Как найти координаты направляющих векторов. Уравнение прямой, проходящей через две точки

УГОЛ МЕЖДУ ПЛОСКОСТЯМИ

Рассмотрим две плоскости α 1 и α 2 , заданные соответственно уравнениями:

Под углом между двумя плоскостями будем понимать один из двугранных углов, образованных этими плоскостями. Очевидно, что угол между нормальными векторами и плоскостей α 1 и α 2 равен одному из указанных смежных двугранных углов или . Поэтому . Т.к. и , то

.

Пример. Определить угол между плоскостями x +2y -3z +4=0 и 2x +3y +z +8=0.

Условие параллельности двух плоскостей.

Две плоскости α 1 и α 2 параллельны тогда и только тогда, когда их нормальные векторы и параллельны, а значит .

Итак, две плоскости параллельны друг другу тогда и только тогда, когда коэффициенты при соответствующих координатах пропорциональны:

или

Условие перпендикулярности плоскостей.

Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, или .

Таким образом, .

Примеры.

ПРЯМАЯ В ПРОСТРАНСТВЕ.

ВЕКТОРНОЕ УРАВНЕНИЕ ПРЯМОЙ.

ПАРАМЕТРИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ

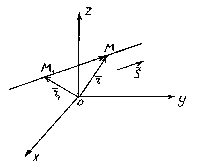
Положение прямой в пространстве вполне определяется заданием какой-либо её фиксированной точки М 1 и вектора , параллельного этой прямой.

Вектор , параллельный прямой, называется направляющим вектором этой прямой.

Итак, пусть прямая l проходит через точку М 1 (x 1 , y 1 , z 1), лежащую на прямой параллельно вектору .

Рассмотрим произвольную точку М(x,y,z) на прямой. Из рисунка видно, что .

Векторы и коллинеарны, поэтому найдётся такое число t , что , где множитель t может принимать любое числовое значение в зависимости от положения точки M на прямой. Множитель t называется параметром. Обозначив радиус-векторы точек М 1 и М соответственно через и , получаем . Это уравнение называется векторным уравнением прямой. Оно показывает, что каждому значению параметра t соответствует радиус-вектор некоторой точки М , лежащей на прямой.

Запишем это уравнение в координатной форме. Заметим, что , и отсюда

Полученные уравнения называются параметрическими уравнениями прямой.

При изменении параметра t изменяются координаты x , y и z и точка М перемещается по прямой.

КАНОНИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ

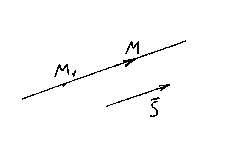
Пусть М 1 (x 1 , y 1 , z 1) – точка, лежащая на прямой l , и – её направляющий вектор. Вновь возьмём на прямой произвольную точку М(x,y,z) и рассмотрим вектор .

Ясно, что векторы и коллинеарные, поэтому их соответствующие координаты должны быть пропорциональны, следовательно,

– канонические уравнения прямой.

Замечание 1. Заметим, что канонические уравнения прямой можно было получить из параметрических,исключив параметр t . Действительно, из параметрических уравнений получаем или .

Пример. Записать уравнение прямой в параметрическом виде.

Обозначим , отсюда x = 2 + 3t , y = –1 + 2t , z = 1 –t .

Замечание 2. Пусть прямая перпендикулярна одной из координатных осей, например оси Ox . Тогда направляющий вектор прямой перпендикулярен Ox , следовательно, m =0. Следовательно, параметрические уравнения прямой примут вид

Исключая из уравнений параметр t , получим уравнения прямой в виде

Однако и в этом случае условимся формально записывать канонические уравнения прямой в виде. Таким образом, еслив знаменателе одной из дробей стоит нуль, то это означает, что прямая перпендикулярна соответствующей координатной оси.

Аналогично, каноническим уравнениям соответствует прямая перпендикулярная осям Ox и Oy или параллельная оси Oz .

Примеры.

ОБЩИЕ УРАВНЕНИЯ ПРЯМОЙ, КАК ЛИНИИ ПЕРЕСЕЧЕНИЯ ДВУХ ПЛОСКОСТЕЙ

Через каждую прямую в пространстве проходит бесчисленное множество плоскостей. Любые две из них, пересекаясь, определяют ее в пространстве. Следовательно, уравнения любых двух таких плоскостей, рассматриваемые совместно представляют собой уравнения этой прямой.

Вообще любые две не параллельные плоскости, заданные общими уравнениями

определяют прямую их пересечения. Эти уравнения называются общими уравнениями прямой.

Примеры.

Построить прямую, заданную уравнениями

Для построения прямой достаточно найти любые две ее точки. Проще всего выбрать точки пересечения прямой с координатными плоскостями. Например, точку пересечения с плоскостью xOy получим из уравнений прямой, полагая z = 0:

Решив эту систему, найдем точку M 1 (1;2;0).

Аналогично, полагая y = 0, получим точку пересечения прямой с плоскостью xOz :

От общих уравнений прямой можно перейтик её каноническим или параметрическим уравнениям. Для этого нужно найти какую-либо точку М 1 на прямой и направляющий вектор прямой.

Координаты точки М 1 получим из данной системы уравнений, придав одной из координат произвольное значение. Для отыскания направляющего вектора, заметим, что этот вектор должен быть перпендикулярен к обоим нормальным векторам и . Поэтому за направляющий вектор прямой l можно взять векторное произведение нормальных векторов:

.

Пример. Привести общие уравнения прямой к каноническому виду.

Найдём точку, лежащую на прямой. Для этого выберем произвольно одну из координат, например, y = 0 и решим систему уравнений:

Нормальные векторы плоскостей, определяющих прямую имеют координаты Поэтому направляющий вектор прямой будет

. Следовательно, l : .

УГОЛ МЕЖДУ ПРЯМЫМИ

Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.

Пусть в пространстве заданы две прямые:

Очевидно, что за угол φ между прямыми можно принять угол между их направляющими векторами и . Так как , то по формуле для косинуса угла между векторами получим

Основные виды уравнений плоскости.

1) -общее уравнение плоскости ;

2) - уравнение плоскости, проходящей через точкуМ 1 (x 1 , y 1 , z 1 ) перпендикулярно нормальному вектору
;

3)
-уравнение плоскости в отрезках , где а , b , с - величины отрезков, отсекаемых плоскостью на координатных осях Ох ,О y , О z соответственно;

4)
-уравнение плоскости , проходящей через три точки М 1 (x 1 , y 1 , z 1 ) , М 2 (x 2 , y 2 , z 2 ) , М 3 (x 3 , y 3 , z 3 ).

Основные виды уравнений прямой.

1)
-общее уравнение прямой , как пересечение двух плоскостей, где направляющий вектор прямой находится из векторного произведения нормальных векторов плоскостей

;

2)
-каноническое уравнение прямой или уравнение прямой, проходящей через точку М 1 (x 1 , y 1 , z 1 ) параллельно вектору;.

3)
- уравнение прямой, проходящей через две точки М 1 (x 1 , y 1 , z 1 ) и М 2 (x 2 , y 2 , z 2 );

4)
-векторное уравнение прямой , где
- радиус-вектор точки, лежащей на прямой,
- направляющий вектор прямой, или в параметрической форме
.

Расстояние от точки
до плоскости определяется по формуле
.

Угол между двумя прямыми , заданными в канонической форме , определяется как угол между их направляющими векторами

.

Угол между прямой
и плоскостью определяется так:

.

Задача. А(1,2,3) параллельно прямой
.

Решение. Так как прямые параллельны, значит направляющий вектор для искомой прямой будет таким же, как и для данной, т.е.
. Поэтому применяем каноническое уравнение прямой, проходящей через точкуА (1,2,3) параллельно вектору
, т.е.
.

Задача. Составить уравнение прямой, проходящей через точку А (2,-3,5) параллельно прямой, заданной в виде пересечения двух плоскостей:
.

Решение. Найдем направляющий вектор заданной прямой через векторное произведение нормальных векторов плоскостей

.

Тогда каноническое уравнение прямой, проходящей через точку А(2,-3,5) параллельно вектору
будет
.

Задача. Дана пирамида АВС D с вершинами А(1,5,7), В(-1,0,1), С (3,-2,4), D (0,1,-1 ). Найти угол между ребром А D и гранью АВС.

Решение. Найдем уравнение грани АВС , т.е. уравнение плоскости, проходящей через три точки А , В и С .

Уравнение ребра AD - уравнение прямой, проходящей через две точки А и D :

Тогда угол между ребром и гранью будем находить по формуле угла между прямой и плоскостью:

Задача. Составить уравнение плоскости, проходящей через точку А(1,2,3) и через прямую, данную в виде пересечения двух плоскостей

.

Решение. Воспользуемся уравнением пучка плоскостей, проходящих через данную прямую . Так как плоскость должна проходить через точкуА , то, подставив ее координаты в уравнение пучка, найдем λ :

.

Теперь, подставив λ в уравнение пучка, получим искомую плоскость:

Задача. Найти точку пересечения прямой
и плоскости
.

Решение. Параметрически уравнения прямой запишутся в виде . Далее, подставив в уравнение плоскости, найдемt :
.

По данному t найдем координаты точки пересечения

Задание 4.1.

Даны координаты вершин пирамиды АВС D . Найти:

1) Уравнение грани АВС ;

2) Уравнение высоты DM , опущенной из точки D на грань АВС;

3) Длину высоты ДМ ;

4) Уравнение ребра DC ;

5) Угол наклона ребра DC к плоскости АВС.

1. А(-3;-2;-4), B (-4;2;-7), C (5;0;3), D (-1;3;0)

2. A(2;-2;1), B(-3;0;-5), C(0;-2;-1), D(-3;4;2)

3. A(5;4;1), B(-1;-2;-2), C(3;-2;2), D(-5;5;4)

4. A(3;6;-2), B(0;2;-3), C(1;-2;0), D(-7;6;6)

5. A(1;-4;1), B(4;4;0), C(-1;2;-4), D(-9;7;8)

6. A(4;6;-1), B(7;2;4), C(-2;0;-4), D(3;1;-4)

7. A(0;6;-5), B(8;2;5), C(2;6;-3), D(5;0;-6)

8. A(-2;4;-6), B(0;-6;1), C(4;2;1), D(7;-1;-8)

9. A(-4;-2;-5), B(1;8;-5), C(0;4;-4), D(9;-2;-10)

10. A(3;4;-1), B(2;-4;2), C(5;6;0), D(11;-3;-12)

11. A(2;1;3), B(3;-2;-4), C(-1;-3;-2), D(5;-3;4)

12. A(4;1;1), B(-2;-1;3), C(1;-3;-4), D(6;-5;5)

13. A(-3;-2;2), B(0;1;5), C(1;-2;-2), D(-1;9;-2)

14. A(-1;0;4), B(2;2;5), C(3;2;4), D(2;3;1)

15. A(-2;0;5), B(1;-4;-6), C(3;2;4), D(2;3;1)

16. A(2;1;-1), B(0;3;-1), C(5;2;1), D(-2;-1;5)

17. A(2;3;0), B(3;4;1), C(-2;5;-1), D(3;4;-5)

18. A(-3;0;-4), B(2;7;2), C(4;-1;-1), D(-3;-2;7)

19. A(1;-4;-4), B(-1;0;-3), C(2;5;1), D(5;6;-9)

20. A(3;2;0), B(5;-2;-1), C(-4;3;-3), D(2;3;-3)

21. A(1;1;1), B(6;3;2), C(0;7;1), D(2;3;4)

22. A(1;0;-1), B(5;1;1), C(2;6;1), D(3;4;5)

23. A(-1;2;0), B(8;1;1), C(2;7;-1), D(4;3;6)

24. A(-1;-1;0), B(9;2;1), C(0;8;-1), D(4;4;7)

25. A(0;1;0), B(8;2;1), C(1;7;2), D(3;5;1)

Задание 4.2.

Даны координаты точек А, В, С . Требуется:

1) составить каноническое уравнение прямой АВ ;

2) составить уравнение прямой, проходящей через точку С параллельно прямой АВ ;

3) составить уравнение плоскости, проходящей через точку С перпендикулярно прямой АВ;

4) найти следы этой плоскости на координатных плоскостях.

1. A(3;-1;5), B(7;1;1), C(4;-2;1). 2. A(-1;2;3), B(3;4;-1), C(0;1;-1).

3. A(2;-3;7), B(6;-1;3), C(3;-4;3). 4. A(0;-2;6), B(4;0;2), C(1;-3;2).

5. A(-3;1;2), B(1;3;-2), C(-2;0;-2). 6. A(-2;3;1), B(2;5;-3), C(-1;2;-3).

7. A(-4;0;8), B(0;2;4), C(-3;-1;4). 8. A(1;4;0), B(5;6;-4), C(2;3;-4).

9. A(4;-4;9), B(8;-2;5), C(5;-5;5). 10. A(5;5;4), B(9;7;0), C(6;4;0).

11. A(3;0;4), B(5;2;6), C(2;3;-3). 12. A(3;-2;2), B(-3;1;2), C(-1;2;1).

13. A(1;-1;1), B(-2;1;3), C(4;-5;-2). 14. A(3;-1;2), B(4;-1;-1), C(2;0;2).

15. A(-1;2;1), B(-3;1;2), C(3;-2;2). 16. A(9;-11;5), B(7;4;2), C(-7;13;-3).

17. A(2;4;-1), B(2;-4;2), C(3;6;0). 18. A(-4;-2;-5), B(1;8;-5), C(0;4;-4).

19. A(-2;4;-6), B(0;-6;1), C(4;2;1). 20. A(4;6;-1), B(7;2;4), C(-2;0;-4).

21. A(3;3;0), B(-1;2;-4), C(-9;7;8). 22. A(7;2;4), B(-2;0-4), C(3;1;-4).

23. A(8;2;5), B(2;6;-3), C(5;0;-6). 24. A(0;-6;1), B(4;2;1), C(7;-1;-8).

25. A(1;8;-5), B(0;4;-4), C(9;-2;-10).

Задание 4.3.

Даны уравнение прямой в виде пересечения двух плоскостей и координаты точки А. Требуется:

1) составить уравнение плоскости, проходящей через данную прямую и точку А;

2) составить каноническое уравнение прямой, проходящей через точку А и параллельно оси О X ;

Прямая на плоскости.

Общее уравнение прямой.

Прежде чем вводить общее уравнение прямой на плоскости введем общее определение линии.

Определение . Уравнение вида

F (x , y )=0 (1)

называется уравнением линии L в заданной системе координат, если этому удовлетворяют координаты х и у любой точки, лежащей на линии L , и не удовлетворяют координаты никакой точки, не лежащей на этой линии.

Степень уравнения (1) определяет порядок линии . Будем говорить, что уравнение (1) определяет (задает) линию L .

Определение . Уравнение вида

Ах+Ву+С=0 (2)

при произвольных коэффициентах А , В , С (А и В одновременно не равны нулю) определяют некоторую прямую в прямоугольной системе координат. Данное уравнение называется общим уравнением прямой .

Уравнение (2) есть уравнение первой степени, таким образом, каждая прямая есть линия первого порядка и, обратно, каждая линия первого порядка есть прямая.

Рассмотрим три частных случая, когда уравнение (2) является неполным, т.е. какой-то из коэффициентов равен нулю.

1)Если С=0 , то уравнение имеет вид Ах+Ву=0 и определяет прямую, проходящую через начало координат т.к. координаты (0,0) удовлетворяют данному уравнению.

2)Если В=0 (А≠0 ), то уравнение имеет вид Ах+С=0 и определяет прямую, параллельную оси ординат. Разрешив это уравнение относительно переменной х получим уравнение вида х=а , гдеа=-С/А , а — величина отрезка, который отсекает прямая на оси абсцисс. Если а=0 (С=0 Оу (рис.1а). Таким образом, прямая х=0 определяет ось ординат.

3)Если А=0 (В≠0 ), то уравнение имеет вид Ву+С=0 и определяет прямую, параллельную оси абсцисс. Разрешив это уравнение относительно переменной у получим уравнение вида у= b , гдеb =-С/В , b — величина отрезка, который отсекает прямая на оси ординат. Если b =0 (С=0 ), то прямая совпадает с осью Ох (рис.1б). Таким образом, прямая у=0 определяет ось абсцисс.

а) б)

Уравнение прямой в отрезках .

Пусть дано уравнение Ах+Ву+С=0 при условии, что ни один из коэффициентов не равен нулю. Перенесем коэффициент С в правую часть и разделим на -С обе части.

Используя обозначения, введенные в первом пункте, получим уравнение прямой «в отрезках »:

Оно имеет такое название потому, что числа а и b являются величинами отрезков, которые прямая отсекает на осях координат.

Пример 2х-3у+6=0 . Составить для этой прямой уравнение «в отрезках» и построить эту прямую.

Решение

Чтобы построить эту прямую, отложим на оси Ох отрезок а=-3 , а на оси Оу отрезок b =2 . Через полученные точки проведем прямую (рис.2).

Уравнение прямой с угловым коэффициентом.

Пусть дано уравнение Ах+Ву+С=0 при условии, что коэффициент В не равен нулю. Выполним следующие преобразования

Уравнение (4), где k =- A / B , называется уравнением прямой с угловым коэффициентом k .

Определение . Углом наклона данной прямой к оси Ох назовем угол α , на который нужно повернуть ось Ох , чтобы её положительное направление совпало с одним из направлений прямой.

Тангенс угла наклона прямой к оси Ох равен угловому коэффициенту, т.е k = tgα . Докажем, что –А/В действительно равно k . Из прямоугольного треугольника ΔОАВ (рис.3) выразим tgα , выполним необходимые преобразования и получим:

Что и требовалось доказать.

Если k =0 , то прямая параллельна оси Ох , и её уравнение имеет вид у= b .

Пример . Прямая задана общим уравнением 4х+2у-2=0 . Составить для этой прямой уравнение с угловым коэффициентом.

Решение . Выполним преобразования, аналогичные описанным выше, получим:

где k=-2, b=1 .

Уравнение прямой, проходящей через заданную точку, с данным угловым коэффициентом.

Пусть задана точка М 0 (х 0 ,у 0) прямой и её угловой коэффициент k . Запишем уравнение прямой в виде (4), где b —пока неизвестное число. Так как точка М 0 принадлежит заданной прямой, то её координаты удовлетворяют уравнению (4): . Подставляя выражение для b в (4), получаем искомое уравнение прямой:

Пример. Записать уравнение прямой, проходящей через точку М(1,2) и под наклоном к оси Ох под углом 45 0 .

Решение . k = tgα = tg 45 0 =1 . Отсюда: .

Уравнение прямой, проходящей через две данные точки.

Пусть даны две точки М 1 (х 1 ,у 1) и М 2 (х 2 ,у 2) . Запишем уравнение прямой в виде (5), где k пока неизвестный коэффициент:

Так как точка М 2 принадлежит заданной прямой, то её координаты удовлетворяют уравнению (5): . Выражая отсюда и подставив его в уравнение (5) получим искомое уравнение:

Если это уравнение можно переписать в виде, более удобном для запоминания:

Пример. Записать уравнение прямой, проходящей через точки М 1 (1,2) и М 2 (-2,3)

Решение . . Используя свойство пропорции, и выполнив необходимые преобразования, получим общее уравнение прямой:

Угол между двумя прямыми

Рассмотрим две прямые l 1 и l 2 :

l 1 : , , и

l 2 : , ,

φ- угол между ними (). Из рис.4 видно: .

Отсюда , или

Если прямые l 1 и l 2 перпендикулярны, то φ=π/2 , α 2 = π/2+ α 1 . . Таким образом, условие перпендикулярности двух прямых состоит в том, что их угловые коэффициенты обратны по величине и противоположны по знаку.