Итак, 7 декабря состоялся очередной пробный ЕГЭ по математике. Как и в прошлый раз, ученикам предложили 16 вариантов - все они в ближайшее время будут опубликованы на сайте.
В целом, об экзамене можно сказать следующее:
Сохраняется деление экзамена на варианты без логарифмов (но с производными) и без производных (но с логарифмами). Это связано с тем, что в школах параллельно существуют две программы: по одной из них производные проходят в 10 классе, а логарифмы - в 11, по другой - наоборот. Однако надо готовиться к тому, что уже в январе-феврале 2012 года во всех вариантах будут и логарифмы, и производные;
Новые варианты стали очень похожими друг на друга, условия задач практически совпадают - отличаются лишь числа и, собственно, ответы. С одной стороны, это хорошо, поскольку все ученики находятся в примерно равных условиях. Но с другой стороны, ничего хорошего в этом нет, поскольку настоящие варианты будут существенно (очень существенно!) отличаться друг от друга;
Как ни странно, появились новые задачи, которые ранее вообще не рассматривались - нигде и никогда. В первую очередь это касается теории вероятностей, о чем я расскажу чуть ниже. Подобные «нововведения» сводят на нет всю работу по унификации вариантов.
Выводы: существенных изменений в новых тренировочных вариантах нет. Сами варианты стали более похожими друг на друга, однако в некоторых из них появились новые задачи, с которыми большинство учеников однозначно не справятся.
Теперь разберем конкретные задачи, особенно «новичков» в теории вероятностей.
Задача B1: почем литр бензина
Согласно спецификациям ЕГЭ по математике, B1 - это задача с практическим содержанием. В нашем случае клиент покупает бензин и получает сдачу. Требуется найти либо размер этой сдачи, либо объем купленного бензина.
Чтобы решить такую задачу, важно знать всего один факт - назовем его законом умножения . Если известна стоимость одного литра бензина p и количество покупаемых литров n , то суммарные расходы составят p · n . Например, если 1 литр стоит 28 рублей, а мы хотим купить 15 литров, то придется заплатить 28 · 15 = 420 рублей.
Кроме того, следует раз и навсегда усвоить, что такое сдача. Задумайтесь: когда вы идете в ларек и покупаете бутылку водки за 350 рублей, но в кармане есть лишь купюра в 1000 рублей, то кассир вернет вам 1000 − 350 = 650 рублей. Это и есть сдача - разность между фактической стоимостью покупки и той суммой, которую вы заплатили. Сдача всегда выражается положительным числом.
Задача. На автозаправке клиент отдал кассиру 1000 рублей и залил в бак 22 литра бензина по цене 31 руб. 80 коп. за литр. Какую сдачу клиент должен получить у кассира? Ответ выразите в рублях.
Для начала выразим цену бензина в рублях (без копеек): 31 руб. 80 коп. - это 31,8 рублей.
Итак, один литр стоит 31,8 рублей. Тогда 22 литра стоят 22 · 31,8 = 699,6 рублей. Но клиент отдал кассиру 1000 рублей, поэтому он должен получить сдачу в размере 1000 − 699,6 = 300,4 рубля. Это и есть ответ - переводить число обратно в копейки не требуется.
Задача. На автозаправке клиент отдал кассиру 1000 рублей и попросил залить бензин до полного бака. Цена бензина - 30 руб. 30 коп. за литр. Сдачи клиент получил 303 руб. 10 коп. Сколько литров бензина было залито в бак?
Снова переведем все цены в рубли: 30 руб. 30 коп - это 30,3 рубля; 303 руб. 10 коп. - это 303,1 рубля.
Теперь смотрим на условие задачи. Если клиент отдал кассиру 1000 рублей, а сдачи получил 303,1 рубля, то фактические расходы (цена покупки) составят 1000 − 303,1 = 696,9 рублей.
Поскольку 1 литр бензина стоит 30,3 рубля, то на 696,9 рублей можно купить 696,9: 30,3 = 23 литра. Это и есть ответ.
Задача B3: учимся резать пиццу. Без клеточек
Как я и предполагал, в некоторых задачах B3 предлагалось найти площадь многоугольника, заданного координатами своих вершин. При этом координатной сетки на чертеже не было. В других задачах требовалось найти площади секторов.
Задачи с многоугольниками решаются элементарно - достаточно построить описанный прямоугольник (см. урок «Площади многоугольников на координатной сетке »). Как работать с секторами, мы тоже знаем (см. урок «Площадь круга »), правда, в этот раз составители задач предложили более изощренные конструкции.
Задача. На клетчатой бумаге нарисован круг, площадь которого равна 16. Найдите площадь закрашенной фигуры.
Разрежем круг на 8 равных секторов, как пиццу. Площадь каждого сектора составит 16: 8 = 2 (см. чертеж).

Очевидно, закрашенная часть состоит из 6 таких секторов, поэтому ее площадь равна 6 · 2 = 12.
Задача. Найдите площадь четырехугольника, вершины которого имеют координаты (1; 1), (10; 1), (7; 9), (2; 9)
Очевидно, что это трапеция, поэтому можно считать по формуле площади трапеции. Но мы пойдем по традиционному пути: построим описанный прямоугольник и отметим длины всех отрезов. Получим следующую картинку:

Осталось найти общую площадь прямоугольника S
, а также площади треугольников S
1 и S
2 , которые надо вырезать:
S
= 9 · 8 = 72;
S
1 = 0,5 · 1 · 8 = 4;
S
2 = 0,5 · 3 · 8 = 12;
S
исх = S
− (S
1 + S
2) = 72 − (4 + 12) = 56.
Задача B7: тригонометрия
Абсолютно стандартная задача на вычисление тригонометрических функций и работу с координатной окружностью. Большинство ошибок пришлось на варианты, в которых требовалось найти тангенс или котангенс, поскольку в самом конце решения таких задач возникают многоэтажные дроби.
К сожалению, большинство учеников 11 класса до сих пор не умеют работать с многоэтажными дробями. Однако виноват в этом только учитель. Удивительно, но большинство школьных преподавателей математики сами не умеют вычислять такие дроби (см. урок «Сложные выражения с дробями. Порядок действий »).
Лично я считаю, что таких людей нельзя допускать к работе в школе. Учитель математики, который не умеет работать с многоэтажными дробями, должен быть немедленно дисквалифицирован и отправлен на рудники - копать уран.
Если у вас также возникают проблемы с многоэтажными дробями, просто изучите урок, приведенный выше, а затем пройдите прилагающиеся к нему тесты. Поверьте, ничего сложного в этих дробях нет.
Задача B10: Петя со своими монетами
Задачи по теории вероятностей всегда отличались разнообразием, но в этот раз составители, похоже, превзошли сами себя. Например, в некоторых вариантах требовалось округлить полученный ответ до сотых. В противном случае получалась бесконечная десятичная дробь. Вот только найти эту дробь большинство учеников сможет лишь при помощи калькулятора, который запрещено использовать на ЕГЭ по математике.
Но округление - это еще полбеды. Гораздо интереснее выглядят задачи про монеты, которые появились в тренировочных вариантах впервые. Для решения таких задач требуется знать, что такое биноминальные коэффициенты - и в ближайшее время мы обязательно рассмотрим эту тему. А пока ограничимся разбором двух конкретных задач из вариантов 1 и 4 (без логарифмов):
Задача. В кармане у Пети было 4 монеты по рублю и 2 монеты по 2 рубля. Петя, не глядя, переложил какие-то три монеты в другой карман. Найдите вероятность того, что обе двухрублевые монеты лежат в одном кармане.
Поскольку обе двухрублевые монеты оказались в одном кармане, то возможны 2 варианта: либо Петя их вообще не перекладывал, либо переложил сразу обе.
В первом случае, когда двухрублевые монеты не перекладывались, придется переложить 3 монеты по рублю. Поскольку всего таких монет 4, число способов это сделать равно числу сочетаний из 4 по 3: C 4 3 .
Во втором случае, когда обе двухрублевые монеты были переложены, придется переложить еще одну рублевую монету. Ее надо выбрать из 4 существующих, и число способов так поступить равно числу сочетаний из 4 по 1: C 4 1 .
Теперь найдем число способов переложить монеты. Поскольку всего монет 4 + 2 = 6, а выбрать надо лишь 3 из них, общее число вариантов равно числу сочетаний из 6 по 3: C 6 3 .
Осталось найти вероятность:
При этом число сочетаний из b по a рассчитывается по формуле, которую обязательно надо знать наизусть:
Задача. В кармане у Пети было 2 монеты по 5 рублей и 4 монеты по 10 рублей. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что пятирублевые монеты лежат теперь в разных карманах.
Чтобы пятирублевые монеты лежали в разных карманах, надо переложить только одну из них. Количество способов это сделать равно числу сочетаний из 2 по 1: C 2 1 .
Поскольку всего Петя переложил 3 монеты, придется переложить еще 2 монеты по 10 рублей. Таких монет у Пети 4, поэтому количество способов равно числу сочетаний из 4 по 2: C 4 2 .
Осталось найти, сколько всего есть вариантов переложить 3 монеты из 6 имеющихся. Это количество, как и в предыдущей задаче, равно числу сочетаний из 6 по 3: C 6 3 .
Находим вероятность:
В последнем шаге мы умножали число способов выбрать двухрублевые монеты и число способов выбрать десятирублевые, поскольку данные события независимы.
Отмечу, что сумма вероятностей оказалась равна 0,4 + 0,6 = 1. Действительно, количество монет в обеих задачах совпадает, а две монеты могут лежать либо в одном кармане, либо в разных - третьего не дано.
Этот факт подтверждает правильность ответов, однако решение получилось далеко не тривиальным и требующим очень хорошего знания теории вероятностей. Большинство школьников такими знаниями не обладает.
Замечания по части C
Задача C1, в которой предлагается решить сложное тригонометрическое уравнение, немного переформулирована и теперь состоит из двух пунктов:
- Собственно, решить тригонометрическое уравнение;
- Найти корни, принадлежащие заданному отрезку.
Остальные задачи перекочевали из предыдущего пробного ЕГЭ практически без изменений. Задача C6 осталась такой же легкой и не идет ни в какое сравнение с настоящими C6, которые встречаются в ЕГЭ по математике.
Здравствуйте, друзья! В состав ЕГЭ по математике входят задачи связанные с нахождением площади круга или его частей (сектора, кольцевых элементов). Фигура задаётся на листе в клетку. В одних задачах масштаб клетки задаётся 1×1 сантиметр, в других он не оговаривается – даётся площадь элемента круга или самого круга.
Задания неглубокие, необходимо помнить формулу площади круга, уметь визуально (по клеткам) определить радиус круга, какую долю от круга составляет выделенный сектор. Кстати, на блоге о площади сектора. Её содержание к решению представленных ниже задач отношения не имеет, но для тех, кто хочет вспомнить формулу площади круга и площади сектора будет весьма полезна. Рассмотрим задачи (взяты из открытого банка заданий):
Найдите (в см 2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см. В ответе запишите S/л.

Для того, чтобы площадь фигуры (кольца) необходимо из площади круга радиусом равным 2 вычесть площадь круга с радиусом 1. Формула площади круга:
Значит,
Разделим результат на число Пи и запишем ответ.
Ответ: 3
На клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 51. Найдите площадь заштрихованной фигуры.

Площадь заштрихованной фигуры можно найти вычислив разность между площадью большего круга и площадью меньшего. Определим во сколько раз площадь большего отличается от площади меньшего. Пусть радиус меньшего равен R, тогда его площадь равна:
Радиус большего круга в два раза больше (видно по клеткам). Значит, его площадь равна:
Получили, что его площадь в 4 раза больше.
Следовательно, она равна 51∙4 = 204 см 2
Таким образом, площадь заштрихованной фигуры равна 204 – 51 = 153 см 2 .
*Второй способ. Можно было вычислить радиус малого круга, затем определить радиус большего. Далее найти площадь большего и вычислить площадь искомой фигуры.
На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 1. Найдите площадь заштрихованной фигуры.

Данная задача по ходу решения практически не отличается от предыдущей, разница состоит лишь в том, что круги имеют разные центры.
Несмотря на то, что видно, что радиус большего круга в 2 раза больше радиуса меньшего, советую вам обозначить размер клетки переменной х (икс).
Так же, как и в предыдущей задаче, определим во сколько раз площадь большего отличается от площади меньшего. Выразим площадь меньшего круга, так как его радиус равен 3х:
![]()
Выразим площадь большего круга, так как его радиус равен 6х:
Как видно, площадь большего круга в 4 раза больше.
Следовательно, она равна 1∙4 = 4 см 2
Таким образом, площадь заштрихованной фигуры равна 4 – 1 = 3 см 2 .
Ответ: 3
На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 9. Найдите площадь заштрихованной фигуры.

Обозначим размер клетки переменной х (икс).
Определим во сколько раз площадь большего круга отличается от площади меньшего. Выразим площадь меньшего круга. Так как его радиус равен 3 ∙ х, то
![]()
Выразим площадь большего круга. Так как его радиус равен 4 ∙ х, то
Разделим площадь большего на площадь меньшего:

То есть, площадь большего круга в 16/9 раза больше площади меньшего, следовательно, она равна:
![]()
Таким образом, площадь заштрихованной фигуры равна 16 – 9 = 7 см 2 .
*Второй способ.
Вычислим радиус меньшего круга. Его площадь равна 9, значит,

Найдём размер клетки и затем сможем определить радиус большего круга. Размер клетки равен:

Так как радиус большего круга соответствует 4 клеткам, то его радиус будет равен:

Определяем площадь большего круга:

Находим разность: 16 – 9 = 7 см 2
Ответ: 7
На клетчатой бумаге нарисован круг площадью 48. Найдите площадь заштрихованного сектора.

В этой задаче очевидно, что заштрихованная часть составляет половину от площади всего круга, то есть равна 24.
Ответ: 24
Небольшой итог.
В задачах связанных с площадью сектора круга необходимо уметь определять какую долю он составляет от площади круга. Это сделать не сложно, так как в подобных задачах центральный угол сектора кратен 30 либо 45.
В задачах связанных с нахождением площадей кольцевых элементов есть разные пути для решения, оба показаны в решённых заданиях. Способ, в котором размер клетки обозначается через переменную х, и затем определяются радиусы более универсален.
Но самое главное – не запоминать эти способы. Можно найти и третий и четвёртый путь решения. Главное – это знать формулу площади круга и уметь логически рассуждать.
На этом всё. Успеха вам!
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Окружности требуют более аккуратного подхода и встречаются в заданиях B5 гораздо реже. Вместе с тем, общая схема решения даже проще, чем в случае с многоугольниками (см. урок «Площади многоугольников на координатной сетке »).
Все, что требуется в таких заданиях - это найти радиус окружности R . Затем можно вычислить площадь круга по формуле S = πR 2 . Из этой формулы также следует, что для решения достаточно найти R 2 .
Чтобы найти указанные величины, достаточно указать на окружности точку, лежащую на пересечении линий сетки. А затем воспользоваться теоремой Пифагора. Рассмотрим конкретные примеры вычисления радиуса:
Задача. Найти радиусы трех окружностей, изображенных на рисунке:
Выполним дополнительные построения в каждой окружности:

В каждом случае точка B выбрана на окружности таким образом, чтобы лежать на пересечении линий сетки. Точка C в окружностях 1 и 3 дополняют фигуру до прямоугольного треугольника. Осталось найти радиусы:
Рассмотрим треугольник ABC в первой окружности. По теореме Пифагора: R 2 = AB 2 = AC 2 + BC 2 = 2 2 + 2 2 = 8.
Для второй окружности все очевидно: R = AB = 2.
Третий случай аналогичен первому. Из треугольника ABC по теореме Пифагора: R 2 = AB 2 = AC 2 + BC 2 = 1 2 + 2 2 = 5.
Теперь мы знаем, как искать радиус окружности (или хотя бы его квадрат). А следовательно, можем найти площадь. Встречаются задачи, где требуется найти площадь сектора, а не всего круга. В таких случаях легко выяснить, какую часть круга составляет этот сектор, и таким образом найти площадь.
Задача. Найти площадь S закрашенного сектора. В ответе укажите S /π .
Очевидно, сектор составляет одну четверть круга. Следовательно, S = 0,25 · S круга.
Остается найти S круга - площадь круга. Для этого выполним дополнительное построение:
Треугольник ABC - прямоугольный. По теореме Пифагора имеем: R 2 = AB 2 = AC 2 + BC 2 = 2 2 + 2 2 = 8.
Теперь находим площади круга и сектора: S круга = πR 2 = 8π ; S = 0,25 · S круга = 2π .
Наконец, искомая величина равна S /π = 2.
Площадь сектора при неизвестном радиусе
Это совершенно новый тип задач, ничего подобного в 2010-2011 годах не было. По условию, нам дан круг определенной площади (именно площади, а не радиуса!). Затем внутри этого круга выделяется сектор, площадь которого и требуется найти.
Хорошая новость состоит в том, что подобные задачи - самые легкие из всех задач на площади, которые бывают в ЕГЭ по математике. К тому же, круг и сектор всегда помещается на координатную сетку. Поэтому, чтобы научиться решать такие задачи, просто взгляните на картинку:
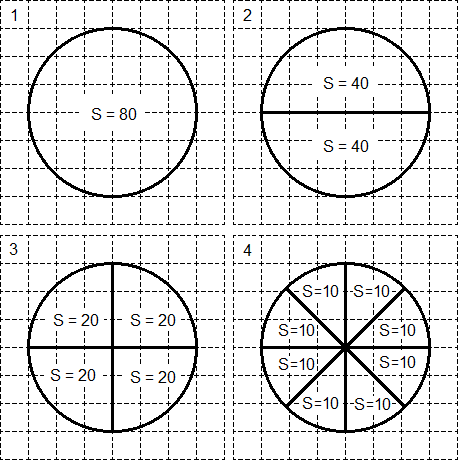
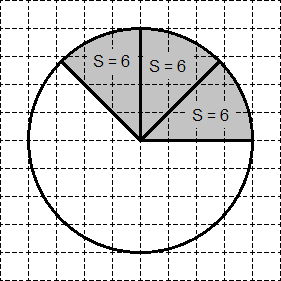
Пусть исходный круг имеет площадь S круга = 80. Тогда его можно разделить на два сектора площадью S = 40 каждый (см. 2 шаг). Аналогично, каждый из этих секторов-«половинок» можно снова разделить пополам - получим четыре сектора площадью S = 20 каждый (см. 3 шаг). Наконец, можно разделить каждый из этих секторов еще на два - получим 8 секторов-«ошметков». Площадь каждого из этих «ошметков» составит S = 10.
Обратите внимание: более мелкого разбиения ни в одной задаче ЕГЭ по математике нет! Таким образом, алгоритм решения задачи B-3 следующий:
- Разрезать исходный круг на 8 секторов-«ошметков». Площадь каждого из них составляет ровно 1/8 часть площади всего круга. Например, если по условию круг имеет площадь S круга = 240, то «ошметки» имеют площадь S = 240: 8 = 30;
- Выяснить, сколько «ошметков» помещается в исходном секторе, площадь которого требуется найти. Например, если в нашем секторе помещается 3 «ошметка» площадью 30, то площадь искомого сектора равна S = 3 · 30 = 90. Это и будет ответ.
Вот и все! Задача решается практически устно. Если все равно что-то непонятно, купите пиццу и порежьте ее на 8 кусков. Каждый такой кусок будет тем самым сектором-«ошметком», которые можно объединить в более крупные куски.
А теперь разберем примеры из пробного ЕГЭ:
Задача. На клетчатой бумаге нарисован круг, площадь которого равна 40. Найдите площадь заштрихованной фигуры.
Итак, площадь круга равна 40. Разделим его на 8 секторов - каждый площадью S = 40: 5 = 8. Получим:
Очевидно, закрашенный сектор состоит ровно из двух секторов-«ошметков». Следовательно, его площадь равна 2 · 5 = 10. Вот и все решение!
Задача. На клетчатой бумаге нарисован круг, площадь которого равна 64. Найдите площадь заштрихованной фигуры.
Снова разделим весь круг на 8 равных секторов. Очевидно, что площадь одного их них как раз и требуется найти. Следовательно, его площадь равна S = 64: 8 = 8.
Задача. На клетчатой бумаге нарисован круг, площадь которого равна 48. Найдите площадь заштрихованной фигуры.
Опять разделим круг на 8 равных секторов. Площадь каждого из них равна S = 48: 8 = 6. В искомом секторе помещается ровно три сектора-«ошметка» (см. рисунок). Следовательно, площадь искомого сектора равна 3 · 6 = 18.