Решу егэ дроби. Сложение дробей с одинаковыми знаменателями

Разбор задания №1 на тему: "Действия с дробями: умножение и вычитание, выделение целой части из неправильной дроби, обратные операции"

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.

Обучающие пособия и тренажеры в интернет-магазине "Интеграл" для 9 класса
Комбинаторика и теория вероятностей Уравнения и неравенства

Ребята, задание №1 охватывает темы, которые, в основном, проходятся в 5-6 классах.

Для правильного решения данного задания требуются умение:

• работать с простыми и десятичными дробями,
• переводить простые дроби в десятичные и обратно,
• возводить числа в целую степень,
• а также понимание понятий рациональных и действительных чисел.

Уроки которые помогут вам при подготовке данного задания:

Давайте подробно разберем примеры заданий, которые вам могут встретиться.

Пример 1.
В данном примере потребуется умение умножать и вычитать дроби, выделять целую часть из неправильной дроби и также проводить обратную операцию.
Найти значение следующего выражения: $1\frac{2}{5}*2\frac{2}{3}-1\frac{2}{3}*3\frac{1}{2}$.

Решение.
Ребята, давайте разобьем решение на несколько действий. Первое, что мы знаем, что умножать дроби с целой частью мы не умеем. Значит, нам надо каждую дробь привести в неправильную дробь.
1. Вспомним правило перевода в неправильную дробь: чтобы получить числитель - целую часть надо умножить на знаменатель и к полученному числу прибавить числитель исходной дроби. Знаменатель остается неизменным, всегда получается числитель больше знаменателя:
$1\frac{2}{5}=\frac{1*5+2}{5}=\frac{7}{5}$.
Давайте выполним аналогичные операции для оставшихся дробей:
$\frac{7}{5}*\frac{2*3+2}{3}-\frac{1*3+2}{3}*\frac{3*2+1}{2}=\frac{7}{5}*\frac{8}{3}-\frac{5}{3}*\frac{7}{2}$.

2. Все прекрасно помнят, что умножение выполняется раньше сложения и вычитания. Далее, нам надо вспомнить правило умножения двух дробей, числитель мы умножаем на числитель, знаменатель на знаменатель:
$\frac{7}{5}*\frac{8}{3}-\frac{5}{3}*\frac{7}{2}=\frac{56}{15}-\frac{35}{6}$.

3. Нам осталось вычесть две дроби. Вспомним, что при сложении и вычитании сначала надо найти общий знаменатель двух дробей, то есть наименьшее общее кратное. У нас есть два знаменателя – числа 15 и 6. Для этих двух чисел наименьшим общим кратным будет число 30.
Если умножить числитель и знаменатель на одно и тоже число, то значение дроби не изменится.
$\frac{56}{15}-\frac{35}{6}=\frac{56*2}{15*2}-\frac{35*5}{6*5}=\frac{112}{30}-\frac{175}{30}=-\frac{63}{30}$.

4. Нам осталось перевести обычную дробь в десятичную, т.к. в бланке ответов ОГЭ мы можем записать числа в десятичном виде.
Выделим целую часть и затем сократим дробь.
$-\frac{63}{30}=-2\frac{3}{30}=-2\frac{1}{10}=-2,1$.

Еще раз распишем решение:
$1\frac{2}{5}*2\frac{2}{3}-1\frac{2}{3}*3\frac{1}{2}=\frac{1*5+2}{5}*\frac{2*3+2}{3}-\frac{1*3+2}{3}*\frac{3*2+1}{2}=\frac{7}{5}*\frac{8}{3}-\frac{5}{3}*\frac{7}{2}=$ $=\frac{56}{15}-\frac{35}{6}=\frac{56*2}{15*2}-\frac{35*5}{6*5}=\frac{112}{30}-\frac{175}{30}=-\frac{63}{30}=-2\frac{3}{30}=-2\frac{1}{10}=-2,1$.
Ответ: $-2,1$.

Пример 2.
Вычислите значение выражения $0,007*0,00007*700$.

Решение.
В данном примере мы можем поступить двумя способами: 1) перемножить все числа "напрямую"; 2) воспользоваться знаниями темы о возведении в целую степень.

1. Первое, на что следует обратить внимание - в каждом числе встречается цифра 7. Это сделано не просто так. Попробуем упростить представленные дробные числа. Как можно представить число 0,007 в виде произведения? $0,007=0,001*7$.

Не стоит бояться упрощать дробные числа. Если в начале дробного числа присутствуют все нули, а заканчивается эта дробь некоторым числом, то его всегда можно представить в виде произведения.
Например: $0,0256=0,0001*256$; $0,00008=0,00001*8$; $0,3562=0,0001*3562$.
Главное сохранять количество цифр в получившейся дроби.
$0,007*0,00007*700=0,001*7*0,00001*7*7*100$.

2. Дальше, нам потребуются знания и умение возводить числа в целую степень.
Если нам задана дробь, в которой все нули и заканчивается она единицей, то ее всегда можно представить в виде числа 10 в отрицательной степени. Причем количество нулей, стоящее перед единицей, будет степенью десятки. Давайте подробно рассмотрим числа в нашем примере. $0,001=10^{-3}$, перед единицей стоит три нуля, значит тройка и будет степенью десятки, только не надо забыть поставить минус.
$0,00001=10^{-5}$, перед единицей стоит пять нулей, значит пятерка и будет степенью десятки.

После преобразований получаем: $0,001*7*0,00001*7*7*100=10^{-3}*7*10^{-5}*7*7*100$.

3. Нам осталось только преобразовать число 100 в виде числа в степени. Если в числе на первом месте стоит единица, а все остальные цифры нули, то любое такое число можно представить в виде степени числа 10, причем степень десятки будет совпадать с количеством нулей.
Например: $10000=10^4$; $1000000=10^6$.
Получаем: $10^{-3}*7*10^{-5}*7*7*10^2=7*7*7*10^{-3}*10^{-5}*10^2$.
В каком порядке будем умножать полученные числа не имеет значения. При перемножении чисел с целым показателем степени и одинаковым основанием – основание степени остается прежним, а показатели складываются.
$7*7*7*10^{-3}*10^{-5}*10^2=243*{10}^{-3-5+2}=243*10^{-6}$.

4. Осталось выполнить операцию, обратную пункту два. В степени десятки у нас стоит -6, значит, число будет дробное, так как минус - в нашем числе будет шесть нулей.
$243*10^{-6}=243*0,000001=0,000243$.

Еще раз распишем решение: $0,007*0,00007*700=0,001*7*0,00001*7*7*100=10^{-3}*7*10^{-5}*7*7*10^2=$ $=7*7*7*10^{-3}*10^{-5}*10^2=243*10^{-3-5+2}=243*10^{-6}=243*0,000001=0,000243$.
Ответ: $0,000243$.

Пример 3.
Найти значение выражения: $6,3*1,8-3,6*2,1$.

Решение.
Данный пример можно решить "в лоб", если вы хорошо умеет умножать дробные числа столбиком. Считать "в лоб" мы данный пример не будем, но приведем два других способа решения.

Способ 1. Если у вас не очень хорошо получается умножать дробные числа столбиком, тогда можно умножить исходное выражение на сто, но главное, потом не забыть опять же поделить на сто.
$\frac{(6,3*1,8-3,6*2,1)*100}{100}=\frac{63*18-36*21}{100}=\frac{1134-756}{100}=\frac{378}{100}$.
Поделим получившиеся число на 100, что довольно таки легко, так как у нас два нуля, то запятая дробного числа сместится на 2 цифры справа налево.
$\frac{378}{100}=3,78$.

Способ 2. Можно заметить, что исходные числа имеют одинаковые сомножители, то есть каждое из представленных чисел нужно представить в виде произведения целого числа и дроби.
$6,3=7*0,9$.
$1,8=6*0,3$.
$3,6=6*0,6$.
$2,1=7*0,3$.
$6,3*1,8-3,6*2,1=7*0,9*6*0,3-6*0,6*7*0,3=42*0,27-42*0,18=$ $=4*(0,27-0,18)=42*0,09=\frac{42*9}{100}=\frac{378}{100}=3,78$.
Выбор способа решения зависит только от ваших предпочтений.

Пример 4.
Запишите номера верных равенств:
1) $2*\frac{1}{3}-\frac{1}{4}=\frac{1}{6}$.
2) $\frac{ \frac{11}{14}}{3\frac{1}{7}}=0,25$.
3) $1,75-2\frac{1}{3}=-\frac{7}{12}$.
4) $\frac{1,6}{\frac{\frac{2}{3}}{\frac{5}{6}}}=4$.

Решение.
Нам ничего не остается, как проверить каждое выражение.

1) В этом примере надо помнить, что умножить целое число на дробь - это не одно и то же, что дробь, в которой выделена целая часть. Решим данный пример.
$2*\frac{1}{3}-\frac{1}{4}=\frac{2}{1}*\frac{1}{3}-\frac{1}{4}=\frac{2}{3}-\frac{1}{4}=\frac{2*4}{3*4}-\frac{1*3}{4*3}=\frac{8}{12}-\frac{3}{12}=\frac{5}{12}$.
Получили, что представленное равенство не верно.

2) Прежде всего надо избавиться от целой части, а потом воспользоваться правилом деления дробей. $\frac{\frac{11}{14}}{3\frac{1}{7}}=\frac{\frac{11}{14}}{\frac{3*7+1}{7}}=\frac{\frac{11}{14}}{\frac{22}{7}}=\frac{11}{14}*\frac{7}{22}$.
Теперь мы можем воспользоваться правилом сокращения дробей.
$\frac{11}{14}*\frac{7}{22}=\frac{1}{2}*\frac{1}{2}=\frac{1}{4}$.
Осталось только перевести полученную дробь в десятичную.
$\frac{1}{4}=0,25$.
Получили верное равенство.

3) В данном примере, для начала, нам надо перевести десятичную дробь в обычную. $1,75=1 \frac{75}{100}=1\frac{3}{4}$.
Теперь избавимся от целой части и получим неправильную дробь: $1\frac{3}{4}-2\frac{1}{3}=\frac{7}{4}-\frac{7}{3}$.
Выполним вычитание двух дробей: $\frac{7}{4}-\frac{7}{3}=\frac{21}{12}-\frac{28}{12}=-\frac{7}{12}$.
Получили верное равенство.

Запишем еще раз решение:
$1,75-2\frac{1}{3}=1\frac{3}{4}-2\frac{1}{3}=\frac{7}{4}-\frac{7}{3}=\frac{21}{12}-\frac{28}{12}=-\frac{7}{12}$.

4) Опять же перейдем от десятичной дроби к обычной.
$1,6=1\frac{6}{10}=\frac{16}{10}$.
Мы хорошо помним, что первое действие выполняется в скобках.
$\frac{\frac{2}{3}}{\frac{5}{6}}=\frac{2}{3}*\frac{6}{5}=\frac{2}{1}*\frac{2}{5}=\frac{4}{5}$.
Выполним деление за скобками: $\frac{\frac{16}{10}}{\frac{4}{5}}=\frac{16}{10}*\frac{5}{4}=\frac{4}{2}*\frac{1}{1}=2$.
Получили, что исходное равенство неверное.
Ответ: 23.

Пример 5.
Найдите значение выражений. В ответ укажите наибольшее из найденных значений.
1) $1,8-\frac{3}{5}$.
2) $\frac{1\frac{1}{3}}{\frac{1}{6}}$.
3) $\frac{0,8+0,3}{1,2}$.
Решение.

1) Перейдем к десятичной дроби.
$1,8-\frac{3}{5}=1,8-0,6=1,2$.

2) Перейдем к неправильной дроби и выполним деление дробей. $\frac{1\frac{1}{3}}{\frac{1}{6}}=\frac{\frac{4}{3}}{\frac{1}{6}}=\frac{4}{3}*\frac{6}{1}=\frac{4}{1}*2=8$.

3) Выполним сложение в числители дроби. $\frac{0,8+0,3}{1,2}=\frac{1,1}{1,2}=\frac{1,1*10}{1,2*0}=\frac{11}{12}$.
Осталось выбрать наибольшее решение, очевидно, что это будет 8.
Ответ: 8.

Александр Шабалин

Действия с дробями. В этой статье разберём примеры, всё подробно с пояснениями. Рассматривать будем обыкновенные дроби. В дальнейшем разберём и десятичные. Рекомендую посмотреть весь и изучать последовательно.

1. Сумма дробей, разность дробей.

Правило: при сложении дробей с равными знаменателями, в результате получаем дробь – знаменатель которой остаётся тот же, а числитель её будет равен сумме числителей дробей.

Правило: при вычислении разности дробей с одинаковыми знаменателями получаем дробь – знаменатель остаётся тот же, а из числителя первой дроби вычитается числитель второй.

Формальная запись суммы и разности дробей с равными знаменателями:

Примеры (1):

Понятно, что когда даны обыкновенные дроби, то всё просто, а если смешанные? Ничего сложного…

Вариант 1 – можно перевести их в обыкновенные и далее вычислять.

Вариант 2 – можно отдельно «работать» с целой и дробной частью.

Примеры (2):

Ещё:

А если будет дана разность двух смешанных дробей и числитель первой дроби будет меньше числителя второй? Тоже можно действовать двумя способами.

Примеры (3):

*Перевели в обыкновенные дроби, вычислили разность, перевели полученную неправильную дробь в смешанную.

*Разбили на целые и дробные части, получили тройку, далее представили 3 как сумму 2 и 1, при чём единицу представили как 11/11, далее нашли разность 11/11 и 7/11 и вычислили результат. Смысл изложенных преобразований заключается в том, чтобы взять (выделить) единицу и представить её в виде дроби с нужным нам знаменателем, далее от этой дроби мы уже можем вычесть другую.

Ещё пример:

Вывод: имеется универсальный подход – для того, чтобы вычислить сумму (разность) смешанных дробей с равными знаменателями их всегда можно перевести в неправильные, далее выполнить необходимое действие. После этого если в результате получаем неправильную дробь переводим её в смешанную.

Выше мы рассмотрели примеры с дробями, у которых равные знаменатели. А если знаменатели будут отличаться? В этом случае дроби приводятся к одному знаменателю и выполняется указанное действие. Для изменения (преобразования) дроби используется основное свойство дроби.

Рассмотрим простые примеры:

В данных примерах мы сразу видим каким образом можно преобразовать одну из дробей, чтобы получить равные знаменатели.

Если обозначить способы приведения дробей к одному знаменателю, то этот назовём СПОСОБ ПЕРВЫЙ .

То есть, сразу при «оценке» дроби нужно прикинуть сработает ли такой подход – проверяем делится ли больший знаменатель на меньший. И если делится, то выполняем преобразование — домножаем числитель и знаменатель так чтобы у обеих дробей знаменатели стали равными.

Теперь посмотрите на эти примеры:

К ним указанный подход не применим. Существуют ещё способы приведения дробей к общему знаменателю, рассмотрим их.

Способ ВТОРОЙ .

Умножаем числитель и знаменатель первой дроби на знаменатель второй, а числитель и знаменатель второй дроби на знаменатель первой:

*Фактически мы приводим дроби к виду, когда знаменатели становятся равными. Далее используем правило сложения робей с равными знаменателями.

Пример:

*Данный способ можно назвать универсальным, и он работает всегда. Единственный минус в том, что после вычислений может получится дробь которую необходимо будет ещё сократить.

Рассмотрим пример:

Видно что числитель и знаменатель делится на 5:

Способ ТРЕТИЙ.

Необходимо найти наименьшее общее кратное (НОК) знаменателей. Это и будет общий знаменатель. Что это за число такое? Это наименьшее натуральное число, которое делится на каждое из чисел.

Посмотрите, вот два числа: 3 и 4, есть множество чисел, которые делятся на них – это 12, 24, 36, … Наименьшее из них 12. Или 6 и 15, на них делятся 30, 60, 90 …. Наименьшее 30. Вопрос – а как определить это самое наименьшее общее кратное?

Имеется чёткий алгоритм, но часто это можно сделать и сразу без вычислений. Например, по указанным выше примерам (3 и 4, 6 и 15) никакого алгоритма не надо, мы взяли большие числа (4 и 15) увеличили их в два раза и увидели, что они делятся на второе число, но пары чисел могут быть и другими, например 51 и 119.

Алгоритм. Для того, чтобы определить наименьшее общее кратное нескольких чисел, необходимо:

— разложить каждое из чисел на ПРОСТЫЕ множители

— выписать разложение БОЛЬШЕГО из них

— умножить его на НЕДОСТАЮЩИЕ множители других чисел

Рассмотрим примеры:

50 и 60 => 50 = 2∙5∙5 60 = 2∙2∙3∙5

в разложении большего числа не хватает одной пятёрки

=> НОК(50,60) = 2∙2∙3∙5∙5 = 300

48 и 72 => 48 = 2∙2∙2∙2∙3 72 = 2∙2∙2∙3∙3

в разложении большего числа не хватает двойки и тройки

=> НОК(48,72) = 2∙2∙2∙2∙3∙3 = 144

* Наименьшее общее кратное двух простых чисел равно их произведению

Вопрос! А чем полезно нахождение наименьшего общего кратного, ведь можно пользоваться вторым способом и полученную дробь просто сократить? Да, можно, но это не всегда удобно. Посмотрите, какой получится знаменатель для чисел 48 и 72, если их просто перемножить 48∙72 = 3456. Согласитесь, что приятнее работать с меньшими числами.

Рассмотрим примеры:

*51 = 3∙17 119 = 7∙17

в разложении большего числа не хватает тройки

=> НОК(51,119) = 3∙7∙17

А теперь применим первый способ:

*Посмотрите какая разница в вычислениях, в первом случае их минимум, а во втором нужно потрудиться отдельно на листочке, да ещё и дробь которую получили сократить необходимо. Нахождение НОК упрощает работу значительно.

Ещё примеры:

*Во втором примере и так видно, что наименьшее число, которое делится на 40 и 60 равно 120.

ИТОГ! ОБЩИЙ АЛГОРИТМ ВЫЧИСЛЕНИЙ!

— приводим дроби к обыкновенным, если есть целая часть.

— приводим дроби к общему знаменателю (сначала смотрим делится ли один знаменатель на другой, если делится то умножаем числитель и знаменатель этой другой дроби; если не делится действуем посредством других указанных выше способов).

— получив дроби с равными знаменателями, выполняем действия (сложение, вычитание).

— если необходимо, то результат сокращаем.

— если необходимо, то выделяем целую часть.

2. Произведение дробей.

Правило простое. При умножении дробей умножаются их числители и знаменатели:

Примеры:

Задача. На базу привезли 13 тонн овощей. Картофель составляет ¾ от всех завезённых овощей. Сколько килограмм картофеля завезли на базу?

С произведением закончим.

*Ранее обещал вам привести формальное объяснение основного свойства дроби через произведение, пожалуйста:

3. Деление дробей.

Деление дробей сводится к их умножению. Здесь важно запомнить, что дробь являющаяся делителем (та, на которую делят) переворачивается и действие меняется на умножение:

Данное действие может быть записано в виде так называемой четырёхэтажной дроби, ведь само деление «:» тоже можно записать как дробь:

Примеры:

На этом всё! Успеха вам!

С уважением, Александр Крутицких.

Умножение и деление дробей.

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно "не очень..."
И для тех, кто "очень даже...")

Эта операция гораздо приятнее сложения-вычитания ! Потому что проще. Напоминаю: чтобы умножить дробь на дробь, нужно перемножить числители (это будет числитель результата) и знаменатели (это будет знаменатель). То есть:

Например:

Всё предельно просто . И, пожалуйста, не ищите общий знаменатель! Не надо его здесь…

Чтобы разделить дробь на дробь, нужно перевернуть вторую (это важно!) дробь и их перемножить, т.е.:

Например:

Если попалось умножение или деление с целыми числами и дробями - ничего страшного. Как и при сложении, делаем из целого числа дробь с единицей в знаменателе - и вперёд! Например:

В старших классах часто приходится иметь дело с трехэтажными (а то и четырехэтажными!) дробями. Например:

Как эту дробь привести к приличному виду? Да очень просто! Использовать деление через две точки:

Но не забывайте о порядке деления! В отличие от умножения, здесь это очень важно! Конечно, 4:2, или 2:4 мы не спутаем. А вот в трёхэтажной дроби легко ошибиться. Обратите внимание, например:

В первом случае (выражение слева):

Во втором (выражение справа):

Чувствуете разницу? 4 и 1/9!

А чем задается порядок деления? Или скобками, или (как здесь) длиной горизонтальных черточек. Развивайте глазомер. А если нет ни скобок, ни черточек, типа:

то делим-умножаем по порядочку, слева направо !

И еще очень простой и важный приём. В действиях со степенями он вам ох как пригодится! Поделим единицу на любую дробь, например, на 13/15:

Дробь перевернулась! И так бывает всегда. При делении 1 на любую дробь, в результате получаем ту же дробь, только перевернутую.

Вот и все действия с дробями. Вещь достаточно простая, но ошибок даёт более, чем достаточно. Примите к сведению практические советы, и их (ошибок) будет меньше!

Практические советы:

1. Самое главное при работе с дробными выражениями - аккуратность и внимательность! Это не общие слова, не благие пожелания! Это суровая необходимость! Все вычисления на ЕГЭ делайте как полноценное задание, сосредоточенно и чётко. Лучше написать две лишние строчки в черновике, чем накосячить при расчёте в уме.

2. В примерах с разными видами дробей - переходим к обыкновенным дробям.

3. Все дроби сокращаем до упора.

4. Многоэтажные дробные выражения сводим к обыкновенным, используя деление через две точки (следим за порядком деления!).

5. Единицу на дробь делим в уме, просто переворачивая дробь.

Вот вам задания, которые нужно обязательно прорешать. Ответы даны после всех заданий. Используйте материалы этой темы и практические советы. Прикиньте, сколько примеров вы смогли решить правильно. С первого раза! Без калькулятора! И сделайте верные выводы...

Помните – правильный ответ, полученный со второго (тем более – третьего) раза – не считается! Такова суровая жизнь.

Итак, решаем в режиме экзамена ! Это уже подготовка к ЕГЭ, между прочим. Решаем пример, проверяем, решаем следующий. Решили все - проверили снова с первого по последний. И только потом смотрим ответы.

Вычислить:

Порешали?

Ищем ответы, которые совпадают с вашими. Я специально их в беспорядке записал, подальше от соблазна, так сказать... Вот они, ответы, через точку с запятой записаны.

0; 17/22; 3/4; 2/5; 1; 25.

А теперь делаем выводы. Если всё получилось - рад за вас! Элементарные вычисления с дробями - не ваша проблема! Можно заняться более серьёзными вещами. Если нет...

Значит, у вас одна из двух проблем. Или обе сразу.) Нехватка знаний и (или) невнимательность. Но... Это решаемые проблемы.

Если Вам нравится этот сайт...

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся - с интересом!)

можно познакомиться с функциями и производными.

1. Правило сложения дробей с одинаковыми знаменателями:

Пример 1:

Пример 2:

Правило сложения дробей с разными знаменателями:

Пример 1:

Пример 2:

Здесь знаменатели не перемножали, а взяли наименьший общий множитель a2.
(В знаменателе старшая степень 2.)
Дополнительный множитель для первой дроби 1, для второй а.

2. Правило вычитания дробей с одинаковыми знаменателями:

Правило вычитания дробей с разными знаменателями:

3. Правило умножения обыкновенных дробей:

4. Правило деления дробей:

Пример:

Обыкновенная (простая) дробь. Числитель и знаменатель дроби.
Правильная и неправильная дробь. Смешанное число.
Неполное частное. Целая и дробная часть. Обратные дроби. Часть единицы или несколько её частей называются обыкновенной или простой дробью . Количество равных частей, на которые делится единица, называется знаменателем , а количество взятых частей – числителем . Дробь записывается в виде:

Здесь 3 – числитель, 7 – знаменатель.

Если числитель меньше знаменателя, то дробь меньше 1 и называется правильной дробью . Если числитель равен знаменателю, то дробь равна 1. Если числитель больше знаменателя, то дробь больше 1. В обоих последних случаях дробь называется неправильной . Если числитель делится на знаменатель, то эта дробь равна частному от деления: 63 / 7 = 9. Если деление выполняется с остатком, то эта неправильная дробь может быть представлена смешанным числом :

Здесь 9 – неполное частное (целая часть смешанного числа), 2 – остаток (числитель дробной части ), 7 – знаменатель.
Часто бывает необходимо решать обратную задачу – обратить смешанное число в дробь . Для этого умножаем целую часть смешанного числа на знаменатель и прибавляем числитель дробной части . Это будет числитель обыкновенной дроби, а знаменатель остаётся прежним.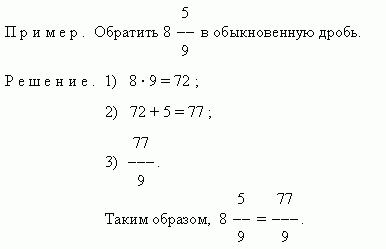

Обратные дроби – это две дроби, произведение которых равно 1. Например, 3 / 7 и 7 / 3 ; 15 / 1 и 1 / 15 и т.д.

Расширение дроби. Сокращение дроби. Сравнение дробей.
Приведение к общему знаменателю. Сложение и вычитание дробей.
Умножение дробей. Деление дробей
Расширение дроби. Значение дроби не меняется, если умножить её числитель и знаменатель на одно и то же число, отличное от нулярасширением дробиНапример,

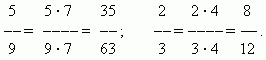
Сокращение дроби. Значение дроби не меняется, если разделить её числитель и знаменатель на одно и то же число, отличное от нуля . Это преобразование называется сокращением дроби . Например,

Сравнение дробей. Из двух дробей с одинаковыми числителями та больше, знаменатель которой меньше:

Из двух дробей с одинаковыми знаменателями та больше, числитель которой больше:

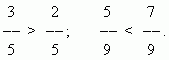
Для сравнения дробей, у которых числители и знаменатели различны, необходимо расширить их, чтобы привести к общему знаменателю.
П р и м е р. Сравнить две дроби:

Использованное здесь преобразование называется приведением дробей к общему знаменателю .
Сложение и вычитание дробей. Если знаменатели дробей одинаковы, то для того, чтобы сложить дроби, надо сложить их числители, а для того, чтобы вычесть дроби, надо вычесть их числители (в том же порядке). Полученная сумма или разность будет числителем результата; знаменатель останется тем же. Если знаменатели дробей различны, необходимо сначала привести дроби к общему знаменателю. При сложении смешанных чисел их целые и дробные части складываются отдельно. При вычитании смешанных чисел мы рекомендуем сначала преобразовать их к виду неправильных дробей, затем вычесть из одной другую, а после этого вновь привести результат, если требуется, к виду смешанного числа.
П р и м е р.

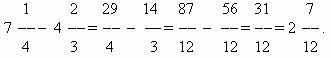
Умножение дробей. Умножить некоторое число на дробь означает умножить его на числитель и разделить произведение на знаменатель. Следовательно, мы имеем общее правило умножения дробей: для перемножения дробей необходимо перемножить отдельно их числители и знаменатели и разделить первое произведение на второе .
П р и м е р.
Деление дробей. я того, чтобы разделить некоторое число на дробь, необходимо умножить это число на обратную дробьЭто правило вытекает из определения деления (см. раздел “Арифметические операции”).
П р и м е р.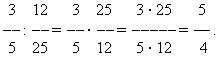

Десятичная дробь. Целая часть. Десятичная точка.
Десятичные знаки. Свойства десятичных дробей.
Периодическая десятичная дробь. Период
Десятичная дробь есть результат деления единицы на десять, сто, тысячу и т.д. частей. Эти дроби очень удобны для вычислений, так как они основаны на той же позиционной системе, на которой построены счёт и запись целых чисел. Благодаря этому запись и правила действий с десятичными дробями фактически те же, что и для целых чисел. При записи десятичных дробей нет необходимости отмечать знаменатель, это определяется местом, которое занимает соответствующая цифра. Сначала пишется целая часть числа, затем справа ставится десятичная точка . Первая цифра после десятичной точки означает число десятых, вторая – число сотых, третья – число тысячных и т.д. Цифры, расположенные после десятичной точки, называются десятичными знаками .
П р и м е р.
Одно из преимуществ десятичных дробей – они легко приводятся к виду обыкновенных: число после десятичной точки (в нашем случае 5047) – это числитель; знаменатель же равен n –ой степени 10, где n - количество десятичных знаков (в нашем случае n = 4):
Если десятичная дробь не содержит целой части, то перед десятичной точкой ставится ноль:

Свойства десятичных дробей.

1. Десятичная дробь не меняется, если справа добавить нули :

2. Десятичная дробь не меняется, если удалить нули, расположенные
в конце десятичной дроби :

0.00123000 = 0.00123 .

Внимание!Нельзя удалять нули, расположенные не в конце десятичной дроби!br />

Эти свойства позволяют быстро умножать и делить десятичные дроби на 10, 100, 1000 и т.д.

Периодическая десятичная дробь одержит бесконечно повторяющуюся группу цифр, называемую периодом . Период записывается в скобках. Например, 0.12345123451234512345… = 0.(12345).

П р и м е р. Если разделить 47 на 11, то получим 4.27272727… = 4.(27).

Умножение десятичных дробей.
Деление десятичных дробей.

Сложение и вычитание десятичных дробей. Эти операции выполняются так же, как и сложение и вычитание целых чисел. Необходимо только записать соответствующие десятичные знаки один под другим.
П р и м е р.

Умножение десятичных дробей. На первом этапе перемножаем десятичные дроби как целые числа, не принимая во внимание десятичную точку. Затем применяется следующее правило: количество десятичных знаков в произведении равно сумме десятичных знаков во всех сомножителях .
Замечание : до простановки десятичной точки в произведении нельзя отбрасывать нули в конце !
П р и м е р.

Сумма чисел десятичных знаков в сомножителях равна: 3 + 4 = 7. Сумма цифр в произведении равна 6. Поэтому необходимо добавить один ноль слева: 0197056 и проставить перед ним десятичную точку: 0.0197056.
Деление десятичных дробей
Деление десятичной дроби на целое число
Если делимое меньше делителя , записываем ноль в целой части частного и ставим после него десятичную точку. Затем, не принимая во внимание десятичную точку делимого, присоединяем к его целой части следующую цифру дробной части и опять сравниваем полученную целую часть делимого с делителем. Если новое число опять меньше делителя, ставим ещё один ноль после десятичной точки в частном и присоединяем к целой части делимого следующую цифру его дробной части. Этот процесс повторяем до тех пор, пока полученное делимое не станет больше делителя. После этого деление выполняется, как для целых чисел. Если делимое больше делителя или равно ему , сначала делим его целую часть, записываем результат деления в частном и ставим десятичную точку. После этого деление продолжается, как в случае целых чисел.
П р и м е р. Разделить 1.328 на 64.
Р е ш е н и е: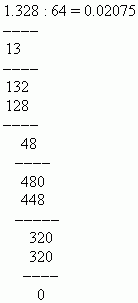
Деление одной десятичной дроби на другую.
Сначала переносим десятичные точки в делимом и делителе на число десятичных знаков в делителе, то есть делаем делитель целым числом. Теперь выполняем деление, как в предыдущем случае.
П р и м е р. Разделить 0.04569 на 0.0006.
Р е ш е н и е. Переносим десятичные точки на 4 позиции вправо и делим 456.9 на 6:

Для того, чтобы обратить десятичную дробь в обыкновенную, надо в качестве числителя взять число, стоящее после десятичной точки, а в качестве знаменателя взять n-ую степень десяти ( здесь n – количество десятичных знаков ). Отличная от нуля целая часть сохраняется в обыкновенной дроби; нулевая целая часть опускается. Например:
Для того, чтобы обратить обыкновенную дробь в десятичную, надо разделить числитель на знаменатель в соответствии с правилами деления .
П р и м е р. Обратить 5 / 8 в десятичную дробь.
Р е ш е н и е. Деля 5 на 8, получаем 0.625. (Проверьте, пожалуйста!).
В большинстве случаев этот процесс может продолжаться бесконечно. Тогда невозможно точно обратить обыкновенную дробь в десятичную. Но на практике это никогда и не требуется. Деление прерывается, если представляющие интерес десятичные знаки уже получены.
П р и м е р. Обратить 1 / 3 в десятичную дробь.
Р е ш е н и е. Деление 1 на 3 будет бесконечным: 1:3 = 0.3333… .
Проверьте это, пожалуйста!