Formeln zur Lösung einfacher trigonometrischer Gleichungen. So lösen Sie trigonometrische Gleichungen

Aufgabe Nr. 1

Die Logik ist einfach: Wir werden wie zuvor vorgehen, ungeachtet der Tatsache, dass trigonometrische Funktionen jetzt ein komplexeres Argument haben!

Wenn wir eine Gleichung der Form lösen würden:

Dann würden wir die folgende Antwort aufschreiben:

Oder (seitdem)

Aber jetzt spielt dieser Ausdruck unsere Rolle:

Dann können wir schreiben:

Unser Ziel ist es, gemeinsam mit Ihnen sicherzustellen, dass die linke Seite einfach und ohne „Verunreinigungen“ steht!

Lasst uns sie nach und nach loswerden!

Entfernen wir zunächst den Nenner bei: Multiplizieren Sie dazu unsere Gleichheit mit:

Lassen Sie uns es nun loswerden, indem wir beide Teile darin aufteilen:

Lassen Sie uns nun die Acht loswerden:

Der resultierende Ausdruck kann als zwei Lösungsreihen geschrieben werden (analog zu einer quadratischen Gleichung, bei der wir die Diskriminante entweder addieren oder subtrahieren).

Wir müssen die größte negative Wurzel finden! Es ist klar, dass wir Ordnung schaffen müssen.

Schauen wir uns zunächst die erste Folge an:

Es ist klar, dass wir, wenn wir sie nehmen, als Ergebnis positive Zahlen erhalten, aber sie interessieren uns nicht.

Man muss es also negativ sehen. Lassen.

Wenn die Wurzel schmaler wird:

Und wir müssen das größte Negativ finden!! Das bedeutet, dass es hier keinen Sinn mehr macht, in die negative Richtung zu gehen. Und die größte negative Wurzel für diese Reihe wird gleich sein.

Schauen wir uns nun die zweite Serie an:

Und wieder ersetzen wir: , dann:

Nicht interessiert!

Dann macht es keinen Sinn mehr zu steigern! Reduzieren wir es! Dann sei:

Passt!

Lassen. Dann

Dann - die größte negative Wurzel!

Antwort:

Aufgabe Nr. 2

Wir lösen erneut, unabhängig vom komplexen Kosinusargument:

Jetzt drücken wir noch einmal links aus:

Multiplizieren Sie beide Seiten mit

Teilen Sie beide Seiten durch

Jetzt müssen Sie ihn nur noch nach rechts verschieben und dabei sein Vorzeichen von Minus auf Plus ändern.

Wir erhalten wieder zwei Wurzelreihen, eine mit und die andere mit.

Wir müssen die größte negative Wurzel finden. Schauen wir uns die erste Folge an:

Es ist klar, dass wir die erste negative Wurzel erhalten werden, sie wird gleich der größten negativen Wurzel in 1 Reihe sein und diese sein.

Für die zweite Serie

Die erste negative Wurzel wird ebenfalls bei erhalten und ist gleich. Denn dann ist die größte negative Wurzel der Gleichung.

Antwort: .

Aufgabe Nr. 3

Wir lösen, unabhängig vom komplexen Tangentenargument.

Nun, es scheint nicht kompliziert zu sein, oder?

Wie zuvor drücken wir auf der linken Seite aus:

Nun, das ist großartig, es gibt hier nur eine Reihe von Wurzeln! Finden wir noch einmal das größte Negativ.

Es ist klar, dass es klappt, wenn man es hinlegt. Und diese Wurzel ist gleich.

Antwort:

Versuchen Sie nun, die folgenden Probleme selbst zu lösen.

Hausaufgaben oder 3 Aufgaben zur eigenständigen Lösung.

Lösen Sie die Gleichung auf.
Lösen Sie die Gleichung auf.
In der Antwort auf die pi-shi-th-die-kleinstmögliche Wurzel.
Lösen Sie die Gleichung auf.
In der Antwort auf die pi-shi-th-die-kleinstmögliche Wurzel.

Bereit? Lass uns das Prüfen. Ich werde nicht den gesamten Lösungsalgorithmus im Detail beschreiben; es scheint mir, dass er oben bereits ausreichend beachtet wurde.

Na, ist alles in Ordnung? Oh, diese fiesen Nebenhöhlen, mit denen gibt es immer irgendwelche Probleme!

Nun können Sie einfache trigonometrische Gleichungen lösen!

Schauen Sie sich die Lösungen und Antworten an:

Aufgabe Nr. 1

Lassen Sie uns ausdrücken

Die kleinste positive Wurzel erhält man, wenn man seit, dann setzt

Antwort:

Aufgabe Nr. 2

Die kleinste positive Wurzel erhält man bei.

Es wird gleich sein.

Antwort: .

Aufgabe Nr. 3

Wann wir bekommen, wann wir haben.

Antwort: .

Dieses Wissen wird Ihnen helfen, viele Probleme zu lösen, auf die Sie in der Prüfung stoßen werden.

Wenn Sie sich für eine „5“-Bewertung bewerben, müssen Sie nur mit dem Lesen des Artikels fortfahren Mittlere Stufe die sich der Lösung komplexerer trigonometrischer Gleichungen widmet (Aufgabe C1).

DURCHSCHNITTSNIVEAU

In diesem Artikel werde ich beschreiben Lösung komplexerer trigonometrischer Gleichungen und wie man ihre Wurzeln auswählt. Dabei werde ich auf folgende Themen zurückgreifen:

Trigonometrische Gleichungen für Anfänger (siehe oben).

Komplexere trigonometrische Gleichungen sind die Grundlage für fortgeschrittene Probleme. Sie erfordern sowohl das Lösen der Gleichung selbst in allgemeiner Form als auch das Finden der Wurzeln dieser Gleichung, die zu einem bestimmten gegebenen Intervall gehören.

Das Lösen trigonometrischer Gleichungen besteht aus zwei Teilaufgaben:

Lösung der Gleichung
Wurzelauswahl

Es ist zu beachten, dass die zweite Option nicht immer erforderlich ist, in den meisten Beispielen jedoch dennoch eine Auswahl erforderlich ist. Aber wenn es nicht erforderlich ist, dann können wir Ihnen recht geben – das bedeutet, dass die Gleichung an sich recht komplex ist.

Meine Erfahrung bei der Analyse von C1-Problemen zeigt, dass sie normalerweise in die folgenden Kategorien unterteilt werden.

Vier Kategorien von Aufgaben mit erhöhter Komplexität (ehemals C1)

Gleichungen, die auf Faktorisierung reduziert werden.
Auf die Form reduzierte Gleichungen.
Gleichungen, die durch Ändern einer Variablen gelöst werden.
Gleichungen, die aufgrund von Irrationalität oder Nenner eine zusätzliche Auswahl von Wurzeln erfordern.

Vereinfacht gesagt: wenn man erwischt wird eine der Gleichungen der ersten drei Typen, dann können Sie sich glücklich schätzen. Für sie müssen Sie in der Regel zusätzlich Wurzeln auswählen, die zu einem bestimmten Intervall gehören.

Wenn Sie auf eine Gleichung vom Typ 4 stoßen, haben Sie weniger Glück: Sie müssen länger und sorgfältiger daran basteln, aber oft ist keine zusätzliche Auswahl von Wurzeln erforderlich. Dennoch werde ich diese Art von Gleichungen im nächsten Artikel analysieren und diesen werde ich der Lösung von Gleichungen der ersten drei Arten widmen.

Gleichungen, die auf Faktorisierung reduziert werden

Das Wichtigste, was Sie beachten müssen, um diese Art von Gleichung zu lösen, ist

Wie die Praxis zeigt, sind diese Kenntnisse in der Regel ausreichend. Schauen wir uns einige Beispiele an:

Beispiel 1. Gleichung reduziert auf Faktorisierung unter Verwendung der Reduktions- und Doppelwinkelsinusformeln

Lösen Sie die Gleichung auf
Finden Sie alle Wurzeln dieser Gleichung, die über dem Schnitt liegen

Hier funktionieren, wie versprochen, die Reduktionsformeln:

Dann sieht meine Gleichung so aus:

Dann wird meine Gleichung die folgende Form annehmen:

Ein kurzsichtiger Student könnte sagen: Jetzt reduziere ich beide Seiten, bekomme die einfachste Gleichung und genieße das Leben! Und er wird sich bitter irren!

Denken Sie daran: Sie können niemals beide Seiten einer trigonometrischen Gleichung durch eine Funktion reduzieren, die ein Unbekanntes enthält! SO VERLIEREN SIE IHRE WURZELN!

Was also tun? Ja, es ist ganz einfach: Schieben Sie alles beiseite und entfernen Sie den gemeinsamen Faktor:

Nun, wir haben es in Faktoren eingerechnet, Hurra! Nun lasst uns entscheiden:

Die erste Gleichung hat Wurzeln:

Und der zweite:

Damit ist der erste Teil des Problems abgeschlossen. Jetzt müssen Sie die Wurzeln auswählen:

Die Lücke sieht so aus:

Oder es kann auch so geschrieben werden:

Schauen wir uns die Wurzeln an:

Lassen Sie uns zunächst mit der ersten Episode arbeiten (und sie ist, gelinde gesagt, einfacher!)

Da unser Intervall vollständig negativ ist, besteht keine Notwendigkeit, nichtnegative Intervalle zu verwenden, sie ergeben immer noch nichtnegative Wurzeln.

Nehmen wir es also – es ist zu viel, es trifft nicht.

Dann lass es sein – ich habe nicht noch einmal zugeschlagen.

Noch ein Versuch – dann – ja, ich habe es geschafft! Die erste Wurzel wurde gefunden!

Ich schieße noch einmal: dann treffe ich erneut!

Na ja, noch einmal: : - das ist schon ein Flug.

Aus der ersten Reihe gibt es also zwei Wurzeln, die zum Intervall gehören: .

Wir arbeiten mit der zweiten Serie (wir bauen zur Potenz gemäß der Regel):

Unterschreiten!

Ich vermisse es schon wieder!

Habe es!

Flug!

Somit hat mein Intervall die folgenden Wurzeln:

Dies ist der Algorithmus, den wir zur Lösung aller anderen Beispiele verwenden werden. Lasst uns gemeinsam mit einem weiteren Beispiel üben.

Beispiel 2. Gleichung mithilfe von Reduktionsformeln auf Faktorisierung reduziert

Löse die Gleichung

Lösung:

Nochmals die berüchtigten Reduktionsformeln:

Versuchen Sie nicht, noch einmal einzuschränken!

Die erste Gleichung hat Wurzeln:

Und der zweite:

Jetzt wieder die Suche nach Wurzeln.

Ich fange mit der zweiten Folge an, ich weiß bereits alles darüber aus dem vorherigen Beispiel! Schauen Sie und stellen Sie sicher, dass die zum Intervall gehörenden Wurzeln wie folgt lauten:

Jetzt die erste Folge und es ist einfacher:

Wenn - geeignet

Wenn das auch in Ordnung ist

Wenn es bereits ein Flug ist.

Dann lauten die Wurzeln wie folgt:

Selbstständige Arbeit. 3 Gleichungen.

Nun, ist Ihnen die Technik klar? Scheint das Lösen trigonometrischer Gleichungen nicht mehr so schwierig zu sein? Dann lösen Sie schnell selbst die folgenden Probleme, und dann lösen wir weitere Beispiele:

Löse die Gleichung
Finden Sie alle Wurzeln dieser Gleichung, die über dem Intervall liegen.
Lösen Sie die Gleichung auf
Geben Sie die Wurzeln der Gleichung an, die über dem Schnitt liegen
Lösen Sie die Gleichung auf
Finden Sie alle Wurzeln dieser Gleichung, die zwischen ihnen liegen.

Gleichung 1.

Und noch einmal die Reduktionsformel:

Erste Wurzelserie:

Zweite Wurzelreihe:

Wir beginnen mit der Auswahl für die Lücke

Antwort: , .

Gleichung 2. Überprüfung selbstständiger Arbeit.

Eine ziemlich knifflige Gruppierung in Faktoren (ich verwende die Doppelwinkelsinusformel):

dann oder

Dies ist eine allgemeine Lösung. Jetzt müssen wir die Wurzeln auswählen. Das Problem besteht darin, dass wir den genauen Wert eines Winkels nicht bestimmen können, dessen Kosinus einem Viertel entspricht. Deshalb kann ich den Arkuskosinus nicht einfach loswerden – so schade!

Was ich tun kann, ist, das so, so, dann herauszufinden.

Erstellen wir eine Tabelle: Intervall:

Nun, durch mühsames Suchen kamen wir zu dem enttäuschenden Schluss, dass unsere Gleichung eine Wurzel im angegebenen Intervall hat: \displaystyle arccos\frac(1)(4)-5\pi

Gleichung 3: Unabhängiger Arbeitstest.

Eine erschreckend aussehende Gleichung. Es lässt sich jedoch ganz einfach lösen, indem man die Doppelwinkelsinusformel anwendet:

Reduzieren wir es um 2:

Lassen Sie uns den ersten Term mit dem zweiten und den dritten mit dem vierten gruppieren und die gemeinsamen Faktoren herausnehmen:

Es ist klar, dass die erste Gleichung keine Wurzeln hat, und nun betrachten wir die zweite:

Im Allgemeinen wollte ich etwas später auf das Lösen solcher Gleichungen eingehen, aber da es aufgetaucht ist, gibt es nichts zu tun, ich muss es lösen...

Gleichungen der Form:

Diese Gleichung wird gelöst, indem beide Seiten geteilt werden durch:

Somit hat unsere Gleichung eine einzige Reihe von Wurzeln:

Wir müssen diejenigen finden, die zum Intervall gehören: .

Lassen Sie uns noch einmal eine Tabelle erstellen, wie ich es zuvor getan habe:

Antwort: .

Gleichungen reduziert auf die Form:

Nun ist es an der Zeit, mit dem zweiten Teil der Gleichungen fortzufahren, insbesondere da ich bereits ausführlich dargelegt habe, woraus die Lösung trigonometrischer Gleichungen eines neuen Typs besteht. Aber es lohnt sich zu wiederholen, dass die Gleichung die Form hat

Gelöst durch Division beider Seiten durch den Kosinus:

Lösen Sie die Gleichung auf
Geben Sie die Wurzeln der Gleichung an, die über dem Schnitt liegen.
Lösen Sie die Gleichung auf
Geben Sie die Wurzeln der Gleichung an, die zwischen ihnen liegen.

Beispiel 1.

Der erste ist ganz einfach. Gehen Sie nach rechts und wenden Sie die Doppelwinkelkosinusformel an:

Ja! Gleichung der Form: . Ich dividiere beide Teile durch

Wir führen Root-Screening durch:

Lücke:

Antwort:

Beispiel 2.

Alles ist auch ganz trivial: Öffnen wir die Klammern rechts:

Grundlegende trigonometrische Identität:

Sinus des Doppelwinkels:

Schließlich erhalten wir:

Root-Screening: Intervall.

Antwort: .

Wie gefällt Ihnen die Technik? Ist sie nicht zu kompliziert? Ich hoffe nicht. Wir können sofort einen Vorbehalt machen: In ihrer reinen Form sind Gleichungen, die sich sofort auf eine Gleichung für den Tangens reduzieren lassen, recht selten. Typischerweise ist dieser Übergang (Division durch Kosinus) nur ein Teil eines komplexeren Problems. Hier ist ein Beispiel zum Üben:

Lösen Sie die Gleichung auf
Finden Sie alle Wurzeln dieser Gleichung, die über dem Schnitt liegen.

Lass uns das Prüfen:

Die Gleichung kann sofort gelöst werden; es genügt, beide Seiten zu dividieren durch:

Wurzelscreening:

Antwort: .

Auf die eine oder andere Weise sind wir bisher noch nicht auf Gleichungen der Art gestoßen, die wir gerade untersucht haben. Allerdings ist es noch zu früh, um Schluss zu machen: Es gibt noch eine weitere „Schicht“ von Gleichungen, die wir nicht analysiert haben. Also:

Lösen trigonometrischer Gleichungen durch Ändern von Variablen

Hier ist alles transparent: Wir schauen uns die Gleichung genau an, vereinfachen sie so weit wie möglich, führen eine Substitution durch, lösen sie, führen eine umgekehrte Substitution durch! In Worten ist alles sehr einfach. Sehen wir es uns in Aktion an:

Beispiel.

Löse die Gleichung: .
Finden Sie alle Wurzeln dieser Gleichung, die über dem Schnitt liegen.

Nun, hier bietet sich uns der Ersatz selbst an!

Dann sieht unsere Gleichung wie folgt aus:

Die erste Gleichung hat Wurzeln:

Und das zweite ist so:

Lassen Sie uns nun die Wurzeln finden, die zum Intervall gehören

Antwort: .

Schauen wir uns gemeinsam ein etwas komplexeres Beispiel an:

Lösen Sie die Gleichung auf
Geben Sie die Wurzeln der gegebenen Gleichung an, die darüber liegen und zwischen ihnen liegen.

Hier ist der Ersatz nicht sofort sichtbar, außerdem ist er nicht sehr offensichtlich. Denken wir zunächst: Was können wir tun?

Wir können es uns zum Beispiel vorstellen

Und gleichzeitig

Dann wird meine Gleichung die Form annehmen:

Und nun Aufmerksamkeit, Fokus:

Teilen wir beide Seiten der Gleichung durch:

Plötzlich haben Sie und ich eine quadratische Gleichung relativ! Machen wir einen Ersatz, dann erhalten wir:

Die Gleichung hat die folgenden Wurzeln:

Unangenehme zweite Wurzelreihe, aber da kann man nichts machen! Wir wählen Wurzeln im Intervall.

Das müssen wir auch bedenken

Seitdem und dann

Antwort:

Um dies zu festigen, bevor Sie die Probleme selbst lösen, ist hier eine weitere Übung für Sie:

Lösen Sie die Gleichung auf
Finden Sie alle Wurzeln dieser Gleichung, die zwischen ihnen liegen.

Hier gilt es, die Augen offen zu halten: Wir haben jetzt Nenner, die Null sein können! Deshalb müssen Sie besonders auf die Wurzeln achten!

Zunächst muss ich die Gleichung umstellen, damit ich eine passende Substitution vornehmen kann. Mir fällt jetzt nichts Besseres ein, als den Tangens in Sinus und Cosinus umzuschreiben:

Jetzt werde ich vom Kosinus zum Sinus wechseln, indem ich die grundlegende trigonometrische Identität verwende:

Und zum Schluss bringe ich alles auf einen gemeinsamen Nenner:

Jetzt kann ich mit der Gleichung fortfahren:

Aber bei (das heißt bei).

Jetzt ist alles zum Austausch bereit:

Dann oder

Beachten Sie jedoch: Wenn, dann gleichzeitig!

Wer leidet darunter? Das Problem mit dem Tangens besteht darin, dass er nicht definiert ist, wenn der Kosinus gleich Null ist (Division durch Null erfolgt).

Somit sind die Wurzeln der Gleichung:

Nun sieben wir die Wurzeln im Intervall heraus:


	- passt
	- übertrieben

Somit hat unsere Gleichung eine einzige Wurzel im Intervall und ist gleich.

Sie sehen: Das Erscheinen eines Nenners (führt genau wie der Tangens zu gewissen Schwierigkeiten mit den Wurzeln! Hier ist mehr Vorsicht geboten!).

Nun, Sie und ich haben die Analyse der trigonometrischen Gleichungen fast abgeschlossen; es bleibt nur noch sehr wenig übrig, um zwei Probleme selbst zu lösen. Hier sind sie.

Löse die Gleichung
Finden Sie alle Wurzeln dieser Gleichung, die über dem Schnitt liegen.
Lösen Sie die Gleichung auf
Geben Sie die Wurzeln dieser Gleichung an, die sich über dem Schnitt befinden.

Entschieden? Ist es nicht sehr schwierig? Lass uns das Prüfen:

Wir arbeiten nach den Reduktionsformeln:
Setzen Sie in die Gleichung ein:
Schreiben wir alles durch Kosinus um, um die Ersetzung einfacher zu machen:
Jetzt ist es ganz einfach, einen Ersatz vorzunehmen:
Es ist klar, dass es sich um eine fremde Wurzel handelt, da die Gleichung keine Lösungen hat. Dann:
Wir suchen nach den Wurzeln, die wir im Intervall brauchen
Antwort: .
Hier ist der Ersatz sofort sichtbar:
Dann oder

- passt! - passt!
- passt! - passt!
- viel! - auch viel!
Antwort:

So, das war's jetzt! Aber die Lösung trigonometrischer Gleichungen endet hier nicht; in den schwierigsten Fällen bleiben wir zurück: wenn die Gleichungen Irrationalität oder verschiedene Arten von „komplexen Nennern“ enthalten. Wie man solche Aufgaben löst, schauen wir uns in einem Artikel für Fortgeschrittene an.

FORTGESCHRITTENES LEVEL

Zusätzlich zu den trigonometrischen Gleichungen, die in den beiden vorherigen Artikeln besprochen wurden, werden wir eine weitere Klasse von Gleichungen betrachten, die eine noch sorgfältigere Analyse erfordern. Diese trigonometrischen Beispiele enthalten entweder Irrationalität oder einen Nenner, was ihre Analyse erschwert. Allerdings kann es durchaus sein, dass Ihnen diese Gleichungen in Teil C der Prüfungsarbeit begegnen. Allerdings hat jede Wolke einen Lichtblick: Bei solchen Gleichungen stellt sich in der Regel nicht mehr die Frage, welche ihrer Wurzeln zu einem bestimmten Intervall gehört. Reden wir nicht um den heißen Brei herum, sondern gehen wir gleich zu den trigonometrischen Beispielen über.

Beispiel 1.

Lösen Sie die Gleichung und finden Sie die Wurzeln, die zum Segment gehören.

Lösung:

Wir haben einen Nenner, der nicht gleich Null sein sollte! Dann ist das Lösen dieser Gleichung dasselbe wie das Lösen des Systems

Lassen Sie uns jede der Gleichungen lösen:

Und jetzt der zweite:

Schauen wir uns nun die Serie an:

Es ist klar, dass diese Option nicht zu uns passt, da in diesem Fall unser Nenner auf Null zurückgesetzt wird (siehe Formel für die Wurzeln der zweiten Gleichung).

Wenn ja, dann ist alles in Ordnung und der Nenner ist nicht Null! Dann lauten die Wurzeln der Gleichung wie folgt: , .

Nun wählen wir die Wurzeln aus, die zum Intervall gehören.


	- ungeeignet	- passt
	- passt	- passt
	Overkill	Overkill

Dann lauten die Wurzeln wie folgt:

Sie sehen, selbst das Auftreten einer kleinen Störung in der Form des Nenners hat die Lösung der Gleichung erheblich beeinflusst: Wir haben eine Reihe von Wurzeln verworfen, die den Nenner zunichte gemacht haben. Noch komplizierter kann es werden, wenn Sie auf trigonometrische Beispiele stoßen, die irrational sind.

Beispiel 2.

Löse die Gleichung:

Lösung:

Nun, zumindest müssen Sie die Wurzeln nicht entfernen, und das ist gut so! Lösen wir zunächst die Gleichung, unabhängig von der Irrationalität:

Also, ist das alles? Nein, leider wäre es zu einfach! Wir müssen bedenken, dass unter der Wurzel nur nicht negative Zahlen erscheinen können. Dann:

Die Lösung dieser Ungleichung lautet:

Jetzt muss noch herausgefunden werden, ob ein Teil der Wurzeln der ersten Gleichung versehentlich dort gelandet ist, wo die Ungleichung nicht gilt.

Dazu können Sie wieder die Tabelle verwenden:


	: , Aber	Nein!
		Ja!
		Ja!

Somit ist eine meiner Wurzeln „herausgefallen“! Es stellt sich heraus, wenn man es hinlegt. Dann kann die Antwort wie folgt geschrieben werden:

Antwort:

Sie sehen, die Wurzel erfordert noch mehr Aufmerksamkeit! Machen wir es komplizierter: Jetzt habe ich eine trigonometrische Funktion unter meiner Wurzel.

Beispiel 3.

Wie zuvor: Zuerst werden wir jedes einzeln lösen und dann darüber nachdenken, was wir getan haben.

Nun die zweite Gleichung:

Am schwierigsten ist es nun herauszufinden, ob sich unter der arithmetischen Wurzel negative Werte ergeben, wenn wir dort die Wurzeln aus der ersten Gleichung einsetzen:

Die Zahl muss im Bogenmaß verstanden werden. Da ein Bogenmaß ungefähr Grad ist, liegt das Bogenmaß in der Größenordnung von Grad. Dies ist die Ecke des zweiten Viertels. Welches Vorzeichen hat der Kosinus des zweiten Viertels? Minus. Was ist mit Sinus? Plus. Was können wir also über den Ausdruck sagen:

Es ist weniger als Null!

Dies bedeutet, dass es nicht die Wurzel der Gleichung ist.

Jetzt ist es Zeit.

Vergleichen wir diese Zahl mit Null.

Kotangens ist eine Funktion, die in einem Viertel abnimmt (je kleiner das Argument, desto größer der Kotangens). Das Bogenmaß ist eine ungefähre Angabe in Grad. Gleichzeitig

seitdem, dann und deshalb
,

Antwort: .

Könnte es noch komplizierter werden? Bitte! Schwieriger wird es, wenn die Wurzel immer noch eine trigonometrische Funktion ist und der zweite Teil der Gleichung wiederum eine trigonometrische Funktion ist.

Je mehr trigonometrische Beispiele, desto besser, siehe unten:

Beispiel 4.

Die Wurzel ist aufgrund des begrenzten Kosinus nicht geeignet

Nun der Zweite:

Gleichzeitig gilt per Definition einer Wurzel:

Wir müssen uns an den Einheitskreis erinnern: nämlich an die Viertel, in denen der Sinus kleiner als Null ist. Was sind das für Viertel? Dritter und vierter. Dann interessieren uns diejenigen Lösungen der ersten Gleichung, die im dritten oder vierten Viertel liegen.

Die erste Reihe ergibt Wurzeln, die am Schnittpunkt des dritten und vierten Viertels liegen. Die zweite Reihe – diametral dazu – führt zu Wurzeln, die an der Grenze des ersten und zweiten Viertels liegen. Daher ist diese Serie für uns nicht geeignet.

Antwort: ,

Und wieder trigonometrische Beispiele mit „schwieriger Irrationalität“. Wir haben die trigonometrische Funktion nicht nur wieder unter der Wurzel, sondern jetzt auch im Nenner!

Beispiel 5.

Nun, es geht nichts – wir machen wie bisher.

Jetzt arbeiten wir mit dem Nenner:

Ich möchte die trigonometrische Ungleichung nicht lösen, also mache ich etwas Schlaues: Ich nehme meine Reihe von Wurzeln und setze sie in die Ungleichung ein:

Wenn - gerade ist, dann gilt:

da alle Blickwinkel im vierten Viertel liegen. Und wieder die heilige Frage: Welches Vorzeichen hat der Sinus im vierten Viertel? Negativ. Dann die Ungleichheit

Wenn -ungerade, dann:

In welchem Viertel liegt der Winkel? Dies ist die Ecke des zweiten Viertels. Dann sind alle Ecken wieder die Ecken des zweiten Viertels. Der Sinus dort ist positiv. Genau das, was Sie brauchen! Also die Serie:

Passt!

Mit der zweiten Wurzelreihe gehen wir genauso um:

Wir setzen in unsere Ungleichung ein:

Wenn – sogar, dann

Ecken im ersten Viertel. Der Sinus dort ist positiv, was bedeutet, dass die Reihe geeignet ist. Wenn nun – seltsam, dann:

passt auch!

Nun, jetzt schreiben wir die Antwort auf!

Antwort:

Nun, das war vielleicht der arbeitsintensivste Fall. Jetzt biete ich Ihnen Probleme an, die Sie selbst lösen können.

Ausbildung

Lösen und finden Sie alle Wurzeln der Gleichung, die zum Segment gehören.

Lösungen:

Erste Gleichung:
oder
Root-ODZ:
Zweite Gleichung:
Auswahl der Wurzeln, die zum Intervall gehören
Antwort:

Oder
oder
Aber

Betrachten wir: . Wenn – sogar, dann
- ungeeignet!
Wenn - ungerade, : - passend!
Das bedeutet, dass unsere Gleichung die folgende Reihe von Wurzeln hat:
oder
Auswahl der Wurzeln im Intervall:


	- ungeeignet	- passt
	- passt	- viel
	- passt	viel

Antwort: , .

Oder
Denn dann ist die Tangente nicht definiert. Diese Wurzelreihe verwerfen wir sofort!

Zweiter Teil:

Gleichzeitig sei dies laut DZ erforderlich

Wir überprüfen die in der ersten Gleichung gefundenen Wurzeln:

Wenn das Zeichen:

Erste Viertelwinkel, bei denen die Tangente positiv ist. Ungeeignet!
Wenn das Zeichen:

Ecke im vierten Viertel. Dort ist die Tangente negativ. Passt. Wir schreiben die Antwort auf:

Antwort: , .

Wir haben uns in diesem Artikel gemeinsam komplexe trigonometrische Beispiele angesehen, Sie sollten die Gleichungen jedoch selbst lösen.

ZUSAMMENFASSUNG UND GRUNDFORMELN

Eine trigonometrische Gleichung ist eine Gleichung, in der die Unbekannte streng unter dem Vorzeichen der trigonometrischen Funktion steht.

Es gibt zwei Möglichkeiten, trigonometrische Gleichungen zu lösen:

Der erste Weg ist die Verwendung von Formeln.

Der zweite Weg führt über den trigonometrischen Kreis.

Ermöglicht das Messen von Winkeln, das Ermitteln ihrer Sinus- und Cosinuswerte usw.

Methoden zur Lösung trigonometrischer Gleichungen.

Das Lösen einer trigonometrischen Gleichung besteht aus zwei Schritten: Gleichungstransformation um es am einfachsten zu bekommen Typ (siehe oben) und Lösungdas resultierende einfachste trigonometrische Gleichung. Es sind sieben grundlegende Methoden zur Lösung trigonometrischer Gleichungen.

1. Algebraische Methode.

(Methode zum Ersetzen und Ersetzen von Variablen).

2. Faktorisierung.

Beispiel 1. Lösen Sie die Gleichung: Sünde X+cos X = 1 .

Lösung: Verschieben wir alle Terme der Gleichung nach links:

Sünde X+cos X – 1 = 0 ,

Lassen Sie uns den Ausdruck transformieren und faktorisieren

Linke Seite der Gleichung:

Beispiel 2. Lösen Sie die Gleichung: cos 2 X+ Sünde X cos X = 1.

Lösung: cos 2 X+ Sünde X cos X– Sünde 2 X– weil 2 X = 0 ,

Sünde X cos X– Sünde 2 X = 0 ,

Sünde X· (cos X– Sünde X ) = 0 ,

Beispiel 3. Lösen Sie die Gleichung: weil 2 X–cos 8 X+ weil 6 X = 1.

Lösung: cos 2 X+ weil 6 X= 1 + cos 8 X,

2 weil 4 X weil 2 X= 2cos² 4 X ,

Denn 4 X · (weil 2 X– weil 4 X) = 0 ,

Denn 4 X · 2 Sünde 3 X Sünde X = 0 ,

1). weil 4 X= 0, 2). Sünde 3 X= 0, 3). Sünde X = 0 ,

3. Reduktion auf homogene Gleichung.

Die gleichung angerufen homogen aus hinsichtlich Sünde Und cos , Wenn alles davon Begriffe gleichen Grades relativ zu Sünde Und cos gleichen Winkel. Um eine homogene Gleichung zu lösen, benötigen Sie:

A) alle seine Mitglieder auf die linke Seite verschieben;

B) Setzen Sie alle gemeinsamen Faktoren aus Klammern;

V) alle Faktoren und Klammern mit Null gleichsetzen;

G) Klammern gleich Null ergeben homogene Gleichung geringeren Grades, in die zerlegt werden soll

cos(oder Sünde) im höheren Studiengang;

D) Lösen Sie die resultierende algebraische Gleichung nachbräunen .

Sünde 2 X+ 4 Sünde X cos X+ 5cos 2 X = 2.

Lösung: 3sin 2 X+ 4 Sünde X cos X+ 5 weil 2 X= 2sin 2 X+ 2cos 2 X ,

Sünde 2 X+ 4 Sünde X cos X+ 3 weil 2 X = 0 ,

Bräune 2 X+ 4 Bräune X + 3 = 0 , von hier j 2 + 4j +3 = 0 ,

Die Wurzeln dieser Gleichung sind:j 1 = - 1, j 2 = - 3, also

1) braun X= –1, 2) tan X = –3,

4. Übergang zum Halbwinkel.

Schauen wir uns diese Methode als Beispiel an:

BEISPIEL Gleichung lösen: 3 Sünde X– 5 cos X = 7.

Lösung: 6 Sünde ( X/ 2) cos ( X/ 2) – 5 cos² ( X/ 2) + 5 sin² ( X/ 2) =

7 sin² ( X/ 2) + 7 cos² ( X/ 2) ,

2 sin² ( X/ 2) – 6 Sünde ( X/ 2) cos ( X/ 2) + 12 cos² ( X/ 2) = 0 ,

tan²( X/ 2) – 3 braun ( X/ 2) + 6 = 0 ,

. . . . . . . . . .

5. Einführung eines Hilfswinkels.

Betrachten Sie eine Gleichung der Form:

A Sünde X + B cos X = C ,

Wo A, B, C– Koeffizienten;X- Unbekannt.

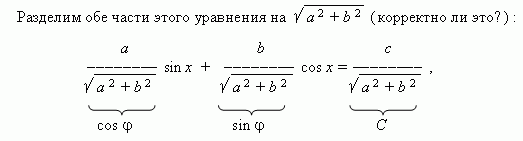
Nun haben die Koeffizienten der Gleichung die Eigenschaften Sinus und Cosinus, nämlich: Modul (absoluter Wert) von jedem davon nicht mehr als 1, und die Summe ihrer Quadrate ist 1. Dann können wir bezeichnen sie entsprechend Wie cos und sin (hier - sogenannt Hilfswinkel), UndNehmen Sie unsere Gleichung

Lektion und Präsentation zum Thema: „Einfache trigonometrische Gleichungen lösen“

Zusätzliche Materialien
Liebe Benutzer, vergessen Sie nicht, Ihre Kommentare, Bewertungen und Wünsche zu hinterlassen! Alle Materialien wurden von einem Antivirenprogramm überprüft.

Handbücher und Simulatoren im Integral Online-Shop für die 10. Klasse von 1C
Wir lösen Probleme in der Geometrie. Interaktive Aufgaben zum Bauen im Weltraum
Softwareumgebung „1C: Mathematical Constructor 6.1“

Was wir studieren werden:
1. Was sind trigonometrische Gleichungen?

3. Zwei Hauptmethoden zur Lösung trigonometrischer Gleichungen.
4. Homogene trigonometrische Gleichungen.
5. Beispiele.

Was sind trigonometrische Gleichungen?

Leute, wir haben bereits Arkussinus, Arkuskosinus, Arkustangens und Arkuskotangens studiert. Schauen wir uns nun trigonometrische Gleichungen im Allgemeinen an.

Trigonometrische Gleichungen sind Gleichungen, in denen eine Variable im Vorzeichen einer trigonometrischen Funktion enthalten ist.

Wiederholen wir die Form der Lösung der einfachsten trigonometrischen Gleichungen:

1)Wenn |a|≤ 1, dann hat die Gleichung cos(x) = a eine Lösung:

X= ± arccos(a) + 2πk

2) Wenn |a|≤ 1, dann hat die Gleichung sin(x) = a eine Lösung:

3) Wenn |a| > 1, dann haben die Gleichungen sin(x) = a und cos(x) = a keine Lösungen. 4) Die Gleichung tg(x)=a hat eine Lösung: x=arctg(a)+ πk

5) Die Gleichung ctg(x)=a hat eine Lösung: x=arcctg(a)+ πk

Für alle Formeln ist k eine ganze Zahl

Die einfachsten trigonometrischen Gleichungen haben die Form: T(kx+m)=a, T ist eine trigonometrische Funktion.

Beispiel.

Lösen Sie die Gleichungen: a) sin(3x)= √3/2

Lösung:

A) Bezeichnen wir 3x=t, dann schreiben wir unsere Gleichung in der Form um:

Die Lösung dieser Gleichung lautet: t=((-1)^n)arcsin(√3 /2)+ πn.

Aus der Wertetabelle erhalten wir: t=((-1)^n)×π/3+ πn.

Kehren wir zu unserer Variablen zurück: 3x =((-1)^n)×π/3+ πn,

Dann ist x= ((-1)^n)×π/9+ πn/3

Antwort: x= ((-1)^n)×π/9+ πn/3, wobei n eine ganze Zahl ist. (-1)^n – minus eins hoch n.

Weitere Beispiele für trigonometrische Gleichungen.

Lösen Sie die Gleichungen: a) cos(x/5)=1 b)tg(3x- π/3)= √3

Lösung:

A) Kommen wir dieses Mal direkt zur Berechnung der Wurzeln der Gleichung:

X/5= ± arccos(1) + 2πk. Dann ist x/5= πk => x=5πk

Antwort: x=5πk, wobei k eine ganze Zahl ist.

B) Wir schreiben es in der Form: 3x- π/3=arctg(√3)+ πk. Wir wissen: arctan(√3)= π/3

3x- π/3= π/3+ πk => 3x=2π/3 + πk => x=2π/9 + πk/3

Antwort: x=2π/9 + πk/3, wobei k eine ganze Zahl ist.

Lösen Sie die Gleichungen: cos(4x)= √2/2. Und finden Sie alle Wurzeln im Segment.

Lösung:

Lösen wir unsere Gleichung in allgemeiner Form: 4x= ± arccos(√2/2) + 2πk

4x= ± π/4 + 2πk;

X= ± π/16+ πk/2;

Sehen wir uns nun an, welche Wurzeln in unserem Segment liegen. Bei k Bei k=0, x= π/16 befinden wir uns im gegebenen Segment.
Mit k=1, x= π/16+ π/2=9π/16 treffen wir erneut.
Für k=2, x= π/16+ π=17π/16, aber hier haben wir nicht getroffen, was bedeutet, dass wir für große k offensichtlich auch nicht getroffen haben.

Antwort: x= π/16, x= 9π/16

Zwei Hauptlösungsmethoden.

Wir haben uns die einfachsten trigonometrischen Gleichungen angesehen, es gibt aber auch komplexere. Um sie zu lösen, werden die Methode der Einführung einer neuen Variablen und die Faktorisierungsmethode verwendet. Schauen wir uns Beispiele an.

Lösen wir die Gleichung:

Lösung:
Um unsere Gleichung zu lösen, verwenden wir die Methode der Einführung einer neuen Variablen mit der Bezeichnung: t=tg(x).

Als Ergebnis der Ersetzung erhalten wir: t 2 + 2t -1 = 0

Finden wir die Wurzeln der quadratischen Gleichung: t=-1 und t=1/3

Dann ist tg(x)=-1 und tg(x)=1/3, wir erhalten die einfachste trigonometrische Gleichung, finden wir ihre Wurzeln.

X=arctg(-1) +πk= -π/4+πk; x=arctg(1/3) + πk.

Antwort: x= -π/4+πk; x=arctg(1/3) + πk.

Ein Beispiel für die Lösung einer Gleichung

Lösen Sie die Gleichungen: 2sin 2 (x) + 3 cos(x) = 0

Lösung:

Verwenden wir die Identität: sin 2 (x) + cos 2 (x)=1

Unsere Gleichung wird die Form annehmen: 2-2cos 2 (x) + 3 cos (x) = 0

2 cos 2 (x) - 3 cos(x) -2 = 0

Führen wir den Ersatz t=cos(x) ein: 2t 2 -3t - 2 = 0

Die Lösung unserer quadratischen Gleichung sind die Wurzeln: t=2 und t=-1/2

Dann ist cos(x)=2 und cos(x)=-1/2.

Weil Kosinus kann keine Werte größer als eins annehmen, dann hat cos(x)=2 keine Wurzeln.

Für cos(x)=-1/2: x= ± arccos(-1/2) + 2πk; x= ±2π/3 + 2πk

Antwort: x= ±2π/3 + 2πk

Homogene trigonometrische Gleichungen.

Definition: Gleichungen der Form a sin(x)+b cos(x) heißen homogene trigonometrische Gleichungen ersten Grades.

Gleichungen der Form

homogene trigonometrische Gleichungen zweiten Grades.

Um eine homogene trigonometrische Gleichung ersten Grades zu lösen, dividieren Sie sie durch cos(x): Sie können nicht durch den Kosinus dividieren, wenn dieser gleich Null ist. Stellen wir sicher, dass dies nicht der Fall ist:
Sei cos(x)=0, dann ist asin(x)+0=0 => sin(x)=0, aber Sinus und Cosinus sind nicht gleichzeitig gleich Null, wir erhalten einen Widerspruch, sodass wir sicher dividieren können um Null.

Löse die Gleichung:
Beispiel: cos 2 (x) + sin(x) cos(x) = 0

Lösung:

Nehmen wir den gemeinsamen Faktor heraus: cos(x)(c0s(x) + sin (x)) = 0

Dann müssen wir zwei Gleichungen lösen:

Cos(x)=0 und cos(x)+sin(x)=0

Cos(x)=0 bei x= π/2 + πk;

Betrachten Sie die Gleichung cos(x)+sin(x)=0. Teilen Sie unsere Gleichung durch cos(x):

1+tg(x)=0 => tg(x)=-1 => x=arctg(-1) +πk= -π/4+πk

Antwort: x= π/2 + πk und x= -π/4+πk

Wie löst man homogene trigonometrische Gleichungen zweiten Grades?
Leute, befolgt immer diese Regeln!

1. Sehen Sie, was der Koeffizient a ist. Wenn a=0, dann nimmt unsere Gleichung die Form cos(x)(bsin(x)+ccos(x)) an, ein Beispiel für die Lösung finden Sie auf der vorherigen Folie

2. Wenn a≠0, dann müssen Sie beide Seiten der Gleichung durch das Kosinusquadrat dividieren, wir erhalten:

Wir ändern die Variable t=tg(x) und erhalten die Gleichung:

Lösen Sie Beispiel Nr.:3

Löse die Gleichung:
Lösung:

Teilen wir beide Seiten der Gleichung durch das Kosinusquadrat:

Wir ändern die Variable t=tg(x): t 2 + 2 t - 3 = 0

Finden wir die Wurzeln der quadratischen Gleichung: t=-3 und t=1

Dann gilt: tg(x)=-3 => x=arctg(-3) + πk=-arctg(3) + πk

Tg(x)=1 => x= π/4+ πk

Antwort: x=-arctg(3) + πk und x= π/4+ πk

Lösen Sie Beispiel Nr.:4

Löse die Gleichung:

Lösung:
Lassen Sie uns unseren Ausdruck umwandeln:

Wir können solche Gleichungen lösen: x= - π/4 + 2πk und x=5π/4 + 2πk

Antwort: x= - π/4 + 2πk und x=5π/4 + 2πk

Beispiel Nr.:5 lösen

Löse die Gleichung:

Lösung:
Lassen Sie uns unseren Ausdruck umwandeln:

Führen wir den Ersatz tg(2x)=t:2 2 - 5t + 2 = 0 ein

Die Lösung unserer quadratischen Gleichung sind die Wurzeln: t=-2 und t=1/2

Dann erhalten wir: tg(2x)=-2 und tg(2x)=1/2
2x=-arctg(2)+ πk => x=-arctg(2)/2 + πk/2

2x= arctg(1/2) + πk => x=arctg(1/2)/2+ πk/2

Antwort: x=-arctg(2)/2 + πk/2 und x=arctg(1/2)/2+ πk/2

Probleme zur unabhängigen Lösung.

1) Lösen Sie die Gleichung

A) sin(7x)= 1/2 b) cos(3x)= √3/2 c) cos(-x) = -1 d) tg(4x) = √3 d) ctg(0,5x) = -1,7

2) Lösen Sie die Gleichungen: sin(3x)= √3/2. Und finden Sie alle Wurzeln auf dem Segment [π/2; π].

3) Lösen Sie die Gleichung: cot 2 (x) + 2 cot (x) + 1 =0

4) Lösen Sie die Gleichung: 3 sin 2 (x) + √3sin (x) cos(x) = 0

5) Lösen Sie die Gleichung: 3sin 2 (3x) + 10 sin(3x)cos(3x) + 3 cos 2 (3x) =0

6) Lösen Sie die Gleichung: cos 2 (2x) -1 - cos(x) =√3/2 -sin 2 (2x)

Beispiele:

\(2\sin(⁡x) = \sqrt(3)\)
tg\((3x)=-\) \(\frac(1)(\sqrt(3))\)
\(4\cos^2⁡x+4\sin⁡x-1=0\)
\(\cos⁡4x+3\cos⁡2x=1\)

So lösen Sie trigonometrische Gleichungen:

Jede trigonometrische Gleichung sollte auf einen der folgenden Typen reduziert werden:

\(\sin⁡t=a\), \(\cos⁡t=a\), tg\(t=a\), ctg\(t=a\)

wobei \(t\) ein Ausdruck mit einem x ist, \(a\) eine Zahl ist. Solche trigonometrischen Gleichungen heißen das einfachste. Sie können leicht mit () oder speziellen Formeln gelöst werden:

Infografiken zum Lösen einfacher trigonometrischer Gleichungen finden Sie hier: und.

Beispiel . Lösen Sie die trigonometrische Gleichung \(\sin⁡x=-\)\(\frac(1)(2)\).
Lösung:

Antwort: \(\left[ \begin(gathered)x=-\frac(π)(6)+2πk, \\ x=-\frac(5π)(6)+2πn, \end(gathered)\right.\) \(k,n∈Z\)

Was jedes Symbol in der Formel für die Wurzeln trigonometrischer Gleichungen bedeutet, siehe.

Aufmerksamkeit! Die Gleichungen \(\sin⁡x=a\) und \(\cos⁡x=a\) haben keine Lösungen, wenn \(a ϵ (-∞;-1)∪(1;∞)\). Da Sinus und Cosinus für jedes x größer oder gleich \(-1\) und kleiner oder gleich \(1\) sind:

\(-1≤\sin x≤1\) \(-1≤\cos⁡x≤1\)

Beispiel . Lösen Sie die Gleichung \(\cos⁡x=-1,1\).
Lösung: \(-1,1<-1\), а значение косинуса не может быть меньше \(-1\). Значит у уравнения нет решения.
Antwort : keine Lösungen.

Beispiel . Lösen Sie die trigonometrische Gleichung tg\(⁡x=1\).
Lösung:

Lösen wir die Gleichung mithilfe des Zahlenkreises. Dafür:
1) Konstruieren Sie einen Kreis)
2) Konstruieren Sie die Achsen \(x\) und \(y\) sowie die Tangentenachse (sie verläuft durch den Punkt \((0;1)\) parallel zur Achse \(y\)).
3) Markieren Sie auf der Tangentenachse den Punkt \(1\).
4) Verbinden Sie diesen Punkt und den Koordinatenursprung – eine gerade Linie.
5) Markieren Sie die Schnittpunkte dieser Linie und des Zahlenkreises.
6) Unterschreiben wir die Werte dieser Punkte: \(\frac(π)(4)\) ,\(\frac(5π)(4)\)
7) Schreiben wir alle Werte dieser Punkte auf. Da sie genau \(π\) voneinander entfernt liegen, lassen sich alle Werte in einer Formel schreiben:

Antwort: \(x=\)\(\frac(π)(4)\) \(+πk\), \(k∈Z\).

Beispiel . Lösen Sie die trigonometrische Gleichung \(\cos⁡(3x+\frac(π)(4))=0\).
Lösung:

Benutzen wir wieder den Zahlenkreis.
1) Konstruieren Sie einen Kreis mit den Achsen \(x\) und \(y\).
2) Markieren Sie auf der Kosinusachse (\(x\)-Achse) \(0\).
3) Zeichnen Sie durch diesen Punkt eine Senkrechte zur Kosinusachse.
4) Markieren Sie die Schnittpunkte der Senkrechten und des Kreises.
5) Unterschreiben wir die Werte dieser Punkte: \(-\) \(\frac(π)(2)\),\(\frac(π)(2)\).
6) Wir schreiben den Gesamtwert dieser Punkte auf und setzen sie mit dem Kosinus (dem, was innerhalb des Kosinus liegt) gleich.

\(3x+\)\(\frac(π)(4)\) \(=±\)\(\frac(π)(2)\) \(+2πk\), \(k∈Z\)

\(3x+\)\(\frac(π)(4)\) \(=\)\(\frac(π)(2)\) \(+2πk\) \(3x+\)\(\frac( π)(4)\) \(=-\)\(\frac(π)(2)\) \(+2πk\)

8) Wie üblich werden wir \(x\) in Gleichungen ausdrücken.
Vergessen Sie nicht, Zahlen mit \(π\) sowie \(1\), \(2\), \(\frac(1)(4)\) usw. zu behandeln. Das sind die gleichen Zahlen wie alle anderen. Keine numerische Diskriminierung!

\(3x=-\)\(\frac(π)(4)\) \(+\)\(\frac(π)(2)\) \(+2πk\) \(3x=-\)\ (\frac(π)(4)\) \(+\)\(\frac(π)(2)\) \(+2πk\)
\(3x=\)\(\frac(π)(4)\) \(+2πk\) \(|:3\) \(3x=-\)\(\frac(3π)(4)\) \(+2πk\) \(|:3\)
\(x=\)\(\frac(π)(12)\) \(+\)\(\frac(2πk)(3)\) \(x=-\)\(\frac(π)( 4)\) \(+\)\(\frac(2πk)(3)\)

Antwort: \(x=\)\(\frac(π)(12)\) \(+\)\(\frac(2πk)(3)\) \(x=-\)\(\frac(π)( 4)\) \(+\)\(\frac(2πk)(3)\) , \(k∈Z\).

Trigonometrische Gleichungen auf das Einfachste zu reduzieren ist eine kreative Aufgabe. Hier müssen Sie sowohl spezielle Methoden zum Lösen von Gleichungen verwenden:
- Methode (die beliebteste im Einheitlichen Staatsexamen).
- Methode.
- Methode der Hilfsargumente.

Betrachten wir ein Beispiel für die Lösung der quadratischen trigonometrischen Gleichung

Beispiel . Lösen Sie die trigonometrische Gleichung \(2\cos^2⁡x-5\cos⁡x+2=0\)
Lösung:

\(2\cos^2⁡x-5\cos⁡x+2=0\)	Machen wir die Ersetzung \(t=\cos⁡x\).

	Unsere Gleichung ist typisch geworden. Sie können es mit lösen.
\(D=25-4 \cdot 2 \cdot 2=25-16=9\)
\(t_1=\)\(\frac(5-3)(4)\) \(=\)\(\frac(1)(2)\) ; \(t_2=\)\(\frac(5+3)(4)\) \(=2\)	Wir machen einen umgekehrten Ersatz.
\(\cos⁡x=\)\(\frac(1)(2)\); \(\cos⁡x=2\)	Wir lösen die erste Gleichung mithilfe des Zahlenkreises. Die zweite Gleichung hat keine Lösungen, weil \(\cos⁡x∈[-1;1]\) und kann für kein x gleich zwei sein.
	Schreiben wir alle Zahlen auf, die an diesen Stellen liegen.

Antwort: \(x=±\)\(\frac(π)(3)\) \(+2πk\), \(k∈Z\).

Ein Beispiel für die Lösung einer trigonometrischen Gleichung mit dem Studium von ODZ:

Beispiel (VERWENDUNG) . Lösen Sie die trigonometrische Gleichung \(=0\)

\(\frac(2\cos^2⁡x-\sin(⁡2x))(ctg x)\)\(=0\)	Es gibt einen Bruch und einen Kotangens – das heißt, wir müssen ihn aufschreiben. Ich möchte Sie daran erinnern, dass ein Kotangens eigentlich ein Bruch ist: ctg\(x=\)\(\frac(\cos⁡x)(\sin⁡x)\) Daher ist die ODZ für ctg\(x\): \(\sin⁡x≠0\).
ODZ: ctg\(x ≠0\); \(\sin⁡x≠0\) \(x≠±\)\(\frac(π)(2)\) \(+2πk\); \(x≠πn\); \(k,n∈Z\)	Markieren wir die „Nichtlösungen“ auf dem Zahlenkreis.

\(\frac(2\cos^2⁡x-\sin(⁡2x))(ctg x)\)\(=0\)	Lassen Sie uns den Nenner in der Gleichung entfernen, indem wir ihn mit ctg\(x\) multiplizieren. Wir können dies tun, da wir oben geschrieben haben, dass ctg\(x ≠0\).
\(2\cos^2⁡x-\sin⁡(2x)=0\)	Wenden wir die Doppelwinkelformel für den Sinus an: \(\sin⁡(2x)=2\sin⁡x\cos⁡x\).
\(2\cos^2⁡x-2\sin⁡x\cos⁡x=0\)	Wenn Sie Ihre Hände ausstrecken, um durch den Kosinus zu dividieren, ziehen Sie sie zurück! Sie können durch einen Ausdruck mit einer Variablen dividieren, wenn diese definitiv nicht gleich Null ist (zum Beispiel diese: \(x^2+1,5^x\)). Nehmen wir stattdessen \(\cos⁡x\) aus der Klammer.
\(\cos⁡x (2\cos⁡x-2\sin⁡x)=0\)	Lassen Sie uns die Gleichung in zwei Teile „teilen“.
\(\cos⁡x=0\); \(2\cos⁡x-2\sin⁡x=0\)	Lösen wir die erste Gleichung mithilfe des Zahlenkreises. Teilen wir die zweite Gleichung durch \(2\) und verschieben wir \(\sin⁡x\) auf die rechte Seite.

\(x=±\)\(\frac(π)(2)\) \(+2πk\), \(k∈Z\). \(\cos⁡x=\sin⁡x\)	Die resultierenden Wurzeln werden nicht in die ODZ einbezogen. Daher werden wir sie nicht als Antwort aufschreiben. Die zweite Gleichung ist typisch. Teilen wir es durch \(\sin⁡x\) (\(\sin⁡x=0\) kann keine Lösung der Gleichung sein, da in diesem Fall \(\cos⁡x=1\) oder \(\cos⁡ x=-1\)).
	Wir verwenden wieder einen Kreis.
\(x=\)\(\frac(π)(4)\) \(+πn\), \(n∈Z\)	Diese Wurzeln werden von ODZ nicht ausgeschlossen, Sie können sie also in die Antwort schreiben.

Antwort: \(x=\)\(\frac(π)(4)\) \(+πn\), \(n∈Z\).

Klasse: 10

„Die Gleichungen werden ewig Bestand haben.“

A. Einstein

Lernziele:

Lehrreich:
- Vertiefung des Verständnisses von Methoden zur Lösung trigonometrischer Gleichungen;
- Entwickeln Sie die Fähigkeiten, Methoden zur Lösung trigonometrischer Gleichungen zu unterscheiden und richtig auszuwählen.
Lehrreich:
- Förderung des kognitiven Interesses am Bildungsprozess;
- Entwicklung der Fähigkeit, eine bestimmte Aufgabe zu analysieren;
- tragen dazu bei, das psychologische Klima im Klassenzimmer zu verbessern.
Entwicklung:
- die Entwicklung der Fähigkeit zum selbstständigen Wissenserwerb fördern;
- die Fähigkeit der Schüler fördern, ihren Standpunkt zu vertreten;

Ausrüstung: Poster mit grundlegenden trigonometrischen Formeln, Computer, Projektor, Leinwand.

1 Lektion

I. Aktualisierung des Referenzwissens

Lösen Sie die Gleichungen mündlich:

1) cosx = 1;
2) 2 cosx = 1;
3) cosx = –;
4) sin2x = 0;
5) sinx = –;
6) sinx = ;
7) tgx = ;
8) cos 2 x – sin 2 x = 0

1) x = 2k;
2) x = ± + 2k;
3) x =± + 2k;
4) x = k;
5) x = (–1) + k;
6) x = (–1) + 2k;
7) x = + k;
8) x = + k; bis Z.

II. Neues Material lernen

– Heute werden wir uns komplexere trigonometrische Gleichungen ansehen. Schauen wir uns 10 Möglichkeiten an, sie zu lösen. Als nächstes gibt es zwei Lektionen zur Festigung und für die nächste Lektion gibt es einen Test. Am „For Lesson“-Stand sind Aufgaben ausgehängt, die denen der Prüfung ähneln und die Sie vor der Prüfung lösen müssen. (Am Tag vor dem Test hängen Sie die Lösungen zu diesen Aufgaben am Stand aus.)

Kommen wir also zu den Möglichkeiten zur Lösung trigonometrischer Gleichungen. Einige dieser Methoden werden Ihnen wahrscheinlich schwierig vorkommen, während andere einfach erscheinen, weil... Sie kennen bereits einige Techniken zum Lösen von Gleichungen.

Vier Schüler der Klasse erhielten eine individuelle Aufgabe: Ihnen vier Möglichkeiten zur Lösung trigonometrischer Gleichungen zu verstehen und zu zeigen.

(Sprechende Schüler haben im Voraus Folien vorbereitet. Der Rest der Klasse schreibt die wichtigsten Schritte zum Lösen von Gleichungen in ein Notizbuch.)

1 Schüler: 1 Weg. Gleichungen durch Faktorisieren lösen

sin 4x = 3 cos 2x

Um die Gleichung zu lösen, verwenden wir die Doppelwinkelsinusformel sin 2 = 2 sin cos
2 sin 2x cos 2x – 3 cos 2x = 0,
cos 2x (2 sin 2x – 3) = 0. Das Produkt dieser Faktoren ist gleich Null, wenn mindestens einer der Faktoren gleich Null ist.

2x = + k, k Z oder sin 2x = 1,5 – es gibt keine Lösungen, weil | Sünde| 1
x = + k; bis Z.
Antwort: x = + k, k Z.

2 Schüler. Methode 2. Lösen von Gleichungen durch Umwandeln der Summe oder Differenz trigonometrischer Funktionen in ein Produkt

cos 3x + sin 2x – sin 4x = 0.

Um die Gleichung zu lösen, verwenden wir die Formel sin–sin = 2 sin сos

cos 3x + 2 sin cos = 0,

сos 3x – 2 sin x cos 3x = 0,

cos 3x (1 – 2 sinx) = 0. Die resultierende Gleichung entspricht einem Satz aus zwei Gleichungen:

Die Lösungsmenge der zweiten Gleichung ist vollständig in der Lösungsmenge der ersten Gleichung enthalten. Bedeutet

Antwort:

3 Schüler. 3-Wege. Lösen von Gleichungen durch Umwandeln des Produkts trigonometrischer Funktionen in eine Summe

sin 5x cos 3x = sin 6x cos2x.

Um die Gleichung zu lösen, verwenden wir die Formel

Antwort:

4 Schüler. 4-Wege. Lösen von Gleichungen, die sich auf quadratische Gleichungen reduzieren lassen

3 sin x – 2 cos 2 x = 0,
3 sin x – 2 (1 – sin 2 x) = 0,
2 Sünde 2 x + 3 Sünde x – 2 = 0,

Sei sin x = t, wobei | t |. Wir erhalten die quadratische Gleichung 2t 2 + 3t – 2 = 0,

D = 9 + 16 = 25.

Auf diese Weise . erfüllt die Bedingung | nicht t |.

Also sin x = . Deshalb .

Antwort:

III. Festigung des Gelernten aus dem Lehrbuch von A. N. Kolmogorov

1. Nr. 164 (a), 167 (a) (quadratische Gleichung)
2. Nr. 168 (a) (Faktorisierung)
3. Nr. 174 (a) (Umrechnung einer Summe in ein Produkt)
4. (Produkt in Summe umwandeln)

(Zeigen Sie am Ende der Lektion die Lösung dieser Gleichungen zur Überprüfung auf dem Bildschirm.)

№ 164 (A)

2 sin 2 x + sin x – 1 = 0.
Sei sin x = t, | t | 1. Dann
2 t 2 + t – 1 = 0, t = – 1, t= . Wo

Antwort: - .

№ 167 (A)

3 tg 2 x + 2 tg x – 1 = 0.

Sei tg x = 1, dann erhalten wir die Gleichung 3 t 2 + 2 t – 1 = 0.

Antwort:

№ 168 (A)

Antwort:

№ 174 (A)

Löse die Gleichung:

Antwort:

Lektion 2 (Unterricht-Vorlesung)

IV. Neues Material lernen(Fortsetzung)

– Lassen Sie uns also weiterhin Möglichkeiten zur Lösung trigonometrischer Gleichungen untersuchen.

5 Wege. Lösung homogener trigonometrischer Gleichungen

Gleichungen der Form a sin x + b cos x = 0, wobei a und b einige Zahlen sind, heißen homogene Gleichungen ersten Grades bezüglich sin x oder cos x.

Betrachten Sie die Gleichung

sin x – cos x = 0. Teilen wir beide Seiten der Gleichung durch cos x. Dies ist möglich; ein Wurzelverlust wird nicht auftreten, weil , Wenn cos x = 0, Das Sünde x = 0. Dies widerspricht jedoch der grundlegenden trigonometrischen Identität Sünde 2 x+cos 2 x = 1.

Wir bekommen tan x – 1 = 0.

tan x = 1,

Gleichungen der Form wie in 2 x + bcos 2 x + c sin x cos x = 0 , Wo a, b, c – Manche Zahlen heißen homogene Gleichungen zweiten Grades bezüglich sin x oder cos x.

Betrachten Sie die Gleichung

sin 2 x – 3 sin x cos x + 2 cos 2 = 0. Teilen wir beide Seiten der Gleichung durch cos x, und die Wurzel geht nicht verloren, weil cos x = 0 ist nicht die Wurzel dieser Gleichung.

tg 2 x – 3tg x + 2 = 0.

Sei tg x = t. D = 9 – 8 = 1.

Dann ist also tg x = 2 oder tg x = 1.

Als Ergebnis ist x = arctan 2 + , x =

Antwort: arctg 2 + ,

Betrachten Sie eine andere Gleichung: 3 sin 2 x – 3 sin x cos x + 4 cos 2 x = 2.
Lassen Sie uns die rechte Seite der Gleichung in die Form 2 = 2 · 1 = 2 · (sin 2 x + cos 2 x) umwandeln. Dann erhalten wir:
3sin 2 x – 3sin x cos x + 4cos 2 x = 2 (sin 2 x + cos 2 x),
3sin 2 x – 3sin x cos x + 4cos 2 x – 2sin 2 x – 2 cos 2 x = 0,
sin 2 x – 3sin x cos x + 2cos 2 x = 0. (Wir haben die 2. Gleichung erhalten, die wir bereits analysiert haben).

Antwort: arctan 2 + k,

6 Wege. Lösen linearer trigonometrischer Gleichungen

Eine lineare trigonometrische Gleichung ist eine Gleichung der Form a sin x + b cos x = c, wobei a, b, c einige Zahlen sind.

Betrachten Sie die Gleichung sin x + cos x= – 1.
Schreiben wir die Gleichung wie folgt um: