Sujet: Formules trigonométriques (25 heures)
Leçon 6 – 7 : La relation entre le sinus, le cosinus et la tangente du même angle.
Cible:étudier la relation entre le sinus, le cosinus et la tangente du même angle. Pour atteindre cet objectif, il faut :
- Savoir:
- formulations de définitions de fonctions trigonométriques de base (sinus, cosinus et tangente) ; signes de fonctions trigonométriques par quartiers ; ensemble de valeurs de fonctions trigonométriques ; formules de base de la trigonométrie.
- Comprendre:
- que l'identité trigonométrique de base ne peut être utilisée que pour le même argument ; algorithme pour calculer une fonction trigonométrique à travers une autre.
- Appliquer:
- capacité à choisir correctement la formule requise pour résoudre une tâche spécifique ; capacité à travailler avec fractions simples; capacité à effectuer des transformations d'expressions trigonométriques.
- Analyse:
- analyser les erreurs dans la logique du raisonnement.
- Synthèse:
- suggérez votre propre façon de résoudre des exemples ; créez des mots croisés en utilisant les connaissances que vous avez acquises.
- Grade:
- connaissances et compétences sur ce sujet pour une utilisation dans d'autres sections de l'algèbre.
- Actualisation des connaissances et des compétences.
- Dans quel quartier se trouve un angle de 1 radian et à quoi est-il approximativement égal ?
- Quel mot manque dans la définition de la fonction sinus ?
- Quel mot manque dans la définition de la fonction cosinus ?
- Quelles valeurs le sinus peut-il prendre ?
 ()
() - Explication du nouveau matériel.
 Représentons un cercle unité dont le centre est le point O. Supposons qu'en faisant tourner le rayon OA, égal à R, d'un angle , on obtient le rayon OB (Fig. 5). Alors par définition
Représentons un cercle unité dont le centre est le point O. Supposons qu'en faisant tourner le rayon OA, égal à R, d'un angle , on obtient le rayon OB (Fig. 5). Alors par définition  Où
Où  – abscisse du point B,
– abscisse du point B, 
 – son ordonnée. Il s'ensuit que le point B appartient au cercle. Par conséquent, ses coordonnées satisfont à l’équation
– son ordonnée. Il s'ensuit que le point B appartient au cercle. Par conséquent, ses coordonnées satisfont à l’équation 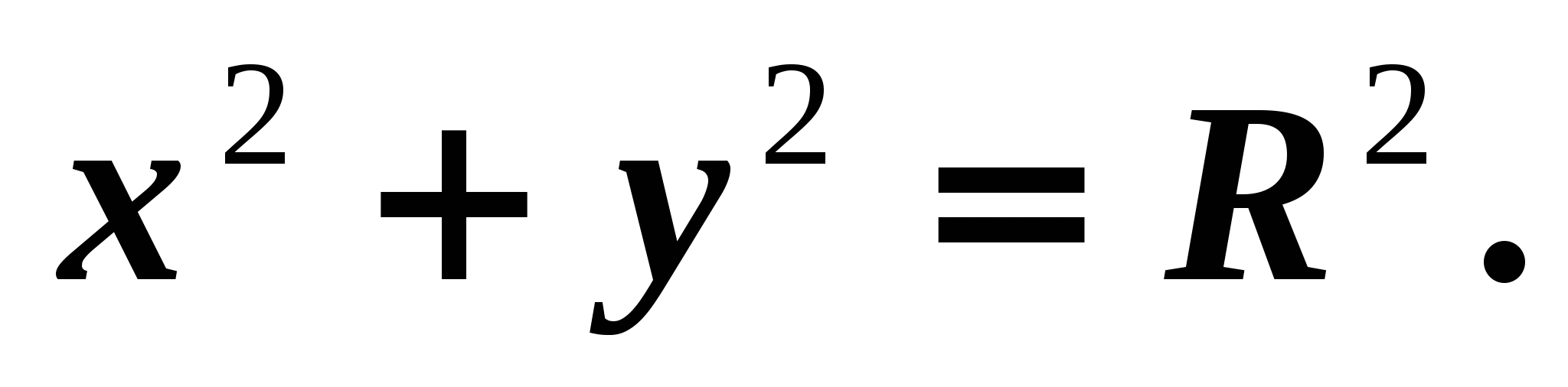 Profiter de ce que nous obtenons
Profiter de ce que nous obtenons  (1).
Nous avons obtenu une égalité valable pour toutes les valeurs des lettres qui y sont incluses. Comment appelle-t-on de telles égalités ? C'est vrai - les identités. L'égalité (1) s'appelle identité trigonométrique de base. Dans l'égalité (1) peut prendre n'importe quelle valeur. Complétez vous-même l'enregistrement :
(1).
Nous avons obtenu une égalité valable pour toutes les valeurs des lettres qui y sont incluses. Comment appelle-t-on de telles égalités ? C'est vrai - les identités. L'égalité (1) s'appelle identité trigonométrique de base. Dans l'égalité (1) peut prendre n'importe quelle valeur. Complétez vous-même l'enregistrement : 1.
Veuillez vérifier que votre saisie est correcte. Ajoutez des points à votre carte de cours pour Tâches n°2. Continuons. Nous avons dérivé l’identité trigonométrique principale, mais pourquoi en avons-nous besoin ? C'est vrai - pour trouver la valeur du cosinus à partir d'une valeur sinusoïdale connue et vice versa. Maintenant, vous et moi pouvons toujours utiliser l'identité trigonométrique de base, mais l'essentiel est le même argument. Dans le cahier, les élèves sont invités à exprimer de manière indépendante à partir du sujet principal identité trigonométrique sinus par cosinus et cosinus par sinus. Deux élèves sont appelés au tableau pour vérifier. On demande à l'un d'exprimer le sinus par le cosinus, au second - le cosinus par le sinus. La bonne réponse s'affiche à l'écran :
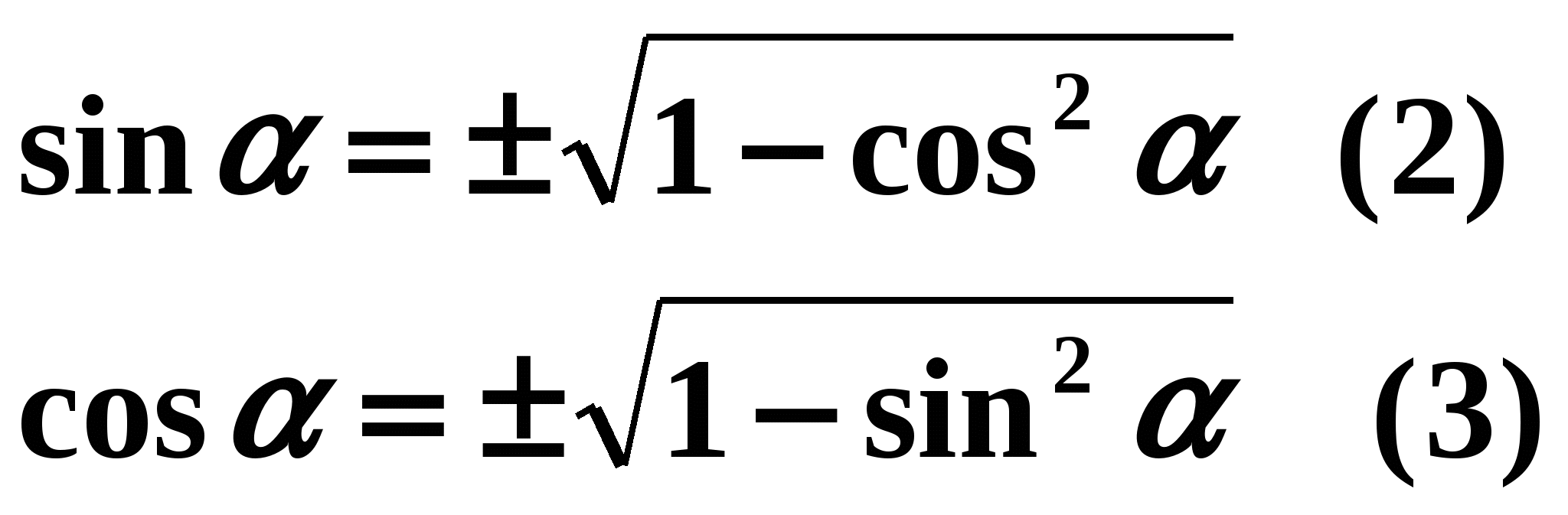 Les élèves vérifient leurs réponses et ajoutent des points à la fiche de cours pour Tâches n°3.
Dans ces formules, de quoi dépend le signe devant la racine ? (Cela dépend du quadrant dans lequel se trouve l'angle de la fonction trigonométrique que nous définissons).
Les élèves vérifient leurs réponses et ajoutent des points à la fiche de cours pour Tâches n°3.
Dans ces formules, de quoi dépend le signe devant la racine ? (Cela dépend du quadrant dans lequel se trouve l'angle de la fonction trigonométrique que nous définissons). Exemple 1 . Calculer
 Si
Si  Déterminer le quartier dans lequel se situe l'angle
Déterminer le quartier dans lequel se situe l'angle  . Trimestre – III. Rappelons que le sinus du troisième quart est négatif, c'est-à-dire dans la formule (2) il faut mettre le signe « - » devant la racine : Exemple 2.
Calculer
. Trimestre – III. Rappelons que le sinus du troisième quart est négatif, c'est-à-dire dans la formule (2) il faut mettre le signe « - » devant la racine : Exemple 2.
Calculer  Si
Si  On détermine le quartier dans lequel se situe l'angle . Trimestre – IV, le cosinus du quatrième trimestre est positif. Par conséquent, dans la formule (3), le signe « + » est nécessaire avant la racine :
On détermine le quartier dans lequel se situe l'angle . Trimestre – IV, le cosinus du quatrième trimestre est positif. Par conséquent, dans la formule (3), le signe « + » est nécessaire avant la racine : Découvrons-le maintenant relation entre tangente et cotangente. Par définition de tangente et cotangente

En multipliant ces égalités, on obtient :

A partir de l'égalité (4) on peut exprimer
 à travers
à travers  et inversement :
et inversement : 
Les égalités (4) – (6) sont vraies pour toutes les valeurs pour lesquelles
 avoir du sens, c'est-à-dire quand
avoir du sens, c'est-à-dire quand 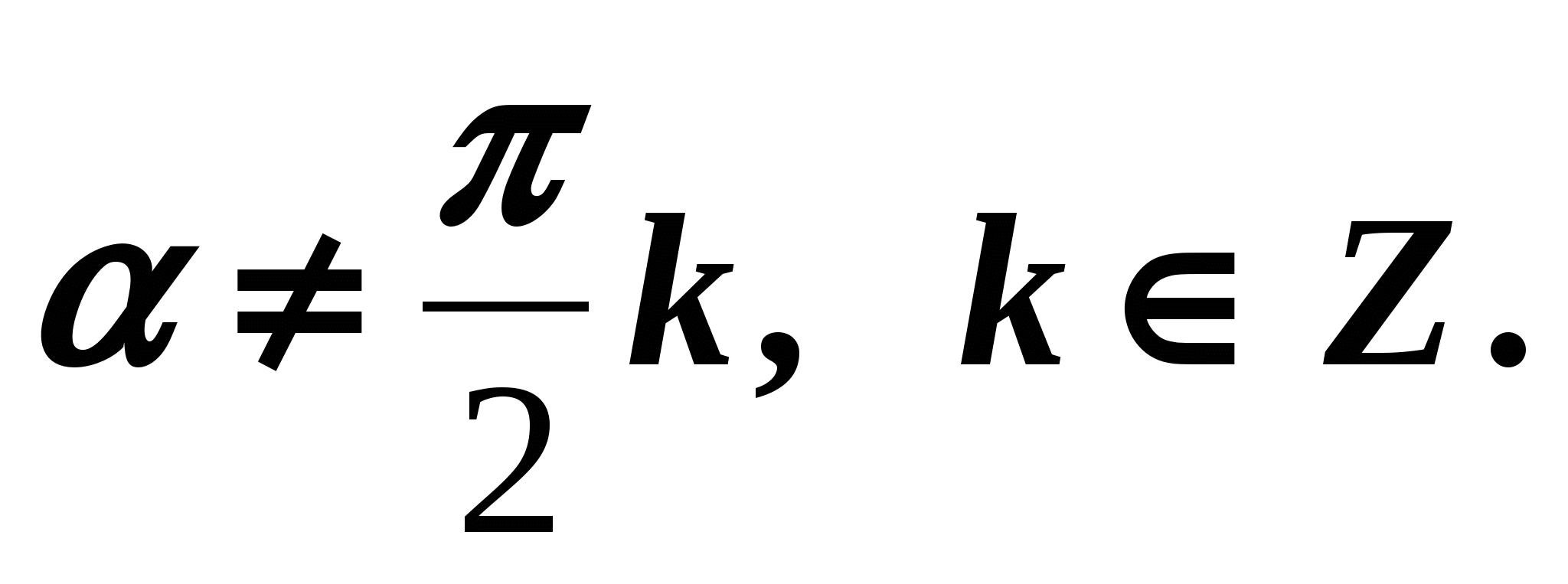 Dérivons maintenant des formules exprimant la relation entre la tangente et le cosinus, ainsi que la cotangente et le sinus du même argument. Diviser les deux côtés de l'égalité (1) par
Dérivons maintenant des formules exprimant la relation entre la tangente et le cosinus, ainsi que la cotangente et le sinus du même argument. Diviser les deux côtés de l'égalité (1) par 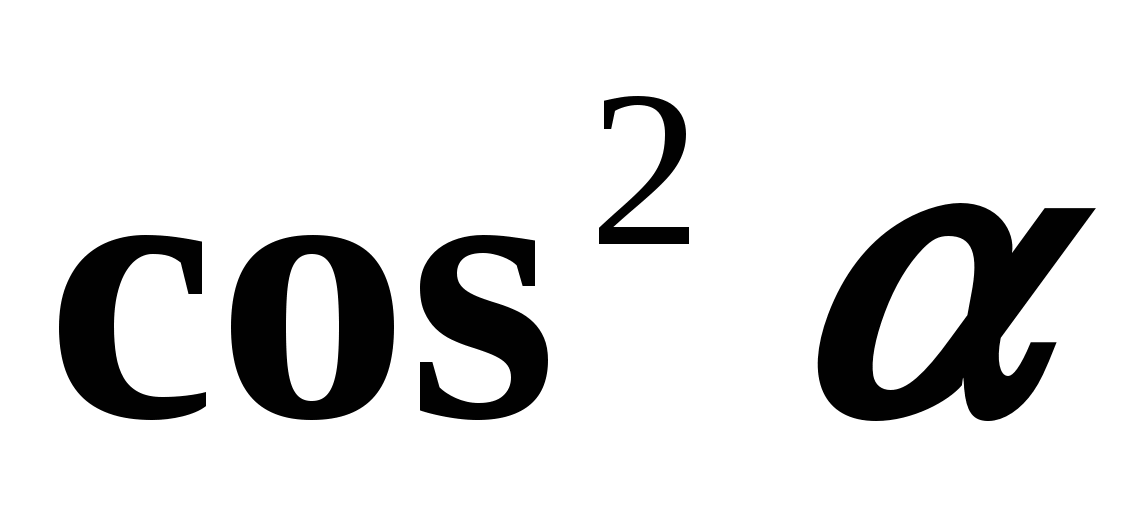 , on obtient :
, on obtient :  ceux.
ceux. 
Si les deux côtés de l’égalité (1) sont divisés par
 , alors nous aurons :
, alors nous aurons :  ceux.
ceux. 
Regardons des exemples d'utilisation des formules dérivées pour trouver les valeurs des fonctions trigonométriques selon valeur connue l'un d'eux.
Exemple 1. Voyons si l'on sait que
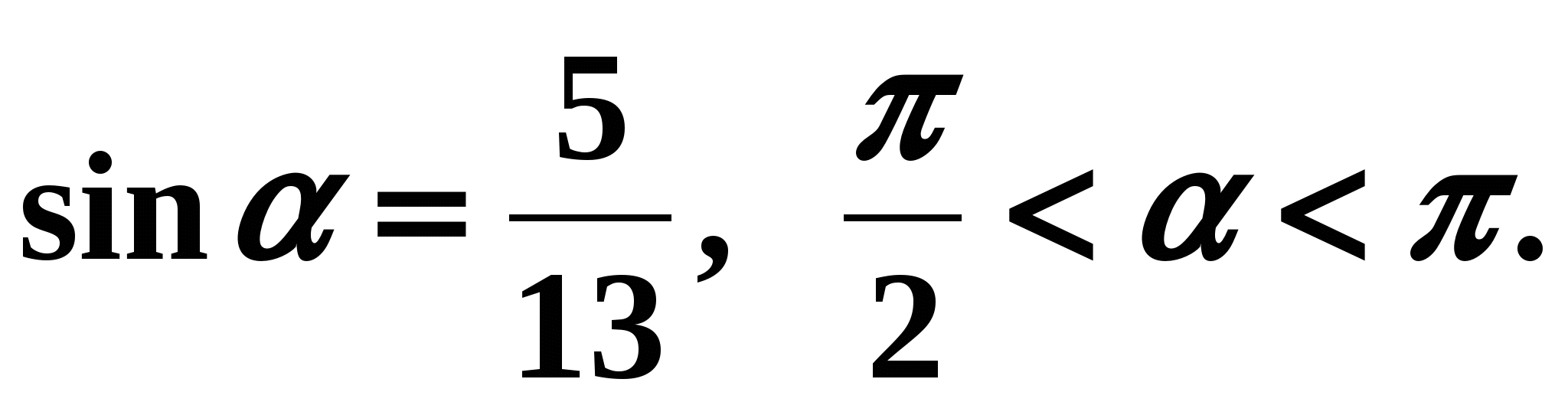 Solution:
Solution: 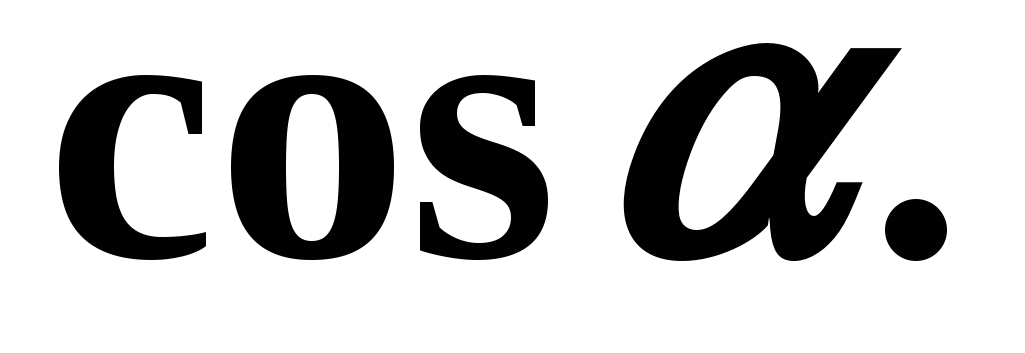
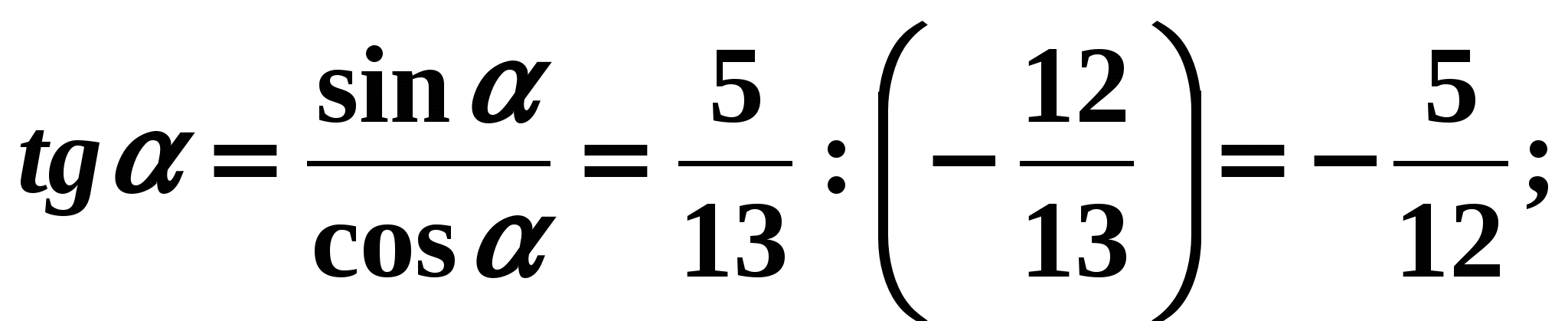
- Pour trouver la cotangente de l'angle , il convient d'utiliser la formule (6) :
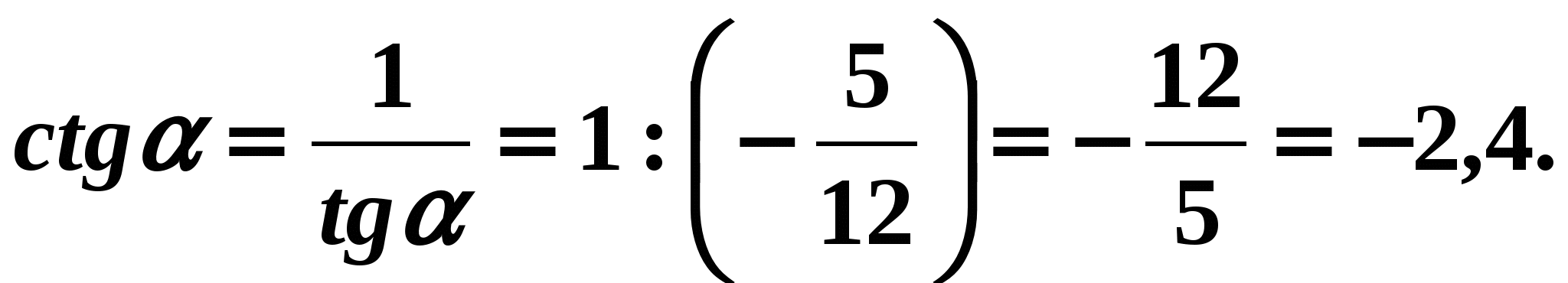 Répondre:
Répondre: Exemple 2. On sait que
 . Retrouvons toutes les autres fonctions trigonométriques. Solution:
. Retrouvons toutes les autres fonctions trigonométriques. Solution: - Utilisons la formule (7).
Nous avons:
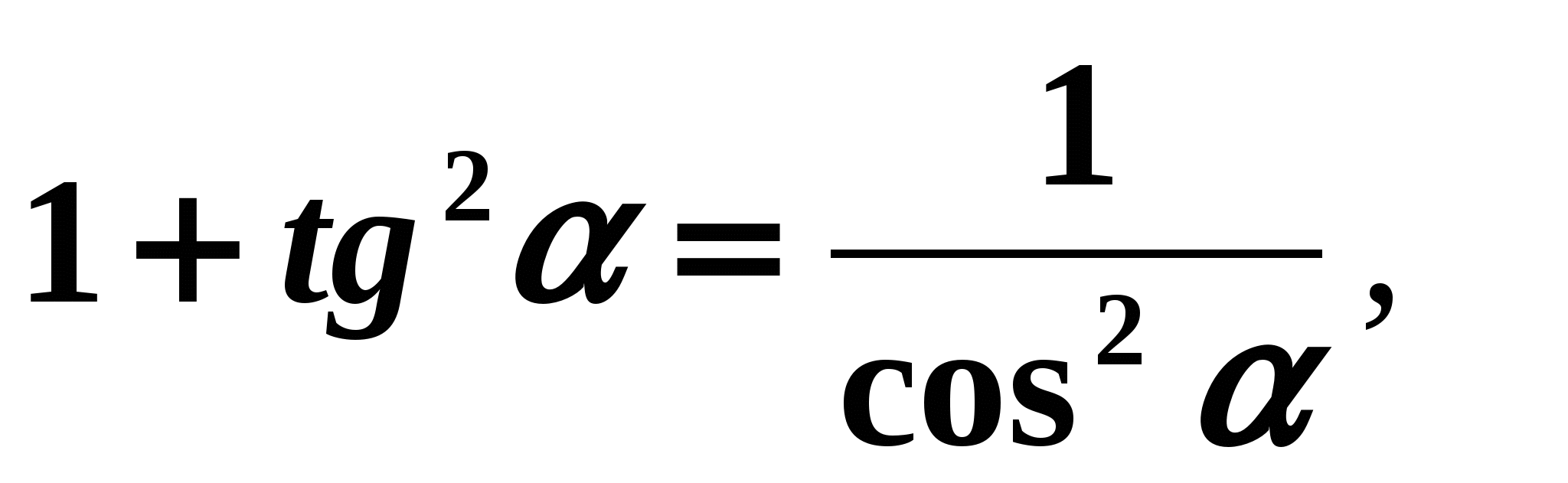
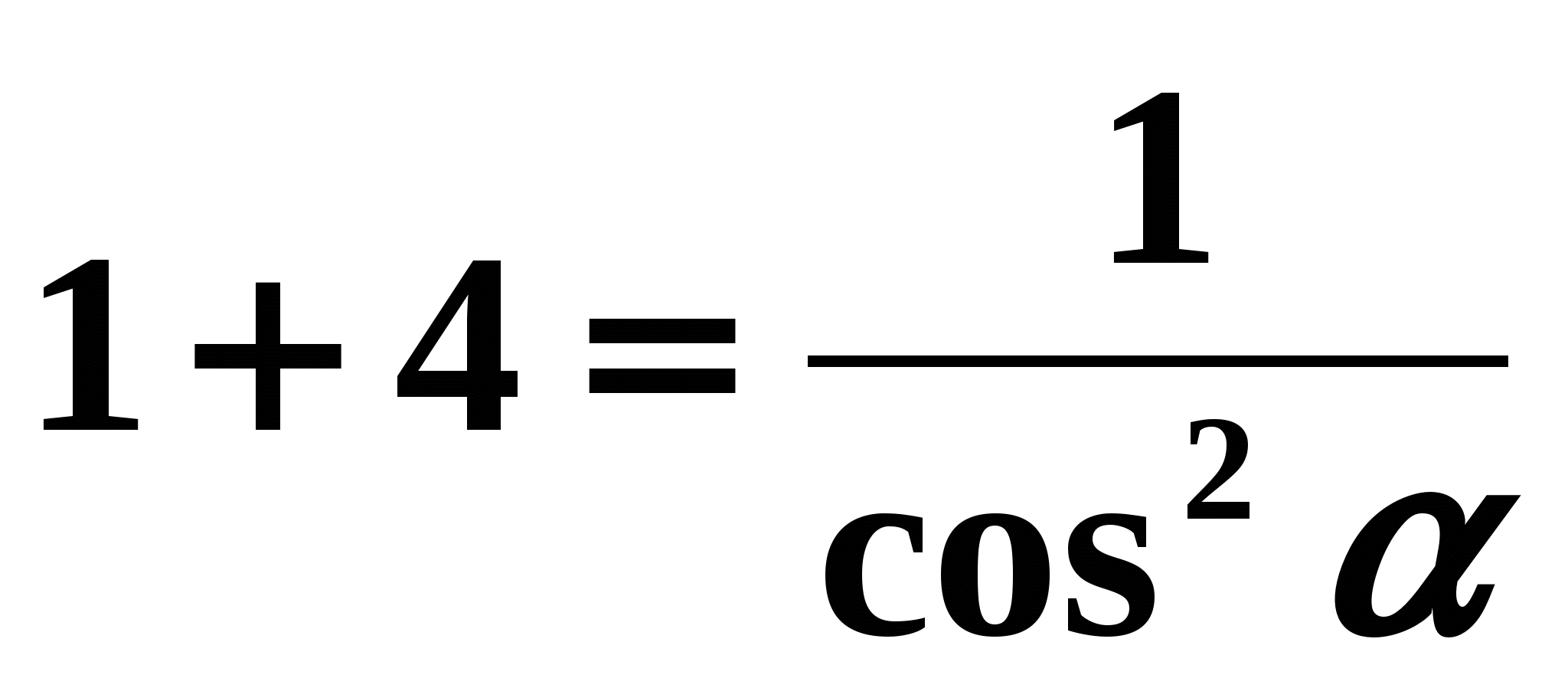 ,
,  . Selon les conditions du problème, l'angle est l'angle de 1 quart, donc son cosinus est positif. Moyens
. Selon les conditions du problème, l'angle est l'angle de 1 quart, donc son cosinus est positif. Moyens 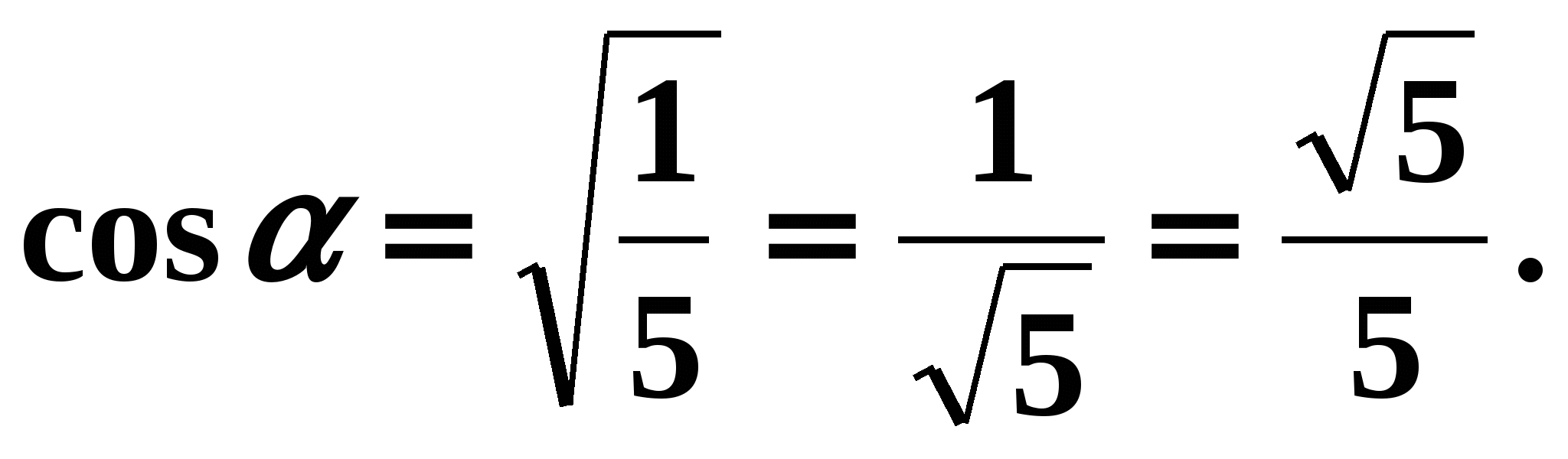

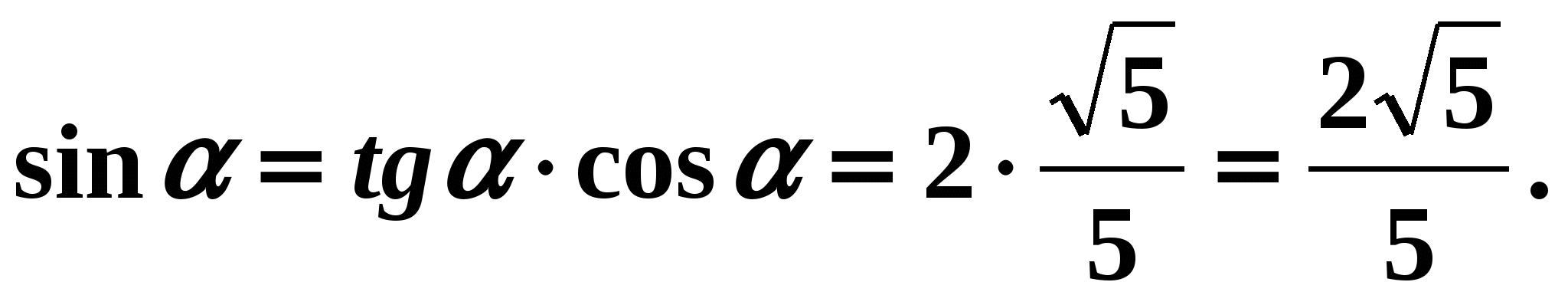
Répondre:
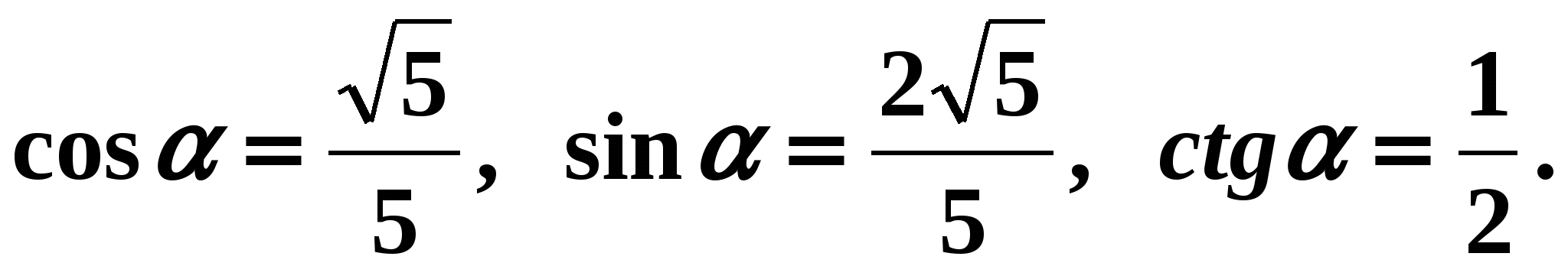 Relations établies entre fonctions trigonométriques du même argument permettent de simplifier les expressions trigonométriques.
Relations établies entre fonctions trigonométriques du même argument permettent de simplifier les expressions trigonométriques. Exemple 3. Simplifions l'expression :
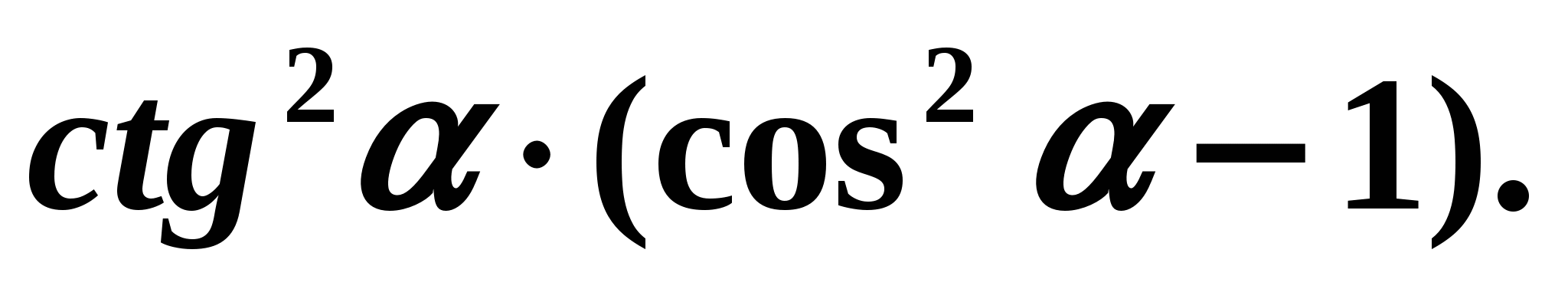 Solution: Utilisons les formules :
Solution: Utilisons les formules :  . On obtient :
. On obtient : - Consolidation.
Et maintenant, l'écran présente des rubriques d'auto-évaluation sur ce sujet. Marquez le niveau que vous aimeriez atteindre aujourd’hui.
J'ai compris le sujet et je peux résoudre des exemples en utilisant l'algorithme, en regardant le cahier, mais à l'aide de questions suggestives (carte - instructions).
J'ai compris le sujet et je peux résoudre des exemples en utilisant l'algorithme, en regardant le cahier, en utilisant les instructions du professeur.
J'ai compris le sujet et je peux résoudre des exemples en utilisant l'algorithme, en regardant le cahier, sans questions ni instructions suggestives.
J'ai compris le sujet et je peux résoudre des exemples en utilisant l'algorithme sans regarder le cahier.
Quel que soit le niveau que vous choisissez, relisez d'abord attentivement toutes les tâches que je vous ai confiées, puis complétez la tâche correspondant au niveau que vous avez choisi (il y a des tâches devant vous en quatre options, le numéro de l'option correspond aux niveaux de l'estime de soi.)
1 possibilité
 Instructions:
Instructions:
Option 4
Maintenant les gars, vérifions les réponses. Les réponses correctes sont affichées à l'écran et les élèves vérifient leur travail et ajoutent des points à la carte de cours pour Tâches n°4. Évaluez-vous à l’aide de la carte de cours. Calculez vos points et mettez-les sur la carte.
- Devoirs.
- Notez toutes les formules dérivées dans l'ouvrage de référence. D'après le manuel n° 459 (3, 5), n° 460 (1)
Dans cet article, nous allons jeter un regard complet. Les identités trigonométriques de base sont des égalités qui établissent une connexion entre le sinus, le cosinus, la tangente et la cotangente d'un angle, et permettent de trouver l'une de ces fonctions trigonométriques à travers un autre connu.
Listons immédiatement les principales identités trigonométriques que nous analyserons dans cet article. Écrivons-les dans un tableau, et ci-dessous nous donnerons le résultat de ces formules et fournirons les explications nécessaires.
Navigation dans les pages.
Relation entre le sinus et le cosinus d'un angle
Parfois, ils ne parlent pas des principales identités trigonométriques énumérées dans le tableau ci-dessus, mais d'une seule. identité trigonométrique de base gentil ![]() . L'explication de ce fait est assez simple : les égalités sont obtenues à partir de l'identité trigonométrique principale après avoir divisé ses deux parties par et respectivement, et les égalités
. L'explication de ce fait est assez simple : les égalités sont obtenues à partir de l'identité trigonométrique principale après avoir divisé ses deux parties par et respectivement, et les égalités  Et
Et ![]() découlent des définitions du sinus, du cosinus, de la tangente et de la cotangente. Nous en parlerons plus en détail dans les paragraphes suivants.
découlent des définitions du sinus, du cosinus, de la tangente et de la cotangente. Nous en parlerons plus en détail dans les paragraphes suivants.
C'est, intérêt particulier représente précisément l'égalité, à laquelle on a donné le nom d'identité trigonométrique principale.
Avant de prouver l'identité trigonométrique principale, donnons sa formulation : la somme des carrés du sinus et du cosinus d'un angle est identiquement égale à un. Maintenant, prouvons-le.
L'identité trigonométrique de base est très souvent utilisée lorsque conversion d'expressions trigonométriques. Il permet de remplacer la somme des carrés du sinus et du cosinus d'un angle par un. Non moins souvent, l'identité trigonométrique de base est utilisée dans ordre inverse: l'unité est remplacée par la somme des carrés du sinus et du cosinus de n'importe quel angle.
Tangente et cotangente par sinus et cosinus
Identités reliant la tangente et la cotangente au sinus et au cosinus d'un angle de vue et ![]() découlent immédiatement des définitions du sinus, du cosinus, de la tangente et de la cotangente. En effet, par définition, le sinus est l'ordonnée de y, le cosinus est l'abscisse de x, la tangente est le rapport de l'ordonnée à l'abscisse, soit
découlent immédiatement des définitions du sinus, du cosinus, de la tangente et de la cotangente. En effet, par définition, le sinus est l'ordonnée de y, le cosinus est l'abscisse de x, la tangente est le rapport de l'ordonnée à l'abscisse, soit ![]() , et la cotangente est le rapport de l'abscisse à l'ordonnée, c'est-à-dire
, et la cotangente est le rapport de l'abscisse à l'ordonnée, c'est-à-dire ![]() .
.
Grâce à une telle évidence des identités et ![]() La tangente et la cotangente sont souvent définies non pas par le rapport de l'abscisse et de l'ordonnée, mais par le rapport du sinus et du cosinus. Ainsi, la tangente d'un angle est le rapport du sinus au cosinus de cet angle, et la cotangente est le rapport du cosinus au sinus.
La tangente et la cotangente sont souvent définies non pas par le rapport de l'abscisse et de l'ordonnée, mais par le rapport du sinus et du cosinus. Ainsi, la tangente d'un angle est le rapport du sinus au cosinus de cet angle, et la cotangente est le rapport du cosinus au sinus.
En conclusion de ce paragraphe, il convient de noter que les identités et ![]() avoir lieu pour tous les angles sous lesquels les fonctions trigonométriques qu'ils contiennent ont un sens. Donc la formule est valable pour tout autre que (sinon le dénominateur aura zéro, et nous n'avons pas défini la division par zéro), et la formule
avoir lieu pour tous les angles sous lesquels les fonctions trigonométriques qu'ils contiennent ont un sens. Donc la formule est valable pour tout autre que (sinon le dénominateur aura zéro, et nous n'avons pas défini la division par zéro), et la formule ![]() - pour tout , différent de , où z est quelconque .
- pour tout , différent de , où z est quelconque .
Relation entre tangente et cotangente
Une identité trigonométrique encore plus évidente que les deux précédentes est l'identité reliant la tangente et la cotangente d'un angle de la forme ![]() . Il est clair que cela est valable pour tous les angles autres que , sinon la tangente ou la cotangente ne sont pas définies.
. Il est clair que cela est valable pour tous les angles autres que , sinon la tangente ou la cotangente ne sont pas définies.
Preuve de la formule ![]() très simple. Par définition et d'où
très simple. Par définition et d'où  . La preuve aurait pu être réalisée un peu différemment. Depuis
. La preuve aurait pu être réalisée un peu différemment. Depuis ![]() , Que
, Que  .
.
Ainsi, la tangente et la cotangente du même angle sous lequel elles ont un sens sont .
Leçon ouverte d'algèbre et principes d'analyse sur le thème : « La relation entre le sinus et le cosinus du même angle » (10e année)
Cible: perception des étudiants et prise de conscience initiale des nouveaux matériel pédagogique, comprendre les connexions et les relations dans les objets d'étude
Pédagogique : dérivation de formules pour la relation entre le sinus et le cosinus du même angle (nombre) ; apprendre à utiliser ces formules pour calculer les valeurs du sinus et du cosinus par valeur définie l'un d'eux.
Du développement : apprendre à analyser, comparer, construire des analogies, généraliser et systématiser, prouver et réfuter, définir et expliquer des concepts, développer et améliorer la capacité d'appliquer les connaissances existantes des élèves dans différentes situations; développer l'alphabétisation discours mathématiqueétudiants, la capacité de donner des formulations concises
Pédagogique: favoriser une attitude consciencieuse envers le travail et attitude positiveà la connaissance, pour cultiver chez les élèves l'exactitude, la capacité d'écouter et d'exprimer leurs opinions ; culture du comportement.
Économie de santé : créer un environnement confortable climat psychologique dans la classe, une ambiance de coopération : élève - enseignant.
Connaissances et compétences : définitions des fonctions trigonométriques de base (sinus, cosinus) ; signes de fonctions trigonométriques par quartiers ; ensembles de valeurs de fonctions trigonométriques ; formules de base trigonométrie.Ula capacité de choisir la bonne formule pour résoudre un problème spécifique ; travailler avec des fractions simples ; Convertissez des expressions trigonométriques.
Progression de la leçon
Point d'organisation :
Vérifiez l'état de préparation des élèves pour la leçon. Ouverture du site Internet de l’enseignant sur ordinateur (Annexe 1).
Travail oral sur le sujet abordé : « Signes du sinus, du cosinus et de la tangente »
Au tableau :
Exercice:
Organiser les numéros de trimestre plan de coordonnées et déterminer les signes du sinus, du cosinus, de la tangente et de la cotangente.
Travail indépendant sur le sujet : "Signes du sinus, du cosinus et de la tangente"
Les étudiants ouvrent la rubrique « Devoirs pour le cours de trigonométrie » sur le site Internet. Auto-test
(Les élèves réalisent la tâche n°1, vérifient leur travail et s'évaluent)
Explication du nouveau matériel
Au tableau :
x = … α , … ≤ cos α≤ … 2)* tan α = , α≠ …
oui= … α, … ≤ péché α≤ … CTG α = , α≠ …
Exercice: ajouter des formules
Professeur : « Vous et moi avons étudié chaque concept séparément. Selon vous, quel sujet est-il logique d’étudier ensuite ? »
( Réponse suggérée : "Dépendance entre ces concepts")
Le sujet de la leçon est formulé : "La relation entre le sinus et le cosinus d'un même angle"
Professeur : « Il existe plusieurs façons de résoudre ce problème »
Utilisation de l'équation du cercle unitéUtiliser le théorème de Pythagore
Professeur : « Regardons les deux et choisissons le plus rationnel »
Au tableau :


Les étudiants bénéficient de l’égalitéparce que 2 α + péché 2 α = 1
Professeur : «Nous avons obtenu une égalité juste pour toutes les valeurs des lettres qui y sont incluses. Comment appelle-t-on de telles égalités ?
( Réponse suggérée : identités)
Professeur : « Rappelez-vous comment s'appelle l'identitéparce que 2 α + péché 2 α = 1 »
Renforcer la matière apprise
A) Enseignant : "Ouvrez le manuel p. 147, n° 457 (2;4)" (les élèves appelés résolvent au tableau)
B) Professeur: « Procédez à la tâche n°2. Nous travaillons sur des options » (Discussion des résultats obtenus)
Au tableau :
Option 1 Option 2
Professeur: « Dans ces formules, les racines sont précédées des signes »±» . Qu’est-ce qui détermine le signe à mettre dans la formule ? »
(Réponse suggérée : "A partir de quel quart se situe l'angle de rotation du point P(1;0)"
B) Enseignant : « Passez à la tâche numéro 3. » (Les élèves résolvent des problèmes, vérifient au tableau)
Résumer la leçon
Professeur: "Bien joué! Nous résumerons la leçon à l’aide de mots croisés » (Tâche 4) (Les élèves travaillent en binôme devant l’ordinateur)
7) Réflexion sous forme de questionnaire (Annexe 2)
Professeur: "Résumez votre performance en classe en complétant le test."
8) Devoirs
§25, n° 456, 457(1;3),460(1;3).
Rapport
Essayons de trouver la relation entre les principales fonctions trigonométriques du même angle.
Relation entre cosinus et sinus du même angle
La figure suivante montre le système de coordonnées Oxy avec la partie du demi-cercle unité ACB représentée avec le centre au point O. Cette partie est l'arc du cercle unité. Le cercle unité est décrit par l'équation
- x 2 +y 2 =1.
Comme on le sait déjà, l'ordonnée y et l'abscisse x peuvent être représentées comme le sinus et le cosinus de l'angle à l'aide des formules suivantes :
- péché(une) = y,
- cos(une) = x.
En substituant ces valeurs dans les équations du cercle unité, nous avons l'égalité suivante
- (sin(a)) 2 + (cos(a)) 2 =1,
Cette égalité est vraie pour toute valeur de l'angle a. C'est ce qu'on appelle l'identité trigonométrique de base.
À partir de l’identité trigonométrique de base, une fonction peut être exprimée en fonction d’une autre.
- péché(une) = ±√(1-(cos(une)) 2),
- cos(une) = ±√(1-(sin(une)) 2).
Le signe à droite de cette formule est déterminé par le signe de l’expression à gauche de cette formule.
Par exemple.
Calculer sin(a) si cos(a)=-3/5 et pi Utilisons la formule donnée ci-dessus : Depuis pi Essayons maintenant de trouver la relation entre la tangente et les cotangentes. Par définition, tg(a) = sin(a)/cos(a), ctg(a) = cos(a)/sin(a). Multiplions ces égalités et obtenons tg(a)*ctg(a) =1. A partir de cette égalité, on peut exprimer une fonction à travers une autre. On obtient : Il faut comprendre que ces égalités ne sont valables que lorsque tg et ctg existent, c'est-à-dire pour tout a, sauf a = k*pi/2, pour tout entier k. Essayons maintenant, en utilisant l'identité trigonométrique de base, de trouver la relation entre la tangente et le cosinus. Divisons l'identité trigonométrique principale par (cos(a)) 2. (cos(a) n’est pas égal à zéro, sinon la tangente n’existerait pas. On obtient l’égalité suivante ((sin(a)) 2 + (cos(a)) 2)/ (cos(a)) 2 =1/(cos(a)) 2. En divisant terme par terme, on obtient : Comme indiqué ci-dessus, cette formule est correcte si cos(a) n'est pas égal à zéro, c'est-à-dire pour tous les angles a, sauf a=pi/2 +pi*k, pour tout entier k.Relation entre tangente et cotangente du même angle








