Antrosios žymiosios ribos formulė yra lim x → ∞ 1 + 1 x x = e. Kita rašymo forma atrodo taip: lim x → 0 (1 + x) 1 x = e.

Kai kalbame apie antrąją žymiąją ribą, turime susidurti su 1 ∞ formos neapibrėžtumu, t.y. vienybė iki begalinio laipsnio.

Yandex.RTB R-A-339285-1

Panagrinėkime problemas, kuriose bus naudinga galimybė apskaičiuoti antrąją nepaprastą ribą.

1 pavyzdys

Raskite ribą lim x → ∞ 1 - 2 x 2 + 1 x 2 + 1 4 .

Sprendimas

Pakeiskime reikiamą formulę ir atlikime skaičiavimus.

lim x → ∞ 1 - 2 x 2 + 1 x 2 + 1 4 = 1 - 2 ∞ 2 + 1 ∞ 2 + 1 4 = 1 - 0 ∞ = 1 ∞

Mūsų atsakymas pasirodė esąs vienas į begalybės galią. Norėdami nustatyti sprendimo metodą, naudojame neapibrėžtumo lentelę. Pasirinkime antrąją reikšmingą ribą ir pakeiskime kintamuosius.

t = - x 2 + 1 2 ⇔ x 2 + 1 4 = - t 2

Jei x → ∞, tai t → - ∞.

Pažiūrėkime, ką gavome po pakeitimo:

lim x → ∞ 1 - 2 x 2 + 1 x 2 + 1 4 = 1 ∞ = lim x → ∞ 1 + 1 t - 1 2 t = rib t → ∞ 1 + 1 t - 1 2 = e - 1 2

Atsakymas: lim x → ∞ 1 - 2 x 2 + 1 x 2 + 1 4 = e - 1 2 .

2 pavyzdys

Apskaičiuokite ribinę ribą x → ∞ x - 1 x + 1 x .

Sprendimas

Pakeiskime begalybę ir gaukime taip.

lim x → ∞ x - 1 x + 1 x = lim x → ∞ 1 - 1 x 1 + 1 x x = 1 - 0 1 + 0 ∞ = 1 ∞

Atsakyme vėl gavome tą patį, ką ir ankstesnėje užduotyje, todėl vėl galime pasinaudoti antrąja nuostabia riba. Tada turime pasirinkti visą maitinimo funkcijos pagrindą:

x - 1 x + 1 = x + 1 - 2 x + 1 = x + 1 x + 1 - 2 x + 1 = 1 - 2 x + 1

Po to limitas įgauna tokią formą:

lim x → ∞ x - 1 x + 1 x = 1 ∞ = lim x → ∞ 1 - 2 x + 1 x

Pakeiskite kintamuosius. Tarkime, kad t = - x + 1 2 ⇒ 2 t = - x - 1 ⇒ x = - 2 t - 1 ; jei x → ∞, tai t → ∞.

Po to užrašome, ką gavome pradiniame limite:

lim x → ∞ x - 1 x + 1 x = 1 ∞ = lim x → ∞ 1 - 2 x + 1 x = lim x → ∞ 1 + 1 t - 2 t - 1 = = lim x → ∞ 1 + 1 t - 2 t 1 + 1 t - 1 = lim x → ∞ 1 + 1 t - 2 t lim x → ∞ 1 + 1 t - 1 = = lim x → ∞ 1 + 1 t t - 2 1 + 1 ∞ = e - 2 · (1 + 0) - 1 = e - 2

Norėdami atlikti šią transformaciją, naudojome pagrindines ribų ir galių savybes.

Atsakymas: lim x → ∞ x - 1 x + 1 x = e - 2 .

3 pavyzdys

Apskaičiuokite ribinę ribą x → ∞ x 3 + 1 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 .

Sprendimas

lim x → ∞ x 3 + 1 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = lim x → ∞ 1 + 1 x 3 1 + 2 x - 1 x 3 3 2 x - 5 x 4 = = 1 + 0 1 + 0 - 0 3 0 - 0 = 1 ∞

Po to turime pakeisti funkciją, kad pritaikytume antrąją didžiąją ribą. Gavome šiuos dalykus:

lim x → ∞ x 3 + 1 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = 1 ∞ = lim x → ∞ x 3 - 2 x 2 - 1 - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = = lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5

lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = = lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5

Kadangi dabar trupmenos skaitiklyje ir vardiklyje turime tuos pačius rodiklius (lygus šešiems), trupmenos riba begalybėje bus lygi šių koeficientų santykiui esant didesnėms galioms.

lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = = lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 6 2 = rib x → ​​∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 3

Pakeitę t = x 2 + 2 x 2 - 1 - 2 x 2 + 2, gauname antrą nepaprastą ribą. Tai reiškia, kad:

lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 3 = lim x → ∞ 1 + 1 t t - 3 = e - 3

Atsakymas: lim x → ∞ x 3 + 1 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = e - 3 .

Išvados

Neapibrėžtis 1 ∞, t.y. vienybė begalinei galiai yra galios dėsnio neapibrėžtis, todėl ją galima atskleisti naudojant eksponentinių laipsnių funkcijų ribų nustatymo taisykles.

Jei tekste pastebėjote klaidą, pažymėkite ją ir paspauskite Ctrl+Enter

Iš aukščiau esančio straipsnio galite sužinoti, kokia yra riba ir su kuo ji valgoma – tai LABAI svarbu. Kodėl? Jūs galite nesuprasti, kas yra determinantai, ir sėkmingai juos išspręsti galite visiškai nesuprasti, kas yra išvestinė ir rasti juos su „A“. Bet jei nesupranti, kas yra riba, tada praktines užduotis išspręsti bus sunku. Taip pat būtų naudinga susipažinti su sprendimų pavyzdžiais ir mano dizaino rekomendacijomis. Visa informacija pateikiama paprasta ir prieinama forma.

O šios pamokos tikslams mums reikės šios mokomosios medžiagos: Nuostabios ribos Ir Trigonometrinės formulės. Juos galima rasti puslapyje. Vadovus geriausia atsispausdinti – taip daug patogiau, be to, dažnai teks jais remtis neprisijungus.

Kuo ypatingos ribos? Stebėtina tai, kad jas įrodė didžiausi žinomų matematikų protai, o dėkingi palikuonys neturi kentėti nuo baisių ribų su krūva trigonometrinių funkcijų, logaritmų, galių. Tai yra, ieškodami ribų, naudosime jau paruoštus rezultatus, kurie buvo įrodyti teoriškai.

Yra keletas nuostabių ribų, tačiau praktiškai 95% atvejų neakivaizdiniai studentai turi dvi nuostabias ribas: Pirma nuostabi riba, Antra nuostabi riba. Pažymėtina, kad tai istoriškai nusistovėję pavadinimai ir, pavyzdžiui, kalbant apie „pirmą nepaprastą ribą“, tai reiškia labai konkretų dalyką, o ne kokią nors atsitiktinę ribą, paimtą iš lubų.

Pirma nuostabi riba

Apsvarstykite šią ribą: (vietoj gimtosios raidės „jis“ naudosiu graikišką raidę „alfa“, tai patogesnė medžiagos pateikimo požiūriu).

Pagal mūsų ribų nustatymo taisyklę (žr Ribos. Sprendimų pavyzdžiai) bandome į funkciją pakeisti nulį: skaitiklyje gauname nulį (nulio sinusas lygus nuliui), o vardiklyje, aišku, irgi yra nulis. Taigi, susiduriame su formos neapibrėžtumu, kurio, laimei, nereikia atskleisti. Matematinės analizės metu įrodoma, kad:

Šis matematinis faktas vadinamas Pirma nuostabi riba. Aš nepateiksiu analitinio ribos įrodymo, bet pažvelgsime į jos geometrinę reikšmę pamokoje apie be galo mažos funkcijos.

Dažnai praktinėse užduotyse funkcijos gali būti išdėstytos skirtingai, tai nieko nekeičia:

- ta pati pirmoji nuostabi riba.

Bet jūs negalite patys pertvarkyti skaitiklio ir vardiklio! Jei riba nurodyta formoje , tai ji turi būti išspręsta ta pačia forma, nieko nepertvarkant.

Praktiškai kaip parametras gali veikti ne tik kintamasis, bet ir elementari arba kompleksinė funkcija. Vienintelis svarbus dalykas yra tai, kad jis linkęs į nulį.

Pavyzdžiai:
, , ,

Čia,,,, , ir viskas gerai – taikoma pirmoji nuostabi riba.

Tačiau šis įrašas yra erezija:

Kodėl? Kadangi daugianomas nelinkęs į nulį, jis linkęs į penkis.

Beje, greitas klausimas: kokia yra riba? ? Atsakymą rasite pamokos pabaigoje.

Praktiškai ne viskas taip sklandu, beveik niekada studentui nepasiūloma išspręsti nemokamą limitą ir gauti lengvą leidimą. Hmm... Rašau šias eilutes, ir į galvą atėjo labai svarbi mintis - juk geriau mintinai prisiminti „nemokamus“ matematinius apibrėžimus ir formules, tai gali suteikti neįkainojamos pagalbos teste, kai klausimas bus nusprendžiama tarp „du“ ir „trys“, o mokytojas nusprendžia užduoti mokiniui kokį nors paprastą klausimą arba pasiūlyti išspręsti paprastą pavyzdį („gal jis (-iai) dar žino ką?!“).

Pereikime prie praktinių pavyzdžių:

1 pavyzdys

Raskite ribą

Jei riboje pastebime sinusą, tai iš karto turėtų paskatinti mus pagalvoti apie galimybę pritaikyti pirmą reikšmingą ribą.

Pirmiausia bandome pakeisti 0 į išraišką po ribos ženklu (tai darome mintyse arba juodraštyje):

Taigi mes turime formos neapibrėžtumą būtinai nurodykite priimant sprendimą. Išraiška po ribos ženklu yra panaši į pirmąją nuostabią ribą, tačiau tai nėra tiksliai ji, ji yra po sinusu, o vardiklyje.

Tokiais atvejais pirmąjį reikšmingą ribą turime organizuoti patys, naudodami dirbtinę techniką. Motyvavimas galėtų būti toks: „po sinusu, kurį turime , o tai reiškia, kad mes taip pat turime patekti į vardiklį“.
Ir tai daroma labai paprastai:

Tai yra, vardiklis šiuo atveju dirbtinai padauginamas iš 7 ir dalinamas iš tų pačių septynių. Dabar mūsų įrašas įgavo pažįstamą formą.
Kai užduotis sudaroma ranka, patartina paprastu pieštuku pažymėti pirmąją žymią ribą:

Kas atsitiko? Tiesą sakant, mūsų apibrėžta išraiška virto vienetu ir išnyko kūrinyje:

Dabar belieka atsikratyti trijų aukštų frakcijos:

Kas pamiršo kelių lygių trupmenų supaprastinimą, atnaujinkite žinyno medžiagą Karštos formulės mokykliniam matematikos kursui .

Paruošta. Galutinis atsakymas:

Jei nenorite naudoti pieštuko ženklų, sprendimą galima parašyti taip:

“

Pasinaudokime pirmąja nuostabia riba

“

2 pavyzdys

Raskite ribą

Vėlgi riboje matome trupmeną ir sinusą. Pabandykime pakeisti nulį į skaitiklį ir vardiklį:

Iš tiesų, turime neapibrėžtumo, todėl turime pabandyti suorganizuoti pirmąją nuostabią ribą. Klasėje Ribos. Sprendimų pavyzdžiai laikėme taisyklę, kad kai turime neapibrėžtumo, skaitiklį ir vardiklį turime koeficientuoti. Čia yra tas pats dalykas, laipsnius pateiksime kaip produktą (daugiklius):

Panašiai kaip ir ankstesniame pavyzdyje, pieštuku nubrėžiame nuostabias ribas (čia yra dvi iš jų) ir nurodome, kad jos linkusios susivienyti:

Tiesą sakant, atsakymas yra paruoštas:

Tolesniuose pavyzdžiuose aš nedarysiu meno „Paint“, manau, kaip teisingai sudaryti sprendimą užrašų knygelėje - jūs jau suprantate.

3 pavyzdys

Raskite ribą

Išraiškoje po ribos ženklu pakeičiame nulį:

Gautas neapibrėžtumas, kurį reikia atskleisti. Jei riboje yra liestinė, ji beveik visada paverčiama sinusu ir kosinusu, naudojant gerai žinomą trigonometrinę formulę (beje, jie daro maždaug tą patį su kotangentu, žr. metodinę medžiagą Karštos trigonometrinės formulės puslapyje Matematinės formulės, lentelės ir pamatinė medžiaga).

Šiuo atveju:

Nulio kosinusas lygus vienetui, ir jo lengva atsikratyti (nepamirškite pažymėti, kad jis linkęs į vienetą):

Taigi, jei riboje kosinusas yra daugiklis, tai, grubiai tariant, jį reikia paversti vienetu, kuris sandaugoje išnyksta.

Čia viskas pasirodė paprasčiau, be daugybos ir dalybos. Pirmoji žymi riba taip pat virsta viena ir dingsta gaminyje:

Dėl to gaunama begalybė, ir tai atsitinka.

4 pavyzdys

Raskite ribą

Pabandykime pakeisti nulį į skaitiklį ir vardiklį:

Gaunamas neapibrėžtis (nulio kosinusas, kaip prisimename, yra lygus vienetui)

Mes naudojame trigonometrinę formulę. Atkreipkite dėmesį! Dėl tam tikrų priežasčių apribojimai naudojant šią formulę yra labai dažni.

Perkelkime pastovius veiksnius už ribos piktogramos:

Suorganizuokime pirmąjį nuostabų limitą:

Čia turime tik vieną nepaprastą ribą, kuri virsta viena ir dingsta gaminyje:

Atsikratykime trijų aukštų struktūros:

Riba iš tikrųjų išspręsta, nurodome, kad likęs sinusas linkęs į nulį:

5 pavyzdys

Raskite ribą

Šis pavyzdys yra sudėtingesnis, pabandykite tai išsiaiškinti patys:

Kai kurias ribas galima sumažinti iki 1-osios reikšmingos ribos pakeitus kintamąjį, apie tai galite perskaityti šiek tiek vėliau straipsnyje Ribų sprendimo būdai.

Antra nuostabi riba

Matematinės analizės teorijoje buvo įrodyta, kad:

Šis faktas vadinamas antra nuostabi riba.

Nuoroda: yra neracionalus skaičius.

Parametras gali būti ne tik kintamasis, bet ir sudėtinga funkcija. Svarbu tik tai, kad ji siekia begalybės.

6 pavyzdys

Raskite ribą

Kai išraiška po ribos ženklu yra laipsniu, tai yra pirmasis ženklas, kad reikia pabandyti pritaikyti antrą nuostabią ribą.

Bet pirmiausia, kaip visada, bandome į išraišką pakeisti be galo didelį skaičių, principas, kuriuo tai daroma, yra aptariamas pamokoje Ribos. Sprendimų pavyzdžiai.

Nesunku pastebėti, kad kai laipsnio pagrindas yra , o eksponentas yra , tai yra, yra formos neapibrėžtumas:

Šis neapibrėžtumas tiksliai atskleidžiamas antrosios nepaprastos ribos pagalba. Tačiau, kaip dažnai nutinka, antroji nuostabi riba slypi ne ant sidabrinio padėklo, o ją reikia dirbtinai organizuoti. Galite samprotauti taip: šiame pavyzdyje parametras yra , tai reiškia, kad mes taip pat turime organizuoti indikatorių. Norėdami tai padaryti, pakeliame bazę į galią, o kad išraiška nepasikeistų, pakeliame ją į galią:

Kai užduotis atliekama ranka, pažymime pieštuku:

Beveik viskas paruošta, baisus laipsnis virto gražiu laišku:

Tokiu atveju pačią ribos piktogramą perkeliame į indikatorių:

7 pavyzdys

Raskite ribą

Dėmesio! Tokio tipo apribojimai pasitaiko labai dažnai, labai atidžiai išstudijuokite šį pavyzdį.

Pabandykime pakeisti be galo didelį skaičių į išraišką po ribos ženklu:

Rezultatas – netikrumas. Tačiau antroji nepaprasta riba taikoma formos neapibrėžtumui. Ką daryti? Turime konvertuoti laipsnio bazę. Mes samprotaujame taip: vardiklyje turime , o tai reiškia, kad skaitiklyje taip pat turime organizuoti .

Šis internetinis matematikos skaičiuotuvas padės jums, jei to prireiks apskaičiuokite funkcijos ribą. Programa sprendimo ribos ne tik duoda atsakymą į problemą, bet ir veda išsamus sprendimas su paaiškinimais, t.y. rodomas limito skaičiavimo procesas.

Ši programa gali praversti bendrojo lavinimo mokyklų gimnazistams ruošiantis įskaitoms ir egzaminams, pasitikrinti žinias prieš Vieningą valstybinį egzaminą, o tėvams kontroliuoti daugelio matematikos ir algebros uždavinių sprendimą.

O gal jums per brangu samdyti dėstytoją ar pirkti naujus vadovėlius? O gal tiesiog norite kuo greičiau atlikti matematikos ar algebros namų darbus? Tokiu atveju taip pat galite naudoti mūsų programas su išsamiais sprendimais.

Apskaičiuokite limitą
Buvo nustatyta, kad kai kurie scenarijai, reikalingi šiai problemai išspręsti, nebuvo įkelti ir programa gali neveikti.
Galbūt esate įjungę „AdBlock“.

Nes Yra daug žmonių, norinčių išspręsti problemą, jūsų prašymas buvo įrašytas į eilę.
Po kelių sekundžių apačioje pasirodys sprendimas.
Palaukite sek...

Jeigu jūs sprendime pastebėjo klaidą, tuomet apie tai galite parašyti atsiliepimų formoje.
Nepamiršk nurodykite, kokia užduotis tu spręsk ką įveskite laukelius.

Mūsų žaidimai, galvosūkiai, emuliatoriai:

Šiek tiek teorijos.

Funkcijos riba x->x 0

Tegul funkcija f(x) yra apibrėžta tam tikroje aibėje X ir tegul taškas \(x_0 \in X\) arba \(x_0 \notin X\)

Paimkime iš X taškų seką, kuri skiriasi nuo x 0:
x 1 , x 2 , x 3 , ..., x n , ... (1)
suartėja su x*. Funkcijų reikšmės šios sekos taškuose taip pat sudaro skaitinę seką
f(x 1), f(x 2), f(x 3), ..., f(x n), ... (2)
ir galima kelti jos ribos egzistavimo klausimą.

Apibrėžimas. Skaičius A vadinamas funkcijos f(x) riba taške x = x 0 (arba x -> x 0), jei bet kuriai argumento x reikšmių sekai (1) skiriasi nuo x 0 konverguojant į x 0, atitinkama reikšmių seka (2) konverguoja į skaičių A.

$$ \lim_(x\to x_0)( f(x)) = A $$

Funkcija f(x) taške x 0 gali turėti tik vieną ribą. Tai išplaukia iš to, kad seka
(f(x n)) turi tik vieną ribą.

Yra ir kitas funkcijos ribos apibrėžimas.

Apibrėžimas Skaičius A vadinamas funkcijos f(x) riba taške x = x 0, jei bet kuriam skaičiui \(\varepsilon > 0\) yra skaičius \(\delta > 0\), kad visiems \ (x \in X, \; x \neq x_0 \), tenkinant nelygybę \(|x-x_0| Naudojant loginius simbolius, šis apibrėžimas gali būti parašytas kaip
\((\forall \varepsilon > 0) (\exists \delta > 0) (\forall x \in X, \; x \neq x_0, \; |x-x_0| Atkreipkite dėmesį, kad nelygybės \(x \neq x_0) , \; x-x_0 | \(\varepsilon - \delta \)“.
Šie du funkcijos ribos apibrėžimai yra lygiaverčiai ir galite naudoti bet kurį iš jų, priklausomai nuo to, kuris iš jų yra patogesnis sprendžiant konkrečią problemą.

Atkreipkite dėmesį, kad funkcijos ribos apibrėžimas „sekų kalba“ dar vadinamas funkcijos ribos apibrėžimu pagal Heine, o funkcijos ribos apibrėžimas „kalba \(\varepsilon - \delta \)“ dar vadinamas funkcijos ribos apibrėžimu pagal Koši.

Funkcijos riba x->x 0 - ir x->x 0 +

Toliau naudosime vienpusių funkcijos ribų sąvokas, kurios apibrėžiamos taip.

Apibrėžimas Skaičius A vadinamas dešiniąja (kairiąja) funkcijos f(x) riba taške x 0, jei bet kuriai sekai (1), konverguojančiai į x 0, kurios elementai x n yra didesni (mažesni už) x 0, atitinkama seka. (2) sutampa su A.

Simboliškai parašyta taip:
$$ \lim_(x \to x_0+) f(x) = A \; \left(\lim_(x \to x_0-) f(x) = A \right) $$

Galime pateikti lygiavertį funkcijos vienpusių ribų apibrėžimą „kalba \(\varepsilon - \delta \)“:

Apibrėžimas skaičius A vadinamas dešiniąja (kairiąja) funkcijos f(x) riba taške x 0, jei bet kuriam \(\varepsilon > 0\) yra \(\delta > 0\) taip, kad visus x atitinka nelygybės \(x_0 simboliniai įrašai:

Šioje temoje analizuosime tas formules, kurias galima gauti naudojant antrą nuostabią ribą (yra tema, skirta tiesiai antrajai nuostabiai ribai). Leiskite jums priminti dvi formuluotes antrosios žymios ribos, kurios bus reikalingos šiame skyriuje: $\lim_(x\to\infty)\left(1+\frac(1)(x)\right)^x=e $ ir $\lim_(x \to\ 0)\left(1+x\right)^\frac(1)(x)=e$.

Paprastai formules pateikiu be įrodymų, bet šiam puslapiui, manau, padarysiu išimtį. Esmė ta, kad antrosios nepaprastos ribos pasekmių įrodyme yra keletas metodų, kurie yra naudingi tiesiogiai sprendžiant problemas. Na, paprastai tariant, patartina žinoti, kaip ta ar kita formulė įrodoma. Tai leidžia geriau suprasti jo vidinę struktūrą, taip pat taikymo ribas. Bet kadangi įrodymai gali būti ne visiems skaitytojams įdomūs, paslėpsiu juos po užrašais, esančiais po kiekvienos pasekmės.

Išvada #1

1 pasekmės įrodymas: rodyti\slėpti

Kadangi nuo $x\iki 0$ turime $\ln(1+x)\iki 0$, tai nagrinėjamoje riboje yra $\frac(0)(0)$ formos neapibrėžtis. Norėdami atskleisti šį neapibrėžtumą, pateiksime išraišką $\frac(\ln(1+x))(x)$ tokia forma: $\frac(1)(x)\cdot\ln(1+x)$ . Dabar įvertinkime $\frac(1)(x)$ į išraiškos $(1+x)$ laipsnį ir pritaikykime antrąją nepaprastą ribą:

$$ \lim_(x\to\ 0) \frac(\ln(1+x))(x)=\left| \frac(0)(0) \right|= \lim_(x\to\ 0) \left(\frac(1)(x)\cdot\ln(1+x)\right)=\lim_(x\ to\ 0)\ln(1+x)^(\frac(1)(x))=\ln e=1. $$

Dar kartą turime formos $\frac(0)(0)$ neapibrėžtį. Pasikliausime formule, kurią jau įrodėme. Kadangi $\log_a t=\frac(\ln t)(\ln a)$, tada $\log_a (1+x)=\frac(\ln(1+x))(\ln a)$.

$$ \lim_(x\to\ 0) \frac(\log_a (1+x))(x)=\left| \frac(0)(0) \right|=\lim_(x\to\ 0)\frac(\ln(1+x))( x \ln a)=\frac(1)(\ln a)\ lim_(x\to\ 0)\frac(\ln(1+x))( x)=\frac(1)(\ln a)\cdot 1=\frac(1)(\ln a). $$

Išvada #2

Išvados Nr. 2 įrodymas: rodyti\slėpti

Kadangi nuo $x\iki 0$ turime $e^x-1\iki 0$, tai nagrinėjamoje riboje yra $\frac(0)(0)$ formos neapibrėžtis. Norėdami atskleisti šį neapibrėžtumą, pakeisime kintamąjį, žymintį $t=e^x-1$. Nuo $x\iki 0$, tada nuo $t\iki 0$. Toliau iš formulės $t=e^x-1$ gauname: $e^x=1+t$, $x=\ln(1+t)$.

$$ \lim_(x\to\ 0) \frac(e^x-1)(x)=\left| \frac(0)(0) \right|=\left | \begin(sulygiuotas) & t=e^x-1;\; t\iki 0.\\ & x=\ln(1+t).\pabaiga (sulygiuota) \right|= \lim_(t\iki 0)\frac(t)(\ln(1+t))= \lim_(t\to 0)\frac(1)(\frac(\ln(1+t))(t))=\frac(1)(1)=1. $$

Dar kartą turime formos $\frac(0)(0)$ neapibrėžtį. Pasikliausime formule, kurią jau įrodėme. Kadangi $a^x=e^(x\ln a)$, tada:

$$ \lim_(x\to\ 0) \frac(a^(x)-1)(x)=\left| \frac(0)(0) \right|=\lim_(x\to 0)\frac(e^(x\ln a)-1)(x)=\ln a\cdot \lim_(x\iki 0 )\frac(e^(x\ln a)-1)(x \ln a)=\ln a \cdot 1=\ln a. $$

Išvada #3

Išvados Nr. 3 įrodymas: rodyti\slėpti

Dar kartą susiduriame su formos $\frac(0)(0)$ neapibrėžtumu. Kadangi $(1+x)^\alpha=e^(\alpha\ln(1+x))$, gauname:

$$ \lim_(x\to\ 0) \frac((1+x)^\alpha-1)(x)= \left| \frac(0)(0) \right|= \lim_(x\to\ 0)\frac(e^(\alpha\ln(1+x))-1)(x)= \lim_(x\to \ 0)\left(\frac(e^(\alpha\ln(1+x))-1)(\alpha\ln(1+x))\cdot \frac(\alpha\ln(1+x) )(x) \right)=\\ =\alpha\lim_(x\to\ 0) \frac(e^(\alpha\ln(1+x))-1)(\alpha\ln(1+x) ))\cdot \lim_(x\to\ 0)\frac(\ln(1+x))(x)=\alpha\cdot 1\cdot 1=\alpha. $$

1 pavyzdys

Apskaičiuokite ribą $\lim_(x\to\ 0) \frac(e^(9x)-1)(\sin 5x)$.

Turime formos $\frac(0)(0)$ neapibrėžtį. Norėdami atskleisti šį neapibrėžtumą, naudosime formulę. Kad atitiktume šios formulės ribą, turėtume turėti omenyje, kad $e$ galios ir vardiklio išraiškos turi sutapti. Kitaip tariant, vardiklyje nėra vietos sinusui. Vardiklis turi būti $9x$. Be to, šio pavyzdžio sprendime bus naudojama pirmoji žymi riba.

$$ \lim_(x\to\ 0) \frac(e^(9x)-1)(\sin 5x)=\left|\frac(0)(0) \right|=\lim_(x\to\ 0) \left(\frac(e^(9x)-1)(9x)\cdot\frac(9x)(\sin 5x) \right) =\frac(9)(5)\cdot\lim_(x\ į\ 0) \left(\frac(e^(9x)-1)(9x)\cdot\frac(1)(\frac(\sin 5x)(5x)) \right)=\frac(9)( 5)\cdot 1 \cdot 1=\frac(9)(5). $$

Atsakymas: $\lim_(x\to\0) \frac(e^(9x)-1)(\sin 5x)=\frac(9)(5)$.

2 pavyzdys

Apskaičiuokite ribą $\lim_(x\to\ 0) \frac(\ln\cos x)(x^2)$.

Turime formos $\frac(0)(0)$ neapibrėžtį (priminsiu, kad $\ln\cos 0=\ln 1=0$). Norėdami atskleisti šį neapibrėžtumą, naudosime formulę. Pirmiausia atsižvelkime į tai, kad $\cos x=1-2\sin^2 \frac(x)(2)$ (žr. spaudinį apie trigonometrines funkcijas). Dabar $\ln\cos x=\ln\left(1-2\sin^2 \frac(x)(2)\right)$, taigi vardiklyje turėtume gauti išraišką $-2\sin^2 \ frac(x)(2)$ (kad mūsų pavyzdys atitiktų formulę). Tolesniame sprendime bus naudojama pirmoji žymi riba.

$$ \lim_(x\to\ 0) \frac(\ln\cos x)(x^2)=\left| \frac(0)(0) \right|=\lim_(x\to\ 0) \frac(\ln\left(1-2\sin^2 \frac(x)(2)\right))(x ^2)= \lim_(x\to\ 0) \left(\frac(\ln\left(1-2\sin^2 \frac(x)(2)\right))(-2\sin^2 \frac(x)(2))\cdot\frac(-2\sin^2 \frac(x)(2))(x^2) \right)=\\ =-\frac(1)(2) \lim_(x\to\ 0) \left(\frac(\ln\left(1-2\sin^2 \frac(x)(2)\right))(-2\sin^2 \frac(x) )(2))\cdot\left(\frac(\sin\frac(x)(2))(\frac(x)(2))\right)^2 \right)=-\frac(1)( 2)\cdot 1\cdot 1^2=-\frac(1)(2). $$

Atsakymas: $\lim_(x\to\ 0) \frac(\ln\cos x)(x^2)=-\frac(1)(2)$.

Yra keletas puikių ribų, tačiau žinomiausios yra pirmoji ir antroji reikšmingos ribos. Nuostabus dalykas, susijęs su šiais apribojimais, yra tai, kad jie yra plačiai naudojami ir su jų pagalba galite rasti kitų daugybės problemų ribų. Tai mes darysime praktinėje šios pamokos dalyje. Norint išspręsti problemas sumažinant jas iki pirmosios ar antrosios nepaprastos ribos, nereikia atskleisti jose esančių neapibrėžtumo, nes šių ribų reikšmes jau seniai nustatė didieji matematikai.

Pirma įspūdinga riba vadinama begalinio mažo lanko sinuso ir to paties lanko santykio riba, išreikšta radianais:

Pereikime prie problemų sprendimo ties pirmąja nuostabia riba. Pastaba: jei po ribos ženklu yra trigonometrinė funkcija, tai yra beveik tikras ženklas, kad šią išraišką galima sumažinti iki pirmosios reikšmingos ribos.

1 pavyzdys. Raskite ribą.

Sprendimas. Vietoj to pakeitimas x nulis sukelia neapibrėžtumą:

.

Vardiklis yra sinusas, todėl išraiška gali būti perkelta iki pirmosios reikšmingos ribos. Pradėkime transformaciją:

.

Vardiklis yra trijų X sinusas, bet skaitiklis turi tik vieną X, o tai reiškia, kad skaitiklyje reikia gauti tris X. Už ką? Norėdami pristatyti 3 x = a ir gaukite išraišką.

Ir mes prieiname prie pirmosios nepaprastos ribos varianto:

nes nesvarbu, kuri raidė (kintamasis) šioje formulėje yra vietoj X.

X padauginame iš trijų ir iš karto padaliname:

.

Atsižvelgdami į pirmą pastebėtą ribą, pakeičiame trupmeninę išraišką:

Dabar pagaliau galime išspręsti šią ribą:

.

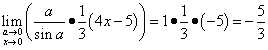2 pavyzdys. Raskite ribą.

Sprendimas. Tiesioginis pakeitimas vėl sukelia „nulis padalintas iš nulio“ neapibrėžtumą:

.

Norint gauti pirmąją reikšmingą ribą, būtina, kad x po sinuso ženklu skaitiklyje ir tik x vardiklyje turėtų tą patį koeficientą. Tegul šis koeficientas yra lygus 2. Norėdami tai padaryti, įsivaizduokite dabartinį x koeficientą, kaip nurodyta toliau, atlikdami operacijas su trupmenomis, gauname:

.

3 pavyzdys. Raskite ribą.

Sprendimas. Keisdami vėl gauname neapibrėžtį „nulis padalytas iš nulio“:

.

Tikriausiai jau supratote, kad iš pirminės išraiškos galite gauti pirmąją nuostabią ribą, padaugintą iš pirmosios nuostabios ribos. Norėdami tai padaryti, išskaidome x kvadratus skaitiklyje ir sinuso vardiklyje į identiškus koeficientus, o norėdami gauti tuos pačius x ir sinuso koeficientus, skaitiklio x padalijame iš 3 ir iš karto padauginame iki 3. Gauname:

.

4 pavyzdys. Raskite ribą.

Sprendimas. Dar kartą gauname neapibrėžtumą „nulis padalintas iš nulio“:

.

Galime gauti pirmųjų dviejų puikių ribų santykį. Tiek skaitiklį, tiek vardiklį padalijame iš x. Tada, kad sinusų ir xų koeficientai sutaptų, viršutinį x padauginame iš 2 ir iškart padalijame iš 2, o apatinį x padauginame iš 3 ir iš karto padaliname iš 3. Gauname:

5 pavyzdys. Raskite ribą.

Sprendimas. Ir vėl neapibrėžtumas „nulis padalintas iš nulio“:

Iš trigonometrijos prisimename, kad liestinė yra sinuso ir kosinuso santykis, o nulio kosinusas lygus vienetui. Atliekame transformacijas ir gauname:

.

6 pavyzdys. Raskite ribą.

Sprendimas. Trigonometrinė funkcija, esanti po ribos ženklu, vėl siūlo naudoti pirmąją reikšmingą ribą. Mes jį pavaizduojame kaip sinuso ir kosinuso santykį.