Функциональ цувралуудын дунд хамгийн чухал байрыг цахилгаан цуваа эзэлдэг.

Хүчтэй цуврал нь цуврал юм

Нөхцөлүүд нь сөрөг бус бүхэл тоог нэмэгдүүлэх замаар зохион байгуулагдсан чадлын функцууд юм x, А в0 , в 1 , в 2 , в n - тогтмол утгууд. Тоонууд в1 , в 2 , в n - цувааны нөхцлийн коэффициент; в0 - чөлөөт гишүүн. Эрчим хүчний цувааны нөхцлүүд нь бүх тооны шугам дээр тодорхойлогддог.

Ингээд ойлголттой танилцацгаая хүчний цувааны ойртох талбарууд. Энэ нь хувьсагчийн утгуудын багц юм x, үүний төлөө цуврал нийлдэг. Эрчим хүчний цувралууд нь нэлээн энгийн нэгдэх мужтай байдаг. Бодит хувьсагчийн утгуудын хувьд xнийлэх муж нь нэг цэгээс бүрдэх, эсвэл тодорхой интервал (нэгдэх интервал) эсвэл бүх тэнхлэгтэй давхцдаг Үхэр .

Утгыг чадлын цувралд орлуулах үед x= 0 нь тооны цуваа үүснэ

в0 +0+0+...+0+... ,

нийлдэг.

Тиймээс, хэзээ x= 0 аливаа чадлын цуваа нийлдэг тул түүний нэгдэх талбар хоосон багц байж болохгүй. Бүх чадлын цувааг нэгтгэх бүсийн бүтэц ижил байна. Үүнийг дараах теоремыг ашиглан тогтоож болно.

Теорем 1 (Абелийн теорем). Хэрэв чадлын цуваа ямар нэг утгаар нийлбэл x = x 0 , тэгээс ялгаатай, дараа нь энэ нь нийлдэг, үүнээс гадна, бүх утгын хувьд туйлын хувьд |x| < |x 0 | . Анхаарна уу: "X нь тэг" гэсэн эхлэлийн утга ба эхлэлийн утгатай харьцуулсан "X" утгыг хоёуланг нь модулиар авна - тэмдгийг харгалзахгүйгээр.

Үр дагавар. Хэрэв хүчний цуваа зөрүүтэй байна ямар нэг үнэ цэнээр x = x 1 , дараа нь бүх утгуудын хувьд ялгаатай байна |x| > |x 1 | .

Өмнө нь олж мэдсэнээр аливаа цахилгаан цуваа нь утгаараа нийлдэг x= 0. Зөвхөн үед нийлдэг хүчний цуваа байдаг x= 0 ба бусад утгуудын хувьд ялгаатай X. Энэ тохиолдлыг авч үзэхээс хассанаар бид чадлын цуваа ямар нэг утгаар нийлдэг гэж таамаглаж байна x = x 0 , тэгээс ялгаатай. Дараа нь Абелийн теоремын дагуу ]-| интервалын бүх цэгүүдэд нийлдэг x0 |, |x 0 |[ (зүүн ба баруун хил хязгаар нь хасах тэмдэг ба нэмэх тэмдгээр авсан хүчин чадлын цуваа нийлэх x утгууд болох интервал), гарал үүслийн хувьд тэгш хэмтэй.

Хэрэв чадлын цуваа нь тодорхой утгаараа зөрүүтэй байвал x = x 1 , дараа нь Абелийн теоремын үр дүнд үндэслэн энэ нь хэрчмээс гадуурх бүх цэгүүдэд хуваагдана [-| x1 |, |x 1 |] . Үүнээс үзэхэд аливаа чадлын цувааны хувьд гарал үүсэлтэй холбоотой тэгш хэмтэй интервал гэж нэрлэгддэг нийлэх интервал , цуваа нийлдэг цэг бүрд, хил хязгаарт нь нийлж, эсвэл салж болох ба энэ нь заавал нэгэн зэрэг байх албагүй, сегментээс гадуур цуваа нь хуваагддаг. Тоо Рхүчийг цуваа нийлэх радиус гэнэ.

Онцгой тохиолдолд чадлын цувааны нэгдэх интервал цэг хүртэл доройтож болно (дараа нь цуваа зөвхөн нийлдэг x= 0 бөгөөд энэ нь гэж тооцогддог Р= 0) эсвэл бүхэл тооны шулууныг төлөөлнө (дараа нь тоон шулууны бүх цэгүүдэд цуваа нийлдэг бөгөөд ).

Тиймээс, чадлын цувааны нийлэх мужийг тодорхойлох нь түүнийг тодорхойлоход оршино нэгдэх радиус Рба нийлэх интервалын зааг дахь цувааны нийлэлтийг судлах ( at ).

Теорем 2.Хэрэв тодорхой нэгээс эхлэн чадлын цувралын бүх коэффициентүүд тэгээс ялгаатай бол түүний нэгдэх радиус нь цувралын нийтлэг гишүүдийн коэффициентүүдийн үнэмлэхүй утгуудын харьцааны хязгаартай тэнцүү байна. , өөрөөр хэлбэл

Жишээ 1. Хүчний цувааны нийлэх мужийг ол

Шийдэл. Энд

(28) томъёог ашиглан бид энэ цувралын нэгдэх радиусыг олно.

Нэгдэх интервалын төгсгөлд цувааны нийлэлтийг судалъя. Жишээ 13-аас харахад энэ цуврал нь нийлдэг x= 1 ба зөрүүтэй байна x= -1. Иймээс нэгдэх бүс нь хагас интервал юм.

Жишээ 2. Хүчний цувааны нийлэх мужийг ол

Шийдэл. Цувралын коэффициентүүд эерэг, ба

Энэ харьцааны хязгаарыг олъё, өөрөөр хэлбэл. Хүчний цувааны ойртох радиус:

Интервалын төгсгөлд цувааны нийлэлтийг судалцгаая. Үнэт зүйлсийг орлуулах x= -1/5 ба xЭнэ эгнээний = 1/5 нь:

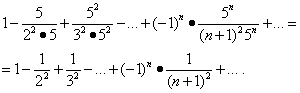
Эдгээр цувралын эхнийх нь нийлдэг (Жишээ 5-ыг үз). Харин дараа нь “Үнэмлэхүй нийлэх” хэсгийн теоремын дагуу хоёр дахь цуваа бас нийлж, түүний нийлэх муж нь хэрчм болно.

Жишээ 3. Хүчний цувааны нийлэх мужийг ол

Шийдэл. Энд

(28) томъёог ашиглан бид цувралын нэгдэх радиусыг олно.

-ийн утгуудын цувааны нийлэлтийг судалцгаая. Эдгээрийг энэ цувралд орлуулж, бид тус тусад нь авна

Нэгтгэх шаардлагатай нөхцөл хангагдаагүй тул хоёр цуваа зөрүүтэй байдаг (тэдгээрийн нийтлэг нэр томъёо нь -д тэг байх хандлагатай байдаггүй). Тэгэхээр нийлбэрийн интервалын хоёр төгсгөлд энэ цуваа нь салж, нийлэх муж нь интервал болно.

Жишээ 5. Хүчний цувааны нийлэх мужийг ол

Шийдэл. Бид хаана, ба гэсэн хамаарлыг олдог :

Томъёоны дагуу (28) энэ цувралын нэгдэх радиус

тэр үед л цуваа нийлдэг x= 0 ба бусад утгуудын хувьд ялгаатай X.

Жишээ нь нийлэх интервалын төгсгөлд цуваа өөр өөрөөр ажилладаг болохыг харуулж байна. 1-р жишээнд нийлэх интервалын нэг төгсгөлд цуваа нийлж, нөгөө талд 2-р жишээнд хоёр төгсгөлд нийлдэг;

Тодорхой цэгээс эхлэн цуваа гишүүний бүх коэффициентүүд тэгээс өөр байна гэсэн таамаглалаар чадлын цувааны нийлэх радиусын томъёог олж авна. Тиймээс (28) томъёог зөвхөн эдгээр тохиолдолд ашиглахыг зөвшөөрнө. Хэрэв энэ нөхцөл зөрчигдсөн бол хүч чадлын цуваа нийлэх радиусыг ашиглан хайх хэрэгтэй. д'Аламберын тэмдэг, эсвэл хувьсагчийг орлуулах замаар цувааг заасан нөхцөл хангагдсан хэлбэрт шилжүүлнэ.

Жишээ 6. Хүчний цувааны нийлэх интервалыг ол

Шийдэл. Энэ цувралд сондгой зэрэгтэй нэр томъёо агуулаагүй болно X. Тиймээс бид цувралыг хувиргаж, тохиргоо . Дараа нь бид цувралыг авна

нийлэх радиусыг олохын тулд (28) томъёог хэрэглэж болно. , a , дараа нь энэ цувааны нийлэх радиус

Бидний олж авсан тэгш байдлаас харахад энэ цуваа интервал дээр нийлдэг.

Хүч чадлын цувааны нийлбэр. Эрчим хүчний цувааг ялгах, нэгтгэх

Эрчим хүчний цувралд орцгооё

нэгдэх радиус Р> 0, өөрөөр хэлбэл. энэ цуваа интервал дээр нийлдэг.

Дараа нь утга бүр Xнийлэх интервалаас цувааны тодорхой нийлбэртэй тохирч байна. Тиймээс чадлын цувааны нийлбэр нь функц юм Xнийлэх интервал дээр. Үүнийг тэмдэглэж байна е(x), бид тэгш байдлыг бичиж болно

цэг бүр дэх цувааны нийлбэр гэсэн утгаар ойлгох Xнийлэх интервалаас функцийн утгатай тэнцүү байна е(x) энэ үед. Үүнтэй ижил утгаараа бид чадлын цуваа (29) функцэд нийлдэг гэж хэлэх болно е(x) нэгдэх интервал дээр.

Нэгдэх интервалаас гадуур тэгш байдал (30) утгагүй болно.

Жишээ 7.Эрчим хүчний цувааны нийлбэрийг ол

Шийдэл. Энэ бол геометрийн цуврал юм а= 1, a q= x. Тиймээс түүний нийлбэр нь функц юм . Цуврал нийлдэг бол , ба түүний нийлэх интервал юм. Тиймээс тэгш байдал

функц хэдий ч зөвхөн утгуудад хүчинтэй бүх утгын хувьд тодорхойлогдсон X, бусад X= 1.

Хүчний цувааны нийлбэр гэдгийг баталж болно е(x) нь нийлэх интервалын аль ч интервалд, ялангуяа цувааны нийлэх интервалын аль ч цэгт тасралтгүй ба дифференциал болно.

Хүчний цувааг гишүүнээр ялгах ба интегралчлалын тухай теоремуудыг танилцуулъя.

Теорем 1.Хүчний цуваа (30) нь нийлэх интервал дахь гишүүнчлэлээр хязгааргүй олон удаа ялгагдах боломжтой ба үр дүнд бий болсон хүчнүүдийн цуваа нь анхны цуваатай ижил нийлэх радиустай бөгөөд тэдгээрийн нийлбэр нь тус тус тэнцүү байна.

Теорем 2.Эрчим хүчний цувралыг (30) 0-ээс хязгааргүй олон удаа нэр томъёогоор нэгтгэж болно. X, хэрэв , ба үр дүнгийн зэрэглэлийн цуваа нь анхны цуваатай ижил нийлэх радиустай ба тэдгээрийн нийлбэрүүд нь харгалзах тэнцүү байна.

Функцуудыг чадлын цуврал болгон өргөжүүлэх

Функцийг өгье е(x), эрчим хүчний цуврал болгон өргөжүүлэх шаардлагатай, i.e. (30) хэлбэрээр илэрхийлнэ:

Даалгавар бол коэффициентийг тодорхойлох явдал юм эгнээ (30). Үүнийг хийхийн тулд тэгш байдлын (30) нэр томъёог нэр томъёогоор нь ялгаж үзвэл бид дараахь зүйлийг байнга олж авдаг.

……………………………………………….. (31)

(30) ба (31) тэнцүү гэж үзвэл X= 0, бид олдог

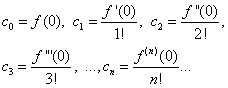
Олдсон илэрхийллийг тэгш байдал (30) болгон орлуулснаар бид олж авна

(32)

Зарим энгийн функцүүдийн Маклаурин цувралын өргөтгөлийг олцгооё.

Жишээ 8.Маклаурин цуврал дахь функцийг өргөжүүлэх

Шийдэл. Энэ функцийн деривативууд нь функцтэй давхцдаг:

Тиймээс, хэзээ X= 0 бидэнд байна

Эдгээр утгыг томъёогоор (32) орлуулснаар бид хүссэн өргөтгөлийг олж авна.

(33)

Энэ цуваа нь бүхэл тооны шулуун дээр нийлдэг (түүний нэгдэх радиус).

Жишээ 1.Хүчний цувааны нийлэх мужийг ол:

A); б) ;

V) ; G)
;

г)
.

A)Нэгдэх радиусыг олъё Р. Учир нь
,
, Тэр

x
, өөрөөр хэлбэл, цуваа нийлэх интервал
.

At
Бид тооны цуврал авдаг . Энэ цуврал нь ерөнхий гармоник цуврал учраас нийлдэг цагт
.

At
Бид тооны цуврал авдаг
. Цуврал нь түүний нөхцлийн үнэмлэхүй утгуудаас бүрддэг тул энэ цуврал нь туйлын нийлдэг , нэгдэх.

б)Нэгдэх радиусыг олъё Р. Учир нь
, Тэр
.

Тиймээс цувралын нийлэх интервал
.

Бид нийлэх интервалын төгсгөлд энэ цувралын нийлэлтийг шалгадаг.

At
Бидэнд тооны цуврал бий

.

At
Бидэнд тооны цуврал бий
. Энэ цуврал нь ялгаатай учраас
байхгүй.

Тэгэхээр энэ цувралын нэгдэх бүс нутаг
.

V)Нэгдэх радиусыг олъё Р. Учир нь
,
Тэр
.

Тиймээс, нийлэх интервал
. Энэ цувралын нийлэх муж нь нийлэх интервалтай давхцаж, өөрөөр хэлбэл хувьсагчийн дурын утгын хувьд цуваа нийлдэг. x.

G)Нэгдэх радиусыг олъё Р. Учир нь
,
Тэр
.

Учир нь
, дараа нь цуваа зөвхөн цэг дээр нийлдэг
. Энэ нь энэ цувралын нэгдэх бүс нэг цэг гэсэн үг юм
.

г)Нэгдэх радиусыг олъё Р.

Учир нь
,
, Тэр

Тиймээс, цуврал нь хүн бүрт нийцдэг x, тэгш бус байдлыг хангаж байна
, тэр нь
.

Эндээс
− нэгдэх интервал,
− нэгдэх радиус.

Энэ цувааг нийлэх интервалын төгсгөлд нэгтгэх эсэхийг шалгацгаая.

At
Бид тооны цуврал авдаг

ялгарах (гармоник цуврал).

At
Бид тооны цуврал авдаг
, энэ нь болзолт нийлдэг (цуврал нь Лейбницийн шалгуурын дагуу нийлдэг бөгөөд түүний гишүүдийн үнэмлэхүй утгуудаас бүрдэх цуврал нь гармоник учраас ялгаатай байдаг).

Тиймээс, цувралын нэгдэх бүс
.

2.3. Тейлор ба Маклаурин цуврал.

Функцуудыг чадлын цуврал болгон өргөжүүлэх.

Хүч чадлын цувааг ойролцоо тооцоонд ашиглах

Асуудлыг шийдвэрлэх жишээ

Жишээ 1.Функцийг чадлын цуврал болгон өргөжүүлнэ үү:

A)
; б)
;

V)
; G)
.

A)Томъёонд орлуулах
xдээр
, бид хүссэн өргөтгөлийг олж авна:

Хаана

б)Тэгш тэгш байдалд орлуулах

Хаана
xдээр
, бид хүссэн өргөтгөлийг олж авна:

V)Энэ функцийг дараах байдлаар бичиж болно.
. Хүссэн цувралаа олохын тулд өргөжүүлэхэд хангалттай

Хаана
орлуулах
. Дараа нь бид авна:

G)Энэ функцийг дараах байдлаар дахин бичиж болно: .

Чиг үүрэг
хоёр нэрийн цуваа оруулснаар хүчирхэг цуваа болгон өргөжүүлж болно
, бид хүлээн авах болно.

Хаана
.

Хүссэн тэлэлтийг олж авахын тулд үүссэн цувралыг үржүүлэхэд хангалттай (эдгээр цувралын үнэмлэхүй нийлбэрийн улмаас).

Тиймээс,

, Хаана
.

Жишээ 2.Эдгээр функцүүдийн ойролцоо утгыг ол:

A)
0.0001 нарийвчлалтай;

б)
0.00001 нарийвчлалтай.

A)Учир нь
, дараа нь функцийн өргөтгөл рүү, хаана
орлуулъя
:

эсвэл

Учир нь
, дараа нь бид зөвхөн үүссэн өргөтгөлийн эхний хоёр нөхцлөөр хязгаарлагдах юм бол шаардлагатай нарийвчлалыг хангах болно.

Бид бином цувралыг ашигладаг

Хаана
.

Итгэж байна
Тэгээд
, бид дараах өргөтгөлийг олж авна:

Хэрэв сүүлийн ээлжийн цувралд зөвхөн эхний хоёр гишүүнийг тооцож, үлдсэнийг нь хассан бол тооцооны алдаа
үнэмлэхүй утгаараа 0.000006-аас хэтрэхгүй. Дараа нь тооцооллын алдаа
тооноос хэтрэхгүй. Тиймээс,

Жишээ 3. 0.001-ийн нарийвчлалтайгаар тооцоол:

A)
; б)
.

A)
.

Интегралыг хүчирхэг цуваа болгон өргөжүүлье. Үүнийг хийхийн тулд дуран цувралд орлуулъя
болон солих xдээр :

Интеграцийн сегментээс хойш
үүссэн цувааны нийлэх мужид хамаарна
, дараа нь бид заасан хязгаарын хүрээнд нэр томъёог нэгтгэх болно:

Үр дүнд нь ээлжлэн тэмдэглэгдсэн цувралд дөрөв дэх гишүүн үнэмлэхүй утгаараа 0.001-ээс бага байна. Тиймээс цувралын эхний гурван нөхцлийг л харгалзан үзвэл шаардлагатай нарийвчлалыг хангах болно.

Хаясан нэр томъёоны эхнийх нь хасах тэмдэгтэй тул үүссэн ойролцоо утга нь илүү байх болно. Тиймээс 0.001 доторх хариулт нь 0.487 байна.

б)Эхлээд интегралыг хүчний цуваа хэлбэрээр төлөөлүүлье. Функцийг өргөтгөхдөө орлуулъя

Хаана

xдээр
, бид авах:

Дараа нь
.

Үүссэн ээлжлэн цуваа нь Лейбницийн шалгуурын нөхцлийг хангаж байна. Цувралын дөрөв дэх гишүүн нь үнэмлэхүй утгаараа 0.001-ээс бага байна. Шаардлагатай нарийвчлалыг хангахын тулд эхний гурван гишүүний нийлбэрийг олоход хангалттай.

Тиймээс,
.

Функциональ цуврал. Эрчим хүчний цуврал.
Цувралын ойртох хүрээ

Ямар ч шалтгаангүйгээр инээх нь д'Аламбертийн шинж юм

Функциональ зэрэглэлийн цаг ирлээ. Сэдвийг, ялангуяа энэ хичээлийг амжилттай эзэмшихийн тулд та энгийн тооны цувралын талаар сайн ойлголттой байх хэрэгтэй. Та цуврал гэж юу болох талаар сайн ойлголттой байх ёстой бөгөөд цувралыг нэгтгэх эсэхийг шалгахын тулд харьцуулах шалгуурыг ашиглах чадвартай байх ёстой. Тиймээс, хэрэв та энэ сэдвийг дөнгөж судалж эхэлсэн эсвэл дээд математикийн анхан шатны суралцагч бол шаардлагатайГурван хичээлийг дарааллаар нь үзээрэй: Дамми нарт зориулсан эгнээ,Д'Аламберын тэмдэг. Кошигийн шинж тэмдэгТэгээд Ээлжит эгнээ. Лейбницийн тест. Мэдээж гурвуулаа! Хэрэв та тооны цуваатай холбоотой асуудлыг шийдвэрлэх үндсэн мэдлэг, чадвартай бол функциональ цувралыг даван туулах нь маш энгийн байх болно, учир нь тийм ч олон шинэ материал байдаггүй.

Энэ хичээлээр бид функциональ цувралын тухай ойлголтыг (энэ нь юу вэ) авч үзэх болно, практик даалгаврын 90% -д байдаг хүчний цуваатай танилцаж, радиусыг олох нийтлэг ердийн асуудлыг хэрхэн шийдвэрлэх талаар сурах болно. зэрэглэлийн цувааны конвергенц, нийлэх интервал ба нийлэх муж. Дараа нь би материалыг авч үзэхийг зөвлөж байна функцуудыг чадлын цуврал болгон өргөжүүлэх, мөн анхлан суралцагчдад анхны тусламж үзүүлнэ. Бага зэрэг амьсгаа авсны дараа бид дараагийн түвшинд шилжинэ.

Мөн функциональ цувралын хэсэгт тэдгээрийн олон тоо байдаг ойролцоогоор тооцоолох програмууд, зарим нь боловсролын уран зохиолд дүрмээр тусдаа бүлгийг өгдөг Фурье цувралаас ялгардаг. Надад ганцхан нийтлэл байна, гэхдээ энэ нь урт бөгөөд олон, олон нэмэлт жишээнүүд байна!

Тиймээс, тэмдэглэгээг тогтоосон тул явцгаая:

Функциональ цуваа ба чадлын цувааны тухай ойлголт

Хэрэв хязгаар нь хязгааргүй болж хувирвал, дараа нь шийдлийн алгоритм нь мөн ажлаа дуусгаж, бид даалгаврын эцсийн хариултыг өгдөг: "Цуврал нь " (эсвэл аль нэг дээр нийлдэг) болно. Өмнөх хэсгийн 3-р хэргийг үзнэ үү.

Хэрэв хязгаар нь тэг ч биш, хязгааргүй ч биш болж хувирвал, дараа нь бид практикт хамгийн түгээмэл тохиолдол №1 - цуврал нь тодорхой интервал дээр нийлдэг.

Энэ тохиолдолд хязгаар нь . Цувралын нэгдэх интервалыг хэрхэн олох вэ? Бид тэгш бус байдлыг бүрдүүлдэг:

IN Энэ төрлийн аливаа ажилтэгш бус байдлын зүүн талд байх ёстой хязгаарын тооцооны үр дүн, мөн тэгш бус байдлын баруун талд - хатуу нэгж. Яагаад ийм тэгш бус байдал, яагаад баруун талд байгаа талаар би яг таг тайлбарлахгүй. Хичээлүүд нь практикт чиглэгддэг бөгөөд миний түүхүүд багш нарын бүрэлдэхүүнийг өлгөж, зарим теоремууд илүү тодорхой болсон нь аль хэдийн маш сайн байсан.

Модультай ажиллах, давхар тэгш бус байдлыг шийдвэрлэх арга техникийг нийтлэлд эхний жилд нарийвчлан авч үзсэн болно. Функцийн домэйн, гэхдээ тухтай байхын тулд би бүх үйлдлүүдийг аль болох нарийвчлан тайлбарлахыг хичээх болно. Сургуулийн дүрмийн дагуу модуль бүхий тэгш бус байдлыг өргөжүүлэх . Энэ тохиолдолд:

Замын тал нь дууслаа.

Хоёрдахь үе шатанд олдсон интервалын төгсгөлд цувралын нийлэлтийг судлах шаардлагатай.

Эхлээд бид интервалын зүүн төгсгөлийг аваад хүчийг цувралдаа орлуулна.

Бид хэд хэдэн цувралыг авсан бөгөөд бид үүнийг нэгтгэх эсэхийг шалгах хэрэгтэй (өмнөх хичээлүүдээс аль хэдийн танил болсон даалгавар).

1) Цуврал ээлжлэн байна.
2) – цувааны нөхцлүүд модулийн бууралт. Түүнээс гадна цувралын дараагийн гишүүн бүр үнэмлэхүй утгаараа өмнөхөөсөө бага байна: , энэ нь бууралт нь нэгэн хэвийн байна гэсэн үг.
Дүгнэлт: цувралууд нийлдэг.

Модулуудаас бүрдсэн цувралыг ашигласнаар бид яг яаж гэдгийг олж мэдэх болно:
– нийлдэг (ерөнхий гармоник цувралын гэр бүлийн стандарт цуврал).

Тиймээс үүссэн тооны цуваа туйлын нийлдэг.

цагт - нийлдэг.

! Би танд сануулж байна аливаа нийлсэн эерэг цуваа бас туйлын нийлдэг.

Ийнхүү хүч чадлын цуваа нь олсон интервалын хоёр төгсгөлд нийлдэг.

Хариулт:Судалгаанд хамрагдаж буй хүч чадлын цувааны нэгдэх талбар:

Хариултын өөр нэг хэлбэр нь амьд явах эрхтэй: Цуврал нэгддэг бол

Заримдаа асуудлын мэдэгдэл нь нэгдэх радиусыг зааж өгөхийг шаарддаг. Энэ нь авч үзсэн жишээн дээр тодорхой харагдаж байна.

Жишээ 2

Хүчний цувааны нийлэх мужийг ол

Шийдэл:Бид цувралын нийлэх интервалыг олно ашигланд'Аламберын тэмдэг (гэхдээ BY шинж чанар биш! - функциональ цувралд ийм шинж чанар байхгүй):

Цуврал нэгдэн нийлдэг

Зүүнбид явах хэрэгтэй зөвхөн, тэгэхээр бид тэгш бус байдлын хоёр талыг 3-аар үржүүлнэ.

-Цуврал ээлжлэн гарч байна.
– – цувааны нөхцлүүд модулийн бууралт. Цувралын дараагийн гишүүн бүр өмнөхөөсөө бага модуль байна: , энэ нь бууралт нь нэгэн хэвийн байна гэсэн үг.

Дүгнэлт: цувралууд нийлдэг.

Үүнийг конвергенцийн шинж чанарын үүднээс авч үзье.

Энэ цувралыг ялгаатай цувралтай харьцуулж үзье.
Бид хязгаарлах харьцуулах шалгуурыг ашигладаг:

Тэгээс ялгаатай хязгаарлагдмал тоо гарч ирдэг бөгөөд энэ нь цуваа цуваанаас салж байна гэсэн үг юм.

Тиймээс цуврал нь нөхцөлт нийлдэг.

2) Хэзээ – зөрүүтэй (батлагдсаны дагуу).

Хариулт:Судалгаанд хамрагдаж буй хүч чадлын цуваа нийлэх талбар: . Цуврал нөхцөлт нийлэх үед.

Харгалзан үзсэн жишээнд чадлын цуваа нийлэх муж нь хагас интервал бөгөөд интервалын бүх цэгүүдэд хүч чадлын цуваа байна. туйлын нийлдэг, мөн тэр үед нь тодорхой болсон шиг - нөхцөлтэйгээр.

Жишээ 3

Хүчний цувааны нийлэх интервалыг олоод олсон интервалын төгсгөлд нийлэлтийг судал.

Энэ бол та өөрөө шийдэх жишээ юм.

Ховор боловч тохиолддог хэд хэдэн жишээг харцгаая.

Жишээ 4

Цувралын нийлэх талбайг ол:

Шийдэл: d'Alembert-ийн тестийг ашиглан бид энэ цувралын нэгдэх интервалыг олно.

(1) Бид цувралын дараагийн гишүүнийг өмнөхтэй харьцуулсан харьцааг бүрдүүлдэг.

(2) Бид дөрвөн давхар фракцаас салсан.

(3) Хүчтэй үйл ажиллагааны дүрмийн дагуу бид кубуудыг нэг хүчний дор авчирдаг. Тоолуур дээр бид зэрэглэлийг ухаалгаар өргөжүүлдэг, өөрөөр хэлбэл. Бид үүнийг дараагийн алхамд бутархайг -ээр багасгахаар зохион байгуулдаг. Бид хүчин зүйлийн талаар дэлгэрэнгүй тайлбарласан.

(4) Шоо дөрвөлжин доор бид хуваагчийг гишүүнээр хувааснаар . Хэсэгчилсэн байдлаар бид багасгаж болох бүх зүйлийг багасгадаг. "Динамик" хувьсагч "en" -ээс хамаарах зүйл байхгүй тул бид хязгаарын тэмдэгээс давсан хүчин зүйлийг авч болно; Модулийн тэмдгийг зураагүй болохыг анхаарна уу, учир нь энэ нь ямар ч "x"-ийн хувьд сөрөг бус утгыг авдаг.

Хязгаарт тэгийг авсан бөгөөд энэ нь бид эцсийн хариултыг өгч чадна гэсэн үг юм.

Хариулт:Цуврал нэгдэн нийлдэг

Гэхдээ эхлээд "аймшигтай дүүргэлт" бүхий энэ хэрүүлийг шийдвэрлэхэд хэцүү байх шиг санагдаж байв. Хязгаарт тэг эсвэл хязгааргүй байдал нь бараг бэлэг юм, учир нь шийдэл нь мэдэгдэхүйц багассан!

Жишээ 5

Цувралын нийлэх талбайг ол

Энэ бол та өөрөө шийдэх жишээ юм. Болгоомжтой байгаарай;-) Бүрэн шийдэл нь хичээлийн төгсгөлд байна.

Техникийн техникийг ашиглах тал дээр шинэлэг байдлын элемент агуулсан хэд хэдэн жишээг авч үзье.

Жишээ 6

Цувралын нийлэх интервалыг олоод олсон интервалын төгсгөлд нийлэлтийг судал.

Шийдэл:Эрчим хүчний цувралын нийтлэг нэр томъёо нь тэмдгийн эргэлтийг баталгаажуулах хүчин зүйлийг агуулдаг. Шийдлийн алгоритм нь бүрэн хадгалагдсан боловч хязгаарыг гаргахдаа модуль нь бүх "хасах" зүйлсийг устгадаг тул бид энэ хүчин зүйлийг үл тоомсорлодог (бичихгүй).

Бид d'Alembert-ийн тестийг ашиглан цувралын нэгдэх интервалыг олно.

Стандарт тэгш бус байдлыг бий болгоё:
Цуврал нэгдэн нийлдэг
Зүүнбид явах хэрэгтэй зөвхөн модуль, тэгэхээр бид тэгш бус байдлын хоёр талыг 5-аар үржүүлнэ.

Одоо бид модулийг танил хэлбэрээр нээж байна:

Давхар тэгш бус байдлын дунд та зөвхөн "X" үлдээх хэрэгтэй, бид тэгш бус байдлын хэсэг бүрээс 2-ыг хасна.

– судалж буй чадлын цувааны нийлэх интервал.

Бид олсон интервалын төгсгөлд цувралын нийлэлтийг судалдаг.

1) Манай чадлын цувралд утгыг орлуулна :

Маш болгоомжтой байгаарай, үржүүлэгч нь ямар ч байгалийн "en"-ийн тэмдгийн ээлжийг өгдөггүй. Үүссэн хасах утгыг цувралаас гадуур авч, мартдаг, учир нь энэ нь (ямар ч хүчин зүйлийн тогтмол гэх мэт) тоон цувааны нэгдэл, зөрүүд ямар ч байдлаар нөлөөлдөггүй.

Дахин анхаарна ууутгыг хүчний цувааны ерөнхий гишүүнд орлуулах явцад бидний хүчин зүйл буурсан. Хэрэв ийм зүйл тохиолдоогүй бол энэ нь бид хязгаарыг буруу тооцоолсон эсвэл модулийг буруу өргөтгөсөн гэсэн үг юм.

Тиймээс бид тооны цувааг нэгтгэхийн тулд шалгах хэрэгтэй. Энд хамгийн хялбар арга бол хязгаарлах харьцуулалтын шалгуурыг ашиглах бөгөөд энэ цувралыг дивергент гармоник цувралтай харьцуулах явдал юм. Гэхдээ үнэнийг хэлэхэд би харьцуулалтын хязгаарлагдмал шинж тэмдгээс маш залхаж байгаа тул шийдэлд олон янз байдлыг нэмж оруулах болно.

Тиймээс цуврал нэгдэж байна

Бид тэгш бус байдлын хоёр талыг 9-ээр үржүүлнэ.

Хуучин сургуулийн хошигнолыг санаж байхдаа бид хоёр хэсгээс үндсийг нь гаргаж авдаг.

Модулийг өргөжүүлэх:

болон бүх хэсэгт нэгийг нэмнэ:

– судалж буй чадлын цувааны нийлэх интервал.

Бид олсон интервалын төгсгөлд хүч чадлын цувааны нийлэлтийг судалж байна.

1) Хэрэв бол дараах тооны цувралыг олж авна.