Комплекс интеграл
Энэ нийтлэл нь тодорхойгүй интегралын сэдвийг төгсгөж, миний нэлээд төвөгтэй гэж үздэг интегралуудыг багтаасан болно. Хичээлийг сайт дээр илүү хэцүү жишээнүүдийг шинжлэхийг хүсч байгаагаа илэрхийлсэн зочдын давтан хүсэлтийн дагуу бүтээсэн.
Энэ текстийг уншигч сайн бэлтгэгдсэн бөгөөд үндсэн интеграцийн арга техникийг хэрхэн ашиглахаа мэддэг гэж үздэг. Дамми болон интегралд тийм ч итгэлтэй биш хүмүүс хамгийн эхний хичээлийг үзэх хэрэгтэй - Тодорхой бус интеграл. Шийдлийн жишээ, та сэдвийг бараг эхнээс нь эзэмших боломжтой. Илүү туршлагатай оюутнууд миний нийтлэлд хараахан гараагүй интеграцийн техник, аргуудтай танилцах боломжтой.
Ямар интегралыг авч үзэх вэ?
Эхлээд бид шийдэлд дараалан ашигладаг үндэстэй интегралуудыг авч үзэх болно хувьсах солихТэгээд хэсгүүдээр нэгтгэх. Өөрөөр хэлбэл, нэг жишээнд хоёр техникийг нэгэн зэрэг хослуулсан болно. Тэгээд бүр илүү.
Дараа нь бид сонирхолтой, эх сурвалжтай танилцах болно интегралыг өөртөө багасгах арга. Цөөн хэдэн интегралыг ингэж шийддэг.
Хөтөлбөрийн гурав дахь дугаар нь өмнөх нийтлэлүүдийн кассын хажуугаар өнгөрч байсан нийлмэл бутархайн интегралууд байх болно.
Дөрөвдүгээрт, тригонометрийн функцүүдийн нэмэлт интегралуудыг шинжлэх болно. Ялангуяа цаг хугацаа их шаарддаг бүх нийтийн тригонометрийн орлуулалтаас зайлсхийх аргууд байдаг.
(2) Интегралд бид хуваагч гишүүнийг гишүүнээр хуваана.
(3) Бид тодорхойгүй интегралын шугаман шинж чанарыг ашигладаг. Сүүлчийн интегралд нэн даруй функцийг дифференциал тэмдгийн доор тавина.
(4) Бид үлдсэн интегралуудыг авдаг. Логарифмд модулийн оронд хаалт хэрэглэж болно гэдгийг анхаарна уу, учир нь .
(5) Бид урвуу орлуулалтыг хийж, шууд орлуулахаас "te"-г илэрхийлнэ.
Масохист оюутнууд миний хийсэн шиг хариултыг ялгаж, анхны интегралыг гаргаж чадна. Үгүй, үгүй ээ, би зөв утгаараа шалгалт хийсэн =)
Таны харж байгаагаар шийдлийн явцад бид хоёроос илүү шийдлийн аргыг ашиглах шаардлагатай болсон тул ийм интегралтай ажиллахын тулд танд өөртөө итгэлтэй интеграцийн ур чадвар, бага зэрэг туршлага хэрэгтэй болно.
Практикт квадрат язгуур нь илүү түгээмэл байдаг: үүнийг өөрөө шийдэх гурван жишээ энд байна.
Жишээ 2
Тодорхойгүй интегралыг ол
Жишээ 3
Тодорхойгүй интегралыг ол
Жишээ 4
Тодорхойгүй интегралыг ол
Эдгээр жишээнүүд нь ижил төрлийнх тул өгүүллийн төгсгөлд байгаа бүрэн шийдэл нь зөвхөн 2-р жишээнд зориулагдсан болно. Жишээ 3-4 нь ижил хариулттай байна. Шийдвэр гаргах эхэнд аль орлуулалтыг ашиглах нь ойлгомжтой гэж бодож байна. Би яагаад ижил төрлийн жишээг сонгосон бэ? Тэдний дүрд ихэвчлэн олддог. Илүү олон удаа, магадгүй, зүгээр л нэг зүйл ![]() .
.
Гэхдээ дандаа биш, арктангенс, синус, косинус, экспоненциал болон бусад функцүүдийн доор шугаман функцийн үндэс байх үед та хэд хэдэн аргыг нэгэн зэрэг ашиглах хэрэгтэй. Хэд хэдэн тохиолдолд "хялбархан гарах" боломжтой, өөрөөр хэлбэл орлуулсны дараа шууд авч болох энгийн интегралыг олж авдаг. Дээр санал болгож буй ажлуудын хамгийн хялбар нь 4-р жишээ бөгөөд орлуулсны дараа харьцангуй энгийн интегралыг олж авдаг.
Интегралыг өөртөө багасгах замаар
Ухаантай, үзэсгэлэнтэй арга. Энэ төрлийн сонгодог бүтээлүүдийг харцгаая.
Жишээ 5
Тодорхойгүй интегралыг ол
Үндэс дор квадрат бином байдаг бөгөөд энэ жишээг нэгтгэх гэж оролдох нь цайны аяганд хэдэн цагийн турш толгой өвдөхөд хүргэдэг. Ийм интегралыг хэсэг хэсгээр нь аваад өөртөө багасгадаг. Зарчмын хувьд энэ нь хэцүү биш юм. Хэрэв та яаж гэдгийг мэддэг бол.
Харж байгаа интегралыг латин үсгээр тэмдэглээд шийдлийг эхлүүлье. ![]()
Хэсэгээр нь нэгтгэж үзье: 

(1) Нэр томъёогоор хуваах интеграл функцийг бэлтгэх.
(2) Бид интеграл функцийн нэр томъёог гишүүнээр нь хуваана. Энэ нь хүн бүрт ойлгомжтой биш байж болох ч би үүнийг илүү дэлгэрэнгүй тайлбарлах болно:
(3) Бид тодорхойгүй интегралын шугаман шинж чанарыг ашигладаг.
(4) Сүүлийн интегралыг ("урт" логарифм) ав.
Одоо шийдлийн эхэн үеийг харцгаая: 
Тэгээд эцэс хүртэл: 
Юу болсон бэ? Бидний заль мэхийн үр дүнд интеграл өөрөө багассан!
Эхлэл ба төгсгөлийг тэнцүүлж үзье: ![]()
Тэмдгийн өөрчлөлтөөр зүүн тал руу шилжинэ: ![]()
Тэгээд бид хоёрыг баруун тийш шилжүүлнэ. Үүний үр дүнд: ![]()
Тогтмол, хатуухан хэлэхэд өмнө нь нэмэх ёстой байсан, гэхдээ би үүнийг төгсгөлд нь нэмсэн. Энд ямар хатуу ширүүн байгааг уншихыг зөвлөж байна:
Жич:
Илүү хатуугаар шийдлийн эцсийн шат дараах байдалтай байна.
Тиймээс:
Тогтмолыг -аар дахин тодорхойлж болно. Яагаад дахин томилогдсон байж болох вэ? Учир нь тэр одоо ч гэсэн үүнийг хүлээн зөвшөөрдөг ямар чутгууд ба энэ утгаараа тогтмол ба хоёрын хооронд ямар ч ялгаа байхгүй.
Үүний үр дүнд:
Тогтмол өөрчлөлттэй ижил төстэй заль мэхийг өргөн ашигладаг дифференциал тэгшитгэл. Тэнд би хатуу байх болно. Энд би ийм эрх чөлөөг зөвхөн шаардлагагүй зүйлээр төөрөлдүүлэхгүйн тулд, интеграцийн аргад анхаарлаа төвлөрүүлэхийн тулд л зөвшөөрч байна.
Жишээ 6
Тодорхойгүй интегралыг ол
Бие даасан шийдлийн өөр нэг ердийн интеграл. Хичээлийн төгсгөлд бүрэн шийдэл, хариулт. Өмнөх жишээн дээрх хариултаас ялгаатай байх болно!
Хэрэв квадрат язгуур дор дөрвөлжин гурвалсан байвал шийдэл нь ямар ч тохиолдолд дүн шинжилгээ хийсэн хоёр жишээнд бууна.
Жишээлбэл, интегралыг авч үзье ![]() . Таны хийх ёстой зүйл бол эхлээд бүрэн дөрвөлжин сонгоно уу:
. Таны хийх ёстой зүйл бол эхлээд бүрэн дөрвөлжин сонгоно уу:
.
Дараа нь шугаман орлуулалт хийгддэг бөгөөд энэ нь "ямар ч үр дагаваргүйгээр" хийдэг.
, үр дүнд нь интеграл . Танил зүйл байна, тийм үү?
Эсвэл квадрат бином бүхий энэ жишээ:
Бүрэн квадратыг сонгоно уу:
Шугаман орлуулсны дараа бид интегралыг олж авдаг бөгөөд үүнийг аль хэдийн хэлэлцсэн алгоритмыг ашиглан шийддэг.
Интегралыг өөртөө хэрхэн бууруулах талаар өөр хоёр ердийн жишээг авч үзье.
– экспоненциалыг синусаар үржүүлсэн интеграл;
– экспоненциалыг косинусаар үржүүлсэн интеграл.
Жагсаалтад орсон интегралуудад та хоёр удаа интегралдах шаардлагатай болно.
Жишээ 7
Тодорхойгүй интегралыг ол
Интеграл нь экспоненциалыг синусаар үржүүлсэн тоо юм.
Бид хэсэг хэсгээр нь хоёр удаа нэгтгэж, интегралыг өөртөө багасгадаг. ![]()



Хэсэгчилсэн давхар интегралын үр дүнд интеграл өөрөө багассан. Бид шийдлийн эхлэл ба төгсгөлийг тэнцүүлж байна:
Бид үүнийг зүүн тал руу тэмдгээр шилжүүлж, интегралыг илэрхийлнэ. 
Бэлэн. Үүний зэрэгцээ баруун талыг самнахыг зөвлөж байна, i.e. илтгэгчийг хаалтнаас гаргаж аваад хаалтанд синус болон косинусыг "сайхан" дарааллаар байрлуул.
Одоо жишээний эхэнд, эсвэл илүү нарийвчлалтайгаар хэсэгчлэн нэгтгэх рүү буцъя:
Бид илтгэгчийг дараах байдлаар тодорхойлсон. Асуулт гарч ирнэ: энэ нь үргэлж тэмдгээр тэмдэглэгдэх ёстой үзүүлэлт мөн үү? Заавал биш. Үнэн хэрэгтээ, авч үзсэн интегралд үндсэндээ хамаагүй, гэж юу гэсэн үг вэ, бид өөр замаар явж болох байсан: 
Энэ яагаад боломжтой вэ? Экспоненциал нь өөрөө болж хувирдаг (дифференциал ба интегралын үед хоёулаа) синус болон косинус нь харилцан бие биедээ (дахин ялгах ба интегралын үед) хувирдаг.
Өөрөөр хэлбэл, бид тригонометрийн функцийг бас илэрхийлж болно. Гэхдээ авч үзсэн жишээн дээр фракцууд гарч ирэх тул энэ нь оновчтой биш юм. Хэрэв та хүсвэл хоёр дахь аргыг ашиглан энэ жишээг шийдэхийг оролдож болно.
Жишээ 8
Тодорхойгүй интегралыг ол
Энэ бол та өөрөө шийдэх жишээ юм. Шийдвэрлэхээсээ өмнө энэ тохиолдолд экспоненциал функц эсвэл тригонометрийн функцээр тэмдэглэх нь илүү ашигтай юу вэ гэдгийг бодоорой. Хичээлийн төгсгөлд бүрэн шийдэл, хариулт.
Мэдээжийн хэрэг, энэ хичээлийн ихэнх хариултыг ялгах замаар шалгахад хялбар гэдгийг мартаж болохгүй!
Үзсэн жишээнүүд нь хамгийн төвөгтэй биш байсан. Практикт интеграл нь тогтмол нь экспонент болон тригонометрийн функцийн аргументад хоёуланд нь байх үед илүү түгээмэл байдаг, жишээ нь: . Ийм интегралд олон хүн төөрөлдөх болно, би өөрөө ихэвчлэн эргэлздэг. Уусмал дахь фракцууд гарч ирэх магадлал өндөр байдаг нь анхаарал болгоомжгүй байдлаас болж ямар нэг зүйлийг алдах нь маш амархан байдаг. Нэмж дурдахад, тэмдгээр алдаа гарах магадлал өндөр байдаг бөгөөд энэ нь хасах тэмдэгтэй байдаг бөгөөд энэ нь нэмэлт хүндрэл үүсгэдэг.
Эцсийн шатанд үр дүн нь ихэвчлэн дараах байдалтай байдаг.
Шийдлийн төгсгөлд ч гэсэн та маш болгоомжтой байж, фракцуудыг зөв ойлгох хэрэгтэй. 
Комплекс бутархайг нэгтгэх
Бид хичээлийн экватор руу аажмаар ойртож, бутархайн интегралуудыг авч үзэж эхэлдэг. Дахин хэлэхэд, тэд бүгд маш нарийн төвөгтэй биш, зүгээр л нэг шалтгааны улмаас жишээнүүд нь бусад нийтлэлд бага зэрэг "сэдвээс гадуур" байсан.
Үндэсийн сэдвийг үргэлжлүүлж байна
Жишээ 9
Тодорхойгүй интегралыг ол
Үндэс дор байгаа хуваагч дээр квадрат гурвалжин ба язгуурын гадна талд "X" хэлбэртэй "хавсралт" байна. Энэ төрлийн интегралыг стандарт орлуулалт ашиглан шийдэж болно.
Бид шийднэ: ![]()
Энд орлуулах нь энгийн: ![]()
Солигдсоны дараах амьдралыг харцгаая: 
(1) Орлуулсны дараа бид язгуурын доорх нэр томъёог нийтлэг хуваагч болгон бууруулна.
(2) Бид үүнийг үндэснээс нь гаргаж авдаг.
(3) Тоолуур ба хуваагчийг -аар багасгасан. Үүний зэрэгцээ, үндэс дор би нөхцөлүүдийг тохиромжтой дарааллаар дахин зохион байгуулав. Зарим туршлагатай бол тайлбар хийсэн үйлдлүүдийг амаар гүйцэтгэх замаар (1), (2) алхмуудыг алгасаж болно.
(4) Үр дүнгийн интеграл, та хичээлээс санаж байна Зарим бутархайг нэгтгэх, шийдвэрлэж байна дөрвөлжин олборлох бүрэн арга. Бүрэн квадратыг сонгоно уу.
(5) Интегралчлалаар бид ердийн "урт" логарифмийг олж авдаг.
(6) Бид урвуу солих ажлыг гүйцэтгэдэг. Хэрэв эхэндээ , дараа нь буцаж: .
(7) Эцсийн үйлдэл нь үр дүнг засахад чиглэгддэг: язгуурын дор бид нэр томъёог дахин нийтлэг хуваагч руу авчирч, үндэснээс нь гаргаж авдаг.
Жишээ 10
Тодорхойгүй интегралыг ол ![]()
Энэ бол та өөрөө шийдэх жишээ юм. Энд ганц "X" дээр тогтмолыг нэмсэн бөгөөд орлуулах нь бараг ижил байна: ![]()
Нэмэлт хийх ёстой цорын ганц зүйл бол орлуулалтаас "x" -ийг илэрхийлэх явдал юм. ![]()
Хичээлийн төгсгөлд бүрэн шийдэл, хариулт.
Заримдаа ийм интегралд язгуур дор квадрат бином байж болох бөгөөд энэ нь шийдлийн аргыг өөрчилдөггүй, бүр илүү хялбар байх болно. Ялгааг мэдэр:
Жишээ 11
Тодорхойгүй интегралыг ол
Жишээ 12
Тодорхойгүй интегралыг ол
Хичээлийн төгсгөлд товч шийдэл, хариултууд. Жишээ 11 нь яг таарч байгааг тэмдэглэх нь зүйтэй бином интеграл, шийдвэрлэх аргыг ангид хэлэлцсэн Иррационал функцүүдийн интегралууд.
2-р зэрэглэлийн задрахгүй олон гишүүнтийн интеграл
(хүлээгчийн олон гишүүнт)
Интегралын илүү ховор төрөл боловч практик жишээн дээр тааралддаг.
Жишээ 13
Тодорхойгүй интегралыг ол
Гэхдээ азтай 13 дугаартай жишээ рүү буцъя (үнэнийг хэлэхэд би буруу таамаглаагүй). Энэ интеграл нь хэрвээ та хэрхэн шийдэхээ мэдэхгүй байгаа бол нэлээд бухимдал төрүүлдэг зүйлсийн нэг юм.
Шийдэл нь хиймэл өөрчлөлтөөс эхэлдэг: 
Хүн бүр тоологчийг хуваагч гишүүнээр хуваахыг аль хэдийн ойлгосон гэж бодож байна.
Үүссэн интегралыг дараах хэсгүүдэд хуваана. 

( – натурал тоо) хэлбэрийн интегралын хувьд бид гаргаж авдаг давтагдахбууруулах томъёо:
, Хаана ![]() - интеграл нэг градусаар бага.
- интеграл нэг градусаар бага.
Шийдвэрлэсэн интегралын хувьд энэ томьёо зөв эсэхийг шалгацгаая.
Энэ тохиолдолд: , , бид томъёог ашиглана: 
Таны харж байгаагаар хариултууд ижил байна.
Жишээ 14
Тодорхойгүй интегралыг ол
Энэ бол та өөрөө шийдэх жишээ юм. Загварын шийдэл нь дээрх томъёог хоёр удаа дараалан ашигладаг.
Хэрэв зэрэгтэй бол хуваагдашгүйдөрвөлжин гурвалсан, дараа нь төгс квадратыг тусгаарлах замаар уусмалыг бином болгон бууруулна, жишээлбэл:
Тоолуурт нэмэлт олон гишүүнт байвал яах вэ? Энэ тохиолдолд тодорхойгүй коэффициентийн аргыг хэрэглэж, интеграл функцийг бутархайн нийлбэр болгон өргөжүүлнэ. Гэхдээ миний практикт ийм жишээ байдаг хэзээ ч уулзаагүй, тиймээс би нийтлэлд энэ хэргийг орхигдуулсан Бутархай-рационал функцүүдийн интеграл, Би үүнийг одоо алгасах болно. Хэрэв та ийм интегралтай тулгарсан хэвээр байгаа бол сурах бичгийг хараарай - тэнд бүх зүйл энгийн байдаг. Материалыг (энгийн ч гэсэн) оруулахыг зөвлөдөггүй гэж би бодож байна, учирч болох магадлал нь тэг байх хандлагатай байдаг.
Нарийн төвөгтэй тригонометрийн функцуудыг нэгтгэх
Ихэнх жишээнүүдийн "цогцолбор" гэсэн нэр томъёо нь ихэвчлэн нөхцөлт байдаг. Өндөр чадлын шүргэгч ба котангентуудаас эхэлье. Ашигласан шийдвэрлэх аргын үүднээс авч үзвэл тангенс ба котангенс нь бараг ижил зүйл тул би тангенсийн талаар илүү их ярих болно, энэ нь интегралыг шийдэх үзүүлсэн арга нь котангентын хувьд ч хүчинтэй гэдгийг илтгэнэ.
Дээрх хичээл дээр бид үзсэн бүх нийтийн тригонометрийн орлуулалттригонометрийн функцүүдийн тодорхой төрлийн интегралыг шийдвэрлэхэд зориулагдсан. Бүх нийтийн тригонометрийн орлуулалтын сул тал нь түүнийг ашигласнаар тооцоолол хийхэд хүндрэлтэй, төвөгтэй интеграл үүсдэг. Мөн зарим тохиолдолд бүх нийтийн тригонометрийн орлуулалтаас зайлсхийх боломжтой!
Нэгийн интегралыг синусаар хуваасан өөр нэг каноник жишээг авч үзье.
Жишээ 17
Тодорхойгүй интегралыг ол
Энд та бүх нийтийн тригонометрийн орлуулалтыг ашиглаж, хариултыг авч болно, гэхдээ илүү оновчтой арга бий. Би алхам бүрийн тайлбар бүхий бүрэн шийдлийг өгөх болно:

(1) Бид давхар өнцгийн синусын тригонометрийн томьёог ашигладаг.
(2) Бид зохиомол хувиргалт хийдэг: хуваарьт хувааж, -ээр үржүүлнэ.
(3) Бид хуваагч дахь сайн мэддэг томьёог ашиглан бутархайг шүргэгч болгон хувиргана.
(4) Бид функцийг дифференциал тэмдгийн дор авчирдаг.
(5) Интегралыг ав.
Та өөрөө шийдэх хэдэн энгийн жишээ:
Жишээ 18
Тодорхойгүй интегралыг ол
Анхаар: Хамгийн эхний алхам бол багасгах томъёог ашиглах явдал юм ![]() өмнөх жишээтэй төстэй үйлдлүүдийг болгоомжтой хийх хэрэгтэй.
өмнөх жишээтэй төстэй үйлдлүүдийг болгоомжтой хийх хэрэгтэй.
Жишээ 19
Тодорхойгүй интегралыг ол
За, энэ бол маш энгийн жишээ юм.
Хичээлийн төгсгөлд шийдлүүд болон хариултуудыг бөглөнө үү.
Одоо хэн ч интегралтай холбоотой асуудал гарахгүй гэж би бодож байна: ![]() гэх мэт.
гэх мэт.
Аргын санаа юу вэ? Энэхүү санаа нь зөвхөн шүргэгч ба шүргэгч деривативыг интеграл болгон зохион байгуулахын тулд хувиргалт ба тригонометрийн томъёог ашиглах явдал юм. Өөрөөр хэлбэл, бид солих тухай ярьж байна: ![]() . 17-19-р жишээн дээр бид энэ орлуулалтыг ашигласан боловч интегралууд нь маш энгийн байсан тул функцийг дифференциал тэмдгийн доор оруулснаар ижил төстэй үйлдлийг гүйцэтгэсэн.
. 17-19-р жишээн дээр бид энэ орлуулалтыг ашигласан боловч интегралууд нь маш энгийн байсан тул функцийг дифференциал тэмдгийн доор оруулснаар ижил төстэй үйлдлийг гүйцэтгэсэн.
Би дээр дурдсанчлан ижил төстэй үндэслэлийг котангентын хувьд хийж болно.
Дээр дурдсан орлуулалтыг хэрэглэх албан ёсны урьдчилсан нөхцөл бас бий.
Косинус ба синусын зэрэглэлийн нийлбэр нь сөрөг бүхэл ТЭГШ тоо юм, Жишээ нь:
интегралын хувьд – сөрөг бүхэл тоо EVEN тоо.
! Анхаарна уу : хэрэв интегралд ЗӨВХӨН синус эсвэл ЗӨВХӨН косинус байвал интегралыг мөн сөрөг сондгой градусаар авна (хамгийн энгийн тохиолдлууд жишээ №17, 18-д байна).
Энэ дүрэмд үндэслэн хэд хэдэн илүү утга учиртай ажлыг авч үзье.
Жишээ 20
Тодорхойгүй интегралыг ол
Синус ба косинусын зэрэглэлийн нийлбэр: 2 – 6 = –4 нь сөрөг бүхэл тоо EVEN тоо бөгөөд энэ нь интегралыг шүргэгч болон түүний дериватив болгон бууруулж болно гэсэн үг юм. 
(1) хуваагчийг өөрчилье.
(2) Сайн мэддэг томьёог ашиглан бид .
(3) Хусагчийг өөрчилье.
(4) Бид томъёог ашигладаг ![]() .
.
(5) Бид функцийг дифференциал тэмдгийн дор авчирдаг.
(6) Бид солих ажлыг гүйцэтгэдэг. Илүү туршлагатай оюутнууд орлуулалтыг хийхгүй байж болох ч шүргэгчийг нэг үсгээр солих нь дээр - төөрөлдөх эрсдэл бага байдаг.
Жишээ 21
Тодорхойгүй интегралыг ол
Энэ бол та өөрөө шийдэх жишээ юм.
Түр хүлээгээрэй, аваргын тойргууд эхлэх гэж байна =)
Ихэнхдээ интеграл нь "hodgepodge"-г агуулдаг:
Жишээ 22
Тодорхойгүй интегралыг ол ![]()
Энэхүү интеграл нь эхлээд шүргэгчийг агуулдаг бөгөөд энэ нь тэр даруй аль хэдийн танил бодолд хүргэдэг:

Бүх зүйлийг дээр дурдсан тул би хиймэл өөрчлөлтийг эхэнд нь, үлдсэн алхмуудыг тайлбаргүйгээр орхих болно.
Өөрийнхөө шийдлийн хэд хэдэн бүтээлч жишээ:
Жишээ 23
Тодорхойгүй интегралыг ол ![]()
Жишээ 24
Тодорхойгүй интегралыг ол ![]()
Тийм ээ, тэдгээрт мэдээжийн хэрэг та синус ба косинусын хүчийг бууруулж, бүх нийтийн тригонометрийн орлуулалтыг ашиглаж болно, гэхдээ шүргэгчээр дамжуулан шийдвэл илүү үр дүнтэй, богино байх болно. Хичээлийн төгсгөлд бүрэн шийдэл, хариултууд
Интегралыг шийдэх нь хялбар ажил боловч зөвхөн сонгогдсон цөөхөн хүмүүст зориулагдсан. Энэ нийтлэл нь интегралуудыг ойлгож сурахыг хүсдэг боловч тэдгээрийн талаар юу ч мэдэхгүй эсвэл бараг юу ч мэдэхгүй хүмүүст зориулагдсан болно. Интеграл... Яагаад хэрэгтэй байна вэ? Үүнийг хэрхэн тооцоолох вэ? Тодорхой ба тодорхойгүй интеграл гэж юу вэ? Хэрэв интегралын хувьд таны мэддэг цорын ганц хэрэглээ бол хүрэхэд хэцүү газраас хэрэгтэй зүйл авахын тулд салшгүй дүрс хэлбэртэй зүүгээр дэгээ ашиглах явдал юм бол тавтай морилно уу! Интегралыг хэрхэн шийдэх, яагаад үүнгүйгээр хийх боломжгүйг олж мэдээрэй.
Бид "интеграл" гэсэн ойлголтыг судалдаг.
Интеграци нь эртний Египетэд мэдэгдэж байсан. Мэдээжийн хэрэг, орчин үеийн хэлбэрээр биш, гэхдээ одоо ч гэсэн. Түүнээс хойш математикчид энэ сэдвээр олон ном бичсэн. Ялангуяа өөрсдийгөө онцолсон Ньютон Тэгээд Лейбниц , гэхдээ юмсын мөн чанар өөрчлөгдөөгүй. Интегралыг эхнээс нь хэрхэн ойлгох вэ? Арга ч үгүй! Энэ сэдвийг ойлгохын тулд танд математик анализын үндсэн суурь мэдлэг хэрэгтэй хэвээр байх болно. Манай блог дээр интегралыг ойлгоход шаардлагатай -ын тухай мэдээлэл аль хэдийн бий.
Тодорхой бус интеграл
Бидэнд ямар нэгэн функцтэй байцгаая f(x) .
Тодорхой бус интеграл функц f(x) энэ функцийг дууддаг F(x) , түүний дериватив нь функцтэй тэнцүү байна f(x) .
Өөрөөр хэлбэл интеграл нь урвуу дериватив эсвэл эсрэг дериватив юм. Дашрамд хэлэхэд, хэрхэн яаж хийх талаар манай нийтлэлээс уншина уу.

Бүх тасралтгүй функцүүдэд эсрэг дериватив байдаг. Мөн тогтмол тэмдэгтээр ялгаатай функцүүдийн деривативууд давхцдаг тул эсрэг дериватив дээр тогтмол тэмдэг нэмж өгдөг. Интегралыг олох үйл явцыг интеграл гэж нэрлэдэг.
Энгийн жишээ:

Энгийн функцүүдийн эсрэг деривативуудыг байнга тооцоолохгүйн тулд тэдгээрийг хүснэгтэд оруулж, бэлэн утгыг ашиглах нь тохиромжтой.

Тодорхой интеграл
Интеграл гэдэг ойлголттой харьцахдаа бид хязгааргүй жижиг хэмжигдэхүүнтэй харьцаж байна. Интеграл нь зургийн талбай, жигд бус биеийн масс, жигд бус хөдөлгөөний үед туулсан зай болон бусад олон зүйлийг тооцоолоход тусална. Интеграл гэдэг нь хязгааргүй олон тооны хязгааргүй жижиг гишүүний нийлбэр гэдгийг санах нь зүйтэй.
Жишээ болгон зарим функцийн графикийг төсөөлөөд үз дээ. Функцийн графикаар хязгаарлагдсан дүрсийн талбайг хэрхэн олох вэ?

Интеграл ашиглах! Координатын тэнхлэгүүд болон функцийн графикаар хязгаарлагдсан муруй шугаман трапецийг хязгааргүй жижиг хэрчмүүдэд хуваацгаая. Ингэснээр зургийг нимгэн багана болгон хуваах болно. Баганын талбайн нийлбэр нь трапецын талбай болно. Гэхдээ ийм тооцоолол нь ойролцоогоор үр дүнг өгөх болно гэдгийг санаарай. Гэсэн хэдий ч сегментүүд нь жижиг, нарийхан байх тусам тооцоолол илүү нарийвчлалтай болно. Хэрэв бид тэдгээрийг урт нь тэг рүү чиглүүлэхээр багасгах юм бол сегментүүдийн талбайн нийлбэр нь зургийн талбай руу чиглэх болно. Энэ бол тодорхой интеграл бөгөөд үүнийг дараах байдлаар бичсэн болно.

a ба b цэгүүдийг интегралын хязгаар гэж нэрлэдэг.
 Бари Алибасов ба "Интеграл" хамтлаг
Бари Алибасов ба "Интеграл" хамтлаг Дашрамд хэлэхэд! Уншигчиддаа зориулж 10% хямдралтай байгаа
Даммигийн интегралыг тооцоолох дүрэм
Тодорхойгүй интегралын шинж чанарууд
Тодорхойгүй интегралыг хэрхэн шийдэх вэ? Энд бид тодорхойгүй интегралын шинж чанаруудыг авч үзэх бөгөөд энэ нь жишээг шийдвэрлэхэд хэрэг болно.
- Интегралын дериватив нь интегралтай тэнцүү байна:

- Тогтмолыг интеграл тэмдгийн доороос гаргаж болно.

- Нийлбэрийн интеграл нь интегралын нийлбэртэй тэнцүү байна. Энэ нь мөн ялгааны хувьд үнэн юм:
Тодорхой интегралын шинж чанарууд
- Шугаман чанар:

- Интегралын хязгаарыг сольсон тохиолдолд интегралын тэмдэг өөрчлөгдөнө.

- At ямар чоноо а, бТэгээд -тай:

Тодорхой интеграл нь нийлбэрийн хязгаар гэдгийг бид аль хэдийн олж мэдсэн. Гэхдээ жишээг шийдэхдээ тодорхой утгыг хэрхэн авах вэ? Үүний тулд Ньютон-Лейбницийн томъёо байдаг:

Интегралыг шийдвэрлэх жишээ
Доор бид тодорхойгүй интеграл олох хэд хэдэн жишээг авч үзэх болно. Бид танд шийдлийн нарийн ширийнийг өөрөө олж мэдэхийг санал болгож байна, хэрэв ямар нэг зүйл тодорхойгүй байвал сэтгэгдэл дээр асуулт асуугаарай.

Материалыг бататгахын тулд интегралыг практикт хэрхэн шийддэг тухай видеог үзээрэй. Хэрэв интегралыг шууд өгөхгүй бол цөхрөл бүү зов. Оюутнуудад зориулсан мэргэжлийн үйлчилгээтэй холбоо бариарай, битүү гадаргуу дээрх гурвалсан эсвэл муруй интеграл нь таны хүчин чадалд багтах болно.
Дараахь томъёог нэрлэнэ хэсгүүдийн томъёогоор нэгтгэх тодорхойгүй интегралд:
Интеграцийг хэсгүүдийн томъёогоор хэрэглэхийн тулд интегралыг хоёр хүчин зүйлд хуваах шаардлагатай. Тэдгээрийн нэгийг нь тэмдэглэв у, үлдсэн хэсэг нь хоёр дахь хүчин зүйлд хамаарах бөгөөд үүнийг тэмдэглэнэ dv. Дараа нь ялгах замаар бид олдог дуба интеграци - функц v. Үүний зэрэгцээ, төлөө у dv- амархан нэгтгэж болох интегралын ийм хэсэг.
Хэзээ хэсэгчлэн нэгтгэх аргыг хэрэглэх нь ашигтай вэ? Тэгээд хэзээ интегралд агуулагддаг :
1) - логарифмын функцууд, түүнчлэн урвуу тригонометрийн функцүүд ("нуман" угтвартай), дараа нь хэсэгчлэн нэгтгэх олон жилийн туршлага дээр үндэслэн эдгээр функцийг дараах байдлаар тэмдэглэв. у;
2) , , - синус, косинус ба илтгэгчийн үржвэр П(x) нь x-д дурын олон гишүүнт байвал эдгээр функцийг дараах байдлаар тэмдэглэнэ dv, мөн олон гишүүнт нь дамжуулан байна у;
3) , , , , энэ тохиолдолд хэсгүүдийн интеграцийг хоёр удаа хэрэглэнэ.
Эхний тохиолдлын жишээг ашиглан хэсгүүдээр нэгтгэх аргын утгыг тайлбарлая. Интеграл тэмдгийн доорх илэрхийлэл нь логарифмын функцийг агуулна (энэ нь жишээ 1 болно). Хэсэгчилсэн интегралыг ашигласнаар ийм интеграл нь зөвхөн алгебрийн функцүүдийн интегралыг (ихэнхдээ олон гишүүнт) тооцоолоход хүргэдэг, өөрөөр хэлбэл логарифм эсвэл урвуу тригонометрийн функцийг агуулдаггүй. Хичээлийн эхэнд өгсөн хэсгүүдийн интеграцийн томъёог ашиглах
бид эхний гишүүнд (интегралгүй) логарифмын функцийг, хоёр дахь гишүүнд (интеграл тэмдгийн дор) логарифм агуулаагүй функцийг олж авдаг. Алгебрийн функцийн интеграл нь логарифм эсвэл урвуу тригонометрийн функцийг тусад нь эсвэл алгебрийн хүчин зүйлтэй хамт олдог тэмдгийн дор байх интегралаас хамаагүй хялбар юм.
Тиймээс ашиглах хэсгүүдийн томъёогоор нэгтгэх интеграл нэн даруй хийгддэггүй: өгөгдсөн интегралыг олох нь нөгөөг олох хүртэл буурдаг. Хэсэгчилсэн интегралын томъёоны утга нь түүнийг хэрэглэсний үр дүнд шинэ интеграл нь хүснэгт хэлбэртэй эсвэл наад зах нь анхныхаасаа илүү хялбар болдог.
Хэсэгээр нэгтгэх арга нь хоёр функцийн бүтээгдэхүүнийг ялгах томъёог ашиглахад суурилдаг.
дараа нь хэлбэрээр бичиж болно
Хичээлийн эхэнд өгсөн.
Функцийг нэгтгэх замаар олох үед vүүний тулд эсрэг дериватив функцүүдийн хязгааргүй багцыг олж авдаг. Интеграцийг хэсгүүдийн томъёогоор ашиглахын тулд та тэдгээрийн аль нэгийг нь авч болно, тиймээс дурын тогтмолд тохирохыг нь авч болно. ХАМТ, тэгтэй тэнцүү. Тиймээс функцийг олох үед vдурын тогтмол ХАМТоруулах ёсгүй.
Хэсэгчилсэн интеграцийн арга нь маш онцгой хэрэглээтэй: интеграл тэмдгийн дор функцүүдийн зэрэглэлийг багасгах шаардлагатай үед эсрэг дериватив функцийг олохын тулд давтагдах томъёог гаргаж авахад ашиглаж болно. Жишээлбэл, синус, косинус гэх мэт функцууд болон тэдгээрийн үржвэрүүдээс их хүчин чадалтай функцүүдийн хувьд хүснэгтэн интеграл байхгүй үед зэрэг бууруулах шаардлагатай. Давтагдах томьёо нь өмнөх гишүүнээр дамжуулан дарааллын дараагийн гишүүнийг олох томьёо юм. Заасан тохиолдлуудын хувьд зэрэглэлийг дараалан бууруулах замаар зорилгодоо хүрдэг. Тэгэхээр хэрэв интеграл нь х-ийн дөрөв дэх зэрэглэлийн синус юм бол хэсгүүдээр интеграл хийснээр синусын интегралыг гуравдахь зэрэгт тооцох томьёог олж болно. Энэ хичээлийн сүүлчийн догол мөр нь тайлбарласан даалгаварт зориулагдсан болно.
Интеграцийг хэсэг хэсгээр нь хамтад нь хэрэглэх
Жишээ 1. Тодорхой бус интегралыг хэсгүүдээр нэгтгэх аргыг ашиглан ол:
Шийдэл. Интеграл илэрхийлэлд - логарифм бөгөөд үүнийг бидний аль хэдийн мэдэж байгаагаар үндэслэлтэйгээр тэмдэглэж болно. у. Бид итгэдэг, .
Бид (онолын лавлагааны тайлбарт дурьдсанчлан бид нэн даруй эхний гишүүнд логарифм функцийг (интегралгүйгээр), хоёр дахь гишүүнд логарифм агуулаагүй функцийг (интеграл тэмдгийн дор) олж авна): ):

Мөн дахин логарифм ...
Жишээ 2.Тодорхой бус интегралыг ол:
Шийдэл. Let, .
Логарифм нь дөрвөлжинд байдаг. Энэ нь нарийн төвөгтэй функц гэж ялгах шаардлагатай гэсэн үг юм. Бид олдог
,
.
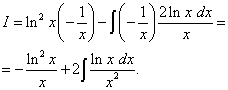
Бид дахин хоёр дахь интегралыг хэсгүүдээр нь олж, аль хэдийн дурдсан давуу талыг олж авдаг (эхний гишүүнд (интегралгүй) логарифм функц байдаг ба хоёр дахь гишүүнд (интеграл тэмдгийн дор) нь агуулаагүй функц байдаг. логарифм).
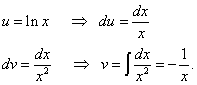

Бид анхны интегралыг олно:

Жишээ 3.
Шийдэл. Логарифмын нэгэн адил арктангенсийг илүү сайн тэмдэглэдэг у. Тиймээс үзье, .
Дараа нь,
.
Интеграцийг хэсэгчилсэн томъёогоор ашигласнаар бид дараахь зүйлийг олж авна.
![]()
Хувьсагчийг өөрчилснөөр бид хоёр дахь интегралыг олно.

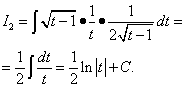
Хувьсагч руу буцах x, бид авдаг
![]() .
.
Бид анхны интегралыг олно:
![]() .
.
Жишээ 4. Тодорхой бус интегралыг хэсгүүдээр нь нэгтгэх аргыг ашиглан ол:
Шийдэл. Экспонентийг -ээр тэмдэглэх нь дээр dv. Бид интегралыг хоёр хүчин зүйл болгон хуваадаг. Үүнд итгэж байна
Жишээ 5. Тодорхой бус интегралыг хэсгүүдээр нэгтгэх аргыг ашиглан ол:
![]() .
.
Шийдэл. Let, . Дараа нь , .
Хэсэгчилсэн интеграцийн томъёог (1) ашиглан бид дараахь зүйлийг олно.
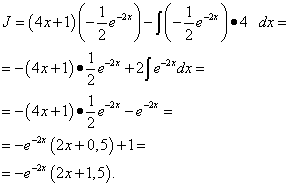
Жишээ 6.Тодорхой бус интегралыг хэсгүүдээр нь интегралаар ол:
Шийдэл. Экспоненциал шиг синусыг хялбархан тэмдэглэж болно dv. Let, .
Хэсэгчилсэн интеграцийн томъёог ашиглан бид дараахь зүйлийг олно.
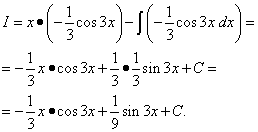
Бид интеграцийг хэсэг хэсгээр нь дахин хэрэгжүүлдэг
Жишээ 10.Тодорхой бус интегралыг хэсгүүдээр нь интегралаар ол:
![]() .
.
Шийдэл. Үүнтэй төстэй бүх тохиолдлын нэгэн адил косинусыг тэмдэглэх нь тохиромжтой dv. Бид , гэж тэмдэглэдэг.
Дараа нь ![]() ,
.
,
.
Хэсэгчилсэн интеграцийн томъёог ашиглан бид дараахь зүйлийг олж авна.
Мөн бид интеграцийг хэсэг хэсгээр нь хоёрдугаар нэр томъёонд ашигладаг. Бид , гэж тэмдэглэдэг.
Эдгээр тэмдэглэгээг ашиглан бид дурдсан нэр томъёог нэгтгэж байна:

Одоо бид шаардлагатай интегралыг олно:

Хэсэгчилсэн интегралчлалын аргаар шийдэж болох интегралуудын дунд онолын хэсэгт дурдсан гурван бүлгийн алинд нь ч ороогүй интегралууд бас байдаг бөгөөд үүнийг практик дээр тэмдэглэсэн нь дээр. у, тэгээд юугаар дамжуулан dv. Тиймээс, эдгээр тохиолдолд та "Хэсгээр нэгтгэх аргын мөн чанар" гэсэн догол мөрөнд өгөгдсөн тав тухтай байдлыг харгалзан үзэх шаардлагатай. уялгах явцад нэг их төвөгтэй болдоггүй интегралын хэсгийг авах хэрэгтэй, гэхдээ dv- амархан нэгтгэж болох интегралын ийм хэсэг. Энэ хичээлийн сүүлчийн жишээ бол яг ийм интегралын шийдэл юм.
Хэсэгээр нэгтгэх томъёо нь дараах байдалтай байна.
.
Хэсэгээр нь нэгтгэх арга нь энэ томъёог хэрэглэхээс бүрдэнэ. Практик хэрэглээний хувьд u ба v нь интеграцийн хувьсагчийн функцууд гэдгийг тэмдэглэх нь зүйтэй. Интеграл хувьсагчийг x (интеграл тэмдэглэгээний төгсгөл дэх дифференциал тэмдгийн d-ийн дараах тэмдэг) гэж тэмдэглэе. Дараа нь u ба v нь x функцууд болно: u(x) ба v(x) .
Дараа нь
, .
Мөн хэсгүүдээр нэгтгэх томъёо нь дараах хэлбэртэй байна.
.
Өөрөөр хэлбэл интеграл функц нь хоёр функцийн үржвэрээс бүрдэх ёстой.
,
нэгийг нь бид u гэж тэмдэглэдэг: g(x) = u, нөгөөгийн хувьд интегралыг тооцоолох шаардлагатай (илүү нарийвчлалтай, эсрэг деривативыг олох ёстой):
, дараа нь dv = f(x) dx .
Зарим тохиолдолд f(x) = 1
.
,
Энэ нь интегралд
бид g(x) = u, x = v гэж тавьж болно.
Үргэлжлэл
;
.
Тиймээс, энэ аргын хувьд хэсгүүдийн интеграцийн томъёог санаж, хоёр хэлбэрээр ашиглах ёстой.
Интегралыг хэсэг хэсгээр нь нэгтгэж тооцсон
Логарифм болон урвуу тригонометрийн (гипербол) функцийг агуулсан интегралууд
Логарифм, урвуу тригонометр эсвэл гипербол функц агуулсан интегралууд нь ихэвчлэн хэсгүүдээр нэгтгэгддэг. Энэ тохиолдолд логарифм буюу урвуу тригонометрийн (гипербол) функцийг агуулсан хэсгийг u, үлдсэн хэсгийг dv гэж тэмдэглэнэ.
, , , , , , .
Хэсэгчилсэн интегралын аргаар тооцоолсон ийм интегралуудын жишээ энд байна.
Олон гишүүнт ба sin x, cos x эсвэл e x-ийн үржвэрийг агуулсан интегралууд
, , ,
Энд P(x) нь х дахь олон гишүүнт юм. Интегралдах үед олон гишүүнт P(x)-ийг u, e ax dx, cos ax dx эсвэлнүгэл сүх dx
- dv-ээр дамжуулан.
, , .
Ийм интегралуудын жишээ энд байна:
Хэсэгээр интегралдах аргыг ашиглан интегралыг тооцоолох жишээ
Логарифм болон урвуу тригонометрийн функц агуулсан интегралын жишээ
Жишээ
Интегралыг тооцоолох:
Нарийвчилсан шийдэл
Энд интеграл нь логарифм агуулна. Сэлгээ хийх у =,
ln x dv = x.
Дараа нь
,
.
2 dx
.
Дараа нь
.
Бид үлдсэн интегралыг тооцоолно:
Тооцооллын төгсгөлд тодорхойгүй интеграл нь бүх антидеривативуудын олонлог тул тогтмол C нэмэх шаардлагатай. Үүнийг мөн завсрын тооцоонд нэмж болох боловч энэ нь зөвхөн тооцооллыг гацаана.
Богино шийдэл
.Та шийдлийг богино хувилбараар танилцуулж болно. Үүнийг хийхийн тулд та u болон v-ээр орлуулалт хийх шаардлагагүй, харин хүчин зүйлсийг бүлэглэж, интеграцийг хэсгүүдийн томъёогоор хоёр дахь хэлбэрээр хэрэглэж болно.
Хариулт
Логарифм болон урвуу тригонометрийн функц агуулсан интегралын жишээ
Жишээ
.
Олон гишүүнт ба sin x, cos x эсвэл ex-ийн үржвэрийг агуулсан интегралын жишээ
Шийдэл
Дифференциал тэмдгийн дор илтгэгчийг танилцуулъя:.
e - x dx = - e - x d(-x) = - d(e - x)
.
Хэсэгээр нь нэгтгэе.
.
.
.
Бид мөн хэсгүүдээр нэгтгэх аргыг ашигладаг.
Эцэст нь бидэнд байна.Хэсэг хэсгүүдээр нэгтгэх
- нэг интеграл нь амархан интегралдах, нөгөө нь дифференциалагдах үед тодорхой ба тодорхойгүй интегралыг шийдвэрлэхэд ашигладаг арга. Тодорхойгүй ба тодорхой интегралыг олох нэлээд түгээмэл арга. Үүнийг ашиглах шаардлагатай үед гол тэмдэг нь хоосон цэгүүдийг нэгтгэж болохгүй хоёр функцийн үржвэрээс бүрдэх тодорхой функц юм.
Томъёо
Энэ аргыг амжилттай ашиглахын тулд та томъёог ойлгож, сурах хэрэгтэй.
Тодорхой бус интеграл дахь хэсгүүдээр интегралчлах томъёо:
$$ \int udv = uv - \int vdu $$
Тодорхой интеграл дахь хэсгүүдээр интеграцийн томъёо:
$$ \int \limits_(a)^(b) udv = uv \bigg |_(a)^(b) - \int \limits_(a)^(b) vdu $$
Шийдлийн жишээ
| Туршилтын үеэр багш нарын санал болгодог хэсгүүдээр нэгтгэх шийдлүүдийн жишээг практик дээр авч үзье. Интеграл тэмдгийн дор хоёр функцийн үржвэр байгааг анхаарна уу. Энэ арга нь шийдэлд тохиромжтой гэсэн дохио юм. |
| Жишээ 1 |
| $ \int xe^xdx $ интегралыг ол |
|
Интеграл нь хоёр функцээс бүрдэх бөгөөд тэдгээрийн нэг нь ялгах үед шууд нэгдмэл болж хувирдаг, нөгөө нь амархан нэгтгэгддэг болохыг бид харж байна. Интегралыг шийдэхийн тулд бид хэсгүүдээр нэгтгэх аргыг ашигладаг. $ u = x \rightarrow du=dx $ ба $ dv = e^x dx \rightarrow v=e^x $ гэж үзье. Бид олсон утгыг эхний интеграцийн томъёонд орлуулж, дараахь зүйлийг авна. $$ \int xe^x dx = xe^x - \int e^x dx = xe^x - e^x + C $$ Хэрэв та асуудлаа шийдэж чадахгүй бол бидэнд илгээнэ үү. Бид нарийвчилсан шийдлийг өгөх болно. Та тооцооллын явцыг харж, мэдээлэл авах боломжтой болно. Энэ нь таныг багшаасаа цаг тухайд нь дүнгээ авахад тусална! |
| Хариулт |
|
$$ \int xe^x dx = xe^x - e^x + C $$ |
| Жишээ 4 |
| $ \int \limits_0 ^1 (x+5) 3^x dx $ интегралыг тооцоол. |
| $ \int xe^xdx $ интегралыг ол |
|
Өмнөх шийдэгдсэн жишээнүүдийн адилаар бид ямар функцийг асуудалгүйгээр нэгтгэх, алийг нь ялгахыг олж мэдэх болно. Хэрэв бид $ (x+5) $ гэж ялгавал энэ илэрхийлэл автоматаар нэгдмэл болж хувирах бөгөөд энэ нь бидний давуу тал болно гэдгийг анхаарна уу. Тиймээс бид үүнийг хийдэг: $$ u=x+5 \rightarrow du=dx, dv=3^x dx \rightarrow v=\frac(3^x)(ln3) $$ Одоо бүх үл мэдэгдэх функцууд олдсон бөгөөд тэдгээрийг тодорхой интегралын хэсгүүдээр нэгтгэх хоёр дахь томьёо руу оруулж болно. $$ \int \limits_0 ^1 (x+5) 3^x dx = (x+5) \frac(3^x)(\ln 3) \bigg |_0 ^1 - \int \limits_0 ^1 \frac (3^x dx)(\ln 3) = $$ $$ = \frac(18)(\ln 3) - \frac(5)(\ln 3) - \frac(3^x)(\ln^2 3)\bigg| _0 ^1 = \frac(13)(\ln 3) - \frac(3)(\ln^2 3)+\frac(1)(\ln^2 3) = \frac(13)(\ln 3) )-\frac(4)(\ln^2 3) $$ |
| Хариулт |
| $$ \int\limits_0 ^1 (x+5)3^x dx = \frac(13)(\ln 3)-\frac(4)(\ln^2 3) $$ |








