Приложение

Степенные ряды на сайт для практических занятий с целью закрепления пройденного материала. И оттачивания навыков студентов для того, чтобы научиться однозначно определять сходимость степенного ряда. Практические занятия в полной мере дают желаемый результат, если в курсе по изучению выделено достаточное количество занятий. Это в полной мере обеспечит высококлассную подготовку учащихся. Но что делать, когда их нет? В этом случае решить степенные ряды онлайн поможет как раз наш сайт, или аналогичный ресурс. Однако не всегда подобные калькуляторы смогут предоставить правильный ответ на поставленную задачу. Как раз для этого на примере одного условия нужно сравнить полученные ответы между решениями подобных сайтов. Можно заметить, что область сходимости ряда вычисляется порой по разным теоремам и ответ, хоть он и правильный, но может быть выражен отличными формами записи. Конечно, такое не будет считаться ошибкой, все дело в том, как именно вам будет удобнее его воспринимать. Короче говоря, найти сходимость степенного ряда с помощью того или иного сайта, решать вам, то есть как будет вам удобно для дальнейших применений ответа. Иногда само решение степенного ряда выражают через записи со знаками неравенств, а чаще всего через знак модуля. Это не случайно, поскольку на практике используют наиболее чаще приемы сравнений общих членов ряда с использованием модулей. Через ряд преобразований выделяют переменную, заключенную в модуль, и остается краткая запись, которая нормально воспринимается для понимания решения. Для наглядного представления радиус сходимости ряда можно представить на числовой оси с указанием граничных точек, это, кстати, тоже приветствуется в ряде случаев. Не нужно загонять себя в какие-то определенные рамки, которые сузят ваш кругозор. Вообще-то говоря, степенные ряды важная тема в математике, поскольку сложная и для того, чтобы её понять, вам придется изучить несколько курсов. Например, теорию предельного перехода и интегральное исчисление, поскольку для доказательства сходимости степенного ряда часто используют именно такие приемы, в которых присутствуют эти действия. Для вас мы предлагаем пройти практические занятия, и проверит свои знаний по изучению степенных рядов онлайн прямо на сайт, поскольку мы даем гарантию, что все решаемые задачи выдаются с точным ответом, в считанные секунды и абсолютно бесплатно в режиме реального времени. Помимо области сходимости ряда, или как её еще называют радиус сходимости ряда, мы предлагаем вашему вниманию много других сопутствующих калькуляторов, которые вы, безусловно, оцените на высочайшем уровне. Если требуется найти сходимость степенного ряда, то предоставьте это сделать за вас именно нам, поскольку сайт есть залог точности и гарантия безупречного качественного ответа. Многие студенты не редко задаются таким вопросом как быстрая подготовка в решении степенного ряда, но не просто решение, а качественное и правильное. Во все времена степенные ряды носили более обширный смысл, чем об этом сейчас рассказывают ученикам. Оно и понятно, потому что объясняется это тем, что нет времени в связи с необходимостью глубокого изучения более важные тем. С одной стороны - ДА, но тогда означает ли это, что можно пренебрегать сходимостью степенного ряда? Скорее всего, нет, так как, не изучив должным образом степенные ряды онлайн, вы попросту не сможете грамотно ответить на очевидные вопросы на защите курсовой или дипломной работы. Допустим, ваша предметная область включает такую дисциплину как механика сплошных сред или строительная механика. Очевидно, что устойчивость систем важна при проектировании стратегических объектов, тем более, если это напрямую касается охраны жизнедеятельности людей. Казалось бы, что можно вынести полезного, если научиться или хотя бы понять суть как находить область сходимости ряда? Трудно в одном предложении передать важность этого определения. Но поверьте на слово, найти сходимость степенного ряда такая же важная и необходимая процедура, как, к примеру, знать теорему Пифагора. Если решение степенного ряда будет выполнено с ошибкой, то в дальнейших расчетах обязательно это сыграет злую шутку со студентом. Бывает порой, что из-за досадной неточности в ошибке происходит крушение летательного аппарата уже на первых испытаниях. Согласитесь, это обидно после проделанных работ и колоссального вклада времени. Поэтому учитесь и еще раз учитесь находить радиус сходимости ряда, прививая тем самым с самого начала правильность т строгость в решении задач. Вернемся к теме степенные ряды и расскажем немного об этом разделе подробнее. В практике множество степенных рядов начинаются именно с первого члена, хотя встречаются такие ряды, в условии которых первый член может начаться и со второго, и с третьего члена. Во многом это связано с тем, что, например, начиная с первого члена, сразу обращается в бесконечность вся сумма ряда, что конечно тривиально, по сути. Сходимость степенного ряда как предмет изучения области его сходимости, на практике применяется не часто, особенно студентами, если они не проходят её на кафедре математического анализа. Суть ясна и задачи все расставлены. Наш калькулятор вычисляет степенные ряды онлайн, а также говорит о сходимости ряда, по какому признаку числовой ряд сходится, короче говоря, умеет определять сходимость степенных рядов. Попасть в область сходимости ряда переменная может, если удовлетворяет конкретному единственному условию, то есть чтобы соответствующий получившийся при этом числовой ряд сходился к конечному действительному числовому значению. Пожалуй, это не одно условие, нужно также, чтобы все члены ряда при любом порядковом натуральном значении параметра n существовал и однозначно определялся. Найти сходимость степенного ряда означает определить область его сходимости на числовой оси абсцисс, если речь идет о декартовой системе координат. Такое сделать представляется возможным по признаку Даламбера, однако, нужно понимать, что лишь по признаку, так как сам принцип устанавливает лишь интервал, в который попадет переменная. Помните, для функциональных рядов признак Даламбера не применим, он только для числовых рядов. Решение степенного ряда напрямую связано с нахождением радиуса сходимости этого ряда, но для краткости выражаются именно так. Мы тоже будем применять этот термин, дабы не отставать от тенденции в научном мире. Степенные ряды в граничных точках изучаются отдельно. Разумеется, это есть часть общей задачи по исследованию на сходимость степенного ряда. В этих граничных точках ряд исследуется как числовой - знакопостоянный или знакопеременный, в зависимости от вида общего члена ряда. Ряды, членами которых являются степенные функции, называются степенными рядами, а калькулятор может решать их онлайн. Когда так говорят, сразу приходит на ум следующее предположение, а если членами ряда будут являться периодические функции, то такой ряд наверно должен называться функциональным периодическим рядом! Забавное дело получается, но все очень серьезно. Когда мы определили область сходимости ряда, необходимо после этого проделать завершающие вычисления, а именно исследовать числовые ряды на сходимость, которые получаются путем подстановок границ определенного интервала вместо переменной x степенного ряда. Дальше сможете написать полноценный ответ с решением. Рассмотрим пример, как можно найти сходимость степенного ряда без применения основных теорем, а лишь сравнительным способом. При этом нужно грамотно составлять сравнения двух функциональных рядов до тех пор, пока не упростим исходный ряд до давно изученного элементарного. По этому принципу возьмем за ответ как раз результат давно известный всем наперед. По решению степенного ряда еще не однозначно можно предположить, какой же точно будет радиус сходимости ряда, поскольку перед этим еще надо произвести исследование как минимум двух числовых рядов на каждой из границ интервала.. По виду все степенные ряды одинаковы тем, что их общий член представляет собой обычную функцию от аргумента. Суть изучения состоит как раз в том, чтобы определить допустимые значения этого аргумента для сходимости ряда (условной или безусловной), а также на каких интервалах соответствующий ему уже числовой ряд будет расходиться. Исследование степенного ряда на сходимость отнимает у вас уйму времени, и мы рекомендуем вам использовать готовый калькулятор сайт. Нужно исследовать и границы интервала тоже, в противном случае задачу будет выполнена не полностью, а значит, гарантировано снимут два балла. На нашем сайте вы можете вычислить сумму степенных рядов онлайн. Всегда быстро, надежно, а главное бесплатно! Удобный интерфейс и понятный запрос данных.. По праву область сходимости ряда есть конкретное условие существования суммы ряда числового. Если значение на границе интервала дает расхождение полученного знакопеременного ряда. то говорят, что ряд сходится условно, то есть он конечно сходится в этой области, но при определенных условиях, что немаловажно в любом случае. Если абстрагироваться от понятия степенного ряда, и на миг просто представить себе сумму степенного ряда как некую функцию по переменной x, то речь уже пойдет не о том, чтобы найти сходимость степенного ряда, а об определении таких условий, при которых будет существовать значение функции при разных значениях её аргумента x. Короче говоря, задачу сведем к простейшему нахождению области определения функции. Правда ведь очень просто и понятно! Любое решение степенного ряда всегда говорит о радиусе сходимости такого степенного ряда и обычно определяется через признак Даламбера, но не напрямую, а лишь с условием. После этого раскрывают модуль полученного неравенства и исследуют числовые ряды на абсолютную или условную сходимость. Потом делают вывод. Очень интересно, когда степенные ряды в первоначальном виде интегрируются или дифференцируются, а потом уже вычисляется сумма ряда от нового степенного ряда. Отсюда следуют много вариантов как себя ведет ряд при тех или иных условиях. Найденная сумма степенного ряда от проинтегрированных членов исходного ряда, есть, по сути, проинтегрированная сумма исходного степенного ряда. Интересно и познавательно, не правда ли? Если грамотно сформулировать текст задачи, то он выглядит примерно так: найти интервал сходимости степенного ряда и исследовать его на границах найденного интервала. Отсюда ряд может сходиться или расходиться абсолютно, что не требует дополнительных исследований. Равномерная сходимость показывает степенные ряды в онлайн вычислении, складывая поочередно все члены исходного ряда, записанного в классическом виде, как в университете. Полагаясь только на свое чутье, студент рискует по неопытности попасть в ловушку своей самоуверенности, когда проще простого взять и воспользоваться калькулятором сайт в самом начале учебы. Из области сходимости ряда делают выводы о сходимости функционального, а точнее степенного ряда, а именно устанавливают сходиться он либо условно, либо абсолютно. Все это необходимо для завершающей записи конечного ответа. Не усложняя ситуацию и не применяя названия сложных теорем, скажем, что найти сходимость степенного ряда будет проще для понимания, если представить в качестве суммы ряда некую функцию и уже исследовать именно ее. А это всем давно ясно и понятно как делать! Радиус сходимости ряда и решение степенного ряда понятия тождественные, так как означают одно и то же, точнее определяют однозначно ту область, значения переменной из которой дает сходимость соответственного числового ряда.

Среди функциональных рядов наиболее важное место занимают степенные ряды.

Степенным рядом называют ряд

члены которого – степенные функции, расположенные по возрастающим целым неотрицательным степеням x , а c 0 , c 1 , c 2 , c n - постоянные величины. Числа c 1 , c 2 , c n - коэффициенты членов ряда, c 0 - свободный член. Члены степенного ряда определены на всей числовой прямой.

Ознакомимся с понятием области сходимости степенного ряда. Это множество значений переменной x , для которых ряд сходится. Степенные ряды имеют довольно простую область сходимости. Для действительных значений переменной x область сходимости состоит либо из одной точки, либо является некоторым интервалом (интервалом сходимости), либо совпадает со всей осью Ox .

При подстановке в степенной ряд значения x = 0 получится числовой ряд

c 0 +0+0+...+0+... ,

который сходится.

Следовательно, при x = 0 сходится любой степенной ряд и, значит, область его сходимости не может быть пустым множеством. Структура области сходимости всех степенных рядов одинакова. Её можно установить с помощью следующей теоремы.

Теорема 1 (теорема Абеля) . Если степенной ряд сходится при некотором значении x = x 0 , отличном от нуля, то он сходится, и притом абсолютно, при всех значениях |x | < |x 0 | . Обратите внимание: и отправное значение "икс нулевое" и любое значение "икса", которое сравнивается с отправным, взяты по модулю - без учёта знака.

Следствие. Если степенной ряд расходится при некотором значении x = x 1 , то он расходится и при всех значениях |x | > |x 1 | .

Как мы уже выяснили ранее, любой степенной ряд сходится при значении x = 0. Есть степенные ряды, которые сходятся только при x = 0 и расходятся при остальных значениях х . Исключая из рассмотрения этот случай, предположим, что степенной ряд сходится при некотором значении x = x 0 , отличном от нуля. Тогда, по теореме Абеля, он сходится во всех точках интервала ]-|x 0 |, |x 0 |[ (интервала, левой и правой границами которого являются значения икса, при котором степенной ряд сходится, взятые соответственно со знаком минус и со знаком плюс), симметричного относительно начала координат.

Если же степенной ряд расходится при некотором значении x = x 1 , то на основании следствия из теоремы Абеля он расходится и во всех точках вне отрезка [-|x 1 |, |x 1 |] . Отсюда следует, что для любого степенного ряда имеется интервал , симметричный относительно начала координат, называемый интервалом сходимости , в каждой точке которого ряд сходится, на границах может сходиться, а может и расходиться, при чем не обязательно одновременно, а вне отрезка ряд расходится. Число R называется радиусом сходимости степенного ряда.

В частных случаях интервал сходимости степенного ряда может вырождаться в точку (тогда ряд сходится только при x = 0 и считается, что R = 0) или представлять собой всю числовую прямую (тогда ряд сходится во всех точках числовой прямой и считается, что ).

Таким образом, определение области сходимости степенного ряда заключается в определении его радиуса сходимости R и исследовании сходимости ряда на границах интервала сходимости (при ).

Теорема 2. Если все коэффициенты степенного ряда, начиная с некоторого, отличны от нуля, то его радиус сходимости равен пределу при отношения абсолютных величин коэффициентов общего следующего за ним членов ряда, т.е..

Пример 1. Найти область сходимости степенного ряда

Решение. Здесь

Используя формулу (28), найдём радиус сходимости данного ряда:

Исследуем сходимость ряда на концах интервала сходимости . В примере 13 показано, что данный ряд сходится при x = 1 и расходится при x = -1. Следовательно, областью сходимости служит полуинтервал .

Пример 2. Найти область сходимости степенного ряда

Решение. Коэффициенты ряда положительны, причём

Найдём предел этого отношения, т.е. радиус сходимости степенного ряда:

Исследуем сходимость ряда на концах интервала . Подстановка значений x = -1/5 и x = 1/5 в данный ряд даёт:

Первый из этих рядов сходится (см. пример 5). Но тогда в силу теоремы параграфа «Абсолютная сходимость» сходится и второй ряд, а область его сходимости – отрезок

Пример 3. Найти область сходимости степенного ряда

Решение. Здесь

По формуле (28) находим радиус сходимости ряда:

Исследуем сходимость ряда при значениях . Подставив их в данный ряд, соответственно получим

Оба ряда расходятся, так как не выполняется необходимое условие сходимости (их общие члены не стремятся к нулю при ). Итак, на обоих концах интервала сходимости данный ряд расходится, а область его сходимости – интервал .

Пример 5. Найти область сходимости степенного ряда

Решение. Находимо отношение , где , а :

Согласно формуле (28) радиус сходимости данного ряда

то есть ряд сходится только при x = 0 и расходится при остальных значениях х .

Примеры показывают, что на концах интервала сходимости ряды ведут себя различно. В примере 1 на одном конце интервала сходимости ряд сходится, а на другом – расходится, в примере 2 – на обоих концах сходится, в примере 3 – на обоих концах расходится.

Формула радиуса сходимости степенного ряда получена в предположении, что все коэффициенты членов ряда, начиная с некоторого, отличны от нуля. Поэтому применение формулы (28) допустимо только в этих случаях. Если это условие нарушается, то радиус сходимости степенного ряда следует искать с помощью признака Даламбера , или же, сделав замену переменной, преобразованием ряда к виду, в котором указанное условие выполняется.

Пример 6. Найти интервал сходимости степенного ряда

Решение. Данный ряд не содержит членов с нечётными степенями х . Поэтому преобразуем ряд, полагая . Тогда получим ряд

для нахождения радиуса сходимости которого можно применить формулу (28). Так как , а , то радиус сходимости этого ряда

Из равенства получаем , следовательно, данный ряд сходится на интервале .

Сумма степенного ряда. Дифференцирование и интегрирование степенных рядов

Пусть для степенного ряда

радиус сходимости R > 0, т.е. этот ряд сходится на интервале .

Тогда каждому значению х из интервала сходимости соответствует некоторая сумма ряда. Следовательно, сумма степенного ряда есть функция от х на интервале сходимости. Обозначая её через f (x ), можем записать равенство

понимая его в том смысле, что сумма ряда в каждой точке х из интервала сходимости равна значению функции f (x ) в этой точке. В этом же смысле будем говорить, что степенной ряд (29) сходится к функции f (x ) на интервале сходимости.

Вне интервала сходимости равенство (30) не имеет смысла.

Пример 7. Найти сумму сумму степенного ряда

Решение. Это геометрический ряд, у которого a = 1, а q = x . Следовательно, его сумма есть функция . Ряд сходится, если , а - его интервал сходимости. Поэтому равенство

справедливо лишь для значений , хотя функция определена для всех значений х , кроме х = 1.

Можно доказать, что сумма степенного ряда f (x ) непрерывна и дифференцируема на любом отрезке внутри интервала сходимости, в частности в любой точке интервала сходимости ряда.

Приведем теоремы о почленном дифференцировании и интегрировании степенных рядов.

Теорема 1. Степенной ряд (30) в интервале его сходимости можно почленно дифференцировать неограниченное число раз, причём получающиеся при этом степенные ряды имеют тот же радиус сходимости, что исходный ряд, а суммы их соответственно равны .

Теорема 2. Степенной ряд (30) можно неограниченное число раз почленно интегрировать в пределах от 0 до х , если , причём получающиеся при этом степенные ряды имеют тот же радиус сходимости, что и исходный ряд, а суммы их соответственно равны

Разложение функций в степенные ряды

Пусть дана функция f (x ), которую требуется разложить в степенной ряд, т.е. представить в виде (30):

Задача состоит в определении коэффициентов ряда (30). Для этого, дифференцируя равенство (30) почленно, последовательно найдём:

……………………………………………….. (31)

Полагая в равенствах (30) и (31) х = 0, находим

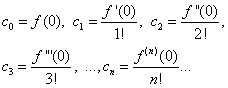
Подставляя найденные выражения в равенство (30), получим

(32)

Найдём разложение в ряд Маклорена некоторых элементарных функций.

Пример 8. Разложить в ряд Маклорена функцию

Решение. Производные этой функции совпадают с самой функцией:

Поэтому при х = 0 имеем

Подставляя эти значения в формулу (32), получим искомое разложение:

(33)

Этот ряд сходится на всей числовой прямой (его радиус сходимости ).

Пример 1. Найти область сходимости степенного ряда:

а) ; б);

в) ; г)
;

д)
.

а) Найдем радиус сходимости R . Так как
,
, то

x
, то есть интервал сходимости ряда
.

При
получаем числовой ряд . Этот ряд сходится, так как является обобщенным гармоническим рядомпри
.

При
получаем числовой ряд
. Этот ряд абсолютно сходящийся, так как ряд, составленный из абсолютных величин его членов, сходящийся.

б) Найдем радиус сходимости R . Так как
, то
.

Итак, интервал сходимости ряда
.

Исследуем на сходимость данный ряд на концах интервала сходимости.

При
имеем числовой ряд

.

При
имеем числовой ряд
. Этот ряд расходящийся, так как
не существует.

Итак, область сходимости данного ряда
.

в) Найдем радиус сходимости R . Так как
,
то
.

Итак, интервал сходимости
. Область сходимости данного ряда совпадает с интервалом сходимости, то есть ряд сходится при любом значении переменнойx .

г) Найдем радиус сходимости R . Так как
,
то
.

Так как
, то ряд сходится только в точке
. Значит, область сходимости данного ряда представляет собой одну точку
.

д) Найдем радиус сходимости R .

Так как
,
, то

Итак, ряд сходится абсолютно для всех x , удовлетворяющих неравенству
, то есть
.

Отсюда
− интервал сходимости,
− радиус сходимости.

Исследуем данный ряд на сходимость на концах интервала сходимости.

При
получаем числовой ряд

который расходится (гармонический ряд).

При
получаем числовой ряд
, который сходится условно (ряд сходится по признаку Лейбница, а ряд, составленный их абсолютных величин его членов, расходится, так как является гармоническим).

Итак, область сходимости ряда
.

2.3. Ряды Тейлора и Маклорена.

Разложение функций в степенной ряд.

Приложение степенных рядов к приближенным вычислениям

Примеры решения задач

Пример 1. Разложить в степенной ряд функции:

а)
; б)
;

в)
; г)
.

а) Заменив в формуле
x на
, получим искомое разложение:

Где

б) Заменяя в равенстве

Где
x на
, получим искомое разложение:

в) Данную функцию можно записать так:
. Чтобы найти искомый ряд, достаточно в разложение

Где
подставить
. Тогда получим:

г) Данную функцию можно переписать так: .

Функцию
можно разложить в степенной ряд, положив в биномиальном ряде
, получим .

Где
.

Чтобы получить искомое разложение, достаточно перемножить полученные ряды (ввиду абсолютной сходимости этих рядов).

Следовательно,

, где
.

Пример 2. Найти приближенные значения данных функций:

а)
с точностью до 0,0001;

б)
с точностью до 0,00001.

а) Так как
, то в разложение функции , где
подставим
:

или

Так как
, то требуемая точность будет обеспечена, если ограничиться только первыми двумя членами полученного разложения.

Используем биномиальный ряд

Где
.

Полагая
и
, получим следующее разложение:

Если в последнем знакочередующемся ряде учитывать только первые два члена, а остальные отбросить, то погрешность при вычислении
не превысит по абсолютной величине 0,000006. Тогда погрешность при вычислении
не превысит числа . Следовательно,

Пример 3. Вычислить с точностью до 0,001:

а)
; б)
.

а)
.

Разложим подынтегральную функцию в степенной ряд. Для этого подставим в биномиальный ряд
и заменим x на :

Так как отрезок интегрирования
принадлежит области сходимости полученного ряда
, то будем интегрировать почленно в указанных пределах:

В полученном знакочередующемся ряде четвертый член по абсолютной величине меньше 0,001. Следовательно, требуемая точность будет обеспечена, если учитывать только первые три члена ряда.

Так как первый из отброшенных членов имеет знак минус, то полученное приближенное значение будет с избытком. Поэтому ответ с точностью до 0,001 равен 0,487.

б) Предварительно представим подынтегральную функцию в виде степенного ряда. Заменим в разложении функции

Где

x на
, получим:

Тогда
.

Полученный знакочередующийся ряд удовлетворяет условиям признака Лейбница. Четвертый член ряда по абсолютной величине меньше 0,001. Чтобы обеспечить требуемую точность, достаточно найти сумму первых трех членов.

Следовательно,
.

Функциональные ряды. Степенные ряды.
Область сходимости ряда

Смех без причины – признак Даламбера

Вот и пробил час функциональных рядов. Для успешного освоения темы, и, в частности, этого урока, нужно хорошо разбираться в обычных числовых рядах. Следует хорошо понимать, что такое ряд, уметь применять признаки сравнения для исследования ряда на сходимость. Таким образом, если Вы только-только приступили к изучению темы или являетесь чайником в высшей математике, необходимо последовательно проработать три урока: Ряды для чайников , Признак Даламбера. Признаки Коши и Знакочередующиеся ряды. Признак Лейбница . Обязательно все три! Если есть элементарные знания и навыки решения задач с числовыми рядами, то справиться с функциональными рядами будет довольно просто, поскольку нового материала не очень и много.

На данном уроке мы рассмотрим понятие функционального ряда (что это вообще такое), познакомимся со степенными рядами, которые встречаются в 90% практических заданий, и научимся решать распространенную типовую задачу на нахождение радиуса сходимости, интервала сходимости и области сходимости степенного ряда. Далее рекомендую рассмотреть материал о разложении функций в степенные ряды , и «скорая помощь» начинающему будет оказана. Немного отдышавшись, переходим на следующий уровень:

Также в разделе функциональных рядов есть их многочисленные приложения к приближённым вычислениям , и некоторым особняком идут Ряды Фурье , которым в учебной литературе, как правило, выделяется отдельная глава. У меня всего лишь одна статья, но зато длиннющая и много-много дополнительных примеров!

Итак, ориентиры расставлены, поехали:

Понятие функционального ряда и степенного ряда

Если в пределе получается бесконечность , то алгоритм решения также заканчивает свою работу, и мы даём окончательный ответ задания: «Ряд сходится при » (или при либо »). Смотрите случай №3 предыдущего параграфа.

Если в пределе получается не ноль и не бесконечность , то у нас самый распространенный на практике случай №1 – ряд сходится на некотором интервале.

В данном случае предел равен . Как найти интервал сходимости ряда? Составляем неравенство:

В ЛЮБОМ задании данного типа в левой части неравенства должен находиться результат вычисления предела , а в правой части неравенства – строго единица . Не буду объяснять, почему именно такое неравенство и почему справа единица. Уроки носят практическую направленность, и уже очень хорошо, что от моих рассказов не повесился профессорско-преподавательский состав стали понятнее некоторые теоремы.

Техника работы с модулем и решения двойных неравенств подробно рассматривалась на первом курсе в статье Область определения функции , но для удобства я постараюсь максимально подробно закомментировать все действия. Раскрываем неравенство с модулем по школьному правилу . В данном случае:

Половина пути позади.

На втором этапе необходимо исследовать сходимость ряда на концах найденного интервала.

Сначала берём левый конец интервала и подставляем его в наш степенной ряд :

При

Получен числовой ряд, и нам нужно исследовать его на сходимость (уже знакомая из предыдущих уроков задача).

1) Ряд является знакочередующимся.
2) – члены ряда убывают по модулю. При этом каждый следующий член ряда по модулю меньше предыдущего: , значит, убывание монотонно.
Вывод: ряд сходится.

С помощью ряда, составленного из модулей, выясним, как именно:
– сходится («эталонный» ряд из семейства обобщенного гармонического ряда).

Таким образом, полученный числовой ряд сходится абсолютно .

при – сходится.

! Напоминаю , что любой сходящийся положительный ряд тоже является абсолютно сходящимся.

Таким образом, степенной ряд сходится, причём абсолютно, на обоих концах найденного интервала.

Ответ: область сходимости исследуемого степенного ряда:

Имеет право на жизнь и другое оформление ответа: Ряд сходится, если

Иногда в условии задачи требуют указать радиус сходимости. Очевидно, что в рассмотренном примере .

Пример 2

Найти область сходимости степенного ряда

Решение: интервал сходимости ряда найдём с помощью признака Даламбера (но не ПО признаку! – для функциональных рядов такого признака не существует) :

Ряд сходится при

Слева нам нужно оставить только , поэтому умножаем обе части неравенства на 3:

– Ряд является знакочередующимся.
– – члены ряда убывают по модулю. Каждый следующий член ряда по модулю меньше предыдущего: , значит, убывание монотонно.

Вывод: ряд сходится.

Исследуем его на характер сходимости:

Сравним данный ряд с расходящимся рядом .
Используем предельный признак сравнения :

Получено конечное число, отличное от нуля, значит, ряд расходится вместе с рядом .

Таким образом, ряд сходится условно .

2) При – расходится (по доказанному).

Ответ: Область сходимости исследуемого степенного ряда: . При ряд сходится условно.

В рассмотренном примере областью сходимости степенного ряда является полуинтервал, причем во всех точках интервала степенной ряд сходится абсолютно , а в точке , как выяснилось – условно .

Пример 3

Найти интервал сходимости степенного ряда и исследовать его сходимость на концах найденного интервала

Это пример для самостоятельного решения.

Рассмотрим пару примеров, которые встречаются редко, но встречаются.

Пример 4

Найти область сходимости ряда:

Решение: с помощью признака Даламбера найдем интервал сходимости данного ряда:

(1) Составляем отношение следующего члена ряда к предыдущему.

(2) Избавляемся от четырехэтажности дроби.

(3) Кубы и по правилу действий со степенями подводим под единую степень. В числителе хитро раскладываем степень , т.е. раскладываем таким образом, чтобы на следующем шаге сократить дробь на . Факториалы расписываем подробно.

(4) Под кубом почленно делим числитель на знаменатель, указывая, что . В дроби сокращаем всё, что можно сократить. Множитель выносим за знак предела, его можно вынести, поскольку в нём нет ничего, зависящего от «динамической» переменной «эн». Обратите внимание, что знак модуля не нарисован – по той причине, что принимает неотрицательные значения при любом «икс».

В пределе получен ноль, а значит, можно давать окончательный ответ:

Ответ: Ряд сходится при

А сначала-то казалось, что этот ряд со «страшной начинкой» будет трудно решить. Ноль или бесконечность в пределе – почти подарок, ведь решение заметно сокращается!

Пример 5

Найти область сходимости ряда

Это пример для самостоятельного решения. Будьте внимательны;-) Полное решение ответ в конце урока.

Рассмотрим еще несколько примеров, содержащих элемент новизны в плане использования технических приемов.

Пример 6

Найти интервал сходимости ряда и исследовать его сходимость на концах найденного интервала

Решение: В общий член степенного ряда входит множитель , обеспечивающий знакочередование. Алгоритм решения полностью сохраняется, но при составлении предела мы игнорируем (не пишем) этот множитель, поскольку модуль уничтожает все «минусы».

Интервал сходимости ряда найдём с помощью признака Даламбера:

Составляем стандартное неравенство:
Ряд сходится при
Слева нам нужно оставить только модуль , поэтому умножаем обе части неравенства на 5:

Теперь раскрываем модуль уже знакомым способом:

В середине двойного неравенства нужно оставить только «икс», в этих целях из каждой части неравенства вычитаем 2:

– интервал сходимости исследуемого степенного ряда.

Исследуем сходимость ряда на концах найденного интервала:

1) Подставляем значение в наш степенной ряд :

Будьте предельно внимательны, множитель не обеспечивает знакочередование, при любом натуральном «эн» . Полученный минус выносим за пределы ряда и забываем про него, поскольку он (как и любая константа-множитель) никак не влияет на сходимость или расходимость числового ряда.

Еще раз заметьте , что в ходе подстановки значения в общий член степенного ряда у нас сократился множитель . Если бы этого не произошло, то это бы значило, что мы либо неверно вычислили предел, либо неправильно раскрыли модуль.

Итак, требуется исследовать на сходимость числовой ряд . Здесь проще всего использовать предельный признак сравнения и сравнить данный ряд с расходящимся гармоническим рядом. Но, если честно, предельный признак сравнения до ужаса мне надоел, поэтому внесу некоторое разнообразие в решение.

Итак, ряд сходится при

Умножаем обе части неравенства на 9:

Извлекаем из обеих частей корень, при этом помним старый школьный прикол :

Раскрываем модуль:

и прибавляем ко всем частям единицу:

– интервал сходимости исследуемого степенного ряда.

Исследуем сходимость степенного ряда на концах найденного интервала:

1) Если , то получается следующий числовой ряд: