Gjendet numri i kërkuar: a 0 = k − 1 (\displaystyle a_(0)=k-1).

Herën e dytë që aksioma e Arkimedit u përdor në mënyrë implicite për të vërtetuar se gjatësitë e segmenteve të sekuencës priren në zero I 0 , I 1 , I 2 , … (\shfaqja e stilit I_(0),I_(1),I_(2),\ldots ):

Një provë rigoroze e këtij propozimi bazohet në aksiomën e Arkimedit. Le të vërtetojmë relacionin ekuivalent

Sipas aksiomës së Arkimedit, cilido qoftë numri real E > 0 (\displaystyle E>0), sekuenca e numrave natyrorë 1 , 2 , … (\shfaqja e stilit 1,2,\ldot) do ta tejkalojë atë, duke u nisur nga një numër i caktuar. Dhe që për të gjithë n (\displaystyle n) ka pabarazi

pastaj sekuenca 10 n (\displaystyle 10^(n)) do të kalojë gjithashtu E (\displaystyle E), duke filluar nga i njëjti numër. Sipas përkufizimit të një sekuence numrash, kjo do të thotë se lim n → ∞ 10 n = ∞ (\displaystyle \lim _(n\to \infty )10^(n)=\infty ).

Dykuptimësia dhjetore

Duke përdorur algoritmin e mësipërm, ne mund të për çdo numër real α (\displaystyle \alfa) ndërtoni një thyesë dhjetore që përfaqëson një numër të caktuar. Megjithatë, mund të ndodhë që i njëjti numër α (\displaystyle \alfa) mund të paraqitet si thyesë dhjetore dhe në mënyra të tjera.

Jo unike e paraqitjes së numrave në formën e thyesave dhjetore rrjedh nga fakti i parëndësishëm se duke caktuar zero në të djathtë pas pikës dhjetore në thyesën përfundimtare, do të marrim thyesa dhjetore të ndryshme që përfaqësojnë të njëjtin numër.

Merrni për shembull thyesën dhjetore

Sipas përkufizimit, kjo thyesë është një paraqitje e një numri 0 + 9 / 10 + 9 / 100 + … = 1 (\stil ekrani 0+9/10+9/100+\pika =1). Megjithatë, ky numër mund të përfaqësohet edhe si thyesë dhjetore 1, 00 … (\shfaqja e stilit 1(,)00\ldot).

Ky shembull mund të përgjithësohet. Mund të tregohet se thyesat

Ku a n ≠ 9 (\displaystyle a_(n)\neq 9), përfaqësojnë të njëjtin numër real.

Rezulton se ky shembull i përgjithshëm shter të gjitha rastet e paqartësisë në paraqitjen e numrave realë në formën e thyesave dhjetore. Në këtë rast, ne, natyrisht, nuk i konsiderojmë rastet e parëndësishme të thyesave të marra duke shtuar zero në fund të njëra-tjetrës, si dhe një palë thyesa dhe .

Këto rezultate mund të përmblidhen në teoremën e mëposhtme.

Teorema. Çdo numër real α (\displaystyle \alfa), e papërfaqësueshme në formë p / 10 s (\displaystyle p/10^(s)), Ku p (\displaystyle p)- e tërë, s (\displaystyle s)- një numër i plotë jo negativ, pranon një paraqitje të vetme në formën e një thyese dhjetore; Për më tepër, kjo pjesë është e pafundme.

Çdo numër real i formularit α = p / 10 s (\displaystyle \alfa =p/10^(s)) mund të paraqitet si dhjetore në më shumë se një mënyrë. Nëse α ≠ 0 (\displaystyle \alfa \neq 0), atëherë mund të paraqitet ose si një thyesë dhjetore e fundme, si dhe një thyesë e pafundme e përftuar duke shtuar zero në fund pas presjes dhjetore, ose si një thyesë e pafundme që përfundon me . Numri α = 0 (\displaystyle \alfa =0) mund të paraqitet me thyesa të formës + 0 , 00 … (\displaystyle +0(,)00\ldpiks), si dhe thyesat e formës − 0 , 00 … (\style display -0(,)00\lds).

Koment. Thyesat e pafundme që mbarojnë me 999 … (\displaystyle 999\ldots), fitohen nëse në algoritmin e mësipërm zgjedhim gjithmonë segmenti i majtë në vend të drejtë.

Zero shtesë dhe gabim

Duhet të theksohet se, nga pikëpamja, shkrimi i një thyese dhjetore me zero në fund nuk është plotësisht identik me shkrimin e tij pa këto zero.

Në përgjithësi pranohet se nëse gabimi nuk është specifikuar, atëherë thyesa dhjetore është e barabartë me plus ose minus gjysmën [ ] njësitë e shifrës së fundit të shkruar. Për shembull, duke shkruar "3.7" do të thotë që gabimi absolut është ±0.05. Dhe në hyrjen "3.700" gabimi absolut është ±0.0005. Shembuj të tjerë:

• "25" - gabimi absolut është ±0.5 (gjithashtu, një hyrje e tillë mund të nënkuptojë vlerën e saktë të 25: për shembull, 25 copë);
• "25.0" - gabimi absolut është ±0.05;
• "25.00" - gabimi absolut është ±0.005.

Dhjetore periodike

Quhet një thyesë dhjetore e pafundme periodike, nëse sekuenca e saj e shifrave pas presjes dhjetore, duke filluar nga një vend i caktuar, është një grup shifrash që përsëriten periodikisht. Me fjalë të tjera, një fraksion periodik është një fraksion dhjetor i formës

Kjo thyesë zakonisht shkruhet shkurt në formë

Përsëritja e grupit të numrave b 1 … b l (\stil ekrani b_(1)\ldpika b_(l)) thirrur periudhë thyesa, numri i shifrave në këtë grup është gjatësia e periudhës.

Nëse në një thyesë periodike perioda vjen menjëherë pas presjes dhjetore, atëherë thyesa quhet periodike e pastër. Nëse ka numra midis pikës dhjetore dhe pikës së parë, thyesa thirret periodike të përziera, dhe grupi i shifrave pas presjes dhjetore para shenjës së pikës së parë është para-periudha thyesat Për shembull, fraksioni 1 , (23) = 1,232 3 … (\style display 1(,)(23)=1(,)2323\ldots )është e pastër periodike, dhe thyesa 0 , 1 (23) = 0,123 23 … (\shfaqja e stilit 0(,)1(23)=0(,)12323\npika )- periodike e përzier.

Vetia kryesore e thyesave periodike, për shkak të së cilës ato dallohen nga i gjithë grupi i thyesave dhjetore, është se thyesat periodike dhe vetëm ato përfaqësojnë . Më saktësisht, vlen propozimi i mëposhtëm.

Teorema. Çdo thyesë dhjetore periodike e pafundme përfaqëson një numër racional. Në të kundërt, nëse një numër racional zgjerohet në një thyesë dhjetore të pafundme, atëherë kjo thyesë është periodike.

Mund të tregohet se thyesat thjesht periodike korrespondojnë me numrat racional, të shkruar si një thyesë e pakalueshme p / q (\displaystyle p/q) emërues q (\displaystyle q) nuk ka

Në këtë artikull ne do të fillojmë të eksplorojmë numrat racionalë. Këtu do të japim përkufizime të numrave racionalë, do të japim shpjegimet e nevojshme dhe do të japim shembuj të numrave racionalë. Pas kësaj, ne do të fokusohemi se si të përcaktojmë nëse një numër i caktuar është racional apo jo.

Navigimi i faqes.

Përkufizimi dhe shembuj të numrave racionalë

Në këtë pjesë do të japim disa përkufizime të numrave racionalë. Pavarësisht dallimeve në formulim, të gjitha këto përkufizime kanë të njëjtin kuptim: numrat racional bashkojnë numrat e plotë dhe thyesat, ashtu si numrat e plotë bashkojnë numrat natyrorë, të kundërtat e tyre dhe numrin zero. Me fjalë të tjera, numrat racional përgjithësojnë numrat e plotë dhe numrat thyesorë.

Le të fillojmë me përkufizimet e numrave racionalë, e cila perceptohet më natyrshëm.

Nga përkufizimi i dhënë rrjedh se një numër racional është:

• Çdo numri natyror n. Në të vërtetë, çdo numër natyror mund të përfaqësohet si një thyesë e zakonshme, për shembull, 3=3/1.
• Çdo numër i plotë, në veçanti numri zero. Në fakt, çdo numër i plotë mund të shkruhet ose si një fraksion pozitiv, një fraksion negativ ose si zero. Për shembull, 26=26/1, .
• Çdo thyesë e zakonshme (pozitive ose negative). Kjo vërtetohet drejtpërdrejt nga përkufizimi i dhënë i numrave racionalë.
• Çdo numër i përzier. Në të vërtetë, ju gjithmonë mund të paraqisni një numër të përzier si një thyesë jo të duhur. Për shembull, dhe.
• Çdo thyesë dhjetore e fundme ose thyesë periodike e pafundme. Kjo për faktin se thyesat dhjetore të treguara shndërrohen në thyesa të zakonshme. Për shembull, dhe 0,(3)=1/3.

Është gjithashtu e qartë se çdo thyesë dhjetore e pafundme jo periodike NUK është një numër racional, pasi nuk mund të përfaqësohet si një thyesë e zakonshme.

Tani mund të japim lehtësisht shembuj të numrave racionalë. Numrat 4, 903, 100,321 janë numra racional sepse janë numra natyrorë. Numrat e plotë 58, −72, 0, −833,333,333 janë gjithashtu shembuj të numrave racionalë. Thyesat e zakonshme 4/9, 99/3 janë gjithashtu shembuj të numrave racionalë. Numrat racional janë gjithashtu numra.

Nga shembujt e mësipërm është e qartë se ekzistojnë numra racionalë pozitivë dhe negativë, dhe numri racional zero nuk është as pozitiv as negativ.

Përkufizimi i mësipërm i numrave racionalë mund të formulohet në një formë më koncize.

Përkufizimi.

Numrat racionalë janë numra që mund të shkruhen si thyesë z/n, ku z është një numër i plotë dhe n është një numër natyror.

Le të vërtetojmë se ky përkufizim i numrave racional është i barabartë me përkufizimin e mëparshëm. Dimë që drejtëzën e thyesës mund ta konsiderojmë si shenjë pjesëtimi, pastaj nga vetitë e pjesëtimit të numrave të plotë dhe rregullat për pjesëtimin e numrave të plotë rrjedh vlefshmëria e barazive të mëposhtme dhe. Kështu, kjo është prova.

Le të japim shembuj të numrave racional bazuar në këtë përkufizim. Numrat −5, 0, 3 dhe janë numra racionalë, pasi mund të shkruhen si thyesa me një numërues të plotë dhe një emërues natyror të formës dhe, përkatësisht.

Përkufizimi i numrave racionalë mund të jepet në formulimin e mëposhtëm.

Përkufizimi.

Numrat racionalë janë numra që mund të shkruhen si thyesë dhjetore periodike të fundme ose të pafundme.

Ky përkufizim është gjithashtu ekuivalent me përkufizimin e parë, pasi çdo thyesë e zakonshme korrespondon me një thyesë dhjetore të fundme ose periodike dhe anasjelltas, dhe çdo numër i plotë mund të shoqërohet me një thyesë dhjetore me zero pas presjes dhjetore.

Për shembull, numrat 5, 0, −13, janë shembuj të numrave racionalë sepse mund të shkruhen si thyesat dhjetore të mëposhtme 5.0, 0.0, -13.0, 0.8 dhe −7, (18).

Le ta përfundojmë teorinë e kësaj pike me pohimet e mëposhtme:

• numrat e plotë dhe thyesat (pozitive dhe negative) përbëjnë bashkësinë e numrave racionalë;
• çdo numër racional mund të paraqitet si thyesë me numërues të plotë dhe emërues natyror, dhe çdo thyesë e tillë paraqet një numër të caktuar racional;
• çdo numër racional mund të përfaqësohet si një thyesë dhjetore periodike e fundme ose e pafundme, dhe çdo thyesë e tillë përfaqëson një numër racional.

A është racional ky numër?

Në paragrafin e mëparshëm, zbuluam se çdo numër natyror, çdo numër i plotë, çdo thyesë e zakonshme, çdo numër i përzier, çdo thyesë dhjetore e fundme, si dhe çdo thyesë dhjetore periodike është një numër racional. Kjo njohuri na lejon të "njohim" numrat racional nga një grup numrash të shkruar.

Por çka nëse numri jepet në formën e disa , ose si , etj., si t'i përgjigjemi pyetjes nëse numri i dhënë racionale? Në shumë raste është shumë e vështirë të përgjigjesh. Le të tregojmë disa drejtime të mendimit.

Nëse numri është dhënë në formular shprehje numerike, i cili përmban vetëm numra dhe shenja racionale veprimet aritmetike(+, −, · dhe:), atëherë vlera e kësaj shprehjeje është një numër racional. Kjo rrjedh nga mënyra se si përcaktohen veprimet me numra racionalë. Për shembull, pasi të kemi kryer të gjitha veprimet në shprehje, marrim numrin racional 18.

Ndonjëherë, pas thjeshtimit të shprehjeve dhe më shumë lloj kompleks, bëhet e mundur të përcaktohet nëse një numër i caktuar është racional.

Le të shkojmë më tej. Numri 2 është një numër racional, pasi çdo numër natyror është racional. Po numri? A është racionale? Rezulton se jo, nuk është një numër racional, është një numër irracional (vërtetimi i këtij fakti me kontradiktë është dhënë në tekstin shkollor të algjebrës për klasën 8, të renditur më poshtë në listën e referencave). Është vërtetuar gjithashtu se Rrenja katrore i një numri natyror është një numër racional vetëm në ato raste kur rrënja përmban një numër që është katrori i përsosur i ndonjë numri natyror. Për shembull, dhe janë numra racionalë, pasi 81 = 9 2 dhe 1 024 = 32 2, dhe numrat dhe nuk janë racionalë, pasi numrat 7 dhe 199 nuk janë katrore perfekte numrat natyrorë.

A është numri racional apo jo? NË në këtë rastËshtë e lehtë të shihet se, prandaj, ky numër është racional. A është numri racional? Është vërtetuar se rrënja k e një numri të plotë është një numër racional vetëm nëse numri nën shenjën e rrënjës është fuqia k e një numri të plotë. Prandaj, nuk është një numër racional, pasi nuk ka asnjë numër të plotë, fuqia e pestë e të cilit është 121.

Metoda me kontradiktë ju lejon të vërtetoni se logaritmet e disa numrave nuk janë numra racionalë për ndonjë arsye. Për shembull, le të vërtetojmë se - nuk është një numër racional.

Le të supozojmë të kundërtën, domethënë, le të themi se është një numër racional dhe mund të shkruhet si një thyesë e zakonshme m/n. Pastaj japim barazitë e mëposhtme: . Barazia e fundit është e pamundur, pasi në anën e majtë është numër i rastësishëm 5 n, dhe në anën e djathtë është numri çift 2 m. Prandaj, supozimi ynë është i pasaktë, pra jo një numër racional.

Si përfundim, vlen të përmendet veçanërisht se kur përcaktohet racionaliteti ose irracionaliteti i numrave, duhet të përmbahen nga nxjerrja e përfundimeve të papritura.

Për shembull, nuk duhet të pohoni menjëherë se prodhimi i numrave iracional π dhe e është një numër irracional, ky është "në dukje i qartë", por jo i provuar. Kjo ngre pyetjen: "Pse një produkt do të ishte një numër racional?" Dhe pse jo, sepse mund të jepni një shembull të numrave irracionalë, prodhimi i të cilëve jep një numër racional: .

Gjithashtu nuk dihet nëse numrat dhe shumë numra të tjerë janë racionalë apo jo. Për shembull, ka numrat irracionalë, shkallë irracionale që është një numër racional. Për ilustrim, ne paraqesim një shkallë të formës, baza e kësaj shkalle dhe eksponenti nuk janë numra racionalë, por , dhe 3 është një numër racional.

Bibliografi.

• Matematika. Klasa e 6-të: arsimore. për arsimin e përgjithshëm institucionet / [N. Ya. Vilenkin dhe të tjerët]. - Botimi i 22-të, rev. - M.: Mnemosyne, 2008. - 288 f.: ill. ISBN 978-5-346-00897-2.
• Algjebra: teksti shkollor për klasën e 8-të. arsimi i përgjithshëm institucionet / [Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; e Redaktuar nga S. A. Telyakovsky. - botimi i 16-të. - M.: Arsimi, 2008. - 271 f. : i sëmurë. - ISBN 978-5-09-019243-9.
• Gusev V. A., Mordkovich A. G. Matematikë (një manual për ata që hyjnë në shkollat ​​teknike): Proc. shtesa.- M.; Më e lartë shkolla, 1984.-351 f., ill.

NË këtë mësim Shqyrtohet shumëzimi dhe pjesëtimi i numrave racionalë.

Shumëzimi i numrave racionalë

Rregullat për shumëzimin e numrave të plotë vlejnë edhe për numrat racionalë. Me fjalë të tjera, për të shumëzuar numrat racional, duhet të jeni në gjendje

Gjithashtu, duhet të dini ligjet bazë të shumëzimit, si: ligjin komutativ të shumëzimit, ligjin asociativ të shumëzimit, ligjin shpërndarës të shumëzimit dhe shumëzimit me zero.

Shembulli 1. Gjeni vlerën e një shprehjeje

Ky është shumëzimi i numrave racionalë me shenja të ndryshme. Për të shumëzuar numrat racionalë me shenja të ndryshme, duhet të shumëzoni modulet e tyre dhe të vendosni një minus përpara përgjigjes që rezulton.

Për të parë qartë se kemi të bëjmë me numra që kanë shenja të ndryshme, çdo numër racional e mbyllim në kllapa së bashku me shenjat e tij.

Moduli i numrit është i barabartë me , dhe moduli i numrit është i barabartë me . Duke shumëzuar modulet që rezultojnë si thyesat pozitive, morëm një përgjigje, por para përgjigjes vendosëm një minus, siç na kërkonte rregulli. Për të siguruar këtë minus para përgjigjes, shumëzimi i moduleve u krye në kllapa, i paraprirë nga një minus.

Zgjidhja e shkurtër duket si kjo:

Shembulli 2. Gjeni vlerën e një shprehjeje

Shembulli 3. Gjeni vlerën e një shprehjeje

Ky është shumëzimi i numrave racionalë negativë. Për të shumëzuar numrat racionalë negativë, duhet të shumëzoni modulet e tyre dhe të vendosni një plus përpara përgjigjes që rezulton.

Zgjidhje për ky shembull mund të shkruhet shkurt:

Shembulli 4. Gjeni vlerën e një shprehjeje

Zgjidhja për këtë shembull mund të shkruhet shkurtimisht:

Shembulli 5. Gjeni vlerën e një shprehjeje

Ky është shumëzimi i numrave racionalë me shenja të ndryshme. Le të shumëzojmë modulet e këtyre numrave dhe të vendosim një minus përpara përgjigjes që rezulton

Zgjidhja e shkurtër do të duket shumë më e thjeshtë:

Shembulli 6. Gjeni vlerën e një shprehjeje

Le ta konvertojmë numrin e përzier në thyesë e papërshtatshme. Le ta rishkruajmë pjesën tjetër siç është

Kemi marrë shumëzimin e numrave racional me shenja të ndryshme. Le të shumëzojmë modulet e këtyre numrave dhe të vendosim një minus përpara përgjigjes që rezulton. Hyrja me module mund të anashkalohet në mënyrë që të mos rrëmojë shprehjen

Zgjidhja për këtë shembull mund të shkruhet shkurt

Shembulli 7. Gjeni vlerën e një shprehjeje

Ky është shumëzimi i numrave racionalë me shenja të ndryshme. Le të shumëzojmë modulet e këtyre numrave dhe të vendosim një minus përpara përgjigjes që rezulton

Në fillim përgjigja doli të ishte një fraksion i gabuar, por ne theksuam të gjithë pjesën në të. vini re se pjesë e tërë u nda nga moduli i fraksionit. Numri i përzier që rezulton u mbyll në kllapa, të paraprirë nga një shenjë minus. Kjo është bërë për të siguruar që kërkesa e rregullit është përmbushur. Dhe rregulli kërkonte që përgjigja e marrë të paraprihej nga një minus.

Zgjidhja për këtë shembull mund të shkruhet shkurtimisht:

Shembulli 8. Gjeni vlerën e një shprehjeje

Së pari, le të shumëzojmë dhe dhe të shumëzojmë numrin që rezulton me numrin e mbetur 5. Ne do ta kalojmë hyrjen me module në mënyrë që të mos rrëmbejmë shprehjen.

Përgjigje: vlera e shprehjes është e barabartë me −2.

Shembulli 9. Gjeni kuptimin e shprehjes:

Le të përkthejmë numra të përzier te thyesat e pahijshme:

Ne morëm shumëzimin e numrave racionalë negativë. Le të shumëzojmë modulet e këtyre numrave dhe të vendosim një plus përpara përgjigjes që rezulton. Hyrja me module mund të anashkalohet në mënyrë që të mos rrëmojë shprehjen

Shembulli 10. Gjeni vlerën e një shprehjeje

Shprehja përbëhet nga disa faktorë. Sipas ligjit asociativ të shumëzimit, nëse një shprehje përbëhet nga disa faktorë, atëherë produkti nuk do të varet nga rendi i veprimeve. Kjo na lejon të llogarisim kjo shprehje në çdo mënyrë.

Le të mos e rishpikim rrotën, por ta llogarisim këtë shprehje nga e majta në të djathtë sipas renditjes së faktorëve. Le të kalojmë hyrjen me module në mënyrë që të mos rrëmbejmë shprehjen

Veprimi i tretë:

Veprimi i katërt:

Përgjigje: vlera e shprehjes është

Shembulli 11. Gjeni vlerën e një shprehjeje

Le të kujtojmë ligjin e shumëzimit me zero. Ky ligj thotë se një produkt është i barabartë me zero nëse të paktën një nga faktorët e barabartë me zero.

Në shembullin tonë, një nga faktorët është i barabartë me zero, kështu që pa humbur kohë përgjigjemi se vlera e shprehjes është e barabartë me zero:

Shembulli 12. Gjeni vlerën e një shprehjeje

Produkti është i barabartë me zero nëse të paktën një nga faktorët është i barabartë me zero.

Në shembullin tonë, një nga faktorët është i barabartë me zero, kështu që pa humbur kohë përgjigjemi se vlera e shprehjes barazohet me zero:

Shembulli 13. Gjeni vlerën e një shprehjeje

Mund të përdorni rendin e veprimeve dhe fillimisht të llogaritni shprehjen në kllapa dhe të shumëzoni përgjigjen që rezulton me një thyesë.

Ju gjithashtu mund të përdorni ligjin shpërndarës të shumëzimit - shumëzoni çdo term të shumës me një fraksion dhe shtoni rezultatet që rezultojnë. Ne do të përdorim këtë metodë.

Sipas rendit të veprimeve, nëse një shprehje përmban mbledhje dhe shumëzim, atëherë duhet të kryhet së pari shumëzimi. Prandaj, në shprehjen e re që rezulton, le të vendosim në kllapa ato parametra që duhet të shumëzohen. Në këtë mënyrë ne mund të shohim qartë se cilat veprime duhet të kryhen më herët dhe cilat më vonë:

Veprimi i tretë:

Përgjigje: vlera e shprehjes barazohet

Zgjidhja për këtë shembull mund të shkruhet shumë më shkurt. Do të duket kështu:

Është e qartë se ky shembull mund të zgjidhet edhe në mendjen e dikujt. Prandaj, duhet të zhvilloni aftësinë për të analizuar një shprehje përpara se ta zgjidhni atë. Ka të ngjarë që mund të zgjidhet mendërisht dhe të kursejë shumë kohë dhe nerva. Dhe në teste dhe provime, siç e dini, koha është shumë e vlefshme.

Shembulli 14. Gjeni vlerën e shprehjes −4,2 × 3,2

Ky është shumëzimi i numrave racionalë me shenja të ndryshme. Le të shumëzojmë modulet e këtyre numrave dhe të vendosim një minus përpara përgjigjes që rezulton

Vini re se si janë shumëzuar modulet e numrave racionalë. Në këtë rast, për të shumëzuar modulin e numrave racional, u desh .

Shembulli 15. Gjeni vlerën e shprehjes −0,15 × 4

Ky është shumëzimi i numrave racionalë me shenja të ndryshme. Le të shumëzojmë modulet e këtyre numrave dhe të vendosim një minus përpara përgjigjes që rezulton

Vini re se si janë shumëzuar modulet e numrave racionalë. Në këtë rast, për të shumëzuar modulin e numrave racionalë, ishte e nevojshme të ishim në gjendje.

Shembulli 16. Gjeni vlerën e shprehjes −4,2 × (−7,5)

Ky është shumëzimi i numrave racionalë negativë. Le të shumëzojmë modulet e këtyre numrave dhe të vendosim një plus përpara përgjigjes që rezulton

Pjestimi i numrave racional

Rregullat për pjesëtimin e numrave të plotë vlejnë edhe për numrat racionalë. Me fjalë të tjera, për të qenë në gjendje të ndani numrat racionalë, duhet të jeni në gjendje

Përndryshe, përdoren të njëjtat metoda për ndarjen e thyesave të zakonshme dhe dhjetore. Për të ndarë një thyesë të përbashkët me një fraksion tjetër, duhet të shumëzoni thyesën e parë me reciprocitetin e thyesës së dytë.

Dhe për të ndarë një thyesë dhjetore në një thyesë tjetër dhjetore, duhet të zhvendosni pikën dhjetore në dividend dhe në pjesëtuesin në të djathtë me aq shifra sa ka pas presjes dhjetore në pjesëtues, pastaj të kryeni pjesëtimin si me një numër i rregullt.

Shembulli 1. Gjeni kuptimin e shprehjes:

Kjo është ndarja e numrave racionalë me shenja të ndryshme. Për të llogaritur një shprehje të tillë, duhet të shumëzoni fraksionin e parë me reciprocitetin e të dytës.

Pra, le të shumëzojmë thyesën e parë me reciprokun e të dytës.

Kemi marrë shumëzimin e numrave racional me shenja të ndryshme. Dhe ne tashmë dimë se si të llogarisim shprehje të tilla. Për ta bërë këtë, ju duhet të shumëzoni modulët e këtyre numrave racionalë dhe të vendosni një minus përpara përgjigjes që rezulton.

Le ta plotësojmë këtë shembull deri në fund. Hyrja me module mund të anashkalohet në mënyrë që të mos rrëmojë shprehjen

Pra, vlera e shprehjes është

Zgjidhja e detajuar është si më poshtë:

Një zgjidhje e shkurtër do të duket kështu:

Shembulli 2. Gjeni vlerën e një shprehjeje

Kjo është ndarja e numrave racionalë me shenja të ndryshme. Për të llogaritur këtë shprehje, duhet të shumëzoni fraksionin e parë me reciprocitetin e të dytës.

Reciproku i thyesës së dytë është thyesa . Le të shumëzojmë me të thyesën e parë:

Një zgjidhje e shkurtër do të duket kështu:

Shembulli 3. Gjeni vlerën e një shprehjeje

Kjo është ndarja e numrave racionalë negativë. Për të llogaritur këtë shprehje, përsëri duhet të shumëzoni fraksionin e parë me reciprocitetin e të dytës.

Reciproku i thyesës së dytë është thyesa . Le të shumëzojmë me të thyesën e parë:

Ne morëm shumëzimin e numrave racionalë negativë. Si llogaritet shprehje e ngjashme ne tashmë e dimë. Ju duhet të shumëzoni modulin e numrave racionalë dhe të vendosni një plus përpara përgjigjes që rezulton.

Le ta përfundojmë këtë shembull deri në fund. Mund ta kaloni hyrjen me module në mënyrë që të mos rrëmbeni shprehjen:

Shembulli 4. Gjeni vlerën e një shprehjeje

Për të llogaritur këtë shprehje, duhet të shumëzoni numrin e parë −3 me thyesën, thyesë reciproke.

Reciprociteti i një thyese është thyesa . Shumëzojeni numrin e parë −3 me të

Shembulli 6. Gjeni vlerën e një shprehjeje

Për të llogaritur këtë shprehje, duhet të shumëzoni fraksionin e parë me numrin reciproke numri 4.

Reciproku i numrit 4 është një thyesë. Shumëzoni me të thyesën e parë

Shembulli 5. Gjeni vlerën e një shprehjeje

Për të llogaritur këtë shprehje, duhet të shumëzoni thyesën e parë me inversin e -3

Anasjellta e −3 është një thyesë. Le të shumëzojmë me të thyesën e parë:

Shembulli 6. Gjeni vlerën e shprehjes −14.4: 1.8

Kjo është ndarja e numrave racionalë me shenja të ndryshme. Për të llogaritur këtë shprehje, duhet të ndani modulin e dividentit me modulin e pjesëtuesit dhe të vendosni një minus përpara përgjigjes që rezulton.

Vini re se si u nda moduli i dividendit me modulin e pjesëtuesit. Në këtë rast, për ta bërë atë në mënyrë korrekte, ishte e nevojshme të ishe në gjendje.

Nëse nuk doni të ngatërroni me numrat dhjetorë (dhe kjo ndodh shpesh), atëherë këto, atëherë kthejini këta numra të përzier në thyesa të papërshtatshme dhe më pas bëni vetë ndarjen.

Le të llogarisim shprehjen e mëparshme −14.4: 1.8 në këtë mënyrë. Le të përkthejmë dhjetore në numra të përzier:

Tani le t'i kthejmë numrat e përzier që rezultojnë në thyesa të pasakta:

Tani mund të bëni pjesëtim drejtpërdrejt, domethënë, të ndani një pjesë me një thyesë. Për ta bërë këtë, ju duhet të shumëzoni fraksionin e parë me fraksionin e kundërt të të dytës:

Shembulli 7. Gjeni vlerën e një shprehjeje

Le ta kthejmë thyesën dhjetore −2.06 në një thyesë të parregullt dhe ta shumëzojmë këtë thyesë me reciprocitetin e thyesës së dytë:

Thyesat shumëkatëshe

Shpesh mund të hasni një shprehje në të cilën ndarja e thyesave shkruhet duke përdorur një vijë thyese. Për shembull, shprehja mund të shkruhet si më poshtë:

Cili është ndryshimi midis shprehjeve dhe ? Nuk ka vërtet asnjë ndryshim. Këto dy shprehje kanë të njëjtin kuptim dhe midis tyre mund të vendoset një shenjë e barabartë:

Në rastin e parë, shenja e ndarjes është dy pika dhe shprehja shkruhet në një rresht. Në rastin e dytë, ndarja e thyesave shkruhet duke përdorur një vijë thyese. Rezultati është një fraksion që njerëzit pranojnë ta quajnë shumëkatëshe.

Kur hasni shprehje të tilla shumëkatëshe, duhet të zbatoni të njëjtat rregulla të ndarjes thyesat e zakonshme. Pjesa e parë duhet të shumëzohet me reciprocitetin e të dytës.

Përdorimi i fraksioneve të tilla në një zgjidhje është jashtëzakonisht i papërshtatshëm, kështu që mund t'i shkruani ato në një formë të kuptueshme duke përdorur një dy pika dhe jo një vijë të pjesshme si shenjë ndarjeje.

Për shembull, le të shkruajmë thyesë shumëkatëshe në mënyrë të kuptueshme. Për ta bërë këtë, së pari duhet të kuptoni se ku është fraksioni i parë dhe ku është i dyti, sepse nuk është gjithmonë e mundur ta bëni këtë si duhet. Thyesat shumëkatëshe kanë disa vija fraksionesh që mund të jenë konfuze. Vija kryesore e fraksionit, e cila ndan fraksionin e parë nga e dyta, zakonisht është më e gjatë se pjesa tjetër.

Pas përcaktimit të vijës kryesore thyesore, mund të kuptoni lehtësisht se ku është thyesa e parë dhe ku është e dyta:

Shembulli 2.

Gjejmë vijën kryesore të thyesës (është më e gjata) dhe shohim që numri i plotë -3 ndahet me një thyesë të përbashkët

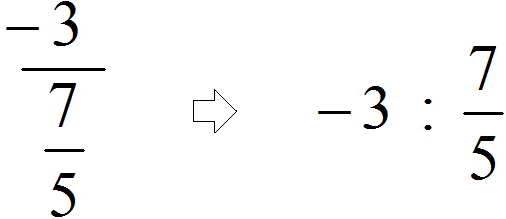
Dhe nëse gabimisht do të kishim marrë si kryesore vijën e dytë thyesore (atë që është më e shkurtër), atëherë do të rezultonte se ne po e pjesëtojmë thyesën me numrin e plotë 5. Në këtë rast, edhe nëse kjo shprehje llogaritet saktë, problemi do të zgjidhet gabimisht, pasi dividenti në këtë Në këtë rast, numri është −3, dhe pjesëtuesi është thyesa .

Shembulli 3. Le ta shkruajmë thyesën me shumë nivele në një formë të kuptueshme

Gjejmë vijën kryesore të thyesës (është më e gjata) dhe shohim që thyesa ndahet me numrin e plotë 2

Dhe nëse gabimisht e merrnim vijën e parë thyesore si atë kryesore (atë që është më e shkurtër), atëherë do të rezultonte se po e ndajmë numrin e plotë -5 me thyesën, edhe nëse kjo shprehje llogaritet saktë. problemi do të zgjidhet gabimisht, pasi dividenti në këtë rast thyesa është , dhe pjesëtuesi është numri i plotë 2.

Përkundër faktit se thyesat me shumë nivele janë të papërshtatshme për të punuar, ne do t'i hasim ato shumë shpesh, veçanërisht kur studiojmë matematikën e lartë.

Natyrisht, duhet Kohe shtese dhe vendin. Prandaj, mund të përdorni më shumë metodë e shpejtë. Kjo metodë është e përshtatshme dhe dalja ju lejon të merrni një shprehje të gatshme në të cilën fraksioni i parë tashmë është shumëzuar me fraksionin reciprok të të dytës.

Kjo metodë zbatohet si më poshtë:

Nëse fraksioni është katërkatësh, për shembull, atëherë numri i vendosur në katin e parë ngrihet në katin e fundit. Dhe figura e vendosur në katin e dytë është ngritur në katin e tretë. Numrat që rezultojnë duhet të lidhen me shenjat e shumëzimit (×)

Si rezultat, duke anashkaluar shënimin e ndërmjetëm, marrim një shprehje të re në të cilën fraksioni i parë tashmë është shumëzuar me fraksionin reciprok të të dytës. Komoditet dhe kaq!

Për të shmangur gabimet gjatë përdorimit këtë metodë, ju mund të udhëhiqeni nga rregulli i mëposhtëm:

Nga e para në të katërt. Nga e dyta në të tretën.

Në rregull po flasim për në lidhje me dyshemetë. Figura nga kati i parë duhet të ngrihet në katin e katërt. Dhe figura nga kati i dytë duhet të ngrihet në katin e tretë.

Le të përpiqemi të llogarisim një fraksion shumëkatësh duke përdorur rregullin e mësipërm.

Pra, ne e ngremë numrin e vendosur në katin e parë në katin e katërt, dhe numrin që ndodhet në katin e dytë në katin e tretë.

Si rezultat, duke anashkaluar shënimin e ndërmjetëm, marrim një shprehje të re në të cilën fraksioni i parë tashmë është shumëzuar me fraksionin reciprok të të dytës. Më pas, mund të përdorni njohuritë tuaja ekzistuese:

Le të përpiqemi të llogarisim një fraksion me shumë nivele duke përdorur një skemë të re.

Ka vetëm katin e parë, të dytë dhe të katërt. Nuk ka kat të tretë. Por ne nuk devijojmë nga skema bazë: e ngremë figurën nga kati i parë në katin e katërt. Dhe duke qenë se nuk ka kat të tretë, e lëmë numrin e vendosur në katin e dytë ashtu siç është

Si rezultat, duke anashkaluar shënimin e ndërmjetëm, morëm një shprehje të re në të cilën numri i parë -3 tashmë është shumëzuar me fraksionin reciprok të të dytit. Më pas, mund të përdorni njohuritë tuaja ekzistuese:

Le të përpiqemi të llogarisim fraksionin shumëkatësh duke përdorur skemën e re.

Ka vetëm katin e dytë, të tretë dhe të katërt. Nuk ka kat të parë. Meqenëse nuk ka kat të parë, nuk ka asgjë për të ngjitur në katin e katërt, por mund ta ngremë figurën nga kati i dytë në të tretën:

Si rezultat, duke anashkaluar shënimin e ndërmjetëm, morëm një shprehje të re në të cilën fraksioni i parë tashmë është shumëzuar me inversin e pjesëtuesit. Më pas, mund të përdorni njohuritë tuaja ekzistuese:

Përdorimi i variablave

Nëse shprehja është komplekse dhe ju duket se do t'ju ngatërrojë në procesin e zgjidhjes së problemit, atëherë një pjesë e shprehjes mund të vendoset në një ndryshore dhe më pas të punohet me këtë ndryshore.

Matematikanë shpesh e bëjnë këtë. Një detyrë e vështirë zbërthejini ato në nëndetyra më të lehta dhe zgjidhni ato. Pastaj nëndetyrat e zgjidhura mblidhen në një tërësi të vetme. Kjo procesi krijues dhe kjo është diçka që njeriu mëson gjatë viteve përmes stërvitjes së vështirë.

Përdorimi i variablave justifikohet kur punoni me fraksione me shumë nivele. Për shembull:

Gjeni vlerën e një shprehjeje

Pra, ekziston një shprehje thyesore në numërues dhe në emërues të së cilës shprehjet thyesore. Me fjalë të tjera, përsëri jemi përballë një fraksioni shumëkatësh, që nuk na pëlqen aq shumë.

Shprehja në numërues mund të futet në një ndryshore me çdo emër, për shembull:

Por në matematikë një rast të tillë Variablave zakonisht u jepen emra duke përdorur shkronja të mëdha latine. Le të mos e thyejmë këtë traditë, dhe të shënojmë shprehjen e parë me një të madhe shkronja latine A

Dhe shprehja në emërues mund të shënohet me shkronjën e madhe B

Tani shprehja jonë origjinale merr formën . Kjo do të thotë, ne zëvendësuam shprehjen numerike me një alfabetik, pasi kemi futur më parë numëruesin dhe emëruesin në variablat A dhe B.

Tani mund të llogarisim veçmas vlerat e ndryshores A dhe vlerën e ndryshores B. Do të fusim vlerat e përfunduara në shprehje.

Le të gjejmë vlerën e ndryshores A

Le të gjejmë vlerën e ndryshores B

Tani le t'i zëvendësojmë vlerat e tyre në shprehjen kryesore në vend të variablave A dhe B:

Ne kemi marrë një fraksion shumëkatësh në të cilin mund të përdorim skemën "nga i pari në të katërtin, nga i dyti në të tretën", domethënë, të ngremë numrin e vendosur në katin e parë në katin e katërt dhe të rrisim numër ndodhet në katin e dytë deri në katin e tretë. Llogaritjet e mëtejshme nuk do të jenë të vështira:

Pra, vlera e shprehjes është −1.

Sigurisht që kemi marrë parasysh shembulli më i thjeshtë, por qëllimi ynë ishte të mësonim se si mund t'i përdorim variablat për t'i bërë gjërat më të lehta për veten tonë, për të minimizuar gabimet.

Vini re gjithashtu se zgjidhja për këtë shembull mund të shkruhet pa përdorur variabla. Do të duket si

Kjo zgjidhje është më e shpejtë dhe më e shkurtër, dhe në këtë rast ka më shumë kuptim ta shkruajmë në këtë mënyrë, por nëse shprehja rezulton e ndërlikuar, e përbërë nga disa parametra, kllapa, rrënjë dhe fuqi, atëherë këshillohet që të llogaritet në disa faza, duke futur një pjesë të shprehjeve të tij në variabla.

Ju pëlqeu mësimi?
Bashkohuni me tonën grup i ri VKontakte dhe filloni të merrni njoftime për mësime të reja

92 kap. II

4) Duke supozuar q nga vlere absolute më pak se 1, provoni

5) Cili është kufiri i një serie të pafundme

1 − 2q + 3q2 − 4q3 + . . . ?

6) Llogaritni kufijtë e shprehjeve

(Udhëzim: Përdorni rezultatet e gjetura në faqet 31–33.)

4. Numrat racional dhe dhjetoret periodike.

Numra të tillë racional p q që nuk mund të paraqiten në

në formën e thyesave dhjetore të fundme, zbërthehen në thyesa dhjetore të pafundme duke përdorur teknikën e zakonshme të pjesëtimit "të gjatë". Në çdo fazë të këtij procesi, lind një mbetje që nuk është e barabartë me zero, përndryshe thyesa do të ishte e fundme. Mbetjet e ndryshme që ndodhin mund të jenë vetëm numra të plotë nga 1 në q − 1, kështu që ekzistojnë vetëm q − 1 mundësi për vlerat e këtyre mbetjeve. Kjo do të thotë që pas pjesëtimeve q do të shfaqet një pjesë e mbetur k për herë të dytë. Por atëherë të gjitha mbetjet e mëvonshme gjithashtu do të përsëriten në të njëjtin rend në të cilin janë shfaqur tashmë pas shfaqjes së parë të mbetjes k. Kështu,

zgjerimi dhjetor i çdo numri racional ka vetinë e periodicitetit; pas një numri të caktuar të numrave dhjetorë fillon të përsëritet i njëjti grup i numrave dhjetorë numër i pafund një herë. Për shembull, 1 6 = 0,166666666. . .;1 7 = 0,142857142857142857 . . .;

11 1 = 0,09090909. . .;1100 122 = 0,1109090909 . . .;11 90 = 0,122222222 . . . etj. (Shënim për ata numra racionalë që përfaqësohen

në formën e një thyese dhjetore përfundimtare që kjo thyesa përfundimtare mund të imagjinohet pas saj të fundit vend decimal shifra 0 që përsëritet pafundësisht, dhe kështu numrat racionalë në fjalë nuk përjashtohen nga formulimi i përgjithshëm i dhënë më sipër.) Nga shembujt e mësipërm është e qartë se për disa nga zgjerimet dhjetore që korrespondojnë me numrat racional, një "bisht" periodik është paraprihet nga një “kokë” jo periodike.

Në të kundërt, mund të tregohet se gjithçka thyesat periodike përfaqësojnë numra racionalë. Konsideroni, për shembull, thyesën periodike të pafundme

p = 0,3322222. . .

Mund të shkruani: p = 100 33 + 10−3 2(1 + 10−1 + 10−2 + . . .). Shprehja në

§ 2 SEGMENTE TË PAKOMASURËSHME. NUMRA IRRACIONAL, KUFIZI93

ka pafundësi në kllapa progresion gjeometrik:

NË rast i përgjithshëm prova është ndërtuar në të njëjtën mënyrë, por është e komplikuar nga nevoja për të futur shënime disi të rënda. Le të shqyrtojmë një pjesë periodike të formës së përgjithshme

p = 0,a1 a2 a3 . . . jam b1 b2 b3 . . . bn b1 b2 b3 . . . bn. . .

Le të shënojmë me B = 0,b1 b2 b3 . . . bn pjesën periodike të zgjerimit tonë. Atëherë mund të shkruani

p = 0,a1 a2 a3 . . . am + 10−m B(1 + 10−n + 10−2n + 10−3n + . . .).

Shprehja në kllapa është një progresion i pafund gjeometrik për të cilin q = 10−n. Shuma e këtij progresioni, sipas formulës (10)

pika tjetër është e barabartë me 1 − 10 −n, dhe për këtë arsye

10−m · Bp = 0.a 1 a 2 a 3 . . . a m + 1 − 10 −n .

Ushtrime. 1) Zbërtheni në thyesa dhjetore numrat racionalë të mëposhtëm: 11 1,13 1,13 2,13 3,17 1,17 2 dhe përcaktoni periudhat e zgjerimit.

2) Numri 142,857 ka vetinë që kur shumëzohet me 2, 3, 4, 5 ose 6, në të kryhen vetëm ndërrime shifrash. Shpjegoni këtë veti bazuar në zbërthimin e numrit 1 7 në një thyesë dhjetore.

3) Faktoroni numrat e dhënë në ushtrimin 1 në thyesat e pafundme me bazat 5, 7 dhe 12.

4) Faktoroni numrin 1 3 në një thyesë binare.

5) Shkruani zgjerimin 0.11212121. . . Përcaktoni cilin numër përfaqëson në bazat 3 ose 5.

5. Përkufizimi i përgjithshëm i numrave irracionalë me anë të segmenteve të kontraktueshëm. Në faqen 82 kemi paraqitur një përkufizim paraprak: "numri" është një thyesë dhjetore e fundme ose e pafundme. Në të njëjtën kohë, ne ramë dakord që thyesat dhjetore që nuk përfaqësojnë një numër racional t'i quajmë numra irracionalë. Bazuar në rezultatet e marra në paragrafin e mëparshëm, tani mund të propozojmë formulimin e mëposhtëm: “një vazhdimësi numerike ose sistem numra realë(Numrat "realë" janë në kontrast këtu me numrat "imagjinarë" ose "kompleks", shih § 5), është një koleksion i të gjitha thyesave dhjetore të pafundme të mundshme." (Duke atribuar zero,

ju mund, siç u përmend tashmë, të shkruani thyesën dhjetore përfundimtare

V formë e pafundme, apo ka një mënyrë tjetër: shifra e fundit zëvendësoni thyesën a me një − 1 dhe shtoni një numër të pafund nëntësh në të. Pra, ne pamë, për shembull, se 0.999. . . = 1, - shih pikën 3.)

Numrat racional janë thyesa periodike; numrat irracionalë janë thyesat jo periodike. Por edhe ky përkufizim nuk duket plotësisht i kënaqshëm: në të vërtetë, ne pamë në kapitullin I se nga vetë natyra e gjërave sistemi dhjetor asgjë e veçantë nuk dallohet nga të tjerat e mundshme; në të njëjtën mënyrë mund të operohet, për shembull, me një sistem binar. Për këtë arsye, është shumë e dëshirueshme të jepet një përkufizim më i përgjithshëm i vazhdimësisë së numrave, pavarësisht nga zgjedhja specifike e bazës 10 ose ndonjë tjetër. Ndoshta, metoda më e thjeshtë për të futur një përgjithësim të tillë është

në atë të radhës.

Le të shohim boshti numerik disa sekuencë I1, I2, I3,. . . , Në , . . . segmente me mbaresa racionale; Le të supozojmë se çdo segment pasues është i përfshirë në atë të mëparshëm dhe se gjatësia e segmentit të n-të In tenton në zero ndërsa n rritet pafundësisht. Ne do ta quajmë një sekuencë të tillë segmentesh "të mbivendosur" në njëri-tjetrin një sekuencë segmentesh kontraktuese. Në rastin e segmenteve dhjetore, gjatësia In është e barabartë me 10−n, por mund të jetë po aq e barabartë me, të themi, 2−n, ose mund ta kufizoni veten në të paktën

me kërkesën që të jetë më pak se n 1. Le të japim tani sa vijon

formulim, të cilin do ta konsiderojmë si postulat kryesor gjeometrik: cilado qoftë sekuenca e segmenteve kontraktuese, ka një dhe vetëm një pikë në boshtin e numrave, e cila gjendet njëkohësisht në të gjitha segmentet. (Është mjaft e qartë se ekziston më së shumti një pikë e tillë, pasi gjatësitë e segmenteve priren në zero dhe dy pika të ndryshme nuk mund të përmbahen në një segment gjatësia e të cilit ishte më e vogël se distanca midis pikave.) Kjo pikë, sipas përkufizimit, dhe quhet një numër real; nëse nuk është racional, quhet numër irracional. Me këtë përkufizim, ne vendosim një korrespondencë të plotë midis pikave dhe numrave. Asgjë thelbësisht e re nuk është shtuar këtu: thjesht përkufizimit të një numri si thyesë dhjetore të pafundme i është dhënë një formë më e përgjithshme.

Megjithatë, lexuesi në këtë pikë mund të kapet nga disa dyshime, të cilat duhen njohur si plotësisht të justifikuara. Cila është në të vërtetë ajo "pikë" në boshtin e numrave, e cila, siç supozojmë, përfshihet njëkohësisht në të gjitha segmentet kontraktuese të sekuencës nëse nuk korrespondon me një numër racional? Përgjigja jonë është: ekzistenca në vijën numerike

§ 2 SEGMENTE TË PAKOMASURËSHME. NUMRA IRRACIONAL, LIMITET95

Oriz. 11. Segmentet kontraktuese. Kufijtë e sekuencës

(i konsideruar si imazh gjeometrik) i një pike të përfshirë në të gjitha segmentet e kontraktueshme me skaje racionale është postulati bazë gjeometrik. Nuk ka nevojë të bëjmë një reduktim, duke e çuar atë në propozime të tjera matematikore. Ne e pranojmë atë, siç pranojmë aksioma ose postulate të tjera në matematikë, bazuar në besueshmërinë e saj intuitive dhe në dobinë e saj, të zbuluar kur ndërtohet në mënyrë logjike. sistemi serik fjalitë matematikore. Thjesht formalisht, ne mund të nisnim nga vija numerike, të cilën do ta mendonim si një koleksion vetëm pikash racionale, dhe më pas do ta përcaktonim pikën iracionale si

një simbol që tregon një sekuencë të caktuar segmentesh të kontraktueshme. Pika irracionale përcaktohet plotësisht nga një sekuencë e segmenteve racionale kontraktuese, gjatësitë e të cilave priren në zero. Kjo do të thotë se postulati ynë bazë është në të vërtetë i aftë të shërbejë si përkufizim. Të pranosh një përkufizim të tillë, pasi të jemi çuar në një sekuencë segmentesh kontraktuese nga një ndjenjë intuitive që pohon "ekzistencën" e një pike irracionale, do të thotë të hedhim poshtë "patericat e intuitës" mbi të cilat mbështetej arsyetimi ynë dhe të kuptojmë se çdo gjë vetitë matematikore pikat irracionale mund të kuptohen dhe paraqiten si veti të sekuencave të segmenteve të kontraktueshme.

Me të pastër pikë matematikore Në këtë rast, fakti i rëndësishëm është se, duke pranuar përkufizimin e një numri irracional si

sekuenca e segmenteve të kontraktueshme, fitojmë mundësinë të japim përkufizime të mbledhjes, shumëzimit, etj., si dhe marrëdhëniet e pabarazisë, të cilat janë përgjithësim i drejtpërdrejtë i përkufizimeve përkatëse në fushën e numrave racionalë dhe, për më tepër, me ruajtjen e të gjitha ligjet bazë që veprojnë në fushën e numrave racionalë. Kështu, për shembull, për të përcaktuar shumën e dy numrave irracionalë a dhe b bazuar në dy sekuenca të segmenteve të kontraktueshëm që përcaktojnë numrat a dhe b, ne ndërtojmë sekuencë e re kontraktimi i segmenteve, duke shtuar fillestarin dhe pikat fundore segmentet e përfshira në këto sekuenca. E njëjta gjë mund të bëhet me prodhimin ab, ndryshimin a − b dhe herësin a/b. Dhe në bazë të këtyre përkufizimeve mund të tregohet se ligjet aritmetike, të diskutuara në § 1 të këtij kreu, nuk cenohen kur kalohet në numra irracionalë. Ne i harrojmë detajet përkatëse këtu.

Verifikimi i të gjitha këtyre ligjeve është i thjeshtë dhe mund të bëhet drejtpërdrejt pa ndonjë vështirësi të veçantë, por mund të duket disi e mërzitshme për një lexues fillestar, i cili natyrisht është i interesuar për sa më shpejt aq më shumëçfarë mund të bëhet me ndihmën e matematikës sesa duke analizuar bazat logjike të saj. Shpesh ndodh që tekstet më të fundit shkollore Matematikanë e sprapsin lexuesin pikërisht sepse që në faqet e para japin një justifikim pedant për sistemin e numrave realë. Lexuesi që i injoron me qetësi këto faqe le të qetësojë ndërgjegjen e tij duke ditur se, deri në fundi i XIX shekuj me radhë, të gjithë matematikanët e mëdhenj bënë zbulimet e tyre në bazë të konceptit "naiv" të vazhdimësisë së numrave, të ofruar drejtpërdrejt nga intuita.

Së fundi, me pikë fizike këndvështrimi, përkufizimi i një numri irracional me anë të një sekuence segmentesh të kontraktueshme krahasohet natyrshëm me përkufizimin vlerë numerike disa sasi të vëzhgueshme - nëpërmjet një sërë matjeve të bëra në mënyrë sekuenciale me saktësi në rritje. Çdo operacion i kryer, le të themi, me qëllim të përcaktimit të gjatësisë së një segmenti të caktuar, është praktikisht kuptimplotë vetëm brenda kufijve të një gabimi të caktuar të mundshëm, madhësia e të cilit përcaktohet nga saktësia e instrumentit. Meqenëse numrat racionalë janë të vendosur dendur kudo në një vijë, asnjë operacion fizik, pavarësisht sa i saktë, nuk do të na lejojë të dallojmë nëse gjatësia e dhënë racionale apo irracionale. Kështu do të duket se nuk ka nevojë që numrat iracionalë të përshkruhen në mënyrë adekuate dukuritë fizike. Por, siç do të shohim në kapitullin VI, kur përshkrimi matematik dukuritë fizike, përparësia e vërtetë e fituar nëpërmjet përdorimit të numrave irracionalë qëndron në thjeshtimin ekstrem të këtij përshkrimi – pikërisht falë përdorimit të lirë të konceptit të limitit, baza e të cilit është vazhdimësia numerike.

§ 2 SEGMENTE TË PAKOMASURËSHME. NUMRA IRRACIONAL, LIMITET97

*6. Metoda të tjera për përcaktimin e numrave irracionalë. Seksionet Dedekind. Një rrugë paksa e ndryshme për përcaktimin e numrave irracionalë u zgjodh nga Richard Dedekind (1831-1916), një nga themeluesit më të shquar të logjikës dhe analiza filozofike bazat e matematikës. Artikujt e tij - “Stetigkeit und irrationale Zahlen”1 (1872) dhe “Was sind und was sollen die Zahlen?”2 (1887) – patën një ndikim të thellë në studimin e parimeve themelore të matematikës. Dedekind parapëlqente konceptet e përgjithshme abstrakte ndaj konstruksioneve konkrete, siç janë sekuencat e segmenteve kontraktuese. Procedura e tij bazohet në idenë e "seksionit"; tani do të përshkruajmë se çfarë është.

Supozoni se në një farë mënyre ishte e mundur të ndahej bashkësia e të gjithë numrave racionalë në dy klasa A dhe B në atë mënyrë që çdo numër b i klasës B të ishte më i madh se çdo numër a i klasës A. Çdo ndarje e këtij lloji quhet një seksion në fushën e numrave racionalë. Nëse bëhet një prerje, atëherë duhet të ndodhë një nga tre mundësitë e mëposhtme logjikisht të imagjinueshme.

1) ekziston elementi më i madh a në klasën A. Kjo gjendje ndodh, për shembull, nëse të gjithë numrat racionalë 6 1 i caktohen klasës A, dhe të gjithë numrat racional > 1 i caktohen klasës B.

2) Ekziston një element më i vogël b në klasën B. Kjo ndodh, për shembull, nëse të gjithë numrat racional i caktohen klasës A< 1, к классу B - все рациональные числа > 1.

3) Nuk ekziston as elementi më i madh në klasën A dhe as më i vogli në klasën B. Një seksion i këtij lloji do të merret, për shembull, nëse

për të Klasa A përfshin të gjithë numrat racional katrori i të cilëve është më i vogël se 2, dhe klasa B përfshin të gjithë numrat racional katrori i të cilëve është më i madh se 2. Klasat A dhe B shterojnë të gjithë numrat racionalë, pasi u tregua se nuk ka numër racional katrori i të cilëve është 2. , nuk ekziston.

Një rast i tillë, kur në klasën A ka një element më të madh a dhe në të njëjtën kohë në klasën B ka një element më të vogël b, është logjikisht i paimagjinueshëm, kështu që

dhe b do të ishte më i madh se elementi më i madh në A dhe më i vogël se elementi më i vogël në B, dhe për këtë arsye nuk mund t'i përkiste as A dhe B.

NË rasti i tretë, kur nuk ka një numër racional më të madh

V klasa A, as më e vogla në klasën B, atëherë, sipas Dedekind, seksioni përcakton, ose, më mirë, përfaqëson disa irracionale

1 “Vazhdimësia dhe numrat irracionalë”. - Përafërsisht. ed.

2 "Cilat janë numrat dhe çfarë duhet të jenë ata?" - Përafërsisht. ed.

Kthehu përpara

Kujdes! Pamjet paraprake të diapozitivëve janë vetëm për qëllime informative dhe mund të mos përfaqësojnë të gjitha tiparet e prezantimit. Ne qofte se je i interesuar kjo pune, ju lutemi shkarkoni versionin e plotë.

Golat:

• Prezantoni përkufizimin e numrave racionalë dhe skemën logjike për zhvillimin e konceptit të numrit.
• Kuptoni konceptet:
• thyesa dhjetore përfundimtare;
• thyesa dhjetore e pafundme;
• thyesë dhjetore e pafundme periodike.
• Mësoni të përcaktoni sipas llojit të një thyese të zakonshme se cila thyesë dhjetore (i fundme apo e pafundme) është.

Detyrat:

• Zhvilloni aftësinë për të hartuar një algoritëm veprimesh dhe për të vepruar sipas algoritmit.
• Zhvilloni aftësinë për të analizuar rezultatet e marra, për të nxjerrë përfundime dhe për të bërë pyetje të reja.
• Zhvilloni aftësinë për të përdorur rregulla të formuluara gjatë zgjidhjes së problemeve.
• Zhvilloni aftësi në hartimin dhe leximin e diagrameve.

Lloji i mësimit: mësimi i materialit të ri.

Metoda: problem-hulumtim.

Forma: grup

Gjatë orëve të mësimit

Pjesa e parë e mësimit.

Qëllimi i pjesës së parë të mësimit (teorik): zbuloni dhe kuptoni se cilët numra quhen dhe janë racionalë dhe nëse ka numra që nuk janë.

1. Përsëriteni shkurtimisht në fillim të mësimit përkufizimet e numrave natyrorë, thyesorë, të plotë.

2. Shpallet tema e orës së mësimit: Numrat racionalë. Thyesat e zakonshme dhe dhjetore. (Rrëshqitje 2). Formulohet qëllimi i pjesës së parë të mësimit.

4. Natyrisht lind pyetja, Cilët nga numrat që dimë janë racionalë?? Gjatë bisedës, në ekran hartohet një diagram logjik i zhvillimit të konceptit të numrit (Figura 1 dhe rrëshqitja 5). Jepim shembuj dhe vërtetojmë se secili nga numrat që njohim është racional.

Oriz. 1

5. Le t'i hedhim një vështrim më të afërt thyesave dhjetore. Le të kujtojmë Rregulli për shndërrimin e një thyese dhjetore në një thyesë të zakonshme (Rrëshqitja 6) dhe ekzekutoni me gojë ushtrim për shndërrimin e thyesave dhjetore në thyesa të zakonshme (Rrëshqitjet 7–12).

(Me gojë)Shndërroni thyesën dhjetore në thyesë të zakonshme: 0,7; 0,75; 0,2; 0,16; 0,125; 0,375.

Pjesa shfaqet në ekran dhe fëmijët marrin kartën me përgjigjen e saktë. Një grup letrash përgatitet paraprakisht (Shtojca 1) dhe shtrihet në tryezën e secilit grup; në kartat janë numrat e mëposhtëm 7/10, 75/100, 15/20, 3/4, 2/10, 1/5, 8/50, 4/25, 25/200, 1/8, 3/8 , 5/8. Ne komentojmë përgjigjet dhe, nëse është e nevojshme, kryejmë një kontroll hap pas hapi (Rrëshqitjet 7–12).

6. Ne vijmë në përfundimi se nëse një dhjetore "rrjedh" nga një thyesë e zakonshme, atëherë ajo dhjetore është një numër racional.

Problemi është formuluar:çfarë mund të jenë thyesat dhjetore dhe nëse të gjitha thyesat dhjetore janë numra racionalë.

7. Për të zgjidhur pyetjet e parashtruara, grupet kryejnë detyrën nr.1 (Rrëshqitjet 13–14), (Shtojca 2).

Detyra nr. 1.1(për grupin 1)

Shprehni thyesat 1/4, 1/3, 1/6 si dhjetore.

Detyra nr 1.2(për grupin 2)

Shprehni thyesat 2/5, 4/11, 7/15 si dhjetore.

Analizoni rezultatet tuaja.

Detyra nr 1.3(për grupin 3)

Shprehni thyesat 3/25, 1/37, 9/44 si dhjetore.

Analizoni rezultatet tuaja.

Duke analizuar rezultatet ( Rrëshqitja 15), dhe nëse është e nevojshme, kontrolloni llogaritjet (Rrëshqitjet 16–18), arrijmë në përfundimin se thyesat dhjetore janë a) të fundme; b) të pafundme. Dhe ato të pafundme kanë një veti të caktuar: duke filluar nga një numër dhjetor, përsëriten një ose më shumë shifra dhjetore. Për këtë veti quhen thyesa dhjetore të tilla të pafundme periodike.

Ndërsa biseda përparon, një diagram hartohet në tabelë. Shenjat me mbishkrime përgatiten paraprakisht (Shtojca 3) dhe ngjiten me magnet në tabelë, dhe shigjetat mund të vizatohen me shkumës.

Oriz. 2

Fëmijët bëjnë përfundimi se dhjetoret e fundme dhe dhjetoret periodike te pafundme jane numra racional. Megjithatë, mësuesi komenton se në këtë fazë të njohurive ky përfundim është vetëm një supozim dhe se ende kërkohet të vërtetohet se ndonjë një thyesë dhjetore periodike mund të përfaqësohet si një thyesë e zakonshme, që do të thotë se është një numër racional dhe këtë do ta vërtetojmë më vonë, në klasën 9. Tani për tani këtë situatë do ta përdorim si fakt.

8. Më pas, fëmijëve u kërkohet të analizojnë diagramin dhe të mendojnë nëse mund të ketë ndonjë thyesë tjetër dhjetore (ose mund t'u kërkojë atyre të nxjerrin një thyesë dhjetore që nuk është as e fundme dhe as pafundësisht periodike). Arrijmë në përfundimin se ka ende thyesa të pafundme jo periodike. Ne japim shembuj të thyesave të tilla (0.01001000100001...; 0.12123123412345123456... etj.), dhe themi se ata nuk do të jenë numra racionalë (dhe përsëri ky është supozimi ynë, të cilin mund ta vërtetojmë, por vetëm më vonë, por tani për tani ne do ta përdorë vetëm si fakt).

Oriz. 3

Pjesa e dytë e mësimit.

Qëllimi i pjesës së dytë të mësimit (praktik): zbuloni se si të kuptoni nga pamja e një thyese të zakonshme nëse ajo mund të përfaqësohet si një thyesë dhjetore e fundme, ose nëse do të rezultojë të jetë një thyesë e pafundme.

9. Le të formulojmë problemin: Si mund të kuptoni nga pamja e një thyese të zakonshme nëse ajo mund të përfaqësohet si një thyesë dhjetore e fundme, apo nëse do të rezultojë të jetë një thyesë e pafundme?

Për të zgjidhur këtë problem, le të plotësojmë detyrat. Secila nga detyrat nr. 2-4 kryhet në grup. Pas përfundimit të secilës detyrë diskutohen rezultatet. Secili grup formulon përfundimet e tij.

10. Detyra nr 2(Rrëshqitja 20, Shtojca 2)

1/20, 1/25, 4/50, 3/125, 5/8, 17/100.

• Faktoroni emëruesit e këtyre thyesave.

Duke analizuar rezultatet (Rrëshqitje 20) (Rrëshqitja 21)

11. Detyra nr.3(Rrëshqitja 22, Shtojca 2)

Shndërroni thyesat në dhjetore dhe përgjigjuni pyetjeve.

1/30, 3/110, 7/9, 8/55, 5/111, 7/82.

• Faktoroni emëruesit e këtyre thyesave
• Çfarë pronë e përbashkët a kanë emëruesit e këtyre thyesave?

Duke analizuar rezultatet (Rrëshqitja 23), duke kontrolluar llogaritjet nëse është e nevojshme (Rrëshqitjet 24–27). Secili grup raporton vëzhgimet e tij dhe nxjerr përfundime paraprake.

12. Detyra nr.4(Rrëshqitja 28, Shtojca 2)

Analizoni rezultatet e tre detyrave të mëparshme dhe përgjigjuni pyetjeve:

• Cilat thyesa dhjetore "rrjedhin" nga thyesat e zakonshme?
• Në cilat kushte një thyesë e zakonshme mund të paraqitet si dhjetore përfundimtare?
• Në çfarë kushti një thyesë e zakonshme mund të përfaqësohet si një thyesë dhjetore periodike e pafundme?

Pasi diskutuam performancën e një përfaqësuesi të secilit grup bazuar në rezultatet e detyrës nr. 4, kalojmë në përfundime.

13. Përfundime(Skema 2, Slides 29–31):

1. Thyesat dhjetore mund të jenë të fundme ose të pafundme.
2. Dhjetorja përfundimtare gjithmonë mund të paraqitet si thyesë dhe një është një numër racional.
3. Një thyesë dhjetore periodike e pafundme mund të përfaqësohet si një fraksion i zakonshëm - ky është një numër racional.
4. Çdo thyesë e zakonshme mund të përfaqësohet si një thyesë dhjetore periodike e fundme ose e pafundme.
5. Thyesa dhjetore përfundimtare do të fitohet nëse në zgjerimin e emëruesit e zakonshme përkatëse fraksion i pareduktueshëm jo të tjerë faktorët kryesorë përveç 2 dhe 5 (Rrëshqitje 30).
6. Një thyesë dhjetore periodike e pafundme do të merret nëse ndonjë faktor tjetër kryesor përveç 2 dhe 5 është i pranishëm në zgjerimin e emëruesit të thyesës së zakonshme të pakësueshme. (Rrëshqitje 31).

14. Zbatimi i rregullit(Rrëshqitjet 32–33):

Detyra nr 5

1. Cila nga thyesat e zakonshme 1/2, 1/3, 7/15, 6/25, 5/16 mund të paraqitet si thyesë dhjetore përfundimtare?
2. Në cilat thyesa (të zakonshme ose dhjetore) është "më i përshtatshëm" për të kryer llogaritjet: a) 3/8 + 0,567; b) 2.378 – 3/14 ?
3. Në cilat thyesa (të zakonshme ose dhjetore) do të shkruani zgjidhjen e ekuacionit:
   1. 3x = 8;
   2. 5u = 12;
   3. 16a = –7?

Ne kontrollojmë detyrën dhe përmbledhim:

15. Përmbledhja dhe ngritja e pyetjeve të reja.(Figura 4, Slides 34–35). Tani e dimë se thyesat pozitive dhe negative mund të paraqiten si thyesa dhjetore të fundme ose periodike. Kjo do të thotë se këta të fundit janë numra racionalë. Por thyesat dhjetore të pafundme jo periodike nuk janë. Me sa duket, ata bien në sferën e disa numrave të tjerë, ende të panjohur për ju, (do t'ju them një sekret që quhen irracionalë). Këta numra irracionalë, së bashku me ata racionalë, formojnë edhe domenin e tyre të numrave, të bashkuar nga vetitë e tyre (numrat realë). Dhe nëse “shtoni” disa numra të tjerë në fushën e numrave realë, atëherë... Por kjo është tema e kërkimit tuaj të ardhshëm.

Oriz. 4

16. Përfundimi i orës së mësimit(Rrëshqitja 36)

Ne e mbyllim mësimin me një citim nga L.N. Tolstoi: "Njohuria është njohuri vetëm kur ajo fitohet nga përpjekjet e mendimit të dikujt, dhe jo nga kujtesa". Në këtë drejtim vlerësojmë punën e secilit grup.

Detyre shtepie:

1. Lexoni paragrafin 37 të tekstit shkollor. Cilat pyetje janë paraqitur në tekst për të cilat nuk kemi diskutuar në klasë?
2. Dilni me pesë thyesa të zakonshme nga të cilat "prodhohen" thyesat dhjetore të fundme dhe pesë thyesa të zakonshme nga të cilat "prodhohen" thyesat dhjetore të pafundme (Shtojca 4) dhe kthejini këto thyesa në dhjetore.

Literatura:

1. Shvartsburd S.I., Vilenkin N.Ya., Zhokhov V.I., Chesnokov A.S. Matematika 6, Mnemosyne, 2006.
2. Mordkovich A.G. Algjebër. Klasa 8: Libër mësuesi për klasat me studim të avancuar të matematikës, Mnemosyne, 2004.