Përgatitja online për provimin. Simulator i Provimit të Unifikuar të Shtetit në anglisht

Udhëzimet

Sipas vetive të një trapezi izoscelular, segmenti n është i barabartë me gjysmën e diferencës së bazave x dhe y. Prandaj, baza më e vogël e trapezit y mund të përfaqësohet si diferencë ndërmjet bazës më të madhe dhe segmentit n të shumëzuar me dy: y = x - 2*n.

Gjeni segmentin më të vogël të panjohur n. Për ta bërë këtë, llogarisni një nga anët e rezultatit trekëndësh kënddrejtë. Një trekëndësh formohet nga një lartësi - h (këmbë), një anë - a (hipotenuzë) dhe një segment - n (këmbë). Sipas teoremës së Pitagorës, këmba e panjohur n² = a² - h². Zëvendësues vlerat numerike dhe njehsoni katrorin e këmbës n. Merrni rrënjën katrore të vlerës që rezulton - kjo do të jetë gjatësia e segmentit n.

Zëvendësoni këtë vlerë në ekuacionin e parë për të llogaritur y. Sipërfaqja e trapezit llogaritet duke përdorur formulën S = ((x + y)*h)/2. Shprehni variablin e panjohur: y = 2*S/h – x.

Burimet:

• lartësia e një trapezi izoscelular

Për të përcaktuar një katërkëndësh të tillë si një trapezoid, duhet të përcaktohen të paktën tre nga anët e tij. Prandaj, për shembull, mund të shqyrtojmë një problem në të cilin jepen gjatësitë e diagonaleve trapezoide, si dhe një nga vektorët anësor.

Udhëzimet

Figura nga kushtet problemore është paraqitur në 1.B në këtë rast duhet supozuar se ajo në shqyrtim është ABCD, në të cilën jepen gjatësitë e diagonaleve AC dhe BD, si dhe anësor AB, e përfaqësuar nga vektori a(ax,ay). Të dhënat fillestare të pranuara na lejojnë t'i gjejmë të dyja bazat trapezoide(si lart ashtu edhe poshtë). NË shembull specifik së pari do të gjendet baza e poshtme AD.

Konsideroni trekëndëshin ABD. Gjatësia e anës së saj AB është e barabartë me vlerën absolute të vektorit a. Le të jetë |a|=sqrt((ax)^2+(ay)^2)=a, pastaj cosф =ax/sqrt(((ax)^2+(ay)^2), si kosinus i drejtimit të a. Le të ketë diagonalja e dhënë BD gjatësia p, dhe AD e dëshiruar gjatësia X. Pastaj, sipas teoremës së kosinusit, P^2=a^2+ x^2-2axcosф. Ose x^2-2axcosф+(a^2-p^2)=0.

Për të gjetur majën bazat BC (gjatësia e tij shënohet edhe me x gjatë kërkimit), përdoret moduli |a|=a, si dhe diagonalja e dytë BD=q dhe kosinusi i këndit ABC, i cili padyshim është i barabartë me (n-ph) .

Më tej ne e konsiderojmë trekëndëshi ABC, për të cilën, si më parë, lind teorema e kosinusit dhe në vijim. Duke marrë parasysh se cos(п-ф)=-cosф, bazuar në zgjidhjen për AD, mund të përdorim formulën e mëposhtme, duke zëvendësuar p me q:ВС=- a*ax|sqrt(((ax)^2+(ay) ^2) +sqrt((((a)^2)(ax^2))/(ax^2+ay^2))-a^2+q^2).

Ky është një katror dhe, në përputhje me rrethanat, ka dy rrënjë. Kështu, në këtë rast mbetet për të zgjedhur vetëm ato rrënjë që kanë vlerë pozitive, pasi gjatësia nuk mund të jetë negative.

Shembull Lëreni trapezoide Ana ABCD AB jepet nga vektori a(1, sqrt3), p=4, q=6. Gjeni bazat trapezoide.Zgjidhja. Duke përdorur algoritmet e marra më sipër, mund të shkruajmë: |a|=a=2, cosф=1/2. AD=1/2+sqrt(4/4 -4+16)=1/2 +sqrt(13)=(sqrt(13)+1)/2.BC=-1/2+sqrt(-3+36 )=(sqrt(33)-1)/2.

Video mbi temën

Një trapez është një katërkëndësh në të cilin dy anët janë paralele dhe dy të tjerat jo. Lartësia e një trapezi është një segment i tërhequr pingul midis dy vijave paralele. Në varësi të të dhënave burimore, ato mund të llogariten në mënyra të ndryshme.

Do t'ju duhet

• Njohuri për anët, bazat, vija e mesme trapezoid, si dhe, sipas dëshirës, ​​sipërfaqja dhe/ose perimetri i tij.

Udhëzimet

Le të themi se ka një trapez me të njëjtat të dhëna si në figurën 1. Le të vizatojmë 2 lartësi, marrim , i cili ka 2 brinjë më të vogla nga këmbët e trekëndëshave kënddrejtë. Le ta shënojmë rrotullën më të vogël si x. Ai vendoset duke e ndarë diferencën në gjatësi midis bazave më të mëdha dhe më të vogla. Pastaj, sipas teoremës së Pitagorës, katrori i lartësisë e barabartë me shumën katrorët e hipotenuzës d dhe këmbës x. Nga kjo shumë nxjerrim dhe marrim lartësinë h. (Fig. 2)

Video mbi temën

Burimet:

• Si të llogarisni lartësinë e një trapezi

Figura matematikore me katër cepa quhet trapez nëse një palë brinjë të kundërta janë paralele dhe çifti tjetër jo. Brinjët paralele quhen arsyet trapezoide, dy të tjerat janë anësore. Në një formë drejtkëndëshe trapezoide njëri nga këndet në anë është i drejtë.

Udhëzimet

Detyra 1. Gjeni bazat BC dhe AD trapezoide, nëse dihet gjatësia AC = f; gjatësia e anës CD = c dhe këndi ADC = α Zgjidhje: Konsideroni një CED drejtkëndëshe. Hipotenuza c dhe këndi ndërmjet hipotenuzës dhe këmbës EDC janë të njohura. Gjeni gjatësitë CE dhe ED: duke përdorur formulën e këndit CE = CD*sin(ADC); ED = CD*cos(ADC). Pra: CE = c*sinα; ED=c*cosα.

Konsideroni trekëndëshin kënddrejtë ACE. Ju e dini hipotenuzën AC dhe CE, gjeni anën AE duke përdorur rregullin: shuma e katrorëve të këmbëve është e barabartë me katrorin e hipotenuzës. Pra: AE(2) = AC(2) - CE(2) = f(2) - c*sinα. Llogaritni rrënjë katrore nga ana e djathtë e barazisë. Ju gjetët pjesën e sipërme drejtkëndore trapezoide.

Gjatësia e bazës AD është shuma e gjatësive të dy segmenteve AE dhe ED. AE = rrënjë katrore(f(2) - c*sinα); ED = c*cosα).Pra: AD = rrenja katrore(f(2) - c*sinα) + c*cosα.Ke gjetur bazen e poshtme te drejtkendeshit trapezoide.

Detyra 2. Gjeni bazat BC dhe AD të drejtkëndëshit trapezoide, nëse dihet gjatësia e diagonales BD = f; gjatësia e anës CD = c dhe këndi ADC = α Zgjidhje: Konsideroni trekëndëshin kënddrejtë CED. Gjeni gjatësitë e brinjëve CE dhe ED: CE = CD*sin(ADC) = c*sinα; ED = CD*cos(ADC) = c*cosα.

Konsideroni drejtkëndëshin ABCE. Nga vetia AB = CE = c*sinα Konsideroni trekëndëshin kënddrejtë ABD. Sipas vetive të trekëndëshit kënddrejtë, katrori i hipotenuzës është shuma e katrorëve të këmbëve. Prandaj AD(2) = BD(2) - AB(2) = f(2) - c*sinα Ju keni gjetur bazën e poshtme të drejtkëndëshit trapezoide AD = rrënjë katrore (f(2) - c*sinα).

Sipas rregullit drejtkëndësh, BC = AE = AD - ED = rrënjë katrore(f(2) - c*sinα) - c*cosα. Keni gjetur bazën e sipërme të drejtkëndëshit trapezoide.

Baza më e vogël e një trapezi është një nga anët e tij paralele, e cila ka një gjatësi minimale. Kjo vlerë mund të llogaritet në disa mënyra duke përdorur të dhëna të caktuara.

Do t'ju duhet

• - kalkulator.

Udhëzimet

Nëse dihen dy gjatësi - baza dhe vija e mesme - përdorni veçorinë trapezoid për të llogaritur bazën më të vogël. Sipas tij, vija e mesme e një trapezi është identike me gjysmën e shumës së bazave. Në këtë rast, baza më e vogël do të jetë e barabartë me diferencën midis dyfishit të gjatësisë së vijës së mesme dhe gjatësisë së bazës së madhe të kësaj figure.

Nëse dihen parametra të tillë të trapezit si , lartësia, gjatësia e bazës së madhe, atëherë llogaritet baza më e vogël e kësaj baze në bazë të trapezit. Në këtë rast rezultati përfundimtar përftohet duke zbritur nga diferenca ndërmjet herësit të dyfishit të sipërfaqes dhe lartësisë një parametër siç është gjatësia e bazës së madhe të trapezit.

Llogaritni gjatësinë e anës anësore në anën tjetër

Në materialet e testeve dhe provimeve të ndryshme, ato gjenden shumë shpesh problemet e trapezit, zgjidhja e të cilave kërkon njohuri për vetitë e tij.

Le të zbulojmë se cilat veti interesante dhe të dobishme ka një trapezoid për zgjidhjen e problemeve.

Pas studimit të vetive të vijës së mesme të një trapezi, mund të formulohet dhe vërtetohet veti e një segmenti që lidh mesin e diagonaleve të një trapezi. Segmenti që lidh mesin e diagonaleve të një trapezi është i barabartë me gjysmën e diferencës së bazave.

MO - vija e mesme trekëndëshi ABC dhe e barabartë me 1/2ВС (Fig. 1).

MQ është vija e mesme e trekëndëshit ABD dhe është e barabartë me 1/2AD.

Pastaj OQ = MQ – MO, pra OQ = 1/2AD – 1/2BC = 1/2(AD – BC).

Kur zgjidhni shumë probleme në një trapezoid, një nga teknikat kryesore është të vizatoni dy lartësi në të.

Merrni parasysh sa vijon detyrë.

Le të jetë BT lartësia e një trapezi dykëndor ABCD me baza BC dhe AD, me BC = a, AD = b. Gjeni gjatësitë e segmenteve AT dhe TD.

Zgjidhje.

Zgjidhja e problemit nuk është e vështirë (Fig. 2), por ju lejon të merrni veti e lartësisë së një trapezi izoscelor të nxjerrë nga kulmi kënd i mpirë : ndahet lartësia e një trapezi izoscelor të nxjerrë nga kulmi i një këndi të mpirë bazë më e madhe në dy segmente, prej të cilëve më i vogli është i barabartë me gjysmën e diferencës së bazave dhe më i madhi është i barabartë me gjysmën e shumës së bazave.

Kur studioni vetitë e një trapezi, duhet t'i kushtoni vëmendje një vetie të tillë si ngjashmëria. Kështu, për shembull, diagonalet e një trapezi e ndajnë atë në katër trekëndësha, dhe trekëndëshat ngjitur me bazat janë të ngjashëm, dhe trekëndëshat ngjitur me anët janë të barabartë në madhësi. Kjo deklaratë mund të quhet veti e trekëndëshave në të cilët ndahet një trapez me diagonalet e tij. Për më tepër, pjesa e parë e pohimit mund të vërtetohet shumë lehtë përmes shenjës së ngjashmërisë së trekëndëshave në dy kënde. Le të provojmë pjesa e dytë e deklaratës.

Trekëndëshat BOC dhe COD kanë një lartësi të përbashkët (Fig. 3), nëse marrim si bazë segmentet BO dhe OD. Atëherë S BOC /S COD = BO/OD = k. Prandaj, S COD = 1/k · S BOC .

Në mënyrë të ngjashme, trekëndëshat BOC dhe AOB kanë një lartësi të përbashkët nëse marrim si bazë segmentet CO dhe OA. Atëherë S BOC /S AOB = CO/OA = k dhe S A O B = 1/k · S BOC .

Nga këto dy fjali rrjedh se S COD = S A O B.

Le të mos ndalemi në deklaratën e formuluar, por të gjejmë marrëdhëniet ndërmjet zonave të trekëndëshave në të cilët ndahet trapezi me diagonalet e tij. Për ta bërë këtë, le të zgjidhim problemin e mëposhtëm.

Le të jetë pika O pika e prerjes së diagonaleve të trapezit ABCD me bazat BC dhe AD. Dihet se sipërfaqet e trekëndëshave BOC dhe AOD janë përkatësisht të barabarta me S 1 dhe S 2. Gjeni zonën e trapezit.

Meqenëse S COD = S A O B, atëherë S ABC D = S 1 + S 2 + 2S COD.

Nga ngjashmëria e trekëndëshave BOC dhe AOD del se BO/OD = √(S1/S 2).

Prandaj, S₁/S COD = BO/OD = √(S1/S 2), që do të thotë S COD = √(S 1 · S 2).

Pastaj S ABC D = S 1 + S 2 + 2√(S 1 · S 2) = (√S 1 + √S 2) 2.

Duke përdorur ngjashmërinë vërtetohet se vetia e një segmenti që kalon nëpër pikën e kryqëzimit të diagonaleve të një trapezi paralel me bazat.

Le të shqyrtojmë detyrë:

Le të jetë pika O pika e prerjes së diagonaleve të trapezit ABCD me bazat BC dhe AD. BC = a, AD = b. Gjeni gjatësinë e segmentit PK që kalon në pikën e prerjes së diagonaleve të trapezit paralel me bazat. Cilat segmente ndahet PK me pikën O (Fig. 4)?

Nga ngjashmëria e trekëndëshave AOD dhe BOC del se AO/OC = AD/BC = b/a.

Nga ngjashmëria e trekëndëshave AOP dhe ACB del se AO/AC = PO/BC = b/(a + b).

Prandaj PO = BC b / (a ​​+ b) = ab / (a ​​+ b).

Në mënyrë të ngjashme, nga ngjashmëria e trekëndëshave DOK dhe DBC, rezulton se OK = ab/(a + b).

Prandaj PO = OK dhe PK = 2ab/(a + b).

Pra, vetia e provuar mund të formulohet si më poshtë: segmenti, paralel me bazat një trapez që kalon nëpër pikën e prerjes së diagonaleve dhe lidh dy pika në anët, përgjysmohet nga pika e kryqëzimit të diagonaleve. Gjatësia e saj është mesatarja harmonike e bazave të trapezit.

Në vijim pronë me katër pikë: në një trapez, pika e prerjes së diagonaleve, pika e kryqëzimit të vazhdimit të brinjëve, mesi i bazave të trapezit shtrihen në të njëjtën vijë.

Trekëndëshat BSC dhe ASD janë të ngjashëm (Fig. 5) dhe në secilën prej tyre medianat ST dhe SG ndajnë këndin e kulmit S në pjesë të barabarta. Prandaj, pikat S, T dhe G shtrihen në të njëjtën linjë.

Në të njëjtën mënyrë, pikat T, O dhe G janë të vendosura në të njëjtën linjë. Kjo rrjedh nga ngjashmëria e trekëndëshave BOC dhe AOD.

Kjo do të thotë që të katër pikat S, T, O dhe G shtrihen në të njëjtën linjë.

Ju gjithashtu mund të gjeni gjatësinë e segmentit që ndan trapezin në dy të ngjashëm.

Nëse trapezoidët ALFD dhe LBCF janë të ngjashëm (Fig. 6), atëherë a/LF = LF/b.

Prandaj LF = √(ab).

Kështu, një segment që ndan një trapezoid në dy trapezoide të ngjashme ka një gjatësi të barabartë me mesataren gjeometrike të gjatësisë së bazave.

Le të provojmë veti e një segmenti që ndan një trapez në dy zona të barabarta.

Le të jetë zona e trapezit S (Fig. 7). h 1 dhe h 2 janë pjesë të lartësisë, dhe x është gjatësia e segmentit të dëshiruar.

Atëherë S/2 = h 1 (a + x)/2 = h 2 (b + x)/2 dhe

S = (h 1 + h 2) · (a + b)/2.

Le të krijojmë një sistem

(h 1 (a + x) = h 2 (b + x)
(h 1 · (a + x) = (h 1 + h 2) · (a + b)/2.

Duke vendosur këtë sistem, marrim x = √(1/2(a 2 + b 2)).

Kështu, gjatësia e segmentit që ndan trapezin në dy të barabarta është e barabartë me √((a 2 + b 2)/2)(katrori mesatar i gjatësisë së bazës).

Pra, për trapezin ABCD me baza AD dhe BC (BC = a, AD = b) vërtetuam se segmenti:

1) MN, që lidh mesin e anëve anësore të trapezit, është paralel me bazat dhe i barabartë me gjysmën e tyre (mesatare numrat aritmetikë a dhe b);

2) PK që kalon nëpër pikën e kryqëzimit të diagonaleve të trapezit paralel me bazat është e barabartë me
2ab/(a + b) (mesatarja harmonike e numrave a dhe b);

3) LF, e cila ndan një trapezoid në dy trapezoide të ngjashme, ka një gjatësi të barabartë me mesataren numrat gjeometrikë a dhe b, √(ab);

4) EH, duke e ndarë një trapez në dy të barabartë, ka gjatësinë √((a 2 + b 2)/2) (rrënja katrore mesatare e numrave a dhe b).

Shenja dhe vetia e një trapezi të mbishkruar dhe të rrethuar.

Vetia e një trapezi të mbishkruar: një trapez mund të brendashkohet në një rreth nëse dhe vetëm nëse është dykëndor.

Vetitë e trapezit të përshkruar. Një trapez mund të përshkruhet rreth një rrethi nëse dhe vetëm nëse shuma e gjatësive të bazave është e barabartë me shumën e gjatësive të anëve.

Pasojat e dobishme të faktit që një rreth është gdhendur në një trapezoid:

1. Lartësia e trapezit të rrethuar është e barabartë me dy rreze të rrethit të brendashkruar.

2. Ana e trapezit të rrethuar është e dukshme nga qendra e rrethit të brendashkruar në një kënd të drejtë.

E para është e qartë. Për të vërtetuar përfundimin e dytë, është e nevojshme të përcaktohet se këndi COD është i drejtë, gjë që gjithashtu nuk është e vështirë. Por njohja e kësaj përfundimi ju lejon të përdorni një trekëndësh kënddrejtë kur zgjidhni probleme.

Le të specifikojmë konkluzionet për një trapezoid të rrethuar izosceles:

Lartësia e një trapezi të rrethuar izosceles është mesatarja bazat gjeometrike trapezoide
h = 2r = √(ab).

Karakteristikat e konsideruara do t'ju lejojnë të kuptoni më thellë trapezin dhe të siguroni sukses në zgjidhjen e problemeve duke përdorur vetitë e tij.

Ende keni pyetje? Nuk dini si të zgjidhni problemet e trapezit?
Për të marrë ndihmë nga një mësues -.
Mësimi i parë është falas!

blog.site, kur kopjoni materialin plotësisht ose pjesërisht, kërkohet një lidhje me burimin origjinal.

Rreth i rrethuar dhe trapez. Përshëndetje! Ekziston një botim tjetër për ju, në të cilin do të shqyrtojmë problemet me trapezoidët. Detyrat janë pjesë e provimit të matematikës. Këtu ato kombinohen në një grup jo vetëm një trapez, por një kombinim trupash - një trapezoid dhe një rreth. Shumica e këtyre problemeve zgjidhen me gojë. Por ka edhe disa që duhen adresuar. vëmendje të veçantë, për shembull, detyra 27926.

Çfarë teorie duhet të mbani mend? Kjo:

Problemet me trapezoidët që janë të disponueshëm në blog mund të shihen Këtu.

27924. Rreth një trapezi është përshkruar një rreth. Perimetri i trapezit është 22, vija e mesme është 5. Gjeni anën e trapezit.

Vini re se një rreth mund të përshkruhet vetëm rreth një trapezi izosceles. Na jepet vija e mesme, që do të thotë se mund të përcaktojmë shumën e bazave, domethënë:

Kjo do të thotë se shuma e anëve do të jetë e barabartë me 22–10=12 (perimetri minus bazën). Meqenëse anët e një trapezi izoscelular janë të barabarta, njëra anë do të jetë e barabartë me gjashtë.

27925. Ana anësore e një trapezi izoscelular është e barabartë me të bazë më e vogël, këndi në bazë është 60 0, baza më e madhe është 12. Gjeni rrezen e rrethit të rrethuar të këtij trapezi.

Nëse keni zgjidhur probleme me një rreth dhe një gjashtëkëndësh të gdhendur në të, atëherë menjëherë do të shprehni përgjigjen - rrezja është 6. Pse?

Shikoni: një trapez izoscelular me një kënd bazë të barabartë me 60 0 dhe anët e barabarta AD, DC dhe CB, përfaqësojnë gjysmën e një gjashtëkëndëshi të rregullt:

Në një gjashtëkëndësh të tillë, segmenti lidh kulme të kundërta kalon nëpër qendër të rrethit. *Qendra e gjashtëkëndëshit dhe qendra e rrethit përkojnë, më shumë detaje

Kjo do të thotë, baza më e madhe e këtij trapezi përkon me diametrin e rrethit të rrethuar. Pra, rrezja është gjashtë.

*Sigurisht, mund të konsiderojmë barazinë e trekëndëshave ADO, DOC dhe OCB. Vërtetoni se janë barabrinjës. Më pas, konkludoni se këndi AOB është i barabartë me 180 0 dhe pika O është e barabartë nga kulmet A, D, C dhe B, dhe për këtë arsye AO=OB=12/2=6.

27926. Bazat e një trapezi dykëndor janë 8 dhe 6. Rrezja e rrethit të rrethuar është 5. Gjeni lartësinë e trapezit.

Vini re se qendra e rrethit të rrethuar shtrihet në boshtin e simetrisë dhe nëse ndërtojmë lartësinë e trapezit që kalon përmes kësaj qendre, atëherë kur ai të kryqëzohet me bazat do t'i ndajë ato në gjysmë. Le ta tregojmë këtë në skicë dhe gjithashtu të lidhim qendrën me kulmet:

Segmenti EF është lartësia e trapezit, ne duhet ta gjejmë atë.

Në trekëndëshin kënddrejtë OFC ne njohim hipotenuzën (kjo është rrezja e rrethit), FC=3 (pasi DF=FC). Duke përdorur teoremën e Pitagorës mund të llogarisim OF:

Në trekëndëshin kënddrejtë OEB, dihet hipotenuza (kjo është rrezja e rrethit), EB=4 (meqë AE=EB). Duke përdorur teoremën e Pitagorës ne mund të llogarisim OE:

Kështu EF=FO+OE=4+3=7.

Tani një nuancë e rëndësishme!

Në këtë problem, figura tregon qartë se bazat shtrihen përgjatë anët e ndryshme nga qendra e rrethit, kështu që problemi zgjidhet në këtë mënyrë.

Po sikur kushtet të mos përfshijnë një skicë?

Atëherë problemi do të kishte dy përgjigje. Pse? Shikoni me kujdes - dy trapezoide me baza të dhëna mund të futen në çdo rreth:

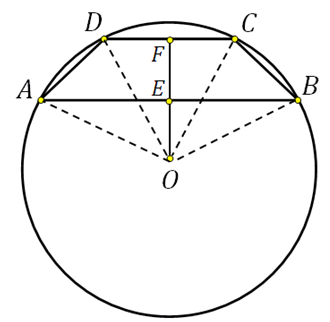
*Dmth, duke pasur parasysh bazat e trapezit dhe rrezen e rrethit, ekzistojnë dy trapezoide.

Dhe zgjidhja për "opsionin e dytë" do të jetë si më poshtë.

Duke përdorur teoremën e Pitagorës ne llogarisim OF:

Le të llogarisim gjithashtu OE:

Kështu EF=FO–OE=4–3=1.

Sigurisht, në një problem me një përgjigje të shkurtër në Provimin e Bashkuar të Shtetit nuk mund të ketë dy përgjigje dhe një problem i ngjashëm nuk do të jepet pa një skicë. Prandaj, kushtojini vëmendje të veçantë skicës! Domethënë: si ndodhen bazat e trapezit. Por në detyrat me një përgjigje të detajuar, kjo ishte e pranishme në vitet e kaluara (me një gjendje pak më të komplikuar). Kushdo që konsideroi vetëm një opsion për vendndodhjen e trapezoidit humbi një pikë në këtë detyrë.

27937. Një trapez është i rrethuar rreth një rrethi, perimetri i të cilit është 40. Gjeni vijën e mesit të tij.

Këtu duhet të kujtojmë menjëherë vetinë e një katërkëndëshi të rrethuar rreth një rrethi:

Shumat anët e kundërtaçdo katërkëndësh i rrethuar rreth një rrethi është i barabartë.

Për të qenë të sigurt dhe për të zgjidhur me sukses problemet në mësimet e gjeometrisë, nuk mjafton të mësosh formulat. Ata duhet të kuptohen së pari. Të kesh frikë, dhe aq më tepër të urresh formulat, është joproduktive. Në këtë artikull gjuhë e aksesueshme do të analizohen mënyra të ndryshme Gjetja e zonës së një trapezi. Për të kuptuar më mirë rregullat dhe teoremat përkatëse, do t'i kushtojmë pak vëmendje vetive të tij. Kjo do t'ju ndihmojë të kuptoni se si funksionojnë rregullat dhe në cilat raste duhet të zbatohen formula të caktuara.

Përcaktimi i një trapezi

Çfarë lloj figure është kjo në përgjithësi? Një trapez është një shumëkëndësh me katër qoshe dhe dy brinjë paralele. Dy anët e tjera të trapezit mund të priren në kënde të ndryshme. Ajo anët paralele quhen baza, dhe për anët jo paralele përdoret emri "anët" ose "ijet". Shifra të tilla janë mjaft të zakonshme në jetën e përditshme. Konturet e trapezoidit mund të shihen në siluetat e veshjeve, sendeve të brendshme, mobiljeve, enëve dhe shumë të tjera. Trapezi ndodh lloje të ndryshme: skalen, barabrinjës dhe drejtkëndor. Ne do të shqyrtojmë llojet dhe vetitë e tyre në më shumë detaje më vonë në artikull.

Vetitë e një trapezi

Le të ndalemi shkurtimisht në vetitë e kësaj figure. Shuma e këndeve ngjitur me çdo anë është gjithmonë 180°. Duhet të theksohet se të gjitha këndet e një trapezi shtohen deri në 360 °. Trapezi ka konceptin e vijës së mesme. Nëse lidhni mesin e anëve me një segment, kjo do të jetë vija e mesme. Është caktuar m. Vija e mesme ka veti të rëndësishme: është gjithmonë paralel me bazat (kujtojmë se edhe bazat janë paralele me njëra-tjetrën) dhe e barabartë me gjysmën e shumës së tyre:

Ky përkufizim duhet mësuar dhe kuptuar, sepse është çelësi i zgjidhjes së shumë problemeve!

Me një trapezoid, gjithmonë mund të ulni lartësinë në bazë. Një lartësi është një pingul, i shënuar shpesh me simbolin h, që tërhiqet nga çdo pikë e një baze në një bazë tjetër ose në shtrirjen e saj. Vija e mesit dhe lartësia do t'ju ndihmojnë të gjeni zonën e trapezit. Detyra të ngjashme janë më të zakonshmet në kursi shkollor gjeometrisë dhe shfaqen rregullisht mes fletëve të testimit dhe provimit.

Formulat më të thjeshta për sipërfaqen e një trapezi

Le të shohim dy më të njohurit dhe formula të thjeshta, me ndihmën e të cilit gjendet zona e një trapezi. Mjafton të shumëzoni lartësinë me gjysmën e shumës së bazave për të gjetur lehtësisht atë që kërkoni:

S = h*(a + b)/2.

Në këtë formulë, a, b tregojnë bazat e trapezit, h - lartësinë. Për lehtësinë e perceptimit, në këtë artikull, shenjat e shumëzimit shënohen me një simbol (*) në ​​formula, megjithëse në librat zyrtarë të referencës shenja e shumëzimit zakonisht hiqet.

Le të shohim një shembull.

Jepet: një trapez me dy baza të barabarta me 10 dhe 14 cm, lartësia është 7 cm.

Le të shohim zgjidhjen e këtij problemi. Duke përdorur këtë formulë, fillimisht duhet të gjeni gjysmën e bazave: (10+14)/2 = 12. Pra, gjysma është e barabartë me 12 cm. Tani shumëzojmë gjysmën e shumës me lartësinë. 12*7 = 84. Ajo që po kërkojmë është gjetur. Përgjigje: Sipërfaqja e trapezit është 84 metra katrorë. cm.

Së dyti formula e famshme thotë: sipërfaqja e një trapezi është e barabartë me produktin e vijës së mesme dhe lartësinë e trapezit. Kjo do të thotë, në fakt rrjedh nga koncepti i mëparshëm i vijës së mesme: S=m*h.

Përdorimi i diagonaleve për llogaritjet

Një mënyrë tjetër për të gjetur zonën e një trapezi nuk është në të vërtetë aq e komplikuar. Ajo është e lidhur me diagonalet e saj. Duke përdorur këtë formulë, për të gjetur zonën, duhet të shumëzoni gjysmën e produktit të diagonaleve të tij (d 1 d 2) me sinusin e këndit midis tyre:

S = ½ d 1 d 2 mëkat a.

Le të shqyrtojmë një problem që tregon zbatimin e kësaj metode. Jepet: një trapez me gjatësinë e diagonaleve përkatësisht 8 dhe 13 cm Këndi a ndërmjet diagonaleve është 30°. Gjeni zonën e trapezit.

Zgjidhje. Duke përdorur formulën e mësipërme, është e lehtë të llogaritet se çfarë kërkohet. Siç e dini, mëkati 30° është 0,5. Prandaj, S = 8*13*0.5=52. Përgjigje: sipërfaqja është 52 metra katrorë. cm.

Gjetja e sipërfaqes së një trapezi izoscelor

Një trapez mund të jetë izosceles (izosceles). Brinjët e tij janë të njëjta dhe këndet në bazat janë të barabarta, gjë që ilustrohet mirë nga figura. Trapezoid isosceles ka të njëjtat veti si ajo e zakonshme, plus një numër të veçantë. Një rreth mund të rrethohet rreth një trapezi izoscelular dhe një rreth mund të brendashkruhet brenda tij.

Cilat metoda ekzistojnë për llogaritjen e sipërfaqes së një figure të tillë? Metoda e mëposhtme do të kërkojë shumë llogaritje. Për ta përdorur atë, duhet të dini vlerat e sinusit (sin) dhe kosinusit (cos) të këndit në bazën e trapezit. Llogaritjet e tyre kërkojnë ose tabela Bradis ose kalkulator inxhinierik. Këtu është formula:

S= c*mëkat a*(a - c*cos a),

Ku Me- kofshë anësore, a- kënd në bazën e poshtme.

Një trapezoid barabrinjës ka diagonale me gjatësi të barabartë. E kundërta është gjithashtu e vërtetë: nëse një trapezoid ka diagonale të barabarta, atëherë ai është dykëndor. Nga këtu formulën e mëposhtme, e cila ndihmon për të gjetur sipërfaqen e një trapezi - gjysma e produktit të katrorit të diagonaleve dhe sinusit të këndit midis tyre: S = ½ d 2 sin a.

Gjetja e sipërfaqes së një trapezi drejtkëndor

I njohur rast i veçantë trapez drejtkëndor. Ky është një trapezoid, në të cilin njëra anë (kofsha e saj) ngjitet me bazat në një kënd të drejtë. Ka vetitë e një trapezi të rregullt. Përveç kësaj, ajo ka shumë tipar interesant. Dallimi në katrorët e diagonaleve të një trapezi të tillë është i barabartë me ndryshimin në katrorët e bazave të tij. Për të përdoren të gjitha metodat e përshkruara më parë për llogaritjen e sipërfaqes.

Ne përdorim zgjuarsinë

Ekziston një truk që mund të ndihmojë nëse harroni formula specifike. Le të hedhim një vështrim më të afërt se çfarë është një trapezoid. Nëse e ndajmë mendërisht në pjesë, do të marrim forma gjeometrike të njohura dhe të kuptueshme: një katror ose drejtkëndësh dhe një trekëndësh (një ose dy). Nëse dihen lartësia dhe anët e trapezit, mund të përdorni formulat për sipërfaqen e një trekëndëshi dhe një drejtkëndëshi dhe më pas të shtoni të gjitha vlerat që rezultojnë.

Le ta ilustrojmë këtë shembullin e mëposhtëm. Dana trapez drejtkëndor. Këndi C = 45°, këndet A, D janë 90°. Baza e sipërme e trapezit është 20 cm, lartësia është 16 cm. Ju duhet të llogarisni sipërfaqen e figurës.

Kjo shifër padyshim përbëhet nga një drejtkëndësh (nëse dy kënde janë të barabarta me 90°) dhe një trekëndësh. Meqenëse trapezi është drejtkëndor, prandaj, lartësia e tij është e barabartë me anën e tij, domethënë 16 cm, kemi një drejtkëndësh me brinjë përkatësisht 20 dhe 16 cm. Tani merrni parasysh një trekëndësh këndi i të cilit është 45°. Ne e dimë se njëra anë e saj është 16 cm meqenëse kjo anë është edhe lartësia e trapezit (dhe dimë që lartësia zbret në bazë në kënd të drejtë), prandaj, këndi i dytë i trekëndëshit është 90°. Prandaj, këndi i mbetur i trekëndëshit është 45°. Si pasojë e kësaj marrim një drejtkëndëshe trekëndëshi dykëndësh, dy anët e të cilit janë të njëjta. Kjo do të thotë që ana tjetër e trekëndëshit është e barabartë me lartësinë, domethënë 16 cm, mbetet vetëm të llogaritet sipërfaqja e trekëndëshit dhe drejtkëndëshit dhe të shtohen vlerat që rezultojnë.

Sipërfaqja e një trekëndëshi kënddrejtë është e barabartë me gjysmën e produktit të këmbëve të tij: S = (16*16)/2 = 128. Sipërfaqja e një drejtkëndëshi është e barabartë me produktin e gjerësisë dhe gjatësisë së tij: S = 20*16 = 320. Gjetëm atë të kërkuar: sipërfaqja e trapezit S = 128 + 320 = 448 sq. shikoni Ju lehtë mund të kontrolloni veten duke përdorur formulat e mësipërme, përgjigja do të jetë identike.

Ne përdorim formulën Pick

S = M/2 + N - 1,

në këtë formulë M është numri i nyjeve, d.m.th. kryqëzimet e vijave të figurës me vijat e qelizës në kufijtë e trapezit (pika portokalli në figurë), N është numri i nyjeve brenda figurës (pika blu). Është më i përshtatshëm për ta përdorur atë kur gjeni zonën shumëkëndësh i çrregullt. Megjithatë, sa më i madh të jetë arsenali i teknikave të përdorura, aq më pak gabime dhe rezultate më të mira.

Sigurisht, informacioni i dhënë nuk shter llojet dhe vetitë e një trapezi, si dhe metodat për gjetjen e zonës së tij. Ky artikull ofron një përmbledhje të karakteristikave të tij më të rëndësishme. Kur zgjidhni probleme gjeometrike, është e rëndësishme të veproni gradualisht, të filloni me formula dhe probleme të thjeshta, të konsolidoni vazhdimisht të kuptuarit tuaj dhe të kaloni në një nivel tjetër kompleksiteti.

Të mbledhura së bashku formulat më të zakonshme do t'i ndihmojnë studentët të lundrojnë në mënyra të ndryshme për të llogaritur sipërfaqen e një trapezi dhe të përgatiten më mirë për teste dhe testet në këtë temë.