Zgjerimi i serisë Taylor të funksioneve trigonometrike të anasjellta. Zgjerimi i serisë Taylor

"Gjeni zgjerimin e serisë Maclaurin të funksionit f(x)"- kjo është pikërisht ajo që tingëllon detyra në matematikën e lartë, të cilën disa nxënës mund ta bëjnë, ndërsa të tjerët nuk mund të përballojnë shembujt. Ka disa mënyra për të zgjeruar një seri në fuqi këtu ne do të japim një teknikë për zgjerimin e funksioneve në një seri Maclaurin. Kur zhvilloni një funksion në një seri, duhet të jeni të mirë në llogaritjen e derivateve.

Shembulli 4.7 Zgjero një funksion në fuqitë e x

Llogaritjet: Zgjerimin e funksionit e kryejmë sipas formulës Maclaurin. Së pari, le të zgjerojmë emëruesin e funksionit në një seri

Së fundi, shumëzojeni zgjerimin me numëruesin.
Termi i parë është vlera e funksionit në zero f (0) = 1/3.
Le të gjejmë derivatet e funksionit të rendit të parë dhe më të lartë f (x) dhe vlerën e këtyre derivateve në pikën x=0.




Më pas, bazuar në modelin e ndryshimeve në vlerën e derivateve në 0, ne shkruajmë formulën për derivatin e n-të

Pra, ne përfaqësojmë emëruesin në formën e një zgjerimi në serinë Maclaurin

Ne shumëzojmë me numëruesin dhe marrim zgjerimin e dëshiruar të funksionit në një seri në fuqi x

Siç mund ta shihni, nuk ka asgjë të komplikuar këtu.
Të gjitha pikat kryesore bazohen në aftësinë për të llogaritur derivatet dhe për të përgjithësuar shpejt vlerën e derivatit të rendit më të lartë në zero. Shembujt e mëposhtëm do t'ju ndihmojnë të mësoni se si të organizoni shpejt një funksion në një seri.

Shembulli 4.10 Gjeni zgjerimin e serisë Maclaurin të funksionit

Llogaritjet: Siç mund ta keni marrë me mend, ne do ta vendosim kosinusin në numërues në një seri. Për ta bërë këtë, ju mund të përdorni formula për sasi infinite të vogla, ose të nxirrni zgjerimin e kosinusit përmes derivateve. Si rezultat, arrijmë në serinë e mëposhtme në fuqinë x

Siç mund ta shihni, ne kemi një minimum llogaritjesh dhe një paraqitje kompakte të zgjerimit të serisë.

Shembulli 4.16 Zgjero një funksion në fuqitë e x:
7/(12-x-x^2)
Llogaritjet: Në këtë lloj shembujsh, është e nevojshme të zgjerohet thyesa përmes shumës së thyesave të thjeshta.
Nuk do të tregojmë se si ta bëjmë këtë tani, por me ndihmën e koeficientëve të pacaktuar do të arrijmë në shumën e thyesave.
Më pas i shkruajmë emëruesit në formë eksponenciale

Mbetet për të zgjeruar termat duke përdorur formulën Maclaurin. Duke përmbledhur termat me të njëjtat fuqi të "x", ne krijojmë një formulë për termin e përgjithshëm të zgjerimit të një funksioni në një seri.



Pjesa e fundit e kalimit në seri në fillim është e vështirë për t'u zbatuar, pasi është e vështirë të kombinohen formulat për indekset (gradat) të çiftuara dhe të paçiftuara, por me praktikë do të përmirësoheni në të.

Shembulli 4.18 Gjeni zgjerimin e serisë Maclaurin të funksionit

Llogaritjet: Le të gjejmë derivatin e këtij funksioni:

Le ta zgjerojmë funksionin në një seri duke përdorur një nga formulat e McLaren:

Ne përmbledhim serinë term pas termi bazuar në faktin se të dyja janë absolutisht identike. Pasi kemi integruar të gjithë serinë term pas termi, marrim zgjerimin e funksionit në një seri në fuqi x

Ekziston një kalim midis dy rreshtave të fundit të zgjerimit që do t'ju marrë shumë kohë në fillim. Përgjithësimi i një formule të serisë nuk është i lehtë për të gjithë, prandaj mos u shqetësoni se nuk mund të merrni një formulë të bukur dhe kompakte.

Shembulli 4.28 Gjeni zgjerimin e serisë Maclaurin të funksionit:

Le ta shkruajmë logaritmin si më poshtë

Duke përdorur formulën e Maclaurin, ne zgjerojmë funksionin e logaritmit në një seri në fuqi x

Konvolucioni përfundimtar është kompleks në shikim të parë, por kur alternoni shenjat, gjithmonë do të merrni diçka të ngjashme. Ka përfunduar mësimi i hyrjes me temën e planifikimit të funksioneve me radhë. Skema të tjera po aq interesante dekompozimi do të diskutohen në detaje në materialet e mëposhtme.

16.1. Zgjerimi i funksioneve elementare në seritë Taylor dhe

Maclaurin

Le të tregojmë se nëse një funksion arbitrar është përcaktuar në një grup
, në afërsi të pikës
ka shumë derivate dhe është shuma e një serie fuqie:

atëherë mund të gjeni koeficientët e kësaj serie.

Le të zëvendësojmë në një seri fuqie
. Pastaj
.

Le të gjejmë derivatin e parë të funksionit
:

Në
:
.

Për derivatin e dytë marrim:

Në
:
.

Vazhdimi i kësaj procedure n sapo të marrim:
.

Kështu, kemi marrë një seri fuqie të formës:

,

që quhet pranë Taylor për funksionin
në afërsi të pikës
.

Një rast i veçantë i serialit Taylor është Seria Maclaurin në
:

Pjesa e mbetur e serisë Taylor (Maclaurin) merret duke hedhur poshtë serinë kryesore n anëtarët e parë dhe shënohet si
. Pastaj funksioni
mund të shkruhet si shumë n anëtarët e parë të serisë
dhe pjesa e mbetur
:,

.

Pjesa e mbetur është zakonisht
të shprehura në formula të ndryshme.

Njëri prej tyre është në formën Lagrange:

, Ku
.
.

Vini re se në praktikë seria Maclaurin përdoret më shpesh. Kështu, për të shkruar funksionin
në formën e shumës së serisë së fuqisë është e nevojshme:

1) gjeni koeficientët e serisë Maclaurin (Taylor);

2) gjeni rajonin e konvergjencës së serisë së fuqisë që rezulton;

3) vërtetoni se kjo seri konvergon me funksionin
.

Teorema1 (kusht i domosdoshëm dhe i mjaftueshëm për konvergjencën e serisë Maclaurin). Lëreni rrezen e konvergjencës së serisë
. Në mënyrë që kjo seri të konvergojë në interval
të funksionojë
, është e nevojshme dhe e mjaftueshme që të plotësohet kushti:
në intervalin e caktuar.

Teorema 2. Nëse derivatet e ndonjë rendi të funksionit
në një farë intervali
kufizuar në vlerë absolute në të njëjtin numër M, pra
, atëherë në këtë interval funksioni
mund të zgjerohet në një seri Maclaurin.

Shembull1 . Zgjerojeni në një seri Taylor rreth pikës
funksionin.

Zgjidhje.

.

,;

,
;

,
;

,

.......................................................................................................................................

,
;

Rajoni i konvergjencës
.

Shembull2 . Zgjeroni një funksion në një seri Taylor rreth një pike
.

Zgjidhja:

Gjeni vlerën e funksionit dhe derivateve të tij në
.

,
;

,
;

...........……………………………

,
.

Le t'i vendosim këto vlera në një rresht. Ne marrim:

ose
.

Le të gjejmë rajonin e konvergjencës së kësaj serie. Sipas testit të d'Alembert, një seri konvergjon nëse

.

Prandaj, për çdo ky kufi është më i vogël se 1, dhe për këtë arsye diapazoni i konvergjencës së serisë do të jetë:
.

Le të shqyrtojmë disa shembuj të zgjerimit të serisë Maclaurin të funksioneve themelore elementare. Kujtojmë se seria Maclaurin:

.

konvergon në interval
të funksionojë
.

Vini re se për të zgjeruar një funksion në një seri është e nevojshme:

a) gjeni koeficientët e serisë Maclaurin për këtë funksion;

b) llogarit rrezen e konvergjencës për serinë që rezulton;

c) vërtetoni se seria që rezulton konvergon me funksionin
.

Shembulli 3. Merrni parasysh funksionin
.

Zgjidhje.

Le të llogarisim vlerën e funksionit dhe derivateve të tij në
.

Atëherë koeficientët numerikë të serisë kanë formën:

për këdo n. Le të zëvendësojmë koeficientët e gjetur në serinë Maclaurin dhe marrim:

Le të gjejmë rrezen e konvergjencës së serisë që rezulton, përkatësisht:

.

Prandaj, seria konvergjon në interval
.

Kjo seri konvergon me funksionin për çdo vlerë , sepse në çdo interval
funksionin dhe derivatet e tij me vlerë absolute janë të kufizuara në numër .

Shembull4 . Merrni parasysh funksionin
.

Zgjidhje.

:

Është e lehtë të shihet se derivatet e rendit të barabartë
, dhe derivatet janë të rendit tek. Le të zëvendësojmë koeficientët e gjetur në serinë Maclaurin dhe të marrim zgjerimin:

Le të gjejmë intervalin e konvergjencës së kësaj serie. Sipas shenjës së d'Alembert:

për këdo . Prandaj, seria konvergjon në interval
.

Kjo seri konvergon me funksionin
, sepse të gjitha derivatet e tij janë të kufizuara në unitet.

Shembull5 .
.

Zgjidhje.

Le të gjejmë vlerën e funksionit dhe derivateve të tij në
:

Kështu, koeficientët e kësaj serie:
Dhe
, pra:

Ngjashëm me rreshtin e mëparshëm, zona e konvergjencës
. Seria konvergon me funksionin
, sepse të gjitha derivatet e tij janë të kufizuara në unitet.

Ju lutemi vini re se funksioni
Zgjerimi tek dhe seri në fuqi tek, funksion
– madje dhe zgjerim në një seri në fuqi çift.

Shembull6 . Seritë binomiale:
.

Zgjidhje.

Le të gjejmë vlerën e funksionit dhe derivateve të tij në
:

Nga kjo shihet se:

Le t'i zëvendësojmë këto vlera të koeficientit në serinë Maclaurin dhe të marrim zgjerimin e këtij funksioni në një seri fuqie:

Le të gjejmë rrezen e konvergjencës së kësaj serie:

Prandaj, seria konvergjon në interval
. Në pikat kufizuese në
Dhe
një seri mund ose nuk mund të konvergojë në varësi të eksponentit
.

Seria e studiuar konvergon në interval
të funksionojë
, domethënë shuma e serisë
në
.

Shembull7 . Le të zgjerojmë funksionin në serinë Maclaurin
.

Zgjidhje.

Për ta zgjeruar këtë funksion në një seri, ne përdorim serinë binomiale në
. Ne marrim:

Bazuar në vetinë e serisë së fuqisë (një seri fuqie mund të integrohet në rajonin e konvergjencës së saj), gjejmë integralin e anës së majtë dhe të djathtë të kësaj serie:

Le të gjejmë zonën e konvergjencës së kësaj serie:
,

domethënë, zona e konvergjencës së kësaj serie është intervali
.

Le të përcaktojmë konvergjencën e serisë në skajet e intervalit. Në
. Kjo seri është një seri harmonike, domethënë divergjente. Në
.

marrim një seri numrash me një term të përbashkët
.

Seria konvergon sipas testit të Leibniz-it. Pra, rajoni i konvergjencës së kësaj serie është intervali

16.2. Zbatimi i serive të fuqisë në llogaritjet e përafërta n Në llogaritjet e përafërta, seritë e fuqisë luajnë një rol jashtëzakonisht të rëndësishëm. Me ndihmën e tyre, janë përpiluar tabelat e funksioneve trigonometrike, tabelat e logaritmeve, tabelat e vlerave të funksioneve të tjera, të cilat përdoren në fusha të ndryshme të njohurive, për shembull, në teorinë e probabilitetit dhe statistikat matematikore. Për më tepër, zgjerimi i funksioneve në një seri fuqie është i dobishëm për studimin e tyre teorik. Çështja kryesore kur përdoret seria e fuqisë në llogaritjet e përafërta është çështja e vlerësimit të gabimit kur zëvendësohet shuma e një serie me shumën e saj të parë.

anëtarët.

Le të shqyrtojmë dy raste:

funksioni është zgjeruar në një seri alternuese të shenjave;

funksioni zgjerohet në një seri shenjash konstante.

Llogaritja duke përdorur seri alternative
Lëreni funksionin zgjeruar në një seri të energjisë alternative. Pastaj kur llogaritet ky funksion për një vlerë specifike n fitojmë një seri numrash për të cilat mund të zbatojmë kriterin e Leibniz-it. Në përputhje me këtë kriter, nëse shuma e një serie zëvendësohet me shumën e së parës së saj
.

Shembull8 . terma, atëherë gabimi absolut nuk e kalon termin e parë të pjesës së mbetur të kësaj serie, domethënë:
Llogaritni

Zgjidhje.

me një saktësi prej 0.0001.
Ne do të përdorim serinë Maclaurin për

, duke zëvendësuar vlerën e këndit në radiane:

Nëse krahasojmë termat e parë dhe të dytë të serisë me një saktësi të caktuar, atëherë: .

Afati i tretë i zgjerimit:
më pak se saktësia e llogaritur e specifikuar. Prandaj, për të llogaritur

.

mjafton të lëmë dy terma të serialit, d.m.th
.

Shembull9 . terma, atëherë gabimi absolut nuk e kalon termin e parë të pjesës së mbetur të kësaj serie, domethënë:
Kështu

Zgjidhje.

me një saktësi prej 0.001.
Do të përdorim formulën e serisë binomiale. Për ta bërë këtë, le të shkruajmë
.

në formën:
,

Në këtë shprehje
Le të krahasojmë secilin nga termat e serisë me saktësinë që është specifikuar. Është e qartë se
. Prandaj, për të llogaritur

ose
.

mjafton të lëmë tre terma të serialit.

Shembull10 . Llogaritja duke përdorur seri pozitive Llogaritni numrin

Zgjidhje.

me një saktësi prej 0.001.
Në një rresht për një funksion
le të zëvendësojmë

Le të vlerësojmë gabimin që lind kur zëvendësohet shuma e një serie me shumën e së parës anëtarët. Le të shkruajmë pabarazinë e dukshme:

që është 2<<3. Используем формулу остаточного члена ряда в форме Лагранжа:
,
.

Sipas problemit, ju duhet të gjeni n të tillë që të jetë pabarazia e mëposhtme:
ose
.

Është e lehtë të kontrollosh se kur n= 6:
.

Prandaj,
.

Shembull11 . terma, atëherë gabimi absolut nuk e kalon termin e parë të pjesës së mbetur të kësaj serie, domethënë:
me një saktësi prej 0.0001.

Zgjidhje.

Vini re se për të llogaritur logaritmet mund të përdorim një seri për funksionin
, por kjo seri konvergon shumë ngadalë dhe për të arritur saktësinë e dhënë do të duhej të merreshin 9999 terma! Prandaj, për të llogaritur logaritmet, si rregull, përdoret një seri për funksionin
, e cila konvergon në interval
.

Le të llogarisim
duke përdorur këtë seri. Le
, Pastaj .

Prandaj,
,

Për të llogaritur
me një saktësi të dhënë, merrni shumën e katër termave të parë:
.

Pjesa tjetër e serisë
le ta hedhim poshtë. Le të vlerësojmë gabimin. Është e qartë se

ose
.

Kështu, në serinë që u përdor për llogaritjen, mjaftonte të merreshin vetëm katër termat e parë në vend të 9999 në serinë për funksionin.
.

Pyetje vetë-diagnostike

1. Çfarë është një seri Taylor?

2. Çfarë forme kishte seria Maclaurin?

3. Formuloni një teoremë mbi zgjerimin e një funksioni në një seri Taylor.

4. Shkruani zgjerimin e serisë Maclaurin të funksioneve kryesore.

5. Tregoni zonat e konvergjencës së serive të konsideruara.

6. Si të vlerësohet gabimi në llogaritjet e përafërta duke përdorur seritë e fuqisë?

Nxënësit e matematikës së lartë duhet të dinë se shuma e një serie fuqie të caktuar që i përket intervalit të konvergjencës së serisë që na është dhënë, rezulton të jetë një funksion i vazhdueshëm dhe i pakufizuar herë i diferencuar. Shtrohet pyetja: a është e mundur të thuhet se një funksion arbitrar i dhënë f(x) është shuma e një serie fuqie të caktuar? Domethënë, në cilat kushte funksioni f(x) mund të përfaqësohet me një seri fuqie? Rëndësia e kësaj pyetjeje qëndron në faktin se është e mundur që përafërsisht të zëvendësohet funksioni f(x) me shumën e disa termave të parë të një serie fuqie, domethënë një polinom. Ky zëvendësim i një funksioni me një shprehje mjaft të thjeshtë - një polinom - është gjithashtu i përshtatshëm kur zgjidhni probleme të caktuara, përkatësisht: kur zgjidhni integrale, kur llogaritni, etj.

Është vërtetuar se për një funksion të caktuar f(x), në të cilin është e mundur të llogariten derivatet deri në rendin (n+1)-të, duke përfshirë të fundit, në afërsi të (α - R; x 0 + R ) disa pikë x = α, është e vërtetë që formula:

Kjo formulë është emëruar pas shkencëtarit të famshëm Brooke Taylor. Seria që është marrë nga ajo e mëparshme quhet seria Maclaurin:

Rregulli që bën të mundur kryerjen e një zgjerimi në një seri Maclaurin:

1. Përcaktoni derivatet e rendit të parë, të dytë, të tretë...
2. Llogaritni se me çfarë janë të barabartë derivatet në x=0.
3. Shkruani serinë Maclaurin për këtë funksion dhe më pas përcaktoni intervalin e konvergjencës së tij.
4. Përcaktoni intervalin (-R;R), ku është pjesa e mbetur e formulës Maclaurin

R n (x) -> 0 në n -> pafundësi. Nëse ekziston një, funksioni f(x) në të duhet të përkojë me shumën e serisë Maclaurin.

Le të shqyrtojmë tani serinë Maclaurin për funksione individuale.

1. Pra, i pari do të jetë f(x) = e x. Natyrisht, sipas karakteristikave të tij, një funksion i tillë ka derivate të rendeve shumë të ndryshme, dhe f (k) (x) = e x, ku k është e barabartë me të gjitha x = 0. Marrim f (k) (0) = e 0 =1, k = 1,2... Bazuar në sa më sipër, seria e x do të duket kështu:

2. Seritë Maclaurin për funksionin f(x) = sin x. Le të sqarojmë menjëherë se funksioni për të gjitha të panjohurat do të ketë derivate, përveç kësaj, f "(x) = cos x = sin(x+n/2), f "" (x) = -sin x = sin(x + 2*n/2)..., f (k) (x) = sin(x+k*n/2), ku k është e barabartë me çdo numër natyror, pra, pasi të kemi bërë llogaritje të thjeshta, mund të arrijmë përfundimi se seria për f(x) = sin x do të duket kështu:

3. Tani le të përpiqemi të marrim parasysh funksionin f(x) = cos x. Për të gjitha të panjohurat ka derivate të rendit arbitrar, dhe |f (k) (x)| = |cos(x+k*n/2)|<=1, k=1,2... Снова-таки, произведя определенные расчеты, получим, что ряд для f(х) = cos х будет выглядеть так:

Pra, ne kemi renditur funksionet më të rëndësishme që mund të zgjerohen në një seri Maclaurin, por ato plotësohen nga seria Taylor për disa funksione. Tani do t'i rendisim ato. Vlen gjithashtu të theksohet se seritë Taylor dhe Maclaurin janë një pjesë e rëndësishme e punës praktike për zgjidhjen e serive në matematikën e lartë. Pra, seri Taylor.

1. E para do të jetë seria për funksionin f(x) = ln(1+x). Ashtu si në shembujt e mëparshëm, për f(x) = ln(1+x) të dhënë mund të shtojmë serinë duke përdorur formën e përgjithshme të serisë Maclaurin. megjithatë, për këtë funksion seria Maclaurin mund të merret shumë më thjeshtë. Pasi kemi integruar një seri të caktuar gjeometrike, marrim një seri për f(x) = ln(1+x) të një kampioni të tillë:

2. Dhe e dyta, e cila do të jetë përfundimtare në artikullin tonë, do të jetë seria për f(x) = arctan x. Për x që i përket intervalit [-1;1] zgjerimi është i vlefshëm:

Kjo është e gjitha. Ky artikull shqyrtoi seritë më të përdorura të Taylor dhe Maclaurin në matematikën e lartë, veçanërisht në universitetet ekonomike dhe teknike.

Ndër seritë funksionale, vendin më të rëndësishëm e zënë seritë e fuqisë.

Një seri fuqie është një seri

termat e të cilëve janë funksione të fuqisë të renditura në rritje të fuqive të plota jo negative x, A c0 , c 1 , c 2 , c n - vlera konstante. Numrat c1 , c 2 , c n - koeficientët e termave të serisë, c0 - anëtar i lirë. Termat e serisë së fuqisë përcaktohen në të gjithë vijën numerike.

Le të njihemi me konceptin zonat e konvergjencës së serisë së fuqisë. Ky është grupi i vlerave të një ndryshoreje x, për të cilën seria konvergon. Seritë e fuqisë kanë një rajon konvergjence mjaft të thjeshtë. Për vlerat reale të ndryshoreve x rajoni i konvergjencës përbëhet ose nga një pikë, ose është një interval i caktuar (intervali i konvergjencës), ose përkon me të gjithë boshtin kau .

Kur zëvendësoni vlerat në serinë e fuqisë x= 0 do të rezultojë në një seri numrash

c0 +0+0+...+0+... ,

e cila konvergon.

Prandaj, kur x= 0 çdo seri fuqie konvergon dhe, për rrjedhojë, zona e saj e konvergjencës nuk mund të jetë grupi bosh. Struktura e rajonit të konvergjencës së të gjitha serive të fuqisë është e njëjtë. Mund të përcaktohet duke përdorur teoremën e mëposhtme.

Teorema 1 (teorema e Abelit). Nëse një seri fuqie konvergon në një vlerë x = x 0 , ndryshe nga zero, atëherë ajo konvergon, dhe, për më tepër, absolutisht, për të gjitha vlerat |x| < |x 0 | . Ju lutemi vini re: si vlera fillestare "X është zero" dhe çdo vlerë e "X" që krahasohet me vlerën fillestare merren modul - pa marrë parasysh shenjën.

Pasoja. Nëse seritë e fuqisë ndryshojnë në një farë vlere x = x 1 , atëherë ai divergjent për të gjitha vlerat |x| > |x 1 | .

Siç e kemi zbuluar tashmë më herët, çdo seri e fuqisë konvergon në vlerë x= 0. Ka seri fuqie që konvergojnë vetëm kur x= 0 dhe divergojnë për vlera të tjera X. Duke e përjashtuar këtë rast nga shqyrtimi, supozojmë se seria e fuqisë konvergon në një vlerë x = x 0 , të ndryshme nga zero. Pastaj, sipas teoremës së Abelit, ajo konvergon në të gjitha pikat e intervalit ]-| x0 |, |x 0 |[ (një interval, kufijtë e majtë dhe të djathtë të të cilit janë vlerat x në të cilat konvergjon seria e fuqisë, e marrë me një shenjë minus dhe një shenjë plus, përkatësisht), simetrike në lidhje me origjinën.

Nëse seria e fuqisë divergon në një vlerë të caktuar x = x 1 , pastaj, bazuar në një konkluzion të teoremës së Abelit, ajo divergon në të gjitha pikat jashtë segmentit [-| x1 |, |x 1 |] . Nga kjo rrjedh se për çdo seri fuqie ekziston një interval simetrik në lidhje me origjinën, i quajtur intervali i konvergjencës , në çdo pikë të së cilës seria konvergjon, në kufijtë mund të konvergojë, ose mund të devijojë, dhe jo domosdoshmërisht në të njëjtën kohë, dhe jashtë segmentit seria divergjente. Numri R quhet rrezja e konvergjencës së serisë së fuqisë.

Në raste të veçanta intervali i konvergjencës së serisë së fuqisë mund të degjenerojë deri në një pikë (atëherë seria konvergjon vetëm kur x= 0 dhe konsiderohet se R= 0) ose përfaqësojnë të gjithë vijën numerike (atëherë seria konvergon në të gjitha pikat e boshtit numerik dhe supozohet se ).

Kështu, përcaktimi i rajonit të konvergjencës së një serie fuqie konsiston në përcaktimin e tij rrezja e konvergjencës R dhe studimi i konvergjencës së serisë në kufijtë e intervalit të konvergjencës (në ).

Teorema 2. Nëse të gjithë koeficientët e një serie fuqie, duke filluar nga një e caktuar, janë të ndryshëm nga zero, atëherë rrezja e saj e konvergjencës është e barabartë me kufirin në raportin e vlerave absolute të koeficientëve të anëtarëve të zakonshëm vijues të serisë. , d.m.th.

Shembulli 1. Gjeni rajonin e konvergjencës së serisë së fuqisë

Zgjidhje. Këtu

Duke përdorur formulën (28), gjejmë rrezen e konvergjencës së kësaj serie:

Le të studiojmë konvergjencën e serisë në skajet e intervalit të konvergjencës. Shembulli 13 tregon se kjo seri konvergon në x= 1 dhe ndryshon në x= -1. Rrjedhimisht, rajoni i konvergjencës është gjysmë-intervali.

Shembulli 2. Gjeni rajonin e konvergjencës së serisë së fuqisë

Zgjidhje. Koeficientët e serisë janë pozitivë, dhe

Le të gjejmë kufirin e këtij raporti, d.m.th. rrezja e konvergjencës së serisë së fuqisë:

Le të studiojmë konvergjencën e serisë në skajet e intervalit. Zëvendësimi i vlerës x= -1/5 dhe x= 1/5 në këtë rresht jep:

E para nga këto seri konvergon (shih Shembullin 5). Por më pas, në bazë të teoremës në seksionin "Konvergjenca absolute", seria e dytë gjithashtu konvergjon, dhe rajoni i konvergjencës së saj është segmenti

Shembulli 3. Gjeni rajonin e konvergjencës së serisë së fuqisë

Zgjidhje. Këtu

Duke përdorur formulën (28) gjejmë rrezen e konvergjencës së serisë:

Le të studiojmë konvergjencën e serisë për vlerat e . Duke i zëvendësuar ato në këtë seri, ne përkatësisht marrim

Të dyja seritë ndryshojnë sepse kushti i nevojshëm për konvergjencë nuk plotësohet (termat e tyre të përbashkët nuk priren në zero në ). Pra, në të dy skajet e intervalit të konvergjencës, kjo seri divergjent, dhe rajoni i konvergjencës së saj është intervali.

Shembulli 5. Gjeni rajonin e konvergjencës së serisë së fuqisë

Zgjidhje. Gjejmë relacionin ku , dhe :

Sipas formulës (28), rrezja e konvergjencës së kësaj serie

,

domethënë, seria konvergjon vetëm kur x= 0 dhe divergjent për vlera të tjera X.

Shembujt tregojnë se në skajet e intervalit të konvergjencës seritë sillen ndryshe. Në shembullin 1, në njërin skaj të intervalit të konvergjencës, seria konvergjon, në shembullin 2, ajo konvergjon në të dy skajet;

Formula për rrezen e konvergjencës së një serie fuqie merret me supozimin se të gjithë koeficientët e termave të serisë, duke filluar nga një pikë e caktuar, janë të ndryshëm nga zero. Prandaj, përdorimi i formulës (28) është i lejueshëm vetëm në këto raste. Nëse ky kusht shkelet, atëherë rrezja e konvergjencës së serisë së fuqisë duhet të kërkohet duke përdorur Shenja e d'Alembert, ose, duke zëvendësuar variablin, duke e transformuar serinë në një formë në të cilën plotësohet kushti i specifikuar.

Shembulli 6. Gjeni intervalin e konvergjencës së serisë së fuqisë

Zgjidhje. Kjo seri nuk përmban terma me shkallë tek X. Prandaj, ne transformojmë serinë, duke vendosur . Pastaj marrim serinë

për të gjetur rrezen e konvergjencës së së cilës mund të zbatojmë formulën (28). Meqenëse , a , atëherë rrezja e konvergjencës së kësaj serie

Nga barazia që marrim, pra, kjo seri konvergon në intervalin .

Shuma e serive të fuqisë. Diferencimi dhe integrimi i serive të fuqisë

Le për serinë e fuqisë

rrezja e konvergjencës R> 0, d.m.th. kjo seri konvergon në intervalin .

Pastaj çdo vlerë X nga intervali i konvergjencës korrespondon një shumë e caktuar e serisë. Prandaj, shuma e serisë së fuqisë është një funksion i X në intervalin e konvergjencës. Duke e shënuar me f(x), mund të shkruajmë barazinë

duke e kuptuar në kuptimin që shuma e serisë në çdo pikë X nga intervali i konvergjencës është i barabartë me vlerën e funksionit f(x) në këtë pikë. Në të njëjtin kuptim, do të themi se seria e fuqisë (29) konvergon me funksionin f(x) në intervalin e konvergjencës.

Jashtë intervalit të konvergjencës, barazia (30) nuk ka kuptim.

Shembulli 7. Gjeni shumën e serisë së fuqisë

Zgjidhje. Kjo është një seri gjeometrike për të cilën a= 1, a q= x. Prandaj, shuma e tij është një funksion . Një seri konvergjon nëse , dhe është intervali i saj i konvergjencës. Prandaj barazia

është e vlefshme vetëm për vlerat, edhe pse funksioni të përcaktuara për të gjitha vlerat X, përveç X= 1.

Mund të vërtetohet se shuma e serisë së fuqisë f(x) është i vazhdueshëm dhe i diferencueshëm në çdo interval brenda intervalit të konvergjencës, veçanërisht në çdo pikë të intervalit të konvergjencës së serisë.

Le të paraqesim teorema mbi diferencimin term pas termi dhe integrimin e serive të fuqisë.

Teorema 1. Seritë e fuqisë (30) në intervalin e konvergjencës së saj mund të diferencohen term pas termi një numër të pakufizuar herë, dhe seritë e fuqisë që rezultojnë kanë të njëjtën rreze konvergjence si seria origjinale, dhe shumat e tyre janë përkatësisht të barabarta me .

Teorema 2. Seritë e fuqisë (30) mund të integrohen term pas termi një numër të pakufizuar herë në intervalin nga 0 në X, nëse , dhe seria e fuqisë që rezulton ka të njëjtën rreze konvergjence si seria origjinale, dhe shumat e tyre janë përkatësisht të barabarta

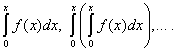
Zgjerimi i funksioneve në seritë e fuqisë

Le të jepet funksioni f(x), e cila duhet të zgjerohet në një seri fuqie, d.m.th. përfaqësojnë në formën (30):

Detyra është të përcaktohen koeficientët rreshti (30). Për ta bërë këtë, duke diferencuar barazinë (30) term pas termi, gjejmë vazhdimisht:

……………………………………………….. (31)

Duke supozuar në barazitë (30) dhe (31) X= 0, gjejmë

Duke zëvendësuar shprehjet e gjetura në barazi (30), marrim

(32)

Le të gjejmë zgjerimin e serisë Maclaurin të disa funksioneve elementare.

Shembulli 8. Zgjero funksionin në një seri Maclaurin

Zgjidhje. Derivatet e këtij funksioni përkojnë me vetë funksionin:

Prandaj, kur X= 0 kemi

Duke zëvendësuar këto vlera në formulën (32), marrim zgjerimin e dëshiruar:

(33)

Kjo seri konvergon në të gjithë vijën numerike (rrezja e saj e konvergjencës).

Nëse funksioni f(x) ka derivate të të gjitha rendeve në një interval të caktuar që përmban pikën a, atëherë formula e Taylor mund të zbatohet për të:
,
Ku r n- i ashtuquajturi termi i mbetur ose pjesa e mbetur e serisë, mund të vlerësohet duke përdorur formulën e Lagranzhit:
, ku numri x është midis x dhe a.

Rregullat për futjen e funksioneve:

Nëse për ndonjë vlerë X r n→ 0 në n→∞, atëherë në kufi formula e Taylor-it bëhet konvergjente për këtë vlerë Seriali Taylor:
,
Kështu, funksioni f(x) mund të zgjerohet në një seri Taylor në pikën x në shqyrtim nëse:
1) ka derivate të të gjitha porosive;
2) seria e ndërtuar konvergon në këtë pikë.

Kur a = 0 marrim një seri të quajtur pranë Maclaurin:
,
Zgjerimi i funksioneve më të thjeshta (elementare) në serinë Maclaurin:
Funksionet eksponenciale
, R=∞
Funksionet trigonometrike
, R=∞
, R=∞
, (-π/2< x < π/2), R=π/2
Funksioni actgx nuk zgjerohet në fuqitë e x, sepse ctg0=∞
Funksionet hiperbolike


Funksionet logaritmike
, -1
Seri binomiale
.

Shembulli nr. 1. Zgjero funksionin në një seri fuqie f(x)= 2x.
Zgjidhje. Le të gjejmë vlerat e funksionit dhe derivatet e tij në X=0
f(x) = 2x, f( 0) = 2 0 =1;
f"(x) = 2x ln2, f"( 0) = 2 0 ln2= ln2;
f""(x) = 2x në 2 2, f""( 0) = 2 0 ln 2 2 = ln 2 2;
…
f(n)(x) = 2x ln n 2, f(n)( 0) = 2 0 ln n 2=ln n 2.
Duke zëvendësuar vlerat e marra të derivateve në formulën e serisë Taylor, marrim:

Rrezja e konvergjencës së kësaj serie është e barabartë me pafundësinë, prandaj ky zgjerim është i vlefshëm për -∞<x<+∞.

Shembulli nr. 2. Shkruani serinë e Taylor në fuqi ( X+4) për funksionin f(x)= e x.
Zgjidhje. Gjetja e derivateve të funksionit e x dhe vlerat e tyre në pikë X=-4.
f(x)= e x, f(-4) = e -4 ;
f"(x)= e x, f"(-4) = e -4 ;
f""(x)= e x, f""(-4) = e -4 ;
…
f(n)(x)= e x, f(n)( -4) = e -4 .
Prandaj, seria e kërkuar Taylor e funksionit ka formën:

Ky zgjerim është gjithashtu i vlefshëm për -∞<x<+∞.

Shembulli nr. 3. Zgjeroni një funksion f(x)=n x në një seri në fuqi ( X- 1),
(d.m.th. në serinë Taylor në afërsi të pikës X=1).
Zgjidhje. Gjeni derivatet e këtij funksioni.
f(x)=lnx , , , ,

f(1)=ln1=0, f"(1)=1, f""(1)=-1, f"""(1)=1*2,..., f (n) =(- 1) n-1 (n-1)!
Duke zëvendësuar këto vlera në formulë, marrim serinë e dëshiruar të Taylor:

Duke përdorur testin e d'Alembert, mund të verifikoni që seria konvergjon në ½x-1½<1 . Действительно,

Seria konvergon nëse ½ X- 1 ½<1, т.е. при 0<x<2. При X=2 marrim një seri alternative që plotëson kushtet e kriterit të Leibniz-it. Kur x=0 funksioni nuk është i përcaktuar. Kështu, rajoni i konvergjencës së serisë Taylor është intervali gjysmë i hapur (0; 2].

Shembulli nr. 4. Zgjero funksionin në një seri fuqie.
Zgjidhje. Në zgjerimin (1) ne zëvendësojmë x me -x 2, marrim:
, -∞

Shembulli nr. 5. Zgjero funksionin në një seri Maclaurin.
Zgjidhje. ne kemi
Duke përdorur formulën (4), mund të shkruajmë:

duke zëvendësuar –x në vend të x në formulë, marrim:

Nga këtu gjejmë: ln(1+x)-ln(1-x) = -
Duke hapur kllapat, duke riorganizuar kushtet e serisë dhe duke sjellë terma të ngjashëm, marrim
. Kjo seri konvergjon në intervalin (-1;1), pasi përftohet nga dy seri, secila prej të cilave konvergjon në këtë interval.

Koment .
Formulat (1)-(5) mund të përdoren gjithashtu për të zgjeruar funksionet përkatëse në një seri Taylor, d.m.th. për zgjerimin e funksioneve në fuqitë e plota pozitive ( Ha). Për ta bërë këtë, është e nevojshme të kryhen transformime të tilla identike në një funksion të caktuar në mënyrë që të merret një nga funksionet (1)-(5), në të cilin në vend të X kushton k( Ha) m, ku k është një numër konstant, m është një numër i plotë pozitiv. Shpesh është e përshtatshme për të bërë një ndryshim të ndryshores t=Ha dhe zgjeroni funksionin që rezulton në lidhje me t në serinë Maclaurin.

Kjo metodë bazohet në teoremën mbi veçantinë e zgjerimit të një funksioni në një seri fuqie. Thelbi i kësaj teoreme është se në afërsi të së njëjtës pikë nuk mund të fitohen dy seri të ndryshme fuqie që do të konvergojnë në të njëjtin funksion, pavarësisht se si kryhet zgjerimi i saj.

Shembulli nr. 5a. Zgjeroni funksionin në një seri Maclaurin dhe tregoni rajonin e konvergjencës.
Zgjidhje. Së pari gjejmë 1-x-6x 2 =(1-3x)(1+2x) , .
në fillore:

Thyesa 3/(1-3x) mund të konsiderohet si shuma e një progresion gjeometrik pafundësisht në rënie me një emërues 3x, nëse |3x|< 1. Аналогично, дробь 2/(1+2x) как сумму бесконечно убывающей геометрической прогрессии знаменателем -2x, если |-2x| < 1. В результате получим разложение в степенной ряд

me rajon konvergjence |x|< 1/3.

Shembulli nr. 6. Zgjero funksionin në një seri Taylor në afërsi të pikës x = 3.
Zgjidhje. Ky problem mund të zgjidhet, si më parë, duke përdorur përkufizimin e serisë Taylor, për të cilën duhet të gjejmë derivatet e funksionit dhe vlerat e tyre në X=3. Sidoqoftë, do të jetë më e lehtë të përdoret zgjerimi ekzistues (5):
=
Seria që rezulton konvergon në ose –3

Shembulli nr. 7. Shkruani serinë Taylor në fuqi (x -1) të funksionit ln(x+2) .
Zgjidhje.


Seria konvergon në , ose -2< x < 5.

Shembulli nr. 8. Zgjero funksionin f(x)=sin(πx/4) në një seri Taylor në afërsi të pikës x =2.
Zgjidhje. Le të bëjmë zëvendësimin t=x-2:

Duke përdorur zgjerimin (3), në të cilin zëvendësojmë π / 4 t në vend të x, marrim:

Seria që rezulton konvergon në funksionin e dhënë në -∞< π / 4 t<+∞, т.е. при (-∞Kështu,
, (-∞

Llogaritjet e përafërta duke përdorur seritë e fuqisë

• nëse seria që rezulton është e alternuar, atëherë përdoret vetia e mëposhtme: për një seri alternative që plotëson kushtet e Leibniz-it, pjesa e mbetur e serisë në vlerë absolute nuk e kalon termin e parë të hedhur poshtë.
• nëse një seri e caktuar është me shenjë konstante, atëherë seria e përbërë nga termat e hedhur poshtë krahasohet me një progresion gjeometrik pafundësisht në rënie.
• në rastin e përgjithshëm, për të vlerësuar pjesën e mbetur të serisë Taylor, mund të përdorni formulën e Lagranzhit: a x ).

Shembulli nr. 1. Llogaritni ln(3) me 0,01 më të afërt.
Zgjidhje. Le të përdorim zgjerimin ku x=1/2 (shih shembullin 5 në temën e mëparshme):

Le të kontrollojmë nëse mund ta heqim pjesën e mbetur pas tre termave të parë të zgjerimit për ta bërë këtë, ne do ta vlerësojmë duke përdorur shumën e një progresion gjeometrik pafundësisht në rënie;

Kështu që ne mund ta hedhim këtë mbetje dhe të marrim

Shembulli nr. 2. Llogaritni me 0,0001 më të afërt.
Zgjidhje. Le të përdorim serinë binomiale. Meqenëse 5 3 është kubi i një numri të plotë më të afërt me 130, këshillohet që numri 130 të përfaqësohet si 130 = 5 3 +5.



pasi që tashmë termi i katërt i serisë alternative që rezulton që plotëson kriterin e Leibniz është më pak se saktësia e kërkuar:
, kështu që ai dhe kushtet pas tij mund të hidhen poshtë.
Shumë integrale të përcaktuara ose të pahijshme praktikisht të nevojshme nuk mund të llogariten duke përdorur formulën Newton-Leibniz, sepse zbatimi i saj shoqërohet me gjetjen e një antiderivati, i cili shpesh nuk ka një shprehje në funksionet elementare. Ndodh gjithashtu që gjetja e një antiderivati ​​është e mundur, por është e panevojshme që kërkon punë intensive. Sidoqoftë, nëse funksioni integrand zgjerohet në një seri fuqie dhe kufijtë e integrimit i përkasin intervalit të konvergjencës së kësaj serie, atëherë është e mundur një llogaritje e përafërt e integralit me një saktësi të paracaktuar.

Shembulli nr. 3. Njehsoni integralin ∫ 0 1 4 sin (x) x brenda 10 -5 .
Zgjidhje. Integrali i pacaktuar përkatës nuk mund të shprehet në funksione elementare, d.m.th. përfaqëson një “integral jo të përhershëm”. Këtu nuk mund të zbatohet formula Newton-Leibniz. Le të llogarisim përafërsisht integralin.
Ndarja term për term i serisë për mëkat x në x, marrim:

Duke integruar këtë seri term pas termi (kjo është e mundur, pasi kufijtë e integrimit i përkasin intervalit të konvergjencës së kësaj serie), marrim:

Meqenëse seria që rezulton plotëson kushtet e Leibniz-it dhe mjafton të merret shuma e dy termave të parë për të marrë vlerën e dëshiruar me një saktësi të caktuar.
Kështu, ne gjejmë
.

Shembulli nr. 4. Njehsoni integralin ∫ 0 1 4 e x 2 me saktësi 0,001.
Zgjidhje.
. Le të kontrollojmë nëse mund ta heqim pjesën e mbetur pas termit të dytë të serisë që rezulton.
0.0001<0.001. Следовательно, .