Бесконечная бесконечность. Правило Лопиталя: теория и примеры решений

Раскрытие неопределённостей вида 0/0 или ∞/∞ и некоторых других неопределённостей, возникающих при вычислении предела отношения двух бесконечно малых или бесконечно больших функций значительно упрощается с помощью правила Лопиталя (на самом деле двух правил и замечаний к ним).

Суть правил Лопиталя состоит в том, что в случае, когда вычисление предела отношений двух бесконечно малых или бесконечно больших функций даёт неопределённости видов 0/0 или ∞/∞, предел отношения двух функций можно заменить пределом отношения их производных и, таким образом, получить определённный результат.

Перейдём к формулировкам правил Лопиталя.

Правило Лопиталя для случая предела двух бесконечно малых величин . Если функции f (x ) и g (x a a , причём в этой окрестности g "(x a равны между собой и равны нулю

().

Правило Лопиталя для случая предела двух бесконечно больших величин . Если функции f (x ) и g (x ) дифференцируемы в некоторой окрестности точки a , за исключением, может быть, самой точки a , причём в этой окрестности g "(x )≠0 и если и если пределы этих функций при стремлении икса к значению функции в точке a равны между собой и равны бесконечности

(),

то предел отношения этих функций равен пределу отношения их производных

().

Иными словами, для неопределённостей вида 0/0 или ∞/∞ предел отношения двух функций равен пределу отношения их производных, если последний существует (конечный или бесконечный).

Замечания .

1. Правила Лопиталя применимы и тогда, когда функции f (x ) и g (x ) не определены при x = a .

2. Если при вычисления предела отношения производных функций f (x ) и g (x ) снова приходим к неопределённости вида 0/0 или ∞/∞, то правила Лопиталя следует применять многократно (минимум дважды).

3. Правила Лопиталя применимы и тогда, когда аргумент функций (икс) стремится не к конечному числу a , а к бесконечности (x → ∞).

К неопределённостям видов 0/0 и ∞/∞ могут быть сведены и неопределённости других видов.

Раскрытие неопределённостей видов "ноль делить на ноль" и "бесконечность делить на бесконечность"

Пример 1.

x =2 приводит к неопределённости вида 0/0. Поэтому производную каждой функции и получаем

В числителе вычисляли производную многочлена, а в знаменателе - производную сложной логарифмической функции . Перед последним знаком равенства вычисляли обычный предел , подставляя вместо икса двойку.

Пример 2. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:

Решение. Подстановка в заданную функцию значения x

Пример 3. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:

Решение. Подстановка в заданную функцию значения x =0 приводит к неопределённости вида 0/0. Поэтому вычисляем производные функций в числителе и знаменателе и получаем:

Пример 4. Вычислить

Решение. Подстановка в заданную функцию значения икса, равного плюс бесконечности, приводит к неопределённости вида ∞/∞. Поэтому применим правило Лопиталя:

Замечание. Переходим к примерам, в которых правило Лопиталя приходится применять дважды, то есть приходить к пределу отношений вторых производных, так как предел отношения первых производных представляет собой неопределённость вида 0/0 или ∞/∞.

Применить правило Лопиталя самостоятельно, а затем посмотреть решение

Раскрытие неопределённостей вида "ноль умножить на бесконечность"

Пример 12. Вычислить

.

Решение. Получаем

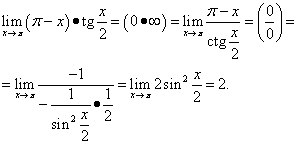
В этом примере использовано тригонометрическое тождество .

Раскрытие неопределённостей видов "ноль в степени ноль", "бесконечность в степени ноль" и "один в степени бесконечность"

Неопределённости вида , или обычно приводятся к виду 0/0 или ∞/∞ с помощью логарифмирования функции вида

Чтобы вычислить предел выражения , следует использовать логарифмическое тождество , частным случаем которого является и свойство логарифма .

Используя логарифмическое тождество и свойство непрерывности функции (для перехода за знак предела), предел следует вычислять следующим образом:

Отдельно следует находить предел выражения в показателе степени и возводить e в найденную степень.

Пример 13.

Решение. Получаем

.

.

Пример 14. Вычислить, пользуясь правилом Лопиталя

Решение. Получаем

Вычисляем предел выражения в показателе степени

.

.

Пример 15. Вычислить, пользуясь правилом Лопиталя

Данную неопределённость «обслуживает» второй замечательный предел , и во второй части того урока мы очень подробно рассмотрели стандартные примеры решений, которые в большинстве случаев встречаются на практике. Сейчас картина с экспонентами будет завершена, кроме того, заключительные задания урока будут посвящены пределам-«обманкам», в которых КАЖЕТСЯ, что необходимо применить 2-ой замечательный предел, хотя это вовсе не так.

Недостаток двух рабочих формул 2-го замечательного предела состоит в том, что аргумент должен стремиться к «плюс бесконечности» либо к нулю. Но что делать, если аргумент стремится к другому числу?

На помощь приходит универсальная формула (которая на самом деле является следствием второго замечательного предела):

Неопределённость можно устранить по формуле:

Где-то вроде уже пояснял, что обозначают квадратные скобки. Ничего особенного, скобки как скобки. Обычно их используют, чтобы чётче выделить математическую запись.

Выделим существенные моменты формулы:

1) Речь идёттолько об определённости и никакой другой .

2) Аргумент «икс» может стремиться к произвольному значению (а не только к нулю или ), в частности, к «минус бесконечности» либо к любому конечному числу.

С помощью данной формулы можно решить все примеры урока Замечательные пределы , которые относятся ко 2-му замечательному пределу. Например, вычислим предел :

В данном случае , и по формуле :

Правда, делать так не советую, в традициях всё-таки применять «обычное» оформление решения, если его можно применить. Однако с помощью формулы очень удобно выполнять проверку «классических» примеров на 2-ой замечательный предел.

Всё это хорошо, правильно, но сейчас в кадре более любопытные кадры:

Пример 18

Вычислить предел

На первом шаге, не устану повторять, подставляем значение «икс» в выражение под знаком предела. А вдруг никакой неопределённости вообще нет? Так бывает! Но не в этот раз. Подставляя «тройку», приходим к выводу, что здесь неопределённость

Используем формулу

Чтобы не таскать за собой букву «е» и не мельчить, показатель удобнее вычислить отдельно:

В данном случае:

Таким образом:

С точки зрения техники вычислений всё рутинно: сначала приводим первое слагаемое к общему знаменателю, затем выносим константы и проводим сокращения, избавляясь от неопределённости 0:0.

В результате:

Обещанный подарок с разностью логарифмов и неопределённостью :

Пример 19

Вычислить предел

Сначала полное решение, потом комменты:

(1)-(2) На первых двух шагах используем формулы . У сложных производных мы «разваливаем» логарифмы, а здесь, наоборот – их нужно «собрать».

(3) Значок предела перемещаем под логарифм. Это можно сделать, поскольку данный логарифм непрерывен на «минус бесконечности». Кроме того, предел же относится к «начинке» логарифма.

(4)-(5) Стандартным приёмом, рассмотренным на базовом уроке про замечательные пределы , преобразуем неопределённость к виду .

(6) Используем формулу .

(7) Экспоненциальная и логарифмическая функция – взаимно обратные функции, поэтому и «е» и логарифм можно убрать. Действительно, согласно свойству логарифма: . Минус перед дробью вносим в знаменатель:

(8) Без комментариев =)

Рассмотренный тип предела не такой редкий, примеров 30-40 у себя нашёл.

Пример 20

Вычислить предел

Это пример для самостоятельного решения. Помимо использования формулы, можно представить предел в виде и заменой свести решение к случаю .

В заключение рассмотрим пределы-«фальшивки».

Вернёмся к неопределённости . Данную неопределённость далеко не всегда можно свести к неопределённости и воспользоваться 2-ым замечательным пределом либо формулой-следствием. Преобразование осуществимо в том случае, если числитель и знаменатель основания степени – эквивалентные бесконечно большие функции . На пример: .

Отвлечёмся от показателя и вычислим предел основания:

В пределе получена единица , значит, числитель и знаменатель не просто одного порядка роста, а ещё и эквивалентны . На уроке Замечательные пределы. Примеры решений мы без проблем свели данный пример к неопределённости и получили ответ.

Аналогичных пределов можно придумать очень много:
и т.д.

Дроби данных примеров объединяет вышеуказанная особенность: . В других случаях при неопределённости 2-ой замечательный предел не применим .

Пример 21

Найти пределы

Как ни старайся, а неопределённость не удастся преобразовать в неопределённость

Здесь числители и знаменатели оснований одного порядка роста, но не эквиваленты : .

Таким образом, 2-ой замечательный предел и, тем более формулу, ПРИМЕНИТЬ НЕЛЬЗЯ .

! Примечание : не путайте с Примером №18, в котором числитель и знаменатель основания не эквивалентны. Там готовая неопределённость , здесь же речь идёт о неопределённости .

Метод решения пределов-«подделок» прост и знакОм: нужно числитель и знаменательоснования разделить на «икс» в старшей степени (невзирая на показатель):

Если числитель и знаменатель основания разного порядка роста, то приём решения точно такой же:

Пример 22

Найти пределы

Это короткие примеры для самостоятельного изучения

Иногда неопределённости может не быть вообще :

Подобные фокусы особенно любимы составителями сборника Кузнецова. Вот почему очень важно ВСЕГДА на первом шаге выполнять подстановку «икса» в выражение под знаком предела!

Пример 2

Старшая степень числителя: 2; старшая степень знаменателя: 3.
:

Пример 4

Разделим числитель и знаменатель на :


Примечание : самым последним действием умножили числитель и знаменатель на , чтобы избавиться от иррациональности в знаменателе.

Пример 6

Разделим числитель и знаменатель на :

Пример 8

Разделим числитель и знаменатель на :

Примечание : слагаемое стремиться к нулю медленнее, чем , поэтому является «главным» нулём знаменателя. .

Пример 22


Примечание : бесконечно малая функция стремится к нулю медленнее, чем , поэтому «более большой» ноль знаменателя играет определяющую роль:

1. Для того, чтобы число А было пределомf(x) приx->a, необходимо и достаточно, чтобы эта функция была представима в видеf(x)=A+альфа(х), где альфа(х) – бесконечно малая.

2. Предел постоянной величины равен самой постоянной.LimC,x->a=C.

3. Еслиf(x)>= 0 (f(x)<=0) в некоторой окрестности точки а, кроме самой точки а, и в этой точке имеет предел, то пределlimf(x),x->a>=0 (limf(x)x->a, <=0)

4. Если функцииf1(x),f2(x) имеют пределы в точке а, то и их сумма, произведение и частное имеет пределы, причемlim(f1(x)+f2(x)),x->a=limf1(x),x->a+limf2(x),x->a, так же с произведением и частным

5. Еслиf(x) имеет предел в точке а, тоlim(f(x))^n,x->a= (limf(x),x->a)^n, гдеn– натуральное число

6. Постоянный множитель можно выносить за знак предела.Lim cf(x), x->a = cLim f(x), x->a.

7. Если для функцийf(x),f1(x),f2(x) в некоторой окрестности в точке а выполняется неравенствоf1(x)<=f(x)<=f2(x) и пределlimf1(x),x->a=limf2(x),x->a=A, тоlimf(x),x->a=A.

8. Limc^x,x->б = бесконечности, еслиc>1 и 0, если 0

Неопределенность вида бесконечность на бесконечность

Разделить все на х в наивысшей степени, учитывая уменьшение степени в корне.

Lim(x->0) sin 5x/sin3x = =lim(x->0) x sin5x/x sin3x = lim(x->0) sin5x/x*lim(x->0) x/sin3x=lim(x->0) 5sin5x/5x*lim 3sin3x/3x)=5/3

Lim(x-unl) (1+1/x) x =e;

1/x=a=>x=1/a, a->0

Lim(a-0) (1+a) 1/2 =e

Lim(x-0) (log a (1+x))/x = lim(x-0) 1/x*log a (1+x)=lim(x-0) log a (1+x) 1/x =log a lim(x-0)(1+x) 1/x =log a e

Lim(x-0) ln(1+x)/x=ln e=1

Lim(x-0) a x -1/x=|a x -1=t;a x =t+1;ln a x =ln(t+1)

Сравнение бесконечно малых функций

Пусть a(x,b(x) – бесконечно малые ф-ции при х->a

1. Lim(x->a)a(x)/b(x)=0 =>a(x) – бесконечно малая более высокого порядка, чемb(x)

2. Lim(x->a)a(x)/b(x) =c<>0=>aиb– бесконечно малые функции одного порядка

3. Lim(x->a)a(x)/b(x) = 1 =>aub– эквивалентные бесконечно малые функции

4. Lim(x->a)d(x)/b n (x) =c<>0 =>a– бесконечно малая функция н-ного порядка относительноb(x)

Cos2x=1-2sin 2 x

Теорема: если б.м. а(х) эквивалентна а 1 (х) иb(x) ~b 1 (x) иlim(x->a)a(x)/b(x) =>lim(x->a)a 1 (x)/b 1 (x)

6. A kx ~kx ln a

8. 1-cos kx ~kx 2 /2

23. Предел функции, теоремы о пределах. Неопределённость вида 0/0.  Бесконечно большие и бесконечно малые.

Функция f (x ) стремится к бесконечности при x стремящимся к a , если для любого M > 0 можно указать такое значение  > 0, что для всех x удовлетворяющих неравенству x a  <  имеет место неравенство f (x ) > M .

lim x  a =

 Функция ограниченная при x  a .

 Функция ограниченная при x  .

 Теорема. Если lim x  a f (x )=b , то функция f (x ) ограниченная при x  a .

 Бесконечно малые и их свойства. lim x  a (x )=0

Теорема. 1. Если f (x )=b +, где  - б.м. при x  a , то lim x  a f (x )=b и обратно, если lim x  a f (x )=b , то можно записать f (x )=b +(x ).

Теорема. 2. Если lim x  a (x )=0 и (x )  0, то 1/ .

Теорема. 3. Сумма конечного числа б.м. есть б.м.

Теорема. 4. Произведение б.м. на ограниченную функцию есть б.м.

 Теоремы о пределах.

Теорема. 1. Предел суммы есть сумма пределов.

Теорема. 2. Предел произведения есть произведение пределов.

Теорема. 3. Предел частного есть частное пределов (если знаменатель не обращается в 0).

Теорема. 4. Если u (x )  z (x )  v (x ), и lim x  a u (x )=lim x  a v (x )=b , то lim x  a z (x )=b . ("Теорема о двух милиционерах").

 Первый замечательный предел.

при n имеет предел, заключенный между 2 и 3. В данной работе мы рассмотрим неопределенность видадля функции. Для нахождения предела функции мы применяем метод преобразования, метод замены и определение бесконечно малых величин.

Пусть требуется найти предел дроби

где P(x) и Q(x) функции определенные в окрестности предельного аргумента a, но в самом предельном значении обращаются в ноль.

Теорема 1 . Пусть число a для многочлена n-й степени P(x) = P n (x) является k кратным решением, а для многочлена m-й степени Q(x) = Q n (x) является r кратным решением, тогда

(2)

где P n-k (a) и Q m-r (a) значения соответствующих многочленов P n-k (x) и Q m-r (x) в точке x = a.

Доказательство . Так как, число a является решением многочленов P n (x) и Q m (x), то их в любое время можно представить в виде:

Биномы (x - a) k и (x - a) r в окрестности точки x = a бесконечно малы, а их основания эквивалентные бесконечно малые. Отсюда

Полагаясь на последнее равенство, можно из (3) предела получить формулу (2). 25. 1-ый Замечательный предел.

ситца идёт на каждое платье для взрослых?

количество бисера, сделанного на фабрике в Усть-Рудицах если его цена за пуд была на 6 рублей меньше?

больше,чем в первый.Сколько килограммов печенья привезли в каждый магазин? Задача№2 Два спорцмена одновременно начали бежать навстречу друг другу.Первый спорцмен бежал со средней скоростью 305м/мин,второй-312м/мин.Спорцмены встретились через 4 мин. Какое расстояние быломежду ними сначала? Решить задачу по действиям с пояснениями. Задача№3 Поезд отправляется в 19ч 35мин.Дорога пассажироа от дома до вокзала занимает 45мин. В котором часу пассажиру надо выехать из дома,чтобы быть на вокзале за 15 мин до отправления поезда? Задача№4 Из 60м ткани сшили 15 одинаковых плащей.Сколько таких плащей можно сшить из 100м такой же ткани? Задача№5 Периметр квадрата равен 8 см. Из двух таких квадратов составили прямоугольник.Найти площадь этого прямоугольника. Задача№6 Площадь сада 192а.Одна десятая часть площади сада занята яблонями,а одна пятая часть оставшейся площади- сливами.Какая площадь сада занята сливами? Задача№7 Масса четырёх одинаковых ящиков с мандаринами 34 кг.Масса пустого ящика 1 кг 500г.Найти массу мандаринов в каждом ящике.

Предел функции на бесконечности:
|f(x) - a| < ε при |x| > N

Определение предела по Коши
Пусть функция f(x) определена в некоторой окрестности бесконечно удаленной точки, при |x| > Число a называется пределом функции f(x) при x стремящемся к бесконечности (), если для любого, сколь угодно малого положительного числа ε > 0 , существует такое число N ε > K , зависящее от ε , что для всех x, |x| > N ε , значения функции принадлежат ε - окрестности точки a :
|f(x) - a| < ε .
Предел функции на бесконечности обозначается так:
.
Или при .

Также часто используется следующее обозначение:
.

Запишем это определение, используя логические символы существования и всеобщности:
.
Здесь подразумевается, что значения принадлежат области определения функции.

Односторонние пределы

Левый предел функции на бесконечности:
|f(x) - a| < ε при x < -N

Часто встречаются случаи, когда функция определена только для положительных или отрицательных значений переменной x (точнее в окрестности точки или ). Также пределы на бесконечности для положительных и отрицательных значений x могут иметь различные значения. Тогда используют односторонние пределы.

Левый предел в бесконечно удаленной точке или предел при x стремящемся к минус бесконечности () определяется так:
.
Правый предел в бесконечно удаленной точке или предел при x стремящемся к плюс бесконечности () :
.
Односторонние пределы на бесконечности часто обозначают так:
; .

Бесконечный предел функции на бесконечности

Бесконечный предел функции на бесконечности:
|f(x)| > M при |x| > N

Определение бесконечного предела по Коши
Пусть функция f(x) определена в некоторой окрестности бесконечно удаленной точки, при |x| > K , где K - положительное число. Предел функции f(x) при x стремящемся к бесконечности (), равен бесконечности , если для любого, сколь угодно большого числа M > 0 , существует такое число N M > K , зависящее от M , что для всех x, |x| > N M , значения функции принадлежат окрестности бесконечно удаленной точки:
|f(x) | > M .
Бесконечный предел при x стремящемся к бесконечности обозначают так:
.
Или при .

С помощью логических символов существования и всеобщности, определение бесконечного предела функции можно записать так:
.

Аналогично вводятся определения бесконечных пределов определенных знаков, равных и :
.
.

Определения односторонних пределов на бесконечности.
Левые пределы.
.
.
.
Правые пределы.
.
.
.

Определение предела функции по Гейне

Пусть функция f(x) определена на некоторой окрестности бесконечно удаленной точки x 0 , где или или .
Число a (конечное или бесконечно удаленное) называется пределом функции f(x) в точке x 0 :
,
если для любой последовательности { x n } , сходящейся к x 0 : ,
элементы которой принадлежат окрестности , последовательность { f(x n )} сходится к a :
.

Если в качестве окрестности взять окрестность бесконечно удаленной точки без знака: , то получим определение предела функции при x стремящемся к бесконечности, . Если взять левостороннюю или правостороннюю окрестность бесконечно удаленной точки x 0 : или , то получим определение предела при x стремящемся к минус бесконечности и плюс бесконечности, соответственно.

Определения предела по Гейне и Коши эквивалентны .

Примеры

Пример 1

Используя определение Коши показать, что
.

Введем обозначения:
.
Найдем область определения функции . Поскольку числитель и знаменатель дроби являются многочленами, то функция определена для всех x кроме точек, в которых знаменатель обращается в нуль. Найдем эти точки. Решаем квадратное уравнение . ;
.
Корни уравнения:
; .
Поскольку , то и .
Поэтому функция определена при . Это мы будем использовать в дальнейшем.

Выпишем определение конечного предела функции на бесконечности по Коши:
.
Преобразуем разность:
.
Разделим числитель и знаменатель на и умножим на -1 :
.

Пусть .
Тогда
;
;
;
.

Итак, мы нашли, что при ,
.
.
Отсюда следует, что
при , и .

Поскольку всегда можно увеличить, то возьмем . Тогда для любого ,
при .
Это означает, что .

Пример 2

Пусть .
Используя определение предела по Коши показать, что:
1) ;
2) .

1) Решение при x стремящемся к минус бесконечности

Поскольку , то функция определена для всех x .
Выпишем определение предела функции при , равного минус бесконечности:
.

Пусть . Тогда
;
.

Итак, мы нашли, что при ,
.
Вводим положительные числа и :
.
Отсюда следует, что для любого положительного числа M , имеется число , так что при ,
.

Это означает, что .

2) Решение при x стремящемся к плюс бесконечности

Преобразуем исходную функцию. Умножим числитель и знаменатель дроби на и применим формулу разности квадратов:
.
Имеем:

.
Выпишем определение правого предела функции при :
.

Введем обозначение: .
Преобразуем разность:
.
Умножим числитель и знаменатель на :
.

Пусть
.
Тогда
;
.

Итак, мы нашли, что при ,
.
Вводим положительные числа и :
.
Отсюда следует, что
при и .

Поскольку это выполняется для любого положительного числа , то
.

Использованная литература:
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.