Equations with change of variable. Integration by change of variable method

Mathematics is a hole through which the logical mind can peek at the ideal world.

Krotov Victor

At school, rational equations occupy a leading place in the algebra course. More time is devoted to their study than to any other topics. This is primarily due to the fact that equations have not only important theoretical significance, but also serve many practical purposes. A huge number of problems in the real world come down to solving various equations, and only after you master the methods of solving them will you find answers to various questions of science and technology.

To develop the ability to solve rational equations, the student’s independent work is of great importance. However, before moving on to independent work, it is necessary to clearly know and be able to apply in practice all possible methods for solving rational equations.

Let's look at it in detail using examples. variable replacement method for solving rational equations.

Example 1.

Solve the equation (2x 2 – 3x + 1) 2 = 22x 2 – 33x + 1.

Solution.

Let us rewrite the equation in the form

(2x 2 – 3x + 1) 2 = 11(2x 2 – 3x) + 1. Let’s make a replacement. Let 2x 2 – 3x = t, then the equation will take the form:

(t + 1) 2 = 11t + 1.

Now let's open the brackets and give similar ones, we get:

t 2 + 2t + 1 = 11t + 1;

In the resulting incomplete quadratic equation, we take the common factor out of brackets and we have:

t = 0 or t = 9.

Now you need to make a reverse substitution and solve each of the resulting equations:

2x 2 – 3x = 0 or 2x 2 – 3x = 9

x(2x – 3) = 0 2x 2 – 3x – 9 = 0

x = 0 or x = 3/2 x = 3 or x = -3/2

Answer: -1.5; 0; 1.5; 3.

Example 2.

Solve the equation (x 2 – 6x) 2 – 2(x – 3) 2 = 81.

Solution.

Let's apply the formula for the squared difference (a – b) 2 = a 2 – 2ab + b 2 . Let us write the original equation in the form

(x 2 – 6x) 2 – 2(x 2 – 6x + 9) = 81. Now you can make a replacement.

Let x 2 – 6x = t, then the equation will look like:

t 2 – 2(t + 9) = 81.

t 2 – 2t – 18 – 81 = 0;

t 2 – 2t – 99 = 0.

According to Vieta's theorem, the roots of the resulting equation will be the numbers -9 and 11.

Let's make a reverse substitution:

x 2 – 6x = -9 or x 2 – 6x = 11

x 2 – 6x + 9 = 0 x 2 – 6x – 11 = 0

(x – 3) 2 = 0 D = 80

x = 3 x 1 = 3 + 2√5; x 2 = 3 – 2√5.

Answer: 3 – 2√5; 3; 3 + 2√5.

Example 3.

Solve the equation (x – 1)(x – 3)(x + 5)(x + 7) = 297 and find the product of its roots.

Solution.

Let’s find a “profitable” way to group factors and open the pairs of brackets:

((x – 1)(x + 5))((x – 3)(x + 7)) = 297;

(x 2 + 5x – x – 5)(x 2 + 7x – 3x – 21) = 297;

(x 2 + 4x – 5)(x 2 + 4x – 21) = 297.

Let's make the replacement x 2 + 4x = t, then the equation will look like this:

(t – 5)(t – 21) = 297.

Let's open the brackets and present similar terms:

t 2 – 21t – 5t + 105 = 297;

t 2 – 26t – 192 = 0.

Using Vieta's theorem, we determine that the roots of the resulting equation will be the numbers -6 and 32.

After reverse substitution we will have:

x 2 + 4x = -6 or x 2 + 4x = 32

x 2 + 4x + 6 = 0 x 2 + 4x – 32 = 0

D = 16 – 24< 0 D = 16 + 128 > 0

No roots x 1 = -8; x 2 = 4

Let's find the product of the roots: -8 · 4 = -32.

Answer: -32.

Example 4.

Find the sum of the roots of the equation (x 2 – 2x + 2) 2 + 3x(x 2 – 2x + 2) = 10x 2.

Solution.

Let x 2 – 2x + 2 = t, then the equation will take the form:

t 2 + 3xt – 10x 2 = 0.

Let us consider the resulting equation as quadratic with respect to t.

D = (3x) 2 – 4 · (-10x 2) = 9x 2 + 40x 2 = 49x 2 ; ≥≤

t 1 = (-3x – 7x) / 2 and t 2 = (-3x + 7x) / 2;

t 1 = -5x and t 2 = 2x.

Since t = x 2 – 2x + 2, then

x 2 – 2x + 2 = -5x or x 2 – 2x + 2 = 2x. Let's solve each of the resulting equations.

x 2 + 3x + 2 = 0 or x 2 – 4x + 2 = 0.

Both equations have roots, because D > 0.

Using Vieta's theorem, we can conclude that the sum of the roots of the first equation is -3, and the second equation is 4. We find that the sum of the roots of the original equation is -3 + 4 = 1

Answer: 1.

Example 5.

Find the root of the equation (x + 1) 4 + (x + 5) 4 = 32, belonging to the interval [-5; 10].

Solution.

Let x = t – 3, then x + 1 = t – 2; x + 5 = t + 2 and the original equation takes the form:

(t – 2) 4 + (t + 2) 4 = 32. To raise expressions to the fourth power, you can use Pascal’s triangle (Fig. 1);

(t – 2) 4 = t 4 – 4t 3 2 + 6t 2 2 2 – 4t 2 3 + 2 4 ;

(t + 2) 4 = t 4 + 4t 3 2 + 6t 2 2 2 + 4t 2 3 + 2 4.

After reducing similar terms we get:

2t 4 – 2 6t 2 2 2 + 2 2 4 = 32;

t 4 + 6t 2 2 2 + 2 4 = 16;

t 4 + 24t 2 + 16 = 16;

t 4 + 24t 2 = 0;

t 2 (t 2 + 24) = 0;

t = 0 or t 2 = -24.

The second equation has no roots, which means t = 0 even after reverse substitution

x = t – 3 = 0 – 3 = -3. The root of the equation -3 belongs to the interval [-5; 10].

Answer: -3.

As you can see, when solving rational equations, you need to know the above formulas and be able to count correctly. Errors most often occur when choosing a replacement and during reverse substitution. To avoid this, you need to describe each action in detail, then there will be no mistakes in your decisions.

blog.site, when copying material in full or in part, a link to the original source is required.

Solving equations using the change of variables method

Most of life's tasks

are solved as algebraic equations:

bringing them to their simplest form.

L.N. Tolstoy.

Purpose of the lesson: organize the educational activities of students to master methods for solving entire equations of higher degrees by the method of substitution of a variable; introduce students to concepts and techniques for solving reciprocal and symmetric equations.

Tasks:educational: continue to develop the ability to use the replacement method

variable when solving equations; developing the ability to see the same method for solving equations in different situations; to form an idea of ​​methods and techniques for solving non-standard problems and algebraic equations at a level exceeding the level of state educational standards;

developing: development of students' thinking; memory development; development

logical thinking, the ability to clearly formulate your thoughts; developing students' imagination; development of oral speech.

educational: education of observation skills; education of neatness

when making notes on the board and in a notebook; nurturing independence when performing practical work.

Lesson progress

Organizational moment.

Updating and systematization of knowledge.

Task No. 1. Solve the crossword puzzle. Write your answers in the nominative case only.

4.What is the expression for a quadratic equation? (discriminant)

6. The value of the variable at which the equation turns into a true equality. (root)

8.Equation of the form
, Where
. (biquadratic)

9.French mathematician related to quadratic equations. (Viet)

10. An equation in which the left and right sides are integer expressions. (whole)

11. Equations with one variable that have the same set of roots. (equivalent)

Vertical:

1. Many roots of the equation. (solution)

2.Solving the equation
. (zero)

3. Equality containing a variable. (equation)

5. Quadratic equation in which one of the coefficients b or c is equal to 0. (incomplete)

7. Quadratic equation in which the first coefficient is equal to one. (given)

What will we devote our lesson to today? ( Solving equations )

Task No. 2. How would you solve the equations for each group?

ANSWERS: Examples of group 1) are best solved by factoring by placing the common factor out of brackets or using abbreviated multiplication formulas.

Examples of group 2) are best solved by grouping and factorization.

Examples of group 3) are better solved by introducing a new variable and moving to a quadratic equation.

1 What factor would you put out of brackets in the examples of group 1?

ANSWERS:

How would you group the terms in the group 2 examples?

ANSWERS:

What would you mean by the new variable in the group 3 examples?

ANSWERS:

How can you factor a polynomial?
?

ANSWERS: .

Today in the lesson you will show your knowledge on the topic “Solving equations using the variable replacement method”

Write down the topic of the lesson in your notebooks.

Today in class we will look at one of the ways to solve equations of higher degrees - the variable replacement method; Let's get acquainted with the concepts and techniques for solving reciprocal and symmetric equations.

The art of making variable substitutions is to see which substitution makes the most sense and leads to success faster.

Task No. 3.

Solve the equation.(2 students solve the task at the board at the same time.)

A) (The first student solves at the board with an explanation.)

b) (The second student solves the equation silently, then explains the solution, the class listens and asks questions if something is not clear.)

1 student Replacement:
.

2 student Replacement:
.

(Additional for those who have mastered the previous equations before).

. .

3 student

(Students comment on the progress of the solution from the seat.)

SOLUTION: Let's add a common factor: ,

where
or
, i.e.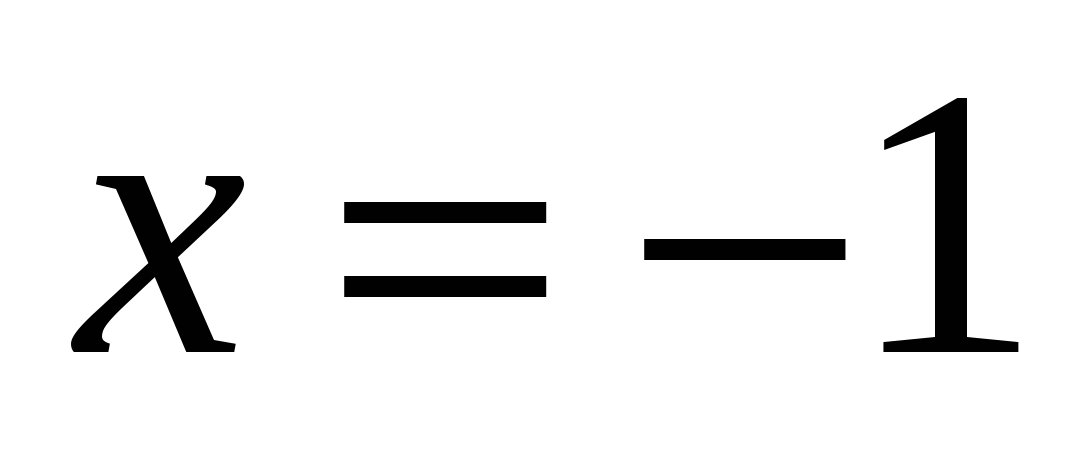

Answer:

Deepening and expanding knowledge

We continue to work. You see the equation on the slide: x 4 -5x 3 +6x 2 -5x+1=0.

How would you propose to solve it? What should we do?

Is it possible to solve it within the framework of school mathematics programs? The answer is no. After all, standard methods for solving equations in school involve solving equations of no higher than the second degree. But we can remember that individual equations of higher degrees were still solved at school. True, the methods for solving them are the creative application of known methods, reducing them to the solution of one or several equations of degree no higher than the second.

Look very closely at this equation? What did you notice ?(in this equation the coefficients equidistant from the ends are equal)

Guys, an equation of this type, when the coefficients equidistant from the ends coincide, is called returnable. This equation can be reduced to a quadratic equation using substitution.

I offer you the following algorithm for solving them:

Algorithm for solving reciprocal equations.

1. Divide both sides of the equation by x 2.

2.Group the terms (the first with the last, the second with the fourth).

Reduce the equation to form A + c = 0

3.Introduce a new variable t = ,then fulfilled t 2 = , i.e. = t 2 – 2.

4. Substitute and solve the quadratic equation.

5.Return to the replacement and solve the resulting equations.

6.Write down the answer.

The guys are studying the algorithm.

The student at the blackboard solves the equation according to the algorithm and with the help of the teacher, the rest write in notebooks.

6x 4 – 5x 3 – 38x 2 – 5x + 6 = 0.

Solution.

6x 2 – 5x – 38 – 5/x + 6/x 2 = 0.

6(x 2 + 1/x 2) – 5(x + 1/x) – 38 = 0.

Enter t: substitution (x + 1/x) = t. Substitution: (x 2 + 1/x 2) = t 2 – 2, we have:

6t 2 – 5t – 50 = 0.

t = -5/2 or t = 10/3.

Let's return to the variable x. After the reverse substitution, we solve the two resulting equations:

1) x + 1/x = -5/2;

x 2 + 5/2 x +1 = 0;

x = -2 or x = -1/2.

2) x + 1/x = 10/3;

x 2 – 10/3 x + 1 = 0;

x = 3 or x = 1/3.

Answer: -2; -1/2; 1/3; 3.

Italian mathematicians of the 16th century N. Tartaglia, A. Fiore, D. Cardano and others made a great contribution to the problem of equations of the 3rd and 4th degrees. In 1535, a scientific duel took place between A. Fiore and N. Tartaglia, at which the latter won. In 2 hours he solved 30 problems proposed by Fiore, and Fiore himself could not solve a single one given to him by Tartaglia.

Guys, I want to offer you one more equation today; I took it from a collection of problems to prepare for the OGE.

. ((x + 1)(x + 4))((x + 2)(x + 3)) = 24,

(x 2 + 5x + 4)(x 2 + 5x + 6) = 24.

Making the substitution x 2 + 5x + 4 = t, we have the equation

t(t + 2) = 24, it is square:

t 2 + 2t – 24 = 0.

t = -6 or t = 4.

After performing the reverse substitution, we easily find the roots of the original equation.

Answer: -5; 0.

Creative transfer of knowledge and skills to new conditions.

At the beginning of the lesson, we talked about the fact that if there are repeating elements in an equation, then you can use the variable substitution method. We do not yet know how to solve trigonometric and irrational equations. Let's see if we can apply this method to them if we know how to solve simple trigonometric and irrational equations.

Task 1: Name the change of variable in the following equations.

Task 2: Compose several equations, the solution of which is based on the variable replacement method.

Summing up.

So guys, our lesson has come to an end. Let's summarize our lesson.

What goals did we set at the beginning of the lesson?

Have our goals been achieved?

What new did we learn in the lesson?

Homework.

4x 4 – 8x 3 + 3x 2 – 8x + 4 = 0

(x+1)(x+2)(x+4)(x+5) = 40

. (equation of Italian mathematicians)

And I would like to end the lesson with the words of the great scientist Einstein A.:

“I have to divide my time between politics and equations. However, the equation, in my opinion, is much more important, because politics exists only for this moment, and the equation will exist forever.”

Thanks for the lesson! Goodbye!

Maintaining your privacy is important to us. For this reason, we have developed a Privacy Policy that describes how we use and store your information. Please review our privacy practices and let us know if you have any questions.

Collection and use of personal information

Personal information refers to data that can be used to identify or contact a specific person.

You may be asked to provide your personal information at any time when you contact us.

Below are some examples of the types of personal information we may collect and how we may use such information.

What personal information do we collect:

• When you submit an application on the site, we may collect various information, including your name, phone number, email address, etc.

How we use your personal information:

• The personal information we collect allows us to contact you with unique offers, promotions and other events and upcoming events.
• From time to time, we may use your personal information to send important notices and communications.
• We may also use personal information for internal purposes, such as conducting audits, data analysis and various research in order to improve the services we provide and provide you with recommendations regarding our services.
• If you participate in a prize draw, contest or similar promotion, we may use the information you provide to administer such programs.

Disclosure of information to third parties

We do not disclose the information received from you to third parties.

Exceptions:

• If necessary - in accordance with the law, judicial procedure, in legal proceedings, and/or on the basis of public requests or requests from government authorities in the territory of the Russian Federation - to disclose your personal information. We may also disclose information about you if we determine that such disclosure is necessary or appropriate for security, law enforcement, or other public importance purposes.
• In the event of a reorganization, merger, or sale, we may transfer the personal information we collect to the applicable successor third party.

Protection of personal information

We take precautions - including administrative, technical and physical - to protect your personal information from loss, theft, and misuse, as well as unauthorized access, disclosure, alteration and destruction.

Respecting your privacy at the company level

To ensure that your personal information is secure, we communicate privacy and security standards to our employees and strictly enforce privacy practices.

Introduction

Mathematical education received in a comprehensive school is an essential component of general education and the general culture of modern man. Almost everything that surrounds modern man is all somehow connected with mathematics. And recent advances in physics, engineering and information technology leave no doubt that in the future the state of affairs will remain the same. Therefore, solving many practical problems comes down to solving various types of equations that you need to learn how to solve.

In elementary mathematics, there are two types of equations: algebraic and transcendental. Algebraic equations include:

10. fractional algebraic equations, i.e. equations containing polynomials and algebraic fractions (fractions of the form

11. irrational equations, i.e. equations containing radicals, under which are polynomials and algebraic fractions;

12. equations containing a modulus, under the modulus of which polynomials and algebraic fractions are contained.

Equations containing transcendental functions, such as the logarithmic, exponential, or trigonometric function, are called transcendental. In our work we will consider algebraic equations in more detail.

Educational and methodological literature traditionally discusses special techniques for solving equations. Meanwhile, the specifics of solving the equations of each section is a secondary matter. Essentially there are four main methods:

Replacing the equation h (f(x))=h (g(x)) with the equation f(x)=g(x);

Variable replacement method;

Factorization method;

Functional-graphic method and their various modifications.

The most common of them is the variable replacement method.

Based on this, we formulate the goal of our work: to study the possibilities of the method of replacing the unknown when solving algebraic equations and to demonstrate their application in standard and non-standard situations. In order to achieve this goal, it is necessary to solve the following tasks:

1. Reveal the content of the basic concepts and statements related to the theory of solving equations: solving an equation, equivalence and corollary, general methods for solving equations.

2. Identify the possibilities of using the method of replacing the unknown when solving algebraic equations in standard and non-standard situations.

3. To typify methods for introducing new unknowns when solving algebraic equations and to identify criteria for their applicability

4. Compose a set of typical problems that boil down to the use of the substitution method when solving equations, and demonstrate their solution.

1. Basic concepts and statements related to the theory of solving equations

In the first chapter of our work, we will reveal the content of the basic concepts and statements related to the theory of solving equations.

We become familiar with the concept of “equation” in mathematics lessons already in elementary school, and the task of “solving an equation” is probably the most frequently encountered problem. Nevertheless, we cannot give an exact definition of the concept of “equation”, define exactly what it means to “solve an equation” without going far beyond the scope of a course in elementary mathematics. To do this, it is necessary to involve very serious logical and even philosophical categories. Familiarity with these concepts at the level of “common sense” is quite enough for us.

Consider two equations A and B with the same unknown. We will say that equation B is consequence equation A if any root of equation A is a root of equation B.

The equations are called equivalent, if any root of one of them is the root of the other and vice versa. Thus, equations are equivalent if each of them is a consequence of the other.

From these definitions it follows, for example, that two equations that have no solutions are equivalent. If A has no solutions, then B is consequence A, whatever the equation B is.

Let us define the concept of “solving an equation.” Solve the equation- means to find all such values ​​of the unknowns included in it that turn the equation into an identity. These values ​​are called the roots of the equation.

The process of solving equations consists mainly of replacing a given equation with another that is equivalent to it.

As previously mentioned, there are four most common methods used in solving equations of any kind. Let's take a closer look at each method.

The method of replacing the equation h (f(x))=h (g(x)) with the equation f(x)=g(x) can only be used when

The essence of the factorization method is as follows: equation

Having solved the equations of this set, you need to take those roots that belong to the domain of definition of the original equation, and discard the rest as extraneous. The idea of ​​​​a graphical method for solving the equation

Let us reveal the essence of the variable replacement method: if the equation

Lesson and presentation on the topic: "Variable replacement method. Examples"

Additional materials
Dear users, do not forget to leave your comments, reviews, wishes! All materials have been checked by an anti-virus program.

Teaching aids and simulators in the Integral online store for grade 11
1C: School. Solving problems in geometry. Interactive tasks on building in space for grades 10–11
Algebraic problems with parameters, grades 9–11

This method is quite common when solving equations, and we have used it more than once. It can be used in the following cases:

• If the original equation $f(x)=0$ has a complex form, but it was possible to transform it to an equation of the form $h(g(x))=0$.
• It is necessary to make a change of variables $u=g(x)$.
• Solve the equation $h(u)=0$, find the roots $u_1$, $u_2$, … $u_n$.
• Enter the reverse substitution $g(x)=u_1$, $g(x)=u_2$, … , $g(x)=u_n$.
• Solve each of the equations $g(x)=u_1$, $g(x)=u_2$, …, $g(x)=u_n$. The roots of each equation will be the solutions to the original equation.

Example.
Solve the equation: $8x^6+7x^3-1=0$.

Solution.
Let us introduce the replacement $y=x^3$. Then our equation reduces to a quadratic equation:
$8y^2+7y-1=0$,
$(8y-1)(y+1)=0$,
$y_1=\frac(1)(8)$ and $y_2=-1$.

At this stage, when solving more complex equations, you should check the obtained roots.
Let's introduce the reverse substitution: $x^3=\frac(1)(8)$ and $x^3=-1$.
The roots of these equations are easy to find: $x_1=\frac(1)(2)$ and $x_2=-1$.

Answer: $x=0.5$ and $x=-1$.

Example.
Solve the equation: $\sqrt(\frac(2x+3)(2x-1))+4\sqrt(\frac(2x-1)(2x+3))=4$.

Solution.
Let's carry out equivalent transformations:
$\sqrt(\frac(2x-1)(2x+3))=(\frac(2x-1)(2x+3))^(\frac(1)(2))=(\frac(2x+ 3)(2x-1))^(-\frac(1)(2))=((\frac(2x+3)(2x-1))^(\frac(1)(2)))^( -1)=\frac(1)(\sqrt(\frac(2x+3)(2x-1)))$.

Let us introduce the replacement: $u=\sqrt(\frac(2x+3)(2x-1))$, then our equation reduces to $u+\frac(4)(u)=4$. $u^2-4u+4=0$, whence $u=2$.

Let's introduce the reverse change: $\sqrt(\frac(2x+3)(2x-1))=2$.

$2x+3=4(2x-1)$ by solving the linear equation $x=1\frac(1)(6)$.

Example.
Solve the equation: $2^x+2^(1-x)=3$.

Solution.
Our equation reduces to an equivalent equation: $2^x+\frac(2)(2^x)=3$.

Let's introduce the replacement: $t=2^x$.
$t+\frac(2)(t)=3$,
$t^2-3t+2=0$,
$(t-2)(t-1)=0$,
$t_1=2$ and $t_2=1$.

Let's introduce the reverse substitution: $2^x=2$ and $2^x=1$. From: $x=1$ and $x=0$.

Answer: $x=1$ and $x=0$.

Example.
Solve the equation: $lg^2(x^2)+lg(10x)-6=0$.

Solution.
Let's transform our equation.
$lg^2(x^2)=(lg(x^2))^2=(2lg(x))^2=4lg^2x$.
$lg(10x)=lg10+lgx=1+lgx$.

The original equation is equivalent to the equation: $4lg^2x+lgx-5=0$.

Let us introduce the replacement: $u=lg(x)$.
$4u^2+u-5=0$,
$(4u+5)(u-1)=0$.

Let's introduce the reverse substitution: $lgx=-1.25$ and $lgx=1$.
Answer: $x=10^(-\frac(5)(4))$ and $x=10$.

Example.
Solve the equation: $sin(x)cos(x)-6sin(x)+6cos(x)+6=0$.

Solution.
Let's introduce the replacement: $cos(x)-sin(x)=y$.

Then: $(cos(x)-sin(x))^2=1-2sin(x)cos(x)$.
$sin(x)cos(x)=\frac(1-y^2)(2)$.

The original equation is equivalent to:
$\frac(1-y^2)(2)+6y+6=0$,
$1-y^2+12y+12=0$,
$y^2-12y-13=0$,
$(y-13)(y+1)=0$.

Let us introduce the inverse substitution: $cos(x)-sin(x)=13$ - it is obvious that there are no solutions, since cosine and sine are limited in modulus by one.

$cos(x)-sin(x)=-1$ - multiply both sides of the equation by $\frac(\sqrt(2))(2)$.
$\frac(\sqrt(2))(2)cos(x)-\frac(\sqrt(2))(2)sin(x)=-\frac(\sqrt(2))(2)$.
$sin(\frac(π)(4)-x)=-\frac(\sqrt(2))(2)$.
$\begin (cases) \frac(π)(4)-x=-\frac(π)(4)+2πn, \\ \frac(π)(4)-x=-\frac(3π)(4 )+2πn. \end (cases)$
$\begin (cases) x=\frac(π)(2)+2πn, \\ x=π+2πn. \end (cases)$

Answer: $x=\frac(π)(2)+2πn$ and $π+2πn$.

Problems to solve independently

2. $\sqrt(\frac(5x-1)(x+3))+5\sqrt(\frac(x+3)(5x-1))=6$.

3. $5^x+5^(2x+1)=-4$.
4. $2cos^2(x)-7cos-4=0$.
5. $5sin(2x)-11sin(x)=11cos(x)-7$.