Menambah dan mengurangi fungsi

fungsi kamu = F(X) disebut bertambah pada interval [ A, B], jika untuk sepasang titik mana pun X Dan X", a ≤ x pertidaksamaan berlaku F(X) ≤ F (X"), dan meningkat secara ketat - jika terjadi ketimpangan F (X) F(X"). Fungsi menurun dan fungsi menurun didefinisikan dengan cara yang sama. Misalnya saja fungsinya pada = X 2 (beras. , a) meningkat tajam pada segmen tersebut , dan

(beras. , b) menurun tajam pada segmen ini. Peningkatan fungsi ditunjuk F (X), dan menurun F (X)↓. F (X Agar fungsinya dapat terdiferensiasi ) meningkat pada segmen [, B A F"(X], perlu dan cukup turunannya ) meningkat pada segmen [, B].

) tidak negatif pada [ pada = F (X Seiring dengan kenaikan dan penurunan suatu fungsi pada suatu ruas, kita perhatikan kenaikan dan penurunan suatu fungsi pada suatu titik. Fungsi X) disebut meningkat pada titik tersebut X 0 jika terdapat interval (α, β) yang memuat titik tersebut X 0, yang untuk titik mana pun dari (α, β), X x> F (X 0) ≤ F (X 0 , pertidaksamaan berlaku X 0, yang untuk titik mana pun ), dan untuk titik mana pun F (X) x 0 , pertidaksamaan berlaku (X≤ f X 0). Peningkatan ketat suatu fungsi pada suatu titik didefinisikan dengan cara yang sama F"(X 0) > 0 . Jika F(X 0, maka fungsinya X 0). Peningkatan ketat suatu fungsi pada suatu titik didefinisikan dengan cara yang sama F (X) meningkat secara ketat pada titik tersebut A, B) meningkat pada setiap titik interval (

), kemudian meningkat selama interval ini.

S.B.Stechkin.. 1969-1978 .

Ensiklopedia Besar Soviet. - M.: Ensiklopedia Soviet

Lihat apa itu “Fungsi menambah dan mengurangi” di kamus lain: Konsep analisis matematis. Fungsi f(x) disebut perbandingan jumlah kelompok umur penduduk yang berbeda yang bertambah pada segmen STRUKTUR USIA PENDUDUK. Tergantung pada angka kelahiran dan kematian, harapan hidup masyarakat...

Kamus Ensiklopedis Besar Konsep analisis matematis. Suatu fungsi f(x) dikatakan meningkat pada ruas tersebut jika untuk sembarang pasangan titik x1 dan x2, a≤x1 ...

Kamus Ensiklopedis<или=х1 <х<или=b, выполняется неравенство f(x1)Konsep matematika. analisa. Fungsi f(x) dipanggil. bertambah pada ruas [a, b], jika untuk sembarang pasangan titik x1 dan x2, dan

Ilmu pengetahuan alam. Kamus Ensiklopedis Cabang matematika yang mempelajari turunan dan diferensial fungsi serta penerapannya dalam studi fungsi. Desain D. dan. menjadi disiplin matematika yang mandiri dikaitkan dengan nama I. Newton dan G. Leibniz (paruh kedua tahun 17 ...

Cabang matematika yang mempelajari konsep turunan dan diferensial serta penerapannya dalam studi fungsi. Perkembangan D. dan. berkaitan erat dengan perkembangan kalkulus integral. Isinya juga tidak dapat dipisahkan. Bersama-sama mereka membentuk dasar...... Ensiklopedia Matematika

Istilah ini memiliki arti lain, lihat fungsinya. Permintaan "Tampilan" dialihkan ke sini; lihat juga arti lainnya... Wikipedia

Aristoteles dan Peripatetik- Pertanyaan Aristoteles Kehidupan Aristoteles Aristoteles lahir pada tahun 384/383. SM e. di Stagira, di perbatasan dengan Makedonia. Ayahnya, bernama Nicomachus, adalah seorang dokter yang melayani raja Makedonia Amyntas, ayah Philip. Bersama keluarganya, Aristoteles muda... ... Filsafat Barat dari asal usulnya hingga saat ini

- (QCD), teori medan kuantum tentang interaksi kuat quark dan gluon, dibangun berdasarkan citra kuantum. elektrodinamika (QED) berdasarkan simetri pengukur "warna". Berbeda dengan QED, fermion di QCD memiliki sifat yang saling melengkapi. derajat kebebasan kuantum nomor,… … Ensiklopedia fisik

I Jantung Jantung (Latin cor, Yunani cardia) adalah organ fibromuskular berongga yang berfungsi sebagai pompa, memastikan pergerakan darah dalam sistem peredaran darah. Anatomi Jantung terletak di mediastinum anterior (Mediastinum) di Perikardium antara... ... Ensiklopedia kedokteran

Kehidupan tumbuhan, seperti organisme hidup lainnya, merupakan serangkaian proses kompleks yang saling terkait; Yang paling penting di antaranya, seperti diketahui, adalah pertukaran zat dengan lingkungan. Lingkungan adalah sumber dari mana... ... Ensiklopedia biologi

Turunan. Jika turunan suatu fungsi positif pada suatu titik dalam interval, maka fungsi tersebut meningkat; jika negatif, maka fungsi tersebut menurun.

Untuk mencari interval kenaikan dan penurunan suatu fungsi, Anda perlu mencari domain definisi, turunannya, menyelesaikan pertidaksamaan bentuk F’(x) > 0 dan F’(x)

Larutan.

3. Selesaikan pertidaksamaan y’ > 0 dan y’ 0;
(4 - x)/x³

Larutan.
1. Temukan domain definisi fungsi. Jelasnya, ekspresi penyebut harus selalu berbeda dari nol. Oleh karena itu, 0 dikecualikan dari domain definisi: fungsi tersebut didefinisikan untuk x ∈ (-∞; 0)∪(0; +∞).

2. Hitung turunan dari fungsi tersebut:
y'(x) = ((3 x² + 2 x - 4)' x² – (3 x² + 2 x - 4) (x²)')/x^4 = ((6 x + 2) x² – (3 x² + 2 x - 4) 2 x)/x^4 = (6 x³ + 2 x² – 6 x³ – 4 x² + 8 x)/x^ 4 = (8 x – 2 x²)/x^4 = 2 (4 - x)/x³.

3. Selesaikan pertidaksamaan y’ > 0 dan y’ 0;
(4 - x)/x³

4. Ruas kiri pertidaksamaan mempunyai satu x = 4 real dan berubah menjadi x = 0. Oleh karena itu, nilai x = 4 termasuk dalam interval dan interval menurun, dan titik 0 tidak termasuk.
Jadi, fungsi yang dibutuhkan bertambah pada interval x ∈ (-∞; 0) ∪ .

4. Ruas kiri pertidaksamaan mempunyai satu x = 4 real dan berubah menjadi x = 0. Oleh karena itu, nilai x = 4 termasuk dalam interval dan interval menurun, dan titik 0 tidak termasuk.
Jadi, fungsi yang dibutuhkan bertambah pada interval x ∈ (-∞; 0) ∪ .

Sumber:

• cara mencari interval penurunan suatu fungsi

Suatu fungsi mewakili ketergantungan ketat suatu bilangan terhadap bilangan lain, atau nilai suatu fungsi (y) pada argumen (x). Setiap proses (tidak hanya dalam matematika) dapat dijelaskan dengan fungsinya masing-masing, yang akan memiliki ciri-ciri: interval penurunan dan kenaikan, titik minimum dan maksimum, dan sebagainya.

Anda akan membutuhkan

• - kertas;
• - pena.

instruksi

Contoh 2.
Tentukan interval penurunan f(x)=sinx +x.
Turunan dari fungsi ini akan sama dengan: f’(x)=cosx+1.
Menyelesaikan pertidaksamaan cosx+1

Selang kesamaan suatu fungsi dapat disebut interval di mana fungsi tersebut hanya bertambah atau berkurang saja. Sejumlah tindakan spesifik akan membantu menemukan rentang fungsi tersebut, yang sering kali diperlukan dalam masalah aljabar semacam ini.

instruksi

Langkah pertama dalam menyelesaikan masalah menentukan interval di mana suatu fungsi naik atau turun secara monoton adalah menghitung fungsi tersebut. Untuk melakukan ini, cari tahu semua nilai argumen (nilai sepanjang sumbu x) yang dapat Anda temukan nilai fungsinya. Tandai titik-titik di mana diskontinuitas teramati. Temukan turunan dari fungsi tersebut. Setelah Anda menentukan ekspresi yang mewakili turunannya, setel ke nol. Setelah ini, Anda harus menemukan akar dari hasil . Bukan soal luas wilayah yang diperbolehkan.

Titik-titik di mana fungsi atau turunannya sama dengan nol mewakili batas-batas interval kesamaan. Rentang ini, serta titik-titik yang memisahkannya, harus dimasukkan secara berurutan ke dalam tabel. Temukan tanda turunan fungsi pada interval yang dihasilkan. Untuk melakukan ini, substitusikan argumen apa pun dari interval ke dalam ekspresi yang sesuai dengan turunannya. Jika hasilnya positif, fungsi dalam rentang ini meningkat, jika tidak maka fungsi tersebut menurun. Hasilnya dimasukkan ke dalam tabel.

Pada baris yang menunjukkan turunan dari fungsi f'(x), nilai argumen yang sesuai ditulis: “+” - jika turunannya positif, “-” - negatif atau “0” - sama dengan nol. Pada baris berikutnya, perhatikan monotonnya ekspresi asli itu sendiri. Panah atas menunjukkan peningkatan, dan panah bawah menunjukkan penurunan. Periksa fungsinya. Ini adalah titik di mana turunannya adalah nol. Titik ekstrem dapat berupa titik maksimum atau titik minimum. Jika bagian fungsi sebelumnya bertambah dan bagian sekarang berkurang, ini adalah titik maksimum. Jika fungsinya menurun sebelum suatu titik tertentu, tetapi sekarang meningkat, maka ini adalah titik minimumnya. Masukkan nilai fungsi pada titik ekstrem ke dalam tabel.

Sumber:

• apa definisi monoton

Perilaku suatu fungsi yang memiliki ketergantungan kompleks pada argumen dipelajari dengan menggunakan turunan. Berdasarkan sifat perubahan turunannya, Anda dapat menemukan titik kritis dan area kenaikan atau penurunan fungsi.

Menaikkan, menurunkan, dan ekstrem suatu fungsi

Menemukan interval kenaikan, penurunan, dan ekstrem suatu fungsi merupakan tugas independen dan merupakan bagian penting dari tugas lain, khususnya, studi fungsi penuh. Informasi awal tentang kenaikan, penurunan, dan ekstrem fungsi diberikan dalam bab teori tentang turunan, yang sangat saya rekomendasikan untuk studi pendahuluan (atau pengulangan)– juga karena alasan bahwa materi berikut ini didasarkan pada hal tersebut pada dasarnya turunan, menjadi kelanjutan yang harmonis dari artikel ini. Meskipun demikian, jika waktunya singkat, maka praktik formal murni dari contoh-contoh dari pelajaran hari ini juga dimungkinkan.

Dan hari ini ada semangat kebulatan suara yang langka di udara, dan saya dapat langsung merasakan bahwa setiap orang yang hadir membara dengan hasrat. belajar mengeksplorasi suatu fungsi menggunakan turunannya. Oleh karena itu, terminologi yang masuk akal, baik, dan abadi segera muncul di layar monitor Anda.

Untuk apa? Salah satu alasannya adalah yang paling praktis: sehingga jelas apa yang umumnya dituntut dari Anda dalam suatu tugas tertentu!

Monotonisitas fungsi. Titik ekstrem dan ekstrem suatu fungsi

Mari kita pertimbangkan beberapa fungsinya. Sederhananya, kita berasumsi bahwa dia kontinu pada seluruh garis bilangan:

Untuk berjaga-jaga, yuk segera hilangkan ilusi-ilusi yang mungkin terjadi, terutama bagi para pembaca yang baru mengenalnya interval tanda konstan fungsi. Sekarang kita TIDAK TERTARIK, bagaimana letak grafik fungsi terhadap sumbu (di atas, di bawah, tempat perpotongan sumbu). Untuk meyakinkan, hapus sumbu secara mental dan sisakan satu grafik. Karena di situlah letak ketertarikannya.

Fungsi meningkat pada suatu interval jika untuk dua titik mana pun pada interval ini yang dihubungkan oleh relasi , pertidaksamaan tersebut benar. Artinya, nilai argumen yang lebih besar berarti nilai fungsi yang lebih besar, dan grafiknya bergerak “dari bawah ke atas”. Fungsi demonstrasi bertambah seiring interval.

Begitu pula fungsinya berkurang pada suatu interval jika untuk dua titik mana pun pada interval tertentu sedemikian rupa sehingga pertidaksamaan tersebut benar. Artinya, nilai argumen yang lebih besar berarti nilai fungsi yang lebih kecil, dan grafiknya bergerak “dari atas ke bawah”. Fungsi kami menurun secara berkala .

Jika suatu fungsi bertambah atau berkurang dalam suatu interval, maka disebut sangat monoton pada interval ini. Apa itu monoton? Anggap saja secara harfiah – monoton.

Anda juga dapat mendefinisikan tidak menurun fungsi (kondisi santai pada definisi pertama) dan tidak meningkat fungsi (kondisi melunak dalam definisi ke-2). Fungsi yang tidak berkurang atau tidak bertambah pada suatu interval disebut fungsi monotonik pada interval tertentu (monotonitas yang ketat adalah kasus khusus dari monotonisitas yang “sederhana”).

Teori ini juga mempertimbangkan pendekatan lain untuk menentukan kenaikan/penurunan suatu fungsi, termasuk setengah interval, segmen, tetapi agar tidak menuangkan minyak-minyak-minyak ke kepala Anda, kami setuju untuk beroperasi dengan interval terbuka dengan definisi kategoris - ini lebih jelas, dan untuk memecahkan banyak masalah praktis sudah cukup.

Dengan demikian, dalam artikel saya, kata-kata "monotonisitas suatu fungsi" hampir selalu disembunyikan interval monoton yang ketat(fungsi yang meningkat secara ketat atau menurun secara ketat).

Lingkungan suatu titik. Kata-kata yang kemudian membuat siswa lari kemanapun mereka bisa dan bersembunyi ketakutan di sudut. ...Meskipun setelah posting Batas Cauchy Mereka mungkin tidak lagi bersembunyi, tetapi hanya sedikit bergidik =) Jangan khawatir, sekarang tidak akan ada bukti teorema analisis matematis - Saya membutuhkan lingkungan untuk merumuskan definisi dengan lebih ketat titik ekstrim. Mari kita ingat:

Lingkungan suatu titik suatu interval yang memuat suatu titik tertentu disebut, dan untuk memudahkan, interval tersebut sering dianggap simetris. Misalnya, suatu titik dan lingkungan standarnya:

Sebenarnya definisinya:

Intinya disebut titik maksimum yang ketat, Jika ada lingkungannya, untuk semua orang yang nilainya, kecuali titik itu sendiri, adalah pertidaksamaan . Dalam contoh spesifik kami, ini adalah sebuah titik.

Intinya disebut titik minimum yang ketat, Jika ada lingkungannya, untuk semua orang yang nilainya, kecuali titik itu sendiri, adalah pertidaksamaan . Pada gambar tersebut terdapat titik “a”.

Catatan : persyaratan kesimetrian lingkungan sama sekali tidak diperlukan. Selain itu, ini penting fakta keberadaan lingkungan (baik kecil atau mikroskopis) yang memenuhi kondisi yang ditentukan

Poinnya disebut titik ekstrem yang ketat atau hanya titik ekstrim fungsi. Artinya, ini adalah istilah umum untuk poin maksimum dan poin minimum.

Bagaimana kita memahami kata “ekstrim”? Ya, sama langsungnya dengan monoton. Titik ekstrim roller coaster.

Seperti dalam kasus monotonisitas, ada postulat longgar dan bahkan lebih umum dalam teori (yang, tentu saja, termasuk dalam kasus-kasus ketat!):

Intinya disebut titik maksimum, Jika ada lingkungannya sedemikian rupa untuk semua orang
Intinya disebut poin minimum, Jika ada lingkungannya sedemikian rupa untuk semua orang nilai-nilai lingkungan ini, kesenjangan tetap ada.

Perhatikan bahwa menurut dua definisi terakhir, setiap titik dari suatu fungsi konstan (atau “bagian datar” dari suatu fungsi) dianggap sebagai titik maksimum dan minimum! Omong-omong, fungsinya tidak bertambah dan tidak berkurang, yaitu monotonik. Namun, kami akan menyerahkan pertimbangan ini kepada para ahli teori, karena dalam praktiknya kami hampir selalu merenungkan “bukit” dan “lubang” tradisional (lihat gambar) dengan “raja bukit” atau “putri rawa” yang unik. Sebagai variasi, hal itu terjadi tip, diarahkan ke atas atau ke bawah, misalnya fungsi minimum pada suatu titik.

Oh, dan berbicara tentang royalti:
– artinya disebut maksimum fungsi;
– artinya disebut minimum fungsi.

Nama umum – ekstrem fungsi.

Harap berhati-hati dengan kata-kata Anda!

Poin ekstrem– ini adalah nilai “X”.
Ekstrem– arti “permainan”.

! Catatan : terkadang istilah yang tercantum merujuk pada titik “X-Y” yang terletak tepat pada GRAFIK fungsi SENDIRI.

Berapa banyak ekstrem yang dapat dimiliki suatu fungsi?

Tidak ada, 1, 2, 3, ... dst. iklan tanpa batas. Misalnya, sinus mempunyai nilai minimum dan maksimum yang tak terhingga banyaknya.

PENTING! Istilah "fungsi maksimum" tidak identik istilah “nilai maksimum suatu fungsi”. Sangat mudah untuk melihat bahwa nilainya maksimal hanya di lingkungan lokal, dan di kiri atas ada “kawan yang lebih keren”. Demikian pula, “nilai minimum suatu fungsi” tidak sama dengan “nilai minimum suatu fungsi”, dan pada gambar kita melihat bahwa nilai minimum hanya di daerah tertentu. Dalam hal ini, titik ekstrem juga disebut titik ekstrem lokal, dan ekstrem – ekstrem lokal. Mereka berjalan dan berkeliaran di dekatnya dan global saudara laki-laki. Jadi, setiap parabola mempunyai titik puncaknya minimum global atau maksimum global. Selanjutnya, saya tidak akan membedakan jenis-jenis ekstrem, dan penjelasannya lebih disuarakan untuk tujuan pendidikan umum - kata sifat tambahan “lokal”/“global” seharusnya tidak mengejutkan Anda.

Mari kita rangkum perjalanan singkat kita ke dalam teori dengan sebuah percobaan: apa yang dimaksud dengan tugas “menemukan interval monotonisitas dan titik ekstrem suatu fungsi”?

Kata-katanya mendorong Anda untuk menemukan:

– interval fungsi naik/turun (tidak menurun, tidak meningkat lebih jarang muncul);

– poin maksimum dan/atau minimum (jika ada). Nah, untuk menghindari kegagalan, lebih baik cari sendiri nilai minimum/maksimumnya ;-)

Bagaimana cara menentukan semua ini? Menggunakan fungsi turunan!

Cara mencari interval kenaikan, penurunan,
titik ekstrem dan ekstrem fungsi?

Banyak aturan yang sebenarnya sudah diketahui dan dipahami pelajaran tentang arti turunan.

Turunan tangen membawa berita gembira bahwa fungsinya semakin meningkat domain definisi.

Dengan kotangen dan turunannya situasinya justru sebaliknya.

Arcsinus bertambah sepanjang interval - turunannya di sini positif: .
Ketika suatu fungsi terdefinisi tetapi tidak terdiferensiasi. Akan tetapi, pada titik kritis terdapat turunan bertangan kanan dan garis singgung bertangan kanan, dan pada sisi lainnya terdapat turunan bertangan kiri.

Saya rasa tidak akan terlalu sulit bagi Anda untuk melakukan penalaran serupa untuk arc cosinus dan turunannya.

Semua kasus di atas, banyak diantaranya turunan tabel, saya ingatkan, ikuti langsung dari definisi turunan.

Mengapa mengeksplorasi suatu fungsi menggunakan turunannya?

Untuk lebih memahami seperti apa grafik fungsi ini: dimana arahnya “bottom up”, dimana “top down”, dimana mencapai minimum dan maksimum (jika mencapai sama sekali). Tidak semua fungsi sesederhana itu - dalam banyak kasus, kita tidak tahu sama sekali tentang grafik fungsi tertentu.

Saatnya beralih ke contoh yang lebih bermakna dan mempertimbangkannya algoritma untuk mencari interval monotonisitas dan ekstrem suatu fungsi:

Contoh 1

Temukan interval kenaikan/penurunan dan ekstrem dari fungsi tersebut

Larutan:

1) Langkah pertama adalah menemukan domain suatu fungsi, dan catat juga break point (jika ada). Dalam hal ini, fungsinya kontinu pada seluruh garis bilangan, dan tindakan ini sampai batas tertentu bersifat formal. Namun dalam beberapa kasus, gairah yang serius berkobar di sini, jadi mari kita perlakukan paragraf tersebut tanpa meremehkan.

2) Poin kedua dari algoritma ini adalah karena

kondisi yang diperlukan untuk ekstrem:

Jika terdapat titik ekstrem pada suatu titik, maka nilainya tidak ada.

Bingung dengan endingnya? Ekstrem dari fungsi “modulus x”. .

Syaratnya perlu, tapi tidak cukup, dan kebalikannya tidak selalu benar. Jadi, persamaan tersebut belum berarti bahwa fungsi tersebut mencapai maksimum atau minimum di titik . Contoh klasik telah disorot di atas - ini adalah parabola kubik dan titik kritisnya.

Namun bagaimanapun juga, kondisi yang diperlukan untuk suatu ekstrem menentukan perlunya menemukan titik-titik yang mencurigakan. Untuk melakukannya, cari turunannya dan selesaikan persamaannya:

Di awal artikel pertama tentang grafik fungsi Saya sudah memberi tahu Anda cara cepat membuat parabola menggunakan sebuah contoh : “...kita ambil turunan pertama dan menyamakannya dengan nol: ...Jadi, penyelesaian persamaan kita: - pada titik inilah titik puncak parabola berada...”. Sekarang, saya rasa, semua orang mengerti mengapa titik puncak parabola terletak tepat di titik ini =) Secara umum, kita harus mulai dengan contoh serupa di sini, tetapi ini terlalu sederhana (bahkan untuk orang bodoh). Selain itu, ada analoginya di akhir pelajaran tentang turunan suatu fungsi. Oleh karena itu, mari kita tingkatkan derajatnya:

Contoh 2

Temukan interval monotonisitas dan ekstrem dari fungsi tersebut

Ini adalah contoh untuk Anda pecahkan sendiri. Solusi lengkap dan perkiraan contoh akhir dari masalah di akhir pelajaran.

Saat yang ditunggu-tunggu untuk bertemu dengan fungsi rasional pecahan telah tiba:

Contoh 3

Jelajahi suatu fungsi menggunakan turunan pertama

Perhatikan betapa bervariasinya satu tugas yang sama dapat dirumuskan ulang.

Larutan:

1) Fungsi tersebut mengalami diskontinuitas tak hingga di titik-titiknya.

2) Kami mendeteksi titik-titik kritis. Mari kita cari turunan pertama dan samakan dengan nol:

Mari kita selesaikan persamaannya. Pecahan bernilai nol bila pembilangnya nol:

Jadi, kita mendapatkan tiga poin penting:

3) Kami memplot SEMUA titik yang terdeteksi pada garis bilangan dan metode interval kami mendefinisikan tanda-tanda DERIVATIF:

Saya ingatkan Anda bahwa Anda perlu mengambil suatu titik dalam interval tersebut dan menghitung nilai turunannya dan tentukan tandanya. Lebih menguntungkan bahkan tidak menghitung, tetapi “memperkirakan” secara lisan. Mari kita ambil, misalnya, sebuah titik yang termasuk dalam interval dan melakukan substitusi: .

Dua “plus” dan satu “minus” menghasilkan “minus”, yang berarti turunannya negatif pada seluruh interval.

Tindakan tersebut, seperti yang Anda pahami, perlu dilakukan untuk masing-masing dari enam interval. Omong-omong, perhatikan bahwa faktor pembilang dan penyebutnya benar-benar positif untuk setiap titik di interval mana pun, yang sangat menyederhanakan tugas.

Jadi, turunannya memberi tahu kita bahwa FUNGSI SENDIRI bertambah sebesar dan berkurang sebesar . Lebih mudah untuk menggabungkan interval dengan tipe yang sama dengan ikon gabung.

Pada saat fungsi mencapai maksimum:
Pada titik tersebut fungsi mencapai minimum:

Pikirkan mengapa Anda tidak perlu menghitung ulang nilai kedua ;-)

Ketika melewati suatu titik, turunannya tidak berubah tanda, sehingga fungsinya TIDAK ADA EKSTREMUMnya - turun dan tetap menurun.

! Mari kita ulangi satu poin penting: poin tidak dianggap kritis - poin tersebut mengandung fungsi tidak ditentukan. Oleh karena itu, di sini Pada prinsipnya tidak ada yang ekstrem(walaupun turunannya berubah tanda).

Menjawab: fungsi meningkat sebesar dan berkurang sebesar Pada titik maksimum fungsi tercapai: , dan pada intinya – minimum: .

Pengetahuan tentang interval monotonisitas dan ekstrem, ditambah dengan mapan asimtot sudah memberikan gambaran yang sangat bagus tentang tampilan grafik fungsi. Seseorang dengan tingkat pelatihan rata-rata mampu menentukan secara verbal bahwa grafik suatu fungsi mempunyai dua asimtot vertikal dan satu asimtot miring. Inilah pahlawan kita:

Coba korelasikan kembali hasil penelitian dengan grafik fungsi ini.
Tidak ada titik ekstrim pada titik kritis, tapi ada infleksi grafik(yang biasanya terjadi dalam kasus serupa).

Contoh 4

Temukan ekstrem dari fungsinya

Contoh 5

Temukan interval monotonisitas, maksimum dan minimum dari fungsi tersebut

…ini hampir seperti liburan “X in a cube” hari ini....
Soooo, siapa di galeri yang menawarkan minuman untuk ini? =)

Setiap tugas memiliki nuansa substantif dan seluk-beluk teknisnya sendiri, yang dikomentari di akhir pelajaran.

Fungsi ekstrem

Definisi 2

Suatu titik $x_0$ disebut titik maksimum suatu fungsi $f(x)$ jika terdapat lingkungan pada titik tersebut sedemikian rupa sehingga untuk semua $x$ dalam lingkungan tersebut terdapat pertidaksamaan $f(x)\le f(x_0) $ ditahan.

Definisi 3

Suatu titik $x_0$ disebut titik maksimum suatu fungsi $f(x)$ jika terdapat lingkungan pada titik tersebut sedemikian rupa sehingga untuk semua $x$ dalam lingkungan tersebut terdapat pertidaksamaan $f(x)\ge f(x_0) $ ditahan.

Konsep titik ekstrem suatu fungsi erat kaitannya dengan konsep titik kritis suatu fungsi. Mari kita perkenalkan definisinya.

Definisi 4

$x_0$ disebut titik kritis fungsi $f(x)$ jika:

1) $x_0$ - titik internal domain definisi;

2) $f"\left(x_0\right)=0$ atau tidak ada.

Untuk konsep ekstrem, kita dapat merumuskan teorema kondisi cukup dan perlu bagi keberadaannya.

Teorema 2

Kondisi cukup untuk ekstrem

Misalkan titik $x_0$ kritis untuk fungsi $y=f(x)$ dan terletak pada interval $(a,b)$. Misalkan pada setiap interval $\left(a,x_0\right)\ dan\ (x_0,b)$ turunan $f"(x)$ ada dan mempunyai tanda konstan. Maka:

1) Jika pada interval $(a,x_0)$ turunannya adalah $f"\left(x\right)>0$, dan pada interval $(x_0,b)$ turunannya adalah $f"\left( x\kanan)

2) Jika pada interval $(a,x_0)$ turunan $f"\left(x\right)0$, maka titik $x_0$ adalah titik minimum untuk fungsi ini.

3) Jika keduanya pada interval $(a,x_0)$ dan pada interval $(x_0,b)$ turunan $f"\left(x\right) >0$ atau turunan $f"\left(x \Kanan)

Teorema ini diilustrasikan pada Gambar 1.

Gambar 1. Kondisi cukup bagi keberadaan ekstrem

Contoh ekstrem (Gbr. 2).

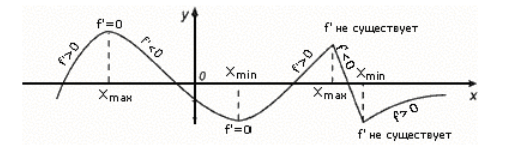
Gambar 2. Contoh titik ekstrim

Aturan untuk mempelajari suatu fungsi ekstrem

2) Temukan turunan $f"(x)$;

7) Menarik kesimpulan tentang keberadaan maxima dan minima pada setiap interval, dengan menggunakan Teorema 2.

Menambah dan mengurangi fungsi

Mari kita perkenalkan terlebih dahulu definisi fungsi naik dan turun.

Definisi 5

Suatu fungsi $y=f(x)$ yang didefinisikan pada interval $X$ dikatakan meningkat jika untuk sembarang titik $x_1,x_2\in X$ di $x_1

Definisi 6

Suatu fungsi $y=f(x)$ yang didefinisikan pada interval $X$ dikatakan menurun jika untuk sembarang titik $x_1,x_2\in X$ untuk $x_1f(x_2)$.

Mempelajari suatu fungsi naik dan turun

Anda dapat mempelajari fungsi naik dan turun menggunakan turunannya.

Untuk memeriksa suatu fungsi pada interval naik dan turun, Anda harus melakukan hal berikut:

1) Temukan domain definisi fungsi $f(x)$;

2) Temukan turunan $f"(x)$;

3) Temukan titik di mana persamaan $f"\left(x\right)=0$;

4) Temukan titik di mana $f"(x)$ tidak ada;

5) Tandai pada garis koordinat semua titik yang ditemukan dan domain definisi fungsi ini;

6) Tentukan tanda turunan $f"(x)$ pada setiap interval yang dihasilkan;

7) Tarik kesimpulan: pada interval di mana $f"\left(x\right)0$ fungsinya meningkat.

Contoh soal mempelajari fungsi kenaikan, penurunan dan keberadaan titik ekstrem

Contoh 1

Periksa fungsi kenaikan dan penurunan, serta keberadaan titik maksimum dan minimum: $f(x)=(2x)^3-15x^2+36x+1$

Karena 6 poin pertama sama, mari kita bahas dulu.

1) Domain definisi - semua bilangan real;

2) $f"\kiri(x\kanan)=6x^2-30x+36$;

3) $f"\kiri(x\kanan)=0$;

\ \ \

4) $f"(x)$ ada di semua titik domain definisi;

5) Garis koordinat:

Gambar 3.

6) Tentukan tanda turunan $f"(x)$ pada setiap interval:

\ \}