İstatistiklerdeki çeşitliliğin ana genelleştirici göstergeleri dağılımlar ve standart sapmalardır.
Dağılım bu aritmetik ortalama Her bir karakteristik değerin genel ortalamadan sapmalarının karesi. Varyansa genellikle sapmaların ortalama karesi denir ve 2 ile gösterilir. Kaynak verilere bağlı olarak varyans, basit veya ağırlıklı aritmetik ortalama kullanılarak hesaplanabilir:
ağırlıklandırılmamış (basit) varyans;
 varyans ağırlıklı.
varyans ağırlıklı.
Standart sapma bu mutlak boyutların genelleştirici bir özelliğidir varyasyonlar toplu olarak işaretler. Nitelik ile aynı ölçü birimleriyle (metre, ton, yüzde, hektar vb.) ifade edilir.
Standart sapma, varyansın kareköküdür ve ile gösterilir:
 ağırlıklandırılmamış standart sapma;
ağırlıklandırılmamış standart sapma;
 ağırlıklı standart sapma.
ağırlıklı standart sapma.
Standart sapma ortalamanın güvenilirliğinin bir ölçüsüdür. Standart sapma ne kadar küçük olursa, aritmetik ortalama temsil edilen popülasyonun tamamını o kadar iyi yansıtır.
Standart sapmanın hesaplanmasından önce varyansın hesaplanması gerekir.
Ağırlıklı varyansın hesaplanmasına ilişkin prosedür aşağıdaki gibidir:
1) ağırlıklı aritmetik ortalamayı belirleyin:
2) seçeneklerin ortalamadan sapmalarını hesaplayın:
3) her seçeneğin ortalamadan sapmasının karesi:
4) sapmaların karelerini ağırlıklarla (frekanslar) çarpın:
5) ortaya çıkan ürünleri özetleyin:
![]()
6) Ortaya çıkan miktar, ağırlıkların toplamına bölünür:

Örnek 2.1

Ağırlıklı aritmetik ortalamayı hesaplayalım:

Ortalamadan sapmaların değerleri ve kareleri tabloda sunulmaktadır. Varyansı tanımlayalım:

Standart sapma şuna eşit olacaktır:

Kaynak veriler aralık şeklinde sunuluyorsa dağıtım serisi , daha sonra önce özelliğin ayrık değerini belirlemeniz ve ardından açıklanan yöntemi uygulamanız gerekir.
Örnek 2.2
Kolektif bir çiftliğin ekili alanının buğday verimine göre dağılımına ilişkin verileri kullanarak aralık serisi için varyans hesaplamasını gösterelim.

Aritmetik ortalama:

Varyansı hesaplayalım:

6.3. Bireysel verilere dayalı bir formül kullanarak varyansın hesaplanması
Hesaplama tekniği farklılıklar karmaşıktır ve büyük seçenek ve frekans değerleriyle hantal olabilir. Hesaplamalar dağılım özellikleri kullanılarak basitleştirilebilir.
Dispersiyon aşağıdaki özelliklere sahiptir.
1. Değişen bir özelliğin ağırlıklarının (frekanslarının) belirli sayıda azaltılması veya arttırılması, dağılımı değiştirmez.
2. Bir özelliğin her değerini aynı sabit miktarda azaltın veya artırın A dağılımını değiştirmez.
3. Her özellik değerini belirli sayıda azaltın veya artırın k varyansı sırasıyla azaltır veya artırır. k 2 kez ve standart sapma içinde k bir kere.
4. Bir özelliğin rastgele bir değere göre dağılımı, ortalama ve isteğe bağlı değerler arasındaki farkın kare başına aritmetik ortalamasına göre dağılımdan her zaman daha büyüktür:
![]()
Eğer A 0 ise aşağıdaki eşitliğe ulaşırız:
yani, özelliğin varyansı, karakteristik değerlerin ortalama karesi ile ortalamanın karesi arasındaki farka eşittir.
Varyans hesaplanırken her özellik bağımsız olarak veya diğerleriyle birlikte kullanılabilir.
Varyansı hesaplama prosedürü basittir:
1) belirlemek aritmetik ortalama :
2) aritmetik ortalamanın karesi:

3) serinin her bir varyantının sapmasının karesi:
X Ben 2 .
4) seçeneklerin karelerinin toplamını bulun:
5) seçeneklerin karelerinin toplamını sayılarına bölün, yani. ortalama kareyi belirleyin:
6) Karakteristiğin ortalama karesi ile ortalamanın karesi arasındaki farkı belirleyin:
Örnek 3.1İşçi verimliliğine ilişkin aşağıdaki veriler mevcuttur:

Aşağıdaki hesaplamaları yapalım:
![]()
Adımlar
Örnek varyansının hesaplanması
-
Örnek değerleri kaydedin.Çoğu durumda istatistikçiler yalnızca belirli popülasyonların örneklerine erişebilir. Örneğin, kural olarak, istatistikçiler Rusya'daki tüm arabaların toplamını korumanın maliyetini analiz etmiyorlar - birkaç bin arabadan oluşan rastgele bir örneği analiz ediyorlar. Böyle bir örnek, bir arabanın ortalama maliyetini belirlemeye yardımcı olacaktır, ancak büyük olasılıkla ortaya çıkan değer gerçek değerden uzak olacaktır.
- Örneğin, bir kafede 6 gün boyunca satılan çörek sayısını rastgele sırayla analiz edelim. Örnek şuna benzer: 17, 15, 23, 7, 9, 13. Bu bir popülasyon değil örnektir çünkü kafenin açık olduğu her gün için satılan çöreklere ilişkin verimiz yoktur.
- Size bir değer örneği yerine bir popülasyon verildiyse bir sonraki bölüme geçin.
-
Örnek varyansını hesaplamak için bir formül yazın. Dağılım, belirli bir miktardaki değerlerin yayılımının bir ölçüsüdür. Varyans değeri sıfıra ne kadar yakınsa değerler birbirine o kadar yakın gruplanır. Bir değer örneğiyle çalışırken varyansı hesaplamak için aşağıdaki formülü kullanın:
- s 2 (\displaystyle s^(2)) = ∑[(x ben (\displaystyle x_(i))- X) 2 (\displaystyle ^(2))] / (n-1)
- s 2 (\displaystyle s^(2))– bu dağılımdır. Dağılım birim kare cinsinden ölçülür.
- x ben (\displaystyle x_(i))– numunedeki her değer.
- x ben (\displaystyle x_(i)) x̅'i çıkarmanız, karesini almanız ve ardından sonuçları eklemeniz gerekir.
- x̅ – örnek ortalaması (örnek ortalaması).
- n – örnekteki değerlerin sayısı.
-
Örnek ortalamasını hesaplayın. X̅ olarak gösterilir. Örnek ortalaması basit bir aritmetik ortalama olarak hesaplanır: örnekteki tüm değerleri toplayın ve ardından sonucu örnekteki değer sayısına bölün.
- Örneğimizde örnekteki değerleri toplayın: 15 + 17 + 23 + 7 + 9 + 13 = 84
Şimdi sonucu örnekteki değer sayısına bölün (örneğimizde 6 tane var): 84 ÷ 6 = 14.
Örnek ortalama x̅ = 14. - Örnek ortalaması, örnekteki değerlerin etrafında dağıldığı merkezi değerdir. Örnek kümedeki değerler örnek ortalamanın etrafında ise varyans küçüktür; aksi takdirde varyans büyüktür.
- Örneğimizde örnekteki değerleri toplayın: 15 + 17 + 23 + 7 + 9 + 13 = 84
-
Örnek ortalamasını örnekteki her değerden çıkarın.Şimdi farkı hesaplayın x ben (\displaystyle x_(i))- x̅, nerede x ben (\displaystyle x_(i))– numunedeki her değer. Elde edilen her sonuç, belirli bir değerin örneklem ortalamasından ne kadar saptığını, yani bu değerin örneklem ortalamasından ne kadar uzak olduğunu gösterir.
- Örneğimizde:
x 1 (\displaystyle x_(1))- x = 17 - 14 = 3
x 2 (\displaystyle x_(2))- x̅ = 15 - 14 = 1
x 3 (\displaystyle x_(3))- x = 23 - 14 = 9
x 4 (\displaystyle x_(4))- x̅ = 7 - 14 = -7
x 5 (\displaystyle x_(5))- x̅ = 9 - 14 = -5
x 6 (\displaystyle x_(6))- x̅ = 13 - 14 = -1 - Toplamlarının sıfıra eşit olması gerektiğinden elde edilen sonuçların doğruluğunu kontrol etmek kolaydır. Bu, ortalamanın tanımıyla ilgilidir, çünkü negatif değerler (ortalamadan daha küçük değerlere olan mesafeler) pozitif değerlerle (ortalamadan daha büyük değerlere olan mesafeler) tamamen dengelenir.
- Örneğimizde:
-
Yukarıda belirtildiği gibi farkların toplamı x ben (\displaystyle x_(i))- x̅ sıfıra eşit olmalıdır. Bu, ortalama varyansın her zaman sıfır olduğu anlamına gelir ve bu da belirli bir miktardaki değerlerin yayılımı hakkında herhangi bir fikir vermez. Bu sorunu çözmek için her farkın karesini alın x ben (\displaystyle x_(i))- X. Bu, yalnızca pozitif sayılar elde etmenize neden olur ve bunların toplamı hiçbir zaman 0'a eşit olmaz.
- Örneğimizde:
(x 1 (\displaystyle x_(1))- X) 2 = 3 2 = 9 (\displaystyle ^(2)=3^(2)=9)
(x 2 (\displaystyle (x_(2))- X) 2 = 1 2 = 1 (\displaystyle ^(2)=1^(2)=1)
9 2 = 81
(-7) 2 = 49
(-5) 2 = 25
(-1) 2 = 1 - Farkın karesini buldunuz - x̅) 2 (\displaystyle ^(2))Örnekteki her değer için.
- Örneğimizde:
-
Farkların karelerinin toplamını hesaplayın. Yani formülün şu şekilde yazılan kısmını bulun: ∑[( x ben (\displaystyle x_(i))- X) 2 (\displaystyle ^(2))] Burada Σ işareti her değer için kare farkların toplamı anlamına gelir x ben (\displaystyle x_(i))örnekte. Karesel farkları zaten buldunuz (x ben (\displaystyle (x_(i))- X) 2 (\displaystyle ^(2)) her değer için x ben (\displaystyle x_(i))örnekte; şimdi sadece bu kareleri ekleyin.
- Örneğimizde: 9 + 1 + 81 + 49 + 25 + 1 = 166 .
-
Sonucu n - 1'e bölün; burada n, örnekteki değerlerin sayısıdır. Bir süre önce istatistikçiler örneklem varyansını hesaplamak için sonucu basitçe n'ye bölüyordu; bu durumda, belirli bir numunenin varyansını tanımlamak için ideal olan kare varyansın ortalamasını elde edersiniz. Ancak herhangi bir örneğin, değerler popülasyonunun yalnızca küçük bir kısmı olduğunu unutmayın. Başka bir örnek alıp aynı hesaplamaları yaparsanız farklı bir sonuç elde edersiniz. Görünen o ki, (sadece n yerine) n - 1'e bölmek, ilgilendiğiniz şey olan popülasyon varyansının daha doğru bir tahminini veriyor. N – 1'e bölme yaygın hale geldi, bu nedenle örnek varyansını hesaplama formülüne dahil edildi.
- Örneğimizde örnek 6 değer içermektedir, yani n = 6.
Örneklem varyansı = s 2 = 166 6 − 1 = (\displaystyle s^(2)=(\frac (166)(6-1))=) 33,2
- Örneğimizde örnek 6 değer içermektedir, yani n = 6.
-
Varyans ve standart sapma arasındaki fark. Formülün bir üs içerdiğini, dolayısıyla dağılımın analiz edilen değerin birim karesi cinsinden ölçüldüğünü unutmayın. Bazen böyle bir büyüklüğün işletilmesi oldukça zordur; bu gibi durumlarda varyansın kareköküne eşit olan standart sapmayı kullanın. Bu nedenle örneklem varyansı şu şekilde gösterilir: s 2 (\displaystyle s^(2)) ve numunenin standart sapması şu şekildedir: s (\displaystyle s).
- Örneğimizde numunenin standart sapması: s = √33,2 = 5,76.
Nüfus Varyansının Hesaplanması
-
Bazı değer kümelerini analiz edin. Set, söz konusu miktarın tüm değerlerini içerir. Örneğin, Leningrad bölgesi sakinlerinin yaşını inceliyorsanız, toplam bu bölgenin tüm sakinlerinin yaşını içerir. Bir popülasyonla çalışırken bir tablo oluşturularak nüfus değerlerinin bu tabloya girilmesi önerilir. Aşağıdaki örneği düşünün:
- Belirli bir odada 6 adet akvaryum bulunmaktadır. Her akvaryumda aşağıdaki sayıda balık bulunur:
x 1 = 5 (\displaystyle x_(1)=5)
x 2 = 5 (\displaystyle x_(2)=5)
x 3 = 8 (\displaystyle x_(3)=8)
x 4 = 12 (\displaystyle x_(4)=12)
x 5 = 15 (\displaystyle x_(5)=15)
x 6 = 18 (\displaystyle x_(6)=18)
- Belirli bir odada 6 adet akvaryum bulunmaktadır. Her akvaryumda aşağıdaki sayıda balık bulunur:
-
Popülasyon varyansını hesaplamak için bir formül yazın. Popülasyon belirli bir miktarın tüm değerlerini içerdiğinden aşağıdaki formül popülasyon varyansının tam değerini elde etmenizi sağlar. Nüfus varyansını örneklem varyansından (ki bu yalnızca bir tahmindir) ayırt etmek için istatistikçiler çeşitli değişkenler kullanır:
- σ 2 (\displaystyle ^(2)) = (∑(x ben (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2)))/N
- σ 2 (\displaystyle ^(2))– nüfus dağılımı (“sigma kare” olarak okunur). Dağılım birim kare cinsinden ölçülür.
- x ben (\displaystyle x_(i))– her değer kendi bütünlüğü içinde.
- Σ – toplam işareti. Yani her değerden x ben (\displaystyle x_(i))μ'yu çıkarmanız, karesini almanız ve ardından sonuçları eklemeniz gerekir.
- μ – nüfus ortalaması.
- n – popülasyondaki değerlerin sayısı.
-
Nüfus ortalamasını hesaplayın. Bir popülasyonla çalışırken ortalaması μ (mu) olarak gösterilir. Popülasyon ortalaması basit bir aritmetik ortalama olarak hesaplanır: popülasyondaki tüm değerleri toplayın ve ardından sonucu popülasyondaki değer sayısına bölün.
- Ortalamaların her zaman aritmetik ortalama olarak hesaplanmadığını unutmayın.
- Örneğimizde popülasyonun anlamı: μ = 5 + 5 + 8 + 12 + 15 + 18 6 (\displaystyle (\frac (5+5+8+12+15+18)(6))) = 10,5
-
Popülasyondaki her değerden popülasyon ortalamasını çıkarın. Fark değeri sıfıra ne kadar yakınsa, spesifik değer popülasyon ortalamasına o kadar yakındır. Popülasyondaki her değer ile ortalaması arasındaki farkı bulun ve değerlerin dağılımı hakkında ilk fikri elde edeceksiniz.
- Örneğimizde:
x 1 (\displaystyle x_(1))- μ = 5 - 10,5 = -5,5
x 2 (\displaystyle x_(2))- μ = 5 - 10,5 = -5,5
x 3 (\displaystyle x_(3))- μ = 8 - 10,5 = -2,5
x 4 (\displaystyle x_(4))- μ = 12 - 10,5 = 1,5
x 5 (\displaystyle x_(5))- μ = 15 - 10,5 = 4,5
x 6 (\displaystyle x_(6))- μ = 18 - 10,5 = 7,5
- Örneğimizde:
-
Elde edilen her sonucun karesini alın. Fark değerleri hem pozitif hem de negatif olacaktır; Bu değerler bir sayı doğrusu üzerinde çizilirse popülasyon ortalamasının sağında ve solunda yer alacaktır. Bu, varyansın hesaplanması için iyi değildir çünkü pozitif ve negatif sayılar birbirini iptal eder. Yani tamamen pozitif sayılar elde etmek için her farkın karesini alın.
- Örneğimizde:
(x ben (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2)) her popülasyon değeri için (i = 1'den i = 6'ya):
(-5,5)2 (\displaystyle ^(2)) = 30,25
(-5,5)2 (\displaystyle ^(2)), Nerede x n (\displaystyle x_(n))– popülasyondaki son değer. - Elde edilen sonuçların ortalama değerini hesaplamak için toplamlarını bulup n'ye bölmeniz gerekir:(( x 1 (\displaystyle x_(1)) - μ) 2 (\displaystyle ^(2)) + (x 2 (\displaystyle x_(2)) - μ) 2 (\displaystyle ^(2)) + ... + (x n (\displaystyle x_(n)) - μ) 2 (\displaystyle ^(2)))/N
- Şimdi yukarıdaki açıklamayı değişkenleri kullanarak yazalım: (∑( x ben (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2))) / n ve popülasyon varyansını hesaplamak için bir formül elde edin.
- Örneğimizde:
Popülasyon incelenen özelliğe göre gruplara ayrılırsa, bu popülasyon için aşağıdaki varyans türleri hesaplanabilir: toplam, grup (grup içi), grup ortalaması (grup içi ortalama), gruplar arası.
Başlangıçta, incelenen özelliğin toplam varyasyonunun ne kadarının gruplar arası varyasyon olduğunu gösteren belirleme katsayısını hesaplar; gruplandırma özelliğinden dolayı:
Ampirik korelasyon ilişkisi, gruplama (faktöriyel) ile performans özellikleri arasındaki bağlantının yakınlığını karakterize eder.
Ampirik korelasyon oranı 0'dan 1'e kadar değerler alabilir.
Ampirik korelasyon oranına dayalı olarak bağlantının yakınlığını değerlendirmek için Chaddock ilişkilerini kullanabilirsiniz:
Örnek 4.Çeşitli mülkiyet biçimlerine sahip tasarım ve araştırma kuruluşlarının iş performansına ilişkin aşağıdaki veriler mevcuttur:
Tanımlamak:
1) toplam varyans;
2) grup farklılıkları;
3) grup varyanslarının ortalaması;
4) gruplar arası varyans;
5) varyansların eklenmesi kuralına dayalı toplam varyans;
6) belirleme katsayısı ve ampirik korelasyon oranı.
Sonuç çıkarın.
Çözüm:
1. İki tür mülkiyete sahip işletmelerin gerçekleştirdiği ortalama iş hacmini belirleyelim:
Toplam varyansı hesaplayalım:
![]()
2. Grup ortalamalarını belirleyin:
![]() milyon ruble;
milyon ruble;
![]() milyon ruble
milyon ruble
Grup farklılıkları:
![]() ;
;
3. Grup varyanslarının ortalamasını hesaplayın:
4. Gruplar arası varyansı belirleyelim:
5. Varyans ekleme kuralına göre toplam varyansı hesaplayın:
6. Belirleme katsayısını belirleyelim:
![]() .
.
Böylece tasarım ve etüt kuruluşlarının gerçekleştirdiği iş hacmi %22 oranında işletmelerin mülkiyet şekline bağlıdır.
Ampirik korelasyon oranı aşağıdaki formül kullanılarak hesaplanır
![]() .
.
Hesaplanan göstergenin değeri, iş hacminin işletmenin mülkiyet biçimine bağımlılığının küçük olduğunu gösterir.
Örnek 5.Üretim alanlarının teknolojik disiplini üzerine yapılan araştırma sonucunda aşağıdaki veriler elde edildi:
Belirleme katsayısını belirleyin
Beklenti ve varyans, bir rastgele değişkenin en yaygın kullanılan sayısal özellikleridir. Dağıtımın en önemli özelliklerini karakterize ederler: konumu ve saçılma derecesi. Pek çok pratik problemde, bir rastgele değişkenin tam ve kapsamlı bir karakteristiği olan dağıtım yasası ya hiç elde edilemez ya da hiç ihtiyaç duyulmaz. Bu durumlarda, sayısal özellikler kullanılarak rastgele bir değişkenin yaklaşık tanımıyla sınırlandırılır.
Beklenen değere genellikle basitçe rastgele bir değişkenin ortalama değeri denir. Rastgele bir değişkenin dağılımı, dağılımın bir özelliğidir, yani rastgele bir değişkenin matematiksel beklentisi etrafında yayılmasıdır.
Ayrık bir rastgele değişkenin beklentisi
Önce ayrık bir rastgele değişkenin dağılımının mekanik yorumuna dayanarak matematiksel beklenti kavramına yaklaşalım. Birim kütlenin x eksenindeki noktalar arasında dağıtılmasına izin verin X1 , X 2 , ..., X N ve her maddi noktanın buna karşılık gelen bir kütlesi vardır. P1 , P 2 , ..., P N. Kütleleri dikkate alınarak tüm malzeme noktaları sisteminin konumunu karakterize eden apsis ekseni üzerinde bir nokta seçilmesi gerekir. Maddi noktalar sisteminin kütle merkezini böyle bir nokta olarak almak doğaldır. Bu rastgele değişkenin ağırlıklı ortalamasıdır X, her noktanın apsisi XBen karşılık gelen olasılığa eşit bir “ağırlık” ile girer. Bu şekilde elde edilen rastgele değişkenin ortalama değeri X matematiksel beklenti denir.
Ayrık bir rastgele değişkenin matematiksel beklentisi, tüm olası değerlerinin çarpımlarının ve bu değerlerin olasılıklarının toplamıdır:

Örnek 1. Kazan-kazan piyangosu düzenlendi. 400'ü 10 ruble olmak üzere 1000 kazanç var. Her biri 300-20 ruble. Her biri 200 - 100 ruble. ve her biri 100 - 200 ruble. Bir bilet alan birinin ortalama kazancı nedir?
Çözüm. 10*400 + 20*300 + 100*200 + 200*100 = 50.000 ruble olan toplam kazanç miktarını 1000'e (toplam kazanç miktarı) bölersek ortalama kazancı buluruz. Sonra 50000/1000 = 50 ruble elde ederiz. Ancak ortalama kazancı hesaplamak için kullanılan ifade aşağıdaki biçimde sunulabilir:

Öte yandan bu koşullar altında kazanma büyüklüğü 10, 20, 100 ve 200 ruble değerlerini alabilen rastgele bir değişkendir. sırasıyla 0,4'e eşit olasılıklarla; 0,3; 0,2; 0.1. Bu nedenle, beklenen ortalama kazanç, kazanç büyüklüğünün ve bunları alma olasılığının çarpımlarının toplamına eşittir.
Örnek 2. Yayıncı yeni bir kitap yayınlamaya karar verdi. Kitabı 280 rubleye satmayı planlıyor, bunun 200'ünü kendisine, 50'sini kitapçıya ve 30'unu yazara alacak. Tablo, bir kitabın basım maliyetleri ve kitabın belirli sayıda nüshasının satılma olasılığı hakkında bilgi sağlar.
Yayıncının beklenen kârını bulun.
Çözüm. Rastgele değişken "kar", satışlardan elde edilen gelir ile maliyetlerin maliyeti arasındaki farka eşittir. Örneğin bir kitabın 500 nüshası satılırsa satıştan elde edilen gelir 200 * 500 = 100.000, basım maliyeti ise 225.000 ruble olur. Böylece yayıncı 125.000 ruble zararla karşı karşıya kalıyor. Aşağıdaki tablo, rastgele değişken - kârın beklenen değerlerini özetlemektedir:
| Sayı | Kâr XBen | Olasılık PBen | XBen P Ben |
| 500 | -125000 | 0,20 | -25000 |
| 1000 | -50000 | 0,40 | -20000 |
| 2000 | 100000 | 0,25 | 25000 |
| 3000 | 250000 | 0,10 | 25000 |
| 4000 | 400000 | 0,05 | 20000 |
| Toplam: | 1,00 | 25000 |
Böylece yayıncının kârının matematiksel beklentisini elde ederiz:
![]() .
.
Örnek 3. Tek atışta vurma ihtimali P= 0,2. Vuruş sayısının 5'e eşit olduğuna dair matematiksel bir beklenti sağlayan mermi tüketimini belirleyin.
Çözüm. Şu ana kadar kullandığımız aynı matematiksel beklenti formülünden, X- kabuk tüketimi:
![]() .
.
Örnek 4. Rastgele bir değişkenin matematiksel beklentisini belirleme X Her atışta bir vuruş olasılığı varsa, üç atıştaki vuruş sayısı P = 0,4 .
İpucu: rastgele değişken değerlerinin olasılığını bulun Bernoulli'nin formülü .
Matematiksel beklentinin özellikleri
Matematiksel beklentinin özelliklerini ele alalım.
Mülk 1. Sabit bir değerin matematiksel beklentisi bu sabite eşittir:
Mülk 2. Sabit faktör matematiksel beklenti işaretinden çıkarılabilir:
![]()
Mülk 3. Rastgele değişkenlerin toplamının (farkının) matematiksel beklentisi, matematiksel beklentilerinin toplamına (farkına) eşittir:
Mülk 4. Rastgele değişkenlerin bir ürününün matematiksel beklentisi, matematiksel beklentilerinin çarpımına eşittir:
Mülk 5. Bir rastgele değişkenin tüm değerleri ise X aynı sayıda azalma (artış) İLE, o zaman matematiksel beklentisi aynı sayı kadar azalacaktır (artacaktır):
![]()
Kendinizi yalnızca matematiksel beklentiyle sınırlayamadığınızda
Çoğu durumda, yalnızca matematiksel beklenti bir rastgele değişkeni yeterince karakterize edemez.
Rastgele değişkenler olsun X Ve e aşağıdaki dağıtım yasalarıyla verilmektedir:
| Anlam X | Olasılık |
| -0,1 | 0,1 |
| -0,01 | 0,2 |
| 0 | 0,4 |
| 0,01 | 0,2 |
| 0,1 | 0,1 |
| Anlam e | Olasılık |
| -20 | 0,3 |
| -10 | 0,1 |
| 0 | 0,2 |
| 10 | 0,1 |
| 20 | 0,3 |
Bu niceliklerin matematiksel beklentileri aynıdır - sıfıra eşittir:


Ancak dağılım şekilleri farklıdır. Rastgele değişken X yalnızca matematiksel beklentiden çok az farklı olan değerleri alabilir ve rastgele değişken e matematiksel beklentiden önemli ölçüde sapan değerler alabilir. Benzer bir örnek: Ortalama ücret, yüksek ve düşük ücretli çalışanların payını değerlendirmeyi mümkün kılmıyor. Başka bir deyişle, matematiksel beklentiden, en azından ortalama olarak, ondan ne tür sapmaların mümkün olduğuna karar verilemez. Bunu yapmak için rastgele değişkenin varyansını bulmanız gerekir.
Ayrık bir rastgele değişkenin varyansı
Varyans ayrık rastgele değişken X matematiksel beklentiden sapmanın karesinin matematiksel beklentisi denir:

Rastgele bir değişkenin standart sapması X varyansının karekökünün aritmetik değerine denir:
![]() .
.
Örnek 5. Rastgele değişkenlerin varyanslarını ve standart sapmalarını hesaplama X Ve e dağıtım yasaları yukarıdaki tablolarda verilmiştir.
Çözüm. Rastgele değişkenlerin matematiksel beklentileri X Ve e yukarıda da görüldüğü gibi sıfıra eşittir. Dispersiyon formülüne göre e(X)=e(sen)=0 şunu elde ederiz:


Daha sonra rastgele değişkenlerin standart sapmaları X Ve e makyaj yapmak
![]() .
.
Böylece aynı matematiksel beklentilerle rastgele değişkenin varyansı Xçok küçük ama rastgele bir değişken e- önemli. Bu, dağılımlarındaki farklılıkların bir sonucudur.
Örnek 6. Yatırımcının 4 alternatif yatırım projesi bulunmaktadır. Tablo, bu projelerde beklenen karı karşılık gelen olasılıkla özetlemektedir.
| Proje 1 | Proje 2 | Proje 3 | Proje 4 |
| 500, P=1 | 1000, P=0,5 | 500, P=0,5 | 500, P=0,5 |
| 0, P=0,5 | 1000, P=0,25 | 10500, P=0,25 | |
| 0, P=0,25 | 9500, P=0,25 |
Her alternatif için matematiksel beklentiyi, varyansı ve standart sapmayı bulun.
Çözüm. 3. alternatif için bu değerlerin nasıl hesaplandığını gösterelim:
Tablo tüm alternatifler için bulunan değerleri özetlemektedir.
Tüm alternatifler aynı matematiksel beklentilere sahiptir. Bu, uzun vadede herkesin aynı gelire sahip olduğu anlamına gelir. Standart sapma bir risk ölçüsü olarak yorumlanabilir; ne kadar yüksek olursa, yatırımın riski de o kadar büyük olur. Fazla risk istemeyen bir yatırımcı, standart sapması en küçük (0) olduğu için proje 1'i seçecektir. Eğer yatırımcı kısa vadede risk ve yüksek getiriyi tercih ediyorsa, standart sapması en büyük olan projeyi (Proje 4) seçecektir.
Dispersiyon özellikleri
Dispersiyonun özelliklerini sunalım.
Mülk 1. Sabit bir değerin varyansı sıfırdır:
Mülk 2. Sabit faktör, karesi alınarak dağılım işaretinden çıkarılabilir:
![]() .
.
Mülk 3. Rastgele bir değişkenin varyansı, bu değerin karesinin matematiksel beklentisine eşittir; bu değerden, değerin kendisinin matematiksel beklentisinin karesi çıkarılır:
![]() ,
,
Nerede ![]() .
.
Mülk 4. Rastgele değişkenlerin toplamının (farkının) varyansı, varyanslarının toplamına (farkına) eşittir:
Örnek 7. Ayrık bir rastgele değişkenin olduğu bilinmektedir. X yalnızca iki değer alır: −3 ve 7. Ayrıca matematiksel beklenti de bilinmektedir: e(X) = 4 . Ayrık bir rastgele değişkenin varyansını bulun.
Çözüm. ile belirtelim P rastgele bir değişkenin değer alma olasılığı X1 = −3 . O zaman değerin olasılığı X2 = 7 1 olacak – P. Matematiksel beklentinin denklemini çıkaralım:
e(X) = X 1 P + X 2 (1 − P) = −3P + 7(1 − P) = 4 ,
olasılıkları nereden alıyoruz: P= 0,3 ve 1 − P = 0,7 .
Rastgele bir değişkenin dağılım yasası:
| X | −3 | 7 |
| P | 0,3 | 0,7 |
Bu rastgele değişkenin varyansını, dağılımın 3. özelliğindeki formülü kullanarak hesaplıyoruz:
D(X) = 2,7 + 34,3 − 16 = 21 .
Bir rastgele değişkenin matematiksel beklentisini kendiniz bulun ve ardından çözüme bakın.
Örnek 8. Ayrık rastgele değişken X yalnızca iki değer alır. 0,4 olasılıkla 3 değerinden büyük olanı kabul eder. Ayrıca rastgele değişkenin varyansı da bilinmektedir. D(X) = 6 . Bir rastgele değişkenin matematiksel beklentisini bulun.
Örnek 9. Torbada 6 beyaz ve 4 siyah top vardır. Torbadan 3 top çekiliyor. Çekilen toplar arasındaki beyaz topların sayısı ayrık bir rastgele değişkendir X. Bu rastgele değişkenin matematiksel beklentisini ve varyansını bulun.
Çözüm. Rastgele değişken X 0, 1, 2, 3 değerlerini alabilir. Karşılık gelen olasılıklar şu şekilde hesaplanabilir: olasılık çarpım kuralı. Rastgele bir değişkenin dağılım yasası:
| X | 0 | 1 | 2 | 3 |
| P | 1/30 | 3/10 | 1/2 | 1/6 |
Dolayısıyla bu rastgele değişkenin matematiksel beklentisi:
M(X) = 3/10 + 1 + 1/2 = 1,8 .
Belirli bir rastgele değişkenin varyansı:
D(X) = 0,3 + 2 + 1,5 − 3,24 = 0,56 .
Sürekli rastgele değişkenin beklentisi ve varyansı
Sürekli bir rastgele değişken için, matematiksel beklentinin mekanik yorumu aynı anlamı koruyacaktır: x ekseni üzerinde yoğunlukla sürekli olarak dağıtılan birim kütlenin kütle merkezi F(X). Fonksiyon argümanı olan ayrık bir rastgele değişkenden farklı olarak XBen aniden değişir; sürekli bir rastgele değişken için argüman sürekli olarak değişir. Ancak sürekli bir rastgele değişkenin matematiksel beklentisi aynı zamanda ortalama değeriyle de ilgilidir.
Sürekli bir rastgele değişkenin matematiksel beklentisini ve varyansını bulmak için belirli integralleri bulmanız gerekir. . Sürekli bir rastgele değişkenin yoğunluk fonksiyonu verilirse, o zaman doğrudan integrale girer. Bir olasılık dağılım fonksiyonu verilirse, bunun farklılığını alarak yoğunluk fonksiyonunu bulmanız gerekir.
Sürekli bir rastgele değişkenin olası tüm değerlerinin aritmetik ortalamasına denir. matematiksel beklenti veya ile gösterilir.
Gruplandırılmış veriler için artık varyans- grup içi varyansların ortalaması:Burada σ 2 j, j'inci grubun grup içi varyansıdır.
Gruplandırılmamış veriler için artık varyans– yaklaşıklık doğruluğunun ölçüsü, yani regresyon çizgisinin orijinal verilere yaklaşımı: 
burada y(t) trend denklemini kullanan tahmindir; y t – başlangıç dinamikleri serisi; n – puan sayısı; p – regresyon denklemi katsayılarının sayısı (açıklayıcı değişkenlerin sayısı).
Bu örnekte buna denir tarafsız varyans tahmincisi.
Örnek No.1. Bir derneğin üç işletmesindeki işçilerin tarife kategorilerine göre dağılımı aşağıdaki verilerle karakterize edilir:
| İşçi tarife kategorisi | İşletmedeki işçi sayısı | ||
| işletme 1 | işletme 2 | işletme 3 | |
| 1 | 50 | 20 | 40 |
| 2 | 100 | 80 | 60 |
| 3 | 150 | 150 | 200 |
| 4 | 350 | 300 | 400 |
| 5 | 200 | 150 | 250 |
| 6 | 150 | 100 | 150 |
Tanımlamak:
1. her işletme için farklılık (grup içi farklılıklar);
2. grup içi varyansların ortalaması;
3. gruplar arası dağılım;
4. toplam varyans.
Çözüm.
Sorunu çözmeye başlamadan önce hangi özelliğin etkili, hangisinin faktöriyel olduğunu bulmak gerekir. Söz konusu örnekte, sonuç niteliği "Tarife kategorisi", faktör niteliği ise "İşletmenin numarası (adı)"dır.
Daha sonra grup ortalamasını ve grup içi varyansları hesaplamanın gerekli olduğu üç grubumuz (işletmelerimiz) var:

| Girişim | Grup ortalaması, | Grup içi varyans, |
| 1 | 4 | 1,8 |
Grup içi varyansların ortalaması ( artık varyans) aşağıdaki formül kullanılarak hesaplanacaktır:

nerede hesaplayabilirsiniz:

veya:

Daha sonra:
Toplam varyans şuna eşit olacaktır: s 2 = 1,6 + 0 = 1,6.
Toplam varyans aşağıdaki iki formülden biri kullanılarak da hesaplanabilir:
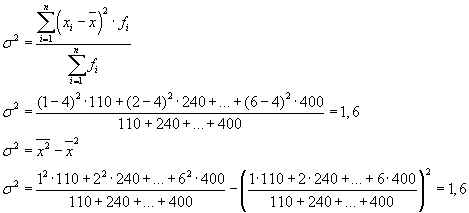
Pratik problemleri çözerken, genellikle yalnızca iki alternatif değer alan bir özellik ile uğraşmak gerekir. Bu durumda bir özelliğin belirli bir değerinin ağırlığından değil, bütünlük içindeki payından bahsediyoruz. İncelenen özelliğe sahip nüfus birimlerinin oranı “ ile gösteriliyorsa R"ve sahip olmayanlar - aracılığıyla " Q", o zaman varyans aşağıdaki formül kullanılarak hesaplanabilir:
s 2 = p×q
Örnek No. 2. Bir ekipteki altı işçinin üretim verilerine dayanarak, gruplar arası varyansı belirleyin ve toplam varyansın 12,2 olması durumunda iş vardiyasının işgücü verimliliği üzerindeki etkisini değerlendirin.
| Ekip çalışanı no. | İşçi çıktısı, adet. | |
| ilk vardiyada | ikinci vardiyada | |
| 1 | 18 | 13 |
| 2 | 19 | 14 |
| 3 | 22 | 15 |
| 4 | 20 | 17 |
| 5 | 24 | 16 |
| 6 | 23 | 15 |
Çözüm. İlk veriler
| X | f1 | f2 | f3 | f4 | f5 | f6 | Toplam |
| 1 | 18 | 19 | 22 | 20 | 24 | 23 | 126 |
| 2 | 13 | 14 | 15 | 17 | 16 | 15 | 90 |
| Toplam | 31 | 33 | 37 | 37 | 40 | 38 |
Daha sonra grup ortalamasını ve grup içi varyansları hesaplamanın gerekli olduğu 6 grubumuz var.
1. Her grubun ortalama değerlerini bulun.
2. Her grubun ortalama karesini bulun.
Hesaplama sonuçlarını bir tabloda özetleyelim:
| Grup numarası | Grup ortalaması | Grup içi varyans |
| 1 | 1.42 | 0.24 |
| 2 | 1.42 | 0.24 |
| 3 | 1.41 | 0.24 |
| 4 | 1.46 | 0.25 |
| 5 | 1.4 | 0.24 |
| 6 | 1.39 | 0.24 |
3. Grup içi varyans gruplandırmanın altında yatan faktör hariç, üzerindeki tüm faktörlerin etkisi altında bir grup içinde incelenen (sonuçsal) özelliğin değişimini (varyasyonunu) karakterize eder:
Grup içi varyansların ortalamasını aşağıdaki formülü kullanarak hesaplıyoruz:
4. Gruplararası varyans Grubun temelini oluşturan bir faktörün (faktöriyel karakteristik) etkisi altında çalışılan (sonuçsal) özelliğin değişimini (varyasyonunu) karakterize eder.
Gruplar arası varyansı şu şekilde tanımlarız:
Nerede
Daha sonra
Toplam varyansİstisnasız tüm faktörlerin (faktöriyel özellikler) etkisi altında çalışılan (sonuçsal) özelliğin değişimini (varyasyonunu) karakterize eder. Problemin koşullarına göre 12,2'ye eşittir.
Ampirik korelasyon ilişkisi ortaya çıkan özelliğin toplam değişkenliğinin ne kadarının incelenen faktörden kaynaklandığını ölçer. Faktör varyansının toplam varyansa oranı:
Ampirik korelasyon ilişkisini tanımlıyoruz:
Karakteristikler arasındaki bağlantılar zayıf ve güçlü (yakın) olabilir. Kriterleri Chaddock ölçeğine göre değerlendirilir:
0,1 0,3 0,5 0,7 0,9 Örneğimizde Y özelliği ile X faktörü arasındaki ilişki zayıf
Belirleme katsayısı.
Belirleme katsayısını belirleyelim:
Yani varyasyonun %0,67'si özellikler arasındaki farklılıklardan, %99,37'si ise diğer faktörlerden kaynaklanmaktadır.
Çözüm: bu durumda, işçilerin çıktısı belirli bir vardiyadaki çalışmaya bağlı değildir; İş vardiyasının işgücü üretkenliği üzerindeki etkisi önemli değildir ve başka faktörlerden kaynaklanmaktadır.
Örnek No. 3. Ortalama ücretler ve iki işçi grubu için değerinden sapmaların kareleri hakkındaki verilere dayanarak, varyansları toplama kuralını uygulayarak toplam varyansı bulun:
Çözüm:Grup içi varyansların ortalaması
Gruplar arası varyansı şu şekilde tanımlarız:
Toplam varyans şöyle olacaktır: 480 + 13824 = 14304








