Değişken değişimi olan denklemler. Değişken yöntemini değiştirerek entegrasyon

Matematik, mantıksal zihnin ideal dünyaya göz atabileceği bir deliktir.

Krotov Victor

Okulda cebir dersinde rasyonel denklemler önde gelen bir yer tutar. Diğer konulara nazaran onların çalışmalarına daha fazla zaman ayrılır. Bunun temel nedeni denklemlerin yalnızca önemli teorik öneme sahip olması değil aynı zamanda birçok pratik amaca da hizmet etmesidir. Gerçek dünyadaki çok sayıda problem, çeşitli denklemlerin çözülmesinden kaynaklanmaktadır ve ancak bunları çözme yöntemlerinde ustalaştıktan sonra, bilim ve teknolojinin çeşitli sorularına yanıt bulacaksınız.

Rasyonel denklemleri çözme yeteneğini geliştirmek için öğrencinin bağımsız çalışması büyük önem taşımaktadır. Bununla birlikte, bağımsız çalışmaya geçmeden önce, rasyonel denklemleri çözmek için olası tüm yöntemleri açıkça bilmek ve pratikte uygulayabilmek gerekir.

Örnekler kullanarak ayrıntılı olarak inceleyelim. değişken değiştirme yöntemi Rasyonel denklemleri çözmek için.

Örnek 1.

(2x 2 – 3x + 1) 2 = 22x 2 – 33x + 1 denklemini çözün.

Çözüm.

Denklemi formda yeniden yazalım.

(2x 2 – 3x + 1) 2 = 11(2x 2 – 3x) + 1. Yerine koyma işlemi yapalım. 2x 2 – 3x = t olsun, o zaman denklem şu şekli alacaktır:

(t + 1) 2 = 11t + 1.

Şimdi parantezleri açıp benzerlerini verelim, şunu elde ederiz:

t2 + 2t + 1 = 11t + 1;

Ortaya çıkan tamamlanmamış ikinci dereceden denklemde, ortak faktörü parantezlerden çıkarırız ve şunu elde ederiz:

t = 0 veya t = 9.

Şimdi ters bir ikame yapmanız ve ortaya çıkan denklemlerin her birini çözmeniz gerekiyor:

2x 2 – 3x = 0 veya 2x 2 – 3x = 9

x(2x – 3) = 0 2x 2 – 3x – 9 = 0

x = 0 veya x = 3/2 x = 3 veya x = -3/2

Cevap: -1.5; 0; 1.5; 3.

Örnek 2.

(x 2 – 6x) 2 – 2(x – 3) 2 = 81 denklemini çözün.

Çözüm.

(a – b) 2 = a 2 – 2ab + b 2 karesi farkının formülünü uygulayalım. Orijinal denklemi formda yazalım.

(x 2 – 6x) 2 – 2(x 2 – 6x + 9) = 81. Şimdi yerine koyabilirsiniz.

x 2 – 6x = t olsun, o zaman denklem şöyle görünecektir:

t 2 – 2(t + 9) = 81.

t2 – 2t – 18 – 81 = 0;

t2 – 2t – 99 = 0.

Vieta teoremine göre ortaya çıkan denklemin kökleri -9 ve 11 sayıları olacaktır.

Ters yerine koyma işlemi yapalım:

x 2 – 6x = -9 veya x 2 – 6x = 11

x 2 – 6x + 9 = 0 x 2 – 6x – 11 = 0

(x – 3) 2 = 0 D = 80

x = 3 x 1 = 3 + 2√5; x 2 = 3 – 2√5.

Cevap: 3 – 2√5; 3; 3 + 2√5.

Örnek 3.

(x – 1)(x – 3)(x + 5)(x + 7) = 297 denklemini çözün ve köklerinin çarpımını bulun.

Çözüm.

Faktörleri gruplandırmanın ve parantez çiftlerini açmanın "kârlı" bir yolunu bulalım:

((x – 1)(x + 5))((x – 3)(x + 7)) = 297;

(x 2 + 5x – x – 5)(x 2 + 7x – 3x – 21) = 297;

(x 2 + 4x – 5)(x 2 + 4x – 21) = 297.

Yerine x 2 + 4x = t koyalım, o zaman denklem şöyle görünecektir:

(t – 5)(t – 21) = 297.

Parantezleri açalım ve benzer terimleri sunalım:

t2 – 21t – 5t + 105 = 297;

t2 – 26t – 192 = 0.

Vieta teoremini kullanarak ortaya çıkan denklemin köklerinin -6 ve 32 sayıları olacağını belirliyoruz.

Ters değiştirmeden sonra elimizde:

x 2 + 4x = -6 veya x 2 + 4x = 32

x 2 + 4x + 6 = 0 x 2 + 4x – 32 = 0

D = 16 – 24< 0 D = 16 + 128 > 0

Kök yok x 1 = -8; x 2 = 4

Köklerin çarpımını bulalım: -8 · 4 = -32.

Cevap: -32.

Örnek 4.

Denklemin köklerinin toplamını bulun (x 2 – 2x + 2) 2 + 3x(x 2 – 2x + 2) = 10x 2.

Çözüm.

x 2 – 2x + 2 = t olsun, o zaman denklem şu şekli alacaktır:

t 2 + 3xt – 10x2 = 0.

Ortaya çıkan denklemi t'ye göre ikinci dereceden olarak ele alalım.

D = (3x) 2 – 4 · (-10x 2) = 9x 2 + 40x 2 = 49x 2 ; ≥≤

t 1 = (-3x – 7x) / 2 ve t 2 = (-3x + 7x) / 2;

t1 = -5x ve t2 = 2x.

t = x 2 – 2x + 2 olduğundan, o zaman

x 2 – 2x + 2 = -5x veya x 2 – 2x + 2 = 2x. Ortaya çıkan denklemlerin her birini çözelim.

x 2 + 3x + 2 = 0 veya x 2 – 4x + 2 = 0.

Her iki denklemin de kökleri vardır çünkü D > 0.

Vieta teoremini kullanarak birinci denklemin kökleri toplamının -3, ikinci denklemin ise 4 olduğu sonucunu çıkarabiliriz. Orijinal denklemin kökleri toplamının -3 + 4 = 1 olduğunu buluruz.

Cevap: 1.

Örnek 5.

[-5; aralığına ait (x + 1) 4 + (x + 5) 4 = 32 denkleminin kökünü bulun; 10].

Çözüm.

x = t – 3 olsun, o zaman x + 1 = t – 2; x + 5 = t + 2 ve orijinal denklem şu şekli alır:

(t – 2) 4 + (t + 2) 4 = 32. İfadeleri dördüncü kuvvete yükseltmek için Pascal üçgenini kullanabilirsiniz (Şekil 1);

(t – 2) 4 = t 4 – 4t 3 2 + 6t 2 2 2 – 4t 2 3 + 2 4;

(t + 2) 4 = t 4 + 4t 3 2 + 6t 2 2 2 + 4t 2 3 + 2 4.

Benzer terimleri azalttıktan sonra şunu elde ederiz:

2t 4 – 2 6t 2 2 2 + 2 2 4 = 32;

t4 + 6t2 2 2 + 2 4 = 16;

t4 + 24t2 + 16 = 16;

t4 + 24t2 = 0;

t2(t2 + 24) = 0;

t = 0 veya t 2 = -24.

İkinci denklemin kökleri yoktur; bu, ters ikameden sonra bile t = 0 anlamına gelir

x = t – 3 = 0 – 3 = -3. -3 denkleminin kökü [-5; 10].

Cevap: -3.

Gördüğünüz gibi rasyonel denklemleri çözerken yukarıdaki formülleri bilmeniz ve doğru sayabilmeniz gerekir. Hatalar çoğunlukla yenisini seçerken ve ters ikame sırasında ortaya çıkar. Bunu önlemek için her eylemi ayrıntılı olarak açıklamanız gerekir, o zaman kararlarınızda hata olmayacaktır.

blog.site, materyalin tamamını veya bir kısmını kopyalarken, orijinal kaynağa bir bağlantı gereklidir.

Değişkenlerin değişimi yöntemini kullanarak denklem çözme

Hayattaki görevlerin çoğu

cebirsel denklemler olarak çözülür:

onları en basit şekline getiriyoruz.

L.N..

Dersin amacı: öğrencilerin eğitim faaliyetlerini, bir değişkenin ikamesi yöntemiyle daha yüksek dereceli denklemlerin tamamını çözme yöntemlerine hakim olmaları için organize etmek; Öğrencilere karşılıklı ve simetrik denklemlerin çözümüne yönelik kavram ve teknikleri tanıtmak.

Görevler:eğitici: değiştirme yöntemini kullanma yeteneğini geliştirmeye devam etmek

denklemleri çözerken değişken; farklı durumlarda denklemleri çözmek için aynı yöntemi görme yeteneğinin geliştirilmesi; standart dışı problemleri ve cebirsel denklemleri devlet eğitim standartlarını aşan bir düzeyde çözmek için yöntem ve teknikler hakkında bir fikir oluşturmak;

gelişmekte:öğrencilerin düşünmesinin gelişimi; hafıza gelişimi; gelişim

mantıksal düşünme, düşüncelerinizi açıkça formüle etme yeteneği; öğrencilerin hayal gücünü geliştirmek; sözlü konuşmanın gelişimi.

eğitici: gözlem becerilerinin eğitimi; temizlik eğitimi

tahtaya ve not defterine not alırken; Pratik çalışmaları gerçekleştirirken bağımsızlığı beslemek.

Ders ilerlemesi

Organizasyon anı.

Bilginin güncellenmesi ve sistemleştirilmesi.

Görev No.1. Bulmacayı çözün. Cevaplarınızı yalnızca yalın durumda yazın.

4.İkinci dereceden bir denklemin ifadesi nedir? (ayrımcı)

6. Denklemin gerçek eşitliğe dönüştüğü değişkenin değeri. (kök)

8. Formun denklemi
, Nerede
. (iki kareli)

9.İkinci dereceden denklemlerle ilgili Fransız matematikçi. (Vietnam)

10. Sol ve sağ tarafları tam sayı ifadeleri olan bir denklem. (tüm)

11. Aynı kök kümesine sahip tek değişkenli denklemler. (eş değer)

Dikey:

1. Denklemin köklerinin çok olması. (çözüm)

2. Denklemin çözümü
. (sıfır)

3. Değişken içeren eşitlik. (denklem)

5. b veya c katsayılarından birinin 0'a eşit olduğu ikinci dereceden denklem. (eksik)

7. Birinci katsayının bire eşit olduğu ikinci dereceden denklem. (verildi)

Bugün dersimizi neye adayacağız? ( Denklemleri çözme )

Görev No.2. Her grup için denklemleri nasıl çözersiniz?

CEVAPLAR: Grup 1) örnekleri en iyi şekilde, ortak faktörü parantezlerin dışına yerleştirerek veya kısaltılmış çarpma formülleri kullanarak çarpanlara ayırma yoluyla çözülür.

Grup 2) örnekleri en iyi şekilde gruplandırma ve çarpanlara ayırma yoluyla çözülür.

Grup 3) örnekleri, yeni bir değişken getirilerek ve ikinci dereceden bir denkleme geçilerek daha iyi çözülür.

1 Grup 1'deki örneklerde hangi faktörü parantez dışına çıkarırsınız?

CEVAPLAR:

Grup 2 örneklerindeki terimleri nasıl gruplandırırsınız?

CEVAPLAR:

Grup 3 örneklerindeki yeni değişkenle neyi kastediyorsunuz?

CEVAPLAR:

Bir polinomu nasıl çarpanlara ayırabilirsiniz?
?

CEVAPLAR: .

Bugün derste “Değişken yerine koyma yöntemini kullanarak denklemleri çözme” konusundaki bilginizi göstereceksiniz.

Dersin konusunu not defterlerinize yazın.

Bugün sınıfta daha yüksek dereceli denklemleri çözmenin yollarından birine bakacağız: değişken yerine koyma yöntemi; Karşılıklı ve simetrik denklemleri çözmeye yönelik kavram ve teknikleri tanıyalım.

Değişken oyuncu değişikliği yapma sanatı, hangi değişikliğin en anlamlı olduğunu ve başarıya daha hızlı yol açtığını görmektir.

Görev No.3.

Denklemi çözün.(2 öğrenci tahtadaki görevi aynı anda çözer.)

A) (Birinci öğrenci tahtada açıklama yaparak çözer.)

B) (İkinci öğrenci denklemi sessizce çözer, sonra çözümü açıklar, sınıf dinler ve anlaşılmayan bir şey varsa sorular sorar.)

1 öğrenci Yenisiyle değiştirme:
.

2 öğrenci Yenisiyle değiştirme:
.

(Daha önce önceki denklemlere hakim olanlar için ek).

. .

3 öğrenci

(Öğrenciler oturduğu yerden çözümün ilerleyişini yorumlarlar.)

ÇÖZÜM: Ortak bir çarpan ekleyelim: ,

Neresi
veya
yani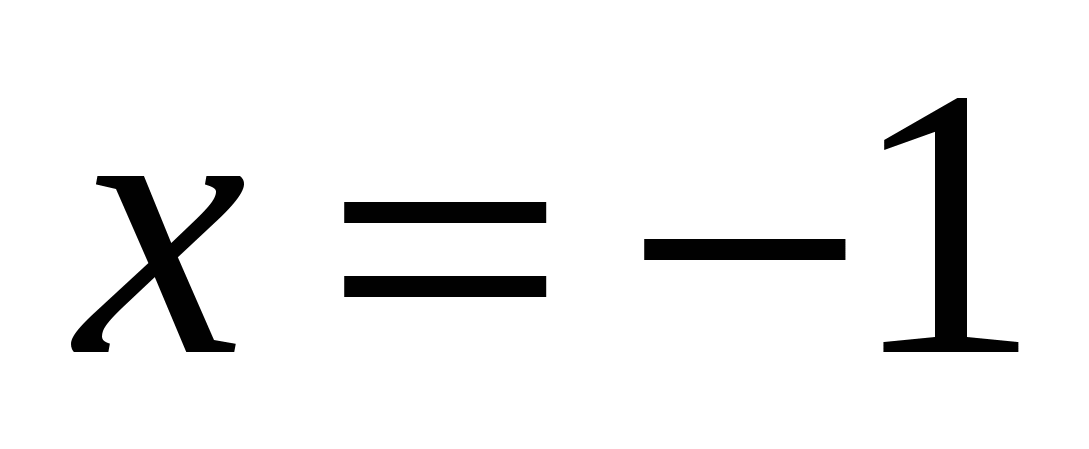

Cevap:

Bilgiyi derinleştirmek ve genişletmek

Çalışmaya devam ediyoruz. Slaytta denklemi görüyorsunuz: x 4 -5x 3 +6x 2 -5x+1=0.

Bunu nasıl çözmeyi önerirsiniz? Ne yapmalıyız?

Okul matematik programları çerçevesinde çözmek mümkün mü? Cevap hayır. Sonuçta, okuldaki denklemleri çözmek için kullanılan standart yöntemler, ikinci dereceden yüksek olmayan denklemlerin çözülmesini içerir. Ancak daha yüksek derecedeki bireysel denklemlerin hâlâ okulda çözüldüğünü hatırlayabiliriz. Doğru, bunları çözme yöntemleri, bilinen yöntemlerin yaratıcı bir şekilde uygulanmasıdır ve bunları ikinciden daha yüksek olmayan bir veya birkaç derece denkleminin çözümüne indirger.

Bu denkleme çok yakından bakar mısınız? Ne fark ettin ?(bu denklemde uçlardan eşit uzaklıktaki katsayılar eşittir)

Arkadaşlar, uçlardan eşit uzaklıktaki katsayılar çakıştığında bu tür bir denklem denir. depozitolu. Bu denklem, ikame kullanılarak ikinci dereceden bir denkleme indirgenebilir.

Bunları çözmek için size aşağıdaki algoritmayı sunuyorum:

Karşılıklı denklemleri çözmek için algoritma.

1. Denklemin her iki tarafını da x 2'ye bölün.

2. Terimleri gruplandırın (birincisi sonuncuyla, ikincisi dördüncüyle).

Denklemi oluşturacak şekilde azaltın A + c = 0

3.Yeni bir değişken tanıtın t = ,sonra yerine getirildi 2 = , yani

= t 2 – 2.

4. İkinci dereceden denklemi değiştirin ve çözün.

5.Değiştirmeye geri dönün ve ortaya çıkan denklemleri çözün.

6. Cevabı yazın.

Adamlar algoritmayı inceliyorlar.

Tahtadaki öğrenci denklemi algoritmaya göre çözer ve öğretmenin yardımıyla geri kalanı not defterlerine yazar. 4 6x 3 – 5x 2 – 38x

Çözüm.

– 5x + 6 = 0.

6x 2 – 5x – 38 – 5/x + 6/x 2 = 0.

6(x 2 + 1/x 2) – 5(x + 1/x) – 38 = 0.

t'yi girin: ikame (x + 1/x) = t. Değiştirme: (x 2 + 1/x 2) = t 2 – 2, elimizde:

6t 2 – 5t – 50 = 0.

t = -5/2 veya t = 10/3.

X değişkenine dönelim. Ters değiştirmeden sonra ortaya çıkan iki denklemi çözeriz:

1) x + 1/x = -5/2;

x 2 + 5/2 x +1 = 0;

x = -2 veya x = -1/2.

2) x + 1/x = 10/3;

x 2 – 10/3 x + 1 = 0;

x = 3 veya x = 1/3.

Cevap: -2; -1/2; 1/3; 3.

16. yüzyıl İtalyan matematikçileri N. Tartaglia, A. Fiore, D. Cardano ve diğerleri 3. ve 4. derece denklem problemine büyük katkı sağladılar. 1535 yılında A. Fiore ve N. İkincisinin kazandığı Tartaglia. 2 saat içinde Fiore'nin önerdiği 30 problemi çözdü ve Fiore, Tartaglia'nın kendisine verdiği tek bir problemi bile çözemedi.

. Arkadaşlar bugün size bir denklem daha sunmak istiyorum; onu OGE'ye hazırlanmak için bir dizi problemden aldım.

((x + 1)(x + 4))((x + 2)(x + 3)) = 24,

(x 2 + 5x + 4)(x 2 + 5x + 6) = 24.

x 2 + 5x + 4 = t yerine koyarsak denklemi elde ederiz

t(t + 2) = 24, karedir:

t2 + 2t – 24 = 0.

t = -6 veya t = 4.

Ters yerine koyma işlemini yaptıktan sonra orijinal denklemin köklerini kolaylıkla buluruz.

Cevap: -5; 0.

Bilgi ve becerilerin yeni koşullara yaratıcı aktarımı.

Dersin başında bir denklemde tekrar eden elemanlar varsa değişken yerine koyma yöntemini kullanabileceğimizden bahsetmiştik. Trigonometrik ve irrasyonel denklemlerin nasıl çözüleceğini henüz bilmiyoruz. Bakalım basit trigonometrik ve irrasyonel denklemleri nasıl çözeceğimizi biliyorsak, bu yöntemi onlara uygulayabilecek miyiz? Görev 1:

Aşağıdaki denklemlerdeki değişken değişimini adlandırın. Görev 2:

Çözümü değişken değiştirme yöntemine dayanan birkaç denklem oluşturun.

Özetle.

Evet arkadaşlar dersimiz sona erdi. Dersimizi özetleyelim.

Dersin başında hangi hedefleri belirledik?

Hedeflerimize ulaşıldı mı?

Derste ne yeni öğrendik?

4x 4 – 8x 3 + 3x 2 – 8x + 4 = 0

(x+1)(x+2)(x+4)(x+5) = 40

. (İtalyan matematikçilerin denklemi)

Ve dersi büyük bilim adamı Einstein A.'nın şu sözleriyle bitirmek istiyorum:

“Zamanımı siyaset ve denklemler arasında bölmek zorundayım. Ancak bana göre denklem çok daha önemli çünkü siyaset sadece şu an için var ve sonsuza kadar da var olacak.”

Ders için teşekkürler! Güle güle!

Gizliliğinizin korunması bizim için önemlidir. Bu nedenle bilgilerinizi nasıl kullandığımızı ve sakladığımızı açıklayan bir Gizlilik Politikası geliştirdik. Lütfen gizlilik uygulamalarımızı inceleyin ve herhangi bir sorunuz varsa bize bildirin.

Kişisel bilgilerin toplanması ve kullanılması

Kişisel bilgiler, belirli bir kişiyi tanımlamak veya onunla iletişim kurmak için kullanılabilecek verileri ifade eder.

Bizimle iletişime geçtiğinizde istediğiniz zaman kişisel bilgilerinizi vermeniz istenebilir.

Aşağıda toplayabileceğimiz kişisel bilgi türlerine ve bu bilgileri nasıl kullanabileceğimize dair bazı örnekler verilmiştir.

Hangi kişisel bilgileri topluyoruz:

• Siteye bir başvuru gönderdiğinizde adınız, telefon numaranız, e-posta adresiniz vb. dahil olmak üzere çeşitli bilgiler toplayabiliriz.

Kişisel bilgilerinizi nasıl kullanıyoruz:

• Topladığımız kişisel bilgiler, benzersiz teklifler, promosyonlar, diğer etkinlikler ve gelecek etkinlikler konusunda sizinle iletişim kurmamıza olanak tanır.
• Zaman zaman kişisel bilgilerinizi önemli bildirimler ve iletişimler göndermek için kullanabiliriz.
• Kişisel bilgileri, sunduğumuz hizmetleri geliştirmek ve size hizmetlerimizle ilgili tavsiyeler sunmak amacıyla denetimler, veri analizi ve çeşitli araştırmalar yapmak gibi şirket içi amaçlarla da kullanabiliriz.
• Bir ödül çekilişine, yarışmaya veya benzer bir promosyona katılırsanız, sağladığınız bilgileri bu tür programları yönetmek için kullanabiliriz.

Bilgilerin üçüncü şahıslara açıklanması

Sizden aldığımız bilgileri üçüncü şahıslara açıklamıyoruz.

İstisnalar:

• Gerekirse - yasaya, adli prosedüre uygun olarak, yasal işlemlerde ve/veya kamunun talepleri veya Rusya Federasyonu topraklarındaki hükümet yetkililerinin talepleri temelinde - kişisel bilgilerinizi ifşa etmek. Ayrıca, bu tür bir açıklamanın güvenlik, kanun yaptırımı veya diğer kamu önemi amaçları açısından gerekli veya uygun olduğunu tespit edersek, hakkınızdaki bilgileri de açıklayabiliriz.
• Yeniden yapılanma, birleşme veya satış durumunda topladığımız kişisel bilgileri ilgili halef üçüncü tarafa aktarabiliriz.

Kişisel bilgilerin korunması

Kişisel bilgilerinizi kayıp, hırsızlık ve kötüye kullanımın yanı sıra yetkisiz erişime, ifşa edilmeye, değiştirilmeye ve imhaya karşı korumak için idari, teknik ve fiziksel önlemler alıyoruz.

Şirket düzeyinde gizliliğinize saygı duymak

Kişisel bilgilerinizin güvende olduğundan emin olmak için gizlilik ve güvenlik standartlarını çalışanlarımıza aktarıyor ve gizlilik uygulamalarını sıkı bir şekilde uyguluyoruz.

giriiş

Kapsamlı bir okulda alınan matematik eğitimi, modern insanın genel eğitiminin ve genel kültürünün önemli bir bileşenidir. Modern insanı çevreleyen hemen hemen her şey bir şekilde matematikle bağlantılıdır. Ve fizik, mühendislik ve bilgi teknolojisindeki son gelişmeler, gelecekte de durumun aynı kalacağı konusunda hiçbir şüpheye yer bırakmıyor. Bu nedenle, birçok pratik problemin çözümü, nasıl çözüleceğini öğrenmeniz gereken çeşitli denklem türlerinin çözülmesine bağlıdır.

İlköğretim matematikte iki tür denklem vardır: cebirsel ve aşkın denklemler şunları içerir:

iki kareli; genel formun dördüncü derecesinin denklemi;

10. kesirli cebirsel denklemler, yani. polinomları ve cebirsel kesirleri içeren denklemler (formun kesirleri)

, burada ve polinomlardır);

Logaritmik, üstel veya trigonometrik fonksiyon gibi aşkın fonksiyonları içeren denklemlere aşkın denir. Çalışmamızda cebirsel denklemleri daha ayrıntılı olarak ele alacağız.

Eğitimsel ve metodolojik literatür geleneksel olarak denklemlerin çözümüne yönelik özel teknikleri tartışır. Bu arada, her bölümün denklemlerini çözmenin özellikleri ikincil bir konudur. Temel olarak dört ana yöntem vardır:

h (f(x))=h (g(x)) denklemini f(x)=g(x) denklemiyle değiştirirsek;

Değişken değiştirme yöntemi;

Çarpanlara ayırma yöntemi;

Fonksiyonel-grafik yöntemi ve çeşitli modifikasyonları.

Bunlardan en yaygın olanı değişken değiştirme yöntemidir.

Buna dayanarak, çalışmamızın amacını formüle ediyoruz: cebirsel denklemleri çözerken bilinmeyeni değiştirme yönteminin olanaklarını incelemek ve bunların standart ve standart dışı durumlarda uygulamalarını göstermek. Bu hedefe ulaşmak için aşağıdaki görevleri çözmek gerekir:

1. Denklem çözme teorisi ile ilgili temel kavram ve ifadelerin içeriğini ortaya koymak: denklem çözme, eşdeğerlik ve sonuç, denklem çözme için genel yöntemler.

2. Standart ve standart dışı durumlarda cebirsel denklemleri çözerken bilinmeyeni değiştirme yöntemini kullanma olanaklarını belirleyin.

3. Cebirsel denklemleri çözerken yeni bilinmeyenleri dahil etmeye yönelik yöntemleri tiplendirmek ve bunların uygulanabilirliğine ilişkin kriterleri belirlemek

4. Denklemleri çözerken yerine koyma yönteminin kullanımına dayanan bir dizi tipik problem oluşturun ve bunların çözümlerini gösterin.

1. Denklem çözme teorisi ile ilgili temel kavramlar ve ifadeler

Çalışmamızın ilk bölümünde denklem çözme teorisi ile ilgili temel kavram ve ifadelerin içeriğini ortaya koyacağız.

Denklem kavramına ilkokul yıllarında matematik derslerinde aşina oluyoruz ve muhtemelen en sık karşılaşılan problemlerden biri de “denklem çözme” görevidir. Ancak ilköğretim matematik dersinin kapsamının çok dışına çıkmadan “denklem” kavramının tam bir tanımını veremeyiz, “denklem çözmenin” ne anlama geldiğini tam olarak tanımlayamayız. Bunun için de çok ciddi mantıksal ve hatta felsefi kategorilerin devreye girmesi gerekiyor. Bu kavramlara “sağduyu” düzeyinde aşinalık bizim için oldukça yeterli.

Aynı bilinmeyene sahip iki A ve B denklemini düşünün. B denkleminin şöyle olduğunu söyleyeceğiz: sonuçlar A denkleminin herhangi bir kökü B denkleminin kökü ise A denklemi.

Denklemler denir eş değer, birinin kökü diğerinin kökü ise veya bunun tersi de geçerlidir. Dolayısıyla, her biri diğerinin sonucu ise denklemler eşdeğerdir.

Bu tanımlardan örneğin çözümü olmayan iki denklemin eşdeğer olduğu sonucu çıkar. A'nın çözümü yoksa B'dir. sonuçlar A, B denklemi ne olursa olsun.

“Denklem çözme” kavramını tanımlayalım. Denklemi çöz- denklemi kimliğe dönüştüren, içinde yer alan bilinmeyenlerin tüm bu değerlerini bulmak anlamına gelir. Bu değerlere denklemin kökleri denir.

Denklem çözme süreci esas olarak belirli bir denklemin ona eşdeğer başka bir denklemle değiştirilmesinden oluşur.

Daha önce de belirtildiği gibi, herhangi bir denklemin çözümünde kullanılan en yaygın dört yöntem vardır. Her yönteme daha yakından bakalım.

h (f(x))=h (g(x)) denklemini f(x)=g(x) denklemiyle değiştirme yöntemi yalnızca şu durumlarda kullanılabilir:

Çarpanlara ayırma yönteminin özü aşağıdaki gibidir: denklem

Bu setin denklemlerini çözdükten sonra, orijinal denklemin tanım alanına ait olan kökleri almanız ve geri kalanını, denklemi çözmek için grafiksel bir yöntem fikri dışında bırakmanız gerekir.

Değişken değiştirme yönteminin özünü açıklayalım: eğer denklem

Konuyla ilgili ders ve sunum: "Değişken değiştirme yöntemi. Örnekler"

Ek malzemeler
Sevgili kullanıcılar, yorumlarınızı, yorumlarınızı, dileklerinizi bırakmayı unutmayın! Tüm materyaller antivirüs programı ile kontrol edilmiştir.

11. sınıf için Integral çevrimiçi mağazasında öğretim yardımcıları ve simülatörler
1C: Okul. Geometride problem çözme. 10-11. Sınıflar için uzayda inşa etmeye ilişkin etkileşimli görevler
Parametrelerle cebirsel problemler, 9-11. Sınıflar

Bu yöntem denklemleri çözerken oldukça yaygındır ve bunu birden fazla kez kullandık. Aşağıdaki durumlarda kullanılabilir:

• Orijinal denklem $f(x)=0$ karmaşık bir forma sahipse, ancak onu $h(g(x))=0$ formundaki bir denkleme dönüştürmek mümkündü.
• $u=g(x)$ değişkenlerinde değişiklik yapmak gereklidir.
• $h(u)=0$ denklemini çözün, $u_1$, $u_2$, … $u_n$ köklerini bulun.
• Ters yerine koyma işlemini girin $g(x)=u_1$, $g(x)=u_2$, … , $g(x)=u_n$.
• $g(x)=u_1$, $g(x)=u_2$, …, $g(x)=u_n$ denklemlerinin her birini çözün. Her denklemin kökleri orijinal denklemin çözümleri olacaktır.

Örnek.
Denklemi çözün: $8x^6+7x^3-1=0$.

Çözüm.
$y=x^3$ yerine geçen ifadeyi tanıtalım. O zaman denklemimiz ikinci dereceden bir denkleme indirgenir:
$8y^2+7y-1=0$,
$(8y-1)(y+1)=0$,
$y_1=\frac(1)(8)$ ve $y_2=-1$.

Bu aşamada daha karmaşık denklemleri çözerken elde edilen kökleri kontrol etmelisiniz.
Ters yerine koyma işlemini tanıtalım: $x^3=\frac(1)(8)$ ve $x^3=-1$.
Bu denklemlerin köklerini bulmak kolaydır: $x_1=\frac(1)(2)$ ve $x_2=-1$.

Cevap: $x=0,5$ ve $x=-1$.

Örnek.
Denklemi çözün: $\sqrt(\frac(2x+3)(2x-1))+4\sqrt(\frac(2x-1)(2x+3))=4$.

Çözüm.
Eşdeğer dönüşümleri gerçekleştirelim:
$\sqrt(\frac(2x-1)(2x+3))=(\frac(2x-1)(2x+3))^(\frac(1)(2))=(\frac(2x+ 3) )(2x-1))^(-\frac(1)(2))=((\frac(2x+3)(2x-1))^(\frac(1)(2)))^( - 1)=\frac(1)(\sqrt(\frac(2x+3)(2x-1))))$.

Değiştirmeyi tanıtalım: $u=\sqrt(\frac(2x+3)(2x-1))$, sonra denklemimiz $u+\frac(4)(u)=4$ olur. $u^2-4u+4=0$, dolayısıyla $u=2$.

Ters değişimi tanıtalım: $\sqrt(\frac(2x+3)(2x-1))=2$.

$2x+3=4(2x-1)$ $x=1\frac(1)(6)$ doğrusal denklemini çözerek.

Örnek.
Denklemi çözün: $2^x+2^(1-x)=3$.

Çözüm.
Denklemimiz eşdeğer bir denkleme indirgenir: $2^x+\frac(2)(2^x)=3$.

Değiştirmeyi tanıtalım: $t=2^x$.
$t+\frac(2)(t)=3$,
$t^2-3t+2=0$,
$(t-2)(t-1)=0$,
$t_1=2$ ve $t_2=1$.

Ters yerine koymayı tanıtalım: $2^x=2$ ve $2^x=1$. Gönderen: $x=1$ ve $x=0$.

Cevap: $x=1$ ve $x=0$.

Örnek.
Denklemi çözün: $lg^2(x^2)+lg(10x)-6=0$.

Çözüm.
Denklemimizi dönüştürelim.
$lg^2(x^2)=(lg(x^2))^2=(2lg(x))^2=4lg^2x$.
$lg(10x)=lg10+lgx=1+lgx$.

Orijinal denklem şu denkleme eşdeğerdir: $4lg^2x+lgx-5=0$.

Yenisini tanıtalım: $u=lg(x)$.
$4u^2+u-5=0$,
$(4u+5)(u-1)=0$.

Ters ikameyi tanıtalım: $lgx=-1.25$ ve $lgx=1$.
Cevap: $x=10^(-\frac(5)(4))$ ve $x=10$.

Örnek.
Denklemi çözün: $sin(x)cos(x)-6sin(x)+6cos(x)+6=0$.

Çözüm.
Değiştirmeyi tanıtalım: $cos(x)-sin(x)=y$.

Sonra: $(cos(x)-sin(x))^2=1-2sin(x)cos(x)$.
$sin(x)cos(x)=\frac(1-y^2)(2)$.

Orijinal denklem şuna eşdeğerdir:
$\frac(1-y^2)(2)+6y+6=0$,
$1-y^2+12y+12=0$,
$y^2-12y-13=0$,
$(y-13)(y+1)=0$.

Ters ikameyi tanıtalım: $cos(x)-sin(x)=13$ - kosinüs ve sinüs modül açısından bir ile sınırlı olduğundan hiçbir çözümün olmadığı açıktır.

$cos(x)-sin(x)=-1$ - denklemin her iki tarafını $\frac(\sqrt(2))(2)$ ile çarpın.
$\frac(\sqrt(2))(2)cos(x)-\frac(\sqrt(2))(2)sin(x)=-\frac(\sqrt(2))(2)$.
$sin(\frac(π)(4)-x)=-\frac(\sqrt(2))(2)$.
$\begin (cases) \frac(π)(4)-x=-\frac(π)(4)+2πn, \\ \frac(π)(4)-x=-\frac(3π)(4 )+2πn. \end (durumlar)$
$\begin (case) x=\frac(π)(2)+2πn, \\ x=π+2πn. \end (durumlar)$

Cevap: $x=\frac(π)(2)+2πn$ ve $π+2πn$.

Bağımsız olarak çözülmesi gereken sorunlar

2. $\sqrt(\frac(5x-1)(x+3))+5\sqrt(\frac(x+3)(5x-1))=6$.

3. $5^x+5^(2x+1)=-4$.
4. $2cos^2(x)-7cos-4=0$.
5. $5sin(2x)-11sin(x)=11cos(x)-7$.