Diyelim ki Aşil kaplumbağadan on kat daha hızlı koşuyor ve onun bin adım gerisinde. Aşil'in bu mesafeyi koştuğu süre boyunca kaplumbağa aynı yönde yüz adım kadar sürünecektir. Aşil yüz adım koştuğunda kaplumbağa on adım daha sürünür ve bu böyle devam eder. Süreç sonsuza kadar devam edecek, Aşil kaplumbağaya asla yetişemeyecek.
Bu akıl yürütme, sonraki tüm nesiller için mantıksal bir şok oldu. Aristoteles, Diogenes, Kant, Hegel, Hilbert... Hepsi öyle ya da böyle Zenon'un açmazını değerlendirdiler. Şok o kadar güçlüydü ki " ... tartışmalar bugüne kadar devam ediyor; bilim camiası paradoksların özü hakkında henüz ortak bir görüşe varamadı ... konunun incelenmesine matematiksel analiz, küme teorisi, yeni fiziksel ve felsefi yaklaşımlar dahil edildi. ; hiçbiri soruna genel kabul görmüş bir çözüm olmadı..."[Wikipedia, "Zeno'nun Aporia'sı". Herkes kandırıldığını anlıyor ama kimse aldatmanın neyden oluştuğunu anlamıyor.
Matematiksel bir bakış açısından Zeno, çıkmazında nicelikten niceliğe geçişi açıkça gösterdi. Bu geçiş, kalıcı olanların yerine uygulamayı ima etmektedir. Anladığım kadarıyla değişken ölçü birimlerini kullanmaya yönelik matematiksel aparat ya henüz geliştirilmedi ya da Zeno'nun açmazına uygulanmadı. Her zamanki mantığımızı uygulamak bizi tuzağa düşürür. Biz düşüncenin ataleti nedeniyle karşılıklı değere sabit zaman birimleri uyguluyoruz. Fiziksel açıdan bakıldığında bu, Aşil'in kaplumbağaya yetiştiği anda tamamen durana kadar zamanın yavaşlaması gibi görünüyor. Zaman durursa Aşil kaplumbağadan daha fazla koşamaz.
Her zamanki mantığımızı tersine çevirirsek her şey yerli yerine oturur. Aşil sabit hızla koşar. Yolunun her bir sonraki bölümü bir öncekinden on kat daha kısadır. Buna göre, bunun üstesinden gelmek için harcanan süre bir öncekine göre on kat daha azdır. Bu duruma “sonsuzluk” kavramını uygularsak o zaman “Aşil kaplumbağaya sonsuz hızla yetişecek” demek doğru olur.
Bu mantıksal tuzaktan nasıl kaçınılır? Sabit zaman birimlerinde kalın ve karşılıklı birimlere geçmeyin. Zeno'nun dilinde şöyle görünür:
Aşil'in bin adım koşması gereken sürede kaplumbağa aynı yönde yüz adım koşacaktır. Bir sonraki birinciye eşit zaman aralığında Aşil bin adım daha koşacak ve kaplumbağa yüz adım daha sürünecektir. Artık Aşil kaplumbağanın sekiz yüz adım ilerisindedir.
Bu yaklaşım, herhangi bir mantıksal paradoks olmaksızın gerçekliği yeterince tanımlamaktadır. Ancak bu soruna tam bir çözüm değildir. Einstein'ın ışık hızının karşı konulmazlığıyla ilgili açıklaması Zeno'nun "Aşil ve Kaplumbağa" açmazına çok benziyor. Hala bu sorunu incelememiz, yeniden düşünmemiz ve çözmemiz gerekiyor. Ve çözümün sonsuz büyük sayılarda değil, ölçü birimlerinde aranması gerekiyor.
Zeno'nun bir başka ilginç açmazı da uçan bir oktan bahseder:
Uçan ok, zamanın her anında hareketsiz olduğundan hareketsizdir ve zamanın her anında hareketsiz olduğundan daima hareketsizdir.
Bu açmazda, mantıksal paradoksun üstesinden çok basit bir şekilde gelinir - uçan bir okun uzayın farklı noktalarında hareketsiz olduğunu, yani aslında hareket olduğunu açıklığa kavuşturmak yeterlidir. Burada bir başka noktaya dikkat çekmek gerekiyor. Yoldaki bir arabanın bir fotoğrafından ne hareketinin gerçekliğini ne de ona olan mesafeyi belirlemek imkansızdır. Bir arabanın hareket edip etmediğini belirlemek için aynı noktadan farklı zamanlarda çekilmiş iki fotoğrafa ihtiyacınız vardır, ancak onlara olan mesafeyi belirleyemezsiniz. Bir arabaya olan mesafeyi belirlemek için, uzayın farklı noktalarından aynı anda çekilmiş iki fotoğrafa ihtiyacınız vardır, ancak bunlardan hareketin gerçeğini belirleyemezsiniz (tabii ki hesaplamalar için yine de ek verilere ihtiyacınız var, trigonometri size yardımcı olacaktır) ). Özellikle dikkat çekmek istediğim şey, zamandaki iki nokta ile uzaydaki iki noktanın birbirine karıştırılmaması gereken farklı şeyler olmasıdır, çünkü bunlar araştırma için farklı fırsatlar sunar.
4 Temmuz 2018 Çarşamba
Küme ve çoklu küme arasındaki farklar Vikipedi'de çok iyi anlatılmıştır. Görelim.
Gördüğünüz gibi “bir kümede iki özdeş eleman olamaz” ama bir kümede özdeş elemanlar varsa bu kümeye “çoklu küme” denir. Makul varlıklar bu kadar saçma mantığı asla anlayamayacaklar. Bu, “tamamen” kelimesinden zekası olmayan, konuşan papağanların ve eğitimli maymunların seviyesidir. Matematikçiler bize saçma fikirlerini vaaz eden sıradan eğitmenler gibi davranırlar.
Bir zamanlar köprüyü inşa eden mühendisler, köprüyü test ederken köprünün altında bir teknedeydiler. Köprü çökerse, vasat mühendis, yarattığı eserin enkazı altında öldü. Köprünün yüke dayanabilmesi durumunda yetenekli mühendis başka köprüler de inşa etti.
Matematikçiler "dikkat edin, evdeyim" veya daha doğrusu "matematik soyut kavramları inceler" ifadesinin arkasına ne kadar saklanırsa saklansınlar, onları gerçeklikle ayrılmaz bir şekilde bağlayan bir göbek bağı vardır. Bu göbek bağı paradır. Matematiksel küme teorisini matematikçilerin kendilerine uygulayalım.
Matematiği çok iyi çalıştık ve şimdi kasanın başında oturup maaş dağıtıyoruz. Yani bir matematikçi parası için bize geliyor. Tutarın tamamını ona sayıyoruz ve içine aynı değerdeki banknotları koyduğumuz farklı yığınlar halinde masamızın üzerine koyuyoruz. Daha sonra her yığından bir banknot alıyoruz ve matematikçiye "matematiksel maaş seti"ni veriyoruz. Matematikçiye, kalan banknotları ancak özdeş elemanları olmayan bir kümenin, aynı elemanları olan bir kümeye eşit olmadığını kanıtladığında alacağını açıklayalım. Eğlencenin başladığı yer burasıdır.
Öncelikle milletvekillerinin mantığı işleyecek: “Bu başkalarına da uygulanabilir ama bana uygulanamaz!” Daha sonra bize, aynı değerdeki banknotların farklı banknot numaralarına sahip olduğu, yani aynı unsurlar olarak kabul edilemeyecekleri konusunda güvence vermeye başlayacaklar. Tamam, maaşları madeni para cinsinden sayalım - madeni paraların üzerinde rakam yok. Burada matematikçi çılgınca fiziği hatırlamaya başlayacak: farklı madeni paraların farklı miktarda kirleri var, kristal yapısı ve atomların düzeni her madeni para için benzersizdir...
Ve şimdi en ilginç sorum var: Çoklu kümenin elemanlarının bir kümenin elemanlarına dönüştüğü ve bunun tersinin de geçerli olduğu çizgi nerede? Böyle bir çizgi yok - her şeye şamanlar karar veriyor, bilim burada yalan söylemeye bile yakın değil.
Buraya bak. Aynı saha alanına sahip futbol stadyumlarını seçiyoruz. Alanların alanları aynıdır; bu da bir çoklu kümeye sahip olduğumuz anlamına gelir. Ancak aynı stadyumların isimlerine baktığımızda çok sayıda isim görüyoruz çünkü isimler farklı. Gördüğünüz gibi aynı eleman kümesi hem bir küme hem de çoklu kümedir. Hangisi doğru? Ve burada matematikçi-şaman-keskinci kolundan bir koz çıkarır ve bize ya bir kümeden ya da bir çoklu kümeden bahsetmeye başlar. Her durumda bizi haklı olduğuna ikna edecektir.
Modern şamanların küme teorisini gerçekliğe bağlayarak nasıl çalıştığını anlamak için bir soruyu yanıtlamak yeterlidir: Bir kümenin öğeleri başka bir kümenin öğelerinden nasıl farklıdır? Size "tek bir bütün olarak düşünülemez" veya "tek bir bütün olarak düşünülemez" olmadan göstereceğim.
18 Mart 2018 Pazar
Bir sayının rakamlarının toplamı, şamanların tef ile dansıdır ve bunun matematikle hiçbir ilgisi yoktur. Evet, matematik derslerinde bize bir sayının rakamlarının toplamını bulmamız ve bunu kullanmamız öğretilir, ancak bu yüzden onlar şamandırlar, nesillerine becerilerini ve bilgeliğini öğretmek için çalışırlar, aksi takdirde şamanlar yok olup giderler.
Kanıta mı ihtiyacınız var? Wikipedia'yı açın ve "Bir sayının rakamlarının toplamı" sayfasını bulmaya çalışın. O yok. Matematikte herhangi bir sayının rakamlarının toplamını bulmak için kullanılabilecek bir formül yoktur. Sonuçta sayılar, sayıları yazdığımız grafik sembollerdir ve matematik dilinde görev şu şekildedir: "Herhangi bir sayıyı temsil eden grafik sembollerin toplamını bulun." Matematikçiler bu problemi çözemezler ama şamanlar bunu kolaylıkla yapabilirler.
Belirli bir sayının rakamlarının toplamını bulmak için ne ve nasıl yapacağımızı bulalım. Peki elimizde 12345 sayısı var. Bu sayının rakamlarının toplamını bulmak için ne yapılması gerekiyor? Tüm adımları sırayla ele alalım.
1. Numarayı bir kağıda yazın. Ne yaptık? Sayıyı grafiksel sayı sembolüne dönüştürdük. Bu matematiksel bir işlem değil.
2. Ortaya çıkan bir resmi, bireysel sayılar içeren birkaç resme kestik. Bir resmi kesmek matematiksel bir işlem değildir.
3. Bireysel grafik sembollerini sayılara dönüştürün. Bu matematiksel bir işlem değil.
4. Ortaya çıkan sayıları ekleyin. Şimdi bu matematik.
12345 sayısının rakamlarının toplamı 15'tir. Bunlar matematikçilerin kullandığı, şamanlar tarafından öğretilen “kesme ve dikme dersleridir”. Ama hepsi bu değil.
Matematiksel açıdan bakıldığında bir sayıyı hangi sayı sisteminde yazdığımız önemli değildir. Yani farklı sayı sistemlerinde aynı sayının rakamlarının toplamı farklı olacaktır. Matematikte sayı sistemi sayının sağında alt simge olarak gösterilir. Büyük sayı olan 12345 ile kafamı kandırmak istemem, yazıdaki 26 sayısını ele alalım. Bu sayıyı ikili, sekizli, onlu ve onaltılı sayı sistemlerinde yazalım. Her adıma mikroskop altında bakmayacağız; bunu zaten yaptık. Sonuca bakalım.
Gördüğünüz gibi farklı sayı sistemlerinde aynı sayının rakamlarının toplamı farklıdır. Bu sonucun matematikle hiçbir ilgisi yoktur. Aynı dikdörtgenin alanını metre ve santimetre olarak belirlerseniz tamamen farklı sonuçlar elde edersiniz.
Sıfır tüm sayı sistemlerinde aynı görünür ve rakam toplamı yoktur. Bu, gerçeğin lehine başka bir argümandır. Matematikçilere soru: Matematikte sayı olmayan bir şey nasıl belirlenir? Ne yani, matematikçiler için sayılardan başka hiçbir şey yok mu? Buna şamanlar için izin verebilirim ama bilim adamları için izin veremem. Gerçeklik sadece sayılardan ibaret değildir.
Elde edilen sonuç, sayı sistemlerinin sayıların ölçü birimleri olduğunun kanıtı olarak değerlendirilmelidir. Sonuçta sayıları farklı ölçü birimleriyle karşılaştıramayız. Aynı niceliğin farklı ölçü birimleriyle yapılan aynı eylemler, karşılaştırıldıktan sonra farklı sonuçlara yol açıyorsa, bunun matematikle hiçbir ilgisi yoktur.
Gerçek matematik nedir? Bu, bir matematiksel işlemin sonucunun sayının büyüklüğüne, kullanılan ölçü birimine ve bu işlemi kimin yaptığına bağlı olmadığı durumdur.
Ah! Burası kadınlar tuvaleti değil mi?
- Genç kadın! Burası, cennete yükselişleri sırasında ruhların ölümsüz kutsallığının incelenmesine yönelik bir laboratuvardır! Halo üstte ve yukarı ok. Başka hangi tuvalet?
Dişi... Üstteki hale ve aşağı ok erkektir.
Böyle bir tasarım sanatı eseri günde birkaç kez gözünüzün önünden geçiyorsa,
O halde arabanızda aniden garip bir simge bulmanız şaşırtıcı değil:
Kişisel olarak ben kaka yapan bir insanda eksi dört dereceyi görmeye çalışıyorum (tek resim) (birkaç resimden oluşan kompozisyon: eksi işareti, dört rakamı, derece işareti). Ve bu kızın fizik bilmeyen bir aptal olduğunu düşünmüyorum. Sadece grafik görüntüleri algılama konusunda güçlü bir stereotipi var. Ve matematikçiler bize bunu her zaman öğretiyorlar. İşte bir örnek.
1A “eksi dört derece” veya “bir a” değildir. Bu "kaka yapan adam" veya onaltılık gösterimle "yirmi altı" sayısıdır. Sürekli olarak bu sayı sisteminde çalışan kişiler, sayıyı ve harfi otomatik olarak tek bir grafik sembol olarak algılarlar.
X sayısının y sayısına oranı, u sayılarının bölümüdür, yani. y/ x veya x: y. Oran, x'in y'den kaç kat büyük olduğunu veya y'nin ne kadarının x olduğunu gösterir. Oran, iki oranın eşitliğidir, yani. a/b = x/y. A ve y sayılarına oranın ekstrem terimleri, x ve b sayılarına ise orta terimleri denir.
Oranın özellikleri
(ana): Bir oranın uç terimlerinin çarpımı orta terimlerinin çarpımına eşittir, yani. a/b = x/y ise ay = bx olur.
Tersine, a, b, x, y sayıları, eğer ay = bx ise, a/b = x/y oranını oluşturur.
Bir orantıda uç noktaları, orta terimleri veya her ikisini de aynı anda değiştirirsek doğru oranı elde ederiz.
Oranın bilinmeyen orta (veya ekstrem) terimini bulmak için, ekstrem (orta) terimlerin çarpımını oranın bilinen orta (ekstrem) terimine bölmeniz gerekir.
Bir sayıyı verilen sayılarla doğru ve ters orantılı parçalara bölmek
Bir sayıyı verilen sayılara orantılı olarak bölmek (belirli bir oranda bölmek) için, bu sayıyı verilen sayıların toplamına bölmeniz ve sonucu her biriyle çarpmanız gerekir.
Bir sayıyı verilen sayılara ters orantılı parçalara bölmek için bu sayıyı, verilen sayılara ters orantılı olan sayılarla doğru orantılı parçalara bölmek yeterlidir.
Mesela 27'yi 4 ve 5 sayılarına ters orantılı olarak bölelim. Verilen sayıların karşılıkları (1/4) : (1/5) = 5:4; o zaman alırız
Yüzde, bir sayının yüzde biri kadardır. Yüzde, % işaretiyle gösterilir.
Bu sayı 1 alınırsa %1 bu sayının 0,01'i, %25'i sayının 0,25'i (veya sayının 1/4'ü) vb. Dolayısıyla yüzde sayısını kesir olarak gösterebilmek için yüzde sayısını 100'e bölmek yeterlidir. Örneğin %125 = 1,25; %2,3 = 0,023.
Yüzdelerle ilgili temel problemler
Belirli bir sayının yüzdesini bulma.
B sayısının %'sini bulmak için yüzdeleri kesir olarak ifade etmeniz gerekir: a /100 ve b sayısını bu kesirle çarpmanız gerekir.
Örneğin, 60 rublenin% 30'u. 0,3 60 = 18 (rub.).
Bir sayıyı yüzdesine göre bulma.
Bir x sayısının % a'sının b'ye eşit olduğu biliniyorsa, formülü kullanarak x sayısını buluruz. Onlar. Yüzdeleri kesir olarak ifade etmeniz ve bilinen b sayısını bu kesre bölmeniz gerekir.
Örneğin, nakit depozitonun% 3'ü 150 ruble ise, depozitonun tamamı 150/0,03 = 5000 (ruble) olur.
Sayıların yüzdesini bulma.
A ve b gibi iki sayının yüzde oranını bulmak için bu sayıların oranını 100 ile çarpmanız gerekir; hesaplamak.
Örneğin, günde 60 araba olarak planlanan hedefte tesis 90 araba ürettiyse bu hedefi şu kadar sürede tamamlamış demektir:
(90/60) 100% = 150%.
“Komedinin Babası” Aristophanes Antik Yunan Aristophanes komedilerinde birkaç kez muhbirler gibi nahoş bir olguya yöneliyor. Mesela “Akharnyan”ın kahramanı Nikarch için...
Rus romanında aşk teması (“Oblomov”, “Babalar ve Oğullar”, “Savaş ve Barış” romanlarından uyarlanmıştır)... Aşk acısı teması en çok "Babalar ve Oğullar" Evgeny Bazarov'un ana karakteri ile ilişkilidir. Duyguları ağır, her şeyi tüketen...
Lise matematiğindeki problemlerin çoğunu çözmek, orantı formüle etme bilgisini gerektirir. Bu basit beceri, yalnızca ders kitabındaki karmaşık alıştırmaları yapmanıza değil, aynı zamanda matematik biliminin özünü derinlemesine incelemenize de yardımcı olacaktır. Orantı nasıl yapılır? Şimdi çözelim.
En basit örnek, üç parametrenin bilindiği ve dördüncüsünün bulunmasının gerektiği bir problemdir. Oranlar elbette farklıdır, ancak çoğu zaman yüzdeleri kullanarak bir sayı bulmanız gerekir. Mesela çocuğun toplam on elması vardı. Dördüncü kısmı annesine verdi. Çocuğun kaç elması kaldı? Bu, orantı oluşturmanıza olanak sağlayacak en basit örnektir. Önemli olan bunu yapmaktır. Başlangıçta on elma vardı. %100 olsun. Bütün elmalarını işaretledik. Dörtte birini verdi. 1/4=25/100. Bu onun bıraktığı anlamına gelir: %100 (başlangıçta öyleydi) - %25 (verdi) = %75. Bu rakam, başlangıçta mevcut olan miktarla karşılaştırıldığında kalan meyve miktarının yüzdesini gösterir. Artık orantıyı çözebileceğimiz üç sayımız var. 10 elma - %100, X elmalar - %75, burada x gerekli miktarda meyvedir. Orantı nasıl yapılır? Ne olduğunu anlamalısın. Matematiksel olarak şöyle görünüyor. Anlamanız için eşittir işareti konulmuştur.

10 elma = %100;
x elma = %75.
10/x = %100/75 olduğu ortaya çıktı. Bu oranların ana özelliğidir. Sonuçta, x ne kadar büyük olursa, bu sayının orijinalden yüzdesi de o kadar büyük olur. Bu oranı çözüyoruz ve x = 7,5 elma olduğunu buluyoruz. Çocuğun neden tamsayılı bir miktar vermeye karar verdiğini bilmiyoruz. Artık orantıyı nasıl yapacağınızı biliyorsunuz. Önemli olan, biri bilinmeyen bilinmeyeni içeren iki ilişki bulmaktır.
Bir orantıyı çözmek genellikle basit çarpma ve ardından bölme işlemine indirgenir. Okullar çocuklara bunun neden böyle olduğunu açıklamıyor. Orantılı ilişkilerin matematik klasikleri, bilimin özü olduğunu anlamak önemli olsa da. Orantıları çözmek için kesirleri kullanabilmeniz gerekir. Örneğin, sıklıkla yüzdeleri kesirlere dönüştürmeniz gerekir. Yani% 95'i kaydetmek işe yaramayacaktır. Ve hemen 95/100 yazarsanız, ana hesaplamaya başlamadan önemli indirimler yapabilirsiniz. Oranınızın iki bilinmeyenli olduğu ortaya çıkarsa çözülemeyeceğini hemen söylemekte fayda var. Burada hiçbir profesör sana yardım edemez. Ve göreviniz büyük olasılıkla doğru eylemler için daha karmaşık bir algoritmaya sahip.

Yüzdelerin olmadığı başka bir örneğe bakalım. Bir sürücü 150 rubleye 5 litre benzin aldı. 30 litre yakıta ne kadar ödeyeceğini düşündü. Bu sorunu çözmek için gerekli para miktarını x ile gösterelim. Bu sorunu kendiniz çözebilir ve ardından cevabı kontrol edebilirsiniz. Oranın nasıl yapılacağını henüz anlamadıysanız, bir göz atın. 5 litre benzin 150 ruble. İlk örnekte olduğu gibi 5l - 150r yazıyoruz. Şimdi üçüncü sayıyı bulalım. Tabii bu 30 litre. Bu durumda bir çift 30 l - x rublenin uygun olduğunu kabul edin. Matematik diline geçelim.
5 litre - 150 ruble;
30 litre - x ruble;
Bu oranı çözelim:
x = 900 ruble.
Biz de karar verdik. Görevinizde cevabın yeterliliğini kontrol etmeyi unutmayın. Yanlış kararla arabaların saatte 5000 kilometre gibi gerçekçi olmayan hızlara ulaşması vb. Artık orantıyı nasıl yapacağınızı biliyorsunuz. Siz de çözebilirsiniz. Gördüğünüz gibi bunda karmaşık bir şey yok.
Oranların temel özellikleri
- Oranın tersine çevrilmesi. Eğer A : B = C : D, O B : A = D : C
- Bir oranın şartlarını çapraz olarak çarpmak. Eğer A : B = C : D, O reklam = M.Ö..
- Orta ve ekstrem terimlerin yeniden düzenlenmesi. Eğer A : B = C : D, O
- Artan ve azalan oranlar. Eğer A : B = C : D, O
- Toplama ve çıkarma yaparak orantı oluşturma. Eğer A : B = C : D, O
Bileşik (sürekli) oranlar
Tarihsel arka plan
Edebiyat
- van der Waerden, B.L. Uyanış Bilimi. Eski Mısır, Babil ve Yunanistan'ın matematiği. - başına. Hollandaca'dan I. N. Veselovsky- M.: GIFML, 1959
Ayrıca bakınız
Wikimedia Vakfı.
2010.:Eş anlamlılar
Diğer sözlüklerde “Oran”ın ne olduğuna bakın: - (Latince, pro for ve portio kısmından, kısım kelimesinden gelir). 1) orantılılık, koordinasyon. 2) Parçaların birbirleriyle ve bütünle ilişkisi. Miktarlar arasındaki ilişki. 3) mimaride: iyi boyutlar. Rusça'da yer alan yabancı kelimeler sözlüğü... ...
Rus dilinin yabancı kelimeler sözlüğü ORAN, oranlar, kadın. (kitap) (enlem. orantı). 1. Orantılılık, parçalar arasında belirli bir ilişki. Vücut parçalarının doğru oranları. Şekeri yumurta sarısı ile şu oranda karıştırın: sarısı başına iki yemek kaşığı şeker. 2. İkinin eşitliği... ...
Ushakov'un Açıklayıcı Sözlüğü Tutum, oran; orantılılık. Karınca. orantısızlık Rusça eşanlamlılar sözlüğü. orantı bkz. oran Rus dilinin eşanlamlıları sözlüğü. Pratik rehber. M.: Rus dili. Z. E. Alexandrova ...
Eşanlamlılar sözlüğü Kadın, Fransız orantılılık; bir şeye karşılık gelen değer veya miktar; | mat. içerik eşitliği, çift-dört haneli özdeş ilişkiler; aritmetikte, eğer ikinci sayı birinciden dördüncü sayı kadar fazla ya da küçükse...
Dahl'ın Açıklayıcı Sözlüğü - (lat. orantı) matematikte, dört niceliğin iki oranı arasındaki eşitlik: a/b =c/d ...
Büyük Ansiklopedik Sözlük ORAN, matematikte dört niceliğin iki oranı arasındaki eşitlik: a/b=c/d. Sürekli orantı, her biri bir sonraki miktarla aynı ilişkiye sahip olan üç veya daha fazla sayıdan oluşan bir gruptur.
Bilimsel ve teknik ansiklopedik sözlük ORAN ve kadın. 1. Matematikte: iki ilişkinin eşitliği (3 değerde). 2. Parçalar arasında belli bir ilişki, orantılılık. P. binanın bazı kısımlarında. Ozhegov'un açıklayıcı sözlüğü. Sİ. Ozhegov, N.Yu. Shvedova. 1949 1992…
Ozhegov'un Açıklayıcı Sözlüğü İngilizce oran; Almanca Oran. 1. Orantılılık, bütünün parçaları arasında belirli bir ilişki. 2. İki ilişkinin eşitliği. Antinazi. Sosyoloji Ansiklopedisi, 2009 ...
Sosyoloji Ansiklopedisi oran - - [A.S. İngilizce-Rusça enerji sözlüğü. 2006] Genel olarak enerji konuları EN oran derecesiD derece oranı ...
Teknik Çevirmen Kılavuzu- ikinin eşitliği (bkz.), yani. a: b = c: d, burada a, b, c, d oranın üyeleridir; a ve d aşırıdır, b ve c ortadadır. Oranın ana özelliği: Oranın aşırı terimlerinin çarpımı ortalamanın çarpımına eşittir: ad = bс ... Büyük Politeknik Ansiklopedisi
Bir orantı oluşturun. Bu yazımda sizlerle orantı hakkında konuşmak istiyorum. Oranın ne olduğunu anlamak ve bunu oluşturabilmek çok önemli, gerçekten kurtarıyor sizi. Bu, matematiğin büyük alfabesinde küçük ve önemsiz bir "harf" gibi görünüyor, ancak o olmadan matematik topal ve eksik olmaya mahkumdur.Öncelikle orantı nedir hatırlatayım. Bu formun bir eşitliğidir:

bu da aynı şeydir (bu farklı bir kayıt şeklidir).
Örnek:
Birin ikiye, dördün sekize eşit olduğunu söylüyorlar. Yani bu iki ilişkinin eşitliğidir (bu örnekte ilişkiler sayısaldır).
Temel orantı kuralı:
a:b=c:d
ekstrem terimlerin çarpımı orta terimlerin çarpımına eşittir
yani
a∙d=b∙c
*Bir orandaki herhangi bir değer bilinmiyorsa her zaman bulunabilir.
Şöyle bir kayıt formu düşünürsek:
o zaman şu kuralı kullanabilirsiniz, buna “çarpı kuralı” denir: köşegen üzerinde duran elemanların (sayılar veya ifadeler) çarpımlarının eşitliği yazılır
a∙d=b∙c
Gördüğünüz gibi sonuç aynı.
Oranın üç unsuru biliniyorsaher zaman dördüncüsünü bulabiliriz.
Faydanın ve gerekliliğin özü tam da budurSorunları çözerken oranlar.
Bilinmeyen x miktarının, a, b, c'nin sayılar olduğu oranda "herhangi bir yerde" bulunduğu tüm seçeneklere bakalım:

X'e çapraz olarak gelen miktar kesrin paydasına, çapraz olarak bilinen miktarlar ise paya çarpım olarak yazılır. Ezberlemenize gerek yok; eğer temel orantı kuralını öğrendiyseniz zaten her şeyi doğru hesaplayacaksınız.
Şimdi asıl soru makalenin başlığıyla ilgili. Oran ne zaman tasarruf sağlar ve nerede kullanılır? Örneğin:
1. Öncelikle bunlar yüzde içeren problemlerdir. Onlara "" ve "" makalelerinde baktık.
2. Birçok formül orantı şeklinde verilmiştir:
>sinüs teoremi
> bir üçgendeki elemanların ilişkisi

> teğet teoremi

> Thales teoremi ve diğerleri.
3. Geometri problemlerinde koşul genellikle kenarların (diğer elemanların) veya alanların oranını belirtir; örneğin 1:2, 2:3 ve diğerleri.
4. Hem bir ölçüdeki birimleri dönüştürmek hem de bir ölçüden diğerine dönüştürmek için kullanılan oran ile ölçü birimlerinin dönüştürülmesi:
- saatlerden dakikalara (ve tam tersi).
- hacim birimleri, alan.
— uzunluklar, örneğin milden kilometreye (ve tersi).
— Dereceden radyana (ve tam tersi).
burada oranlar çizmeden yapamazsınız.
Önemli olan yazışmaları doğru bir şekilde kurmanız gerektiğidir, basit örneklere bakalım:
700'ün %35'i kadar bir sayı belirlemeniz gerekiyor.
Yüzde içeren problemlerde karşılaştırdığımız değer %100 olarak alınır. Bilinmeyen sayıyı x olarak gösteririz. Yazışma kuralım:
Yedi yüz otuz beşin yüzde 100'e karşılık geldiğini söyleyebiliriz.
X yüzde 35'e karşılık gelir. Araç,
700 – 100%
x – %35
Haydi karar verelim

Cevap: 245
50 dakikayı saate çevirelim.
Bir saatin 60 dakikaya eşit olduğunu biliyoruz. Yazışmaları belirtelim -x saat 50 dakikadır. Araç
1 – 60
x – 50
Biz karar veriyoruz:
Yani 50 dakika bir saatin altıda beşidir.
Cevap: 5/6
Nikolai Petrovich 3 kilometre sürdü. Mil cinsinden ne kadar olacak (1 milin 1,6 km olduğunu düşünün)?
1 milin 1,6 kilometre olduğu biliniyor. Nikolai Petrovich'in kat ettiği mil sayısını x olarak alalım. Eşleşebiliriz:
Bir mil 1,6 kilometreye karşılık gelir.
X mil üç kilometredir.
1 – 1,6
x – 3
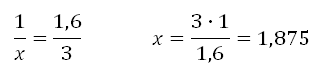
Cevap: 1.875 mil
Dereceleri radyana (ve tam tersi) dönüştürmek için formüller olduğunu biliyorsunuz. Bunları yazmıyorum çünkü ezberlemenin gereksiz olduğunu ve bu nedenle birçok bilgiyi hafızanızda tutmanız gerektiğini düşünüyorum. Orantı kullanıyorsanız dereceleri her zaman radyana (veya tam tersi) dönüştürebilirsiniz.
65 dereceyi radyan birimine çevirelim.
Hatırlanması gereken en önemli şey 180 derecenin Pi radyan olmasıdır.
İstenilen miktarı x olarak gösterelim. Yazışmalar kuruyoruz.
Yüz seksen derece Pi radyanına karşılık gelir.
Altmış beş derece x radyana karşılık gelir. makaleyi inceleyin bu konu hakkında blogda. İçindeki materyal biraz farklı sunuluyor, ancak prensip aynı. Bununla bitireceğim. Kesinlikle daha ilginç bir şey olacak, kaçırmayın!
Matematiğin tanımını hatırlarsak, şu kelimeleri içerir: matematik çalışmaları niceliksel İLİŞKİLER (İLİŞKİLER)- anahtar kelime burada). Gördüğünüz gibi matematiğin tanımı orantıyı içeriyor. Genel olarak orantısız matematik matematik değildir!!!
Herşey gönlünce olsun!
Saygılarımla, İskender
Not: Siteyi sosyal ağlarda anlatırsanız sevinirim.








