Ваша цель: знать методы доказательства неравенств и уметь их применять.
Понятие доказательства неравенства . Некоторые неравенства обращаются в верное числовое неравенство при всех допустимых значениях переменных или на некотором заданном множестве значений переменных. Например, неравенства а 2 ³0, (а –b ) 2 ³ 0, a 2 + b 2 + c 2 " ³ 0 верны при любых действительных значениях переменных, а неравенство ³ 0 – при любых действительных неотрицательных значениях а. Иногда возникает задача доказательства неравенства.
Доказать неравенство – значит показать, что данное неравенство обращается в верное числовое неравенство при всех допустимых значениях переменных или на заданном множестве значений этих переменных.
Методы доказательства неравенств. Заметим, что общего метода доказательства неравенств не существует. Однако некоторые из них можно указать.
1. Метод оценки знака разности между левой и правой частями неравенства. Составляется разность левой и правой частей неравенства и устанавливается, положительна или отрицательна эта разность при рассматриваемых значениях переменных (для нестрогих неравенств надо установить, неотрицательна или неположительна эта разность).
Пример 1. Для любых действительных чисел а и b имеет место неравенство
a 2 +b 2 ³ 2ab. (1)
Доказательство. Составим разность левой и правой частей неравенства:
a 2 +b 2 – 2ab = a 2 – 2ab + b 2 = (a – b ) 2 .
Так как квадрат любого действительного числа есть число неотрицательное, то (a – b ) 2 ³ 0, а, значит, a 2 +b 2 ³ 2ab для любых действительных чисел а и b. Равенство в (1) имеет место в том и только в том случае, когда а = b.
Пример 2. Доказать, что если а ³ 0 и b ³ 0, то ³ , т.е. среднее арифметическое неотрицательных действительных чисел а и b не меньше их среднего геометрического.
Доказательство. Если а ³ 0 и b ³ 0, то
³ 0. Значит, ³ .
2. Дедуктивный метод доказательства неравенств. Сущность этого метода заключается в следующем: с помощью ряда преобразований выводят требуемое неравенство из некоторых известных (опорных) неравенств. В качестве опорных могут использоваться, например, неравенства: а 2 ³ 0 при любом a Î R ; (a – b ) 2 ³ 0 при любых а и b Î R ; (а 2 + b 2) ³ 2ab при любых a, b Î R ; ³ при а ³ 0, b ³ 0.
Пример 3. Доказать, что для любых действительных чисел а и b имеет место неравенство
а 2 + b 2 + с 2 ³ ab + bc + ac.
Доказательство. Из верных неравенств (a – b ) 2 ³ 0, (b – c ) 2 ³ 0 и (c – a ) 2 ³ 0 следует, что а 2 + b 2 ³ 2ab , b 2 + c 2 ³ 2bc , c 2 + a 2 ³ 2ac. Сложив почленно все три неравенства и разделив обе части нового на 2, получим требуемое неравенство.
Исходное неравенство можно доказать и первым методом. В самом деле, а 2 + b 2 + с 2 – ab – bc – ac = 0,5(2а 2 + 2b 2 + 2с 2 – 2ab – 2bc – 2ac ) = = 0,5((a – b ) 2 + (a – c ) 2 + (b – c ) 2)³ 0.
Разность между а 2 + b 2 + с 2 и ab + bc + ac больше или равна нулю, а это значит, что а 2 + b 2 + с 2 ³ ab + bc + ac (равенство справедливо тогда и только тогда, когда а = b = с).
3. Метод оценок при доказательстве неравенств.
Пример 4. Доказать неравенство
+ + + … + >
Доказательство. Легко заметить, что левая часть неравенства содержит 100 слагаемых, каждое из которых не меньше. В таком случае говорят, что левую часть неравенства можно оценить снизу следующим образом:
+ + + … + > = 100 = .
4. Метод полной индукции. Сущность метода состоит в рассмотрении всех частных случаев, охватывающих условие задачи в целом.
Пример 5. Доказать, что если х > ïу ï, то х > у.
Доказательство. Возможны два случая:
а) у ³ 0; тогда ïу ï = у, а по условию х > ïу ï. Значит, х > у;
б) у < 0; тогда ïу ï > у и по условию х > ïу ï, значит, х > у.
Практическая часть
Задание 0. Возьмите чистый лист бумаги и на нем запишите ответы на все устные упражнения приведенные ниже. Затем свои ответы сверьте с ответами или краткими указания, помещенными в конце этого учебного элемента в рубрике «Ваш помощник».
Устные упражнения
1. Сравните сумму квадратов двух неравных чисел и с их удвоенным произведением.
2. Докажите неравенство:
а) ![]() ;
;
б) ![]() ;
;
в) ![]() ;
;
3. Известно, что . Докажите, что .
4. Известно, что . Докажите, что .
Задание 1. Что больше:
а) 2 + 11 или 9; г) + или;
б) или + ; д) – или;
в) + или 2; е) + 2 или + ?
Задание 2. Докажите, что при любом действительном x имеет место неравенство:
а) 3(x + 1) + x – 4(2 + x ) < 0; г) 4x 2 + 1 ³ 4x ;
б) (x + 2)(x + 4) > (x + 1)(x + 5); д) ³ 2x;
в) (x – 2) 2 > x (x – 4); е) l + 2x 4 > x 2 + 2x 3 .
Задание 3. Докажите, что:
а) x 3 + 1 ³ x 2 + x, если x ³ –1;
б) x 3 + 1 £ x 2 + x, если x £ –1.
Задание 4. Докажите, что если a ³ 0, b ³ 0, с ³ 0, d ³ 0, то
(a 2 + b 2)(c 2 + d 2) ³ (ac + bd ) 2 .
Задание 5. Докажите неравенство, выделив полный квадрат:
а) x 2 – 2xy + 9y 2 ³ 0;
б) x 2 + y 2 + 2³2(x + y );
в) 10x 2 + 10xy + 5y 2 + 1 > 0;
г) x 2 – xy + y 2 ³ 0;
д) x 2 + y 2 + z 2 + 3³ 2(х + у + z );
e) (x + l)(x – 2y + l) + y 2 ³ 0.
Задание 6. Докажите, что:
а) x 2 + 2y 2 + 2xy + 6y + l0 > 0;
б) x 2 + y 2 – 2xy + 2x – 2у + 1 > 0;
в) 3x 2 + y 2 + 8x + 4y – 2xy + 22 ³ 0;
г) x 2 + 2xy + 3y 2 + 2x + 6y + 3 > 0.
Задание 7. Докажите, что если n ³ k ³ 1, то k (n – k + 1) ³ n.
Задание 8. Докажите, что если 4а + 2b = 1, то a 2 + b 2 ³ .
Определите значения а и b, при которых имеет место равенство.
Задание 9. Докажите неравенство:
а) х 3 + у 3 ³ х 2 у + ху 2 при x ³ 0 и y ³ 0;
б) х 4 + у 4 ³ х 3 у + ху 3 при любых x и у ;
в) х 5 + у 5 ³ х 4 у + ху 4 при x ³ 0 и y ³ 0;
г) х n + у n ³ х n -1 у + ху n -1 при x ³ 0 и y ³ 0.
Методы доказательства неравенств.
Решение неравенств. Равносильные неравенства.
Метод интервалов. Системы неравенств.
Доказательство неравенств. Существует несколько методов доказатель ства неравенств. Мы рассмотрим их на примере неравенства:
где a – положительное число.
1). Использование известного или ранее доказанного неравенства.
Известно, что ( a – 1 )² 0 .
2). Оценка знака разности между частями неравенства .
Рассмотрим разность между левой и правой частью:
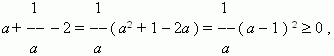
более того, равенство имеет место только при
a = 1 .3). Доказательство от противного.
Предположим противное:a , получим: a 2 + 1 < 2 a , т. e .
a 2 + 1 – 2 a < 0 , или ( a – 1 ) 2 < 0, что неверно. (Почему?) .
Полученное противоречие доказывает справедливость
Рассматриваемого неравенства.
4). Метод неопределённого неравенства.
Неравенство называется неопределённым , если у него знак \/ или /\ ,
т.е. когда мы не знаем в какую сторону следует повернуть этот знак,
чтобы получить справедливое неравенство.
Здесь действуют те же правила, что и с обычными неравенствами.
Рассмотрим неопределённое неравенство:
Умножая обе части неравенства на a , получим: a 2 + 1 \/ 2 a , т. e .
а 2 + 1 – 2 a \/ 0 , или ( a – 1) 2 \/ 0 , но здесь мы уже знаем, как повернуть
Знак \/ , чтобы получить верное неравенство (Как?). Поворачивая его
В нужном направлении по
всей цепочке неравенств снизу вверх, мы
получим требуемое неравенство.
Решение неравенств. Два неравенства, содержащие одни и те же неизвестные, называются равносильными , если они справедливы при одних и тех же значениях этих неизвестных . Такое же определение используется для равносильности двух систем неравенств. Решение неравенств - это процесс перехода от одного неравенства к другому, равносильному неравенству. Для этого используются основные свойства неравенств (см. ). Кроме того, может быть использована замена любого выражения другим, тождественным данному. Неравенства могут быть алгебраические ( содержащие только многочлены ) и трансцендентные (например, логарифмические или тригонометрические ). Мы рассмотрим здесь один очень важный метод, используемый часто при решении алгебраических неравенств.
Метод интервалов. Решить неравенство: ( x – 3)( x – 5) < 2( x – 3). Здесь нельзя делить обе части неравенства на (x – 3), так как мы не знаем знака этого двучлена (он содержит неизвестное x ). Поэтому мы перенесём все члены неравенства в левую часть:
( x – 3)( x – 5) – 2( x – 3) < 0 ,
разложим её на множители:
( x – 3)( x – 5 – 2) < 0 ,
и получим: ( x – 3)( x – 7) < 0. Теперь определим знак произведения в левой части неравенства в различных числовых интервалах. Заметим, что x = 3 и x = 7 - корни этого выражения. Поэтому вся числовая ось разделится этими корнями на следующие три интервала:
В интервале I (x < 3 ) оба сомножителя отрицательны, следовательно , их произведение положительно ; в интервале II (3 < x < 7 ) первый множитель (x – 3 ) положителен, а второй (x – 7 ) отрицателен, поэтому их произведение отрицательно ; в интервале III (x > 7 ) оба сомножителя положительны, следовательно, их произведение также положительно . Теперь остаётся выбрать интервал, в котором наше произведение отрицательно . Это интервал II , следовательно, решение неравенства: 3 < x < 7. Последнее выражение - так называемое двойное неравенство . Оно означает, что x должен быть одновременно больше 3 и меньше 7.
П р и м е р. Решить следующее неравенство методом интервалов:
( x – 1)(x – 2)(x – 3) … (x –100) > 0 .
Р е ш е н и е. Корни левой части неравенства очевидны: 1, 2, 3, …, 100.
Они разбивают числовую ось на 101 интервал:
Так как количество скобок в левой части чётно (равно 100), то
При x < 1, когда все множители отрицательны, их произведение
Положительно. При переходе через корень происходит смена
Знака произведения. Поэтому следующим интервалом, внутри
Которого произведение положительно, будет (2, 3), затем (4, 5),
Затем (6, 7), … , (98, 99) и наконец , x >100.
Таким образом, данное неравенство имеет решение:
x < 1, 2 < x < 3, 4 < x < 5 ,…, x >100.
Итак, чтобы решить алгебраическое неравенство, надо перенести все его члены в левую (или правую) часть и решить соответствующее уравнение. После этого найденные корни нанести на числовую ось; в результате она разбивается на некоторое число интервалов. На последнем этапе решения нужно определить, какой знак имеет многочлен внутри каждого из этих интервалов, и выбрать нужные интервалы в соответствии со знаком решаемого неравенства.
Заметим, что большинство трансцендентных неравенств заменой неизвестного приводятся к алгебраическому неравенству. Его надо решить относительно нового неизвестного, а затем путём обратной замены найти решение для исходного неравенства.
Системы неравенств. Чтобы решить систему неравенств, необходимо решить каждое из них, и совместить их решения. Это совмещение приводит к одному из двух возможных случаев: либо система имеет решение, либо нет.
П р и м е р 1. Решить систему неравенств:

Р е ш е н и е. Решение первого неравенства:
x < 4 ; а второго: x > 6.Таким образом, эта система неравенств не имеет решения.
(Почему?)
П р и м е р 2. Решить систему неравенств:
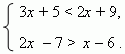
Р е ш е н и е. Первое неравенство, как и прежде, даёт: x < 4; но решение
Второго неравенства в данном примере: x > 1.
Таким образом, решение системы неравенств: 1 < x < 4.
Учебное заведение: МОУ Лицей№1 г.Комсомольск-на-Амуре
Руководитель: Будлянская Наталья Леонидовна
Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой, пока есть к тому возможность. Она окажет вам потом огромную помощь во всей вашей работе. (М.И. Калинин)

Представление левой части неравенства в виде суммы неотрицательных слагаемых (правая часть равна 0) с использованием тождеств.
Пример 1
. Доказать что для любого хϵR
Доказательство. 1 способ
.
2 способ
.
для квадратичной функции что означает её положительность при любом действительном х
.

Пример 2
. Доказать, что для любых x и y
Доказательство. Пример 3
. Доказать, что
Доказательство. Пример 4
. Доказать, что для любых a и b
Доказательство.

2. Метод от противного
Вот хороший пример применения данного метода. Доказать, что для a, b ϵ R.
Доказательство. Предположим, что. Но,что явно доказывает, что наше предположение неверно. Ч.Т.Д.

Пример 5
. Доказать, что для любых чисел А,В,С справедливо неравенство
Доказательство.
Очевидно, что данное неравенство достаточно установить для неотрицательных А, В
и С,
так как будем иметь следующее отношения: ,
что является обоснованием исходного неравенства.

Пусть теперь нашлись такие неотрицательные числа А, В
и С
, для которых выполняется неравенство , что невозможно ни при каких действительных А,В
и С
. Сделанное выше предположение опровергнуто, что доказывает исследуемое исходное неравенство.

Использование свойств квадратного трехчлена
Метод основан на свойстве неотрицательности квадратного трехчлена, если и. Пример 6
. Доказать, что
Доказательство. Пусть, a=2, 2>0
=>

Пример 7
. Доказать, что для любых действительных х и у имеет место быть неравенство
Доказательство. Рассмотрим левую часть неравенство как квадратный трехчлен относительно х:
, а>0, D D= => P(x)>0
и верно при любых действительных значениях х
и у.

Пример 8
. Доказать, что
для любых действительных значениях х и у.
Доказательство. Пусть
, Это означает, что для любых действительных у
и неравенство выполняется при любых действительных х
и у.

Метод введения новых переменных или метод подстановки
Пример 9
. Доказать, что для любых неотрицательных чисел х, у, z
Доказательство. Воспользуемся верным неравенством для, . Получаем исследуемое неравенство

Использование свойств функций.
Пример 10
. Докажем неравенство
для любых а и b.
Доказательство. Рассмотрим 2 случая: Если а=b,то верно
причем равенство достигается только при а=b=0. 2)Если , на R => ()* ()>0, что доказывает неравенство

Пример 11
. Докажем, что для любых
Доказательство. на R. Если, то знаки чисел и совпадают, что означает положительность исследуемой разности =>

Применение метода математической индукции
Данный метод применяется для доказательства неравенств относительно натуральных чисел. Пример 12
. Доказать, что для любого nϵN
Проверим истинность утверждения при
- (верно) 2) Предположим верность утверждения при (k>1)

3) Докажем истинность утверждения при n=k+1. Сравним и: , Имеем: Вывод: утверждение верно для любого nϵN.

Использование замечательных неравенств
Теорема о средних (неравенство Коши)
Неравенство Коши – Буняковского
Неравенство Бернулли
Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)
Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического , где Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.
Доказательство. 1 способ
.
2 способ
.
для квадратичной функции что означает её положительность при любом действительном х
.

Пример 2
. Доказать, что для любых x и y
Доказательство. Пример 3
. Доказать, что
Доказательство. Пример 4
. Доказать, что для любых a и b
Доказательство.

2. Метод от противного
Вот хороший пример применения данного метода. Доказать, что для a, b ϵ R.
Доказательство. Предположим, что. Но,что явно доказывает, что наше предположение неверно. Ч.Т.Д.

Пример 5
. Доказать, что для любых чисел А,В,С справедливо неравенство
Доказательство.
Очевидно, что данное неравенство достаточно установить для неотрицательных А, В
и С,
так как будем иметь следующее отношения: ,
что является обоснованием исходного неравенства.

Пусть теперь нашлись такие неотрицательные числа А, В
и С
, для которых выполняется неравенство , что невозможно ни при каких действительных А,В
и С
. Сделанное выше предположение опровергнуто, что доказывает исследуемое исходное неравенство.

Использование свойств квадратного трехчлена
Метод основан на свойстве неотрицательности квадратного трехчлена, если и. Пример 6
. Доказать, что
Доказательство. Пусть, a=2, 2>0
=>

Пример 7
. Доказать, что для любых действительных х и у имеет место быть неравенство
Доказательство. Рассмотрим левую часть неравенство как квадратный трехчлен относительно х:
, а>0, D D= => P(x)>0
и верно при любых действительных значениях х
и у.

Пример 8
. Доказать, что
для любых действительных значениях х и у.
Доказательство. Пусть
, Это означает, что для любых действительных у
и неравенство выполняется при любых действительных х
и у.

Метод введения новых переменных или метод подстановки
Пример 9
. Доказать, что для любых неотрицательных чисел х, у, z
Доказательство. Воспользуемся верным неравенством для, . Получаем исследуемое неравенство

Использование свойств функций.
Пример 10
. Докажем неравенство
для любых а и b.
Доказательство. Рассмотрим 2 случая: Если а=b,то верно
причем равенство достигается только при а=b=0. 2)Если , на R => ()* ()>0, что доказывает неравенство

Пример 11
. Докажем, что для любых
Доказательство. на R. Если, то знаки чисел и совпадают, что означает положительность исследуемой разности =>

Применение метода математической индукции
Данный метод применяется для доказательства неравенств относительно натуральных чисел. Пример 12
. Доказать, что для любого nϵN
Проверим истинность утверждения при
- (верно) 2) Предположим верность утверждения при (k>1)

3) Докажем истинность утверждения при n=k+1. Сравним и: , Имеем: Вывод: утверждение верно для любого nϵN.

Использование замечательных неравенств
Теорема о средних (неравенство Коши)
Неравенство Коши – Буняковского
Неравенство Бернулли
Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)
Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического , где Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.
2 способ
.
для квадратичной функции что означает её положительность при любом действительном х
.

Пример 2
. Доказать, что для любых x и y
Доказательство. Пример 3
. Доказать, что
Доказательство. Пример 4
. Доказать, что для любых a и b
Доказательство.

2. Метод от противного
Вот хороший пример применения данного метода. Доказать, что для a, b ϵ R.
Доказательство. Предположим, что. Но,что явно доказывает, что наше предположение неверно. Ч.Т.Д.

Пример 5
. Доказать, что для любых чисел А,В,С справедливо неравенство
Доказательство.
Очевидно, что данное неравенство достаточно установить для неотрицательных А, В
и С,
так как будем иметь следующее отношения: ,
что является обоснованием исходного неравенства.

Пусть теперь нашлись такие неотрицательные числа А, В
и С
, для которых выполняется неравенство , что невозможно ни при каких действительных А,В
и С
. Сделанное выше предположение опровергнуто, что доказывает исследуемое исходное неравенство.

Использование свойств квадратного трехчлена
Метод основан на свойстве неотрицательности квадратного трехчлена, если и. Пример 6
. Доказать, что
Доказательство. Пусть, a=2, 2>0
=>

Пример 7
. Доказать, что для любых действительных х и у имеет место быть неравенство
Доказательство. Рассмотрим левую часть неравенство как квадратный трехчлен относительно х:
, а>0, D D= => P(x)>0
и верно при любых действительных значениях х
и у.

Пример 8
. Доказать, что
для любых действительных значениях х и у.
Доказательство. Пусть
, Это означает, что для любых действительных у
и неравенство выполняется при любых действительных х
и у.

Метод введения новых переменных или метод подстановки
Пример 9
. Доказать, что для любых неотрицательных чисел х, у, z
Доказательство. Воспользуемся верным неравенством для, . Получаем исследуемое неравенство

Использование свойств функций.
Пример 10
. Докажем неравенство
для любых а и b.
Доказательство. Рассмотрим 2 случая: Если а=b,то верно
причем равенство достигается только при а=b=0. 2)Если , на R => ()* ()>0, что доказывает неравенство

Пример 11
. Докажем, что для любых
Доказательство. на R. Если, то знаки чисел и совпадают, что означает положительность исследуемой разности =>

Применение метода математической индукции
Данный метод применяется для доказательства неравенств относительно натуральных чисел. Пример 12
. Доказать, что для любого nϵN
Проверим истинность утверждения при
- (верно) 2) Предположим верность утверждения при (k>1)

3) Докажем истинность утверждения при n=k+1. Сравним и: , Имеем: Вывод: утверждение верно для любого nϵN.

Использование замечательных неравенств
Теорема о средних (неравенство Коши)
Неравенство Коши – Буняковского
Неравенство Бернулли
Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)
Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического , где Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.
для квадратичной функции что означает её положительность при любом действительном х
.

Пример 2
. Доказать, что для любых x и y
Доказательство. Пример 3
. Доказать, что
Доказательство. Пример 4
. Доказать, что для любых a и b
Доказательство.

2. Метод от противного
Вот хороший пример применения данного метода. Доказать, что для a, b ϵ R.
Доказательство. Предположим, что. Но,что явно доказывает, что наше предположение неверно. Ч.Т.Д.

Пример 5
. Доказать, что для любых чисел А,В,С справедливо неравенство
Доказательство.
Очевидно, что данное неравенство достаточно установить для неотрицательных А, В
и С,
так как будем иметь следующее отношения: ,
что является обоснованием исходного неравенства.

Пусть теперь нашлись такие неотрицательные числа А, В
и С
, для которых выполняется неравенство , что невозможно ни при каких действительных А,В
и С
. Сделанное выше предположение опровергнуто, что доказывает исследуемое исходное неравенство.

Использование свойств квадратного трехчлена
Метод основан на свойстве неотрицательности квадратного трехчлена, если и. Пример 6
. Доказать, что
Доказательство. Пусть, a=2, 2>0
=>

Пример 7
. Доказать, что для любых действительных х и у имеет место быть неравенство
Доказательство. Рассмотрим левую часть неравенство как квадратный трехчлен относительно х:
, а>0, D D= => P(x)>0
и верно при любых действительных значениях х
и у.

Пример 8
. Доказать, что
для любых действительных значениях х и у.
Доказательство. Пусть
, Это означает, что для любых действительных у
и неравенство выполняется при любых действительных х
и у.

Метод введения новых переменных или метод подстановки
Пример 9
. Доказать, что для любых неотрицательных чисел х, у, z
Доказательство. Воспользуемся верным неравенством для, . Получаем исследуемое неравенство

Использование свойств функций.
Пример 10
. Докажем неравенство
для любых а и b.
Доказательство. Рассмотрим 2 случая: Если а=b,то верно
причем равенство достигается только при а=b=0. 2)Если , на R => ()* ()>0, что доказывает неравенство

Пример 11
. Докажем, что для любых
Доказательство. на R. Если, то знаки чисел и совпадают, что означает положительность исследуемой разности =>

Применение метода математической индукции
Данный метод применяется для доказательства неравенств относительно натуральных чисел. Пример 12
. Доказать, что для любого nϵN
Проверим истинность утверждения при
- (верно) 2) Предположим верность утверждения при (k>1)

3) Докажем истинность утверждения при n=k+1. Сравним и: , Имеем: Вывод: утверждение верно для любого nϵN.

Использование замечательных неравенств
Теорема о средних (неравенство Коши)
Неравенство Коши – Буняковского
Неравенство Бернулли
Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)
Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического , где Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.
что означает её положительность при любом действительном х
.

Пример 2
. Доказать, что для любых x и y
Доказательство. Пример 3
. Доказать, что
Доказательство. Пример 4
. Доказать, что для любых a и b
Доказательство.

2. Метод от противного
Вот хороший пример применения данного метода. Доказать, что для a, b ϵ R.
Доказательство. Предположим, что. Но,что явно доказывает, что наше предположение неверно. Ч.Т.Д.

Пример 5
. Доказать, что для любых чисел А,В,С справедливо неравенство
Доказательство.
Очевидно, что данное неравенство достаточно установить для неотрицательных А, В
и С,
так как будем иметь следующее отношения: ,
что является обоснованием исходного неравенства.

Пусть теперь нашлись такие неотрицательные числа А, В
и С
, для которых выполняется неравенство , что невозможно ни при каких действительных А,В
и С
. Сделанное выше предположение опровергнуто, что доказывает исследуемое исходное неравенство.

Использование свойств квадратного трехчлена
Метод основан на свойстве неотрицательности квадратного трехчлена, если и. Пример 6
. Доказать, что
Доказательство. Пусть, a=2, 2>0
=>

Пример 7
. Доказать, что для любых действительных х и у имеет место быть неравенство
Доказательство. Рассмотрим левую часть неравенство как квадратный трехчлен относительно х:
, а>0, D D= => P(x)>0
и верно при любых действительных значениях х
и у.

Пример 8
. Доказать, что
для любых действительных значениях х и у.
Доказательство. Пусть
, Это означает, что для любых действительных у
и неравенство выполняется при любых действительных х
и у.

Метод введения новых переменных или метод подстановки
Пример 9
. Доказать, что для любых неотрицательных чисел х, у, z
Доказательство. Воспользуемся верным неравенством для, . Получаем исследуемое неравенство

Использование свойств функций.
Пример 10
. Докажем неравенство
для любых а и b.
Доказательство. Рассмотрим 2 случая: Если а=b,то верно
причем равенство достигается только при а=b=0. 2)Если , на R => ()* ()>0, что доказывает неравенство

Пример 11
. Докажем, что для любых
Доказательство. на R. Если, то знаки чисел и совпадают, что означает положительность исследуемой разности =>

Применение метода математической индукции
Данный метод применяется для доказательства неравенств относительно натуральных чисел. Пример 12
. Доказать, что для любого nϵN
Проверим истинность утверждения при
- (верно) 2) Предположим верность утверждения при (k>1)

3) Докажем истинность утверждения при n=k+1. Сравним и: , Имеем: Вывод: утверждение верно для любого nϵN.

Использование замечательных неравенств
Теорема о средних (неравенство Коши)
Неравенство Коши – Буняковского
Неравенство Бернулли
Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)
Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического , где Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.

Пример 2
. Доказать, что для любых x и y
Доказательство. Пример 3
. Доказать, что
Доказательство. Пример 4
. Доказать, что для любых a и b
Доказательство.

2. Метод от противного
Вот хороший пример применения данного метода. Доказать, что для a, b ϵ R.
Доказательство. Предположим, что. Но,что явно доказывает, что наше предположение неверно. Ч.Т.Д.

Пример 5
. Доказать, что для любых чисел А,В,С справедливо неравенство
Доказательство.
Очевидно, что данное неравенство достаточно установить для неотрицательных А, В
и С,
так как будем иметь следующее отношения: ,
что является обоснованием исходного неравенства.

Пусть теперь нашлись такие неотрицательные числа А, В
и С
, для которых выполняется неравенство , что невозможно ни при каких действительных А,В
и С
. Сделанное выше предположение опровергнуто, что доказывает исследуемое исходное неравенство.

Использование свойств квадратного трехчлена
Метод основан на свойстве неотрицательности квадратного трехчлена, если и. Пример 6
. Доказать, что
Доказательство. Пусть, a=2, 2>0
=>

Пример 7
. Доказать, что для любых действительных х и у имеет место быть неравенство
Доказательство. Рассмотрим левую часть неравенство как квадратный трехчлен относительно х:
, а>0, D D= => P(x)>0
и верно при любых действительных значениях х
и у.

Пример 8
. Доказать, что
для любых действительных значениях х и у.
Доказательство. Пусть
, Это означает, что для любых действительных у
и неравенство выполняется при любых действительных х
и у.

Метод введения новых переменных или метод подстановки
Пример 9
. Доказать, что для любых неотрицательных чисел х, у, z
Доказательство. Воспользуемся верным неравенством для, . Получаем исследуемое неравенство

Использование свойств функций.
Пример 10
. Докажем неравенство
для любых а и b.
Доказательство. Рассмотрим 2 случая: Если а=b,то верно
причем равенство достигается только при а=b=0. 2)Если , на R => ()* ()>0, что доказывает неравенство

Пример 11
. Докажем, что для любых
Доказательство. на R. Если, то знаки чисел и совпадают, что означает положительность исследуемой разности =>

Применение метода математической индукции
Данный метод применяется для доказательства неравенств относительно натуральных чисел. Пример 12
. Доказать, что для любого nϵN
Проверим истинность утверждения при
- (верно) 2) Предположим верность утверждения при (k>1)

3) Докажем истинность утверждения при n=k+1. Сравним и: , Имеем: Вывод: утверждение верно для любого nϵN.

Использование замечательных неравенств
Теорема о средних (неравенство Коши)
Неравенство Коши – Буняковского
Неравенство Бернулли
Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)
Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического , где Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.
Доказательство. Пример 3
. Доказать, что
Доказательство. Пример 4
. Доказать, что для любых a и b
Доказательство.

2. Метод от противного
Вот хороший пример применения данного метода. Доказать, что для a, b ϵ R.
Доказательство. Предположим, что. Но,что явно доказывает, что наше предположение неверно. Ч.Т.Д.

Пример 5
. Доказать, что для любых чисел А,В,С справедливо неравенство
Доказательство.
Очевидно, что данное неравенство достаточно установить для неотрицательных А, В
и С,
так как будем иметь следующее отношения: ,
что является обоснованием исходного неравенства.

Пусть теперь нашлись такие неотрицательные числа А, В
и С
, для которых выполняется неравенство , что невозможно ни при каких действительных А,В
и С
. Сделанное выше предположение опровергнуто, что доказывает исследуемое исходное неравенство.

Использование свойств квадратного трехчлена
Метод основан на свойстве неотрицательности квадратного трехчлена, если и. Пример 6
. Доказать, что
Доказательство. Пусть, a=2, 2>0
=>

Пример 7
. Доказать, что для любых действительных х и у имеет место быть неравенство
Доказательство. Рассмотрим левую часть неравенство как квадратный трехчлен относительно х:
, а>0, D D= => P(x)>0
и верно при любых действительных значениях х
и у.

Пример 8
. Доказать, что
для любых действительных значениях х и у.
Доказательство. Пусть
, Это означает, что для любых действительных у
и неравенство выполняется при любых действительных х
и у.

Метод введения новых переменных или метод подстановки
Пример 9
. Доказать, что для любых неотрицательных чисел х, у, z
Доказательство. Воспользуемся верным неравенством для, . Получаем исследуемое неравенство

Использование свойств функций.
Пример 10
. Докажем неравенство
для любых а и b.
Доказательство. Рассмотрим 2 случая: Если а=b,то верно
причем равенство достигается только при а=b=0. 2)Если , на R => ()* ()>0, что доказывает неравенство

Пример 11
. Докажем, что для любых
Доказательство. на R. Если, то знаки чисел и совпадают, что означает положительность исследуемой разности =>

Применение метода математической индукции
Данный метод применяется для доказательства неравенств относительно натуральных чисел. Пример 12
. Доказать, что для любого nϵN
Проверим истинность утверждения при
- (верно) 2) Предположим верность утверждения при (k>1)

3) Докажем истинность утверждения при n=k+1. Сравним и: , Имеем: Вывод: утверждение верно для любого nϵN.

Использование замечательных неравенств
Теорема о средних (неравенство Коши)
Неравенство Коши – Буняковского
Неравенство Бернулли
Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)
Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического , где Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.
Доказательство. Пример 4
. Доказать, что для любых a и b
Доказательство.

2. Метод от противного
Вот хороший пример применения данного метода. Доказать, что для a, b ϵ R.
Доказательство. Предположим, что. Но,что явно доказывает, что наше предположение неверно. Ч.Т.Д.

Пример 5
. Доказать, что для любых чисел А,В,С справедливо неравенство
Доказательство.
Очевидно, что данное неравенство достаточно установить для неотрицательных А, В
и С,
так как будем иметь следующее отношения: ,
что является обоснованием исходного неравенства.

Пусть теперь нашлись такие неотрицательные числа А, В
и С
, для которых выполняется неравенство , что невозможно ни при каких действительных А,В
и С
. Сделанное выше предположение опровергнуто, что доказывает исследуемое исходное неравенство.

Использование свойств квадратного трехчлена
Метод основан на свойстве неотрицательности квадратного трехчлена, если и. Пример 6
. Доказать, что
Доказательство. Пусть, a=2, 2>0
=>

Пример 7
. Доказать, что для любых действительных х и у имеет место быть неравенство
Доказательство. Рассмотрим левую часть неравенство как квадратный трехчлен относительно х:
, а>0, D D= => P(x)>0
и верно при любых действительных значениях х
и у.

Пример 8
. Доказать, что
для любых действительных значениях х и у.
Доказательство. Пусть
, Это означает, что для любых действительных у
и неравенство выполняется при любых действительных х
и у.

Метод введения новых переменных или метод подстановки
Пример 9
. Доказать, что для любых неотрицательных чисел х, у, z
Доказательство. Воспользуемся верным неравенством для, . Получаем исследуемое неравенство

Использование свойств функций.
Пример 10
. Докажем неравенство
для любых а и b.
Доказательство. Рассмотрим 2 случая: Если а=b,то верно
причем равенство достигается только при а=b=0. 2)Если , на R => ()* ()>0, что доказывает неравенство

Пример 11
. Докажем, что для любых
Доказательство. на R. Если, то знаки чисел и совпадают, что означает положительность исследуемой разности =>

Применение метода математической индукции
Данный метод применяется для доказательства неравенств относительно натуральных чисел. Пример 12
. Доказать, что для любого nϵN
Проверим истинность утверждения при
- (верно) 2) Предположим верность утверждения при (k>1)

3) Докажем истинность утверждения при n=k+1. Сравним и: , Имеем: Вывод: утверждение верно для любого nϵN.

Использование замечательных неравенств
Теорема о средних (неравенство Коши)
Неравенство Коши – Буняковского
Неравенство Бернулли
Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)
Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического , где Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.
Доказательство.

2. Метод от противного
Вот хороший пример применения данного метода. Доказать, что для a, b ϵ R.
Доказательство. Предположим, что. Но,что явно доказывает, что наше предположение неверно. Ч.Т.Д.

Пример 5
. Доказать, что для любых чисел А,В,С справедливо неравенство
Доказательство.
Очевидно, что данное неравенство достаточно установить для неотрицательных А, В
и С,
так как будем иметь следующее отношения: ,
что является обоснованием исходного неравенства.

Пусть теперь нашлись такие неотрицательные числа А, В
и С
, для которых выполняется неравенство , что невозможно ни при каких действительных А,В
и С
. Сделанное выше предположение опровергнуто, что доказывает исследуемое исходное неравенство.

Использование свойств квадратного трехчлена
Метод основан на свойстве неотрицательности квадратного трехчлена, если и. Пример 6
. Доказать, что
Доказательство. Пусть, a=2, 2>0
=>

Пример 7
. Доказать, что для любых действительных х и у имеет место быть неравенство
Доказательство. Рассмотрим левую часть неравенство как квадратный трехчлен относительно х:
, а>0, D D= => P(x)>0
и верно при любых действительных значениях х
и у.

Пример 8
. Доказать, что
для любых действительных значениях х и у.
Доказательство. Пусть
, Это означает, что для любых действительных у
и неравенство выполняется при любых действительных х
и у.

Метод введения новых переменных или метод подстановки
Пример 9
. Доказать, что для любых неотрицательных чисел х, у, z
Доказательство. Воспользуемся верным неравенством для, . Получаем исследуемое неравенство

Использование свойств функций.
Пример 10
. Докажем неравенство
для любых а и b.
Доказательство. Рассмотрим 2 случая: Если а=b,то верно
причем равенство достигается только при а=b=0. 2)Если , на R => ()* ()>0, что доказывает неравенство

Пример 11
. Докажем, что для любых
Доказательство. на R. Если, то знаки чисел и совпадают, что означает положительность исследуемой разности =>

Применение метода математической индукции
Данный метод применяется для доказательства неравенств относительно натуральных чисел. Пример 12
. Доказать, что для любого nϵN
Проверим истинность утверждения при
- (верно) 2) Предположим верность утверждения при (k>1)

3) Докажем истинность утверждения при n=k+1. Сравним и: , Имеем: Вывод: утверждение верно для любого nϵN.

Использование замечательных неравенств
Теорема о средних (неравенство Коши)
Неравенство Коши – Буняковского
Неравенство Бернулли
Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)
Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического , где Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.
Доказать, что для a, b ϵ R.
Доказательство. Предположим, что. Но,что явно доказывает, что наше предположение неверно. Ч.Т.Д.

Пример 5
. Доказать, что для любых чисел А,В,С справедливо неравенство
Доказательство.
Очевидно, что данное неравенство достаточно установить для неотрицательных А, В
и С,
так как будем иметь следующее отношения: ,
что является обоснованием исходного неравенства.

Пусть теперь нашлись такие неотрицательные числа А, В
и С
, для которых выполняется неравенство , что невозможно ни при каких действительных А,В
и С
. Сделанное выше предположение опровергнуто, что доказывает исследуемое исходное неравенство.

Использование свойств квадратного трехчлена
Метод основан на свойстве неотрицательности квадратного трехчлена, если и. Пример 6
. Доказать, что
Доказательство. Пусть, a=2, 2>0
=>

Пример 7
. Доказать, что для любых действительных х и у имеет место быть неравенство
Доказательство. Рассмотрим левую часть неравенство как квадратный трехчлен относительно х:
, а>0, D D= => P(x)>0
и верно при любых действительных значениях х
и у.

Пример 8
. Доказать, что
для любых действительных значениях х и у.
Доказательство. Пусть
, Это означает, что для любых действительных у
и неравенство выполняется при любых действительных х
и у.

Метод введения новых переменных или метод подстановки
Пример 9
. Доказать, что для любых неотрицательных чисел х, у, z
Доказательство. Воспользуемся верным неравенством для, . Получаем исследуемое неравенство

Использование свойств функций.
Пример 10
. Докажем неравенство
для любых а и b.
Доказательство. Рассмотрим 2 случая: Если а=b,то верно
причем равенство достигается только при а=b=0. 2)Если , на R => ()* ()>0, что доказывает неравенство

Пример 11
. Докажем, что для любых
Доказательство. на R. Если, то знаки чисел и совпадают, что означает положительность исследуемой разности =>

Применение метода математической индукции
Данный метод применяется для доказательства неравенств относительно натуральных чисел. Пример 12
. Доказать, что для любого nϵN
Проверим истинность утверждения при
- (верно) 2) Предположим верность утверждения при (k>1)

3) Докажем истинность утверждения при n=k+1. Сравним и: , Имеем: Вывод: утверждение верно для любого nϵN.

Использование замечательных неравенств
Теорема о средних (неравенство Коши)
Неравенство Коши – Буняковского
Неравенство Бернулли
Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)
Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического , где Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.
Предположим, что. Но,что явно доказывает, что наше предположение неверно. Ч.Т.Д.

Пример 5
. Доказать, что для любых чисел А,В,С справедливо неравенство
Доказательство.
Очевидно, что данное неравенство достаточно установить для неотрицательных А, В
и С,
так как будем иметь следующее отношения: ,
что является обоснованием исходного неравенства.

Пусть теперь нашлись такие неотрицательные числа А, В
и С
, для которых выполняется неравенство , что невозможно ни при каких действительных А,В
и С
. Сделанное выше предположение опровергнуто, что доказывает исследуемое исходное неравенство.

Использование свойств квадратного трехчлена
Метод основан на свойстве неотрицательности квадратного трехчлена, если и. Пример 6
. Доказать, что
Доказательство. Пусть, a=2, 2>0
=>

Пример 7
. Доказать, что для любых действительных х и у имеет место быть неравенство
Доказательство. Рассмотрим левую часть неравенство как квадратный трехчлен относительно х:
, а>0, D D= => P(x)>0
и верно при любых действительных значениях х
и у.

Пример 8
. Доказать, что
для любых действительных значениях х и у.
Доказательство. Пусть
, Это означает, что для любых действительных у
и неравенство выполняется при любых действительных х
и у.

Метод введения новых переменных или метод подстановки
Пример 9
. Доказать, что для любых неотрицательных чисел х, у, z
Доказательство. Воспользуемся верным неравенством для, . Получаем исследуемое неравенство

Использование свойств функций.
Пример 10
. Докажем неравенство
для любых а и b.
Доказательство. Рассмотрим 2 случая: Если а=b,то верно
причем равенство достигается только при а=b=0. 2)Если , на R => ()* ()>0, что доказывает неравенство

Пример 11
. Докажем, что для любых
Доказательство. на R. Если, то знаки чисел и совпадают, что означает положительность исследуемой разности =>

Применение метода математической индукции
Данный метод применяется для доказательства неравенств относительно натуральных чисел. Пример 12
. Доказать, что для любого nϵN
Проверим истинность утверждения при
- (верно) 2) Предположим верность утверждения при (k>1)

3) Докажем истинность утверждения при n=k+1. Сравним и: , Имеем: Вывод: утверждение верно для любого nϵN.

Использование замечательных неравенств
Теорема о средних (неравенство Коши)
Неравенство Коши – Буняковского
Неравенство Бернулли
Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)
Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического , где Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.
Ч.Т.Д.

Пример 5
. Доказать, что для любых чисел А,В,С справедливо неравенство
Доказательство.
Очевидно, что данное неравенство достаточно установить для неотрицательных А, В
и С,
так как будем иметь следующее отношения: ,
что является обоснованием исходного неравенства.

Пусть теперь нашлись такие неотрицательные числа А, В
и С
, для которых выполняется неравенство , что невозможно ни при каких действительных А,В
и С
. Сделанное выше предположение опровергнуто, что доказывает исследуемое исходное неравенство.

Использование свойств квадратного трехчлена
Метод основан на свойстве неотрицательности квадратного трехчлена, если и. Пример 6
. Доказать, что
Доказательство. Пусть, a=2, 2>0
=>

Пример 7
. Доказать, что для любых действительных х и у имеет место быть неравенство
Доказательство. Рассмотрим левую часть неравенство как квадратный трехчлен относительно х:
, а>0, D D= => P(x)>0
и верно при любых действительных значениях х
и у.

Пример 8
. Доказать, что
для любых действительных значениях х и у.
Доказательство. Пусть
, Это означает, что для любых действительных у
и неравенство выполняется при любых действительных х
и у.

Метод введения новых переменных или метод подстановки
Пример 9
. Доказать, что для любых неотрицательных чисел х, у, z
Доказательство. Воспользуемся верным неравенством для, . Получаем исследуемое неравенство

Использование свойств функций.
Пример 10
. Докажем неравенство
для любых а и b.
Доказательство. Рассмотрим 2 случая: Если а=b,то верно
причем равенство достигается только при а=b=0. 2)Если , на R => ()* ()>0, что доказывает неравенство

Пример 11
. Докажем, что для любых
Доказательство. на R. Если, то знаки чисел и совпадают, что означает положительность исследуемой разности =>

Применение метода математической индукции
Данный метод применяется для доказательства неравенств относительно натуральных чисел. Пример 12
. Доказать, что для любого nϵN
Проверим истинность утверждения при
- (верно) 2) Предположим верность утверждения при (k>1)

3) Докажем истинность утверждения при n=k+1. Сравним и: , Имеем: Вывод: утверждение верно для любого nϵN.

Использование замечательных неравенств
Теорема о средних (неравенство Коши)
Неравенство Коши – Буняковского
Неравенство Бернулли
Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)
Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического , где Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.
Доказательство.
Очевидно, что данное неравенство достаточно установить для неотрицательных А, В
и С,
так как будем иметь следующее отношения: ,
что является обоснованием исходного неравенства.

Пусть теперь нашлись такие неотрицательные числа А, В
и С
, для которых выполняется неравенство , что невозможно ни при каких действительных А,В
и С
. Сделанное выше предположение опровергнуто, что доказывает исследуемое исходное неравенство.

Использование свойств квадратного трехчлена
Метод основан на свойстве неотрицательности квадратного трехчлена, если и. Пример 6
. Доказать, что
Доказательство. Пусть, a=2, 2>0
=>

Пример 7
. Доказать, что для любых действительных х и у имеет место быть неравенство
Доказательство. Рассмотрим левую часть неравенство как квадратный трехчлен относительно х:
, а>0, D D= => P(x)>0
и верно при любых действительных значениях х
и у.

Пример 8
. Доказать, что
для любых действительных значениях х и у.
Доказательство. Пусть
, Это означает, что для любых действительных у
и неравенство выполняется при любых действительных х
и у.

Метод введения новых переменных или метод подстановки
Пример 9
. Доказать, что для любых неотрицательных чисел х, у, z
Доказательство. Воспользуемся верным неравенством для, . Получаем исследуемое неравенство

Использование свойств функций.
Пример 10
. Докажем неравенство
для любых а и b.
Доказательство. Рассмотрим 2 случая: Если а=b,то верно
причем равенство достигается только при а=b=0. 2)Если , на R => ()* ()>0, что доказывает неравенство

Пример 11
. Докажем, что для любых
Доказательство. на R. Если, то знаки чисел и совпадают, что означает положительность исследуемой разности =>

Применение метода математической индукции
Данный метод применяется для доказательства неравенств относительно натуральных чисел. Пример 12
. Доказать, что для любого nϵN
Проверим истинность утверждения при
- (верно) 2) Предположим верность утверждения при (k>1)

3) Докажем истинность утверждения при n=k+1. Сравним и: , Имеем: Вывод: утверждение верно для любого nϵN.

Использование замечательных неравенств
Теорема о средних (неравенство Коши)
Неравенство Коши – Буняковского
Неравенство Бернулли
Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)
Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического , где Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.
,
что является обоснованием исходного неравенства.

Пусть теперь нашлись такие неотрицательные числа А, В
и С
, для которых выполняется неравенство , что невозможно ни при каких действительных А,В
и С
. Сделанное выше предположение опровергнуто, что доказывает исследуемое исходное неравенство.

Использование свойств квадратного трехчлена
Метод основан на свойстве неотрицательности квадратного трехчлена, если и. Пример 6
. Доказать, что
Доказательство. Пусть, a=2, 2>0
=>

Пример 7
. Доказать, что для любых действительных х и у имеет место быть неравенство
Доказательство. Рассмотрим левую часть неравенство как квадратный трехчлен относительно х:
, а>0, D D= => P(x)>0
и верно при любых действительных значениях х
и у.

Пример 8
. Доказать, что
для любых действительных значениях х и у.
Доказательство. Пусть
, Это означает, что для любых действительных у
и неравенство выполняется при любых действительных х
и у.

Метод введения новых переменных или метод подстановки
Пример 9
. Доказать, что для любых неотрицательных чисел х, у, z
Доказательство. Воспользуемся верным неравенством для, . Получаем исследуемое неравенство

Использование свойств функций.
Пример 10
. Докажем неравенство
для любых а и b.
Доказательство. Рассмотрим 2 случая: Если а=b,то верно
причем равенство достигается только при а=b=0. 2)Если , на R => ()* ()>0, что доказывает неравенство

Пример 11
. Докажем, что для любых
Доказательство. на R. Если, то знаки чисел и совпадают, что означает положительность исследуемой разности =>

Применение метода математической индукции
Данный метод применяется для доказательства неравенств относительно натуральных чисел. Пример 12
. Доказать, что для любого nϵN
Проверим истинность утверждения при
- (верно) 2) Предположим верность утверждения при (k>1)

3) Докажем истинность утверждения при n=k+1. Сравним и: , Имеем: Вывод: утверждение верно для любого nϵN.

Использование замечательных неравенств
Теорема о средних (неравенство Коши)
Неравенство Коши – Буняковского
Неравенство Бернулли
Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)
Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического , где Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.
, что невозможно ни при каких действительных А,В
и С
. Сделанное выше предположение опровергнуто, что доказывает исследуемое исходное неравенство.

Использование свойств квадратного трехчлена
Метод основан на свойстве неотрицательности квадратного трехчлена, если и. Пример 6
. Доказать, что
Доказательство. Пусть, a=2, 2>0
=>

Пример 7
. Доказать, что для любых действительных х и у имеет место быть неравенство
Доказательство. Рассмотрим левую часть неравенство как квадратный трехчлен относительно х:
, а>0, D D= => P(x)>0
и верно при любых действительных значениях х
и у.

Пример 8
. Доказать, что
для любых действительных значениях х и у.
Доказательство. Пусть
, Это означает, что для любых действительных у
и неравенство выполняется при любых действительных х
и у.

Метод введения новых переменных или метод подстановки
Пример 9
. Доказать, что для любых неотрицательных чисел х, у, z
Доказательство. Воспользуемся верным неравенством для, . Получаем исследуемое неравенство

Использование свойств функций.
Пример 10
. Докажем неравенство
для любых а и b.
Доказательство. Рассмотрим 2 случая: Если а=b,то верно
причем равенство достигается только при а=b=0. 2)Если , на R => ()* ()>0, что доказывает неравенство

Пример 11
. Докажем, что для любых
Доказательство. на R. Если, то знаки чисел и совпадают, что означает положительность исследуемой разности =>

Применение метода математической индукции
Данный метод применяется для доказательства неравенств относительно натуральных чисел. Пример 12
. Доказать, что для любого nϵN
Проверим истинность утверждения при
- (верно) 2) Предположим верность утверждения при (k>1)

3) Докажем истинность утверждения при n=k+1. Сравним и: , Имеем: Вывод: утверждение верно для любого nϵN.

Использование замечательных неравенств
Теорема о средних (неравенство Коши)
Неравенство Коши – Буняковского
Неравенство Бернулли
Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)
Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического , где Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.
и. Пример 6
. Доказать, что
Доказательство. Пусть, a=2, 2>0
=>

Пример 7
. Доказать, что для любых действительных х и у имеет место быть неравенство
Доказательство. Рассмотрим левую часть неравенство как квадратный трехчлен относительно х:
, а>0, D D= => P(x)>0
и верно при любых действительных значениях х
и у.

Пример 8
. Доказать, что
для любых действительных значениях х и у.
Доказательство. Пусть
, Это означает, что для любых действительных у
и неравенство выполняется при любых действительных х
и у.

Метод введения новых переменных или метод подстановки
Пример 9
. Доказать, что для любых неотрицательных чисел х, у, z
Доказательство. Воспользуемся верным неравенством для, . Получаем исследуемое неравенство

Использование свойств функций.
Пример 10
. Докажем неравенство
для любых а и b.
Доказательство. Рассмотрим 2 случая: Если а=b,то верно
причем равенство достигается только при а=b=0. 2)Если , на R => ()* ()>0, что доказывает неравенство

Пример 11
. Докажем, что для любых
Доказательство. на R. Если, то знаки чисел и совпадают, что означает положительность исследуемой разности =>

Применение метода математической индукции
Данный метод применяется для доказательства неравенств относительно натуральных чисел. Пример 12
. Доказать, что для любого nϵN
Проверим истинность утверждения при
- (верно) 2) Предположим верность утверждения при (k>1)

3) Докажем истинность утверждения при n=k+1. Сравним и: , Имеем: Вывод: утверждение верно для любого nϵN.

Использование замечательных неравенств
Теорема о средних (неравенство Коши)
Неравенство Коши – Буняковского
Неравенство Бернулли
Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)
Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического , где Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.
Доказательство. Пусть, a=2, 2>0
=>

Пример 7
. Доказать, что для любых действительных х и у имеет место быть неравенство
Доказательство. Рассмотрим левую часть неравенство как квадратный трехчлен относительно х:
, а>0, D D= => P(x)>0
и верно при любых действительных значениях х
и у.

Пример 8
. Доказать, что
для любых действительных значениях х и у.
Доказательство. Пусть
, Это означает, что для любых действительных у
и неравенство выполняется при любых действительных х
и у.

Метод введения новых переменных или метод подстановки
Пример 9
. Доказать, что для любых неотрицательных чисел х, у, z
Доказательство. Воспользуемся верным неравенством для, . Получаем исследуемое неравенство

Использование свойств функций.
Пример 10
. Докажем неравенство
для любых а и b.
Доказательство. Рассмотрим 2 случая: Если а=b,то верно
причем равенство достигается только при а=b=0. 2)Если , на R => ()* ()>0, что доказывает неравенство

Пример 11
. Докажем, что для любых
Доказательство. на R. Если, то знаки чисел и совпадают, что означает положительность исследуемой разности =>

Применение метода математической индукции
Данный метод применяется для доказательства неравенств относительно натуральных чисел. Пример 12
. Доказать, что для любого nϵN
Проверим истинность утверждения при
- (верно) 2) Предположим верность утверждения при (k>1)

3) Докажем истинность утверждения при n=k+1. Сравним и: , Имеем: Вывод: утверждение верно для любого nϵN.

Использование замечательных неравенств
Теорема о средних (неравенство Коши)
Неравенство Коши – Буняковского
Неравенство Бернулли
Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)
Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического , где Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.
=>

Пример 7
. Доказать, что для любых действительных х и у имеет место быть неравенство
Доказательство. Рассмотрим левую часть неравенство как квадратный трехчлен относительно х:
, а>0, D D= => P(x)>0
и верно при любых действительных значениях х
и у.

Пример 8
. Доказать, что
для любых действительных значениях х и у.
Доказательство. Пусть
, Это означает, что для любых действительных у
и неравенство выполняется при любых действительных х
и у.

Метод введения новых переменных или метод подстановки
Пример 9
. Доказать, что для любых неотрицательных чисел х, у, z
Доказательство. Воспользуемся верным неравенством для, . Получаем исследуемое неравенство

Использование свойств функций.
Пример 10
. Докажем неравенство
для любых а и b.
Доказательство. Рассмотрим 2 случая: Если а=b,то верно
причем равенство достигается только при а=b=0. 2)Если , на R => ()* ()>0, что доказывает неравенство

Пример 11
. Докажем, что для любых
Доказательство. на R. Если, то знаки чисел и совпадают, что означает положительность исследуемой разности =>

Применение метода математической индукции
Данный метод применяется для доказательства неравенств относительно натуральных чисел. Пример 12
. Доказать, что для любого nϵN
Проверим истинность утверждения при
- (верно) 2) Предположим верность утверждения при (k>1)

3) Докажем истинность утверждения при n=k+1. Сравним и: , Имеем: Вывод: утверждение верно для любого nϵN.

Использование замечательных неравенств
Теорема о средних (неравенство Коши)
Неравенство Коши – Буняковского
Неравенство Бернулли
Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)
Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического , где Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.
Доказательство. Рассмотрим левую часть неравенство как квадратный трехчлен относительно х:
, а>0, D D= => P(x)>0
и верно при любых действительных значениях х
и у.

Пример 8
. Доказать, что
для любых действительных значениях х и у.
Доказательство. Пусть
, Это означает, что для любых действительных у
и неравенство выполняется при любых действительных х
и у.

Метод введения новых переменных или метод подстановки
Пример 9
. Доказать, что для любых неотрицательных чисел х, у, z
Доказательство. Воспользуемся верным неравенством для, . Получаем исследуемое неравенство

Использование свойств функций.
Пример 10
. Докажем неравенство
для любых а и b.
Доказательство. Рассмотрим 2 случая: Если а=b,то верно
причем равенство достигается только при а=b=0. 2)Если , на R => ()* ()>0, что доказывает неравенство

Пример 11
. Докажем, что для любых
Доказательство. на R. Если, то знаки чисел и совпадают, что означает положительность исследуемой разности =>

Применение метода математической индукции
Данный метод применяется для доказательства неравенств относительно натуральных чисел. Пример 12
. Доказать, что для любого nϵN
Проверим истинность утверждения при
- (верно) 2) Предположим верность утверждения при (k>1)

3) Докажем истинность утверждения при n=k+1. Сравним и: , Имеем: Вывод: утверждение верно для любого nϵN.

Использование замечательных неравенств
Теорема о средних (неравенство Коши)
Неравенство Коши – Буняковского
Неравенство Бернулли
Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)
Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического , где Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.
D= => P(x)>0
и верно при любых действительных значениях х
и у.

Пример 8
. Доказать, что
для любых действительных значениях х и у.
Доказательство. Пусть
, Это означает, что для любых действительных у
и неравенство выполняется при любых действительных х
и у.

Метод введения новых переменных или метод подстановки
Пример 9
. Доказать, что для любых неотрицательных чисел х, у, z
Доказательство. Воспользуемся верным неравенством для, . Получаем исследуемое неравенство

Использование свойств функций.
Пример 10
. Докажем неравенство
для любых а и b.
Доказательство. Рассмотрим 2 случая: Если а=b,то верно
причем равенство достигается только при а=b=0. 2)Если , на R => ()* ()>0, что доказывает неравенство

Пример 11
. Докажем, что для любых
Доказательство. на R. Если, то знаки чисел и совпадают, что означает положительность исследуемой разности =>

Применение метода математической индукции
Данный метод применяется для доказательства неравенств относительно натуральных чисел. Пример 12
. Доказать, что для любого nϵN
Проверим истинность утверждения при
- (верно) 2) Предположим верность утверждения при (k>1)

3) Докажем истинность утверждения при n=k+1. Сравним и: , Имеем: Вывод: утверждение верно для любого nϵN.

Использование замечательных неравенств
Теорема о средних (неравенство Коши)
Неравенство Коши – Буняковского
Неравенство Бернулли
Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)
Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического , где Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.

Пример 8
. Доказать, что
для любых действительных значениях х и у.
Доказательство. Пусть
, Это означает, что для любых действительных у
и неравенство выполняется при любых действительных х
и у.

Метод введения новых переменных или метод подстановки
Пример 9
. Доказать, что для любых неотрицательных чисел х, у, z
Доказательство. Воспользуемся верным неравенством для, . Получаем исследуемое неравенство

Использование свойств функций.
Пример 10
. Докажем неравенство
для любых а и b.
Доказательство. Рассмотрим 2 случая: Если а=b,то верно
причем равенство достигается только при а=b=0. 2)Если , на R => ()* ()>0, что доказывает неравенство

Пример 11
. Докажем, что для любых
Доказательство. на R. Если, то знаки чисел и совпадают, что означает положительность исследуемой разности =>

Применение метода математической индукции
Данный метод применяется для доказательства неравенств относительно натуральных чисел. Пример 12
. Доказать, что для любого nϵN
Проверим истинность утверждения при
- (верно) 2) Предположим верность утверждения при (k>1)

3) Докажем истинность утверждения при n=k+1. Сравним и: , Имеем: Вывод: утверждение верно для любого nϵN.

Использование замечательных неравенств
Теорема о средних (неравенство Коши)
Неравенство Коши – Буняковского
Неравенство Бернулли
Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)
Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического , где Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.

Пример 8
. Доказать, что
для любых действительных значениях х и у.
Доказательство. Пусть
, Это означает, что для любых действительных у
и неравенство выполняется при любых действительных х
и у.

Метод введения новых переменных или метод подстановки
Пример 9
. Доказать, что для любых неотрицательных чисел х, у, z
Доказательство. Воспользуемся верным неравенством для, . Получаем исследуемое неравенство

Использование свойств функций.
Пример 10
. Докажем неравенство
для любых а и b.
Доказательство. Рассмотрим 2 случая: Если а=b,то верно
причем равенство достигается только при а=b=0. 2)Если , на R => ()* ()>0, что доказывает неравенство

Пример 11
. Докажем, что для любых
Доказательство. на R. Если, то знаки чисел и совпадают, что означает положительность исследуемой разности =>

Применение метода математической индукции
Данный метод применяется для доказательства неравенств относительно натуральных чисел. Пример 12
. Доказать, что для любого nϵN
Проверим истинность утверждения при
- (верно) 2) Предположим верность утверждения при (k>1)

3) Докажем истинность утверждения при n=k+1. Сравним и: , Имеем: Вывод: утверждение верно для любого nϵN.

Использование замечательных неравенств
Теорема о средних (неравенство Коши)
Неравенство Коши – Буняковского
Неравенство Бернулли
Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)
Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического , где Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.
Доказательство. Пусть
, Это означает, что для любых действительных у
и неравенство выполняется при любых действительных х
и у.

Метод введения новых переменных или метод подстановки
Пример 9
. Доказать, что для любых неотрицательных чисел х, у, z
Доказательство. Воспользуемся верным неравенством для, . Получаем исследуемое неравенство

Использование свойств функций.
Пример 10
. Докажем неравенство
для любых а и b.
Доказательство. Рассмотрим 2 случая: Если а=b,то верно
причем равенство достигается только при а=b=0. 2)Если , на R => ()* ()>0, что доказывает неравенство

Пример 11
. Докажем, что для любых
Доказательство. на R. Если, то знаки чисел и совпадают, что означает положительность исследуемой разности =>

Применение метода математической индукции
Данный метод применяется для доказательства неравенств относительно натуральных чисел. Пример 12
. Доказать, что для любого nϵN
Проверим истинность утверждения при
- (верно) 2) Предположим верность утверждения при (k>1)

3) Докажем истинность утверждения при n=k+1. Сравним и: , Имеем: Вывод: утверждение верно для любого nϵN.

Использование замечательных неравенств
Теорема о средних (неравенство Коши)
Неравенство Коши – Буняковского
Неравенство Бернулли
Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)
Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического , где Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.
выполняется при любых действительных х
и у.

Метод введения новых переменных или метод подстановки
Пример 9
. Доказать, что для любых неотрицательных чисел х, у, z
Доказательство. Воспользуемся верным неравенством для, . Получаем исследуемое неравенство

Использование свойств функций.
Пример 10
. Докажем неравенство
для любых а и b.
Доказательство. Рассмотрим 2 случая: Если а=b,то верно
причем равенство достигается только при а=b=0. 2)Если , на R => ()* ()>0, что доказывает неравенство

Пример 11
. Докажем, что для любых
Доказательство. на R. Если, то знаки чисел и совпадают, что означает положительность исследуемой разности =>

Применение метода математической индукции
Данный метод применяется для доказательства неравенств относительно натуральных чисел. Пример 12
. Доказать, что для любого nϵN
Проверим истинность утверждения при
- (верно) 2) Предположим верность утверждения при (k>1)

3) Докажем истинность утверждения при n=k+1. Сравним и: , Имеем: Вывод: утверждение верно для любого nϵN.

Использование замечательных неравенств
Теорема о средних (неравенство Коши)
Неравенство Коши – Буняковского
Неравенство Бернулли
Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)
Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического , где Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.

Метод введения новых переменных или метод подстановки
Пример 9
. Доказать, что для любых неотрицательных чисел х, у, z
Доказательство. Воспользуемся верным неравенством для, . Получаем исследуемое неравенство

Использование свойств функций.
Пример 10
. Докажем неравенство
для любых а и b.
Доказательство. Рассмотрим 2 случая: Если а=b,то верно
причем равенство достигается только при а=b=0. 2)Если , на R => ()* ()>0, что доказывает неравенство

Пример 11
. Докажем, что для любых
Доказательство. на R. Если, то знаки чисел и совпадают, что означает положительность исследуемой разности =>

Применение метода математической индукции
Данный метод применяется для доказательства неравенств относительно натуральных чисел. Пример 12
. Доказать, что для любого nϵN
Проверим истинность утверждения при
- (верно) 2) Предположим верность утверждения при (k>1)

3) Докажем истинность утверждения при n=k+1. Сравним и: , Имеем: Вывод: утверждение верно для любого nϵN.

Использование замечательных неравенств
Теорема о средних (неравенство Коши)
Неравенство Коши – Буняковского
Неравенство Бернулли
Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)
Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического , где Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.
. Получаем исследуемое неравенство

Использование свойств функций.
Пример 10
. Докажем неравенство
для любых а и b.
Доказательство. Рассмотрим 2 случая: Если а=b,то верно
причем равенство достигается только при а=b=0. 2)Если , на R => ()* ()>0, что доказывает неравенство

Пример 11
. Докажем, что для любых
Доказательство. на R. Если, то знаки чисел и совпадают, что означает положительность исследуемой разности =>

Применение метода математической индукции
Данный метод применяется для доказательства неравенств относительно натуральных чисел. Пример 12
. Доказать, что для любого nϵN
Проверим истинность утверждения при
- (верно) 2) Предположим верность утверждения при (k>1)

3) Докажем истинность утверждения при n=k+1. Сравним и: , Имеем: Вывод: утверждение верно для любого nϵN.

Использование замечательных неравенств
Теорема о средних (неравенство Коши)
Неравенство Коши – Буняковского
Неравенство Бернулли
Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)
Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического , где Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.

Использование свойств функций.
Пример 10
. Докажем неравенство
для любых а и b.
Доказательство. Рассмотрим 2 случая: Если а=b,то верно
причем равенство достигается только при а=b=0. 2)Если , на R => ()* ()>0, что доказывает неравенство

Пример 11
. Докажем, что для любых
Доказательство. на R. Если, то знаки чисел и совпадают, что означает положительность исследуемой разности =>

Применение метода математической индукции
Данный метод применяется для доказательства неравенств относительно натуральных чисел. Пример 12
. Доказать, что для любого nϵN
Проверим истинность утверждения при
- (верно) 2) Предположим верность утверждения при (k>1)

3) Докажем истинность утверждения при n=k+1. Сравним и: , Имеем: Вывод: утверждение верно для любого nϵN.

Использование замечательных неравенств
Теорема о средних (неравенство Коши)
Неравенство Коши – Буняковского
Неравенство Бернулли
Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)
Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического , где Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.
Доказательство. Рассмотрим 2 случая: Если а=b,то верно
причем равенство достигается только при а=b=0. 2)Если , на R => ()* ()>0, что доказывает неравенство

Пример 11
. Докажем, что для любых
Доказательство. на R. Если, то знаки чисел и совпадают, что означает положительность исследуемой разности =>

Применение метода математической индукции
Данный метод применяется для доказательства неравенств относительно натуральных чисел. Пример 12
. Доказать, что для любого nϵN
Проверим истинность утверждения при
- (верно) 2) Предположим верность утверждения при (k>1)

3) Докажем истинность утверждения при n=k+1. Сравним и: , Имеем: Вывод: утверждение верно для любого nϵN.

Использование замечательных неравенств
Теорема о средних (неравенство Коши)
Неравенство Коши – Буняковского
Неравенство Бернулли
Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)
Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического , где Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.
Если а=b,то верно
2)Если , на R => ()* ()>0, что доказывает неравенство

Пример 11
. Докажем, что для любых
Доказательство. на R. Если, то знаки чисел и совпадают, что означает положительность исследуемой разности =>

Применение метода математической индукции
Данный метод применяется для доказательства неравенств относительно натуральных чисел. Пример 12
. Доказать, что для любого nϵN
Проверим истинность утверждения при
- (верно) 2) Предположим верность утверждения при (k>1)

3) Докажем истинность утверждения при n=k+1. Сравним и: , Имеем: Вывод: утверждение верно для любого nϵN.

Использование замечательных неравенств
Теорема о средних (неравенство Коши)
Неравенство Коши – Буняковского
Неравенство Бернулли
Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)
Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического , где Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.
()* ()>0, что доказывает неравенство

Пример 11
. Докажем, что для любых
Доказательство. на R. Если, то знаки чисел и совпадают, что означает положительность исследуемой разности =>

Применение метода математической индукции
Данный метод применяется для доказательства неравенств относительно натуральных чисел. Пример 12
. Доказать, что для любого nϵN
Проверим истинность утверждения при
- (верно) 2) Предположим верность утверждения при (k>1)

3) Докажем истинность утверждения при n=k+1. Сравним и: , Имеем: Вывод: утверждение верно для любого nϵN.

Использование замечательных неравенств
Теорема о средних (неравенство Коши)
Неравенство Коши – Буняковского
Неравенство Бернулли
Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)
Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического , где Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.
Доказательство. на R. Если, то знаки чисел и совпадают, что означает положительность исследуемой разности =>

Применение метода математической индукции
Данный метод применяется для доказательства неравенств относительно натуральных чисел. Пример 12
. Доказать, что для любого nϵN
Проверим истинность утверждения при
- (верно) 2) Предположим верность утверждения при (k>1)

3) Докажем истинность утверждения при n=k+1. Сравним и: , Имеем: Вывод: утверждение верно для любого nϵN.

Использование замечательных неравенств
Теорема о средних (неравенство Коши)
Неравенство Коши – Буняковского
Неравенство Бернулли
Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)
Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического , где Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.
на R. Если, то знаки чисел и совпадают, что означает положительность исследуемой разности =>

Применение метода математической индукции
Данный метод применяется для доказательства неравенств относительно натуральных чисел. Пример 12
. Доказать, что для любого nϵN
Проверим истинность утверждения при
- (верно) 2) Предположим верность утверждения при (k>1)

3) Докажем истинность утверждения при n=k+1. Сравним и: , Имеем: Вывод: утверждение верно для любого nϵN.

Использование замечательных неравенств
Теорема о средних (неравенство Коши)
Неравенство Коши – Буняковского
Неравенство Бернулли
Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)
Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического , где Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.

Применение метода математической индукции
Данный метод применяется для доказательства неравенств относительно натуральных чисел. Пример 12
. Доказать, что для любого nϵN
Проверим истинность утверждения при
- (верно) 2) Предположим верность утверждения при (k>1)

3) Докажем истинность утверждения при n=k+1. Сравним и: , Имеем: Вывод: утверждение верно для любого nϵN.

Использование замечательных неравенств
Теорема о средних (неравенство Коши)
Неравенство Коши – Буняковского
Неравенство Бернулли
Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)
Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического , где Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.
Проверим истинность утверждения при
- (верно) 2) Предположим верность утверждения при (k>1)

3) Докажем истинность утверждения при n=k+1. Сравним и: , Имеем: Вывод: утверждение верно для любого nϵN.

Использование замечательных неравенств
Теорема о средних (неравенство Коши)
Неравенство Коши – Буняковского
Неравенство Бернулли
Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)
Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического , где Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.
Проверим истинность утверждения при
2) Предположим верность утверждения при (k>1)

3) Докажем истинность утверждения при n=k+1. Сравним и: , Имеем: Вывод: утверждение верно для любого nϵN.

Использование замечательных неравенств
Теорема о средних (неравенство Коши)
Неравенство Коши – Буняковского
Неравенство Бернулли
Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)
Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического , где Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.

3) Докажем истинность утверждения при n=k+1. Сравним и: , Имеем: Вывод: утверждение верно для любого nϵN.

Использование замечательных неравенств
Теорема о средних (неравенство Коши)
Неравенство Коши – Буняковского
Неравенство Бернулли
Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)
Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического , где Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.
Имеем: Вывод: утверждение верно для любого nϵN.

Использование замечательных неравенств
Теорема о средних (неравенство Коши)
Неравенство Коши – Буняковского
Неравенство Бернулли
Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)
Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического , где Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.

Использование замечательных неравенств
Теорема о средних (неравенство Коши)
Неравенство Коши – Буняковского
Неравенство Бернулли
Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)
Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического , где Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.

Применение теоремы о средних (неравенства Коши)
Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического , где Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.
Знак равенства достигается тогда и только тогда, когда Рассмотрим частные случаи этой теоремы:

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.

Пусть n=2, тогда
Пусть n=2, a>0, тогда
Пусть n=3, тогда
Пример 13
. Доказать, что для всех неотрицательных a,b,c выполняется неравенство
Доказательство.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.

Неравенство Коши - Буняковского
Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.

Пример 14.
Доказательство. Запишем исследуемое неравенство в следующем виде:
Это заведомо истинное неравенство, так как является частным случаем неравенства Коши – Буняковского.
Пример 15. Доказать, что для любых a,b,c ϵ R справедливо неравенство
Доказательство. Достаточно записать данное неравенство в виде
и сослаться на неравенство Коши – Буняковского.

Неравенство Бернулли
Неравенство Бернулли утверждает, что если х>-1, то для всех натуральных значений n выполняется неравенство Неравенство может применяться для выражений вида Кроме того, очень большая группа неравенств может быть легко доказана с помощью теоремы Бернулли.

Кроме того, очень большая группа неравенств может быть легко доказана с помощью теоремы Бернулли.

Пример 16 .
Доказательство. Положив х=0,5 и применив теорему Бернулли для выражения
Получим требуемое неравенство.
Пример 17 . Доказать, что для любых n ϵ N
Доказательство.
по теореме Бернулли, что и требовалось. 
Давида Гильберта спросили об одном из его бывших учеников. "А, такой-то? - вспомнил Гильберт. - Он стал поэтом. Для математики у него было слишком мало воображения.

МОУ Гришино -Слободская средняя общеобразовательная школа
Программа модуля
« Методы доказательства неравенств»
в рамках элективного курса
«За страницами учебника математики»
для учащихся 10-11 классов
Составил:
учитель математики
Панкова Е.Ю
Пояснительная записка
«Математику называют тавтологической наукой: другими словами, про математиков говорят, что они тратят время на доказательство того, что предметы равны самим себе. Это утверждение весьма неточно по двум причинам. Во-первых, математика, несмотря на свойственный ей научный язык, не является наукой; скорее ее можно назвать искусством. Во- вторых основные результаты математики чаще выражаются неравенствами, а не равенствами.»
Неравенства используются в практической работе математика постоянно. Они применяются для получения ряда интересных и важных экстремальных свойств «симметричных» фигур: квадрата, куба, равностороннего треугольника, а также для доказательства сходимости итерационных процессов и вычисления некоторых пределов. Важна роль неравенств и в различных вопросах естествознания и техники.
Задачи на доказательство неравенств самые трудные и интересные из традиционных. Доказательства неравенств требуют истинной изобретательности, творчества, которые делают математику тем захватывающим воображение предметом, каким она является.
Обучение доказательствам играет большую роль в развитии дедуктивно- математического мышления и общих мыслительных способностей учащихся. Как же научить школьников самостоятельно проводить доказательства неравенств? Ответ гласит: только путем рассмотрения многих приемов и методов доказательств и регулярного их применения.
Применяемые для доказательства неравенств идеи почти столь же разнообразны, как и сами неравенства. В конкретных ситуациях общие методы часто приводят к некрасивым решениям. Но неочевидное комбинирование нескольких «базовых» неравенств удается лишь немногим школьникам. И, кроме того, ничто не мешает ученику в каждом конкретном случае поискать лучшее решение, нежели полученное общим методом. По этой причине доказательства неравенств нередко относят к области искусства. И как во всяком искусстве здесь есть свои технические приемы, набор которых весьма широк и овладеть всеми очень сложно, но каждый учитель должен стремится к расширению имеющегося в его запасе математического инструмента.
Данный модуль рекомендуется для учащихся 10-11 классов. Здесь рассматриваются не все возможные методы доказательства неравенств (не затронуты метод замены переменной, доказательство неравенств с помощью производной, метод исследования и обобщения, прием упорядочения). Предложить рассмотреть остальные методы можно на втором этапе (например, в 11 классе), если данный модуль курса вызовет интерес у учащихся, а также ориентируясь на успехи усвоения первой части курса.
|
Уравнения и неравенства с параметром. |
||
|
Методы доказательства неравенств. |
||
|
Уравнения и неравенства, содержащие неизвестное под знаком модуля. |
||
|
Системы неравенств с двумя переменными. |
«За страницами учебника математики»
«Методы доказательства неравенств»
|
Введение. |
||
|
Доказательство неравенств на основании определения. |
||
|
Метод математической индукции. |
||
|
Применение классических неравенств. |
||
|
Графический метод. |
||
|
Метод от противного. |
||
|
Прием рассмотрения неравенств относительно одной из переменных. |
||
|
Идея усиления. |
||
|
Урок - контроль. |
Урок1. Введение.
Доказательство неравенств -увлекательная и непростая тема элементарной математики. Отсутствие единого подхода к проблеме доказательства неравенств, приводит к поиску ряда приемов, пригодных для доказательства неравенств определенных видов. На данном элективном курсе будут рассматриваться следующие методы доказательства неравенств:
Повторение:
Провести доказательства некоторых свойств.
Классические неравенства:
1)
 (неравенство Коши)
(неравенство Коши)
2)

3)

4)

Историческая справка:
Неравенство (1) называют в честь
французского математика Огюста Коши.
Число
 называют средним арифметическим
чисел a
и b;
называют средним арифметическим
чисел a
и b;
число
 называют средним геометрическим
чисел a
и b.
Таким образом, неравенство означает,
что среднее арифметическое двух
положительных чисел не меньше их среднего
геометрического.
называют средним геометрическим
чисел a
и b.
Таким образом, неравенство означает,
что среднее арифметическое двух
положительных чисел не меньше их среднего
геометрического.
Дополнительно:
Рассмотреть несколько математических софизмов с неравенствами.
Математический софизм - удивительное утверждение, в доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки.
Софизмы – это ложные результаты, полученные с помощью рассуждений, которые только кажутся правильными, но обязательно содержат ту или иную ошибку.
Пример:
Четыре больше двенадцати
Урок2.Доказательство неравенств на основании определения.
Суть этого метода заключается в следующем: для того чтобы установить справедливость неравенства F(x,y,z)>S(x,y,z) составляют разность F(x,y,z)-S(x,y,z) и доказывают, что она положительна. Применяя этот метод, часто выделяют квадрат, куб суммы или разности, неполный квадрат суммы или разности. Это помогает определить знак разности.
Пример.
Доказать неравенство (x+y)(x+y+2cosx)+2 2sin 2 x
2sin 2 x
Доказательство:
Рассмотрим разность (x+y)(x+y+2cosx)+2- 2sin 2 x =(x+y)(x+y+2cosx)+2cos 2 x=(x+y)(x+y+2cosx)+ cos 2 x +cos 2 x= (x+y) 2 +2(x+y)cosx+ cos 2 x +cos 2 x=((x+y)+cosx) 2 + cos 2 x 0.
Доказать неравенство:
1.ab(a+b)+bc(b+c)+ac(a+c) 6abc
3.
4. >2x-20
>2x-20
5.

6.(a+b)(b+c)(c+a) 8abc
7.
Урок3.Метод математической индукции.
При доказательстве неравенств, в которые входят натуральные числа часто прибегают к методу математической индукции. Метод состоит в следующем:
1) проверяем истинность теоремы для n=1;
2)допускаем, что теорема верна для некоторого n=k, и исходя из этого допущения доказываем истинность теоремы для n=k+1;
3) на основании первых двух шагов и принципа математической индукции заключаем, что теорема верна для любого n.
Пример.
Доказать неравенство
Доказательство:
1) при n=2 неравенство верно:
2)Пусть
неравенство верно для n=k
т.е.
 (*)
(*)
Докажем,
что неравенство верно при n=k+1,
т.е.
 .
Умножим обе части неравенства (*) на
.
Умножим обе части неравенства (*) на
 получим
3)Из
п1.и п.2 делаем вывод, что неравенство
верно для любого n.
получим
3)Из
п1.и п.2 делаем вывод, что неравенство
верно для любого n.
Задания для работы в классе и дома
Доказать неравенство:
1)
2)
3)
4)
5)
6) .
.
Урок4. Применение классических неравенств.
Суть этого метода заключается в следующем: с помощью ряда преобразований выводят требуемое неравенство с помощью некоторых классических неравенств.
Пример.
Доказать неравенство:
Доказательство:
В
качестве опорного неравенства используем
 .
.
Приведем данное неравенство к следующему виду:
 ,
тогда
,
тогда
Но
= ,
тогда
,
тогда
Доказать неравенство:
1)(p+2)(q+2)(p+q)16pq(для док-ва используется неравенство )
2)
 (для
док-ва используется неравенство
)
(для
док-ва используется неравенство
)
3) (a+b)(b+c)(c+a) 8abc (для док-ва используется неравенство )
4)
 (для
док-ва используется неравенство
).
(для
док-ва используется неравенство
).
Урок5. Графический метод.
Доказательство неравенств графическим методом заключается в следующем: если доказываем неравенство f(x)>g(x)(f(x)
1) построить графики функций y=f(x) и y=g(x);
2)если график функции y=f(x) расположен выше (ниже) графика функции y=g(x), то доказываемое неравенство верно.
Пример.
Доказать неравенство:
cosx
 ,x0
,x0
Доказательство:
Построим в одной системе координат графики функций y=cosx и

Из графика видно, что при x0 график функции y=cosx лежит выше графика функции y= .
Задания для работы в классе и дома.
Доказать неравенство:
1)
5)
Урок6.Метод от противного
Суть этого метода заключается в следующем: пусть нужно доказать истинность неравенства F(x,y,z) S(x,y,z)(1). Предполагают противное, т. е что хотя бы для одного набора переменных справедливо неравенство F(x,y,z) S(x,y,z) (2). Используя свойства неравенств, выполняют преобразования неравенства (2). Если в результате этих преобразований получается ложное неравенство, то это означает, что предположение о справедливости неравенства (2) неверно, а потому верно неравенство (1).
Пример.
Доказать неравенство:
Доказательство:
Предположим противное, т. е .
Возведем
обе части неравенства в квадрат, получим
,
откуда
 и далее
и далее
 .
Но это противоречит неравенству Коши.
Значит наше предположение неверно, т.
е справедливо неравенствоЗадания
для работы в классе и дома.
.
Но это противоречит неравенству Коши.
Значит наше предположение неверно, т.
е справедливо неравенствоЗадания
для работы в классе и дома.
Урок9. Урок- контроль знаний учащихся.
Работу на этом уроке можно организовать в парах или если большая численность класса в группах. В конце урока каждый учащийся должен быть оценен. Это и есть зачетная форма по данному курсу. По данной теме не рекомендуется проводить контрольную работу т.к. доказательство неравенств, как это уже говорилось в пояснительной записке, относят к области искусства. В начале учащимся предлагается самим определить метод доказательства предложенных неравенств. Если же у учащихся возникнут затруднения, то учитель сообщаем им рациональный метод, предупредив группу, что это, конечно же, повлияет на их оценку.
Работа по парам.
Примеры заданий.
________________________________________________________________
Доказать неравенство:
1. (метод
мат. индукции)
(метод
мат. индукции)
2. (по
определению)
(по
определению)
Модулем . Уравнения и неравенства с параметрами. ... свойств, формулировка и доказательство теорем, вывод формул... простейшие неравенства . 7. Уметь пользоваться методом интервалов...
Программа Открытой олимпиады и требования к подготовке по математике для учащихся 9 классов
ПрограммаПонятие модуля действительного числа. Арифметическое и геометрическое определения модуля . Раскрытие модулей . ... неравенства . Доказательство неравенств . Решение линейных, квадратных, дробно-рациональных неравенств с одной переменной. Решение неравенств ...
Программа факультатива по математике для 8 класса
ПрограммаПродемонстрировать методы доказательства чуть более сложных неравенств с помощью этого простого неравенства ? Итак, в этой министерской программе ...








