DEFINITION OF MATRIX. TYPES OF MATRICES
Matrix of size m× n called a set m·n numbers arranged in a rectangular table of m lines and n columns. This table is usually enclosed in parentheses. For example, the matrix might look like:
For brevity, a matrix can be denoted by a single capital letter, for example, A or IN.
In general, a matrix of size m× n write it like this
.
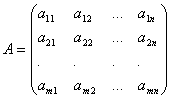The numbers that make up the matrix are called matrix elements. It is convenient to provide matrix elements with two indices a ij: The first indicates the row number and the second indicates the column number. For example, a 23– the element is in the 2nd row, 3rd column.
If a matrix has the same number of rows as the number of columns, then the matrix is called square, and the number of its rows or columns is called in order matrices. In the examples above, the second matrix is square - its order is 3, and the fourth matrix is its order 1.
A matrix in which the number of rows is not equal to the number of columns is called rectangular. In the examples this is the first matrix and the third.
There are also matrices that have only one row or one column.
A matrix with only one row is called matrix - row(or string), and a matrix with only one column matrix - column.
A matrix whose elements are all zero is called null and is denoted by (0), or simply 0. For example,
.
Main diagonal of a square matrix we call the diagonal going from the upper left to the lower right corner.
A square matrix in which all elements below the main diagonal are equal to zero is called triangular matrix.
.
A square matrix in which all elements, except perhaps those on the main diagonal, are equal to zero, is called diagonal matrix. For example, or.
A diagonal matrix in which all diagonal elements are equal to one is called single matrix and is denoted by the letter E. For example, the 3rd order identity matrix has the form 
.
ACTIONS ON MATRICES
Matrix equality. Two matrices A And B are said to be equal if they have the same number of rows and columns and their corresponding elements are equal a ij = b ij. So if 
And 
, That A=B, If a 11 = b 11, a 12 = b 12, a 21 = b 21 And a 22 = b 22.
Transpose. Consider an arbitrary matrix A from m lines and n columns. It can be associated with the following matrix B from n lines and m columns, in which each row is a matrix column A with the same number (hence each column is a row of the matrix A with the same number). So if 
, That 
.
This matrix B called transposed matrix A, and the transition from A To B transposition.
Thus, transposition is a reversal of the roles of the rows and columns of a matrix. Matrix transposed to matrix A, usually denoted A T.
Communication between matrix A and its transpose can be written in the form .
For example. Find the matrix transposed of the given one.
Matrix addition. Let the matrices A And B consist of the same number of rows and the same number of columns, i.e. have same sizes. Then in order to add matrices A And B needed for matrix elements A add matrix elements B standing in the same places. Thus, the sum of two matrices A And B called a matrix C, which is determined by the rule, for example,
Examples. Find the sum of matrices:
It is easy to verify that matrix addition obeys the following laws: commutative A+B=B+A and associative ( A+B)+C=A+(B+C).
Multiplying a matrix by a number. To multiply a matrix A per number k every element of the matrix is needed A multiply by this number. Thus, the matrix product A per number k there is a new matrix, which is determined by the rule 
or .
For any numbers a And b and matrices A And B the following equalities hold:
Examples.
Matrix multiplication. This operation is carried out according to a peculiar law. First of all, we note that the sizes of the factor matrices must be consistent. You can multiply only those matrices in which the number of columns of the first matrix coincides with the number of rows of the second matrix (i.e., the length of the first row is equal to the height of the second column). The work matrices A not a matrix B called the new matrix C=AB, the elements of which are composed as follows:
Thus, for example, to obtain the product (i.e. in the matrix C) element located in the 1st row and 3rd column from 13, you need to take the 1st row in the 1st matrix, the 3rd column in the 2nd, and then multiply the row elements by the corresponding column elements and add the resulting products. And other elements of the product matrix are obtained using a similar product of the rows of the first matrix and the columns of the second matrix.
In general, if we multiply a matrix A = (a ij) size m× n to the matrix B = (b ij) size n× p, then we get the matrix C size m× p, whose elements are calculated as follows: element c ij is obtained as a result of the product of elements i th row of the matrix A to the corresponding elements j th matrix column B and their additions.
From this rule it follows that you can always multiply two square matrices of the same order, and as a result we obtain a square matrix of the same order. In particular, a square matrix can always be multiplied by itself, i.e. square it.
Another important case is the multiplication of a row matrix by a column matrix, and the width of the first must be equal to the height of the second, resulting in a first-order matrix (i.e. one element). Really,
.
Examples.
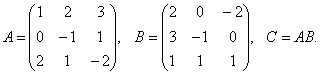
Thus, these simple examples show that matrices, generally speaking, do not commute with each other, i.e. A∙B ≠ B∙A . Therefore, when multiplying matrices, you need to carefully monitor the order of the factors.
It can be verified that matrix multiplication obeys associative and distributive laws, i.e. (AB)C=A(BC) And (A+B)C=AC+BC.
It is also easy to check that when multiplying a square matrix A to the identity matrix E of the same order we again obtain a matrix A, and AE=EA=A.
The following interesting fact can be noted. As you know, the product of 2 non-zero numbers is not equal to 0. For matrices this may not be the case, i.e. the product of 2 non-zero matrices may turn out to be equal to the zero matrix.
For example, If 
, That
.
THE CONCEPT OF DETERMINANTS
Let a second-order matrix be given - a square matrix consisting of two rows and two columns .
Second order determinant, corresponding to this matrix, is the number obtained as follows: a 11 a 22 – a 12 a 21.
The determinant is indicated by the symbol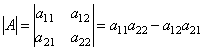 
.
So, in order to find the second-order determinant, you need to subtract the product of the elements along the second diagonal from the product of the elements of the main diagonal.
Examples. Calculate second order determinants.
Similarly, we can consider a third-order matrix and its corresponding determinant.
Third order determinant, corresponding to a given third-order square matrix, is a number denoted and obtained as follows:
.
Thus, this formula gives the expansion of the third-order determinant in terms of the elements of the first row a 11 , a 12 , a 13 and reduces the calculation of the third-order determinant to the calculation of the second-order determinants.
Examples. Calculate the third order determinant.
Similarly, one can introduce the concepts of determinants of the fourth, fifth, etc. orders, lowering their order by expanding into the elements of the 1st row, with the “+” and “–” signs of the terms alternating.
So, unlike a matrix, which is a table of numbers, a determinant is a number that is assigned to the matrix in a certain way.
consisting of T lines and n columns is called the size matrix n× m. Numbers A 11 , A 12 , ..., A mn are called her elements. The table denoting the matrix is written in parentheses and denoted A = (a ij ).
If the number of rows of a matrix is equal to the number of its columns, then the matrix is called square, and the number of its rows is equal to the number of columns - in order square matrix.
The set of all elements of a square matrix that lie on the segment connecting the upper left corner to the lower right corner is called main diagonal, and on the segment connecting the upper right corner with the lower left - side diagonal.
The square matrix is called diagonal, if all its elements not lying on the main diagonal are equal to zero. A square matrix in which the elements along the main diagonal are equal to one, and the rest are zeros, is called single and is designated E.
The two matrices are called equal if the number of their rows and columns are equal and if the elements in the corresponding places of these matrices are equal.
A matrix whose elements are all zero is called null and is denoted by N.
By definition, to multiply a matrix A for the number r, you need each element of the matrix A multiply by r.
Example. Given a matrix A =
, find matrix 3 A.
3
A = 3
=
Sum of matrices A And IN is called a matrix C, the elements of which are equal to the sums of the corresponding elements of the matrices A And IN. Only matrices with the same number of rows and columns can be added.
Example. Given matrices A =
And IN
=
. Find matrix C = A + B.
C =
Properties of matrix addition:
A+B=B+A
(A+ B)+ C = A+ (B + C)
A + N = A
Matrix product A to the matrix IN defined only if the number of matrix columns A equal to the number of rows of the matrix IN. The result of multiplication is the matrix AB, which has the same number of rows as there are in the matrix A, and the same number of columns as there are in the matrix IN.
Product of two matrices A (m× p) And IN(p× n) called a matrix WITH (m× n), the elements of which are determined by the rule
WITH ij
=
Comment. In order to multiply two matrices you need the elements i multiply the th row of the first matrix by elements j th column of the second matrix and add the resulting products. Let's get the element of the new matrix with the index ij.
Example. Given matrices a and b. ;. Find the product of matrices ab.
AB= 
=
=
Example. Given matrices A And IN.
A=
And B =
.
Solution: A =(2X3), IN= (3X2) => AB =(2X2)
AB=
=
=
Properties of matrix multiplication:
AB VA;
(AB)C=A(BC);
AE= EA= A
(AB)k = (AB)k= A(Bk)
(A+B)C = AB +BC
A(B+C) = AB + AC/
Transposed matrix A T is a matrix in which rows are written instead of columns, and columns are written instead of rows.
Example. Let the matrix be given A=
, Then
A T
=
Determinants.
Second order determinant corresponding to matrix A
=
, called the number 
=A 11 A 22
- A 12 A 21 .
Example. Calculate using a second-order determinant.
= 1 · (-3) – 2 · 4 = -11.
Third order determinant corresponding to matrix
A
=
, called the number 
=A 11
A 22
A 33
+a 12
A 23
A 31
+ a 13
A 21
A 32
- A 13
A 22
A 31
- A 12
A 21
A 33
-A 11
A 23
A 32.
To remember which products on the right side of the equality should be taken with the “+” sign and which with the “-” sign, a useful rule is called the triangle rule, shown in Fig. 1.
«
+ » « - »
Figure 1.
Example. Compute determinant
The second way to calculate third-order determinants is to add the first two columns, find the products along the main diagonal and parallels to it and along the secondary diagonal and parallels to it.
=
A 11
A 22
A 33
+a 12
A 23
A 31
+ a 13
A 21
A 32
- A 13
A 22
A 31
- A 12
A 21
A 33
-A 11
A 23
A 32.
Properties of determinants:
If two rows (columns) are swapped in the determinant, its sign will change to the opposite.
If the rows and columns in the determinant are swapped, then its sign and magnitude will not change.
If two lines in the determinant are proportional (equal), then it is equal to zero.
If any row (column) in the determinant is multiplied by a certain number and added to another row (column), its value will not change.
If in the determinant the elements of any row (column) have a common factor, then it can be taken out of the sign of the determinant.
If the determinant contains a null row or column, then it is equal to zero.
Minor M ij determinant element A ij is a determinant obtained from the original by deleting i- oh lines and j th column on which this element is located.
Algebraic complement A ij determinant element A ij called minor multiplied by (-1) i + j .
The third way to calculate determinants is using the decomposition theorem.
Decomposition theorem: The determinant is equal to the sum of the products of the elements of any row (column) and their algebraic complements.
Example. Calculate third order determinant 
, expanding the determinant into the elements of the first row.
= 5· (-1) 1+1 · 
+ 3 · (-1) 1+2 · 
+ 2·(-1) 1+3 · 
= 68.
The same determinant can be calculated using property 4), and then the expansion theorem can be applied. In our example, we create zeros in the first column. To do this, we add to the elements of the first row the elements of the second row, multiplied by 5, and to the elements of the third row we add the elements of the second row, multiplied by 7. And we decompose the resulting matrix into the elements of the first column.
=
=
0
- (-1)
+0
=
=13 · 34 – 17 · 22 = 68.
Instructions. For an online solution, you need to specify a matrix expression. At the second stage, it will be necessary to clarify the dimension of the matrices.
Valid operations: multiplication (*), addition (+), subtraction (-), inverse matrix A^(-1), exponentiation (A^2, B^3), matrix transposition (A^T).Valid operations: multiplication (*), addition (+), subtraction (-), inverse matrix A^(-1), exponentiation (A^2, B^3), matrix transposition (A^T).
To perform a list of operations, use a semicolon (;) separator. For example, to perform three operations:
a) 3A+4B
b) AB-VA
c) (A-B) -1
you will need to write it like this: 3*A+4*B;A*B-B*A;(A-B)^(-1)
A matrix is a rectangular numeric table with m rows and n columns, so the matrix can be schematically represented as a rectangle.
Zero matrix (null matrix) is a matrix whose elements are all equal to zero and are denoted by 0.
Identity matrix is called a square matrix of the form
Two matrices A and B are equal, if they are the same size and their corresponding elements are equal.
Singular matrix is a matrix whose determinant is equal to zero (Δ = 0).
Let's define basic operations on matrices.
Matrix addition
Definition . The sum of two matrices of the same size is a matrix of the same dimensions, the elements of which are found according to the formula
. Denoted by C = A+B. Example 6. .
The operation of matrix addition extends to the case of any number of terms. Obviously A+0=A .
Let us emphasize once again that only matrices of the same size can be added; For matrices of different sizes, the addition operation is not defined.
Subtraction of matrices
Definition . The difference B-A of matrices B and A of the same size is a matrix C such that A+ C = B.Matrix multiplication
Definition . The product of a matrix by a number α is a matrix obtained from A by multiplying all its elements by α, .Definition . Let two matrices be given
and , and the number of columns of A is equal to the number of rows of B. The product of A by B is a matrix whose elements are found according to the formula 
.
Denoted by C = A·B.
Schematically, the operation of matrix multiplication can be depicted as follows:
and the rule for calculating an element in a product:
Let us emphasize once again that the product A·B makes sense if and only if the number of columns of the first factor is equal to the number of rows of the second, and the product produces a matrix whose number of rows is equal to the number of rows of the first factor, and the number of columns is equal to the number of columns of the second. You can check the result of multiplication using a special online calculator.
Example 7. Given matrices 
And 
. Find matrices C = A·B and D = B·A.
Solution.
First of all, note that the product A·B exists because the number of columns of A is equal to the number of rows of B.
Note that in the general case A·B≠B·A, i.e. the product of matrices is anticommutative.
Let's find B·A (multiplication is possible).
Example 8. Given a matrix 
. Find 3A 2 – 2A.
Solution.
.
; 
.
.
Let us note the following interesting fact.
As you know, the product of two non-zero numbers is not equal to zero. For matrices, a similar circumstance may not occur, that is, the product of non-zero matrices may turn out to be equal to the null matrix.
