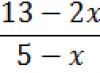How to find the decimal logarithm of a number. Decimal logarithm: how to calculate

The power of a given number is a mathematical term coined centuries ago. In geometry and algebra, there are two options - decimal and natural logarithms. They are calculated by different formulas, and equations that differ in spelling are always equal to each other. This identity characterizes the properties that relate to the useful potential of the function.

Features and important signs

There are currently ten known mathematical qualities. The most common and popular of them are:

• The radical log divided by the magnitude of the root is always the same as the decimal logarithm √.
• The product log is always equal to the producer's sum.
• Lg = the magnitude of the power multiplied by the number that is raised to it.
• If you subtract the divisor from log of the dividend, you get log of the quotient.

In addition, there is an equation based on the main identity (considered the key), a transition to an updated basis, and several minor formulas.

Calculating the decimal logarithm is a fairly specialized task, so integrating properties into a solution must be approached carefully and regularly checked your actions and consistency. We must not forget about the tables, which must be constantly consulted, and be guided only by the data found there.

Varieties of mathematical term

The main differences between a mathematical number are “hidden” in the base (a). If it has an exponent of 10, then it is log decimal. In the opposite case, “a” is transformed into “y” and has transcendental and irrational characteristics. It is also worth noting that the natural value is calculated by a special equation, where the proof is a theory studied outside the high school curriculum.

Decimal logarithms are widely used in the calculation of complex formulas. Entire tables have been compiled to facilitate calculations and clearly show the process of solving the problem. In this case, before directly getting down to business, you need to raise log to In addition, in every school supply store you can find a special ruler with a printed scale that helps solve an equation of any complexity.

The decimal logarithm of a number is called Brigg's number, or Euler's number, in honor of the researcher who first published the quantity and discovered the contrast between the two definitions.

Two types of formula

All types and varieties of problems for calculating the answer, having the term log in the condition, have a separate name and a strict mathematical structure. The exponential equation is an almost exact copy of logarithmic calculations, if you look at the correctness of the solution. It’s just that the first option includes a specialized number that helps you quickly understand the condition, and the second replaces log with an ordinary power. In this case, calculations using the last formula must include a variable value.

Difference and terminology

Both main indicators have their own characteristics that distinguish the numbers from each other:

• Decimal logarithm. An important detail of the number is the mandatory presence of a base. The standard version of the value is 10. It is marked with the sequence - log x or log x.
• Natural. If its base is the sign "e", which is a constant identical to a strictly calculated equation, where n is rapidly moving towards infinity, then the approximate size of the number in digital equivalent is 2.72. The official marking, adopted both in school and in more complex professional formulas, is ln x.
• Different. In addition to basic logarithms, there are hexadecimal and binary types (base 16 and 2, respectively). There is an even more complex option with a base indicator of 64, which falls under a systematic adaptive type control that calculates the final result with geometric accuracy.

The terminology includes the following quantities included in the algebraic problem:

• meaning;
• argument;
• base.

Calculating log number

There are three ways to quickly and verbally make all the necessary calculations to find the result of interest, with the obligatory correct outcome of the solution. Initially, we bring the decimal logarithm closer to its order (the scientific notation of a number to a power). Each positive value can be specified by an equation where it is equal to the mantissa (a number from 1 to 9) multiplied by ten to the nth power. This calculation option is based on two mathematical facts:

• the product and sum log always have the same exponent;
• the logarithm taken from a number from one to ten cannot exceed a value of 1 point.

1. If an error in the calculation does occur, then it is never less than one in the direction of subtraction.
2. Accuracy increases if you consider that lg with base three has a final result of five tenths of one. Therefore, any mathematical value greater than 3 automatically adds one point to the answer.
3. Almost perfect accuracy is achieved if you have a specialized table at hand that can be easily used in your assessment activities. With its help you can find out what the decimal logarithm is equal to tenths of a percent of the original number.

History of real log

The sixteenth century was in dire need of more complex calculus than was known to science at the time. This was especially true for dividing and multiplying multi-digit numbers with great consistency, including fractions.

At the end of the second half of the era, several minds immediately came to the conclusion about adding numbers using a table that compared two and a geometric one. In this case, all basic calculations had to rest on the last value. Scientists have integrated subtraction in the same way.

The first mention of lg took place in 1614. This was done by an amateur mathematician named Napier. It is worth noting that, despite the enormous popularization of the results obtained, an error was made in the formula due to ignorance of some definitions that appeared later. It began with the sixth digit of the indicator. The closest to the understanding of the logarithm were the Bernoulli brothers, and the debut legalization occurred in the eighteenth century by Euler. He also extended the function to the field of education.

History of complex log

Debut attempts to integrate lg into the general public were made at the dawn of the 18th century by Bernoulli and Leibniz. But they were never able to draw up comprehensive theoretical calculations. There was a whole discussion about this, but no exact definition was given to the number. Later the dialogue resumed, but between Euler and d'Alembert.

The latter agreed in principle with many of the facts proposed by the founder of the value, but believed that positive and negative indicators should be equal. In the middle of the century the formula was demonstrated as a final version. In addition, Euler published the derivative of the decimal logarithm and compiled the first graphs.

Tables

The properties of numbers indicate that multi-digit numbers can not be multiplied, but their log can be found and added using specialized tables.

This indicator has become especially valuable for astronomers who are forced to work with a large set of sequences. In Soviet times, the decimal logarithm was looked for in the Bradis collection, published in 1921. Later, in 1971, the Vega edition appeared.

Instructions

Write the given logarithmic expression. If the expression uses the logarithm of 10, then its notation is shortened and looks like this: lg b is the decimal logarithm. If the logarithm has the number e as its base, then write the expression: ln b – natural logarithm. It is understood that the result of any is the power to which the base number must be raised to obtain the number b.

When finding the sum of two functions, you simply need to differentiate them one by one and add the results: (u+v)" = u"+v";

When finding the derivative of the product of two functions, it is necessary to multiply the derivative of the first function by the second and add the derivative of the second function multiplied by the first function: (u*v)" = u"*v+v"*u;

In order to find the derivative of the quotient of two functions, it is necessary to subtract from the product of the derivative of the dividend multiplied by the divisor function the product of the derivative of the divisor multiplied by the function of the dividend, and divide all this by the divisor function squared. (u/v)" = (u"*v-v"*u)/v^2;

If a complex function is given, then it is necessary to multiply the derivative of the internal function and the derivative of the external one. Let y=u(v(x)), then y"(x)=y"(u)*v"(x).

Using the results obtained above, you can differentiate almost any function. So let's look at a few examples:

y=x^4, y"=4*x^(4-1)=4*x^3;

y=2*x^3*(e^x-x^2+6), y"=2*(3*x^2*(e^x-x^2+6)+x^3*(e^x-2 *x));
There are also problems involving calculating the derivative at a point. Let the function y=e^(x^2+6x+5) be given, you need to find the value of the function at the point x=1.
1) Find the derivative of the function: y"=e^(x^2-6x+5)*(2*x +6).

2) Calculate the value of the function at a given point y"(1)=8*e^0=8

Video on the topic

Useful advice

Learn the table of elementary derivatives. This will significantly save time.

Sources:

• derivative of a constant

So, what is the difference between an irrational equation and a rational one? If the unknown variable is under the square root sign, then the equation is considered irrational.

Instructions

The main method for solving such equations is the method of constructing both sides equations into a square. However. this is natural, the first thing you need to do is get rid of the sign. This method is not technically difficult, but sometimes it can lead to trouble. For example, the equation is v(2x-5)=v(4x-7). By squaring both sides you get 2x-5=4x-7. Solving such an equation is not difficult; x=1. But the number 1 will not be given equations. Why? Substitute one into the equation instead of the value of x. And the right and left sides will contain expressions that do not make sense, that is. This value is not valid for a square root. Therefore, 1 is an extraneous root, and therefore this equation has no roots.

So, an irrational equation is solved using the method of squaring both its sides. And having solved the equation, it is necessary to cut off extraneous roots. To do this, substitute the found roots into the original equation.

Consider another one.
2х+vх-3=0
Of course, this equation can be solved using the same equation as the previous one. Move Compounds equations, which do not have a square root, to the right side and then use the squaring method. solve the resulting rational equation and roots. But also another, more elegant one. Enter a new variable; vх=y. Accordingly, you will receive an equation of the form 2y2+y-3=0. That is, an ordinary quadratic equation. Find its roots; y1=1 and y2=-3/2. Next, solve two equations vх=1; vх=-3/2. The second equation has no roots; from the first we find that x=1. Don't forget to check the roots.

Solving identities is quite simple. To do this, it is necessary to carry out identical transformations until the set goal is achieved. Thus, with the help of simple arithmetic operations, the task at hand will be solved.

You will need

• - paper;
• - pen.

Instructions

The simplest of such transformations are algebraic abbreviated multiplications (such as the square of the sum (difference), difference of squares, sum (difference), cube of the sum (difference)). In addition, there are many trigonometric formulas, which are essentially the same identities.

Indeed, the square of the sum of two terms is equal to the square of the first plus twice the product of the first by the second and plus the square of the second, that is, (a+b)^2= (a+b)(a+b)=a^2+ab +ba+b ^2=a^2+2ab+b^2.

Simplify both

General principles of the solution

Variable Replacement Method

Solving integrals of the second kind

Substitution of integration limits

SECTION XIII.

LOGARITHMAS AND THEIR APPLICATIONS.

§ 2. Decimal logarithms.

The decimal logarithm of the number 1 is 0. Decimal logarithms of positive powers of 10, i.e. the numbers 10, 100, 1000,.... are essentially positive numbers 1, 2, 3,...., so in general the logarithm of a number denoted by one with zeros is equal to the number of zeros. Decimal logarithms of negative powers of 10, i.e. the fractions 0.1, 0.01, 0.001,.... are negative numbers -1, -2, -3....., so in general the logarithm of a decimal fraction with a numerator of one is equal to the negative number of zeros of the denominator.

The logarithms of all other commensurable numbers are incommensurable. Such logarithms are calculated approximately, usually with an accuracy of one hundred thousandth, and therefore are expressed in five-digit decimal fractions; for example, log 3 = 0.47712.

When presenting the theory of decimal logarithms, all numbers are assumed to be composed according to the decimal system of their units and fractions, and all logarithms are expressed through a decimal fraction containing 0 integers, with an integer increase or decrease. The fractional part of a logarithm is called its mantissa, and the whole increase or decrease is called its characteristic. Logarithms of numbers greater than one are always positive and therefore have a positive characteristic; logarithms of numbers less than one are always negative, but they are represented in such a way that their mantissa turns out to be positive, and one characteristic is negative: for example, log 500 = 0.69897 + 2 or shorter 2.69897, and log 0.05 = 0, 69897-2, which for brevity is denoted as 2.69897, putting the characteristic in place of integers, but with a sign above it. Thus, the logarithm of a number greater than one represents the arithmetic sum of a positive integer and a positive fraction, and the logarithm of a number less than one represents the algebraic sum of a negative integer with a positive fraction.

Any negative logarithm can be reduced to the indicated artificial form. For example, we have log 3 / 5 = log 3 - log 5 = 0.47712-0.69897 = -0.22185. To convert this true logarithm into an artificial form, we add 1 to it and, after algebraic addition, we indicate the subtraction of one for correction.

We get log 3 / 5 = log 0.6 = (1-0.22185)-1 = 0.77815-1. It turns out that the mantissa 0.77815 is the same one that corresponds to the numerator 6 of this number, represented in the decimal system in the form of the fraction 0.6.

In the indicated representation of decimal logarithms, their mantissa and characteristics have important properties in connection with the designation of the numbers corresponding to them in the decimal system. To explain these properties, we note the following. Let us take as the main type of number some arbitrary number contained between 1 and 10, and, expressing it in the decimal system, present it in the form a,b,c,d,e,f ...., Where A there is one of the significant figures 1, 2, 3, 4, 5, 6, 7, 8, 9, and the decimal places, b,c,d,e,f ....... are any numbers, between which there may be zeros. Due to the fact that the taken number is contained between 1 and 10, its logarithm is contained between 0 and 1 and therefore this logarithm consists of one mantissa without characteristic or with characteristic 0. Let us denote this logarithm in the form 0 ,α β γ δ ε ...., Where α, β ,γ ,δ, ε the essence of some numbers. Let us now multiply this number on the one hand by the numbers 10, 100, 1000,.... and on the other hand by the numbers 0.1, 0.01, 0.001,... and apply the theorems on the logarithms of the product and the quotient. Then we get a series of numbers greater than one and a series of numbers less than one with their logarithms:

lg A ,bcde f ....= 0 ,α β γ δ ε ....

lg ab,cde f ....= 1 ,α β γ δ ε ....lg 0,abcde f ....= 1 ,α β γ δ ε ....

lg аbc,de f ....= 2 ,α β γ δ ε ....lg 0.0abcde f ....= 2 ,α β γ δ ε ....

lg аbcd,e f ....= 3 ,α β γ δ ε ....lg 0.00abcde f ....= 3 ,α β γ δ ε ....

When considering these equalities, the following properties of the mantissa and characteristics are revealed:

Mantissa property. The mantissa depends on the location and type of the gapping digits of the number, but does not at all depend on the place of the comma in the designation of this number. Mantissas of logarithms of numbers having a decimal ratio, i.e. those whose multiple ratio is equal to any positive or negative power of ten are the same.

Characteristic property. The characteristic depends on the rank of the highest units or decimal fractions of a number, but does not at all depend on the type of digits in the designation of this number.

If we name the numbers A ,bcde f ...., ab,cde f ...., аbc,de f .... numbers of positive digits - first, second, third, etc., digit of number 0,abcde f .... we will consider zero, and the digits of numbers 0.0abcde f ...., 0.00abcde f ...., 0.000abcde f .... if we express negative numbers minus one, minus two, minus three, etc., then we can generally say that the characteristic of the logarithm of any decimal number is one less than the number indicating the digit

101. Knowing that log 2 =0.30103, find the logarithms of the numbers 20.2000, 0.2 and 0.00002.

101. Knowing that log 3=0.47712, find the logarithms of the numbers 300, 3000, 0.03 and 0.0003.

102. Knowing that log 5 = 0.69897, find the logarithms of the numbers 2.5, 500, 0.25 and 0.005.

102. Knowing that log 7 = 0.84510, find the logarithms of the numbers 0.7, 4.9, 0.049 and 0.0007.

103. Knowing log 3=0.47712 and log 7=0.84510, find the logarithms of the numbers 210, 0.021, 3/7, 7/9 and 3/49.

103. Knowing log 2=0.30103 and log 7=0.84510, find the logarithms of the numbers 140, 0.14, 2/7, 7/8 and 2/49.

104. Knowing log 3 = 0.47712 and log 5 = O.69897, find the logarithms of the numbers 1.5, 3 / 5, 0.12, 5 / 9 and 0.36.

104. Knowing log 5 = 0.69897 and log 7 = 0.84510, find the logarithms of the numbers 3.5, 5 / 7, 0.28, 5 / 49 and 1.96.

Decimal logarithms of numbers expressed in no more than four digits are found directly from the tables, and from the tables the mantissa of the desired logarithm is found, and the characteristic is set in accordance with the rank of the given number.

If the number contains more than four digits, then finding the logarithm is accompanied by an additional calculation. The rule is: to find the logarithm of a number containing more than four digits, you need to find in the tables the number indicated by the first four digits and write the mantissa corresponding to these four digits; then multiply the tabular difference of the mantissa by the number made up of the discarded digits, in the product, discard as many digits from the right as were discarded in the given number, and add the result to the last digits of the found mantissa; put the characteristic in accordance with the rank of the given number.

When a number is searched for using a given logarithm and this logarithm is contained in tables, then the digits of the sought number are found directly from the tables, and the rank of the number is determined in accordance with the characteristics of the given logarithm.

If this logarithm is not contained in the tables, then searching for the number is accompanied by an additional calculation. The rule is: to find the number corresponding to a given logarithm, the mantissa of which is not contained in the tables, you need to find the nearest smaller mantissa and write down the digits of the number corresponding to it; then multiply the difference between the given mantissa and the found one by 10 and divide the product by the tabulated difference; add the resulting digit of the quotient to the right to the written digits of the number, which is why you get the desired set of digits; The rank of the number must be determined in accordance with the characteristics of the given logarithm.

105. Find the logarithms of the numbers 8, 141, 954, 420, 640, 1235, 3907, 3010, 18.43, 2.05, 900.1, 0.73, 0.0028, 0.1008, 0.00005.

105. Find the logarithmic of the numbers 15.154, 837, 510, 5002,1309-, 8900, 8.315, 790.7, 0.09, 0.6745, 0.000745, 0.04257, 0.00071.

106. Find the logarithms of the numbers 2174.6, 1445.7, 2169.5, 8437.2, 46.472, 6.2853, 0.7893B, 0.054294, 631.074, 2.79556, 0.747428, 0.00237158.

106. Find the logarithms of the numbers 2578.4, 1323.6, 8170.5, 6245.3, 437.65, 87.268, 0.059372, 0.84938, 62.5475, 131.037, 0.593946, 0.00234261.

107. Find the numbers corresponding to the logarithms 3.16227, 3.59207, 2.93318, 0.41078, 1.60065, 2.756.86, 3.23528, 1.79692. 4.87800 5.14613.

107. Find the numbers corresponding to the logarithms 3.07372, 3.69205, 1.64904, 2.16107, 0.70364, 1.31952, 4.30814, 3.00087, 2.69949, 6.57978.

108. Find the number corresponding to the logarithms 3.57686, 3.16340, 2.40359, 1.09817, 4.49823, 2.83882, 1.50060, 3.30056, 1.17112, 4.25100.

108. Find the numbers corresponding to the logarithms 3.33720, 3.09875, 0.70093, 4.04640, 2.94004, 1.41509, 2.32649, 4.14631, 3.01290, 5.39003.

Positive logarithms of numbers greater than one are the arithmetic sums of their characteristics and mantissas. Therefore, operations with them are carried out according to ordinary arithmetic rules.

Negative logarithms of numbers less than one are the algebraic sums of a negative characteristic and a positive mantissa. Therefore, operations with them are carried out according to algebraic rules, which are supplemented by special instructions relating to the reduction of negative logarithms to their normal form. The normal form of a negative logarithm is one in which the characteristic is a negative integer and the mantissa is a positive proper fraction.

To convert a true reflective logarithm into its normal artificial form, you need to increase the absolute value of its integer term by one and make the result a negative characteristic; then add all the digits of the fractional term to 9, and the last one to 10 and make the result a positive mantissa. For example, -2.57928 = 3.42072.

To convert the normal artificial form of the logarithm into its true negative value, you need to reduce the negative characteristic by one and make the result an integer term of the negative sum; then add all the digits of the mantissa to 9, and the last one to 10 and make the result a fractional term of the same negative sum. For example: 4.57406= -3.42594.

109. Convert logarithms to artificial form -2.69537, -4, 21283, -0.54225, -1.68307, -3.53820, -5.89990.

109. Convert logarithms to artificial form -3.21729, -1.73273, -5.42936, -0.51395, -2.43780, -4.22990.

110. Find the true values ​​of logarithms 1.33278, 3.52793, 2.95426, 4.32725, 1.39420, 5.67990.

110. Find the true values ​​of logarithms 2.45438, 1.73977, 3.91243, 5.12912, 2.83770, 4.28990.

The rules for algebraic operations with negative logarithms are expressed as follows:

To apply a negative logarithm in its artificial form, you need to apply the mantissa and subtract the absolute value of the characteristic. If a positive integer number emerges from the addition of mantissas, then you need to attribute it to the characteristic of the result, making the appropriate correction to it. For example,

3,89573 + 2 ,78452 = 1 1 ,68025 = 2,68025

1 ,54978 + 2 ,94963=3 1 ,49941=2 ,49941.

To subtract a negative logarithm in its artificial form, you need to subtract the mantissa and add the absolute value of the characteristic. If the subtracted mantissa is large, then you need to make an adjustment in the characteristic of the minuend so as to separate a positive unit from the minuend. For example,

2,53798-3 ,84582=1 1 ,53798-3 ,84582 = 4,69216,

2 ,22689-1 ,64853=3 1 ,22689-1 ,64853=2 ,57836.

To multiply a negative logarithm by a positive integer, you need to multiply its characteristic and mantissa separately. If, when multiplying the mantissa, a whole positive number is identified, then you need to attribute it to the characteristic of the result, making an appropriate amendment to it. For example,

2 ,53729 5=10 2 ,68645=8 ,68645.

When multiplying a negative logarithm by a negative quantity, you must replace the multiplicand with its true value.

To divide a negative logarithm by a positive integer, you need to separate its characteristic and mantissa separately. If the characteristic of the dividend is not exactly divisible by the divisor, then you need to make an amendment to it so as to include several positive units in the mantissa, and make the characteristic a multiple of the divisor. For example,

3 ,79432: 5=5 2 ,79432: 5=1 ,55886.

When dividing a negative logarithm by a negative quantity, you need to replace the dividend with its true value.

Perform the following calculations using logarithmic tables and check the results in the simplest cases using ordinary methods:

174. Determine the volume of a cone whose generatrix is ​​0.9134 feet and whose base radius is 0.04278 feet.

175. Calculate the 15th term of a multiple progression, the first term of which is 2 3 / 5 and the denominator is 1.75.

175. Calculate the first term of a multiple progression, the 11th term of which is equal to 649.5 and the denominator is 1.58.

176. Determine the number of factors A , A 3 , A 5 r . Find something like this A , in which the product of 10 factors is equal to 100.

176. Determine the number of factors. A 2 , A 6 , A 10 ,.... so that their product equals the given number r . Find something like this A , in which the product of 5 factors is equal to 10.

177. The denominator of the multiple progression is 1.075, the sum of its 10 terms is 2017.8. Find the first term.

177. The denominator of the multiple progression is 1.029, the sum of its 20 terms is 8743.7. Find the twentieth term.

178 . Express the number of terms of a multiple progression given the first term A , last and denominator q , and then, randomly choosing numeric values a And u , pick up q so that n

178. Express the number of terms of a multiple progression given the first term A , last And and denominator q And And q , pick up A so that n was some integer.

179. Determine the number of factors so that their product is equal to r . What it must be like r in order to A =0.5 and b =0.9 the number of factors was 10.

179. Determine the number of factors so that their product is equal r . What it must be like r in order to A =0.2 and b =2 the number of factors was 10.

180. Express the number of terms of a multiple progression given the first term A , I'll follow And and the product of all members r , and then, randomly selecting numeric values A And r , pick up And and then the denominator q so that And was some integer.

160. Express the number of terms of a multiple progression given the first term A , the last and and the product of all terms r , and then, randomly selecting numeric values And And r , pick up A and then the denominator q so that n was some integer.

Solve the following equations, where possible - without the help of tables, and where not, with tables:

They often take the number ten. Logarithms of numbers based on base ten are called decimal. When performing calculations with the decimal logarithm, it is common to operate with the sign lg, not log; in this case, the number ten, which defines the base, is not indicated. Yes, let's replace log 10 105 to simplified lg105; A log 10 2 on lg2.

For decimal logarithms the same features that logarithms have with a base greater than one are typical. Namely, decimal logarithms are characterized exclusively for positive numbers. The decimal logarithms of numbers greater than one are positive, and those of numbers less than one are negative; of two non-negative numbers, the larger one is equivalent to the larger decimal logarithm, etc. Additionally, decimal logarithms have distinctive features and peculiar features, which explain why it is comfortable to prefer the number ten as the base of logarithms.

Before examining these properties, let us familiarize ourselves with the following formulations.

Integer part of the decimal logarithm of a number A is called characteristic, and the fractional one is mantissa this logarithm.

Characteristics of the decimal logarithm of a number A is indicated as , and the mantissa as (lg A}.

Let's take, say, log 2 ≈ 0.3010. Accordingly = 0, (log 2) ≈ 0.3010.

Likewise for log 543.1 ≈2.7349. Accordingly, = 2, (log 543.1)≈ 0.7349.

The calculation of decimal logarithms of positive numbers from tables is quite widely used.

Characteristic features of decimal logarithms.

The first sign of the decimal logarithm. a non-negative integer represented by a one followed by zeros is a positive integer equal to the number of zeros in the record of the selected number .

Let's take log 100 = 2, log 1 00000 = 5.

Generally speaking, if

That A= 10n , from which we get

lg a = lg 10 n = n lg 10 =n.

Second sign. The ten logarithm of a positive decimal, shown as a one with leading zeros, is - n, Where n- the number of zeros in the representation of this number, taking into account zero integers.

Let's consider , log 0.001 = - 3, log 0.000001 = -6.

Generally speaking, if

,

That a= 10-n and it turns out

lga= lg 10n =-n log 10 =-n

Third sign. The characteristic of the decimal logarithm of a non-negative number greater than one is equal to the number of digits in the integer part of this number excluding one.

Let's analyze this feature: 1) The characteristic of the logarithm lg 75.631 is equal to 1.

Indeed, 10< 75,631 < 100. Из этого можно сделать вывод

lg 10< lg 75,631 < lg 100,

1 < lg 75,631 < 2.

It follows from this,

log 75.631 = 1 +b,

Shifting a decimal point in a decimal fraction to the right or left is equivalent to the operation of multiplying this fraction by a power of ten with an integer exponent n(positive or negative). And therefore, when the decimal point in a positive decimal fraction is shifted to the left or right, the mantissa of the decimal logarithm of this fraction does not change.

So, (log 0.0053) = (log 0.53) = (log 0.0000053).

Which is very easy to use, does not require any additional programs to be installed in its interface. All you have to do is go to the Google website and enter the appropriate query in the only field on this page. For example, to calculate the decimal logarithm for 900, enter lg 900 in the search query field and immediately (even without pressing a button) you will get 2.95424251.

Use a calculator if you don't have access to a search engine. This could also be a software calculator from the standard Windows OS set. The easiest way to run it is to press the WIN +R key combination, enter the calc command and click the OK button. Another way is to open the menu on the “Start” button and select “All Programs” from it. Then you need to open the “Standard” section and go to the “Service” subsection to click on the “Calculator” link there. If you're using Windows 7, you can press the WIN key and type "Calculator" in the search box, and then click the appropriate link in the search results.

Switch the calculator interface to advanced mode, since the basic version that opens by default does not provide the operation you need. To do this, open the “View” section in the program menu and select “ ” or “engineering” - depending on the version of the operating system installed on your computer.

Nowadays you won't surprise anyone with discounts. Sellers understand that discounts are not a means of increasing revenue. The most effective is not 1-2 discounts on a specific product, but a system of discounts, which should be simple and understandable to the company’s employees and its customers.

Instructions

You have probably noticed that currently the most common one is growing with increasing production volumes. In this case, the seller develops a scale of discount percentages, which increases with the growth of purchase volumes over a certain period. For example, you bought a kettle and coffee maker and received discount 5%. If you also buy an iron this month, you will receive discount 8% on all purchased goods. At the same time, the company's profit received at a discounted price and increased sales volume should be no less than the expected profit at a price without a discount and the same sales level.

Calculating the discount scale is easy. First, determine the sales volume from which the discount begins. You can take as a lower limit. Then calculate the expected amount of profit you would like to make on the product you sell. Its upper limit will be limited by the purchasing power of the product and its competitive properties. Maximum discount can be calculated as follows: (profit – (profit x minimum sales / expected volume) / unit price.

Another fairly common discount is the contract discount. This may be a discount on, when purchasing certain types of goods, as well as when paying in a particular currency. Sometimes discounts of this type are provided when purchasing goods and ordering for delivery. For example, you buy a company’s products, order transport from the same company and receive discount 5% on purchased goods.

The amount of pre-holiday and seasonal discounts is determined based on the cost of the goods in the warehouse and the likelihood of selling the goods at the set price. Typically, retailers resort to such discounts, for example, when selling clothes from last season's collections. Supermarkets use similar discounts to relieve the store's work load in the evenings and weekends. In this case, the size of the discount is determined by the amount of lost profits when consumer demand is not satisfied during peak hours.

Sources:

• how to calculate the discount percentage in 2019

Calculating logarithms may be necessary to find values ​​using formulas containing exponents as unknown variables. Two types of logarithms, unlike all others, have their own names and notations - these are logarithms to bases 10 and the number e (an irrational constant). Let's look at some simple ways to calculate the base 10 logarithm - the "decimal" logarithm.

Instructions

Use for calculations built into the Windows operating system. To run it, press the win key, select “Run” in the main menu of the system, enter calc and click OK. The standard interface of this program does not have a function for calculating algorithms, so open the “View” section in its menu (or press the alt + “and” key combination) and select the “scientific” or “engineering” line.