In modern mathematics, a complex number is one of the most fundamental concepts, finding application both in “pure science” and in applied fields. It is clear that this was not always the case. In ancient times, when even ordinary negative numbers seemed a strange and dubious innovation, the need to extend the square root operation to them was not at all obvious. However, in the middle of the 16th century, mathematician Raphael Bombelli introduced complex (in this case, more precisely, imaginary) numbers into circulation. Actually, I propose to look at what was the essence of the difficulties that eventually brought the respectable Italian to such extremes.
There is a common misconception that complex numbers were required in order to solve quadratic equations. In fact, this is completely wrong: the task of finding the roots of a quadratic equation in no way motivates the introduction of complex numbers. That's perfect.
Let's see for ourselves. Any quadratic equation can be represented as:
.
Geometrically, this means that we want to find the intersection points of a certain line and a parabola
I even made a picture here for illustration.

As we all know well from school, the roots of a quadratic equation (in the above notation) are found by the following formula: ![]()
There are 3 possible options:
1. The radical expression is positive.
2. The radical expression is equal to zero.
3. The radical expression is negative.
In the first case there are 2 different roots, in the second there are two coinciding ones, in the third the equation “cannot be solved.” All these cases have a very clear geometric interpretation:
1. A straight line intersects a parabola (blue line in the figure).
2. A straight line touches a parabola.
3. The straight line has no common points with the parabola (lilac straight line in the figure).
The situation is simple, logical, and consistent. There is absolutely no reason to try to take the square root of a negative number. Nobody even tried.
The situation changed significantly when inquisitive mathematical thought reached cubic equations. A little less obvious, using some simple substitution , any cubic equation can be reduced to the form: . From a geometric point of view, the situation is similar to the previous one: we are looking for the intersection point of a straight line and a cubic parabola.
Take a look at the picture: 
The significant difference from the case of a quadratic equation is that no matter what line we take, it will always intersect the parabola. That is, from purely geometric considerations, a cubic equation always has at least one solution.
You can find it using the Cardano formula: ![]()
Where ![]() .
.
A little bulky, but so far everything seems to be in order. Or not?
In general, Cardano's formula is a vivid example of the “Arnold's principle” in action. And what is characteristic is that Cardano never claimed authorship of the formula.
Let us return, however, to our sheep. The formula is remarkable, without exaggeration, a great achievement of mathematics in the early to mid-16th century. But she has one nuance.
Let's take a classic example, which Bombelli considered: ![]() .
.
Suddenly,
,
and, accordingly,
.
We've arrived. It’s a pity for the formula, but the formula is good. Dead end. Despite the fact that the equation certainly has a solution.
Rafael Bombelli's idea was as follows: let's pretend to be a hose and pretend that the root of a negative is some kind of number. We, of course, know that there are no such numbers, but nevertheless, let's imagine that it exists and, like ordinary numbers, it can be added to others, multiplied, raised to a power, etc.
Using a similar approach, Bombelli found, in particular, that ![]() ,
,
And ![]() .
.
Let's check:
.
Please note that in the calculations no assumptions were made about the properties of the square roots of negative numbers, except for the assumption mentioned above that they behave like “ordinary” numbers.
In total we get . Which is quite the correct answer, which can be easily verified by direct substitution. It was a real breakthrough. Breakthrough into the complex plane.
Nevertheless, such calculations look like some kind of magic, a mathematical trick. The attitude towards them as some kind of trick persisted among mathematicians for a very long time. Actually, the name “imaginary numbers”, invented by Rene Descartes for roots of negative numbers, fully reflects the attitude of mathematicians of those times towards such entertainment.
However, as time passed, the “trick” was used with constant success, the authority of “imaginary numbers” in the eyes of the mathematical community grew, restrained, however, by the inconvenience of their use. Only the receipt by Leonhard Euler (by the way, it was he who introduced the now commonly used designation for the imaginary unit) of the famous formula
opened the way for complex numbers to various areas of mathematics and its applications. But that's a completely different story.
Complex numbers
Imaginary And complex numbers. Abscissa and ordinate
complex number. Conjugate complex numbers.
Operations with complex numbers. Geometric
representation of complex numbers. Complex plane.
Modulus and argument of a complex number. Trigonometric
complex number form. Operations with complex
numbers in trigonometric form. Moivre's formula.
Basic information about imaginary And complex numbers are given in the section “Imaginary and complex numbers”. The need for these numbers of a new type arose when solving quadratic equations for the case
D< 0 (здесь D– discriminant of a quadratic equation). For a long time, these numbers did not find physical application, which is why they were called “imaginary” numbers. However, now they are very widely used in various fields of physicsand technology: electrical engineering, hydro- and aerodynamics, elasticity theory, etc.
Complex numbers are written in the form:a+bi. Here a And b – real numbers , A i – imaginary unit, i.e. e. i 2 = –1. Number a called abscissa,a b – ordinatecomplex numbera + bi.Two complex numbersa+bi And a–bi are called conjugate complex numbers.
Main agreements:
1. Real number
Acan also be written in the formcomplex number:a+ 0 i or a – 0 i. For example, records 5 + 0i and 5 – 0 imean the same number 5 .2. Complex number 0 + bicalled purely imaginary number. Recordbimeans the same as 0 + bi.
3. Two complex numbersa+bi Andc + diare considered equal ifa = c And b = d. Otherwise complex numbers are not equal.
Addition. Sum of complex numbersa+bi And c + diis called a complex number (a+c ) + (b+d ) i.Thus, when adding complex numbers, their abscissas and ordinates are added separately.
This definition corresponds to the rules for operations with ordinary polynomials.
Subtraction. The difference of two complex numbersa+bi(diminished) and c + di(subtrahend) is called a complex number (a–c ) + (b–d ) i.
Thus, When subtracting two complex numbers, their abscissas and ordinates are subtracted separately.
Multiplication. Product of complex numbersa+bi And c + di is called a complex number:
(ac–bd ) + (ad+bc ) i.This definition follows from two requirements:
1) numbers a+bi And c + dimust be multiplied like algebraic binomials,
2) number ihas the main property:i 2 = – 1.
EXAMPLE ( a+ bi )(a–bi) =a 2 +b 2 . Hence, work
two conjugate complex numbers is equal to the real
a positive number.
Division. Divide a complex numbera+bi (divisible) by anotherc + di(divider) - means to find the third numbere + f i(chat), which when multiplied by a divisorc + di, results in the dividenda + bi.
If the divisor is not zero, division is always possible.
EXAMPLE Find (8 +i ) : (2 – 3 i) .
Solution. Let's rewrite this ratio as a fraction:
Multiplying its numerator and denominator by 2 + 3i
AND Having performed all the transformations, we get:

Geometric representation of complex numbers. Real numbers are represented by points on the number line:
Here is the point Ameans the number –3, dotB– number 2, and O- zero. In contrast, complex numbers are represented by points on the coordinate plane. For this purpose, we choose rectangular (Cartesian) coordinates with the same scales on both axes. Then the complex numbera+bi will be represented by a dot P with abscissa a and ordinate b (see picture). This coordinate system is called complex plane .
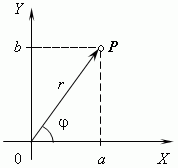
Module complex number is the length of the vectorOP, representing a complex number on the coordinate ( comprehensive) plane. Modulus of a complex numbera+bi denoted | a+bi| or letter r
Complex numbers for dummies. Lesson 1. What are they and what do you eat them with? Imaginary unit.
In order to understand what complex numbers are, let's remember about ordinary numbers and take a comprehensive look at them. And so, the simplest thing is natural numbers. They are called natural because through them something can be expressed “in kind,” that is, something can be counted. Here are two apples. They can be counted. There are five boxes of chocolates. We can count them. In other words, natural numbers are numbers with which we can count specific objects. You know very well that these numbers can be added, subtracted, multiplied and divided. Everything is clear with addition and multiplication. There were two apples, they added three, it became five. We took three boxes of chocolates, 10 pieces each, which means a total of thirty chocolates. Now let's move on to whole numbers. If natural numbers denote a specific number of objects, then abstractions are introduced into the set of integers. This zero And negative numbers. Why are these abstractions? Zero is the absence of something. But can we touch, feel what is not there? We can touch two apples, here they are. We can even eat them. What does zero apples mean? Can we touch, feel this zero? No, we can't. So this is abstraction. You have to somehow indicate the absence of something. So we designated zero as a number. But why signify this somehow? Let's imagine that we had two apples. We ate two. How much do we have left? That's right, not at all. We will write this operation (we ate two apples) as subtraction 2-2. And what did we end up with? How should we label the result? Only by introducing a new abstraction (zero), which will indicate that as a result of subtraction (eating) it turns out that we do not have a single apple left. But we can subtract not 2, but 3 from two. It would seem that this operation is meaningless. If we only have two apples, how can we eat three?
Let's look at another example. We go to the store for beer. We have 100 rubles with us. Beer costs 60 rubles per bottle. We want to buy two bottles, but we don’t have enough money. We need 120 rubles. And then we meet our old friend and borrow twenty from him. We buy beer. Question. How much money do we have left? Common sense dictates that not at all. But from a mathematical point of view this would be absurd. Why? Because in order to get zero as a result, you need to subtract 100 from 100. And we do 100-120. Here we should get something different. What did we get? And the fact that we still owe our friend 20 rubles. The next time we have 140 rubles with us, we will come to the store for beer, meet a friend, pay off our debts with him and be able to buy two more bottles of beer. As a result, we get 140-120-20=0. Note -20. This is another abstraction - negative number. That is, our debt to a friend is a number with a minus sign, because when we repay the debt, we subtract this amount. I will say more, this is an even greater abstraction than zero. Zero means something that doesn't exist. And a negative number is like something that will be taken away from us in the future.
And so, using an example, I showed how abstractions are born in mathematics. And that, it would seem, despite all the absurdity of such abstractions (like taking away more than was), they find application in real life. In the case of dividing integers, another abstraction arises - fractional numbers. I will not dwell on them in detail, and it is clear that they are needed in the case when we have integers that are not divisible by an integer. For example, we have four apples, but we need to divide them among three people. It’s clear here that we divide the one remaining apple into three parts and get fractions.
Now let’s very smoothly get to the complex numbers themselves. But first, remember that when you multiply two negative numbers, you get a positive number. Someone ask - why is this so? Let's first understand multiplying a negative number by a positive one. Let's say we multiply -20 by 2. That is, we need to add -20+-20. The result is -40, since adding a negative number is a subtraction. Why subtraction - see above, a negative number is a debt; when we take it away, something is taken away from us. There is another everyday meaning. What happens if the debt increases? For example, in the case when we were given a loan at interest? As a result, the same number with a minus sign remained, the one that became larger after the minus. What does it mean to multiply by a negative number? What does 3*-2 mean? This means that the number three must be taken minus two times. That is, put a minus before the result of multiplication. By the way, this is the same as -3*2, since rearranging the factors does not change the product. Now pay attention. Multiply -3 by -2. We take the number -3 minus two times. If we take the number -3 twice, then the result will be -6, you understand that. What if we take minus two times? But what does it mean to take minus times? If you take a positive number minus times, you end up with a negative number, its sign changes. If we take a negative number minus times, then its sign changes and it becomes positive.
Why did we talk about multiplying minus by minus? And in order to consider another abstraction, this time it is directly related to complex numbers. This imaginary unit. The imaginary unit is equal to the square root of minus 1:
Let me remind you what a square root is. This is the inverse operation of squaring. And squaring is multiplying a number by itself. So the square root of 4 is 2 because 2*2=4. The square root of 9 is 3, since 3*3=9. The square root of one also turns out to be one, and the square root of zero is zero. But how do we take the square root of minus one? What number must be multiplied by itself to get -1? But there is no such number! If we multiply -1 by itself, we will ultimately get 1. If we multiply 1 by 1, we will get 1. But we will not get minus -1 in this way. But, nevertheless, we may encounter a situation where there is a negative number under the root. What to do? You can, of course, say that there is no solution. It's like dividing by zero. Until some time, we all believed that it was impossible to divide by zero. But then we learned about such an abstraction as infinity, and it turned out that dividing by zero is still possible. Moreover, abstractions such as division by zero, or the uncertainty obtained by dividing zero by zero or infinity by infinity, as well as other similar operations, are widely used in higher mathematics (), and higher mathematics is the basis of many exact sciences, which move forward technical progress. So maybe there is some secret meaning in the imaginary unit? Eat. And you will understand it by reading my further lessons on complex numbers. In the meantime, I will talk about some areas where complex numbers (numbers that contain an imaginary unit) are used.
And so, here is a list of areas where complex numbers are used:
Electrical engineering. Calculation of alternating current circuits. The use of complex numbers in this case greatly simplifies the calculation; without them, differential and integral equations would have to be used.
Quantum mechanics.In short, in quantum mechanics there is such a thing as a wave function, which itself is complex-valued and whose square (already a real number) is equal to the probability density of finding a particle at a given point. See also the series of lessons
Digital signal processing. The theory of digital signal processing includes such a concept as the z-transform, which greatly facilitates various calculations related to the calculation of the characteristics of various signals, such as frequency and amplitude characteristics, etc.
Description of processes of plane flow of liquids.
Liquid flow around profiles.
Wave movements of liquid.
And this is far from an exhaustive list of where complex numbers are used. This completes the first acquaintance with complex numbers, until we meet again.
Complex or imaginary numbers first appeared in Cardano's famous work "The Great Art, or on the Rules of Algebra" in 1545. In the opinion of the author, these numbers were not suitable for use. However, this claim was later refuted. In particular, Bombelli in 1572, when solving a cubic equation, substantiated the use of imaginary numbers. He compiled the basic rules for operations with complex numbers.
And yet, for a long time in the mathematical world there was no single idea about the essence of complex numbers.
The symbol for imaginary numbers was first proposed by the outstanding mathematician Euler. The proposed symbolism looked like this: i = sqr -1, where i is imaginarius, which means fictitious. Euler's merit also includes the idea of the algebraic closedness of the field of complex numbers.
So, the need for numbers of a new type arose when solving quadratic equations for the case D< 0 (где D - дискриминант квадратного уравнения). В настоящее время комплексные числа нашли широкое применение в физике и технике, гидро- и аэродинамике, теории упругости и т.п.
The graphical representation of complex numbers has the form: a + bi, where a and b are real numbers, and i is an imaginary unit, i.e. i 2 = -1. The number a is called the abscissa, and b is the ordinate of the complex number a + bi. Two complex numbers a + bi and a - bi are called conjugate complex numbers.
There are a number of rules associated with complex numbers:
- First, the real number a can be written in complex number form: a+ 0 i or a - 0 i. For example, 5 + 0 i and 5 - 0 i mean the same number 5.
- Secondly, the complex number 0+ bi is called a purely imaginary number. The notation bi means the same as 0+ bi .
- Third, two complex numbers a + bi and c + di are considered equal if a = c and b = d. Otherwise, complex numbers are not equal.
Basic operations on complex numbers include:

In geometric representation, complex numbers, unlike real numbers, which are represented on the number line by points, are marked by points on the coordinate plane. For this we take rectangular (Cartesian) coordinates with identical scales on the axes. In this case, the complex number a + bi will be represented by point P with abscissa a and ordinate b. This coordinate system is called complex plane.
Module complex number is the length of the vector OP representing the complex number of the complex plane. The modulus of a complex number a + bi is written as |a + bi| or the letter r and is equal to: r = |a + ib| = sqr a 2 + b 2 .Conjugate complex numbers have the same modulus.








