Random variable A variable is called a variable that, as a result of each test, takes on one previously unknown value, depending on random reasons. Random variables are denoted by capital Latin letters: $X,\ Y,\ Z,\ \dots $ According to their type, random variables can be discrete And continuous.
Discrete random variable- this is a random variable whose values can be no more than countable, that is, either finite or countable. By countability we mean that the values of a random variable can be numbered.
Example 1 . Here are examples of discrete random variables:
a) the number of hits on the target with $n$ shots, here the possible values are $0,\ 1,\ \dots ,\ n$.
b) the number of emblems dropped when tossing a coin, here the possible values are $0,\ 1,\ \dots ,\ n$.
c) the number of ships arriving on board (a countable set of values).
d) the number of calls arriving at the PBX (countable set of values).
1. Law of probability distribution of a discrete random variable.
A discrete random variable $X$ can take values $x_1,\dots ,\ x_n$ with probabilities $p\left(x_1\right),\ \dots ,\ p\left(x_n\right)$. The correspondence between these values and their probabilities is called law of distribution of a discrete random variable. As a rule, this correspondence is specified using a table, in the first line of which the values $x_1,\dots ,\ x_n$ are indicated, and in the second line the probabilities $p_1,\dots ,\ p_n$ corresponding to these values are indicated.
$\begin(array)(|c|c|)
\hline
X_i & x_1 & x_2 & \dots & x_n \\
\hline
p_i & p_1 & p_2 & \dots & p_n \\
\hline
\end(array)$
Example 2 . Let the random variable $X$ be the number of points rolled when tossing a die. Such a random variable $X$ can take the following values: $1,\ 2,\ 3,\ 4,\ 5,\ 6$. The probabilities of all these values are equal to $1/6$. Then the law of probability distribution of the random variable $X$:
$\begin(array)(|c|c|)
\hline
1 & 2 & 3 & 4 & 5 & 6 \\
\hline
\hline
\end(array)$
Comment. Since in the distribution law of a discrete random variable $X$ the events $1,\ 2,\ \dots ,\ 6$ form a complete group of events, then the sum of the probabilities must be equal to one, that is, $\sum(p_i)=1$.
2. Mathematical expectation of a discrete random variable.
Expectation of a random variable sets its “central” meaning. For a discrete random variable, the mathematical expectation is calculated as the sum of the products of the values $x_1,\dots ,\ x_n$ and the probabilities $p_1,\dots ,\ p_n$ corresponding to these values, that is: $M\left(X\right)=\sum ^n_(i=1)(p_ix_i)$. In English-language literature, another notation $E\left(X\right)$ is used.
Properties of mathematical expectation$M\left(X\right)$:
- $M\left(X\right)$ lies between the smallest and largest values of the random variable $X$.
- The mathematical expectation of a constant is equal to the constant itself, i.e. $M\left(C\right)=C$.
- The constant factor can be taken out of the sign of the mathematical expectation: $M\left(CX\right)=CM\left(X\right)$.
- The mathematical expectation of the sum of random variables is equal to the sum of their mathematical expectations: $M\left(X+Y\right)=M\left(X\right)+M\left(Y\right)$.
- The mathematical expectation of the product of independent random variables is equal to the product of their mathematical expectations: $M\left(XY\right)=M\left(X\right)M\left(Y\right)$.
Example 3 . Let's find the mathematical expectation of the random variable $X$ from example $2$.
$$M\left(X\right)=\sum^n_(i=1)(p_ix_i)=1\cdot ((1)\over (6))+2\cdot ((1)\over (6) )+3\cdot ((1)\over (6))+4\cdot ((1)\over (6))+5\cdot ((1)\over (6))+6\cdot ((1 )\over (6))=3.5.$$
We can notice that $M\left(X\right)$ lies between the smallest ($1$) and largest ($6$) values of the random variable $X$.
Example 4 . It is known that the mathematical expectation of the random variable $X$ is equal to $M\left(X\right)=2$. Find the mathematical expectation of the random variable $3X+5$.
Using the above properties, we get $M\left(3X+5\right)=M\left(3X\right)+M\left(5\right)=3M\left(X\right)+5=3\cdot 2 +5=$11.
Example 5 . It is known that the mathematical expectation of the random variable $X$ is equal to $M\left(X\right)=4$. Find the mathematical expectation of the random variable $2X-9$.
Using the above properties, we get $M\left(2X-9\right)=M\left(2X\right)-M\left(9\right)=2M\left(X\right)-9=2\cdot 4 -9=-1$.
3. Dispersion of a discrete random variable.
Possible values of random variables with equal mathematical expectations can disperse differently around their average values. For example, in two student groups the average score for the exam in probability theory turned out to be 4, but in one group everyone turned out to be good students, and in the other group there were only C students and excellent students. Therefore, there is a need for a numerical characteristic of a random variable that would show the spread of the values of the random variable around its mathematical expectation. This characteristic is dispersion.
Variance of a discrete random variable$X$ is equal to:
$$D\left(X\right)=\sum^n_(i=1)(p_i(\left(x_i-M\left(X\right)\right))^2).\ $$
In English literature the notation $V\left(X\right),\ Var\left(X\right)$ is used. Very often the variance $D\left(X\right)$ is calculated using the formula $D\left(X\right)=\sum^n_(i=1)(p_ix^2_i)-(\left(M\left(X \right)\right))^2$.
Dispersion properties$D\left(X\right)$:
- The variance is always greater than or equal to zero, i.e. $D\left(X\right)\ge 0$.
- The variance of the constant is zero, i.e. $D\left(C\right)=0$.
- The constant factor can be taken out of the sign of the dispersion provided that it is squared, i.e. $D\left(CX\right)=C^2D\left(X\right)$.
- The variance of the sum of independent random variables is equal to the sum of their variances, i.e. $D\left(X+Y\right)=D\left(X\right)+D\left(Y\right)$.
- The variance of the difference between independent random variables is equal to the sum of their variances, i.e. $D\left(X-Y\right)=D\left(X\right)+D\left(Y\right)$.
Example 6 . Let's calculate the variance of the random variable $X$ from example $2$.
$$D\left(X\right)=\sum^n_(i=1)(p_i(\left(x_i-M\left(X\right)\right))^2)=((1)\over (6))\cdot (\left(1-3.5\right))^2+((1)\over (6))\cdot (\left(2-3.5\right))^2+ \dots +((1)\over (6))\cdot (\left(6-3.5\right))^2=((35)\over (12))\approx 2.92.$$
Example 7 . It is known that the variance of the random variable $X$ is equal to $D\left(X\right)=2$. Find the variance of the random variable $4X+1$.
Using the above properties, we find $D\left(4X+1\right)=D\left(4X\right)+D\left(1\right)=4^2D\left(X\right)+0=16D\ left(X\right)=16\cdot 2=32$.
Example 8 . It is known that the variance of the random variable $X$ is equal to $D\left(X\right)=3$. Find the variance of the random variable $3-2X$.
Using the above properties, we find $D\left(3-2X\right)=D\left(3\right)+D\left(2X\right)=0+2^2D\left(X\right)=4D\ left(X\right)=4\cdot 3=12$.
4. Distribution function of a discrete random variable.
The method of representing a discrete random variable in the form of a distribution series is not the only one, and most importantly, it is not universal, since a continuous random variable cannot be specified using a distribution series. There is another way to represent a random variable - the distribution function.
Distribution function random variable $X$ is called a function $F\left(x\right)$, which determines the probability that the random variable $X$ will take a value less than some fixed value $x$, that is, $F\left(x\right )=P\left(X< x\right)$
Properties of the distribution function:
- $0\le F\left(x\right)\le 1$.
- The probability that the random variable $X$ will take values from the interval $\left(\alpha ;\ \beta \right)$ is equal to the difference between the values of the distribution function at the ends of this interval: $P\left(\alpha< X < \beta \right)=F\left(\beta \right)-F\left(\alpha \right)$
- $F\left(x\right)$ - non-decreasing.
- $(\mathop(lim)_(x\to -\infty ) F\left(x\right)=0\ ),\ (\mathop(lim)_(x\to +\infty ) F\left(x \right)=1\ )$.
Example 9 . Let us find the distribution function $F\left(x\right)$ for the distribution law of the discrete random variable $X$ from example $2$.
$\begin(array)(|c|c|)
\hline
1 & 2 & 3 & 4 & 5 & 6 \\
\hline
1/6 & 1/6 & 1/6 & 1/6 & 1/6 & 1/6 \\
\hline
\end(array)$
If $x\le 1$, then, obviously, $F\left(x\right)=0$ (including for $x=1$ $F\left(1\right)=P\left(X< 1\right)=0$).
If $1< x\le 2$, то $F\left(x\right)=P\left(X=1\right)=1/6$.
If $2< x\le 3$, то $F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)=1/6+1/6=1/3$.
If $3< x\le 4$, то $F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right)=1/6+1/6+1/6=1/2$.
If $4< x\le 5$, то $F\left(X\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right)+P\left(X=4\right)=1/6+1/6+1/6+1/6=2/3$.
If $5< x\le 6$, то $F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right)+P\left(X=4\right)+P\left(X=5\right)=1/6+1/6+1/6+1/6+1/6=5/6$.
If $x > 6$, then $F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right) +P\left(X=4\right)+P\left(X=5\right)+P\left(X=6\right)=1/6+1/6+1/6+1/6+ 1/6+1/6=1$.
So $F(x)=\left\(\begin(matrix)
0,\ at\ x\le 1,\\
1/6,at\ 1< x\le 2,\\
1/3,\ at\ 2< x\le 3,\\
1/2,at\ 3< x\le 4,\\
2/3,\ at\ 4< x\le 5,\\
5/6,\ at\ 4< x\le 5,\\
1,\ for\ x > 6.
\end(matrix)\right.$
As is already known, the distribution law completely characterizes a random variable. However, often the distribution law is unknown and one has to limit oneself to less information. Sometimes it is even more profitable to use numbers that describe the random variable in total; such numbers are called numerical characteristics of a random variable. One of the important numerical characteristics is the mathematical expectation.
The mathematical expectation, as will be shown below, is approximately equal to the average value of the random variable. To solve many problems, it is enough to know the mathematical expectation. For example, if it is known that the mathematical expectation of the number of points scored by the first shooter is greater than that of the second, then the first shooter, on average, scores more points than the second, and, therefore, shoots better than the second. Although the mathematical expectation provides much less information about a random variable than the law of its distribution, knowledge of the mathematical expectation is sufficient for solving problems like the one above and many others.
§ 2. Mathematical expectation of a discrete random variable
Mathematical expectation A discrete random variable is the sum of the products of all its possible values and their probabilities.
Let the random variable X can only take values X 1 , X 2 , ..., X n , whose probabilities are respectively equal r 1 , r 2 , . . ., r n . Then the mathematical expectation M(X) random variable X is determined by equality
M(X) = X 1 r 1 + X 2 r 2 + … + x n p n .
If a discrete random variable X takes a countable set of possible values, then
M(X)=
Moreover, the mathematical expectation exists if the series on the right side of the equality converges absolutely.
Comment. From the definition it follows that the mathematical expectation of a discrete random variable is a non-random (constant) quantity. We recommend that you remember this statement, since it will be used many times later. It will be shown later that the mathematical expectation of a continuous random variable is also a constant value.
Example 1. Find the mathematical expectation of a random variable X, knowing the law of its distribution:
Solution. The required mathematical expectation is equal to the sum of the products of all possible values of the random variable and their probabilities:
M(X)= 3* 0, 1+ 5* 0, 6+ 2* 0, 3= 3, 9.
Example 2. Find the mathematical expectation of the number of occurrences of an event A in one trial, if the probability of the event A equal to r.
Solution. Random variable X - number of occurrences of the event A in one test - can take only two values: X 1 = 1 (event A occurred) with probability r And X 2 = 0 (event A did not occur) with probability q= 1 -r. The required mathematical expectation
M(X)= 1* p+ 0* q= p
So, the mathematical expectation of the number of occurrences of an event in one trial is equal to the probability of this event. This result will be used below.
§ 3. Probabilistic meaning of mathematical expectation
Let it be produced n tests in which the random variable X accepted T 1 times value X 1 , T 2 times value X 2 ,...,m k times value x k , and T 1 + T 2 + …+t To = p. Then the sum of all values taken X, equal to
X 1 T 1 + X 2 T 2 + ... + X To T To .
Let's find the arithmetic mean  all values accepted by a random variable, for which we divide the found sum by the total number of tests:
all values accepted by a random variable, for which we divide the found sum by the total number of tests:
 =
(X 1 T 1
+
X 2 T 2 +
... +
X To T To)/p,
=
(X 1 T 1
+
X 2 T 2 +
... +
X To T To)/p,
 =
X 1
(m 1 /
n)
+
X 2
(m 2 /
n)
+ ... +
X To
(T To /n).
(*)
=
X 1
(m 1 /
n)
+
X 2
(m 2 /
n)
+ ... +
X To
(T To /n).
(*)
Noticing that the attitude m 1 / n- relative frequency W 1 values X 1 , m 2 / n - relative frequency W 2 values X 2 etc., we write the relation (*) like this:
 =X 1
W 1
+
x 2 W 2
+ ..
. + X To W k .
(**)
=X 1
W 1
+
x 2 W 2
+ ..
. + X To W k .
(**)
Let us assume that the number of tests is large enough. Then the relative frequency is approximately equal to the probability of the event occurring (this will be proven in Chapter IX, § 6):
W 1
 p 1 ,
W 2
p 1 ,
W 2
 p 2 ,
…,
W k
p 2 ,
…,
W k
 p k .
p k .
Replacing the relative frequencies with the corresponding probabilities in relation (**), we obtain

 x 1 p 1
+
X 2 r 2
+ … +
X To r To .
x 1 p 1
+
X 2 r 2
+ … +
X To r To .
The right side of this approximate equality is M(X). So,

 M(X).
M(X).
The probabilistic meaning of the result obtained is as follows: mathematical expectation is approximately equal(the more accurate, the greater the number of tests) the arithmetic mean of the observed values of a random variable.
Remark 1. It is easy to understand that the mathematical expectation is greater than the smallest and less than the largest possible value. In other words, on the number line, possible values are located to the left and right of the mathematical expectation. In this sense, the mathematical expectation characterizes the location of the distribution and is therefore often called distribution center.
This term is borrowed from mechanics: if the masses r 1 , p 2 , ..., r n located at the abscissa points x 1 ,
X 2 ,
...,
X n, and  then the abscissa of the center of gravity
then the abscissa of the center of gravity
x c =
 .
.
Considering that
 =
M
(X)
And
=
M
(X)
And  we get M(X)= x With .
we get M(X)= x With .
So, the mathematical expectation is the abscissa of the center of gravity of a system of material points, the abscissas of which are equal to the possible values of the random variable, and the masses are equal to their probabilities.
Remark 2. The origin of the term “mathematical expectation” is associated with the initial period of the emergence of probability theory (XVI - XVII centuries), when the scope of its application was limited to gambling. The player was interested in the average value of the expected win, or, in other words, the mathematical expectation of winning.
Each individual value is completely determined by its distribution function. Also, to solve practical problems, it is enough to know several numerical characteristics, thanks to which it becomes possible to present the main features of a random variable in a short form.
These quantities include primarily mathematical expectation And dispersion .
Expectation— the average value of a random variable in probability theory. Denoted as .
In the simplest way, the mathematical expectation of a random variable X(w), find how integralLebesgue in relation to the probability measure R original probability space![]()
You can also find the mathematical expectation of a value as Lebesgue integral from X by probability distribution R X quantities X:
![]()
where is the set of all possible values X.
Mathematical expectation of functions from a random variable X found through distribution R X. For example, If X- a random variable with values in and f(x)- unambiguous Borel'sfunction X , That:
If F(x)- distribution function X, then the mathematical expectation is representable integralLebesgue - Stieltjes (or Riemann - Stieltjes):
![]()
in this case integrability X In terms of ( * ) corresponds to the finiteness of the integral
![]()
In specific cases, if X has a discrete distribution with probable values x k, k=1, 2, . , and probabilities, then
![]()
If X has an absolutely continuous distribution with probability density p(x), That
![]()
in this case, the existence of a mathematical expectation is equivalent to the absolute convergence of the corresponding series or integral.
Properties of the mathematical expectation of a random variable.
- The mathematical expectation of a constant value is equal to this value:
C- constant;
- M=C.M[X]
- The mathematical expectation of the sum of randomly taken values is equal to the sum of their mathematical expectations:
![]()
- The mathematical expectation of the product of independent randomly taken variables = the product of their mathematical expectations:
M=M[X]+M[Y]
If X And Y independent.
if the series converges:
![]()
Algorithm for calculating mathematical expectation.
Properties of discrete random variables: all their values can be renumbered by natural numbers; assign each value a non-zero probability.
1. Multiply the pairs one by one: x i on p i.
2. Add the product of each pair x i p i.
For example, For n = 4 :
Distribution function of a discrete random variable stepwise, it increases abruptly at those points whose probabilities have a positive sign.
Example: Find the mathematical expectation using the formula.
Expectation and variance are the most commonly used numerical characteristics of a random variable. They characterize the most important features of the distribution: its position and degree of scattering. In many practical problems, a complete, exhaustive characteristic of a random variable - the distribution law - either cannot be obtained at all, or is not needed at all. In these cases, one is limited to an approximate description of a random variable using numerical characteristics.
The expected value is often called simply the average value of a random variable. Dispersion of a random variable is a characteristic of dispersion, the spread of a random variable around its mathematical expectation.
Expectation of a discrete random variable
Let us approach the concept of mathematical expectation, first based on the mechanical interpretation of the distribution of a discrete random variable. Let the unit mass be distributed between the points of the x-axis x1 , x 2 , ..., x n, and each material point has a corresponding mass of p1 , p 2 , ..., p n. It is required to select one point on the abscissa axis, characterizing the position of the entire system of material points, taking into account their masses. It is natural to take the center of mass of the system of material points as such a point. This is the weighted average of the random variable X, to which the abscissa of each point xi enters with a “weight” equal to the corresponding probability. The average value of the random variable obtained in this way X is called its mathematical expectation.
The mathematical expectation of a discrete random variable is the sum of the products of all its possible values and the probabilities of these values:

Example 1. A win-win lottery has been organized. There are 1000 winnings, of which 400 are 10 rubles. 300 - 20 rubles each. 200 - 100 rubles each. and 100 - 200 rubles each. What is the average winnings for someone who buys one ticket?
Solution. We will find the average winnings if we divide the total amount of winnings, which is 10*400 + 20*300 + 100*200 + 200*100 = 50,000 rubles, by 1000 (total amount of winnings). Then we get 50000/1000 = 50 rubles. But the expression for calculating the average winnings can be presented in the following form:

On the other hand, under these conditions, the winning size is a random variable, which can take values of 10, 20, 100 and 200 rubles. with probabilities equal to 0.4, respectively; 0.3; 0.2; 0.1. Therefore, the expected average win is equal to the sum of the products of the size of the wins and the probability of receiving them.
Example 2. The publisher decided to publish a new book. He plans to sell the book for 280 rubles, of which he himself will receive 200, 50 to the bookstore and 30 to the author. The table provides information about the costs of publishing a book and the probability of selling a certain number of copies of the book.
Find the publisher's expected profit.
Solution. The random variable “profit” is equal to the difference between the income from sales and the cost of costs. For example, if 500 copies of a book are sold, then the income from the sale is 200 * 500 = 100,000, and the cost of publication is 225,000 rubles. Thus, the publisher faces a loss of 125,000 rubles. The following table summarizes the expected values of the random variable - profit:
| Number | Profit xi | Probability pi | xi p i |
| 500 | -125000 | 0,20 | -25000 |
| 1000 | -50000 | 0,40 | -20000 |
| 2000 | 100000 | 0,25 | 25000 |
| 3000 | 250000 | 0,10 | 25000 |
| 4000 | 400000 | 0,05 | 20000 |
| Total: | 1,00 | 25000 |
Thus, we obtain the mathematical expectation of the publisher’s profit:
![]() .
.
Example 3. Probability of hitting with one shot p= 0.2. Determine the consumption of projectiles that provide a mathematical expectation of the number of hits equal to 5.
Solution. From the same mathematical expectation formula that we have used so far, we express x- shell consumption:
![]() .
.
Example 4. Determine the mathematical expectation of a random variable x number of hits with three shots, if the probability of a hit with each shot p = 0,4 .
Hint: find the probability of random variable values by Bernoulli's formula .
Properties of mathematical expectation
Let's consider the properties of mathematical expectation.
Property 1. The mathematical expectation of a constant value is equal to this constant:
Property 2. The constant factor can be taken out of the mathematical expectation sign:
![]()
Property 3. The mathematical expectation of the sum (difference) of random variables is equal to the sum (difference) of their mathematical expectations:
Property 4. The mathematical expectation of a product of random variables is equal to the product of their mathematical expectations:
Property 5. If all values of a random variable X decrease (increase) by the same number WITH, then its mathematical expectation will decrease (increase) by the same number:
![]()
When you can’t limit yourself only to mathematical expectation
In most cases, only the mathematical expectation cannot sufficiently characterize a random variable.
Let the random variables X And Y are given by the following distribution laws:
| Meaning X | Probability |
| -0,1 | 0,1 |
| -0,01 | 0,2 |
| 0 | 0,4 |
| 0,01 | 0,2 |
| 0,1 | 0,1 |
| Meaning Y | Probability |
| -20 | 0,3 |
| -10 | 0,1 |
| 0 | 0,2 |
| 10 | 0,1 |
| 20 | 0,3 |
The mathematical expectations of these quantities are the same - equal to zero:
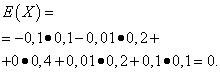

However, their distribution patterns are different. Random variable X can only take values that differ little from the mathematical expectation, and the random variable Y can take values that deviate significantly from the mathematical expectation. A similar example: the average wage does not make it possible to judge the share of high- and low-paid workers. In other words, one cannot judge from the mathematical expectation what deviations from it, at least on average, are possible. To do this, you need to find the variance of the random variable.
Variance of a discrete random variable
Variance discrete random variable X is called the mathematical expectation of the square of its deviation from the mathematical expectation:

The standard deviation of a random variable X the arithmetic value of the square root of its variance is called:
![]() .
.
Example 5. Calculate variances and standard deviations of random variables X And Y, the distribution laws of which are given in the tables above.
Solution. Mathematical expectations of random variables X And Y, as found above, are equal to zero. According to the dispersion formula at E(X)=E(y)=0 we get:
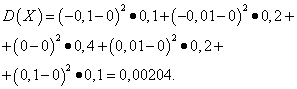
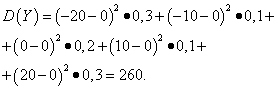
Then the standard deviations of random variables X And Y make up
![]() .
.
Thus, with the same mathematical expectations, the variance of the random variable X very small, but a random variable Y- significant. This is a consequence of differences in their distribution.
Example 6. The investor has 4 alternative investment projects. The table summarizes the expected profit in these projects with the corresponding probability.
| Project 1 | Project 2 | Project 3 | Project 4 |
| 500, P=1 | 1000, P=0,5 | 500, P=0,5 | 500, P=0,5 |
| 0, P=0,5 | 1000, P=0,25 | 10500, P=0,25 | |
| 0, P=0,25 | 9500, P=0,25 |
Find for each alternative the mathematical expectation, variance and standard deviation.
Solution. Let us show how these values are calculated for the 3rd alternative:
The table summarizes the found values for all alternatives.
All alternatives have the same mathematical expectations. This means that in the long run everyone has the same income. Standard deviation can be interpreted as a measure of risk - the higher it is, the greater the risk of the investment. An investor who does not want much risk will choose project 1 since it has the smallest standard deviation (0). If the investor prefers risk and high returns in a short period, then he will choose the project with the largest standard deviation - project 4.
Dispersion properties
Let us present the properties of dispersion.
Property 1. The variance of a constant value is zero:
Property 2. The constant factor can be taken out of the dispersion sign by squaring it:
![]() .
.
Property 3. The variance of a random variable is equal to the mathematical expectation of the square of this value, from which the square of the mathematical expectation of the value itself is subtracted:
![]() ,
,
Where ![]() .
.
Property 4. The variance of the sum (difference) of random variables is equal to the sum (difference) of their variances:
Example 7. It is known that a discrete random variable X takes only two values: −3 and 7. In addition, the mathematical expectation is known: E(X) = 4 . Find the variance of a discrete random variable.
Solution. Let us denote by p the probability with which a random variable takes a value x1 = −3 . Then the probability of the value x2 = 7 will be 1 − p. Let us derive the equation for the mathematical expectation:
E(X) = x 1 p + x 2 (1 − p) = −3p + 7(1 − p) = 4 ,
where we get the probabilities: p= 0.3 and 1 − p = 0,7 .
Law of distribution of a random variable:
| X | −3 | 7 |
| p | 0,3 | 0,7 |
We calculate the variance of this random variable using the formula from property 3 of dispersion:
D(X) = 2,7 + 34,3 − 16 = 21 .
Find the mathematical expectation of a random variable yourself, and then look at the solution
Example 8. Discrete random variable X takes only two values. It accepts the greater of the values 3 with probability 0.4. In addition, the variance of the random variable is known D(X) = 6 . Find the mathematical expectation of a random variable.
Example 9. There are 6 white and 4 black balls in an urn. 3 balls are drawn from the urn. The number of white balls among the drawn balls is a discrete random variable X. Find the mathematical expectation and variance of this random variable.
Solution. Random variable X can take values 0, 1, 2, 3. The corresponding probabilities can be calculated from probability multiplication rule. Law of distribution of a random variable:
| X | 0 | 1 | 2 | 3 |
| p | 1/30 | 3/10 | 1/2 | 1/6 |
Hence the mathematical expectation of this random variable:
M(X) = 3/10 + 1 + 1/2 = 1,8 .
The variance of a given random variable is:
D(X) = 0,3 + 2 + 1,5 − 3,24 = 0,56 .
Expectation and variance of a continuous random variable
For a continuous random variable, the mechanical interpretation of the mathematical expectation will retain the same meaning: the center of mass for a unit mass distributed continuously on the x-axis with density f(x). Unlike a discrete random variable, whose function argument xi changes abruptly; for a continuous random variable, the argument changes continuously. But the mathematical expectation of a continuous random variable is also related to its average value.
To find the mathematical expectation and variance of a continuous random variable, you need to find definite integrals . If the density function of a continuous random variable is given, then it directly enters into the integrand. If a probability distribution function is given, then by differentiating it, you need to find the density function.
The arithmetic average of all possible values of a continuous random variable is called its mathematical expectation, denoted by or .
– the number of boys among 10 newborns.
It is absolutely clear that this number is not known in advance, and the next ten children born may include:
Or boys - one and only one from the listed options.
And, in order to keep in shape, a little physical education:
– long jump distance (in some units).
Even a master of sports cannot predict it :)
However, your hypotheses?
2) Continuous random variable – accepts All numerical values from some finite or infinite interval.
Note : the abbreviations DSV and NSV are popular in educational literature
First, let's analyze the discrete random variable, then - continuous.
Distribution law of a discrete random variable
- This correspondence between possible values of this quantity and their probabilities. Most often, the law is written in a table: 
The term is used quite often row
distribution, but in some situations it sounds ambiguous, and so I will stick to the "law".
And now very important point: since the random variable Necessarily will accept one of the values, then the corresponding events form full group and the sum of the probabilities of their occurrence is equal to one:
or, if written condensed:
So, for example, the law of probability distribution of points rolled on a die has the following form: 
No comments.
You may be under the impression that a discrete random variable can only take on “good” integer values. Let's dispel the illusion - they can be anything:
Example 1
Some game has the following winning distribution law: 
...you've probably dreamed of such tasks for a long time :) I'll tell you a secret - me too. Especially after I finished working on field theory.
Solution: since a random variable can take only one of three values, the corresponding events form full group, which means the sum of their probabilities is equal to one: ![]()
Exposing the “partisan”: ![]()
– thus, the probability of winning conventional units is 0.4.
Control: that’s what we needed to make sure of.
Answer:
It is not uncommon when you need to draw up a distribution law yourself. For this they use classical definition of probability, multiplication/addition theorems for event probabilities and other chips tervera:
Example 2
The box contains 50 lottery tickets, among which 12 are winning, and 2 of them win 1000 rubles each, and the rest - 100 rubles each. Draw up a law for the distribution of a random variable - the size of the winnings, if one ticket is drawn at random from the box.
Solution: as you noticed, the values of a random variable are usually placed in in ascending order. Therefore, we start with the smallest winnings, and that is rubles.
There are 50 such tickets in total - 12 = 38, and according to classical definition:
– the probability that a randomly drawn ticket will be a loser.
In other cases everything is simple. The probability of winning rubles is:
Check: – and this is a particularly pleasant moment of such tasks!
Answer: the desired law of distribution of winnings: ![]()
The following task is for you to solve on your own:
Example 3
The probability that the shooter will hit the target is . Draw up a distribution law for a random variable - the number of hits after 2 shots.
...I knew that you missed him :) Let's remember multiplication and addition theorems. The solution and answer are at the end of the lesson.
The distribution law completely describes a random variable, but in practice it can be useful (and sometimes more useful) to know only some of it numerical characteristics .
Expectation of a discrete random variable
In simple terms, this is average expected value when testing is repeated many times. Let the random variable take values with probabilities ![]() respectively. Then the mathematical expectation of this random variable is equal to sum of products all its values to the corresponding probabilities:
respectively. Then the mathematical expectation of this random variable is equal to sum of products all its values to the corresponding probabilities:
or collapsed: ![]()
Let us calculate, for example, the mathematical expectation of a random variable - the number of points rolled on a die:
Now let's remember our hypothetical game: 
The question arises: is it profitable to play this game at all? ...who has any impressions? So you can’t say it “offhand”! But this question can be easily answered by calculating the mathematical expectation, essentially - weighted average by probability of winning:
Thus, the mathematical expectation of this game losing.
Don't trust your impressions - trust the numbers!
Yes, here you can win 10 and even 20-30 times in a row, but in the long run we will face inevitable ruin. And I wouldn't advise you to play such games :) Well, maybe only for fun.
From all of the above it follows that the mathematical expectation is no longer a RANDOM value.
Creative task for independent research:
Example 4
Mr. X plays European roulette using the following system: he constantly bets 100 rubles on “red”. Draw up a law of distribution of a random variable - its winnings. Calculate the mathematical expectation of winnings and round it to the nearest kopeck. How many on average Does the player lose for every hundred he bet?
Reference : European roulette contains 18 red, 18 black and 1 green sector (“zero”). If a “red” appears, the player is paid double the bet, otherwise it goes to the casino’s income
There are many other roulette systems for which you can create your own probability tables. But this is the case when we do not need any distribution laws or tables, because it has been established for certain that the player’s mathematical expectation will be exactly the same. The only thing that changes from system to system is








