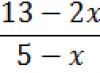In technology and the world around us we often have to deal with periodic(or almost periodic) processes that repeat at regular intervals. Such processes are called oscillatory.
Oscillations are one of the most common processes in nature and technology. The wings of insects and birds in flight, high-rise buildings and high-voltage wires under the influence of the wind, the pendulum of a wound clock and a car on springs while driving, the river level throughout the year and the temperature of the human body during illness, sound is fluctuations in air density and pressure, radio waves - periodic changes in the strengths of electric and magnetic fields, visible light is also electromagnetic vibrations, only with slightly different wavelengths and frequencies, earthquakes are soil vibrations, the pulse is periodic contractions of the human heart muscle, etc.
Vibrations can be mechanical, electromagnetic, chemical, thermodynamic and various others. Despite such diversity, they all have much in common.
Oscillatory phenomena of various physical natures are subject to general laws. For example, current oscillations in an electrical circuit and oscillations of a mathematical pendulum can be described by the same equations. The commonality of oscillatory patterns allows us to consider oscillatory processes of various natures from a single point of view. A sign of oscillatory motion is its periodicity.
Mechanical vibrations –Thismovements that are repeated exactly or approximately at regular intervals.
Examples of simple oscillatory systems are a load on a spring (spring pendulum) or a ball on a string (mathematical pendulum).


During mechanical vibrations, kinetic and potential energies change periodically.
At maximum deviation body from its equilibrium position, its speed, and therefore kinetic energy goes to zero. In this position potential energy oscillating body reaches maximum value. For a load on a spring, potential energy is the energy of elastic deformation of the spring. For a mathematical pendulum, this is the energy in the Earth’s gravitational field.
When a body, in its movement, passes through equilibrium position, its speed is maximum. The body overshoots the equilibrium position according to the law of inertia. At this moment it has maximum kinetic and minimum potential energy. An increase in kinetic energy occurs due to a decrease in potential energy.
With further movement, potential energy begins to increase due to a decrease in kinetic energy, etc.
Thus, during harmonic oscillations, a periodic transformation of kinetic energy into potential energy and vice versa occurs.
If there is no friction in the oscillatory system, then the total mechanical energy during mechanical vibrations remains unchanged.
For spring load:
![]()
At the position of maximum deflection, the total energy of the pendulum is equal to the potential energy of the deformed spring:
When passing through the equilibrium position, the total energy is equal to the kinetic energy of the load:

For small oscillations of a mathematical pendulum:

At the position of maximum deviation, the total energy of the pendulum is equal to the potential energy of the body raised to a height h:

When passing through the equilibrium position, the total energy is equal to the kinetic energy of the body:

Here h m– the maximum height of the pendulum in the Earth’s gravitational field, x m and υ m = ω 0 x m– maximum values of the pendulum’s deviation from the equilibrium position and its speed.
Harmonic oscillations and their characteristics. Equation of harmonic vibration.
The simplest type of oscillatory process are simple harmonic vibrations, which are described by the equation
x = x m cos(ω t + φ 0).
Here x– displacement of the body from the equilibrium position,
x m– amplitude of oscillations, that is, the maximum displacement from the equilibrium position,
ω – cyclic or circular frequency hesitation,
t- time.
Characteristics of oscillatory motion.
Offset x – deviation of an oscillating point from its equilibrium position. The unit of measurement is 1 meter.
Oscillation amplitude A – the maximum deviation of an oscillating point from its equilibrium position. The unit of measurement is 1 meter.
Oscillation periodT– the minimum time interval during which one complete oscillation occurs is called. The unit of measurement is 1 second.
T=t/N
where t is the oscillation time, N is the number of oscillations completed during this time.
From the graph of harmonic oscillations, you can determine the period and amplitude of the oscillations:

Oscillation frequency ν – a physical quantity equal to the number of oscillations per unit time.
ν=N/t
Frequency is the reciprocal of the oscillation period:
Frequency oscillations ν shows how many oscillations occur in 1 s. The unit of frequency is hertz(Hz).
Cyclic frequency ω– number of oscillations in 2π seconds.
The oscillation frequency ν is related to cyclic frequency ω and oscillation period T ratios:
Phase harmonic process - a quantity under the sine or cosine sign in the equation of harmonic oscillations φ = ω t + φ 0 . At t= 0 φ = φ 0 , therefore φ 0 called initial phase.
Harmonic graph represents a sine or cosine wave.
In all three cases for blue curves φ 0 = 0:

only greater amplitude(x" m > x m);

the red curve is different from the blue one only meaning period(T" = T / 2);

the red curve is different from the blue one only meaning initial phase(glad).
When a body oscillates along a straight line (axis OX) the velocity vector is always directed along this straight line. The speed of movement of the body is determined by the expression
![]()
In mathematics, the procedure for finding the limit of the ratio Δх/Δt at Δ t→ 0 is called calculating the derivative of the function x(t) by time t and is denoted as x"(t).The speed is equal to the derivative of the function x( t) by time t.
For the harmonic law of motion x = x m cos(ω t+ φ 0) calculating the derivative leads to the following result:
υ X =x"(t)= ω x m sin (ω t + φ 0)
Acceleration is determined in a similar way a x bodies during harmonic vibrations. Acceleration a is equal to the derivative of the function υ( t) by time t, or the second derivative of the function x(t). Calculations give:
and x =υ x "(t) =x""(t)= -ω 2 x m cos(ω t+ φ 0)=-ω 2 x
The minus sign in this expression means that the acceleration a(t) always has the opposite sign of the displacement x(t), and, therefore, according to Newton’s second law, the force causing the body to perform harmonic oscillations is always directed towards the equilibrium position ( x = 0).
The figure shows graphs of the coordinates, speed and acceleration of a body performing harmonic oscillations.

Graphs of coordinates x(t), velocity υ(t) and acceleration a(t) of a body performing harmonic oscillations.
Spring pendulum.
Spring pendulumis a load of some mass m attached to a spring of stiffness k, the second end of which is fixedly fixed.
Natural frequencyω 0 free oscillations of the load on the spring is found by the formula:
Period T harmonic vibrations of the load on the spring is equal to

This means that the period of oscillation of a spring pendulum depends on the mass of the load and the stiffness of the spring.
Physical properties of the oscillatory system determine only the natural frequency of oscillations ω 0 and the period T . Parameters of the oscillation process such as amplitude x m and the initial phase φ 0 are determined by the way in which the system was brought out of equilibrium at the initial moment of time.
Mathematical pendulum.
Mathematical pendulumcalled a small body suspended on a thin inextensible thread, the mass of which is negligible compared to the mass of the body.
In the equilibrium position, when the pendulum hangs plumb, the force of gravity is balanced by the tension force of the thread N. When the pendulum is deflected from the equilibrium position by a certain angle φ, a tangential component of the force of gravity appears F τ = – mg sin φ. The minus sign in this formula means that the tangential component is directed in the direction opposite to the deflection of the pendulum.

Mathematical pendulum.φ – angular deviation of the pendulum from the equilibrium position,
x= lφ – displacement of the pendulum along the arc
The natural frequency of small oscillations of a mathematical pendulum is expressed by the formula:
Period of oscillation of a mathematical pendulum:

This means that the period of oscillation of a mathematical pendulum depends on the length of the thread and on the acceleration of free fall of the area where the pendulum is installed.
Free and forced vibrations.
Mechanical vibrations, like oscillatory processes of any other physical nature, can be free And forced.
Free vibrations –These are oscillations that occur in a system under the influence of internal forces, after the system has been removed from a stable equilibrium position.
Oscillations of a weight on a spring or oscillations of a pendulum are free oscillations.
In order for free vibrations to occur according to the harmonic law, it is necessary that the force tending to return the body to the equilibrium position be proportional to the displacement of the body from the equilibrium position and directed in the direction opposite to the displacement.
In real conditions, any oscillatory system is under the influence of friction forces (resistance). In this case, part of the mechanical energy is converted into internal energy of thermal motion of atoms and molecules, and vibrations become fading.
Fading called oscillations whose amplitude decreases with time.

To prevent the oscillations from fading, it is necessary to provide the system with additional energy, i.e. influence the oscillatory system with a periodic force (for example, to rock a swing).
Oscillations occurring under the influence of an external periodically changing force are calledforced.
An external force does positive work and provides an energy flow to the oscillatory system. It does not allow vibrations to die out, despite the action of friction forces.
A periodic external force can change over time according to various laws. Of particular interest is the case when an external force, varying according to a harmonic law with a frequency ω, acts on an oscillatory system capable of performing its own oscillations at a certain frequency ω 0.
If free oscillations occur at a frequency ω 0, which is determined by the parameters of the system, then steady forced oscillations always occur at frequency ω external force .
The phenomenon of a sharp increase in the amplitude of forced oscillations when the frequency of natural oscillations coincides with the frequency of the external driving force is calledresonance.
Amplitude dependence x m forced oscillations from the frequency ω of the driving force is called resonant characteristic or resonance curve.

Resonance curves at various attenuation levels:
1 – oscillatory system without friction; at resonance, the amplitude x m of forced oscillations increases indefinitely;
2, 3, 4 – real resonance curves for oscillatory systems with different friction.
In the absence of friction, the amplitude of forced oscillations during resonance should increase without limit. In real conditions, the amplitude of steady-state forced oscillations is determined by the condition: the work of the external force during the oscillation period must be equal to the loss of mechanical energy during the same time due to friction. The less friction, the greater the amplitude of forced oscillations during resonance.
The phenomenon of resonance can cause the destruction of bridges, buildings and other structures if the natural frequencies of their oscillations coincide with the frequency of a periodically acting force, which arises, for example, due to the rotation of an unbalanced motor.
The period of oscillation of a physical pendulum depends on many circumstances: on the size and shape of the body, on the distance between the center of gravity and the point of suspension and on the distribution of body mass relative to this point; Therefore, calculating the period of a suspended body is a rather difficult task. The situation is simpler for a mathematical pendulum. From observations of such pendulums, the following simple laws can be established.
1. If, while maintaining the same length of the pendulum (the distance from the point of suspension to the center of gravity of the load), you hang different loads, then the period of oscillation will be the same, although the masses of the loads are very different. The period of a mathematical pendulum does not depend on the mass of the load.
2. If, when starting a pendulum, we deflect it at different (but not too large) angles, then it will oscillate with the same period, although with different amplitudes. As long as the amplitudes are not too large, the oscillations are quite close in their form to harmonic (§ 5) and the period of a mathematical pendulum does not depend on the amplitude of the oscillations. This property is called isochronism (from the Greek words “isos” - equal, “chronos” - time).
This fact was first established in 1655 by Galileo, allegedly under the following circumstances. Galileo observed in the Pisa Cathedral the swing of a chandelier on a long chain, which was pushed when lit. During the service, the swings gradually faded (§ 11), that is, the amplitude of the vibrations decreased, but the period remained the same. Galileo used his own pulse as a time indicator.
Let us now derive a formula for the period of oscillation of a mathematical pendulum.
Rice. 16. Oscillations of a pendulum in a plane (a) and movement along a cone (b)
When the pendulum swings, the load moves accelerated along an arc (Fig. 16, a) under the influence of a restoring force, which changes during movement. Calculating the motion of a body under the action of a variable force is quite complicated. Therefore, for simplicity, we will proceed as follows.
Let's make the pendulum not oscillate in one plane, but describe a cone so that the load moves in a circle (Fig. 16, b). This movement can be obtained as a result of the addition of two independent vibrations: one - still in the plane of the drawing and the other - in a perpendicular plane. Obviously, the periods of both of these plane oscillations are the same, since any plane of oscillation is no different from any other. Consequently, the period of complex motion - the rotation of the pendulum along the cone - will be the same as the period of the swing of the water plane. This conclusion can be easily illustrated by direct experience by taking two identical pendulums and giving one of them a swing in a plane, and the other a rotation along a cone.
But the period of revolution of the “conical” pendulum is equal to the length of the circle described by the load, divided by the speed:
If the angle of deviation from the vertical is small (small amplitudes), then we can assume that the restoring force is directed along the radius of the circle, i.e., equal to the centripetal force:
On the other hand, from the similarity of triangles it follows that . Since then from here
Equating both expressions to each other, we obtain for the circulation rate
Finally, substituting this into the period expression, we find
So, the period of a mathematical pendulum depends only on the acceleration of gravity and on the length of the pendulum, i.e., the distance from the point of suspension to the center of gravity of the load. From the resulting formula it follows that the period of the pendulum does not depend on its mass and amplitude (provided that it is small enough). In other words, we obtained by calculation those basic laws that were previously established from observations.
But our theoretical conclusion gives us more: it allows us to establish a quantitative relationship between the period of the pendulum, its length and the acceleration of gravity. The period of a mathematical pendulum is proportional to the square root of the ratio of the length of the pendulum to the acceleration of gravity. The proportionality coefficient is .
A very accurate method for determining this acceleration is based on the dependence of the period of the pendulum on the acceleration of gravity. Having measured the length of the pendulum and determined the period from a large number of oscillations, we can calculate using the resulting formula. This method is widely used in practice.
It is known (see Volume I, §53) that the acceleration of gravity depends on the geographic latitude of the place (at the pole and at the equator). Observations of the swing period of a certain standard pendulum make it possible to study the distribution of gravitational acceleration over latitude. This method is so accurate that it can be used to detect more subtle differences in value on the earth's surface. It turns out that even on the same parallel, the values at different points on the earth’s surface are different. These anomalies in the distribution of gravity acceleration are associated with the uneven density of the earth's crust. They are used to study the distribution of density, in particular to detect the occurrence of any minerals in the earth's crust. Extensive gravimetric changes, which made it possible to judge the occurrence of dense masses, were carried out in the USSR in the area of the so-called Kursk magnetic anomaly (see volume II, § 130) under the leadership of the Soviet physicist Pyotr Petrovich Lazarev. In combination with data on the anomaly of the earth's magnetic field, these gravimetric data made it possible to establish the distribution of the occurrence of iron masses that determine the Kursk magnetic and gravitational anomalies.
What is a mathematical pendulum?
From previous lessons you should already know that a pendulum, as a rule, means a body that oscillates under the influence of gravitational interaction. That is, we can say that in physics, this concept is generally considered to be a solid body that, under the influence of gravity, performs oscillatory movements that occur around a fixed point or axis.
Operating principle of a mathematical pendulum
Now let's look at the principle of operation of a mathematical pendulum and find out what it is.
The principle of operation of a mathematical pendulum is that when a material point deviates from the equilibrium position by a small angle a, that is, an angle at which the condition sina=a would be satisfied, then a force F = -mgsina = -mga will act on the body.
We see that force F has a negative exponent, and it follows that the minus sign tells us that this force is directed in the direction opposite to the displacement. And since the force F is proportional to the displacement S, it follows that under the influence of such a force the material point will perform harmonic oscillations.
Properties of a pendulum
If we take any other pendulum, its period of oscillation depends on many factors. These factors include:
Firstly, body size and shape;
Secondly, the distance that exists between the point of suspension and the center of gravity;
Thirdly, also the distribution of body weight relative to a given point.
In connection with these various circumstances of pendulums, determining the period of a hanging body is quite difficult.

And if we take a mathematical pendulum, then it has all those properties that can be proven using known physical laws and its period can be easily calculated using a formula.
Having carried out many different observations on such mechanical systems, physicists were able to determine such patterns as:
Firstly, the period of the pendulum does not depend on the mass of the load. That is, if, with the same length of the pendulum, we suspend weights that have different masses from it, then the period of their oscillations will still be the same, even if their masses have quite striking differences.
Secondly, if we deflect the pendulum by small but different angles when starting the system, then its oscillations will have the same period, but the amplitudes will be different. With small deviations from the center of equilibrium, the vibrations in their form will have an almost harmonic character. That is, we can say that the period of such a pendulum does not depend on the amplitude of oscillations. Translated from Greek, this property of this mechanical system is called isochronism, where “isos” means equal, and “chronos” means time.
Practical use of pendulum oscillations
A mathematical pendulum is used for various studies by physicists, astronomers, surveyors and other scientists. With the help of such a pendulum they search for minerals. By observing the acceleration of a mathematical pendulum and counting the number of its oscillations, one can find deposits of coal and ore in the bowels of our Earth.
K. Flammarion, the famous French astronomer and naturalist, claimed that with the help of a mathematical pendulum he was able to make many important discoveries, including the appearance of the Tunguska meteorite and the discovery of a new planet.
Nowadays, many psychics and occultists use such a mechanical system to search for missing people and make prophetic predictions.
Math pendulum
Introduction
Oscillation period
Conclusions
Literature
Introduction
Now it is no longer possible to verify the legend about how Galileo, standing in prayer in the cathedral, carefully watched the swinging of bronze chandeliers. I observed and determined the time spent by the chandelier moving back and forth. This time was later called the oscillation period. Galileo did not have a watch, and to compare the period of oscillation of chandeliers suspended on chains of different lengths, he used the frequency of his pulse.
Pendulums are used to adjust the speed of clocks, since any pendulum has a very specific period of oscillation. The pendulum also finds important applications in geological exploration. It is known that in different places around the globe the values g are different. They are different because the Earth is not a completely regular sphere. In addition, in areas where dense rocks occur, such as some metal ores, the value g abnormally high. Accurate measurements g with the help of a mathematical pendulum it is sometimes possible to detect such deposits.
Equation of motion of a mathematical pendulum
A mathematical pendulum is a heavy material point that moves either along a vertical circle (flat mathematical pendulum) or along a sphere (spherical pendulum). To a first approximation, a small weight suspended on an inextensible flexible thread can be considered a mathematical pendulum.
Let us consider the motion of a flat mathematical pendulum along a circle of radius l centered at a point ABOUT(Fig. 1). We will determine the position of the point M(pendulum) angle of deviation j radius OM from the vertical. Directing a tangent M t towards the positive angle j, we will compose a natural equation of motion. This equation is formed from the equation of motion
mW=F+N, (1)
Where F is the active force acting on the point, and N- communication reaction.
Figure 1
We obtained equation (1) according to Newton’s second law, which is the fundamental law of dynamics and states that the time derivative of the momentum of a material point is equal to the force acting on it, i.e.
Assuming the mass is constant, we can represent the previous equation in the form
Where W is the acceleration of the point.
So equation (1) in projection onto the t axis will give us one of the natural equations for the motion of a point along a given fixed smooth curve:
In our case, we obtain in projection onto the t axis
 ,
,
Where m there is a mass of the pendulum.
Since or , from here we find
 .
.
Reducing by m and believing
, (3)
we will finally have:
 ,
,
 ,
,
 ,
,
 . (4)
. (4)
Let us first consider the case of small oscillations. Let at the initial moment the pendulum be deflected from the vertical by an angle j and lowered without initial speed. Then the initial conditions will be:
at t= 0, ![]() . (5)
. (5)
From the energy integral:
 , (6)
, (6)
Where V- potential energy, and h is the integration constant, it follows that under these conditions at any time the angle jЈj 0 . Constant value h determined from the initial data. Let us assume that the angle j 0 is small (j 0 Ј1); then the angle j will also be small and we can approximately set sinj»j. In this case, equation (4) will take the form
 . (7)
. (7)
Equation (7) is the differential equation of a simple harmonic oscillation. The general solution to this equation is
, (8)
Where A And B or a and e are constants of integration.
From here we immediately find the period ( T) small oscillations of a mathematical pendulum (period - the period of time during which the point returns to its previous position at the same speed)
![]() And
And ![]()
![]() ,
,
because sin has a period equal to 2p, then w T=2p Yu
 (9)
(9)
To find the law of motion under initial conditions (5), we calculate:
. (10)
Substituting values (5) into equations (8) and (10), we obtain:
j 0 = A, 0 = w B,
those. B=0. Consequently, the law of motion for small oscillations under conditions (5) will be:
j = j 0 cos wt. (11)
Let us now find the exact solution to the problem of a flat mathematical pendulum. Let us first determine the first integral of the equation of motion (4). Because
 ,
,
then (4) can be represented as
 .
.
Hence, multiplying both sides of the equation by d j and integrating, we get:
 . (12)
. (12)
Let us denote here j 0 the angle of maximum deflection of the pendulum; then for j = j 0 we will have, whence C= w 2 cosj 0 . As a result, integral (12) gives:
, (13)
where w is determined by equality (3).
This integral is the energy integral and can be directly obtained from the equation
 , (14)
, (14)
where is work on moving M 0 M active force F, if we take into account that in our case v 0 =0, and (see figure).
From equation (13) it is clear that when the pendulum moves, angle j will change between the values +j 0 and -j 0 (|j|Јj 0, since), i.e. the pendulum will perform an oscillating motion. Let's agree to count down the time t from the moment the pendulum passes through the vertical O.A. when it moves to the right (see figure). Then we will have the initial condition:
at t=0, j=0. (15)
In addition, when moving from a point A will ; taking the square root from both sides of equality (13), we obtain:
 .
.
Separating the variables here, we have:
 . (16)
. (16)
 ,
,  ,
,
That
 .
.
Substituting this result into equation (16), we obtain.
The period of oscillation of a mathematical pendulum depends on the length of the thread: as the length of the thread decreases, the period of oscillation decreases
For a mathematical pendulum, some laws are satisfied:
1 law. If, while maintaining the same length of the pendulum, we suspend different loads (for example, 5 kg and 100 kg), then the period of oscillation will be the same, although the masses of the loads are very different. The period of a mathematical pendulum does not depend on the mass of the load.
2nd law. If the pendulum is deflected by different but small angles, then it will oscillate with the same period, although with different amplitudes. As long as the amplitude of the pendulum is small, the oscillations in their form will be similar to harmonic ones, and then the period of the mathematical pendulum does not depend on the amplitude of the oscillations. This property is called isochronism.

Let's derive the formula for the period of a mathematical pendulum.
The load m of a mathematical pendulum is acted upon by the force of gravity mg and the elastic force of the thread Fynp. Let's direct the 0X axis along the tangent to the upward movement trajectory. Let's write down Newton's second law for this case:
![]()
We project everything onto the OX axis:
At small angles
![]()
After making substitutions and small transformations, we get that the equation looks like:
Comparing the resulting expression with the equation of harmonic vibrations, we get:
From the equation it can be seen that the cyclic frequency of the spring pendulum will have the form:
Then the period of the mathematical pendulum will be equal to:
![]()
The period of a mathematical pendulum depends only on the acceleration of gravity g and on the length of the pendulum l. From the resulting formula it follows that the period of the pendulum does not depend on its mass and amplitude (provided that it is small enough). We also established a quantitative relationship between the period of the pendulum, its length and the acceleration of gravity. The period of a mathematical pendulum is proportional to the square root of the ratio of the length of the pendulum to the acceleration of gravity. The proportionality factor is 2p
There is also:
Period of a spring pendulum
Period of a physical pendulum ![]()
Period of a torsion pendulum