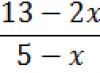Based on the data in the correlation table, construct a correlation field. See pages where the term correlation field is mentioned

Regression and correlation analysis are statistical research methods. These are the most common ways to show the dependence of a parameter on one or more independent variables.

Below, using specific practical examples, we will consider these two very popular analyzes among economists. We will also give an example of obtaining results when combining them.

Regression Analysis in Excel

Shows the influence of some values (independent, independent) on the dependent variable. For example, how does the number of economically active population depend on the number of enterprises, wages and other parameters. Or: how do foreign investments, energy prices, etc. affect the level of GDP.

The result of the analysis allows you to highlight priorities. And based on the main factors, predict, plan the development of priority areas, and make management decisions.

Regression happens:

linear (y = a + bx);
parabolic (y = a + bx + cx 2);
exponential (y = a * exp(bx));
power (y = a*x^b);
hyperbolic (y = b/x + a);
logarithmic (y = b * 1n(x) + a);
exponential (y = a * b^x).

Let's look at an example of building a regression model in Excel and interpreting the results. Let's take the linear type of regression.

Task. At 6 enterprises, the average monthly salary and the number of quitting employees were analyzed. It is necessary to determine the dependence of the number of quitting employees on the average salary.

The linear regression model looks like this:

Y = a 0 + a 1 x 1 +…+a k x k.

Where a are regression coefficients, x are influencing variables, k is the number of factors.

In our example, Y is the indicator of quitting employees. The influencing factor is wages (x).

Excel has built-in functions that can help you calculate the parameters of a linear regression model. But the “Analysis Package” add-on will do this faster.

Let's activate a powerful analytical tool:

Once activated, the add-on will be available in the Data tab.

Now let's do the regression analysis itself.

First of all, we pay attention to R-squared and coefficients.

R-squared is the coefficient of determination. In our example – 0.755, or 75.5%. This means that the calculated parameters of the model explain 75.5% of the relationship between the studied parameters. The higher the coefficient of determination, the better the model. Good - above 0.8. Bad – less than 0.5 (such an analysis can hardly be considered reasonable). In our example – “not bad”.

The coefficient 64.1428 shows what Y will be if all variables in the model under consideration are equal to 0. That is, the value of the analyzed parameter is also influenced by other factors not described in the model.

The coefficient -0.16285 shows the weight of variable X on Y. That is, the average monthly salary within this model affects the number of quitters with a weight of -0.16285 (this is a small degree of influence). The “-” sign indicates a negative impact: the higher the salary, the fewer people quit. Which is fair.

Correlation Analysis in Excel

Correlation analysis helps determine whether there is a relationship between indicators in one or two samples. For example, between the operating time of a machine and the cost of repairs, the price of equipment and the duration of operation, the height and weight of children, etc.

If there is a connection, then does an increase in one parameter lead to an increase (positive correlation) or a decrease (negative) of the other. Correlation analysis helps the analyst determine whether the value of one indicator can be used to predict the possible value of another.

The correlation coefficient is denoted by r. Varies from +1 to -1. The classification of correlations for different areas will be different. When the coefficient is 0, there is no linear relationship between samples.

Let's look at how to find the correlation coefficient using Excel.

To find paired coefficients, the CORREL function is used.

Objective: Determine whether there is a relationship between the operating time of a lathe and the cost of its maintenance.

Place the cursor in any cell and press the fx button.

In the “Statistical” category, select the CORREL function.
Argument “Array 1” - the first range of values – machine operating time: A2:A14.
Argument “Array 2” - second range of values – repair cost: B2:B14. Click OK.

To determine the type of connection, you need to look at the absolute number of the coefficient (each field of activity has its own scale).

For correlation analysis of several parameters (more than 2), it is more convenient to use “Data Analysis” (the “Analysis Package” add-on). You need to select correlation from the list and designate the array. All.

The resulting coefficients will be displayed in the correlation matrix. Like this:

Correlation and regression analysis

In practice, these two techniques are often used together.

Example:

Now the regression analysis data has become visible.

For experimental study of dependencies between random variables x and y carry out a number of independent experiments. Result i- experiment gives a pair of values (x r, y g), i = 1, 2,..., p.

Quantities characterizing various properties of objects can be independent or interrelated. The forms of manifestation of relationships are very diverse. The two most common types are functional (complete) and correlation (incomplete) connections.

When two quantities are functionally dependent on the value of one -x h necessarily corresponds to one or more precisely defined values of another quantity -y ( . Quite often, functional connections appear in physics and chemistry. In real situations, there is an infinitely large number of properties of the object itself and the external environment that influence each other, so this kind of connection does not exist, in other words, functional connections are mathematical abstractions.

The influence of general factors and the presence of objective patterns in the behavior of objects only lead to the manifestation of statistical dependence. Statistical is a dependence in which a change in one of the quantities entails a change in the distribution of others (another), and these other quantities take on certain values with certain probabilities. In this case, functional dependence should be considered a special case of statistical dependence: the value of one factor corresponds to the values of other factors with a probability equal to one. A more important special case of statistical dependence is the correlation dependence, which characterizes the relationship between the values of some random variables and the average value of others, although in each individual case any interrelated value can take on different values.

A correlation relationship (which is also called incomplete, or statistical) appears on average, for mass observations, when the given values of the dependent variable correspond to a certain number of probable values of the independent variable. Explanation - the complexity of the relationships between the analyzed factors, the interaction of which is influenced by unaccounted random variables. Therefore, the connection between the signs appears only on average, in the mass of cases. In a correlation connection, each argument value corresponds to function values randomly distributed in a certain interval.

The term “correlation” was first used by the French paleontologist J. Cuvier, who derived the “law of correlation of animal parts and organs” (this law allows one to reconstruct the appearance of the entire animal from found body parts). This term was introduced into statistics by the English biologist and statistician F. Galton (not just a relation, but “as if a connection” - corelation).

Correlation dependencies are found everywhere. For example, in agriculture, this could be the relationship between yield and the amount of fertilizer applied. Obviously, the latter are involved in the formation of the crop. But for each specific field or plot, the same amount of applied fertilizer will cause a different increase in yield, since a number of other factors interact (weather, soil condition, etc.), which form the final result. However, on average, such a relationship is observed - an increase in the mass of applied fertilizers leads to an increase in yield.

The simplest method for identifying connections between the characteristics being studied is to construct a correlation table; its visual representation is the correlation field. It is a graph where jq values are plotted on the abscissa axis, and on the ordinate axis y x. By the location of the points and their concentration in a certain direction, one can qualitatively judge the presence of a connection.

Rice. 7.3.

A positive correlation between random variables, close to a parabolic functional one, is shown in Fig. 6.1 , A. In Fig. 6.1, b shows an example of a weak negative correlation, and in Fig. 6.1, V - an example of practically uncorrelated random variables. The correlation is high if the dependence “can be represented” on the graph by a straight line (with a positive or negative slope).

1. Topic of the work.

2. Brief theoretical information.

3. The order of work.

4. Initial data for developing a mathematical model.

5. Results of developing a mathematical model.

6. Results of the model study. Building a forecast.

7. Conclusions.

In tasks 2-4, you can use Excel PPP to calculate model characteristics.

Job No. 1.

Construction of paired regression models. Checking residuals for heteroscedasticity.

For 15 enterprises producing the same type of product, the values of two characteristics are known:

X - production output, thousand units;

y - production costs, million rubles.

x	y
5,3	18,4
15,1	22,0
24,2	32,3
7,1	16,4
11,0	22,2
8,5	21,7
14,5	23,6
10,2	18,5
18,6	26,1
19,7	30,2
21,3	28,6
22,1	34,0
4,1	14,2
12,0	22,1
18,3	28,2

Required:

1. Construct a correlation field and formulate a hypothesis about the form of the connection.

2. Build models:

Linear pair regression.

Semilogarithmic pairwise regression.

2.3 Power pair regression.
To do this:

2. Assess the closeness of the connection using a coefficient (index)
correlations.

3. Assess the quality of the model using the coefficient (index)
determination and average error of approximation.

4. Give using the average elasticity coefficient
comparative assessment of the strength of the relationship between the factor and the result.

5. With F-Fisher criterion to evaluate the statistical reliability of regression modeling results.

Based on the values of the characteristics calculated in paragraphs 2-5, select the best regression equation.

Using the Golfreld-Quandt method, check the residuals for heteroskedasticity.

We build a correlation field.

Analyzing the location of the points of the correlation field, we assume that the relationship between the signs X And at can be linear, i.e. y=a+bx, or nonlinear type: y=a+blnx, y = ax b.

Based on the theory of the relationship being studied, we assume to obtain the relationship at from X kind y=a+bx, because production costs y can be divided into two types: constant, independent of production volume - a, such as rent, administration maintenance, etc.; and variables that change proportionally to output bx, such as material consumption, electricity, etc.

2.1.Linear pair regression model.

2.1.1. Let's calculate the parameters a And b linear regression y=a+bx.

We build calculation table 1.

Table 1

Options a And b equations

Y x = a + bx

Divided by n b:

Regression equation:

=11.591+0.871x

With an increase in product output by 1 thousand rubles. production costs increase by 0.871 million rubles. on average, fixed costs are equal to 11.591 million rubles.

2.1.2. We will evaluate the closeness of the connection using the linear pair correlation coefficient.

Let us first determine the standard deviations of the characteristics.

Standard deviations:

Correlation coefficient:

Between the signs X And Y a very close linear correlation is observed.

2.1.3. Let us evaluate the quality of the constructed model.

i.e. this model explains 90.5% of the total variance at, the share of unexplained variance accounts for 9.5%.

Therefore, the quality of the model is high.

A i .

First, from the regression equation, we determine the theoretical values for each factor value.

Approximation error A i, i=1…15:

Average approximation error:

2.1.4. Let's determine the average elasticity coefficient:

It shows that with an increase in output by 1%, production costs increase by an average of 0.515%.

2.1.5. Let us evaluate the statistical significance of the resulting equation.
Let's check the hypothesis H 0 that the identified dependence at from X is random in nature, i.e. the resulting equation is statistically insignificant. Let's take α=0.05. Let's find the table (critical) value F- Fisher test:

Let's find the actual value F- Fisher criterion:

hence the hypothesis H 0 H 1 x And y is not accidental.

Let's construct the resulting equation.

2.2. Semi-log pairwise regression model.

2.2.1. Let's calculate the parameters A And b in regression:

y x =a +blnх.

Let us linearize this equation, denoting:

y=a + bz.

Options a And b equations

= a+bz

determined by the least squares method:

We calculate Table 2.

Table 2

Divided by n and solving by Cramer's method, we obtain a formula for determining b:

Regression equation:

= -1.136 + 9.902z

2.2.2. Let us evaluate the closeness of the connection between the characteristics at And X.

Because the equation y = a + bln x linear with respect to parameters A And b and its linearization was not related to the transformation of the dependent variable _ at, then the closeness of the relationship between the variables at And X, estimated using the pair correlation index Rxy, can also be determined using the linear pair correlation coefficient r yz

standard deviation z:

The correlation index value is close to 1, therefore, between the variables at And X there is a very close correlation of the type = a + bz.

2.2.3. Let us evaluate the quality of the constructed model.

Let's determine the coefficient of determination:

i.e. this model explains 83.8% of the total variation in the result at, the share of unexplained variation accounts for 16.2%. Therefore, the quality of the model is high.

Let's find the value of the average approximation error A i .

First, from the regression equation, we determine the theoretical values for each factor value. Approximation error A i,:

, i=1…15.

Average approximation error:

The error is small, the quality of the model is high.

2.2.4. Let's determine the average elasticity coefficient:

It shows that with an increase in output by 1%, production costs increase by an average of 0.414%.

2.2.5. Let us evaluate the statistical significance of the resulting equation.
Let's check the hypothesis H 0 that the identified dependence at from X is random in nature, i.e. the resulting equation is statistically insignificant. Let's take α=0.05.

Let's find the table (critical) value F-Fisher criterion:

Let's find the actual value F-Fisher criterion:

hence the hypothesis H 0 rejected, alternative hypothesis accepted H 1: with probability 1-α=0.95, the resulting equation is statistically significant, the relationship between the variables x And y is not accidental.

Let's construct a regression equation on the correlation field

2.3. Power pair regression model.

2.3.1. Let's calculate the parameters A And b power regression:

The calculation of parameters is preceded by the procedure of linearization of this equation:

and changing variables:

Y=lny, X=lnx, A=lna

Equation parameters:

determined by the least squares method:

We calculate Table 3.

We define b:

Regression equation:

Let's construct a regression equation on the correlation field:

2.3.2. Let us evaluate the closeness of the connection between the characteristics at And X using the pair correlation index Ryx.

Let's first calculate the theoretical value for each factor value x, and then:

Correlation index value Rxy close to 1, therefore between variables at And X There is a very close correlation of the form:

2.3.3. Let us evaluate the quality of the constructed model.

Let's determine the index of determination:

R 2=0,936 2 =0,878,

i.e. this model explains 87.6% of the total variation in the result y, and unexplained variation accounts for 12.4%.

The quality of the model is high.

Let us find the value of the average approximation error.

Approximation error A i, i=1…15:

Average approximation error:

The error is small, the quality of the model is high.

2.3.4. Let's determine the average elasticity coefficient:

It shows that with an increase in output by 1%, production costs increase by an average of 0.438%.

2.3.5. Let us evaluate the statistical significance of the resulting equation.

Let's check the hypothesis H 0 that the identified dependence at from X is random in nature, i.e. the resulting equation is statistically insignificant. Let's take α=0.05.

table (critical) value F-Fisher criterion:

actual value F-Fisher criterion:

Table 3

3. Choosing the best equation.

Let's make a table of the research results obtained.

Table 4

We analyze the table and draw conclusions.

ú All three equations turned out to be statistically significant and reliable, have a correlation coefficient (index) close to 1, a high (close to 1) determination coefficient (index) and an approximation error within acceptable limits.

ú At the same time, the characteristics of the linear model indicate that it describes the relationship between characteristics somewhat better than the semilogarithmic and power models x And u.

ú Therefore, we choose a linear model as the regression equation.

When raising the question of the correlation between two statistical characteristics X and Y, an experiment is carried out with parallel recording of their values.

Example 8.1.

Determine whether the result of a running long jump (sign X) depends on the value of the final run-up speed (sign Y). To answer this question, in parallel with recording the result X of each jump of an athlete or group of athletes, the value of the final take-off speed Y is also recorded. Let them be like this:

Table 5

I
xi (cm)
yi (m/s)	10,7	10,5	10,1	9,8	10,1	10,5	9,1	9,6

Let us present Table 5 in the form of a graph in a rectangular coordinate system, where we will plot the length of the jump (X) on the horizontal axis, and the value of the final take-off speed in this jump (Y) on the vertical axis.
function PlayMyFlash(cmd)( Corel_.TPlay(cmd); )

№1 !!! №2 !!! №3 !!! №4 !!! №5!!! №6 !!! №7 !!! №8!!!

Rice. 8. Correlation field graph.

We will call the correlation field the scatter zone of the points obtained in this way on the graph. Visually analyzing the correlation field in Figure 8, you can see that it seems to be elongated along some straight line. This picture is typical for the so-called linear correlation relationship between characteristics. In this case, it can be generally assumed that with an increase in the final take-off speed, the length of the jump also increases, and vice versa. Those. There is a direct (positive) relationship between the characteristics under consideration.

Along with this example, from the many other possible correlation fields, the following can be distinguished (Fig. 9-11):

Figure 9 also shows a linear relationship, but as the values of one attribute increase, the values of the other decrease, and vice versa, i.e. feedback or negative. It can be assumed that in Figure 11 the points of the correlation field are scattered around some kind of curved line. In this case, they say that there is a curvilinear correlation between the characteristics.

With regard to the correlation field shown in Figure 10, it cannot be said that the points are located along some straight or curved line; it has a spherical shape. In this case, they say that characteristics X and Y do not depend on each other.

In addition, the correlation field can be used to approximately judge the closeness of the correlation connection, if this connection exists. Here they say: the fewer points are scattered around the imaginary average line, the closer the correlation between the characteristics under consideration.

Visual analysis of correlation fields helps to understand the essence of the correlation relationship and allows us to make assumptions about the presence, direction and closeness of the connection. But it is impossible to say for sure whether there is a connection between the signs or not, a linear connection or a curvilinear one, a close connection (reliable) or a weak one (unreliable), using this method. The most accurate method for identifying and assessing the linear relationship between characteristics is the method of determining various correlation indicators from statistical data.

3. Correlation coefficients and their properties

Often to determine the reliability of the relationship between two characteristics (X, Y) use nonparametric (rank) Spearman correlation coefficient and parametric Pearson correlation coefficient . The value of these correlation indicators is determined by the following formulas:

(1)

Where: dx - ranks of statistical data of characteristic x;

dy - ranks of statistical data of the characteristic y.

(2)

Where: - statistical data of characteristic x,

Statistical data of the characteristic y.

These coefficients have the following powerful features:

1. Based on correlation coefficients, one can only judge a linear correlation between characteristics. Nothing can be said about a curvilinear connection with their help.
2. The values of the correlation coefficients are a dimensionless quantity that cannot be less than -1 or more than +1, i.e.
3.
4. If the values of the correlation coefficients are zero, i.e. = 0 or = 0, then the connection between the characteristics x, y absent.
5. If the values of the correlation coefficients are negative, i.e.< 0 или < 0, то связь между признаками Х и Y reverse.
6. If the values of the correlation coefficients are positive, i.e. > 0 or y> 0, then the relationship between features X and Y straight(positive).
7. If the correlation coefficients take values +1 or -1, i.e. = ± 1 or = ± 1, then the relationship between characteristics X and Y linear (functional).
8. The reliability of the correlation between characteristics cannot be judged only by the magnitude of the correlation coefficients. This reliability also depends on number of degrees of freedom.

Where: n is the number of correlated pairs of statistical data of characteristics X and Y.

The larger n, the higher the reliability of the relationship with the same correlation coefficient.

In addition to the listed common properties, the correlation coefficients under consideration also have differences. Their main difference is that the Pearson coefficient ( can be used only if the distribution of characteristics X and Y is normal, the Spearman coefficient () can be used for characteristics with any type of distribution. If the characteristics in question have a normal distribution, then it is more expedient to determine the presence of a correlation connection using the Pearson coefficient (), since in this case it will have a smaller error than the Spearman coefficient ().

Example 8.2.

Using Spearman's rank correlation coefficient, determine whether there is a relationship between the results of the running long jump (X) and the final running speed (Y) of a group of athletes (data from Example 8.1, Table 5).

In formula (1) dx and dy are the ranks of statistical data, i.e. places option in their ranked set. If in the aggregate there are several identical data, then their ranks are equal and are determined as the average value of the places occupied by these options. For example,

Data xi
dx ranks			4,5	4,5	4,5	4,5	7,5	7,5

			3 + 4 + 5 + 6	7 + 8

Using this rule, we will determine the ranks of the data in Table 5. For convenience, we will write everything in the form of Table 6.

Table 6

dx		dy	dx-dy
	9,1		1 - 1 = 0	02 = 0
	9,6		2 - 2 = 0	02 = 0
	9,8		3 - 3 = 0	02 = 0
	10,1		4 - 4 = 0	02 = 0
	10,5	6,5	5 - 6,5 = - 1,5	(- 1,5)2 = 2,25
	10,5	6,5	6 - 6,5 = - 0,5	(- 0,5)2 = 0,25
	10,3		7 - 5 = 2	22 = 4
	10,7		8 - 8 = 0	02 = 0
			(dx-dy) = 0

In this case we have 8 pairs of values, i.e. 8 correlated pairs. This means n = 8. Substituting the result in formula (1), we will have:

Conclusion:

(0,92 > 0) , then between the signs X and Y U X), and vice versa - with a decrease in take-off speed, the length of the jump decreases. The reliability of the Spearman correlation coefficient is determined from the table of critical values of the rank correlation coefficient.

b) because the resulting value of the correlation coefficient = 0.9 is greater than the table value = 0.88, corresponding to level b = 99%, then the confidence in the correctness of conclusion (a) is greater than 99%. Such reliability allows us to extend conclusion (a) to the entire population, i.e. for all long jumpers.

If a preliminary check of the populations under consideration for normality of distribution is not carried out, then, if the Pearson correlation coefficient is unreliable, the presence of a connection should also be checked using the Spearman coefficient.

Example 8.3.

The rank correlation coefficient can be used to identify relationships between variables that have any statistical distribution. But if these variables have a normal (Gaussian) distribution, then the relationship can be established more accurately using the normalized (Bravais-Pearson) correlation coefficient.

Let's assume that in our example and - correspond to the law of normal distribution, and check the existence of a connection between the test results X and Y using the calculation of the normalized correlation coefficient.

From formula (1) it is clear that for the calculation it is necessary to find the average values of the characteristics X, Y and the deviation of each statistical data from its mean. Knowing these values, you can find the amounts for which it is not difficult to calculate

Based on the data in Table 5, fill out Table 7:

Table 7



	962 = 9216	10,7	0,6	0,62 = 0,36	96 · 0.6 = 57.6
	262 = 676	10,5	0,4	0,42 = 0,16	26 · 0.4 = 10.4
		10,3	0,2	0,04	5,4
- 4		9,8	- 0,3	0,09	1,2
		10,1		0,00	1,0
		10,5	0,4	0,16	3,2
- 92		9,1	- 1,0	1,00	9,2
- 64		9,6	- 0,5	0,25	32,0
	= 23262			= 2,06	= 201

Substituting the sum of column 7 into the numerator of formula (1), and the sums of columns 3 and 6 into the denominator, we obtain:

Conclusion:

a) because the correlation coefficient value is positive (0.92>0) , then between X and Y there is a direct connection, i.e. with increasing take-off speed (sign Y) the length of the jump increases (sign X) and vice versa - with a decrease in take-off speed, the length of the jump decreases. It is very important to know the confidence in the correctness of the conclusion obtained.

Theoretical part

To differentiate the direction of influence of one characteristic on another, the concepts of positive and negative connections were introduced.

If with an increase (decrease) in one attribute, the values of another generally increase (decrease), then such a correlation is called direct or positive.

If with an increase (decrease) in one attribute the values of another generally decrease (increase), then such a correlation is called inverse or negative.

Correlation fields and their use in preliminary correlation analysis

When raising the question of the correlation between two statistical characteristics X and Y, an experiment is carried out with parallel recording of their values.

Example -
We will call the correlation field the scatter zone of the points obtained in this way on the graph. Visually analyzing the correlation field in Figure 8, you can see that it seems to be elongated along some straight line. This picture is typical for the so-called linear correlation relationship between characteristics. In this case, it can be generally assumed that with an increase in the final take-off speed, the length of the jump also increases, and vice versa. Those. There is a direct (positive) relationship between the characteristics under consideration.

Along with this example, from the many other possible correlation fields, the following can be distinguished (Fig. 9-11):