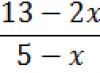The concepts of speed and acceleration are naturally generalized to the case of a material point moving along curvilinear trajectory. The position of the moving point on the trajectory is specified by the radius vector r drawn to this point from some fixed point ABOUT, for example, the origin of coordinates (Fig. 1.2). Let at a moment in time t the material point is in position M with radius vector r = r (t). After a short time D t, it will move to position M 1 with radius - vector r 1 = r (t+ D t). Radius - the vector of the material point will receive an increment determined by the geometric difference D r = r 1 - r . Average speed over time D t is called the quantity
Average speed direction V Wed matches with vector direction D r .

Average speed limit at D t® 0, i.e. derivative of the radius - vector r by time
![]() (1.9)
(1.9)
called true or instant speed of a material point. Vector V directed tangentially to the trajectory of a moving point.
Acceleration A is called a vector equal to the first derivative of the velocity vector V or the second derivative of the radius - vector r by time:
![]() (1.10)
(1.10)
 (1.11)
(1.11)
Let us note the following formal analogy between speed and acceleration. From an arbitrary fixed point O 1 we will plot the velocity vector V moving point at all possible times (Fig. 1.3).

End of vector V called speed point. The geometric locus of the velocity points is a curve called speed hodograph. When a material point describes a trajectory, the corresponding velocity point moves along the hodograph.
Rice. 1.2 differs from Fig. 1.3 by notation only. Radius – vector r replaced by velocity vector V , the material point - to the velocity point, the trajectory - to the hodograph. Mathematical operations on a vector r when finding the speed and above the vector V when found, the accelerations are completely identical.
Speed V directed along a tangential trajectory. That's why accelerationa will be directed tangentially to the speed hodograph. It can be said that acceleration is the speed of movement of the speed point along the hodograph. Hence,
Depending on the shape of the trajectory, movement can be divided into rectilinear and curvilinear. Most often you encounter curvilinear movements when the trajectory is represented as a curve. An example of this type of motion is the path of a body thrown at an angle to the horizon, the movement of the Earth around the Sun, planets, and so on.
Figure 1. Trajectory and movement in curved motion
Definition 1Curvilinear movement called a movement whose trajectory is a curved line. If a body moves along a curved path, then the displacement vector s → is directed along the chord, as shown in Figure 1, and l is the length of the path. The direction of the instantaneous speed of the body moves along a tangent at the same point of the trajectory where the moving object is currently located, as shown in Figure 2.

Figure 2. Instantaneous speed during curved motion
Definition 2
Curvilinear motion of a material point called uniform when the velocity module is constant (circular motion), and uniformly accelerated when the direction and velocity module are changing (movement of an thrown body).
Curvilinear motion is always accelerated. This is explained by the fact that even with an unchanged velocity module and a changed direction, acceleration is always present.
In order to study the curvilinear motion of a material point, two methods are used.
The path is divided into separate sections, at each of which it can be considered straight, as shown in Figure 3.

Figure 3. Partitioning curvilinear motion into translational ones
Now the law of rectilinear motion can be applied to each section. This principle is allowed.
The most convenient solution method is considered to represent the path as a set of several movements along circular arcs, as shown in Figure 4. The number of partitions will be much less than in the previous method, in addition, the movement along the circle is already curvilinear.

Figure 4. Partitioning curvilinear motion into motion along circular arcs
Note 1
To record curvilinear movement, you must be able to describe movement in a circle, and represent arbitrary movement in the form of sets of movements along the arcs of these circles.
The study of curvilinear motion includes the compilation of a kinematic equation that describes this motion and allows us to determine all the characteristics of the motion based on the available initial conditions.
Example 1
Given a material point moving along a curve, as shown in Figure 4. The centers of circles O 1, O 2, O 3 are located on the same straight line. Need to find displacement
s → and path length l while moving from point A to B.
Solution
By condition, we have that the centers of the circle belong to the same straight line, hence:
s → = R 1 + 2 R 2 + R 3 .
Since the trajectory of movement is the sum of semicircles, then:
l ~ A B = π R 1 + R 2 + R 3 .
Answer: s → = R 1 + 2 R 2 + R 3, l ~ A B = π R 1 + R 2 + R 3.
Example 2
The dependence of the distance traveled by the body on time is given, represented by the equation s (t) = A + B t + C t 2 + D t 3 (C = 0.1 m / s 2, D = 0.003 m / s 3). Calculate after what period of time after the start of movement the acceleration of the body will be equal to 2 m / s 2
Solution

Answer: t = 60 s.
If you notice an error in the text, please highlight it and press Ctrl+Enter
6. Curvilinear movement. Angular displacement, angular velocity and acceleration of a body. Path and displacement during curvilinear movement of a body.
Curvilinear movement– this is a movement whose trajectory is a curved line (for example, a circle, ellipse, hyperbola, parabola). An example of curvilinear motion is the movement of planets, the end of a clock hand along a dial, etc. In general curvilinear speed changes in magnitude and direction.
Curvilinear motion of a material point is considered uniform motion if the module speed constant (for example, uniform motion in a circle), and uniformly accelerated if the module and direction speed changes (for example, the movement of a body thrown at an angle to the horizontal).
Rice. 1.19. Trajectory and vector of movement during curvilinear movement.
When moving along a curved path displacement vector directed along the chord (Fig. 1.19), and l- length trajectories . The instantaneous speed of the body (that is, the speed of the body at a given point of the trajectory) is directed tangentially at the point of the trajectory where the moving body is currently located (Fig. 1.20).
 Rice. 1.20. Instantaneous speed during curved motion.
Rice. 1.20. Instantaneous speed during curved motion.
Curvilinear motion is always accelerated motion. That is acceleration during curved motion is always present, even if the speed module does not change, but only the direction of speed changes. The change in speed per unit time is tangential acceleration :
 or
or 
Where v τ ,v 0 – velocity values at the moment of time t 0 +Δt And t 0 respectively.
Tangential acceleration at a given point of the trajectory, the direction coincides with the direction of the speed of movement of the body or is opposite to it.
Normal acceleration is the change in speed in direction per unit time:

Normal acceleration directed along the radius of curvature of the trajectory (towards the axis of rotation). Normal acceleration is perpendicular to the direction of velocity.
Centripetal acceleration is the normal acceleration during uniform circular motion.
Total acceleration during uniform curvilinear motion of a body equals:

The movement of a body along a curved path can be approximately represented as movement along the arcs of certain circles (Fig. 1.21).
 Rice. 1.21. Movement of a body during curvilinear motion.
Rice. 1.21. Movement of a body during curvilinear motion.
Curvilinear movement
Curvilinear movements– movements whose trajectories are not straight, but curved lines. Planets and river waters move along curvilinear trajectories.
Curvilinear motion is always motion with acceleration, even if the absolute value of the velocity is constant. Curvilinear motion with constant acceleration always occurs in the plane in which the acceleration vectors and initial velocities of the point are located. In the case of curvilinear motion with constant acceleration in the plane xOy projections v x And v y its speed on the axis Ox And Oy and coordinates x And y points at any time t determined by formulas
![]()
![]()
A special case of curvilinear motion is circular motion. Circular motion, even uniform, is always accelerated motion: the velocity module is always directed tangentially to the trajectory, constantly changing direction, so circular motion always occurs with centripetal acceleration where r– radius of the circle.
The acceleration vector when moving in a circle is directed towards the center of the circle and perpendicular to the velocity vector.
In curvilinear motion, acceleration can be represented as the sum of normal and tangential components:
Normal (centripetal) acceleration is directed towards the center of curvature of the trajectory and characterizes the change in speed in the direction:
v – instantaneous speed value, r– radius of curvature of the trajectory at a given point.
Tangential (tangential) acceleration is directed tangentially to the trajectory and characterizes the change in speed modulo.
The total acceleration with which a material point moves is equal to:

In addition to centripetal acceleration, the most important characteristics of uniform circular motion are the period and frequency of rotation.
Circulation period- this is the time during which the body completes one revolution .
The period is indicated by the letter T(c) and is determined by the formula:
Where t- circulation time, n- the number of revolutions completed during this time.
Frequency- this is a quantity numerically equal to the number of revolutions completed per unit of time.
Frequency is denoted by a Greek letter (nu) and is found using the formula:
The frequency is measured in 1/s.
Period and frequency are mutually inverse quantities:
If a body moves in a circle with speed v, makes one revolution, then the distance traveled by this body can be found by multiplying the speed v for the time of one revolution:
l = vT. On the other hand, this path is equal to the circumference of the circle 2π r. That's why
vT = 2π r,
![]()
Where w(s -1) - angular velocity.
At a constant rotation frequency, centripetal acceleration is directly proportional to the distance from the moving particle to the center of rotation.
Angular velocity (w) – a value equal to the ratio of the angle of rotation of the radius at which the rotating point is located to the period of time during which this rotation occurred:
![]() .
.
Relationship between linear and angular speeds:
The motion of a body can be considered known only when it is known how each point moves. The simplest motion of solid bodies is translational. Progressive is the motion of a rigid body in which any straight line drawn in this body moves parallel to itself.
You are well aware that depending on the shape of the trajectory, movement is divided into rectilinear And curvilinear. We learned how to work with rectilinear motion in previous lessons, namely, to solve the main problem of mechanics for this type of motion.
However, it is clear that in the real world we most often deal with curvilinear motion, when the trajectory is a curved line. Examples of such movement are the trajectory of a body thrown at an angle to the horizon, the movement of the Earth around the Sun, and even the trajectory of the movement of your eyes, which are now following this note.
This lesson will be devoted to the question of how the main problem of mechanics is solved in the case of curvilinear motion.
To begin with, let’s determine what fundamental differences exist in curvilinear movement (Fig. 1) relative to rectilinear movement and what these differences lead to.
Rice. 1. Trajectory of curvilinear movement
Let's talk about how it is convenient to describe the movement of a body during curvilinear motion.
The movement can be divided into separate sections, in each of which the movement can be considered rectilinear (Fig. 2).

Rice. 2. Dividing curvilinear movement into sections of rectilinear movement
However, the following approach is more convenient. We will imagine this movement as a combination of several movements along circular arcs (Fig. 3). Please note that there are fewer such partitions than in the previous case, in addition, the movement along the circle is curvilinear. In addition, examples of motion in a circle are very common in nature. From this we can conclude:
In order to describe curvilinear movement, you need to learn to describe movement in a circle, and then represent arbitrary movement in the form of sets of movements along circular arcs.

Rice. 3. Partitioning curvilinear motion into motion along circular arcs
So, let's begin the study of curvilinear motion by studying uniform motion in a circle. Let's figure out what are the fundamental differences between curvilinear movement and rectilinear movement. To begin with, let us remember that in ninth grade we studied the fact that the speed of a body when moving in a circle is directed tangent to the trajectory (Fig. 4). By the way, you can observe this fact experimentally if you watch how sparks move when using a sharpening stone.

Let's consider the movement of a body along a circular arc (Fig. 5).

Rice. 5. Speed of a body when moving in a circle
Please note that in this case the modulus of the velocity of the body at a point is equal to the modulus of the velocity of the body at the point:
However, a vector is not equal to a vector. So, we have a velocity difference vector (Fig. 6):

Rice. 6. Velocity difference vector
Moreover, the change in speed occurred after some time. So we get the familiar combination:
![]()
This is nothing more than a change in speed over a period of time, or acceleration of a body. A very important conclusion can be drawn:
Movement along a curved path is accelerated. The nature of this acceleration is a continuous change in the direction of the velocity vector.
Let us note once again that, even if it is said that the body moves uniformly in a circle, it is meant that the modulus of the body’s velocity does not change. However, such movement is always accelerated, since the direction of speed changes.
In ninth grade, you studied what this acceleration is equal to and how it is directed (Fig. 7). Centripetal acceleration is always directed towards the center of the circle along which the body is moving.

Rice. 7. Centripetal acceleration
The centripetal acceleration module can be calculated using the formula:
Let us move on to the description of the uniform motion of a body in a circle. Let's agree that the speed that you used while describing the translational motion will now be called linear speed. And by linear speed we will understand the instantaneous speed at the point of the trajectory of a rotating body.

Rice. 8. Movement of disk points
Consider a disk that rotates clockwise for definiteness. On its radius we mark two points and (Fig. 8). Let's consider their movement. Over time, these points will move along the arcs of the circle and become points and. It is obvious that the point has moved more than the point . From this we can conclude that the farther a point is from the axis of rotation, the greater the linear speed it moves
However, if you look closely at the points and , we can say that the angle by which they turned relative to the axis of rotation remained unchanged. It is the angular characteristics that we will use to describe the movement in a circle. Note that to describe circular motion we can use corner characteristics.
Let's start considering motion in a circle with the simplest case - uniform motion in a circle. Let us recall that uniform translational motion is a movement in which the body makes equal movements over any equal intervals of time. By analogy, we can give the definition of uniform motion in a circle.
Uniform circular motion is a motion in which the body rotates through equal angles over any equal intervals of time.
Similar to the concept of linear velocity, the concept of angular velocity is introduced.
Angular velocity of uniform motion ( is a physical quantity equal to the ratio of the angle through which the body turned to the time during which this rotation occurred.
In physics, the radian measure of angle is most often used. For example, angle b is equal to radians. Angular velocity is measured in radians per second:
Let's find the connection between the angular speed of rotation of a point and the linear speed of this point.

Rice. 9. Relationship between angular and linear speed
When rotating, a point passes an arc of length , turning at an angle . From the definition of the radian measure of an angle we can write:
Let's divide the left and right sides of the equality by the period of time during which the movement was made, then use the definition of angular and linear velocities:
Please note that the further a point is from the axis of rotation, the higher its linear speed. And the points located on the axis of rotation itself are motionless. An example of this is a carousel: the closer you are to the center of the carousel, the easier it is for you to stay on it.
This dependence of linear and angular velocities is used in geostationary satellites (satellites that are always located above the same point on the earth's surface). Thanks to such satellites, we are able to receive television signals.
Let us remember that earlier we introduced the concepts of period and frequency of rotation.
The rotation period is the time of one full revolution. The rotation period is indicated by a letter and measured in SI seconds:
Rotation frequency is a physical quantity equal to the number of revolutions that a body makes per unit time.
Frequency is indicated by a letter and measured in reciprocal seconds:
They are related by the relation:
There is a relationship between angular velocity and the frequency of rotation of the body. If we remember that a full revolution is equal to , it is easy to see that the angular velocity is:
![]()
Substituting these expressions into the relationship between angular and linear speed, we can obtain the dependence of linear speed on period or frequency:
![]()
Let us also write down the relationship between centripetal acceleration and these quantities:
Thus, we know the relationship between all the characteristics of uniform circular motion.
Let's summarize. In this lesson we began to describe curvilinear motion. We understood how we can connect curvilinear motion with circular motion. Circular motion is always accelerated, and the presence of acceleration determines the fact that the speed always changes its direction. This acceleration is called centripetal. Finally, we remembered some characteristics of circular motion (linear speed, angular speed, period and frequency of rotation) and found the relationships between them.
References
- G.Ya. Myakishev, B.B. Bukhovtsev, N.N. Sotsky. Physics 10. - M.: Education, 2008.
- A.P. Rymkevich. Physics. Problem book 10-11. - M.: Bustard, 2006.
- O.Ya. Savchenko. Physics problems. - M.: Nauka, 1988.
- A.V. Peryshkin, V.V. Krauklis. Physics course. T. 1. - M.: State. teacher ed. min. education of the RSFSR, 1957.
- Аyp.ru ().
- Wikipedia ().
Homework
Having solved the problems for this lesson, you will be able to prepare for questions 1 of the State Examination and questions A1, A2 of the Unified State Exam.
- Problems 92, 94, 98, 106, 110 - Sat. problems A.P. Rymkevich, ed. 10
- Calculate the angular velocity of the minute, second and hour hands of the clock. Calculate the centripetal acceleration acting on the tips of these arrows if the radius of each of them is one meter.
Depending on the shape of the trajectory, movement is divided into rectilinear and curvilinear. In the real world, we most often deal with curvilinear motion, when the trajectory is a curved line. Examples of such movement are the trajectory of a body thrown at an angle to the horizon, the movement of the Earth around the Sun, the movement of the planets, the end of a clock hand on a dial, etc.
Figure 1. Trajectory and displacement during curved motion
Definition
Curvilinear motion is a motion whose trajectory is a curved line (for example, a circle, ellipse, hyperbola, parabola). When moving along a curved path, the displacement vector $\overrightarrow(s)$ is directed along the chord (Fig. 1), and l is the length of the path. The instantaneous speed of the body (that is, the speed of the body at a given point of the trajectory) is directed tangentially at the point of the trajectory where the moving body is currently located (Fig. 2).

Figure 2. Instantaneous speed during curved motion
However, the following approach is more convenient. This movement can be represented as a combination of several movements along circular arcs (see Fig. 4.). There will be fewer such partitions than in the previous case, in addition, the movement along the circle is itself curvilinear.

Figure 4. Breakdown of curvilinear motion into motion along circular arcs
Conclusion
In order to describe curvilinear movement, you need to learn to describe movement in a circle, and then represent arbitrary movement in the form of sets of movements along circular arcs.
The task of studying the curvilinear motion of a material point is to compile a kinematic equation that describes this motion and allows, based on given initial conditions, to determine all the characteristics of this motion.