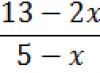The simplest equation of a parabola. How to build a parabola using a quadratic equation

Let us introduce a rectangular coordinate system, where . Let the axis pass through the focus F parabola and perpendicular to the directrix, and the axis passes midway between the focus and the directrix. Let us denote by the distance between the focus and the directrix. Then the directrix equation.

The number is called the focal parameter of the parabola. Let be the current point of the parabola. Let be the focal radius of the point of the hyperbola. Let be the distance from the point to the directrix. Then( drawing 27.)

Drawing 27.

By definition of a parabola. Hence,

Let's square the equation and get:

(15)

where (15) is the canonical equation of a parabola that is symmetrical about the axis and passes through the origin.

Study of the properties of a parabola

1) Vertex of the parabola:

Equation (15) is satisfied by numbers and, therefore, the parabola passes through the origin.

2) Parabola symmetry:

Let it belong to the parabola, i.e. true equality. The point is symmetrical to the point relative to the axis, therefore, the parabola is symmetrical relative to the abscissa axis.

Parabola eccentricity:

Definition 4.2. The eccentricity of a parabola is a number equal to one.

Since by definition of a parabola.

4) Tangent of the parabola:

The tangent to a parabola at the point of tangency is given by the equation

Where ( drawing 28.)

Drawing 28.

Parabola image

Drawing 29.

Using ESO-Mathcad:

drawing 30.)

Drawing 30.

a) Construction without the use of ICT: To construct a parabola, we set a rectangular coordinate system with a center at point O and a unit segment. We mark the focus on the OX axis, since we draw such that, and the directrix of the parabola. We construct a circle at a point with a radius equal to the distance from the straight line to the directrix of the parabola. The circle intersects the line at points . We construct a parabola so that it passes through the origin and through the points.( drawing 31.)

Drawing 31.

b)Using ESO-Mathcad:

The resulting equation looks like: . To construct a second-order line in the Mathcad program, we reduce the equation to the form: .( drawing 32.)

Drawing 32.

In order to summarize the work on the theory of second-order lines in elementary mathematics and for the convenience of using information about lines when solving problems, we will include all the data on second-order lines in Table No. 1.

Table No. 1.

Second order lines in elementary mathematics

Possibilities of using ICT in the study of second-order lines

The process of informatization, which today has covered all aspects of the life of modern society, has several priority areas, which, of course, should include the informatization of education. It is the fundamental basis for the global rationalization of human intellectual activity through the use of information and communication technologies (ICT).

The mid-90s of the last century until today is characterized by the widespread use and availability of personal computers in Russia, the widespread use of telecommunications, which allows the introduction of developed educational information technologies into the educational process, improving and modernizing it, improving the quality of knowledge, increasing motivation to learn, making maximum use of the principle of individualization of learning. Information technologies for education are a necessary tool at this stage of informatization of education.

Information technologies not only facilitate access to information and open up opportunities for variability in educational activities, their individualization and differentiation, but also make it possible to reorganize the interaction of all subjects of learning in a new way, to build an educational system in which the student would be an active and equal participant in educational activities.

The formation of new information technologies within the framework of subject lessons stimulates the need to create new software and methodological complexes aimed at qualitatively increasing the effectiveness of the lesson. Therefore, for the successful and purposeful use of information technology tools in the educational process, teachers must know the general description of the principles of operation and the didactic capabilities of software applications, and then, based on their experience and recommendations, “build” them into the educational process.

The study of mathematics is currently associated with a number of features and difficulties in the development of school education in our country.

A so-called crisis in mathematics education has emerged. The reasons for this are as follows:

In changing priorities in society and in science, that is, the priority of the humanities is currently growing;

In reducing the number of mathematics lessons in school;

The isolation of the content of mathematical education from life;

Has little impact on the feelings and emotions of students.

Today the question remains open: “How to most effectively use the potential capabilities of modern information and communication technologies when teaching schoolchildren, including when teaching mathematics?”

A computer is an excellent assistant in studying a topic such as “Quadratic Function”, because using special programs you can build graphs of various functions, explore the function, easily determine the coordinates of intersection points, calculate the areas of closed figures, etc. For example, in a 9th grade algebra lesson devoted to graph transformation (stretching, compressing, moving coordinate axes), you can only see the frozen result of the construction, while the entire dynamics of the sequential actions of the teacher and student can be seen on the monitor screen.

The computer, like no other technical tool, accurately, visually and excitingly reveals ideal mathematical models to the student, i.e. what a child should strive for in his practical actions.

How many difficulties does a mathematics teacher have to go through in order to convince students that the tangent to the graph of a quadratic function at the point of tangency practically merges with the graph of the function. It is very easy to demonstrate this fact on a computer—it is enough to narrow the interval along the Ox axis and discover that in a very small neighborhood of the tangency point, the graph of the function and the tangent line coincide. All these actions take place in front of the students. This example provides an impetus for active reflection in the lesson. The use of a computer is possible both during the explanation of new material in class and at the control stage. With the help of these programs, for example “My Test”, the student can independently test his level of knowledge in theory and complete theoretical and practical tasks. The programs are convenient due to their versatility. They can be used for both self-control and teacher control.

Reasonable integration of mathematics and computer technology will allow us to take a richer and deeper look at the process of solving a problem and the process of understanding mathematical laws. In addition, the computer will help to form a graphic, mathematical and mental culture of students, and with the help of a computer you can prepare didactic materials: cards, survey sheets, tests, etc. At the same time, give the children the opportunity to independently develop tests on the topic, during which interest and creative approach.

Thus, there is a need to use computers in mathematics lessons as widely as possible. The use of information technology will help improve the quality of knowledge, expand the horizons of studying the quadratic function, and therefore help find new prospects for maintaining students’ interest in the subject and topic, and therefore for a better, more attentive attitude towards it. Today, modern information technologies are becoming the most important tool for modernizing the school as a whole - from management to education and ensuring accessibility of education.

A parabola is the locus of points in the plane that are equidistant from a given point F and a given straight line d that does not pass through the given point. This geometric definition expresses directorial property of a parabola.

Directorial property of a parabola

Point F is called the focus of the parabola, line d is the directrix of the parabola, the midpoint O of the perpendicular lowered from the focus to the directrix is ​​the vertex of the parabola, the distance p from the focus to the directrix is ​​the parameter of the parabola, and the distance \frac(p)(2) from the vertex of the parabola to its focus is the focal length (Fig. 3.45a). The straight line perpendicular to the directrix and passing through the focus is called the axis of the parabola (focal axis of the parabola). The segment FM connecting an arbitrary point M of the parabola with its focus is called the focal radius of the point M. The segment connecting two points of a parabola is called a chord of the parabola.

For an arbitrary point of a parabola, the ratio of the distance to the focus to the distance to the directrix is ​​equal to one. Comparing the directorial properties of , and parabolas, we conclude that parabola eccentricity by definition equal to one (e=1).

Geometric definition of a parabola, expressing its directorial property, is equivalent to its analytical definition - the line defined by the canonical equation of a parabola:

Indeed, let us introduce a rectangular coordinate system (Fig. 3.45, b). We take the vertex O of the parabola as the origin of the coordinate system; let us take the straight line passing through the focus perpendicular to the directrix as the abscissa axis (the positive direction on it is from point O to point F); Let us take the straight line perpendicular to the abscissa axis and passing through the vertex of the parabola as the ordinate axis (the direction on the ordinate axis is chosen so that the rectangular coordinate system Oxy is right).

Let's create an equation for a parabola using its geometric definition, which expresses the directorial property of a parabola. In the selected coordinate system, we determine the coordinates of the focus F\!\left(\frac(p)(2);\,0\right) and the directrix equation x=-\frac(p)(2) . For an arbitrary point M(x,y) belonging to a parabola, we have:

FM=MM_d,

Where M_d\!\left(\frac(p)(2);\,y\right)- orthogonal projection of the point M(x,y) onto the directrix. We write this equation in coordinate form:

\sqrt((\left(x-\frac(p)(2)\right)\^2+y^2}=x+\frac{p}{2}. !}

We square both sides of the equation: (\left(x-\frac(p)(2)\right)\^2+y^2=x^2+px+\frac{p^2}{4} !}. Bringing similar terms, we get canonical parabola equation

y^2=2\cdot p\cdot x, those. the chosen coordinate system is canonical.

Carrying out the reasoning in reverse order, we can show that all points whose coordinates satisfy equation (3.51), and only they, belong to the locus of points called a parabola. Thus, the analytical definition of a parabola is equivalent to its geometric definition, which expresses the directorial property of a parabola.

Parabola equation in polar coordinate system

The equation of a parabola in the polar coordinate system Fr\varphi (Fig. 3.45, c) has the form

r=\frac(p)(1-e\cdot\cos\varphi), where p is the parameter of the parabola, and e=1 is its eccentricity.

In fact, as the pole of the polar coordinate system we choose the focus F of the parabola, and as the polar axis - a ray with a beginning at point F, perpendicular to the directrix and not intersecting it (Fig. 3.45, c). Then for an arbitrary point M(r,\varphi) belonging to a parabola, according to the geometric definition (directional property) of a parabola, we have MM_d=r. Because MM_d=p+r\cos\varphi, we obtain the parabola equation in coordinate form:

p+r\cdot\cos\varphi \quad \Leftrightarrow \quad r=\frac(p)(1-\cos\varphi),

Q.E.D. Note that in polar coordinates the equations of the ellipse, hyperbola and parabola coincide, but describe different lines, since they differ in eccentricities (0\leqslant e<1 для , e=1 для параболы, e>1 for ).

Geometric meaning of the parameter in the parabola equation

Let's explain geometric meaning of the parameter p in the canonical parabola equation. Substituting x=\frac(p)(2) into equation (3.51), we obtain y^2=p^2, i.e. y=\pm p . Therefore, the parameter p is half the length of the chord of the parabola passing through its focus perpendicular to the axis of the parabola.

The focal parameter of the parabola, as well as for an ellipse and a hyperbola, is called half the length of the chord passing through its focus perpendicular to the focal axis (see Fig. 3.45, c). From the parabola equation in polar coordinates at \varphi=\frac(\pi)(2) we get r=p, i.e. the parameter of the parabola coincides with its focal parameter.

Notes 3.11.

1. The parameter p of a parabola characterizes its shape. The larger p, the wider the branches of the parabola, the closer p is to zero, the narrower the branches of the parabola (Fig. 3.46).

2. The equation y^2=-2px (for p>0) defines a parabola, which is located to the left of the ordinate axis (Fig. 3.47,a). This equation is reduced to the canonical one by changing the direction of the x-axis (3.37). In Fig. 3.47,a shows the given coordinate system Oxy and the canonical Ox"y".

3. Equation (y-y_0)^2=2p(x-x_0),\,p>0 defines a parabola with vertex O"(x_0,y_0), the axis of which is parallel to the abscissa axis (Fig. 3.47,6). This equation is reduced to the canonical one using parallel translation (3.36).

Equation (x-x_0)^2=2p(y-y_0),\,p>0, also defines a parabola with vertex O"(x_0,y_0), the axis of which is parallel to the ordinate axis (Fig. 3.47, c). This equation is reduced to the canonical one using parallel translation (3.36) and renaming the coordinate axes (3.38). In Fig. Figure 3.47, b, c shows the given coordinate systems Oxy and the canonical coordinate systems Ox"y".

4. y=ax^2+bx+c,~a\ne0 is a parabola with vertex at the point O"\!\left(-\frac(b)(2a);\,-\frac(b^2-4ac)(4a)\right), the axis of which is parallel to the ordinate axis, the branches of the parabola are directed upward (for a>0) or downward (for a<0 ). Действительно, выделяя полный квадрат, получаем уравнение

y=a\left(x+\frac(b)(2a)\right)^2-\frac(b^2)(4a)+c \quad \Leftrightarrow \quad \!\left(x+\frac(b) (2a)\right)^2=\frac(1)(a)\left(y+\frac(b^2-4ac)(4a)\right)\!,

which is reduced to the canonical form (y")^2=2px" , where p=\left|\frac(1)(2a)\right|, using replacement y"=x+\frac(b)(2a) And x"=\pm\!\left(y+\frac(b^2-4ac)(4a)\right).

The sign is chosen to coincide with the sign of the leading coefficient a. This replacement corresponds to the composition: parallel transfer (3.36) with x_0=-\frac(b)(2a) And y_0=-\frac(b^2-4ac)(4a), renaming the coordinate axes (3.38), and in the case of a<0 еще и изменения направления координатной оси (3.37). На рис.3.48,а,б изображены заданные системы координат Oxy и канонические системы координат O"x"y" для случаев a>0 and a<0 соответственно.

5. The x-axis of the canonical coordinate system is axis of symmetry of the parabola, since replacing the variable y with -y does not change equation (3.51). In other words, the coordinates of the point M(x,y), belonging to the parabola, and the coordinates of the point M"(x,-y), symmetrical to the point M relative to the x-axis, satisfy equation (3.S1). The axes of the canonical coordinate system are called the main axes of the parabola.

Example 3.22. Draw the parabola y^2=2x in the canonical coordinate system Oxy. Find the focal parameter, focal coordinates and directrix equation.

Solution. We construct a parabola, taking into account its symmetry relative to the abscissa axis (Fig. 3.49). If necessary, determine the coordinates of some points of the parabola. For example, substituting x=2 into the parabola equation, we get y^2=4~\Leftrightarrow~y=\pm2. Consequently, points with coordinates (2;2),\,(2;-2) belong to the parabola.

Comparing the given equation with the canonical one (3.S1), we determine the focal parameter: p=1. Focus coordinates x_F=\frac(p)(2)=\frac(1)(2),~y_F=0, i.e. F\!\left(\frac(1)(2),\,0\right). We compose the equation of the directrix x=-\frac(p)(2) , i.e. x=-\frac(1)(2) .

General properties of ellipse, hyperbola, parabola

1. The directorial property can be used as a single definition of an ellipse, hyperbola, parabola (see Fig. 3.50): the locus of points in the plane, for each of which the ratio of the distance to a given point F (focus) to the distance to a given straight line d (directrix) not passing through a given point is constant and equal to eccentricity e, is called:

a) if 0\leqslant e<1 ;

b) if e>1;

c) parabola if e=1.

2. An ellipse, hyperbola, and parabola are obtained as planes in sections of a circular cone and are therefore called conic sections. This property can also serve as a geometric definition of an ellipse, hyperbola, and parabola.

3. Common properties of the ellipse, hyperbola and parabola include bisectoral property their tangents. Under tangent to a line at some point K is understood to be the limiting position of the secant KM when the point M, remaining on the line under consideration, tends to the point K. A straight line perpendicular to a tangent to a line and passing through the point of tangency is called normal to this line.

The bisectoral property of tangents (and normals) to an ellipse, hyperbola and parabola is formulated as follows: the tangent (normal) to an ellipse or to a hyperbola forms equal angles with the focal radii of the tangent point(Fig. 3.51, a, b); the tangent (normal) to the parabola forms equal angles with the focal radius of the point of tangency and the perpendicular dropped from it to the directrix(Fig. 3.51, c). In other words, the tangent to the ellipse at point K is the bisector of the external angle of the triangle F_1KF_2 (and the normal is the bisector of the internal angle F_1KF_2 of the triangle); the tangent to the hyperbola is the bisector of the internal angle of the triangle F_1KF_2 (and the normal is the bisector of the external angle); the tangent to the parabola is the bisector of the internal angle of the triangle FKK_d (and the normal is the bisector of the external angle). The bisectoral property of a tangent to a parabola can be formulated in the same way as for an ellipse and a hyperbola, if we assume that the parabola has a second focus at a point at infinity.

4. From the bisectoral properties it follows optical properties of ellipse, hyperbola and parabola, explaining the physical meaning of the term "focus". Let us imagine surfaces formed by rotating an ellipse, hyperbola or parabola around the focal axis. If a reflective coating is applied to these surfaces, elliptical, hyperbolic and parabolic mirrors are obtained. According to the law of optics, the angle of incidence of a light ray on a mirror is equal to the angle of reflection, i.e. the incident and reflected rays form equal angles with the normal to the surface, and both rays and the axis of rotation are in the same plane. From here we get the following properties:

– if the light source is located at one of the focuses of an elliptical mirror, then the rays of light, reflected from the mirror, are collected at another focus (Fig. 3.52, a);

– if the light source is located in one of the focuses of a hyperbolic mirror, then the rays of light, reflected from the mirror, diverge as if they came from another focus (Fig. 3.52, b);

– if the light source is at the focus of a parabolic mirror, then the light rays, reflected from the mirror, go parallel to the focal axis (Fig. 3.52, c).

5. Diametric property ellipse, hyperbola and parabola can be formulated as follows:

– the midpoints of parallel chords of an ellipse (hyperbola) lie on one straight line passing through the center of the ellipse (hyperbola);

– the midpoints of parallel chords of a parabola lie on the straight, collinear axis of symmetry of the parabola.

The geometric locus of the midpoints of all parallel chords of an ellipse (hyperbola, parabola) is called diameter of the ellipse (hyperbola, parabola), conjugate to these chords.

This is the definition of diameter in the narrow sense (see example 2.8). Previously, a definition of diameter was given in a broad sense, where the diameter of an ellipse, hyperbola, parabola, and other second-order lines is a straight line containing the midpoints of all parallel chords. In a narrow sense, the diameter of an ellipse is any chord passing through its center (Fig. 3.53, a); the diameter of a hyperbola is any straight line passing through the center of the hyperbola (with the exception of asymptotes), or part of such a straight line (Fig. 3.53,6); The diameter of a parabola is any ray emanating from a certain point of the parabola and collinear to the axis of symmetry (Fig. 3.53, c).

Two diameters, each of which bisects all chords parallel to the other diameter, are called conjugate. In Fig. 3.53, bold lines show the conjugate diameters of an ellipse, hyperbola, and parabola.

The tangent to the ellipse (hyperbola, parabola) at point K can be defined as the limit position of parallel secants M_1M_2, when points M_1 and M_2, remaining on the line under consideration, tend to point K. From this definition it follows that a tangent parallel to the chords passes through the end of the diameter conjugate to these chords.

6. Ellipse, hyperbola and parabola have, in addition to those given above, numerous geometric properties and physical applications. For example, Fig. 3.50 can serve as an illustration of the trajectories of space objects located in the vicinity of the center of gravity F.

A parabola is an infinite curve that consists of points equidistant from a given line, called the directrix of the parabola, and a given point, the focus of the parabola. A parabola is a conic section, that is, it represents the intersection of a plane and a circular cone.

In general, the mathematical equation of a parabola has the form: y=ax^2+bx+c, where a is not equal to zero, b reflects the horizontal displacement of the function graph relative to the origin, and c is the vertical displacement of the function graph relative to the origin. Moreover, if a>0, then when plotting the graph they will be directed upward, and if aProperties of the parabola

A parabola is a second-order curve that has an axis of symmetry passing through the focus of the parabola and perpendicular to the directrix of the parabola.

A parabola has a special optical property, which consists in focusing light rays parallel to its axis of symmetry and directed into the parabola at the vertex of the parabola and defocusing a beam of light directed at the vertex of the parabola into parallel light rays relative to the same axis.

If you reflect a parabola relative to any tangent, then the image of the parabola will appear on its directrix. All parabolas are similar to each other, that is, for every two points A and B of one parabola, there are points A1 and B1 for which the statement |A1,B1| = |A,B|*k, where k is the similarity coefficient, which in numerical value is always greater than zero.

Manifestation of a parabola in life

Some cosmic bodies, such as comets or asteroids, passing near large space objects at high speed have a parabola-shaped trajectory. This property of small cosmic bodies is used in gravitational maneuvers of spacecraft.

To train future cosmonauts, special aircraft flights are carried out on the ground along a parabolic trajectory, thereby achieving the effect of weightlessness in the gravitational field of the earth.

In everyday life, parabolas can be found in various lighting fixtures. This is due to the optical property of a parabola. One of the latest ways to use the parabola, based on its properties of focusing and defocusing light rays, is solar panels, which are increasingly included in the energy supply sector in the southern regions of Russia.

Level III

3.1. Hyperbole touches lines 5 x – 6y – 16 = 0, 13x – 10y– – 48 = 0. Write down the equation of the hyperbola provided that its axes coincide with the coordinate axes.

3.2. Write equations for tangents to a hyperbola

1) passing through a point A(4, 1), B(5, 2) and C(5, 6);

2) parallel to straight line 10 x – 3y + 9 = 0;

3) perpendicular to straight line 10 x – 3y + 9 = 0.

Parabola is the geometric locus of points in the plane whose coordinates satisfy the equation

Parabola parameters:

Dot F(p/2, 0) is called focus parabolas, magnitude p – parameter , point ABOUT(0, 0) – top . In this case, the straight line OF, about which the parabola is symmetrical, defines the axis of this curve.

Magnitude Where M(x, y) – an arbitrary point of a parabola, called focal radius , straight D: x = –p/2 – headmistress (it does not intersect the interior region of the parabola). Magnitude is called the eccentricity of the parabola.

The main characteristic property of a parabola: all points of the parabola are equidistant from the directrix and focus (Fig. 24).

There are other forms of the canonical parabola equation that determine other directions of its branches in the coordinate system (Fig. 25):

For parametric definition of a parabola as a parameter t the ordinate value of the parabola point can be taken:

Where t is an arbitrary real number.

Example 1. Determine the parameters and shape of a parabola using its canonical equation:

Solution. 1. Equation y 2 = –8x defines a parabola with vertex at point ABOUT Oh. Its branches are directed to the left. Comparing this equation with the equation y 2 = –2px, we find: 2 p = 8, p = 4, p/2 = 2. Therefore, the focus is at the point F(–2; 0), directrix equation D: x= 2 (Fig. 26).

2. Equation x 2 = –4y defines a parabola with vertex at point O(0; 0), symmetrical about the axis Oy. Its branches are directed downwards. Comparing this equation with the equation x 2 = –2py, we find: 2 p = 4, p = 2, p/2 = 1. Therefore, the focus is at the point F(0; –1), directrix equation D: y= 1 (Fig. 27).

Example 2. Determine parameters and type of curve x 2 + 8x – 16y– 32 = 0. Make a drawing.

Solution. Let's transform the left side of the equation using the complete square extraction method:

x 2 + 8x– 16y – 32 =0;

(x + 4) 2 – 16 – 16y – 32 =0;

(x + 4) 2 – 16y – 48 =0;

(x + 4) 2 – 16(y + 3).

As a result we get

(x + 4) 2 = 16(y + 3).

This is the canonical equation of a parabola with the vertex at the point (–4, –3), the parameter p= 8, branches pointing upward (), axis x= –4. Focus is on point F(–4; –3 + p/2), i.e. F(–4; 1) Headmistress D given by the equation y = –3 – p/2 or y= –7 (Fig. 28).

Example 4. Write an equation for a parabola with its vertex at the point V(3; –2) and focus at the point F(1; –2).

Solution. The vertex and focus of a given parabola lie on a straight line parallel to the axis Ox(same ordinates), the branches of the parabola are directed to the left (the abscissa of the focus is less than the abscissa of the vertex), the distance from the focus to the vertex is p/2 = 3 – 1 = 2, p= 4. Hence, the required equation

(y+ 2) 2 = –2 4( x– 3) or ( y + 2) 2 = = –8(x – 3).

Tasks for independent solution

I level

1.1. Determine the parameters of the parabola and construct it:

1) y 2 = 2x; 2) y 2 = –3x;

3) x 2 = 6y; 4) x 2 = –y.

1.2. Write the equation of a parabola with its vertex at the origin if you know that:

1) the parabola is located in the left half-plane symmetrically relative to the axis Ox And p = 4;

2) the parabola is located symmetrically relative to the axis Oy and passes through the point M(4; –2).

3) the directrix is ​​given by equation 3 y + 4 = 0.

1.3. Write an equation for a curve all points of which are equidistant from the point (2; 0) and the straight line x = –2.

Level II

2.1. Determine the type and parameters of the curve.

Throughout this chapter it is assumed that in the plane (in which all the figures considered below lie) a certain scale has been chosen; Only rectangular coordinate systems with this scale are considered.

§ 1. Parabola

A parabola is known to the reader from a school mathematics course as a curve, which is the graph of a function

(Fig. 76). (1)

Graph of any quadratic trinomial

is also a parabola; is possible by simply shifting the coordinate system (by some vector OO), i.e. transforming

ensure that the graph of the function (in the second coordinate system) coincides with graph (2) (in the first coordinate system).

In fact, let us substitute (3) into equality (2). We get

We want to choose so that the coefficient at and the free term of the polynomial (with respect to ) on the right side of this equality are equal to zero. To do this, we determine from the equation

which gives

Now we determine from the condition

into which we substitute the already found value. We get

So, by means of shift (3), in which

we moved to a new coordinate system, in which the equation of the parabola (2) took the form

(Fig. 77).

Let's return to equation (1). It can serve as the definition of a parabola. Let us recall its simplest properties. The curve has an axis of symmetry: if a point satisfies equation (1), then a point symmetrical to point M relative to the ordinate axis also satisfies equation (1) - the curve is symmetrical relative to the ordinate axis (Fig. 76).

If , then parabola (1) lies in the upper half-plane, having a single common point O with the abscissa axis.

With an unlimited increase in the absolute value of the abscissa, the ordinate also increases without limit. A general view of the curve is shown in Fig. 76, a.

If (Fig. 76, b), then the curve is located in the lower half-plane symmetrically relative to the abscissa axis to the curve.

If we move to a new coordinate system, obtained from the old one by replacing the positive direction of the ordinate axis with the opposite one, then the parabola, which has the equation y in the old system, will receive the equation y in the new coordinate system. Therefore, when studying parabolas, we can limit ourselves to equations (1), in which .

Let us finally change the names of the axes, i.e., we will move to a new coordinate system, in which the ordinate axis will be the old abscissa axis, and the abscissa axis will be the old ordinate axis. In this new system, equation (1) will be written in the form

Or, if the number is denoted by , in the form

Equation (4) is called in analytical geometry the canonical equation of a parabola; the rectangular coordinate system in which a given parabola has equation (4) is called the canonical coordinate system (for this parabola).

Now we will establish the geometric meaning of the coefficient. To do this we take the point

called the focus of parabola (4), and the straight line d, defined by the equation

This line is called the directrix of the parabola (4) (see Fig. 78).

Let be an arbitrary point of the parabola (4). From equation (4) it follows that Therefore, the distance of the point M from the directrix d is the number

The distance of point M from focus F is

But, therefore

So, all points M of the parabola are equidistant from its focus and directrix:

Conversely, every point M satisfying condition (8) lies on parabola (4).

In fact,

Hence,

and, after opening the parentheses and bringing like terms,

We have proven that each parabola (4) is the locus of points equidistant from the focus F and from the directrix d of this parabola.

At the same time, we have established the geometric meaning of the coefficient in equation (4): the number is equal to the distance between the focus and the directrix of the parabola.

Let us now assume that a point F and a line d not passing through this point are given arbitrarily on the plane. Let us prove that there exists a parabola with focus F and directrix d.

To do this, draw a line g through point F (Fig. 79), perpendicular to line d; let us denote the point of intersection of both lines by D; the distance (i.e. the distance between point F and straight line d) will be denoted by .

Let us turn the straight line g into an axis, taking the direction DF on it as positive. Let us make this axis the abscissa axis of a rectangular coordinate system, the origin of which is the middle O of the segment

Then straight line d also receives the equation .

Now we can write the canonical equation of the parabola in the selected coordinate system:

where point F will be the focus, and straight line d will be the directrix of the parabola (4).

We established above that a parabola is the locus of points M equidistant from point F and line d. So, we can give such a geometric (i.e., independent of any coordinate system) definition of a parabola.

Definition. A parabola is the locus of points equidistant from some fixed point (the “focus” of the parabola) and some fixed line (the “directrix” of the parabola).

Denoting the distance between the focus and the directrix of a parabola by , we can always find a rectangular coordinate system that is canonical for a given parabola, that is, one in which the equation of the parabola has the canonical form:

Conversely, any curve that has such an equation in some rectangular coordinate system is a parabola (in the geometric sense just established).

The distance between the focus and the directrix of a parabola is called the focal parameter, or simply the parameter of the parabola.

The line passing through the focus perpendicular to the directrix of the parabola is called its focal axis (or simply axis); it is the axis of symmetry of the parabola - this follows from the fact that the axis of the parabola is the abscissa axis in the coordinate system, relative to which the equation of the parabola has the form (4).

If a point satisfies equation (4), then this equation is also satisfied by a point symmetric to point M relative to the abscissa axis.

The point of intersection of a parabola with its axis is called the vertex of the parabola; it is the origin of the coordinate system canonical for a given parabola.

Let's give another geometric interpretation of the parabola parameter.

Let us draw a straight line through the focus of the parabola, perpendicular to the axis of the parabola; it will intersect the parabola at two points (see Fig. 79) and determine the so-called focal chord of the parabola (i.e., the chord passing through the focus parallel to the directrix of the parabola). Half the length of the focal chord is the parameter of the parabola.

In fact, half the length of the focal chord is the absolute value of the ordinate of any of the points, the abscissa of each of which is equal to the abscissa of the focus, i.e. Therefore, for the ordinate of each point we have

Q.E.D.