કાર્યાત્મક શ્રેણીઓમાં, સૌથી મહત્વપૂર્ણ સ્થાન પાવર શ્રેણી દ્વારા કબજે કરવામાં આવે છે.

પાવર શ્રેણી એ શ્રેણી છે

જેની શરતો બિન-નકારાત્મક પૂર્ણાંક શક્તિઓને વધારવામાં ગોઠવાયેલા પાવર ફંક્શન્સ છે x, એ c0 , c 1 , c 2 , c n - સતત મૂલ્યો. સંખ્યાઓ c1 , c 2 , c n - શ્રેણીની શરતોના ગુણાંક, c0 - મફત સભ્ય. પાવર શ્રેણીની શરતો સમગ્ર સંખ્યા રેખા પર વ્યાખ્યાયિત કરવામાં આવી છે.

ચાલો ખ્યાલથી પરિચિત થઈએ પાવર શ્રેણીના કન્વર્જન્સના ક્ષેત્રો. આ ચલ મૂલ્યોનો સમૂહ છે x, જેના માટે શ્રેણી એકરૂપ થાય છે. પાવર શ્રેણી એકદમ સરળ કન્વર્જન્સ પ્રદેશ ધરાવે છે. વાસ્તવિક ચલ મૂલ્યો માટે xકન્વર્જન્સ પ્રદેશમાં એક બિંદુનો સમાવેશ થાય છે, અથવા ચોક્કસ અંતરાલ (કન્વર્જન્સ અંતરાલ) હોય છે અથવા સમગ્ર ધરી સાથે એકરુપ હોય છે બળદ .

જ્યારે મૂલ્યોને પાવર શ્રેણીમાં બદલી રહ્યા હોય x= 0 એ સંખ્યા શ્રેણીમાં પરિણમશે

c0 +0+0+...+0+... ,

જે એકરૂપ થાય છે.

તેથી, જ્યારે x= 0 કોઈપણ પાવર શ્રેણી કન્વર્જ થાય છે અને તેથી, તેનું સંકલન ક્ષેત્ર ખાલી સેટ ન હોઈ શકે. તમામ પાવર સીરીઝના કન્વર્જન્સના પ્રદેશનું માળખું સમાન છે. તે નીચેના પ્રમેયનો ઉપયોગ કરીને સ્થાપિત કરી શકાય છે.

પ્રમેય 1 (અબેલનું પ્રમેય). જો પાવર શ્રેણી અમુક મૂલ્ય પર કન્વર્જ થાય છે x = x 0 , શૂન્યથી અલગ, પછી તે કન્વર્જ થાય છે, અને વધુમાં, એકદમ, તમામ મૂલ્યો માટે |x| < |x 0 | . મહેરબાની કરીને નોંધ કરો: બંને પ્રારંભિક મૂલ્ય "X શૂન્ય છે" અને "X" નું કોઈપણ મૂલ્ય જે પ્રારંભિક મૂલ્ય સાથે સરખાવવામાં આવે છે તે મોડ્યુલો લેવામાં આવે છે - ચિહ્નને ધ્યાનમાં લીધા વિના.

પરિણામ. જો પાવર શ્રેણી અલગ પડે છે અમુક કિંમતે x = x 1 , પછી તે તમામ મૂલ્યો માટે અલગ પડે છે |x| > |x 1 | .

જેમ આપણે પહેલાથી જ શોધી કાઢ્યું છે, કોઈપણ પાવર શ્રેણી મૂલ્ય પર કન્વર્જ થાય છે x= 0. ત્યાં પાવર શ્રેણીઓ છે જે ફક્ત ત્યારે જ કન્વર્જ થાય છે x= 0 અને અન્ય મૂલ્યો માટે અલગ કરો એક્સ. વિચારણામાંથી આ કેસને બાદ કરતાં, અમે ધારીએ છીએ કે પાવર શ્રેણી અમુક મૂલ્ય પર કન્વર્જ થાય છે x = x 0 , શૂન્યથી અલગ. પછી, એબેલના પ્રમેય મુજબ, તે અંતરાલના તમામ બિંદુઓ પર એકરૂપ થાય છે ]-| x0 |, |x 0 |[ (એક અંતરાલ જેની ડાબી અને જમણી સીમાઓ એ x મૂલ્યો છે કે જેના પર પાવર સિરીઝ કન્વર્જ થાય છે, અનુક્રમે ઓછા ચિહ્ન અને વત્તા ચિહ્ન સાથે લેવામાં આવે છે), મૂળના સંદર્ભમાં સપ્રમાણતા.

જો પાવર શ્રેણી ચોક્કસ મૂલ્ય પર અલગ પડે છે x = x 1 , તો પછી, એબેલના પ્રમેયની કોરોલરીના આધારે, તે સેગમેન્ટની બહારના તમામ બિંદુઓ પર અલગ પડે છે [-| x1 |, |x 1 |] . તે અનુસરે છે કે કોઈપણ પાવર શ્રેણી માટે મૂળના સંદર્ભમાં એક અંતરાલ સપ્રમાણ હોય છે, જેને કહેવાય છે કન્વર્જન્સ અંતરાલ , જેમાંથી દરેક બિંદુએ શ્રેણી એકરૂપ થાય છે, તે સીમાઓ પર એકરૂપ થઈ શકે છે, અથવા તે અલગ થઈ શકે છે, અને તે જ સમયે જરૂરી નથી, અને સેગમેન્ટની બહાર શ્રેણી અલગ પડે છે. નંબર આરપાવર શ્રેણીના કન્વર્જન્સની ત્રિજ્યા કહેવાય છે.

ખાસ કિસ્સાઓમાં પાવર શ્રેણીનું કન્વર્જન્સ અંતરાલ એક બિંદુ સુધી અધોગતિ કરી શકે છે (પછી શ્રેણી માત્ર ત્યારે જ કન્વર્જ થાય છે જ્યારે x= 0 અને તે માનવામાં આવે છે આર= 0) અથવા સમગ્ર સંખ્યા રેખાનું પ્રતિનિધિત્વ કરો (પછી શ્રેણી સંખ્યા રેખાના તમામ બિંદુઓ પર કન્વર્જ થાય છે અને એવું માનવામાં આવે છે કે ).

આમ, પાવર સીરીઝના કન્વર્જન્સનો વિસ્તાર નક્કી કરવામાં તેનો સમાવેશ થાય છે કન્વર્જન્સ ત્રિજ્યા આરઅને કન્વર્જન્સ અંતરાલ (એટ) ની સીમાઓ પર શ્રેણીના કન્વર્જન્સનો અભ્યાસ કરવો.

પ્રમેય 2.જો પાવર સિરીઝના તમામ ગુણાંક, ચોક્કસથી શરૂ કરીને, શૂન્યથી અલગ હોય, તો તેની સંપાતની ત્રિજ્યા શ્રેણીના સામાન્ય નીચેના સભ્યોના ગુણાંકના ચોક્કસ મૂલ્યોના ગુણોત્તર પરની મર્યાદા જેટલી હોય છે. , એટલે કે

ઉદાહરણ 1. પાવર શ્રેણીના કન્વર્જન્સનો પ્રદેશ શોધો

ઉકેલ. અહીં

સૂત્ર (28) નો ઉપયોગ કરીને, આપણે આ શ્રેણીના કન્વર્જન્સની ત્રિજ્યા શોધીએ છીએ:

ચાલો કન્વર્જન્સ અંતરાલના અંતે શ્રેણીના કન્વર્જન્સનો અભ્યાસ કરીએ. ઉદાહરણ 13 બતાવે છે કે આ શ્રેણી પર કન્વર્જ થાય છે x= 1 અને પર અલગ પડે છે x= -1. પરિણામે, કન્વર્જન્સનો પ્રદેશ અર્ધ-અંતરાલ છે.

ઉદાહરણ 2. પાવર શ્રેણીના કન્વર્જન્સનો પ્રદેશ શોધો

ઉકેલ. શ્રેણીના ગુણાંક હકારાત્મક છે, અને

ચાલો આ ગુણોત્તરની મર્યાદા શોધીએ, એટલે કે. પાવર શ્રેણીના કન્વર્જન્સની ત્રિજ્યા:

ચાલો અંતરાલના અંતે શ્રેણીના કન્વર્જન્સનો અભ્યાસ કરીએ. મૂલ્ય અવેજી x= -1/5 અને xઆ પંક્તિમાં = 1/5 આપે છે:

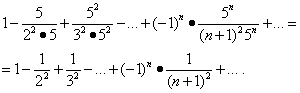
આ શ્રેણીમાંથી પ્રથમ કન્વર્જ થાય છે (ઉદાહરણ 5 જુઓ). પરંતુ પછી, "સંપૂર્ણ કન્વર્જન્સ" વિભાગમાં પ્રમેયના આધારે, બીજી શ્રેણી પણ કન્વર્જ થાય છે, અને તેના કન્વર્જન્સનો વિસ્તાર સેગમેન્ટ છે

ઉદાહરણ 3. પાવર શ્રેણીના કન્વર્જન્સનો પ્રદેશ શોધો

ઉકેલ. અહીં

ફોર્મ્યુલા (28) નો ઉપયોગ કરીને આપણે શ્રેણીના કન્વર્જન્સની ત્રિજ્યા શોધીએ છીએ:

ચાલો ની કિંમતો માટે શ્રેણીના કન્વર્જન્સનો અભ્યાસ કરીએ. આ શ્રેણીમાં તેમને બદલીને, અમે અનુક્રમે મેળવીએ છીએ

બંને શ્રેણીઓ અલગ પડે છે કારણ કે કન્વર્જન્સ માટે જરૂરી સ્થિતિ સંતુષ્ટ નથી (તેમની સામાન્ય શરતો શૂન્ય પર વલણ ધરાવતી નથી). તેથી, કન્વર્જન્સ અંતરાલના બંને છેડે, આ શ્રેણી અલગ પડે છે, અને તેના કન્વર્જન્સનો પ્રદેશ અંતરાલ છે.

ઉદાહરણ 5. પાવર શ્રેણીના કન્વર્જન્સનો પ્રદેશ શોધો

ઉકેલ. અમે સંબંધ શોધીએ છીએ જ્યાં , અને :

સૂત્ર (28) અનુસાર, આ શ્રેણીના કન્વર્જન્સની ત્રિજ્યા

,

એટલે કે, શ્રેણી ત્યારે જ કન્વર્જ થાય છે જ્યારે x= 0 અને અન્ય મૂલ્યો માટે અલગ પડે છે એક્સ.

ઉદાહરણો દર્શાવે છે કે કન્વર્જન્સ અંતરાલના અંતે શ્રેણી અલગ રીતે વર્તે છે. ઉદાહરણ 1 માં, કન્વર્જન્સ અંતરાલના એક છેડે, તે અલગ પડે છે, ઉદાહરણ 2 માં, તે બંને છેડે અલગ પડે છે;

પાવર સિરીઝના કન્વર્જન્સના ત્રિજ્યા માટેનું સૂત્ર એ ધારણા હેઠળ મેળવવામાં આવે છે કે ચોક્કસ બિંદુથી શરૂ થતા શ્રેણીના તમામ ગુણાંક શૂન્યથી અલગ છે. તેથી, સૂત્ર (28) નો ઉપયોગ ફક્ત આ કિસ્સાઓમાં જ માન્ય છે. જો આ શરતનું ઉલ્લંઘન કરવામાં આવે છે, તો પાવર સીરીઝના કન્વર્જન્સની ત્રિજ્યાનો ઉપયોગ કરીને શોધ કરવી જોઈએ ડી'એલેમ્બર્ટની નિશાની, અથવા, ચલને બદલીને, શ્રેણીને એવા સ્વરૂપમાં રૂપાંતરિત કરો કે જેમાં ઉલ્લેખિત સ્થિતિ સંતુષ્ટ હોય.

ઉદાહરણ 6. પાવર શ્રેણીના કન્વર્જન્સનું અંતરાલ શોધો

ઉકેલ. આ શ્રેણીમાં વિષમ ડિગ્રી સાથેના શબ્દો શામેલ નથી એક્સ. તેથી, અમે શ્રેણીને બદલીએ છીએ, સેટિંગ કરીએ છીએ. પછી અમે શ્રેણી મેળવીએ છીએ

કન્વર્જન્સની ત્રિજ્યા શોધવા માટે કે જેના માટે આપણે સૂત્ર (28) લાગુ કરી શકીએ. ત્યારથી , a , પછી આ શ્રેણીના કન્વર્જન્સની ત્રિજ્યા

સમાનતામાંથી આપણે મેળવીએ છીએ, તેથી, આ શ્રેણી અંતરાલ પર કન્વર્જ થાય છે.

શક્તિ શ્રેણીનો સરવાળો. પાવર શ્રેણીનો તફાવત અને એકીકરણ

પાવર શ્રેણી માટે ચાલો

કન્વર્જન્સની ત્રિજ્યા આર> 0, એટલે કે. આ શ્રેણી અંતરાલ પર એકરૂપ થાય છે.

પછી દરેક મૂલ્ય એક્સકન્વર્જન્સ અંતરાલમાંથી શ્રેણીના ચોક્કસ સરવાળાને અનુલક્ષે છે. તેથી, પાવર શ્રેણીનો સરવાળો એક કાર્ય છે એક્સકન્વર્જન્સ અંતરાલ પર. દ્વારા સૂચિત કરવું f(x), આપણે સમાનતા લખી શકીએ છીએ

દરેક બિંદુ પર શ્રેણીનો સરવાળો એ અર્થમાં સમજવું એક્સકન્વર્જન્સ અંતરાલમાંથી ફંક્શનના મૂલ્યની બરાબર છે f(x) આ બિંદુએ. તે જ અર્થમાં, આપણે કહીશું કે પાવર શ્રેણી (29) ફંક્શનમાં કન્વર્જ થાય છે f(x) કન્વર્જન્સ અંતરાલ પર.

કન્વર્જન્સ અંતરાલની બહાર, સમાનતા (30) નો કોઈ અર્થ નથી.

ઉદાહરણ 7.શક્તિ શ્રેણીનો સરવાળો શોધો

ઉકેલ. આ એક ભૌમિતિક શ્રેણી છે જેના માટે a= 1, એ q= x. તેથી, તેનો સરવાળો એક કાર્ય છે . શ્રેણી કન્વર્જ થાય છે જો , અને તેનું કન્વર્જન્સ અંતરાલ છે. તેથી સમાનતા

માત્ર મૂલ્યો માટે જ માન્ય છે, જો કે કાર્ય બધા મૂલ્યો માટે વ્યાખ્યાયિત એક્સ, સિવાય એક્સ= 1.

તે સાબિત કરી શકાય છે કે શક્તિ શ્રેણીનો સરવાળો f(x) એ કન્વર્જન્સ અંતરાલની અંદર કોઈપણ અંતરાલ પર સતત અને ભિન્ન છે, ખાસ કરીને શ્રેણીના કન્વર્જન્સ અંતરાલના કોઈપણ બિંદુએ.

ચાલો ટર્મ-બાય-ટર્મ ડિફરન્સિએશન અને પાવર સિરીઝના એકીકરણ પર પ્રમેય રજૂ કરીએ.

પ્રમેય 1.તેના કન્વર્જન્સના અંતરાલમાં પાવર સિરીઝ (30) ને શબ્દ દ્વારા અમર્યાદિત સંખ્યામાં અલગ કરી શકાય છે, અને પરિણામી પાવર સિરીઝ મૂળ શ્રેણીની સમાન કન્વર્જન્સની ત્રિજ્યા ધરાવે છે, અને તેમના સરવાળો અનુક્રમે .

પ્રમેય 2.પાવર સિરીઝ (30) ને 0 થી રેન્જમાં અમર્યાદિત સંખ્યામાં ટર્મ દ્વારા સંકલિત કરી શકાય છે એક્સ, જો , અને પરિણામી શક્તિ શ્રેણીમાં મૂળ શ્રેણીની સમાન કન્વર્જન્સની ત્રિજ્યા હોય છે, અને તેમના સરવાળો અનુરૂપ સમાન હોય છે

પાવર શ્રેણીમાં કાર્યોનું વિસ્તરણ

ફંક્શન આપવા દો f(x), જેને પાવર શ્રેણીમાં વિસ્તૃત કરવાની જરૂર છે, એટલે કે. ફોર્મમાં રજૂ કરો (30):

કાર્ય એ ગુણાંક નક્કી કરવાનું છે પંક્તિ (30). આ કરવા માટે, સમાનતા (30) શબ્દને શબ્દ દ્વારા અલગ કરીને, અમે સતત શોધીએ છીએ:

……………………………………………….. (31)

સમાનતામાં ધારવું (30) અને (31) એક્સ= 0, આપણે શોધીએ છીએ

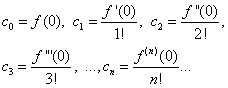
મળેલા સમીકરણોને સમાનતામાં બદલીને (30), આપણે મેળવીએ છીએ

(32)

ચાલો આપણે કેટલાક પ્રાથમિક કાર્યોના મેકલોરિન શ્રેણીના વિસ્તરણને શોધીએ.

ઉદાહરણ 8. Maclaurin શ્રેણીમાં કાર્યને વિસ્તૃત કરો

ઉકેલ. આ ફંક્શનના ડેરિવેટિવ્ઝ ફંક્શન સાથે મેળ ખાય છે:

તેથી, જ્યારે એક્સ= 0 અમારી પાસે છે

આ મૂલ્યોને સૂત્ર (32) માં બદલીને, અમે ઇચ્છિત વિસ્તરણ મેળવીએ છીએ:

(33)

આ શ્રેણી સમગ્ર સંખ્યા રેખા (તેની સંપાત ત્રિજ્યા) પર કન્વર્જ થાય છે.

ઉદાહરણ 1.પાવર શ્રેણીના કન્વર્જન્સનો પ્રદેશ શોધો:

એ); b) ;

વી) ; જી)
;

ડી)
.

અ)ચાલો કન્વર્જન્સની ત્રિજ્યા શોધીએ આર. કારણ કે
,
, તે

.

x
, એટલે કે, શ્રેણીના કન્વર્જન્સનું અંતરાલ
.

મુ
અમને સંખ્યાની શ્રેણી મળે છે . આ શ્રેણી કન્વર્જ થાય છે કારણ કે તે સામાન્ય હાર્મોનિક શ્રેણી છે ખાતે
.

મુ
અમને સંખ્યાની શ્રેણી મળે છે
. આ શ્રેણી એકદમ કન્વર્જન્ટ છે, કારણ કે તેની શરતોના સંપૂર્ણ મૂલ્યોની બનેલી શ્રેણી , કન્વર્જન્ટ.

.

b)ચાલો કન્વર્જન્સની ત્રિજ્યા શોધીએ આર. કારણ કે
, તે
.

તેથી, શ્રેણીનું કન્વર્જન્સ અંતરાલ
.

અમે કન્વર્જન્સ અંતરાલના અંતે આ શ્રેણીના કન્વર્જન્સનું પરીક્ષણ કરીએ છીએ.

મુ
અમારી પાસે સંખ્યાની શ્રેણી છે

.

મુ
અમારી પાસે સંખ્યાની શ્રેણી છે
. આ શ્રેણી અલગ છે કારણ કે
અસ્તિત્વમાં નથી.

તેથી, આ શ્રેણીના કન્વર્જન્સનો પ્રદેશ
.

વી)ચાલો કન્વર્જન્સની ત્રિજ્યા શોધીએ આર. કારણ કે
,
તે
.

તેથી, કન્વર્જન્સ અંતરાલ
. આ શ્રેણીનો કન્વર્જન્સ ક્ષેત્ર કન્વર્જન્સ અંતરાલ સાથે એકરુપ છે, એટલે કે, ચલના કોઈપણ મૂલ્ય માટે શ્રેણી કન્વર્જ થાય છે x.

જી)ચાલો કન્વર્જન્સની ત્રિજ્યા શોધીએ આર. કારણ કે
,
તે
.

કારણ કે
, પછી શ્રેણી માત્ર બિંદુ પર એકરૂપ થાય છે
. આનો અર્થ એ છે કે આ શ્રેણીના કન્વર્જન્સનો પ્રદેશ એક બિંદુ છે
.

ડી)ચાલો કન્વર્જન્સની ત્રિજ્યા શોધીએ આર.

કારણ કે
,
, તે

.

તેથી, શ્રેણી સંપૂર્ણપણે દરેક માટે એકરૂપ થાય છે x, અસમાનતાને સંતોષે છે
, એટલે કે
.

અહીંથી
- કન્વર્જન્સ અંતરાલ,
- કન્વર્જન્સની ત્રિજ્યા.

ચાલો કન્વર્જન્સ અંતરાલના અંતે કન્વર્જન્સ માટે આ શ્રેણીનું પરીક્ષણ કરીએ.

મુ
અમને સંખ્યાની શ્રેણી મળે છે

,

જે અલગ પડે છે (હાર્મોનિક શ્રેણી).

મુ
અમને સંખ્યાની શ્રેણી મળે છે
, જે શરતી રીતે કન્વર્જ થાય છે (શ્રેણી લીબનીઝના માપદંડ અનુસાર કન્વર્જ થાય છે, અને તેના સભ્યોના સંપૂર્ણ મૂલ્યોથી બનેલી શ્રેણી અલગ પડે છે, કારણ કે તે હાર્મોનિક છે).

તેથી, શ્રેણીના કન્વર્જન્સનો પ્રદેશ
.

2.3. ટેલર અને મેકલોરિન શ્રેણી.

પાવર શ્રેણીમાં કાર્યોનું વિસ્તરણ.

અંદાજિત ગણતરીઓ માટે પાવર શ્રેણીનો ઉપયોગ

સમસ્યા હલ કરવાના ઉદાહરણો

ઉદાહરણ 1.કાર્યને પાવર શ્રેણીમાં વિસ્તૃત કરો:

અ)
; b)
;

વી)
; જી)
.

અ)ફોર્મ્યુલામાં બદલીને
xપર
, અમે ઇચ્છિત વિસ્તરણ મેળવીએ છીએ:

જ્યાં

b)સમાનતામાં અવેજી

જ્યાં
xપર
, અમે ઇચ્છિત વિસ્તરણ મેળવીએ છીએ:

વી)આ કાર્ય આ રીતે લખી શકાય છે:
. ઇચ્છિત શ્રેણી શોધવા માટે, તે વિસ્તૃત કરવા માટે પૂરતું છે

જ્યાં
અવેજી
. પછી આપણને મળે છે:

જી)આ કાર્યને આ રીતે ફરીથી લખી શકાય છે: .

કાર્ય
દ્વિપદી શ્રેણીમાં મૂકીને પાવર શ્રેણીમાં વિસ્તૃત કરી શકાય છે
, અમે પ્રાપ્ત કરીશું.

જ્યાં
.

ઇચ્છિત વિસ્તરણ મેળવવા માટે, પરિણામી શ્રેણીને ગુણાકાર કરવા માટે તે પૂરતું છે (આ શ્રેણીના સંપૂર્ણ કન્વર્જન્સને કારણે).

આથી,

, ક્યાં
.

ઉદાહરણ 2.આ કાર્યોના અંદાજિત મૂલ્યો શોધો:

અ)
0.0001 ની ચોકસાઈ સાથે;

b)
0.00001 ની ચોકસાઈ સાથે.

અ)કારણ કે
, પછી કાર્યના વિસ્તરણમાં, જ્યાં
ચાલો અવેજી કરીએ
:

અથવા

કારણ કે
, તો જરૂરી ચોકસાઈ સુનિશ્ચિત કરવામાં આવશે જો આપણે પોતાને પરિણામી વિસ્તરણની માત્ર પ્રથમ બે શરતો સુધી મર્યાદિત રાખીએ.

.

અમે દ્વિપદી શ્રેણીનો ઉપયોગ કરીએ છીએ

જ્યાં
.

માનતા
અને
, અમે નીચેનું વિસ્તરણ મેળવીએ છીએ:

જો છેલ્લી વૈકલ્પિક શ્રેણીમાં ફક્ત પ્રથમ બે શબ્દો ધ્યાનમાં લેવામાં આવે છે અને બાકીના કાઢી નાખવામાં આવે છે, તો ગણતરીમાં ભૂલ
સંપૂર્ણ મૂલ્યમાં 0.000006 કરતાં વધી જશે નહીં. પછી ગણતરીમાં ભૂલ
સંખ્યા કરતાં વધી જશે નહીં. આથી,

ઉદાહરણ 3.નજીકના 0.001 સુધી ગણતરી કરો:

અ)
; b)
.

અ)
.

ચાલો ઇન્ટિગ્રેન્ડને પાવર સિરીઝમાં વિસ્તૃત કરીએ. આ કરવા માટે, ચાલો દ્વિપદી શ્રેણીમાં બદલીએ
અને બદલો xપર :

.

એકીકરણ ના સેગમેન્ટ થી
પરિણામી શ્રેણીના કન્વર્જન્સના પ્રદેશથી સંબંધિત છે
, તો પછી અમે ઉલ્લેખિત મર્યાદામાં ટર્મ દ્વારા ટર્મને એકીકૃત કરીશું:

.

વૈકલ્પિક ચિહ્નોની પરિણામી શ્રેણીમાં, ચોથો શબ્દ સંપૂર્ણ મૂલ્યમાં 0.001 કરતાં ઓછો છે. પરિણામે, જો શ્રેણીની માત્ર પ્રથમ ત્રણ શરતોને ધ્યાનમાં લેવામાં આવે તો જરૂરી ચોકસાઈની ખાતરી કરવામાં આવશે.

.

કાઢી નાખવામાં આવેલી શરતોમાંથી પ્રથમમાં બાદબાકીનું ચિહ્ન હોવાથી, પરિણામી અંદાજિત મૂલ્ય વધુ હશે. તેથી, 0.001 ની અંદરનો જવાબ 0.487 છે.

b)ચાલો સૌપ્રથમ ઈન્ટીગ્રેન્ડને પાવર સીરીઝ તરીકે રજૂ કરીએ. ચાલો ફંક્શનના વિસ્તરણમાં બદલીએ

જ્યાં

xપર
, અમને મળે છે:

પછી
.

પરિણામી વૈકલ્પિક શ્રેણી લીબનીઝના માપદંડની શરતોને સંતોષે છે. શ્રેણીની ચોથી મુદત સંપૂર્ણ મૂલ્યમાં 0.001 કરતાં ઓછી છે. જરૂરી ચોકસાઈની ખાતરી કરવા માટે, પ્રથમ ત્રણ શબ્દોનો સરવાળો શોધવા માટે તે પૂરતું છે.

આથી,
.

કાર્યાત્મક શ્રેણી. પાવર શ્રેણી.
શ્રેણીના કન્વર્જન્સની શ્રેણી

કોઈ કારણ વિના હાસ્ય એ ડી'અલેમ્બર્ટની નિશાની છે

કાર્યાત્મક રેન્કનો કલાક ત્રાટક્યો છે. વિષયને સફળતાપૂર્વક માસ્ટર કરવા માટે, અને ખાસ કરીને, આ પાઠ, તમારે સામાન્ય સંખ્યાની શ્રેણીની સારી સમજ હોવી જરૂરી છે. તમને શ્રેણી શું છે તેની સારી સમજ હોવી જોઈએ અને કન્વર્જન્સ માટે શ્રેણીની તપાસ કરવા માટે સરખામણી માપદંડ લાગુ કરવા સક્ષમ હોવા જોઈએ. આમ, જો તમે હમણાં જ વિષયનો અભ્યાસ શરૂ કર્યો હોય અથવા ઉચ્ચ ગણિતમાં શિખાઉ છો, જરૂરીક્રમમાં ત્રણ પાઠો દ્વારા કાર્ય કરો: ડમી માટે પંક્તિઓ,ડી'એલેમ્બર્ટનું ચિહ્ન. કોચીના ચિહ્નોઅને વૈકલ્પિક પંક્તિઓ. લીબનીઝની કસોટી. ચોક્કસપણે ત્રણેય! જો તમારી પાસે સંખ્યા શ્રેણીની સમસ્યાઓ હલ કરવામાં મૂળભૂત જ્ઞાન અને કુશળતા હોય, તો કાર્યાત્મક શ્રેણીનો સામનો કરવો એકદમ સરળ હશે, કારણ કે ત્યાં ઘણી બધી નવી સામગ્રી નથી.

આ પાઠમાં, આપણે કાર્યાત્મક શ્રેણીની વિભાવના જોઈશું (તે શું પણ છે), પાવર શ્રેણીથી પરિચિત થઈશું, જે 90% વ્યવહારુ કાર્યોમાં જોવા મળે છે, અને ત્રિજ્યા શોધવાની સામાન્ય લાક્ષણિક સમસ્યાને કેવી રીતે હલ કરવી તે શીખીશું. પાવર શ્રેણીના કન્વર્જન્સ, કન્વર્જન્સ ઇન્ટરવલ અને કન્વર્જન્સ રિજન. આગળ, હું વિશેની સામગ્રીને ધ્યાનમાં લેવાની ભલામણ કરું છું પાવર શ્રેણીમાં કાર્યોનું વિસ્તરણ, અને શિખાઉ માણસને પ્રાથમિક સારવાર આપવામાં આવશે. અમારા શ્વાસને થોડો પકડ્યા પછી, અમે આગલા સ્તર પર આગળ વધીએ છીએ:

કાર્યાત્મક શ્રેણીના વિભાગમાં પણ તેમાંના અસંખ્ય છે અંદાજિત કમ્પ્યુટિંગ માટેની એપ્લિકેશનો, અને કેટલીક રીતે ફ્યુરિયર શ્રેણી બહાર આવે છે, જે, એક નિયમ તરીકે, શૈક્ષણિક સાહિત્યમાં એક અલગ પ્રકરણ આપવામાં આવે છે. મારી પાસે ફક્ત એક જ લેખ છે, પરંતુ તે લાંબો છે અને ઘણા બધા વધારાના ઉદાહરણો છે!

તેથી, સીમાચિહ્નો સેટ છે, ચાલો જઈએ:

કાર્યાત્મક શ્રેણી અને પાવર શ્રેણીનો ખ્યાલ

જો મર્યાદા અનંત છે, પછી સોલ્યુશન એલ્ગોરિધમ પણ તેનું કાર્ય પૂર્ણ કરે છે, અને અમે કાર્યનો અંતિમ જવાબ આપીએ છીએ: "શ્રેણી " (અથવા ક્યાં તો ") પર કન્વર્જ થાય છે. અગાઉના ફકરાનો કેસ નંબર 3 જુઓ.

જો મર્યાદા શૂન્ય અથવા અનંત ન હોવાનું બહાર આવે છે, તો પછી અમારી પાસે પ્રેક્ટિસ નંબર 1 માં સૌથી સામાન્ય કેસ છે - શ્રેણી ચોક્કસ અંતરાલ પર કન્વર્જ થાય છે.

આ કિસ્સામાં, મર્યાદા છે. શ્રેણીના કન્વર્જન્સનું અંતરાલ કેવી રીતે શોધવું? અમે અસમાનતા બનાવીએ છીએ:

IN આ પ્રકારનું કોઈપણ કાર્યઅસમાનતાની ડાબી બાજુ હોવી જોઈએ મર્યાદા ગણતરીનું પરિણામ, અને અસમાનતાની જમણી બાજુએ - કડક રીતે એકમ. હું બરાબર સમજાવીશ નહીં કે આવી અસમાનતા શા માટે છે અને શા માટે જમણી બાજુએ છે. પાઠ વ્યવહારીક રીતે લક્ષી છે, અને તે પહેલેથી જ ખૂબ જ સારું છે કે મારી વાર્તાઓએ શિક્ષણ કર્મચારીઓને અટકી ન હતી અને કેટલાક પ્રમેય સ્પષ્ટ થયા હતા.

મોડ્યુલ સાથે કામ કરવાની અને બેવડી અસમાનતાઓને હલ કરવાની તકનીકની લેખમાં પ્રથમ વર્ષમાં વિગતવાર ચર્ચા કરવામાં આવી હતી. કાર્ય ડોમેન, પરંતુ સગવડ માટે, હું શક્ય તેટલી વધુ વિગતવાર બધી ક્રિયાઓ પર ટિપ્પણી કરવાનો પ્રયાસ કરીશ. અમે શાળાના નિયમ અનુસાર મોડ્યુલસ સાથે અસમાનતા જાહેર કરીએ છીએ . આ કિસ્સામાં:

અડધો રસ્તો પૂરો થઈ ગયો.

બીજા તબક્કે, મળેલા અંતરાલના અંતે શ્રેણીના કન્વર્જન્સની તપાસ કરવી જરૂરી છે.

પ્રથમ, અમે અંતરાલનો ડાબો છેડો લઈએ છીએ અને તેને અમારી પાવર શ્રેણીમાં બદલીએ છીએ:

મુ

અમે સંખ્યાની શ્રેણી મેળવી છે, અને અમારે તેને કન્વર્જન્સ માટે તપાસવાની જરૂર છે (અગાઉના પાઠોથી પહેલેથી જ પરિચિત કાર્ય).

1) શ્રેણી વૈકલ્પિક છે.
2) - શ્રેણીની શરતો મોડ્યુલસમાં ઘટાડો કરે છે. તદુપરાંત, શ્રેણીના દરેક આગામી સભ્ય નિરપેક્ષ મૂલ્યમાં અગાઉના એક કરતા ઓછા છે: , જેનો અર્થ છે કે ઘટાડો એકવિધ છે.
નિષ્કર્ષ: શ્રેણી એકરૂપ થાય છે.

મોડ્યુલોથી બનેલી શ્રેણીનો ઉપયોગ કરીને, આપણે બરાબર કેવી રીતે શોધીશું:
- કન્વર્જ (સામાન્યકૃત હાર્મોનિક શ્રેણીના પરિવારમાંથી "માનક" શ્રેણી).

આમ, પરિણામી સંખ્યા શ્રેણી એકદમ કન્વર્જ થાય છે.

ખાતે - એકરૂપ થાય છે.

! હું તમને યાદ કરાવું છું કે કોઈપણ કન્વર્જન્ટ ધન શ્રેણી પણ એકદમ કન્વર્જન્ટ છે.

આમ, પાવર સીરિઝ કન્વર્જ થાય છે, અને એકદમ, મળેલા અંતરાલના બંને છેડે.

જવાબ:અધ્યયન હેઠળ પાવર શ્રેણીના કન્વર્જન્સનો વિસ્તાર:

જવાબના અન્ય સ્વરૂપમાં જીવનનો અધિકાર છે: શ્રેણી કન્વર્જ થાય છે જો

કેટલીકવાર સમસ્યાના નિવેદનમાં તમારે કન્વર્જન્સની ત્રિજ્યા દર્શાવવાની જરૂર પડે છે. તે સ્પષ્ટ છે કે માનવામાં આવેલા ઉદાહરણમાં.

ઉદાહરણ 2

પાવર શ્રેણીના કન્વર્જન્સનો પ્રદેશ શોધો

ઉકેલ:આપણે શ્રેણીના કન્વર્જન્સનું અંતરાલ શોધીએ છીએ ઉપયોગ કરીનેડી'એલેમ્બર્ટની નિશાની (પરંતુ વિશેષતા દ્વારા નહીં! - કાર્યાત્મક શ્રેણી માટે આવી વિશેષતા અસ્તિત્વમાં નથી):

શ્રેણી ખાતે કન્વર્જ થાય છે

ડાબીઆપણે છોડવાની જરૂર છે માત્ર, તેથી આપણે અસમાનતાની બંને બાજુઓને 3 વડે ગુણાકાર કરીએ છીએ:

- શ્રેણી વૈકલ્પિક છે.
– - શ્રેણીની શરતો મોડ્યુલસમાં ઘટાડો કરે છે. શ્રેણીનો દરેક આગામી સભ્ય નિરપેક્ષ મૂલ્યમાં પાછલા સભ્ય કરતાં ઓછો છે: , જેનો અર્થ છે કે ઘટાડો એકવિધ છે.

નિષ્કર્ષ: શ્રેણી એકરૂપ થાય છે.

ચાલો તેને કન્વર્જન્સની પ્રકૃતિ માટે તપાસીએ:

ચાલો આ શ્રેણીની તુલના એક અલગ શ્રેણી સાથે કરીએ.
અમે મર્યાદિત સરખામણી માપદંડનો ઉપયોગ કરીએ છીએ:

એક મર્યાદિત સંખ્યા પ્રાપ્ત થાય છે જે શૂન્યથી અલગ હોય છે, જેનો અર્થ છે કે શ્રેણી શ્રેણીમાંથી અલગ પડે છે.

આમ, શ્રેણી શરતી રીતે કન્વર્જ થાય છે.

2) ક્યારે - અલગ પડે છે (જે સાબિત થયું છે તે મુજબ).

જવાબ:અધ્યયન હેઠળની પાવર શ્રેણીના કન્વર્જન્સનો વિસ્તાર: . જ્યારે શ્રેણી શરતી રીતે કન્વર્જ થાય છે.

ધ્યાનમાં લેવાયેલ ઉદાહરણમાં, પાવર શ્રેણીના સંપાતનો પ્રદેશ અર્ધ-અંતરાલ છે, અને અંતરાલના તમામ બિંદુઓ પર પાવર શ્રેણી સંપૂર્ણપણે એકરૂપ થાય છે, અને બિંદુએ, જેમ તે બહાર આવ્યું છે - શરતી.

ઉદાહરણ 3

પાવર સિરીઝના કન્વર્જન્સનું અંતરાલ શોધો અને મળેલા અંતરાલના અંતે તેના કન્વર્જન્સની તપાસ કરો

આ તમારા માટે એક ઉદાહરણ છે જે તમે જાતે જ હલ કરી શકો છો.

ચાલો કેટલાક ઉદાહરણો જોઈએ જે દુર્લભ છે, પરંતુ થાય છે.

ઉદાહરણ 4

શ્રેણીના કન્વર્જન્સનું ક્ષેત્રફળ શોધો:

ઉકેલ:ડી'એલેમ્બર્ટની કસોટીનો ઉપયોગ કરીને આપણે આ શ્રેણીના કન્વર્જન્સનું અંતરાલ શોધીએ છીએ:

(1) અમે શ્રેણીના આગલા સભ્યનો પાછલા સભ્યનો ગુણોત્તર કંપોઝ કરીએ છીએ.

(2) આપણે ચાર માળના અપૂર્ણાંકમાંથી છૂટકારો મેળવીએ છીએ.

(3) શક્તિઓ સાથેની કામગીરીના નિયમ અનુસાર, અમે ક્યુબ્સને એક પાવર હેઠળ લાવીએ છીએ. અંશમાં આપણે ચતુરાઈથી ડિગ્રીને વિસ્તૃત કરીએ છીએ, એટલે કે. અમે તેને એવી રીતે ગોઠવીએ છીએ કે આગળના પગલામાં આપણે અપૂર્ણાંકને ઘટાડી શકીએ. અમે ફેક્ટોરિયલ્સનું વિગતવાર વર્ણન કરીએ છીએ.

(4) ક્યુબ હેઠળ, આપણે અંશને છેદ શબ્દ દ્વારા પદ દ્વારા વિભાજીત કરીએ છીએ, જે દર્શાવે છે. અપૂર્ણાંકમાં આપણે બધું ઘટાડીએ છીએ જે ઘટાડી શકાય છે. અમે પરિબળને મર્યાદા ચિહ્નની બહાર લઈએ છીએ; તે બહાર લઈ શકાય છે, કારણ કે તેમાં "ડાયનેમિક" ચલ "en" પર આધાર રાખતું નથી. મહેરબાની કરીને નોંધ કરો કે મોડ્યુલસ ચિહ્ન દોરવામાં આવ્યું નથી - કારણ કે તે કોઈપણ "x" માટે બિન-નકારાત્મક મૂલ્યો લે છે.

મર્યાદામાં, શૂન્ય પ્રાપ્ત થાય છે, જેનો અર્થ છે કે આપણે અંતિમ જવાબ આપી શકીએ છીએ:

જવાબ:શ્રેણી ખાતે કન્વર્જ થાય છે

પરંતુ શરૂઆતમાં એવું લાગતું હતું કે "ભયંકર ભરણ" સાથેની આ પંક્તિ હલ કરવી મુશ્કેલ હશે. મર્યાદામાં શૂન્ય અથવા અનંત લગભગ એક ભેટ છે, કારણ કે ઉકેલ નોંધપાત્ર રીતે ઘટાડો થયો છે!

ઉદાહરણ 5

શ્રેણીના કન્વર્જન્સનું ક્ષેત્રફળ શોધો

આ તમારા માટે એક ઉદાહરણ છે જે તમે જાતે જ હલ કરી શકો છો. સાવચેત રહો;-) સંપૂર્ણ ઉકેલ પાઠના અંતે છે.

ચાલો કેટલાક વધુ ઉદાહરણો જોઈએ જેમાં તકનીકી તકનીકોના ઉપયોગની દ્રષ્ટિએ નવીનતાનું તત્વ છે.

ઉદાહરણ 6

શ્રેણીના કન્વર્જન્સ અંતરાલને શોધો અને મળેલા અંતરાલના અંતે તેના કન્વર્જન્સની તપાસ કરો

ઉકેલ:પાવર શ્રેણીના સામાન્ય શબ્દમાં એક પરિબળનો સમાવેશ થાય છે જે ચિહ્નના ફેરબદલને સુનિશ્ચિત કરે છે. સોલ્યુશન એલ્ગોરિધમ સંપૂર્ણપણે સચવાયેલું છે, પરંતુ મર્યાદા દોરતી વખતે, અમે આ પરિબળને અવગણીએ છીએ (લખતા નથી), કારણ કે મોડ્યુલ તમામ "બાદબાકી" નો નાશ કરે છે.

અમે ડી'એલેમ્બર્ટની કસોટીનો ઉપયોગ કરીને શ્રેણીના કન્વર્જન્સનું અંતરાલ શોધીએ છીએ:

ચાલો પ્રમાણભૂત અસમાનતા બનાવીએ:
શ્રેણી ખાતે કન્વર્જ થાય છે
ડાબીઆપણે છોડવાની જરૂર છે માત્ર મોડ્યુલ, તેથી આપણે અસમાનતાની બંને બાજુઓને 5 વડે ગુણાકાર કરીએ છીએ:

હવે આપણે મોડ્યુલને પરિચિત રીતે ખોલીએ છીએ:

ડબલ અસમાનતાની મધ્યમાં, તમારે આ હેતુ માટે ફક્ત "X" છોડવાની જરૂર છે, અમે અસમાનતાના દરેક ભાગમાંથી 2 બાદ કરીએ છીએ:

- અભ્યાસ હેઠળ પાવર શ્રેણીના કન્વર્જન્સનું અંતરાલ.

અમે મળેલા અંતરાલના અંતે શ્રેણીના કન્વર્જન્સની તપાસ કરીએ છીએ:

1) મૂલ્યને અમારી પાવર શ્રેણીમાં બદલો :

અત્યંત સાવચેત રહો, ગુણક કોઈપણ કુદરતી "en" માટે સાઇન વૈકલ્પિક પ્રદાન કરતું નથી. અમે પરિણામી માઈનસને શ્રેણીની બહાર લઈએ છીએ અને તેના વિશે ભૂલી જઈએ છીએ, કારણ કે તે (કોઈપણ પરિબળ સ્થિરતાની જેમ) કોઈપણ રીતે સંખ્યા શ્રેણીના કન્વર્જન્સ અથવા ડાયવર્જન્સને અસર કરતું નથી.

મહેરબાની કરીને ફરીથી નોંધ કરોકે પાવર સિરીઝના સામાન્ય શબ્દમાં મૂલ્યને બદલવાની પ્રક્રિયામાં, અમારું પરિબળ ઘટાડવામાં આવ્યું હતું. જો આવું ન થયું હોય, તો તેનો અર્થ એ થશે કે અમે મર્યાદાની ગણતરી ખોટી રીતે કરી છે અથવા મોડ્યુલને ખોટી રીતે વિસ્તૃત કર્યું છે.

તેથી, આપણે કન્વર્જન્સ માટે સંખ્યા શ્રેણીની તપાસ કરવાની જરૂર છે. અહીં સૌથી સહેલો રસ્તો એ છે કે મર્યાદિત સરખામણી માપદંડનો ઉપયોગ કરવો અને આ શ્રેણીને વિવિધ હાર્મોનિક શ્રેણી સાથે સરખાવી. પરંતુ, સાચું કહું તો, હું સરખામણીના મર્યાદિત સંકેતથી ખૂબ જ કંટાળી ગયો છું, તેથી હું ઉકેલમાં કેટલીક વિવિધતા ઉમેરીશ.

તેથી, શ્રેણી અહીં કન્વર્જ થાય છે

અમે અસમાનતાની બંને બાજુઓને 9 વડે ગુણાકાર કરીએ છીએ:

અમે બંને ભાગોમાંથી રુટ કાઢીએ છીએ, જ્યારે જૂની શાળાની મજાક યાદ રાખીએ છીએ:


મોડ્યુલનું વિસ્તરણ:

અને બધા ભાગોમાં એક ઉમેરો:

- અભ્યાસ હેઠળ પાવર શ્રેણીના કન્વર્જન્સનું અંતરાલ.

ચાલો મળેલ અંતરાલના અંતે પાવર શ્રેણીના કન્વર્જન્સની તપાસ કરીએ:

1) જો , તો નીચેની સંખ્યા શ્રેણી પ્રાપ્ત થાય છે:

ગુણક ટ્રેસ વિના અદૃશ્ય થઈ ગયો, કારણ કે કોઈપણ કુદરતી મૂલ્ય માટે "en" .