ત્રિકોણમિતિ કાર્યોના મૂલ્યોનું કોષ્ટક
નોંધ. ત્રિકોણમિતિ કાર્ય મૂલ્યોનું આ કોષ્ટક વર્ગમૂળ દર્શાવવા માટે √ ચિહ્નનો ઉપયોગ કરે છે. અપૂર્ણાંક દર્શાવવા માટે, "/" ચિહ્નનો ઉપયોગ કરો.
પણ જુઓઉપયોગી સામગ્રી:
માટે ત્રિકોણમિતિ કાર્યનું મૂલ્ય નક્કી કરવું, તેને ત્રિકોણમિતિ કાર્ય દર્શાવતી રેખાના આંતરછેદ પર શોધો. ઉદાહરણ તરીકે, સાઈન 30 ડિગ્રી - અમે હેડિંગ sin (sine) સાથે કૉલમ શોધીએ છીએ અને "30 ડિગ્રી" પંક્તિ સાથે આ કોષ્ટક કૉલમનું આંતરછેદ શોધીએ છીએ, તેમના આંતરછેદ પર આપણે પરિણામ વાંચીએ છીએ - અડધા. એ જ રીતે આપણે શોધીએ છીએ કોસાઇન 60ડિગ્રી સાઈન 60ડિગ્રી (ફરી એક વાર, પાપ કૉલમ અને 60 ડિગ્રી રેખાના આંતરછેદ પર આપણને મૂલ્ય sin 60 = √3/2 મળે છે), વગેરે. અન્ય “લોકપ્રિય” ખૂણાઓના સાઈન, કોસાઈન્સ અને સ્પર્શકોના મૂલ્યો એ જ રીતે જોવા મળે છે.
સાઈન પાઈ, કોસાઈન પાઈ, ટેન્જેન્ટ પાઈ અને રેડિયનમાં અન્ય ખૂણો
કોસાઇન્સ, સાઇન અને ટેન્જેન્ટનું નીચેનું કોષ્ટક ત્રિકોણમિતિ વિધેયોનું મૂલ્ય શોધવા માટે પણ યોગ્ય છે જેની દલીલ છે રેડિયનમાં આપેલ છે. આ કરવા માટે, કોણ મૂલ્યોની બીજી કૉલમનો ઉપયોગ કરો. આનો આભાર, તમે લોકપ્રિય ખૂણાના મૂલ્યને ડિગ્રીથી રેડિયનમાં રૂપાંતરિત કરી શકો છો. ઉદાહરણ તરીકે, ચાલો પ્રથમ લીટીમાં 60 ડિગ્રીનો કોણ શોધીએ અને તેની નીચેની રેડિયનમાં તેની કિંમત વાંચીએ. 60 ડિગ્રી π/3 રેડિયનની બરાબર છે.
નંબર pi અસ્પષ્ટપણે કોણના ડિગ્રી માપ પર પરિઘની અવલંબનને વ્યક્ત કરે છે. આમ, પાઇ રેડિયન 180 ડિગ્રી બરાબર છે.
પાઇ (રેડિયન) ની દ્રષ્ટિએ વ્યક્ત કરાયેલ કોઈપણ સંખ્યાને પાઇ (π) ને 180 સાથે બદલીને સરળતાથી ડિગ્રીમાં રૂપાંતરિત કરી શકાય છે..
ઉદાહરણો:
1. સાઈન પી.
sin π = sin 180 = 0
આમ, pi ની સાઈન 180 ડિગ્રીની સાઈન જેટલી જ છે અને તે શૂન્યની બરાબર છે.
2. કોસાઇન પી.
cos π = cos 180 = -1
આમ, pi નો કોસાઇન 180 ડિગ્રીના કોસાઇન જેટલો જ છે અને તે માઇનસ વન બરાબર છે.
3. સ્પર્શક પી
tg π = tg 180 = 0
આમ, સ્પર્શક pi એ સ્પર્શક 180 ડિગ્રી સમાન છે અને તે શૂન્યની બરાબર છે.
કોણ 0 - 360 ડિગ્રી (સામાન્ય મૂલ્યો) માટે સાઈન, કોસાઈન, સ્પર્શક મૂલ્યોનું કોષ્ટક
|
કોણ α મૂલ્ય (ડિગ્રી) |
કોણ α મૂલ્ય (pi દ્વારા) |
પાપ (સાઇનસ) |
cos (કોસાઇન) |
tg (સ્પર્શક) |
સીટીજી (સહસ્પર્શક) |
સેકન્ડ (સેકન્ટ) |
કોસેક (કોસેકન્ટ) |
| 0 | 0 | 0 | 1 | 0 | - | 1 | - |
| 15 | π/12 | 2 - √3 | 2 + √3 | ||||
| 30 | π/6 | 1/2 | √3/2 | 1/√3 | √3 | 2/√3 | 2 |
| 45 | π/4 | √2/2 | √2/2 | 1 | 1 | √2 | √2 |
| 60 | π/3 | √3/2 | 1/2 | √3 | 1/√3 | 2 | 2/√3 |
| 75 | 5π/12 | 2 + √3 | 2 - √3 | ||||
| 90 | π/2 | 1 | 0 | - | 0 | - | 1 |
| 105 | 7π/12 |
- |
- 2 - √3 | √3 - 2 | |||
| 120 | 2π/3 | √3/2 | -1/2 | -√3 | -√3/3 | ||
| 135 | 3π/4 | √2/2 | -√2/2 | -1 | -1 | -√2 | √2 |
| 150 | 5π/6 | 1/2 | -√3/2 | -√3/3 | -√3 | ||
| 180 | π | 0 | -1 | 0 | - | -1 | - |
| 210 | 7π/6 | -1/2 | -√3/2 | √3/3 | √3 | ||
| 240 | 4π/3 | -√3/2 | -1/2 | √3 | √3/3 | ||
| 270 | 3π/2 | -1 | 0 | - | 0 | - | -1 |
| 360 | 2π | 0 | 1 | 0 | - | 1 | - |
જો ત્રિકોણમિતિ વિધેયોના મૂલ્યોના કોષ્ટકમાં ફંક્શન વેલ્યુ (ટેન્જેન્ટ (ટીજી) 90 ડિગ્રી, કોટેન્જેન્ટ (સીટીજી) 180 ડિગ્રી) ને બદલે ડેશ સૂચવવામાં આવે છે, તો પછી કોણના ડિગ્રી માપના આપેલ મૂલ્ય માટે ફંક્શન ચોક્કસ મૂલ્ય નથી. જો ત્યાં કોઈ ડૅશ નથી, તો કોષ ખાલી છે, જેનો અર્થ છે કે અમે હજી સુધી જરૂરી મૂલ્ય દાખલ કર્યું નથી. અમને રસ છે કે વપરાશકર્તાઓ અમારી પાસે કઈ પ્રશ્નો માટે આવે છે અને કોષ્ટકને નવા મૂલ્યો સાથે પૂરક બનાવે છે, એ હકીકત હોવા છતાં કે સૌથી સામાન્ય કોણ મૂલ્યોના કોસાઇન્સ, સાઇન અને ટેન્જેન્ટના મૂલ્યો પરનો વર્તમાન ડેટા મોટાભાગના ઉકેલવા માટે પૂરતો છે. સમસ્યાઓ
સૌથી વધુ લોકપ્રિય ખૂણાઓ માટે ત્રિકોણમિતિ વિધેયો sin, cos, tg ના મૂલ્યોનું કોષ્ટક
0, 15, 30, 45, 60, 90 ... 360 ડિગ્રી
(સંખ્યાત્મક મૂલ્યો "બ્રાડિસ કોષ્ટકો મુજબ")
| કોણ α મૂલ્ય (ડિગ્રી) | રેડિયનમાં કોણ α મૂલ્ય | પાપ (પાપ) | cos (કોસાઇન) | tg (સ્પર્શક) | સીટીજી (કોટેન્જેન્ટ) |
|---|---|---|---|---|---|
| 0 | 0 | ||||
| 15 |
0,2588 |
0,9659
|
0,2679 |
||
| 30 |
0,5000 |
0,5774 |
|||
| 45 |
0,7071 |
||||
|
0,7660 |
|||||
| 60 |
0,8660 |
0,5000
|
1,7321 |
||
|
7π/18 |
ત્રિકોણમિતિ કાર્યોના મૂલ્યોનું કોષ્ટક
ત્રિકોણમિતિ વિધેયોના મૂલ્યોનું કોષ્ટક 0, 30, 45, 60, 90, 180, 270 અને 360 ડિગ્રીના ખૂણાઓ અને વ્રાડિયનમાં અનુરૂપ ખૂણાના મૂલ્યો માટે સંકલિત કરવામાં આવે છે. ત્રિકોણમિતિ વિધેયોમાંથી, કોષ્ટક સાઈન, કોસાઈન, ટેન્જેન્ટ, કોટેન્જેન્ટ, સેકન્ટ અને કોસેકન્ટ દર્શાવે છે. શાળાના ઉદાહરણો ઉકેલવાની સગવડ માટે, કોષ્ટકમાં ત્રિકોણમિતિ કાર્યોના મૂલ્યો અપૂર્ણાંકના રૂપમાં લખવામાં આવે છે જ્યારે સંખ્યાઓના વર્ગમૂળને કાઢવા માટેના ચિહ્નોને સાચવવામાં આવે છે, જે ઘણી વાર જટિલ ગાણિતિક સમીકરણોને ઘટાડવામાં મદદ કરે છે. સ્પર્શક અને કોટિંજન્ટ માટે, કેટલાક ખૂણાઓની કિંમતો નક્કી કરી શકાતી નથી. આવા ખૂણાઓના સ્પર્શક અને કોટિંજન્ટના મૂલ્યો માટે, ત્રિકોણમિતિ વિધેયોના મૂલ્યોના કોષ્ટકમાં આડંબર છે. તે સામાન્ય રીતે સ્વીકારવામાં આવે છે કે આવા ખૂણાઓની સ્પર્શક અને સહસ્પર્શક અનંત સમાન છે. એક અલગ પૃષ્ઠ પર ત્રિકોણમિતિ કાર્યોને ઘટાડવા માટેના સૂત્રો છે.
ત્રિકોણમિતિ કાર્ય સાઈન માટેના મૂલ્યોનું કોષ્ટક નીચેના ખૂણાઓ માટેના મૂલ્યો બતાવે છે: sin 0, sin 30, sin 45, sin 60, sin 90, sin 180, sin 270, sin 360 ડિગ્રી માપમાં, જે અનુરૂપ છે માટે sin 0 pi, sin pi/6 , sin pi/4, sin pi/3, sin pi/2, sin pi, sin 3 pi/2, sin 2 pi ખૂણાના રેડિયન માપમાં. સાઇન્સનું શાળા ટેબલ.
ત્રિકોણમિતિ કોસાઇન ફંક્શન માટે, કોષ્ટક નીચેના ખૂણાઓ માટેના મૂલ્યો બતાવે છે: cos 0, cos 30, cos 45, cos 60, cos 90, cos 180, cos 270, cos 360 ડિગ્રીમાં, જે cos 0 pi ને અનુરૂપ છે , cos pi બાય 6, cos pi બાય 4, cos pi બાય 3, cos pi બાય 2, cos pi, cos 3 pi by 2, cos 2 pi બાય 2, cos 2 pi ખૂણોના રેડિયન માપમાં. કોસાઇન્સનું શાળા ટેબલ.
ત્રિકોણમિતિ કાર્ય સ્પર્શક માટેનું ત્રિકોણમિતિ કોષ્ટક નીચેના ખૂણાઓ માટે મૂલ્યો આપે છે: tg 0, tg 30, tg 45, tg 60, tg 180, tg 360 ડિગ્રી માપમાં, જે tg 0 pi, tg pi/6, tg pi/4, tg pi/3, tg pi, tg 2 pi ખૂણાઓના રેડિયન માપમાં. ત્રિકોણમિતિ સ્પર્શક કાર્યોના નીચેના મૂલ્યો tan 90, tan 270, tan pi/2, tan 3 pi/2 વ્યાખ્યાયિત નથી અને તેને અનંતની સમાન ગણવામાં આવે છે.
ત્રિકોણમિતિ કોષ્ટકમાં ત્રિકોણમિતિ ફંક્શન કોટેન્જેન્ટ માટે નીચેના ખૂણાઓની કિંમતો આપવામાં આવી છે: ctg 30, ctg 45, ctg 60, ctg 90, ctg 270 ડિગ્રી માપમાં, જે ctg pi/6, ctg pi/4 ને અનુરૂપ છે , ctg pi/3, tg pi/ 2, tan 3 pi/2 ખૂણાઓના રેડિયન માપમાં. ત્રિકોણમિતિ કોટેન્જેન્ટ ફંક્શનના નીચેના મૂલ્યો ctg 0, ctg 180, ctg 360, ctg 0 pi, ctg pi, ctg 2 pi તરીકે વ્યાખ્યાયિત નથી અને તેને અનંતની સમાન ગણવામાં આવે છે.
ત્રિકોણમિતિ વિધેયો સેકન્ટ અને કોસેકન્ટના મૂલ્યો સાઈન, કોસાઈન, ટેન્જેન્ટ, કોટેન્જેન્ટ જેવા ડિગ્રી અને રેડિયનમાં સમાન ખૂણાઓ માટે આપવામાં આવે છે.

બિન-પ્રમાણભૂત ખૂણાઓના ત્રિકોણમિતિ કાર્યોના મૂલ્યોનું કોષ્ટક 15, 18, 22.5, 36, 54, 67.5 72 ડિગ્રી અને રેડિયન pi/12 માં કોણ માટે સાઈન, કોસાઈન, સ્પર્શક અને કોટેન્જેન્ટના મૂલ્યો દર્શાવે છે. , pi/10, pi/8, pi/5, 3pi/8, 2pi/5 રેડિયન. શાળાના ઉદાહરણોમાં અપૂર્ણાંક ઘટાડવાનું સરળ બનાવવા માટે ત્રિકોણમિતિ કાર્યોના મૂલ્યો અપૂર્ણાંક અને વર્ગમૂળની દ્રષ્ટિએ વ્યક્ત કરવામાં આવે છે.

ત્રણ વધુ ત્રિકોણમિતિ રાક્ષસો. પ્રથમ 1.5 દોઢ ડિગ્રીની સ્પર્શક છે અથવા 120 વડે પાઈ ભાગ્યા છે. બીજું 240, pi/240 વડે ભાગ્યા pi નું કોસાઈન છે. સૌથી લાંબો એ 17, pi/17 વડે વિભાજિત pi ની કોસાઇન છે.

સાઈન અને કોસાઈન ફંક્શનના મૂલ્યોનું ત્રિકોણમિતિ વર્તુળ દૃષ્ટિની રીતે કોણની તીવ્રતાના આધારે સાઈન અને કોસાઈનના ચિહ્નોનું પ્રતિનિધિત્વ કરે છે. ખાસ કરીને બ્લોન્ડ્સ માટે, મૂંઝવણ ઘટાડવા માટે કોસાઇન મૂલ્યો લીલા આડંબર સાથે રેખાંકિત છે. જ્યારે રેડિયનને pi ની દ્રષ્ટિએ વ્યક્ત કરવામાં આવે છે ત્યારે રેડિયનમાં ડિગ્રીનું રૂપાંતર પણ ખૂબ જ સ્પષ્ટ રીતે રજૂ થાય છે.

આ ત્રિકોણમિતિ કોષ્ટક એક-ડિગ્રી અંતરાલ પર 0 શૂન્યથી 90 નેવું અંશ સુધીના ખૂણાઓ માટે સાઈન, કોસાઈન, ટેન્જેન્ટ અને કોટેન્જેન્ટના મૂલ્યો રજૂ કરે છે. પ્રથમ પિસ્તાળીસ ડિગ્રી માટે, ત્રિકોણમિતિ કાર્યોના નામ કોષ્ટકની ટોચ પર જોવા જોઈએ. પ્રથમ સ્તંભમાં ડિગ્રી હોય છે, પછીની ચાર કૉલમમાં સાઈન, કોસાઈન્સ, ટેન્જેન્ટ અને કોટેન્જેન્ટના મૂલ્યો લખવામાં આવે છે.
પિસ્તાળીસ ડિગ્રીથી નેવું ડિગ્રી સુધીના ખૂણાઓ માટે, ત્રિકોણમિતિ કાર્યોના નામ કોષ્ટકની નીચે લખેલા છે. છેલ્લા સ્તંભમાં ડિગ્રી હોય છે; અગાઉના ચાર કૉલમમાં કોસાઇન્સ, સાઇન, કોટેન્જન્ટ અને ટેન્જેન્ટના મૂલ્યો લખેલા છે. તમારે સાવચેત રહેવું જોઈએ કારણ કે ત્રિકોણમિતિ કોષ્ટકના તળિયે ત્રિકોણમિતિ કાર્યોના નામ કોષ્ટકની ટોચ પરના નામોથી અલગ છે. સાઇન્સ અને કોસાઇન્સ એકબીજા સાથે બદલાય છે, જેમ કે ટેન્જેન્ટ અને કોટેન્જેન્ટ. આ ત્રિકોણમિતિ કાર્યોના મૂલ્યોની સમપ્રમાણતાને કારણે છે.

ત્રિકોણમિતિ કાર્યોના ચિહ્નો ઉપરની આકૃતિમાં દર્શાવવામાં આવ્યા છે. સાઈન 0 થી 180 ડિગ્રી અથવા 0 થી pi સુધીના સકારાત્મક મૂલ્યો ધરાવે છે. સાઈન 180 થી 360 ડિગ્રી અથવા pi થી 2 pi સુધીના નકારાત્મક મૂલ્યો ધરાવે છે. કોસાઇન મૂલ્યો 0 થી 90 અને 270 થી 360 ડિગ્રી, અથવા 0 થી 1/2 pi અને 3/2 થી 2 pi સુધી હકારાત્મક છે. સ્પર્શક અને કોટેન્જેન્ટ 0 થી 90 ડિગ્રી અને 180 થી 270 ડિગ્રી સુધીના હકારાત્મક મૂલ્યો ધરાવે છે, જે 0 થી 1/2 pi અને pi થી 3/2 pi ના મૂલ્યોને અનુરૂપ છે. સ્પર્શક અને કોટેન્જેન્ટના નકારાત્મક મૂલ્યો 90 થી 180 ડિગ્રી અને 270 થી 360 ડિગ્રી સુધી અથવા 1/2 pi થી pi અને 3/2 pi થી 2 pi છે. 360 ડિગ્રી અથવા 2 pi કરતા વધારે ખૂણાઓ માટે ત્રિકોણમિતિ વિધેયોના ચિહ્નો નક્કી કરતી વખતે, તમારે આ વિધેયોના સામયિક ગુણધર્મોનો ઉપયોગ કરવો જોઈએ.
ત્રિકોણમિતિ વિધેયો સાઈન, ટેન્જેન્ટ અને કોટેન્જેન્ટ વિષમ વિધેયો છે. ઋણ ખૂણાઓ માટેના આ કાર્યોના મૂલ્યો નકારાત્મક હશે. કોસાઇન એક સમાન ત્રિકોણમિતિ કાર્ય છે - નકારાત્મક કોણ માટે કોસાઇન મૂલ્ય હકારાત્મક હશે. ત્રિકોણમિતિ કાર્યોનો ગુણાકાર અને ભાગાકાર કરતી વખતે સાઇન નિયમોનું પાલન કરવું આવશ્યક છે.
ત્રિકોણમિતિ સાઈન ફંક્શન માટેના મૂલ્યોનું કોષ્ટક નીચેના ખૂણાઓ માટેના મૂલ્યો દર્શાવે છે
દસ્તાવેજએક અલગ પેજ પર રિડક્શન ફોર્મ્યુલા છે ત્રિકોણમિતિકાર્યો. IN ટેબલમૂલ્યોમાટેત્રિકોણમિતિકાર્યોસાઇનસઆપેલમૂલ્યોમાટેનીચેનાખૂણા: પાપ 0, પાપ 30, પાપ 45 ...
સૂચિત ગાણિતિક ઉપકરણ એ n-પરિમાણીય હાઇપરકોમ્પ્લેક્સ સંખ્યાઓ માટે n ની સ્વતંત્રતા n ની કોઈપણ સંખ્યા સાથે જટિલ કેલ્ક્યુલસનું સંપૂર્ણ એનાલોગ છે અને તે બિનરેખીયના ગાણિતિક મોડેલિંગ માટે બનાવાયેલ છે.
દસ્તાવેજ... કાર્યોબરાબર કાર્યોછબીઓ આ પ્રમેયમાંથી જોઈએ, શું માટે U, V કોઓર્ડિનેટ્સ શોધવા, તે ગણતરી કરવા માટે પૂરતું છે કાર્ય... ભૂમિતિ; પોલિનાર કાર્યો(દ્વિ-પરિમાણીયના બહુપરિમાણીય એનાલોગ ત્રિકોણમિતિકાર્યો), તેમની મિલકતો, કોષ્ટકોઅને એપ્લિકેશન; ...
- પૂર્વે પાંચમી સદીમાં, એલિયાના પ્રાચીન ગ્રીક ફિલસૂફ ઝેનોએ તેમના પ્રખ્યાત એપોરિયાસની રચના કરી, જેમાંથી સૌથી પ્રસિદ્ધ એપોરિયા "એચિલીસ અને કાચબો" છે. તે આના જેવું લાગે છે તે અહીં છે:
ચાલો કહીએ કે એચિલીસ કાચબા કરતા દસ ગણી ઝડપથી દોડે છે અને તેની પાછળ એક હજાર પગલાં છે. એચિલીસને આ અંતર ચલાવવા માટે જે સમય લાગશે તે દરમિયાન કાચબો તે જ દિશામાં સો ડગલાં ચાલશે. જ્યારે એચિલીસ સો ડગલાં ચાલે છે, ત્યારે કાચબો બીજા દસ ડગલાં ચાલે છે, વગેરે. પ્રક્રિયા અનંત સુધી ચાલુ રહેશે, એચિલીસ ક્યારેય કાચબાને પકડી શકશે નહીં.
આ તર્ક અનુગામી તમામ પેઢીઓ માટે તાર્કિક આંચકો બની ગયો. એરિસ્ટોટલ, ડાયોજીનીસ, કાન્ત, હેગેલ, હિલ્બર્ટ... આ બધાએ એક યા બીજી રીતે ઝેનોના અપોરિયાને માની લીધું. આંચકો એટલો જોરદાર હતો કે " ... ચર્ચાઓ આજ સુધી ચાલુ છે; વૈજ્ઞાનિક સમુદાય હજુ સુધી વિરોધાભાસના સાર પર એક સામાન્ય અભિપ્રાય પર આવવા સક્ષમ નથી ... આ મુદ્દાના અભ્યાસમાં ગાણિતિક વિશ્લેષણ, સેટ થિયરી, નવા ભૌતિક અને દાર્શનિક અભિગમો સામેલ હતા. ; તેમાંથી કોઈ સમસ્યાનો સામાન્ય રીતે સ્વીકૃત ઉકેલ બન્યો નથી..."[વિકિપીડિયા, "ઝેનોઝ એપોરિયા." દરેક વ્યક્તિ સમજે છે કે તેઓને મૂર્ખ બનાવવામાં આવી રહ્યા છે, પરંતુ કોઈ સમજી શકતું નથી કે છેતરપિંડી શું છે.
ગાણિતિક દૃષ્ટિકોણથી, ઝેનોએ તેના એપોરિયામાં સ્પષ્ટપણે જથ્થામાંથી સંક્રમણ દર્શાવ્યું. આ સંક્રમણ સ્થાયીને બદલે એપ્લિકેશન સૂચવે છે. જ્યાં સુધી હું સમજું છું, માપનના ચલ એકમોનો ઉપયોગ કરવા માટેનું ગાણિતિક ઉપકરણ કાં તો હજી વિકસિત થયું નથી, અથવા તે ઝેનોના એપોરિયા પર લાગુ કરવામાં આવ્યું નથી. આપણા સામાન્ય તર્કને લાગુ પાડવાથી આપણે જાળમાં ફસાઈ જઈએ છીએ. આપણે, વિચારની જડતાને લીધે, પારસ્પરિક મૂલ્ય પર સમયના સતત એકમો લાગુ કરીએ છીએ. ભૌતિક દૃષ્ટિકોણથી, આ એચિલીસ કાચબાને પકડે ત્યારે તે ક્ષણે સંપૂર્ણપણે બંધ ન થાય ત્યાં સુધી સમય ધીમો પડી જાય તેવું લાગે છે. જો સમય અટકી જાય, તો એચિલીસ કાચબાથી આગળ નીકળી શકશે નહીં.
જો આપણે આપણા સામાન્ય તર્કને ફેરવીએ, તો બધું જ જગ્યાએ પડે છે. એચિલીસ સતત ઝડપે દોડે છે. તેના પાથનો દરેક અનુગામી સેગમેન્ટ પાછલા એક કરતા દસ ગણો નાનો છે. તદનુસાર, તેના પર કાબુ મેળવવા માટે ખર્ચવામાં આવેલો સમય અગાઉના એક કરતા દસ ગણો ઓછો છે. જો આપણે આ પરિસ્થિતિમાં "અનંત" ની વિભાવના લાગુ કરીએ, તો તે કહેવું યોગ્ય રહેશે કે "એકિલિસ કાચબાને અનંત ઝડપથી પકડી લેશે."
આ લોજિકલ ટ્રેપથી કેવી રીતે બચવું? સમયના સતત એકમોમાં રહો અને પારસ્પરિક એકમો પર સ્વિચ કરશો નહીં. ઝેનોની ભાષામાં તે આના જેવું દેખાય છે:
એચિલીસને એક હજાર પગથિયાં ચલાવવામાં જેટલો સમય લાગે છે, કાચબો એ જ દિશામાં સો ડગલાં ચાલશે. આગલા સમયના અંતરાલમાં પહેલાના સમાન અંતરાલ દરમિયાન, એચિલીસ બીજા હજાર પગથિયાં દોડશે, અને કાચબો સો પગલાંઓ ક્રોલ કરશે. હવે એચિલીસ કાચબા કરતાં આઠસો ડગલાં આગળ છે.
આ અભિગમ કોઈપણ તાર્કિક વિરોધાભાસ વિના વાસ્તવિકતાનું પર્યાપ્ત રીતે વર્ણન કરે છે. પરંતુ આ સમસ્યાનો સંપૂર્ણ ઉકેલ નથી. પ્રકાશની ગતિની અનિવાર્યતા વિશે આઈન્સ્ટાઈનનું નિવેદન ઝેનોના એપોરિયા “એચિલીસ એન્ડ ધ ટોર્ટોઈઝ” જેવું જ છે. આપણે હજુ આ સમસ્યાનો અભ્યાસ, પુનર્વિચાર અને ઉકેલ લાવવાનો છે. અને ઉકેલ અનંત મોટી સંખ્યામાં નહીં, પરંતુ માપના એકમોમાં શોધવો જોઈએ.
ઝેનોનો બીજો રસપ્રદ એપોરિયા ઉડતા તીર વિશે કહે છે:
ઉડતું તીર ગતિહીન છે, કારણ કે સમયની દરેક ક્ષણે તે આરામમાં છે, અને તે સમયની દરેક ક્ષણે આરામમાં હોવાથી, તે હંમેશા આરામમાં છે.
આ અપોરિયામાં, તાર્કિક વિરોધાભાસને ખૂબ જ સરળ રીતે દૂર કરવામાં આવે છે - તે સ્પષ્ટ કરવા માટે પૂરતું છે કે સમયની દરેક ક્ષણે ઉડતું તીર અવકાશમાં વિવિધ બિંદુઓ પર આરામ કરે છે, જે હકીકતમાં, ગતિ છે. અહીં અન્ય એક મુદ્દાની નોંધ લેવી જરૂરી છે. રસ્તા પરની કારના એક ફોટોગ્રાફ પરથી તેની હિલચાલની હકીકત અથવા તેનાથી અંતર નક્કી કરવું અશક્ય છે. કાર આગળ વધી રહી છે કે કેમ તે નિર્ધારિત કરવા માટે, તમારે એક જ બિંદુ પરથી સમયાંતરે અલગ-અલગ બિંદુઓ પર લીધેલા બે ફોટોગ્રાફ્સની જરૂર છે, પરંતુ તમે તેમાંથી અંતર નક્કી કરી શકતા નથી. કારનું અંતર નક્કી કરવા માટે, તમારે એક સમયે અવકાશના જુદા જુદા બિંદુઓથી લેવામાં આવેલા બે ફોટોગ્રાફ્સની જરૂર છે, પરંતુ તેમાંથી તમે હલનચલનની હકીકત નક્કી કરી શકતા નથી (અલબત્ત, તમારે હજુ પણ ગણતરીઓ માટે વધારાના ડેટાની જરૂર છે, ત્રિકોણમિતિ તમને મદદ કરશે. ). હું જેના પર વિશેષ ધ્યાન દોરવા માંગુ છું તે એ છે કે સમયના બે બિંદુઓ અને અવકાશમાંના બે બિંદુઓ જુદી જુદી વસ્તુઓ છે જે મૂંઝવણમાં ન હોવી જોઈએ, કારણ કે તે સંશોધન માટે વિવિધ તકો પ્રદાન કરે છે.
બુધવાર, જુલાઈ 4, 2018
સેટ અને મલ્ટિસેટ વચ્ચેના તફાવતોનું વિકિપીડિયા પર ખૂબ જ સારી રીતે વર્ણન કરવામાં આવ્યું છે. ચાલો જોઈએ.
જેમ તમે જોઈ શકો છો, "સેટમાં બે સરખા તત્વો હોઈ શકતા નથી," પરંતુ જો સમૂહમાં સમાન તત્વો હોય, તો આવા સમૂહને "મલ્ટીસેટ" કહેવામાં આવે છે. વાજબી માણસો આવા વાહિયાત તર્કને ક્યારેય સમજી શકશે નહીં. આ બોલતા પોપટ અને પ્રશિક્ષિત વાંદરાઓનું સ્તર છે, જેમને "સંપૂર્ણપણે" શબ્દની કોઈ બુદ્ધિ નથી. ગણિતશાસ્ત્રીઓ સામાન્ય પ્રશિક્ષકો તરીકે કાર્ય કરે છે, અમને તેમના વાહિયાત વિચારોનો ઉપદેશ આપે છે.
એક સમયે, બ્રિજ બનાવનાર એન્જિનિયરો પુલનું પરીક્ષણ કરતી વખતે પુલની નીચે બોટમાં હતા. જો પુલ તૂટી પડ્યો, તો સામાન્ય એન્જિનિયર તેની બનાવટના કાટમાળ હેઠળ મૃત્યુ પામ્યો. જો બ્રિજ ભારને ટકી શકે, તો પ્રતિભાશાળી એન્જિનિયરે અન્ય પુલ બનાવ્યા.
"મને ધ્યાનમાં રાખો, હું ઘરમાં છું" અથવા તેના બદલે, "ગણિત અમૂર્ત ખ્યાલોનો અભ્યાસ કરે છે" વાક્ય પાછળ ગણિતશાસ્ત્રીઓ કેવી રીતે છુપાવે છે તે મહત્વનું નથી, ત્યાં એક નાળ છે જે તેમને વાસ્તવિકતા સાથે અસ્પષ્ટ રીતે જોડે છે. આ નાળ એટલે પૈસા. ચાલો આપણે ગણિતશાસ્ત્રીઓ માટે ગણિતીય સમૂહ સિદ્ધાંત લાગુ કરીએ.
અમે ગણિતનો ખૂબ જ સારી રીતે અભ્યાસ કર્યો અને હવે અમે કેશ રજિસ્ટર પર બેઠા છીએ, પગાર આપીએ છીએ. તેથી એક ગણિતશાસ્ત્રી તેના પૈસા માટે અમારી પાસે આવે છે. અમે તેને આખી રકમ ગણીએ છીએ અને તેને અમારા ટેબલ પર જુદા જુદા થાંભલાઓમાં મૂકીએ છીએ, જેમાં અમે સમાન સંપ્રદાયના બિલો મૂકીએ છીએ. પછી અમે દરેક ખૂંટોમાંથી એક બિલ લઈએ છીએ અને ગણિતશાસ્ત્રીને તેના "પગારનો ગાણિતિક સમૂહ" આપીએ છીએ. ચાલો આપણે ગણિતશાસ્ત્રીને સમજાવીએ કે તેને બાકીના બિલ ત્યારે જ મળશે જ્યારે તે સાબિત કરે કે સમાન તત્વો વિનાનો સમૂહ સમાન તત્વોવાળા સમૂહની બરાબર નથી. આ તે છે જ્યાં મજા શરૂ થાય છે.
સૌ પ્રથમ, ડેપ્યુટીઓનું તર્ક કામ કરશે: "આ અન્ય લોકો પર લાગુ થઈ શકે છે, પરંતુ મને નહીં!" પછી તેઓ અમને આશ્વાસન આપવાનું શરૂ કરશે કે સમાન સંપ્રદાયના બિલમાં અલગ-અલગ બિલ નંબરો હોય છે, જેનો અર્થ છે કે તેમને સમાન તત્વો ગણી શકાય નહીં. ઠીક છે, ચાલો સિક્કાઓમાં પગારની ગણતરી કરીએ - સિક્કા પર કોઈ સંખ્યાઓ નથી. અહીં ગણિતશાસ્ત્રી ભૌતિકશાસ્ત્રને ઉગ્રતાથી યાદ રાખવાનું શરૂ કરશે: વિવિધ સિક્કાઓમાં ગંદકીનું પ્રમાણ અલગ-અલગ હોય છે, દરેક સિક્કા માટે ક્રિસ્ટલનું માળખું અને અણુઓની ગોઠવણી અનન્ય છે...
અને હવે મારી પાસે સૌથી રસપ્રદ પ્રશ્ન છે: તે રેખા ક્યાં છે જેની બહાર મલ્ટિસેટના ઘટકો સમૂહના ઘટકોમાં ફેરવાય છે અને તેનાથી ઊલટું? આવી લાઇન અસ્તિત્વમાં નથી - બધું શામન દ્વારા નક્કી કરવામાં આવે છે, વિજ્ઞાન અહીં જૂઠું બોલવાની નજીક પણ નથી.
અહીં જુઓ. અમે સમાન ક્ષેત્ર વિસ્તાર સાથે ફૂટબોલ સ્ટેડિયમ પસંદ કરીએ છીએ. ક્ષેત્રોના વિસ્તારો સમાન છે - જેનો અર્થ છે કે આપણી પાસે મલ્ટિસેટ છે. પરંતુ જો આપણે આ જ સ્ટેડિયમોના નામ જોઈએ, તો આપણને ઘણા મળે છે, કારણ કે નામ અલગ-અલગ છે. જેમ તમે જોઈ શકો છો, તત્વોનો સમાન સમૂહ સમૂહ અને મલ્ટિસેટ બંને છે. જે સાચું છે? અને અહીં ગણિતશાસ્ત્રી-શામન-શાર્પિસ્ટ તેની સ્લીવમાંથી ટ્રમ્પનો પાસા ખેંચે છે અને અમને સેટ અથવા મલ્ટિસેટ વિશે કહેવાનું શરૂ કરે છે. કોઈ પણ સંજોગોમાં, તે આપણને ખાતરી આપશે કે તે સાચો છે.
આધુનિક શામન સેટ થિયરી સાથે કેવી રીતે કાર્ય કરે છે તે સમજવા માટે, તેને વાસ્તવિકતા સાથે જોડીને, એક પ્રશ્નનો જવાબ આપવા માટે તે પૂરતું છે: એક સમૂહના તત્વો બીજા સમૂહના તત્વોથી કેવી રીતે અલગ પડે છે? હું તમને બતાવીશ, કોઈપણ "એક સંપૂર્ણ તરીકે કલ્પી શકાય તેવું નથી" અથવા "એક સંપૂર્ણ તરીકે કલ્પનાશીલ નથી."
રવિવાર, માર્ચ 18, 2018
સંખ્યાના અંકોનો સરવાળો એ ખંજરી સાથે શામનનું નૃત્ય છે, જેને ગણિત સાથે કોઈ લેવાદેવા નથી. હા, ગણિતના પાઠોમાં આપણને સંખ્યાના અંકોનો સરવાળો શોધવા અને તેનો ઉપયોગ કરવાનું શીખવવામાં આવે છે, પરંતુ તેથી જ તેઓ શામન છે, તેમના વંશજોને તેમની કુશળતા અને ડહાપણ શીખવવા માટે, અન્યથા શમન ખાલી મરી જશે.
શું તમને પુરાવાની જરૂર છે? વિકિપીડિયા ખોલો અને "સંખ્યાના અંકોનો સરવાળો" પૃષ્ઠ શોધવાનો પ્રયાસ કરો. તેણી અસ્તિત્વમાં નથી. ગણિતમાં એવું કોઈ સૂત્ર નથી કે જેનો ઉપયોગ કોઈપણ સંખ્યાના અંકોનો સરવાળો શોધવા માટે થઈ શકે. છેવટે, સંખ્યાઓ એ ગ્રાફિક પ્રતીકો છે જેની સાથે આપણે સંખ્યાઓ લખીએ છીએ, અને ગણિતની ભાષામાં કાર્ય આના જેવું લાગે છે: "કોઈપણ સંખ્યાને રજૂ કરતા ગ્રાફિક પ્રતીકોનો સરવાળો શોધો." ગણિતશાસ્ત્રીઓ આ સમસ્યાને હલ કરી શકતા નથી, પરંતુ શામન તે સરળતાથી કરી શકે છે.
ચાલો જોઈએ કે આપેલ સંખ્યાના અંકોનો સરવાળો શોધવા માટે આપણે શું અને કેવી રીતે કરીએ છીએ. અને તેથી, ચાલો આપણે 12345 નંબર મેળવીએ. આ સંખ્યાના અંકોનો સરવાળો શોધવા માટે શું કરવાની જરૂર છે? ચાલો ક્રમમાં તમામ પગલાંઓ ધ્યાનમાં લઈએ.
1. કાગળના ટુકડા પર નંબર લખો. અમે શું કર્યું છે? અમે સંખ્યાને ગ્રાફિકલ નંબર સિમ્બોલમાં રૂપાંતરિત કરી છે. આ કોઈ ગાણિતિક ક્રિયા નથી.
2. અમે એક પરિણામી ચિત્રને વ્યક્તિગત નંબરો ધરાવતા અનેક ચિત્રોમાં કાપીએ છીએ. ચિત્ર કાપવું એ ગાણિતિક ક્રિયા નથી.
3. વ્યક્તિગત ગ્રાફિક પ્રતીકોને સંખ્યામાં રૂપાંતરિત કરો. આ કોઈ ગાણિતિક ક્રિયા નથી.
4. પરિણામી સંખ્યાઓ ઉમેરો. હવે આ ગણિત છે.
12345 નંબરના અંકોનો સરવાળો 15 છે. આ શામનના "કટીંગ અને સીવિંગ કોર્સ" છે જેનો ગણિતશાસ્ત્રીઓ ઉપયોગ કરે છે. પરંતુ તે બધુ જ નથી.
ગાણિતિક દૃષ્ટિકોણથી, આપણે કઈ નંબર સિસ્ટમમાં સંખ્યા લખીએ છીએ તેનાથી કોઈ ફરક પડતો નથી. તેથી, વિવિધ નંબર સિસ્ટમ્સમાં સમાન સંખ્યાના અંકોનો સરવાળો અલગ હશે. ગણિતમાં, નંબર સિસ્ટમ નંબરની જમણી બાજુએ સબસ્ક્રિપ્ટ તરીકે સૂચવવામાં આવે છે. મોટી સંખ્યા 12345 સાથે, હું મારા માથાને મૂર્ખ બનાવવા માંગતો નથી, ચાલો લેખમાંથી 26 નંબરને ધ્યાનમાં લઈએ. ચાલો આ સંખ્યાને બાઈનરી, ઓક્ટલ, ડેસિમલ અને હેક્સાડેસિમલ નંબર સિસ્ટમમાં લખીએ. અમે દરેક પગલાને માઇક્રોસ્કોપ હેઠળ જોશું નહીં; અમે તે પહેલાથી જ કર્યું છે. ચાલો પરિણામ જોઈએ.
જેમ તમે જોઈ શકો છો, વિવિધ નંબર સિસ્ટમ્સમાં સમાન સંખ્યાના અંકોનો સરવાળો અલગ હોય છે. આ પરિણામને ગણિત સાથે કોઈ લેવાદેવા નથી. તે સમાન છે જો તમે મીટર અને સેન્ટિમીટરમાં લંબચોરસનો વિસ્તાર નક્કી કરો છો, તો તમને સંપૂર્ણપણે અલગ પરિણામો મળશે.
શૂન્ય તમામ સંખ્યા પ્રણાલીઓમાં સમાન દેખાય છે અને તેમાં અંકોનો કોઈ સરવાળો નથી. આ હકીકતની તરફેણમાં બીજી દલીલ છે. ગણિતશાસ્ત્રીઓ માટે પ્રશ્ન: ગણિતમાં નિયુક્ત નંબર ન હોય તેવી વસ્તુ કેવી રીતે છે? શું, ગણિતશાસ્ત્રીઓ માટે સંખ્યાઓ સિવાય કંઈ જ અસ્તિત્વમાં નથી? હું શામન માટે આની મંજૂરી આપી શકું છું, પરંતુ વૈજ્ઞાનિકો માટે નહીં. વાસ્તવિકતા માત્ર સંખ્યાઓ વિશે નથી.
પ્રાપ્ત પરિણામ એ સાબિતી તરીકે ગણવું જોઈએ કે સંખ્યા પ્રણાલીઓ સંખ્યાઓના માપનના એકમો છે. છેવટે, અમે માપનના વિવિધ એકમો સાથે સંખ્યાઓની તુલના કરી શકતા નથી. જો સમાન જથ્થાના માપનના વિવિધ એકમો સાથેની સમાન ક્રિયાઓ તેમની સરખામણી કર્યા પછી વિવિધ પરિણામો તરફ દોરી જાય છે, તો તેને ગણિત સાથે કોઈ લેવાદેવા નથી.
વાસ્તવિક ગણિત શું છે? આ ત્યારે થાય છે જ્યારે ગાણિતિક ક્રિયાનું પરિણામ સંખ્યાના કદ, વપરાયેલ માપન એકમ અને આ ક્રિયા કોણ કરે છે તેના પર નિર્ભર નથી.
દરવાજા પર સહી કરો ઓહ! શું આ મહિલા શૌચાલય નથી?
- યુવાન સ્ત્રી! સ્વર્ગમાં તેમના આરોહણ દરમિયાન આત્માઓની અનિશ્ચિત પવિત્રતાના અભ્યાસ માટે આ એક પ્રયોગશાળા છે! પ્રભામંડળ ટોચ પર અને તીર ઉપર. બીજું શું શૌચાલય?સ્ત્રી... ઉપરનું પ્રભામંડળ અને નીચેનું તીર પુરુષ છે.
જો ડિઝાઇન આર્ટનું આવું કામ તમારી આંખો સામે દિવસમાં ઘણી વખત ચમકતું હોય,
પછી તે આશ્ચર્યજનક નથી કે તમને અચાનક તમારી કારમાં એક વિચિત્ર ચિહ્ન મળે છે:
અંગત રીતે, હું પોપિંગ વ્યક્તિ (એક ચિત્ર) માં માઈનસ ચાર ડિગ્રી જોવાનો પ્રયાસ કરું છું (ઘણા ચિત્રોની રચના: માઈનસ ચિહ્ન, નંબર ચાર, ડિગ્રી હોદ્દો). અને મને નથી લાગતું કે આ છોકરી મૂર્ખ છે જે ભૌતિકશાસ્ત્ર નથી જાણતી. તેણી પાસે ગ્રાફિક છબીઓ સમજવાની એક મજબૂત સ્ટીરિયોટાઇપ છે. અને ગણિતશાસ્ત્રીઓ આપણને આ બધું શીખવે છે. અહીં એક ઉદાહરણ છે.
1A એ "માઈનસ ચાર ડિગ્રી" અથવા "એક a" નથી. આ હેક્સાડેસિમલ નોટેશનમાં "પોપિંગ મેન" અથવા નંબર "છવીસ" છે. જે લોકો આ નંબર સિસ્ટમમાં સતત કામ કરે છે તેઓ આપમેળે એક નંબર અને એક અક્ષરને એક ગ્રાફિક પ્રતીક તરીકે સમજે છે.
આ લેખ સમાવે છે સાઈન, કોસાઈન્સ, ટેન્જેન્ટ અને કોટેન્જન્ટ્સનાં કોષ્ટકો. પ્રથમ, આપણે ત્રિકોણમિતિ કાર્યોના મૂળભૂત મૂલ્યોનું કોષ્ટક પ્રદાન કરીશું, એટલે કે, 0, 30, 45, 60, 90, ..., 360 ડિગ્રી ( 0, π/6, π/4, π/3, π/2, …, 2πરેડિયન). આ પછી, અમે સાઇન્સ અને કોસાઇન્સનું કોષ્ટક આપીશું, તેમજ વી.એમ. બ્રાડિસ દ્વારા સ્પર્શકો અને કોટિન્જન્ટ્સનું કોષ્ટક આપીશું, અને ત્રિકોણમિતિ વિધેયોના મૂલ્યો શોધતી વખતે આ કોષ્ટકોનો ઉપયોગ કેવી રીતે કરવો તે બતાવીશું.
પૃષ્ઠ નેવિગેશન.
0, 30, 45, 60, 90, ... ડિગ્રીના ખૂણાઓ માટે સાઈન, કોસાઈન્સ, સ્પર્શક અને કોટેન્જેન્ટનું કોષ્ટક
સંદર્ભો.
- બીજગણિત:પાઠ્યપુસ્તક 9મા ધોરણ માટે. સરેરાશ શાળા/યુ. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova; એડ. એસ. એ. ટેલિયાકોવ્સ્કી - એમ.: એજ્યુકેશન, 1990. - 272 પીપી. - ISBN 5-09-002727-7
- બશ્માકોવ એમ. આઇ.બીજગણિત અને વિશ્લેષણની શરૂઆત: પાઠ્યપુસ્તક. 10-11 ગ્રેડ માટે. સરેરાશ શાળા - 3જી આવૃત્તિ. - એમ.: શિક્ષણ, 1993. - 351 પૃષ્ઠ: બીમાર. - ISBN 5-09-004617-4.
- બીજગણિતઅને વિશ્લેષણની શરૂઆત: પ્રોક. 10-11 ગ્રેડ માટે. સામાન્ય શિક્ષણ સંસ્થાઓ / A. N. Kolmogorov, A. M. Abramov, Yu P. Dudnitsyn અને અન્ય; એડ. એ. એન. કોલમોગોરોવ - 14મી આવૃત્તિ - એમ.: એજ્યુકેશન, 2004. - 384 પીપી.
- ગુસેવ વી.એ., મોર્ડકોવિચ એ.જી.ગણિત (તકનીકી શાળાઓમાં પ્રવેશ કરનારાઓ માટે માર્ગદર્શિકા): પ્રોક. ભથ્થું.- એમ.; ઉચ્ચ શાળા, 1984.-351 પૃ., બીમાર.
- બ્રાડીસ વી. એમ.ચાર-અંકના ગણિત કોષ્ટકો: સામાન્ય શિક્ષણ માટે. પાઠ્યપુસ્તક સંસ્થાઓ - 2જી આવૃત્તિ. - એમ.: બસ્ટાર્ડ, 1999.- 96 પૃષ્ઠ: બીમાર. ISBN 5-7107-2667-2
લેખમાં, અમે સંપૂર્ણપણે સમજીશું કે તે શું દેખાય છે ત્રિકોણમિતિ મૂલ્યોનું કોષ્ટક, સાઈન, કોસાઈન, સ્પર્શક અને કોટેન્જેન્ટ. ચાલો 0,30,45,60,90,...,360 ડિગ્રીના ખૂણાથી ત્રિકોણમિતિ વિધેયોના મૂળ અર્થને ધ્યાનમાં લઈએ. અને ચાલો જોઈએ કે ત્રિકોણમિતિ વિધેયોના મૂલ્યોની ગણતરીમાં આ કોષ્ટકોનો ઉપયોગ કેવી રીતે કરવો.
પહેલા ચાલો જોઈએ કોસાઈન, સાઈન, ટેન્જેન્ટ અને કોટેન્જેન્ટનું કોષ્ટક 0, 30, 45, 60, 90,... ડિગ્રીના ખૂણામાંથી. આ જથ્થાઓની વ્યાખ્યા અમને 0 અને 90 ડિગ્રીના ખૂણાઓના કાર્યોનું મૂલ્ય નક્કી કરવાની મંજૂરી આપે છે:sin 0 0 =0, cos 0 0 = 1. tg 00 = 0, 00 માંથી કોટેન્જેન્ટ અવ્યાખ્યાયિત હશે
sin 90 0 = 1, cos 90 0 =0, ctg90 0 = 0, 90 0 માંથી સ્પર્શક અનિશ્ચિત હશેજો તમે કાટકોણ ત્રિકોણ લો કે જેના ખૂણા 30 થી 90 ડિગ્રી છે. અમને મળે છે:
sin 30 0 = 1/2, cos 30 0 = √3/2, tan 30 0 = √3/3, cos 30 0 = √3
sin 45 0 = √2/2, cos 45 0 = √2/2, tan 45 0 = 1, cos 45 0 = 1
sin 60 0 = √3/2, cos 60 0 = 1/2, tg 60 0 =√3, cot 60 0 = √3/3ચાલો ફોર્મમાં તમામ પ્રાપ્ત મૂલ્યોનું પ્રતિનિધિત્વ કરીએ ત્રિકોણમિતિ કોષ્ટક:
સાઈન, કોસાઈન્સ, ટેન્જેન્ટ અને કોટેન્જેન્ટ્સનું કોષ્ટક!
જો આપણે ઘટાડા સૂત્રનો ઉપયોગ કરીએ, તો આપણું ટેબલ વધશે, 360 ડિગ્રી સુધીના ખૂણાઓ માટે મૂલ્યો ઉમેરશે. તે આના જેવું દેખાશે:

ઉપરાંત, સામયિકતાના ગુણધર્મોના આધારે, જો આપણે ખૂણાઓને 0 0 +360 0 *z .... 330 0 +360 0 *z સાથે બદલીએ તો કોષ્ટક વધારી શકાય છે, જેમાં z એ પૂર્ણાંક છે. આ કોષ્ટકમાં એક વર્તુળમાંના બિંદુઓને અનુરૂપ તમામ ખૂણાઓની કિંમતની ગણતરી કરવી શક્ય છે.

સોલ્યુશનમાં કોષ્ટકનો ઉપયોગ કેવી રીતે કરવો તે જોઈએ.
બધું ખૂબ જ સરળ છે. કારણ કે આપણને જે મૂલ્યની જરૂર છે તે કોષોના આંતરછેદ બિંદુ પર આવેલું છે. ઉદાહરણ તરીકે, 60 ડિગ્રીના ખૂણાના કોસ લો, કોષ્ટકમાં તે આના જેવું દેખાશે:
ત્રિકોણમિતિ કાર્યોના મુખ્ય મૂલ્યોના અંતિમ કોષ્ટકમાં, આપણે તે જ રીતે આગળ વધીએ છીએ. પરંતુ આ કોષ્ટકમાં 1020 ડિગ્રીના ખૂણોમાંથી સ્પર્શક કેટલી છે તે શોધવાનું શક્ય છે, તે = -√3 ચાલો 1020 0 = 300 0 +360 0 *2 તપાસીએ. ચાલો કોષ્ટકનો ઉપયોગ કરીને તેને શોધીએ.

બ્રેડિસ ટેબલ. સાઈન, કોસાઈન, ટેન્જેન્ટ અને કોટેન્જેન્ટ માટે.
બ્રાડીસ કોષ્ટકોને કેટલાક ભાગોમાં વિભાજિત કરવામાં આવે છે, જેમાં કોસાઈન અને સાઈન, ટેન્જેન્ટ અને કોટેન્જેન્ટના કોષ્ટકોનો સમાવેશ થાય છે - જે બે ભાગોમાં વિભાજિત થાય છે (90 ડિગ્રી સુધીના ખૂણાઓનો tg અને નાના ખૂણાના ctg).
સાઈન અને કોસાઈન


00 થી શરૂ થતા કોણનો tg 760 સાથે સમાપ્ત થાય છે, 140 થી શરૂ થતા કોણનો ctg 900 સાથે સમાપ્ત થાય છે.
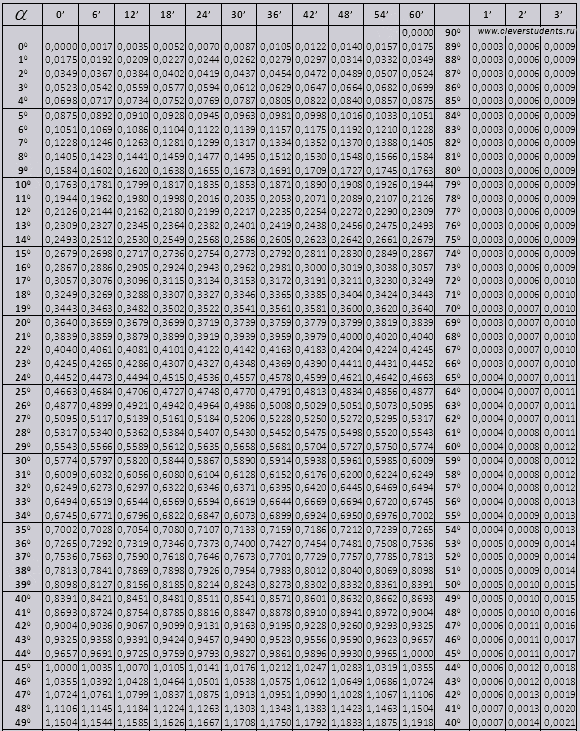

900 સુધી tg અને નાના ખૂણાઓનો ctg.
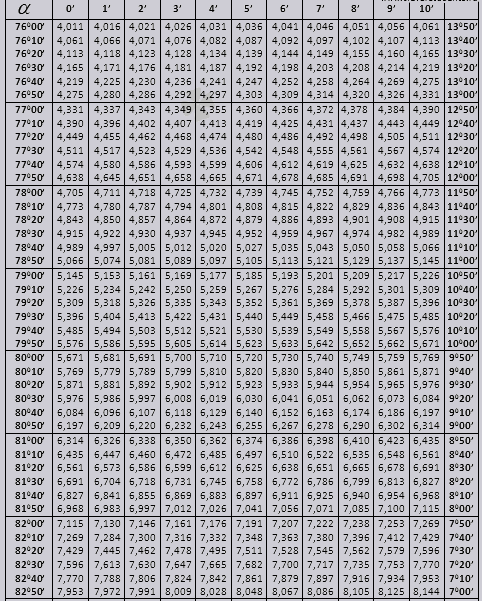

ચાલો જાણીએ કે સમસ્યાઓ ઉકેલવા માટે બ્રાડિસ કોષ્ટકોનો ઉપયોગ કેવી રીતે કરવો.
ચાલો હોદ્દો શોધીએ (ડાબી ધાર પરના સ્તંભમાં હોદ્દો) 42 મિનિટ (હોદ્દો ટોચની લાઇન પર છે). આંતરછેદ દ્વારા આપણે હોદ્દો શોધીએ છીએ, તે = 0.3040.
મિનિટના મૂલ્યો છ મિનિટના અંતરાલ સાથે સૂચવવામાં આવે છે, જો આપણને જરૂરી મૂલ્ય આ અંતરાલમાં બરાબર આવે તો શું કરવું. ચાલો 44 મિનિટ લઈએ, પરંતુ કોષ્ટકમાં ફક્ત 42 છે અમે 42 ને આધાર તરીકે લઈએ છીએ અને જમણી બાજુના વધારાના કૉલમનો ઉપયોગ કરીએ છીએ, 2જી સુધારો લઈએ અને 0.3040 + 0.0006 માં ઉમેરીએ તો અમને 0.3046 મળે છે.
પાપ 47 મિનિટ સાથે, અમે આધાર તરીકે 48 મિનિટ લઈએ છીએ અને તેમાંથી 1 કરેક્શન બાદ કરીએ છીએ, એટલે કે 0.3057 - 0.0003 = 0.3054
cos ની ગણતરી કરતી વખતે, આપણે પાપની જેમ જ કામ કરીએ છીએ, માત્ર આપણે કોષ્ટકની નીચેની પંક્તિને આધાર તરીકે લઈએ છીએ. ઉદાહરણ તરીકે cos 20 0 = 0.9397
90 0 સુધીના tg એંગલની કિંમતો અને નાના કોણની કોટ સાચી છે અને તેમાં કોઈ સુધારા નથી. ઉદાહરણ તરીકે, tg 78 0 37min = 4.967 શોધો
અને ctg 20 0 13min = 25.83
સારું, અમે મૂળભૂત ત્રિકોણમિતિ કોષ્ટકો જોયા છે. અમે આશા રાખીએ છીએ કે આ માહિતી તમારા માટે અત્યંત ઉપયોગી હતી. જો તમને કોષ્ટકો વિશે કોઈ પ્રશ્નો હોય, તો તેમને ટિપ્પણીઓમાં લખવાનું ભૂલશો નહીં!
નોંધ: વોલ બમ્પર્સ એ દિવાલોને સુરક્ષિત કરવા માટેનું બમ્પર બોર્ડ છે. લિંક ફ્રેમલેસ વોલ બમ્પર્સ (http://www.spi-polymer.ru/otboyniki/) ને અનુસરો અને વધુ જાણો.








