Dört boyutlu uzayın ne olduğunu açıklayarak başlayalım.
Bu tek boyutlu bir uzaydır, yani basitçe OX eksenidir. Üzerindeki herhangi bir nokta bir koordinatla karakterize edilir.

Şimdi OY eksenini OX eksenine dik olarak çizelim. Böylece iki boyutlu bir uzay, yani XOY düzlemi elde ederiz. Üzerindeki herhangi bir nokta iki koordinatla karakterize edilir - apsis ve ordinat.

OZ eksenini OX ve OY eksenlerine dik olarak çizelim. Sonuç, herhangi bir noktanın apsis, ordinat ve uygulama alanına sahip olduğu üç boyutlu bir alandır.

Dördüncü eksen olan OQ'nun aynı anda OX, OY ve OZ eksenlerine dik olması mantıklıdır. Ancak böyle bir ekseni doğru bir şekilde inşa edemeyiz ve bu nedenle onu yalnızca hayal etmeye çalışabiliriz. Dört boyutlu uzaydaki her noktanın dört koordinatı vardır: x, y, z ve q.
Şimdi dört boyutlu küpün nasıl ortaya çıktığını görelim.

Resimde tek boyutlu uzayda bir şekil, bir çizgi gösterilmektedir.

Bu çizginin OY ekseni boyunca paralel ötelemesini yaparsanız ve ardından ortaya çıkan iki çizginin karşılık gelen uçlarını birleştirirseniz bir kare elde edersiniz.

Benzer şekilde, karenin OZ ekseni boyunca paralel ötelemesini yaparsanız ve ilgili köşeleri birleştirirseniz bir küp elde edersiniz.

Ve eğer küpün OQ ekseni boyunca paralel ötelemesini yaparsak ve bu iki küpün köşelerini birleştirirsek, o zaman dört boyutlu bir küp elde ederiz. Bu arada, buna denir tesseract.
Bir düzleme küp çizmek için buna ihtiyacınız var proje. Görsel olarak şöyle görünüyor: 
Yüzeyin üzerinde havada asılı kaldığını hayal edelim. tel kafes modeli küp, yani “telden yapılmış” gibi ve üstünde bir ampul var. Ampulü açarsanız, küpün gölgesini bir kalemle çizerseniz ve ardından ampulü kapatırsanız, yüzeyde küpün bir izdüşümü gösterilecektir.
Biraz daha karmaşık bir şeye geçelim. Ampulün olduğu çizime tekrar bakın: gördüğünüz gibi tüm ışınlar bir noktada birleşiyor. Buna denir ufuk noktası ve inşa etmek için kullanılır perspektif projeksiyonu(ve aynı zamanda tüm ışınlar birbirine paralel olduğunda paralel de olur. Sonuç olarak hacim hissi yaratılmaz, ancak daha hafif olur ve ayrıca, ufuk noktası yansıtılan nesneden oldukça uzaktaysa, o zaman bu iki projeksiyon arasındaki fark çok az fark edilir). Belirli bir noktayı belirli bir düzleme bir ufuk noktası kullanarak yansıtmak için, ufuk noktasından ve verilen noktadan geçen düz bir çizgi çizmeniz ve ardından ortaya çıkan düz çizgi ile düzlemin kesişme noktasını bulmanız gerekir. Ve daha karmaşık bir şekli, örneğin bir küpü yansıtmak için, onun köşelerinin her birini yansıtmanız ve ardından karşılık gelen noktaları birleştirmeniz gerekir. Şunu belirtmek gerekir ki uzayı alt uzaya yansıtma algoritması sadece 3D->2D değil, 4D->3D durumuna da genelleştirilebilir.
Dediğim gibi, tıpkı tesseract gibi OQ ekseninin de tam olarak neye benzediğini hayal edemiyoruz. Ancak bunu bir hacme yansıtıp daha sonra bilgisayar ekranına çizersek, bununla ilgili sınırlı bir fikir sahibi olabiliriz!
Şimdi tesseract projeksiyonundan bahsedelim.

Solda küpün düzlem üzerindeki izdüşümü, sağda ise hacim üzerindeki tesseract yer almaktadır. Oldukça benzerler: Bir küpün izdüşümü, biri diğerinin içinde olan ve karşılık gelen köşeleri çizgilerle birbirine bağlanan küçük ve büyük iki kareye benzer. Ve tesseractın izdüşümü, biri diğerinin içinde olan ve karşılık gelen köşeleri birbirine bağlı olan küçük ve büyük iki küp gibi görünüyor. Ama hepimiz küpü görmüşüzdür ve hem küçük karenin hem de büyük karenin ve küçük karenin üstündeki, altındaki, sağındaki ve solundaki dört yamuğun aslında kare olduğunu ve eşit olduklarını güvenle söyleyebiliriz. . Ve tesseract'ta da aynı şey var. Ve büyük bir küp, bir küçük küp ve küçük bir küpün yanlarındaki altı kesik piramit - bunların hepsi küp ve eşittir.
Programım yalnızca bir tesseractın projeksiyonunu bir hacme çizmekle kalmıyor, aynı zamanda onu döndürebiliyor. Bunun nasıl yapıldığına bakalım.
İlk önce sana ne olduğunu anlatacağım düzleme paralel dönüş.
Küpün OZ ekseni etrafında döndüğünü hayal edin. Daha sonra köşelerinin her biri OZ ekseni etrafındaki bir daireyi tanımlar. 
Daire düz bir şekildir. Ve bu dairelerin her birinin düzlemleri birbirine paraleldir ve bu durumda XOY düzlemine paraleldir. Yani sadece OZ ekseni etrafında dönmeden değil, XOY düzlemine paralel dönmeden de bahsedebiliriz. Görüldüğü gibi XOY eksenine paralel dönen noktalarda sadece apsis ve ordinat değişir, uygulama kalır. Ve aslında ancak üç boyutlu uzay söz konusu olduğunda düz bir çizgi etrafında dönmekten bahsedebiliriz. İki boyutlu uzayda her şey bir noktanın etrafında döner, dört boyutlu uzayda her şey bir düzlemin etrafında döner, beş boyutlu uzayda ise bir hacmin etrafında dönmekten söz ederiz. Ve eğer bir nokta etrafında dönmeyi hayal edebiliyorsak, o zaman bir düzlem ve hacim etrafında dönme düşünülemez bir şeydir. Ve eğer düzleme paralel dönüşten bahsedersek, o zaman herhangi bir n boyutlu uzayda bir nokta düzleme paralel olarak dönebilir.
Birçoğunuz muhtemelen rotasyon matrisini duymuşsunuzdur. Noktayı bununla çarptığımızda, düzleme paralel olarak phi açısı kadar döndürülmüş bir nokta elde ederiz. İki boyutlu uzay için şöyle görünür: 
Nasıl çarpılır: phi açısıyla döndürülmüş bir noktanın x'i = orijinal noktanın phi*ix açısının kosinüsü eksi orijinal noktanın phi*ig açısının sinüsü;
phi açısıyla döndürülmüş bir noktanın ig'si = orijinal noktanın phi * ix açısının sinüsü artı orijinal noktanın phi * ig açısının kosinüsü.
Xa`=cosф*Xa - sinф*Ya
Ya`=sinф*Xa + cosф*Ya
burada Xa ve Ya döndürülecek noktanın apsisi ve ordinatıdır, Xa' ve Ya' zaten döndürülmüş noktanın apsisi ve ordinatıdır
Üç boyutlu uzay için bu matris şu şekilde genelleştirilir: 
XOY düzlemine paralel dönüş. Gördüğünüz gibi Z koordinatı değişmiyor sadece X ve Y değişiyor
Xa`=cosф*Xa - sinф*Ya + Za*0
Ya`=sinф*Xa +cosф*Ya + Za*0
Za'=Xa*0 + Ya*0 + Za*1 (esasen Za'=Za)

XOZ düzlemine paralel dönüş. Yeni bir şey yok
Xa`=cosф*Xa + Ya*0 - sinф*Za
Ya`=Xa*0 + Ya*1 + Za*0 (esasen Ya`=Ya)
Za`=sinф*Xa + Ya*0 + cosф*Za

Ve üçüncü matris.
Xa`=Xa*1 + Ya*0 + Za*0 (esasen, Xa`=Xa)
Ya`=Xa*0 + cosф*Ya - sinф*Za
Za`=Xa*0 + sinф*Ya + cosф*Za
Ve dördüncü boyut için şöyle görünürler: 
Sanırım neyle çarpmanız gerektiğini zaten anladınız, bu yüzden tekrar ayrıntıya girmeyeceğim. Ancak bunun, üç boyutlu uzayda bir düzleme paralel dönüş için bir matrisle aynı şeyi yaptığını not ediyorum! Her ikisi de yalnızca koordinatı ve uygulamayı değiştirir ve diğer koordinatlara dokunmaz, bu nedenle dördüncü koordinata dikkat edilmeden üç boyutlu durumda kullanılabilir.
Ancak projeksiyon formülüyle her şey o kadar basit değil. Ne kadar forum okursam okuyayım, projeksiyon yöntemlerinin hiçbiri işime yaramadı. Projeksiyon üç boyutlu görünmeyeceği için paralel olan bana uygun değildi. Bazı projeksiyon formüllerinde, bir noktayı bulmak için bir denklem sistemini çözmeniz gerekir (ve bunları bir bilgisayara çözmeyi nasıl öğreteceğimi bilmiyorum), diğerlerini ise anlamadım... Genel olarak, şunu yapmaya karar verdim: kendi yolumu bul. Bu amaçla 2D->1D projeksiyonunu düşünün.

pov "Bakış açısı" anlamına gelir, ptp "Yansıtma noktası" (yansıtılacak nokta) anlamına gelir ve ptp` OX ekseni üzerinde istenen noktadır.
povptpB ve ptpptp`A açıları karşılık gelen şekilde eşittir (noktalı çizgi OX eksenine paraleldir, düz çizgi povptp bir kesendir).
ptp' noktasının x'i, ptp noktasının x'i eksi ptp'A parçasının uzunluğuna eşittir. Bu parça ptpptp`A üçgeninden bulunabilir: ptp`A = ptpA/ptpptp`A açısının tanjantı. Bu teğeti povptpB üçgeninden bulabiliriz: teğet ptpptp`A = (Ypov-Yptp)(Xpov-Xptp).
Cevap: Xptp`=Xptp-Yptp/ptpptp`A açısının tanjantı.
Formülün biraz değiştiği birçok özel durum olduğundan, bu algoritmayı burada ayrıntılı olarak açıklamadım. İlgilenen varsa programın kaynak koduna bakın, her şey orada yorumlarda anlatılıyor.
Üç boyutlu uzayda bir noktayı bir düzleme yansıtmak için, iki düzlemi (XOZ ve YOZ) ele alıyoruz ve bu sorunu her biri için çözüyoruz. Dört boyutlu uzay durumunda üç düzlemin dikkate alınması gerekir: XOQ, YOQ ve ZOQ.
Ve son olarak program hakkında. Şu şekilde çalışır: tesseract'ın on altı köşesini başlatın -> kullanıcı tarafından girilen komutlara bağlı olarak döndürün -> hacmin üzerine yansıtın -> kullanıcı tarafından girilen komutlara bağlı olarak, projeksiyonunu döndürün -> üzerine yansıtın uçak -> çiz.
Projeksiyonları ve rotasyonları kendim yazdım. Az önce anlattığım formüllere göre çalışıyorlar. OpenGL kütüphanesi çizgiler çizer ve aynı zamanda renk karışımını da yönetir. Ve tesseract köşelerinin koordinatları şu şekilde hesaplanır:
Başlangıç noktası ve uzunluğu 2 - (1) ve (-1) olan bir çizginin köşelerinin koordinatları;
- " - " - kare - " - " - ve kenarı 2 uzunluğunda:
(1; 1), (-1; 1), (1; -1) ve (-1; -1);
- " - " - küp - " - " -:
(1; 1; 1), (-1; 1; 1), (1; -1; 1), (-1; -1; 1), (1; 1; -1), (-1; 1; -1), (1; -1; -1), (-1; -1; -1);
Gördüğünüz gibi kare, OY ekseninin bir çizgi üstünde ve OY ekseninin bir çizgi altındadır; küp, XOY düzleminin bir kare önünde ve bir karenin arkasındadır; Tesseract, XOYZ hacminin diğer tarafında ve bu tarafta bir küptür. Ancak birler ve eksiler arasındaki bu değişimi bir sütuna yazılmışlarsa algılamak çok daha kolaydır
1; 1; 1
-1; 1; 1
1; -1; 1
-1; -1; 1
1; 1; -1
-1; 1; -1
1; -1; -1
-1; -1; -1
İlk sütunda bir ve eksi bir dönüşümlüdür. İkinci sütunda önce iki artı, sonra iki eksi var. Üçüncüsünde - dört artı bir ve ardından dört eksi bir. Bunlar küpün köşeleriydi. Tesseract'ta bunlardan iki kat daha fazla var ve bu nedenle bunları bildirmek için bir döngü yazmak gerekliydi, aksi takdirde kafanın karışması çok kolaydır.
Programım aynı zamanda anaglif de çizebiliyor. Mutlu 3D gözlük sahipleri stereoskopik bir görüntüyü gözlemleyebilir. Bir resim çizmenin zor bir yanı yoktur; sağ ve sol gözler için düzlem üzerine iki projeksiyon çizmeniz yeterlidir. Ancak program çok daha görsel ve ilgi çekici hale geliyor ve en önemlisi dört boyutlu dünya hakkında daha iyi bir fikir veriyor.
Daha az önemli işlevler, dönüşlerin daha iyi görülebilmesi için kenarlardan birinin kırmızı renkte aydınlatılmasının yanı sıra küçük kolaylıklardır - "göz" noktalarının koordinatlarının düzenlenmesi, dönüş hızının artırılması ve azaltılması.
Programı, kaynak kodunu ve kullanım talimatlarını içeren arşiv.
Bakalyar Maria
Dört boyutlu küp (tesseract) kavramını tanıtma yöntemleri, yapısı ve bazı özellikleri incelenmektedir. Dört boyutlu bir küp, üç boyutlu yüzlerine paralel hiperdüzlemlerle kesiştiğinde hangi üç boyutlu nesnelerin elde edildiği sorusu incelenmektedir. , yanı sıra ana köşegenine dik olan hiperdüzlemler de ele alınmaktadır. Araştırma için kullanılan çok boyutlu analitik geometri aparatı dikkate alınmaktadır.
İndirmek:
Önizleme:
Giriş……………………………………………………………………………….2
Ana bölüm……………………………………………………………..4
Sonuçlar………….. ………………………………………………………..12
Referanslar………………………………………………………..13
giriiş
Dört boyutlu uzay uzun zamandır hem profesyonel matematikçilerin hem de bu bilimi incelemekten uzak insanların dikkatini çekmiştir. Dördüncü boyuta ilgi, tıpkı bir düzlemin üç boyutlu uzaya "batırılması" gibi, düz bir çizginin de dört boyutlu uzaya "batırılması" gibi, üç boyutlu dünyamızın dört boyutlu uzaya "batırıldığı" varsayımından kaynaklanıyor olabilir. düzlemdir ve bir nokta düz bir çizgi üzerindedir. Ayrıca dört boyutlu uzay, modern görelilik teorisinde (uzay-zaman veya Minkowski uzayı olarak da bilinir) önemli bir rol oynar ve özel bir durum olarak da değerlendirilebilir.boyutlu Öklid uzayı (ile).
Dört boyutlu bir küp (tesseract), dört boyutlu uzayda mümkün olan maksimum boyuta sahip bir nesnedir (tıpkı sıradan bir küpün üç boyutlu uzayda bir nesne olması gibi). Aynı zamanda doğrudan ilgi çekici olduğuna da dikkat edin, yani doğrusal programlamanın optimizasyon problemlerinde (dört değişkenli bir doğrusal fonksiyonun minimum veya maksimumunun bulunduğu bir alan olarak) görünebilir ve ayrıca dijital mikroelektronikte de kullanılır (ne zaman elektronik saat ekranının çalışmasının programlanması). Ek olarak, dört boyutlu bir küpü inceleme süreci, mekansal düşünme ve hayal gücünün gelişmesine katkıda bulunur.
Sonuç olarak, dört boyutlu bir küpün yapısının ve spesifik özelliklerinin incelenmesi oldukça önemlidir. Dört boyutlu küpün yapı açısından oldukça iyi çalışıldığını belirtmekte fayda var. Çok daha ilginç olanı, çeşitli hiperdüzlemlerle bölümlerinin doğasıdır. Bu nedenle, bu çalışmanın temel amacı tesseractın yapısını incelemek ve dört boyutlu bir küpün üç boyutlu küplerinden birine paralel hiperdüzlemler tarafından kesilmesi durumunda hangi üç boyutlu nesnelerin elde edileceği sorusunu açıklığa kavuşturmaktır. boyutlu yüzler veya ana köşegenine dik hiperdüzlemler tarafından. Dört boyutlu uzaydaki bir hiperdüzlem, üç boyutlu bir altuzay olarak adlandırılacaktır. Bir düzlemdeki düz bir çizginin tek boyutlu bir hiperdüzlem olduğunu, üç boyutlu uzaydaki bir düzlemin ise iki boyutlu bir hiperdüzlem olduğunu söyleyebiliriz.
Hedef, çalışmanın hedeflerini belirledi:
1) Çok boyutlu analitik geometrinin temel gerçeklerini inceleyin;
2) 0'dan 3'e kadar boyutlarda küpler oluşturmanın özelliklerini inceleyin;
3) Dört boyutlu bir küpün yapısını inceleyin;
4) Dört boyutlu bir küpü analitik ve geometrik olarak tanımlar;
5) Üç boyutlu ve dört boyutlu küplerin gelişme modellerini ve merkezi projeksiyonlarını yapar.
6) Çok boyutlu analitik geometri aygıtını kullanarak, dört boyutlu bir küpün, üç boyutlu yüzlerinden birine paralel hiperdüzlemlerle veya ana köşegenine dik hiperdüzlemlerle kesişmesinden kaynaklanan üç boyutlu nesneleri tanımlayın.
Bu şekilde elde edilen bilgiler, tesseractın yapısını daha iyi anlamamızın yanı sıra, farklı boyutlardaki küplerin yapısı ve özelliklerindeki derin analojileri tespit etmemizi sağlayacaktır.
Ana bölüm
Öncelikle bu çalışma sırasında kullanacağımız matematiksel aparatları tanımlıyoruz.
1) Vektör koordinatları: eğer, O
2) Bir hiperdüzlemin normal bir vektörle denklemi Buraya benziyor
3) Uçaklar ve paraleldir ancak ve ancak
4) İki nokta arasındaki mesafe şu şekilde belirlenir:, O
5) Vektörlerin diklik koşulu:
Öncelikle dört boyutlu bir küpün nasıl tanımlanacağını bulalım. Bu iki şekilde yapılabilir: geometrik ve analitik.
Geometrik belirleme yöntemi hakkında konuşursak, sıfır boyuttan başlayarak küp oluşturma sürecinin izlenmesi tavsiye edilir. Sıfır boyutlu bir küp bir noktadır (bu arada, bir noktanın aynı zamanda sıfır boyutlu bir topun rolünü de oynayabileceğini unutmayın). Daha sonra, ilk boyutu (x ekseni) tanıtıyoruz ve karşılık gelen eksende, birbirinden 1 uzaklıkta bulunan iki noktayı (iki sıfır boyutlu küp) işaretliyoruz. Sonuç bir segmenttir; tek boyutlu bir küp. Hemen karakteristik bir özelliği belirtelim: Tek boyutlu bir küpün (parçanın) sınırları (uçları) iki sıfır boyutlu küptür (iki nokta). Daha sonra ikinci boyutu (koordinat ekseni) ve düzlemi tanıtıyoruzUçları birbirinden 1 uzaklıkta olan iki tek boyutlu küp (iki parça) oluşturalım (aslında parçalardan biri diğerinin dik izdüşümüdür). Segmentlerin karşılık gelen uçlarını bağlayarak, iki boyutlu bir küp olan bir kare elde ederiz. Yine, iki boyutlu bir küpün (karenin) sınırının dört adet tek boyutlu küp (dört parça) olduğuna dikkat edin. Son olarak üçüncü boyutu tanıtıyoruz (ekseni uyguluyoruz) ve uzayda kurguluyoruzbiri diğerinin dik izdüşümü olacak şekilde iki kare (karelerin karşılık gelen köşeleri birbirinden 1 uzaklıkta olacaktır). Karşılık gelen köşeleri bölümlere bağlayalım - üç boyutlu bir küp elde ederiz. Üç boyutlu bir küpün sınırının altı adet iki boyutlu küp (altı kare) olduğunu görüyoruz. Açıklanan yapılar aşağıdaki modeli tanımlamamızı sağlar: her adımdaboyutlu küp “bir iz bırakarak hareket eder”e hareket yönü küpe dik iken 1 mesafede ölçüm. Dört boyutlu küp kavramına ulaşmamızı sağlayan da bu sürecin biçimsel devamıdır. Yani üç boyutlu küpü dördüncü boyut yönünde (küpe dik) 1 mesafe hareket etmeye zorlayacağız. Bir öncekine benzer şekilde hareket ederek yani küplerin karşılık gelen köşelerini birleştirerek, dört boyutlu bir küp elde edeceğiz. Uzayımızda böyle bir yapının geometrik olarak imkansız olduğunu (üç boyutlu olduğu için) belirtmek gerekir, ancak burada mantıksal açıdan herhangi bir çelişkiyle karşılaşmıyoruz. Şimdi dört boyutlu bir küpün analitik açıklamasına geçelim. Aynı zamanda analoji kullanılarak resmi olarak da elde edilir. Dolayısıyla, sıfır boyutlu bir birim küpün analitik spesifikasyonu şu şekildedir:
Tek boyutlu bir birim küpün analitik görevi şu şekildedir:
İki boyutlu bir birim küpün analitik görevi şu şekildedir:
Üç boyutlu bir birim küpün analitik görevi şu şekildedir:
Artık dört boyutlu bir küpün analitik temsilini vermek çok kolaydır:
Görüldüğü gibi, dört boyutlu bir küpü tanımlamanın hem geometrik hem de analitik yöntemlerinde analojiler yöntemi kullanılmıştır.
Şimdi analitik geometri aparatını kullanarak dört boyutlu bir küpün yapısının ne olduğunu öğreneceğiz. Öncelikle hangi unsurları içerdiğini öğrenelim. Burada yine bir benzetme kullanabiliriz (bir hipotez ileri sürmek için). Tek boyutlu bir küpün sınırları noktalardır (sıfır boyutlu küpler), iki boyutlu bir küpün parçalarıdır (tek boyutlu küpler), üç boyutlu bir küpün sınırları karelerdir (iki boyutlu yüzler). Tesseractın sınırlarının üç boyutlu küpler olduğu varsayılabilir. Bunu kanıtlamak için köşe, kenar ve yüzlerden ne kastedildiğini açıklayalım. Bir küpün köşeleri onun köşe noktalarıdır. Yani köşelerin koordinatları sıfır veya bir olabilir. Böylece küpün boyutu ile köşe sayısı arasında bir bağlantı ortaya çıkar. Kombinatoryal çarpım kuralını uygulayalım - tepe noktasından itibarenölçülen küp tam olarakher biri sıfıra veya bire eşit olan (diğerlerinden bağımsız) koordinatlar, o zaman toplamdazirveler Böylece herhangi bir köşe noktası için tüm koordinatlar sabittir ve şuna eşit olabilir: veya . Tüm koordinatları sabitlersek (her birini eşitleyerek) veya , diğerlerinden bağımsız olarak), biri hariç, küpün kenarlarını içeren düz çizgiler elde ederiz. Bir öncekine benzer şekilde, tam olarak var olduğunu sayabilirsiniz.şeyler. Ve şimdi tüm koordinatları düzeltirsek (her birini eşitleyerek) veya , diğerlerinden bağımsız olarak), birkaç tanesi hariç, küpün iki boyutlu yüzlerini içeren düzlemler elde ederiz. Kombinatorik kuralını kullanarak tam olarak var olduğunu görüyoruz.şeyler. Sonra, benzer şekilde - tüm koordinatları sabitlemek (her birini eşit koymak) veya , diğerlerinden bağımsız olarak), üçü hariç, küpün üç boyutlu yüzlerini içeren hiperdüzlemler elde ederiz. Aynı kuralı kullanarak sayılarını hesaplıyoruz - tam olarakvesaire. Bu araştırmamız için yeterli olacaktır. Elde edilen sonuçları dört boyutlu bir küpün yapısına, yani koyduğumuz tüm türetilmiş formüllere uygulayalım.. Bu nedenle, dört boyutlu bir küpün: 16 köşesi, 32 kenarı, 24 iki boyutlu yüzü ve 8 üç boyutlu yüzü vardır. Açıklık sağlamak için, tüm unsurlarını analitik olarak tanımlayalım.
Dört boyutlu bir küpün köşeleri:
Dört boyutlu bir küpün kenarları ():
Dört boyutlu bir küpün iki boyutlu yüzleri (benzer kısıtlamalar):
Dört boyutlu bir küpün üç boyutlu yüzleri (benzer kısıtlamalar):
Artık dört boyutlu bir küpün yapısı ve onu tanımlama yöntemleri yeterince ayrıntılı olarak açıklandığı için, ana hedefin uygulanmasına geçelim - küpün çeşitli bölümlerinin doğasını açıklığa kavuşturmak. Bir küpün bölümlerinin üç boyutlu yüzlerinden birine paralel olduğu temel durumla başlayalım. Örneğin, yüzeye paralel hiperdüzlemlere sahip bölümlerini düşününAnalitik geometriden böyle bir bölümün denklemle verileceği bilinmektedir.İlgili bölümleri analitik olarak tanımlayalım:
Görebildiğimiz gibi, hiperdüzlemde bulunan üç boyutlu bir birim küp için analitik bir spesifikasyon elde ettik.
Bir benzetme yapmak için üç boyutlu bir küpün düzlemle kesitini yazalım.Şunu elde ederiz:
Bu bir düzlemde uzanan bir kare. Analoji açıktır.
Dört boyutlu bir küpün hiperdüzlemlerle bölümleritamamen benzer sonuçlar verir. Bunlar aynı zamanda hiperdüzlemlerde yer alan üç boyutlu tek küpler olacak sırasıyla.
Şimdi dört boyutlu bir küpün hiperdüzlemleri ana köşegenine dik olan bölümlerini ele alalım. Öncelikle bu problemi üç boyutlu bir küp için çözelim. Yukarıda açıklanan üç boyutlu küp birimini tanımlama yöntemini kullanarak, ana köşegen olarak örneğin uçları olan bir parçanın alınabileceği sonucuna varır. Ve . Bu, ana köşegenin vektörünün koordinatlara sahip olacağı anlamına gelir. Bu nedenle ana köşegene dik olan herhangi bir düzlemin denklemi şöyle olacaktır:
Parametre değişiminin sınırlarını belirleyelim. Çünkü sonra bu eşitsizlikleri terim terim topladığımızda şunu elde ederiz:
Veya .
Eğer öyleyse (kısıtlamalar nedeniyle). Aynı şekilde - eğer, O . Peki ne zaman ve ne zaman kesme düzlemi ve küpün tam olarak bir ortak noktası vardır ( Ve sırasıyla). Şimdi şunu not edelim. Eğer(yine değişken sınırlamalar nedeniyle). Karşılık gelen düzlemler aynı anda üç yüzü keser, çünkü aksi takdirde kesme düzlemi bunlardan birine paralel olacaktır ki bu durum duruma göre geçerli değildir. Eğerise düzlem küpün tüm yüzleriyle kesişir. Eğer, sonra düzlem yüzlerle kesişir. İlgili hesaplamaları sunalım.
İzin vermek Daha sonra uçakçizgiyi geçiyor düz bir çizgide ve . Üstelik kenar. Kenar düzlem düz bir çizgide kesişiyor, Ve
İzin vermek Daha sonra uçakçizgiyi aşıyor:
düz bir çizgide kenar ve .
düz bir çizgide kenar ve .
düz bir çizgide kenar ve .
düz bir çizgide kenar ve .
düz bir çizgide kenar ve .
düz bir çizgide kenar ve .
Bu sefer sıralı olarak ortak amaçlara sahip altı bölüm elde ediyoruz:
İzin vermek Daha sonra uçakçizgiyi geçiyor düz bir çizgide ve . Kenar düzlem düz bir çizgide kesişiyor, Ve . Kenar düzlem düz bir çizgide kesişiyor, Ve . Yani, ikili olarak ortak uçları olan üç segment elde ederiz:Böylece belirtilen parametre değerleri içindüzlem küpü köşeleri olan normal bir üçgen boyunca kesecek
İşte burada, bir küp ana köşegenine dik bir düzlemle kesiştiğinde elde edilen düzlem figürlerinin kapsamlı bir açıklaması bulunmaktadır. Ana fikir şuydu. Düzlemin hangi yüzleri kesiştiğini, hangi kümeler boyunca kesiştiğini ve bu kümelerin birbirleriyle nasıl ilişkili olduğunu anlamak gerekir. Örneğin, düzlemin çift olarak ortak uçları olan bölümler boyunca tam olarak üç yüzle kesiştiği ortaya çıkarsa, o zaman bölüm, köşeleri bu uçlar olan eşkenar bir üçgendir (bölümlerin uzunlukları doğrudan sayılarak kanıtlanır). segmentlerden.
Aynı aparatı ve aynı bölümleri inceleme fikrini kullanarak, aşağıdaki gerçekler tamamen benzer bir şekilde çıkarılabilir:
1) Dört boyutlu birim küpün ana köşegenlerinden birinin vektörü şu koordinatlara sahiptir:
2) Dört boyutlu bir küpün ana köşegenine dik olan herhangi bir hiperdüzlem şu şekilde yazılabilir:.
3) Sekant hiperdüzlem denkleminde parametre0'dan 4'e kadar değişebilir;
4) Ne zaman ve bir sekant hiperdüzlemi ve dört boyutlu bir küpün tek bir ortak noktası vardır ( Ve sırasıyla);
5) Ne zaman kesit düzenli bir tetrahedron üretecektir;
6) Ne zaman kesitte sonuç bir oktahedron olacaktır;
7) Ne zaman kesit düzenli bir tetrahedron üretecektir.
Buna göre, burada hiperdüzlem, değişkenlerin sınırlamaları nedeniyle üçgen bir bölgenin tahsis edildiği bir düzlem boyunca tesseract'ı keser (bir benzetme - düzlem, küpü düz bir çizgi boyunca kesiyordu; değişkenler için bir segment tahsis edildi). Durum 5'te, hiperdüzlem tesseractın tam olarak dört üç boyutlu yüzünü keser, yani çift olarak ortak kenarları olan, başka bir deyişle bir tetrahedron oluşturan dört üçgen elde edilir (bunun nasıl hesaplanabileceği doğrudur). Durum 6'da, hiperdüzlem tesseractın tam olarak sekiz üç boyutlu yüzünü keser, yani sıralı olarak ortak kenarları olan, başka bir deyişle bir oktahedron oluşturan sekiz üçgen elde edilir. Durum 7), durum 5) ile tamamen benzerdir.
Bunu spesifik bir örnekle açıklayalım. Yani, dört boyutlu bir küpün kesitini bir hiperdüzlemle inceliyoruzDeğişken kısıtlamalar nedeniyle bu hiperdüzlem aşağıdaki üç boyutlu yüzlerle kesişir: Kenar bir düzlem boyunca kesişiyorDeğişkenlerin sınırlamaları nedeniyle elimizde:Köşeleri olan üçgen bir alan elde ediyoruzSonraki,bir üçgen elde ediyoruzBir hiperdüzlem bir yüzle kesiştiğindebir üçgen elde ediyoruzBir hiperdüzlem bir yüzle kesiştiğindebir üçgen elde ediyoruzBöylece tetrahedronun köşeleri aşağıdaki koordinatlara sahiptir:. Hesaplanması kolay olduğu gibi bu tetrahedron gerçekten düzenlidir.
Sonuçlar
Böylece, bu araştırma sürecinde çok boyutlu analitik geometrinin temel gerçekleri incelendi, 0'dan 3'e kadar boyutlarda küpler oluşturmanın özellikleri incelendi, dört boyutlu bir küpün yapısı incelendi, dört boyutlu bir küpün yapısı incelendi. analitik ve geometrik olarak tanımlanmış, üç boyutlu ve dört boyutlu küplerin gelişim modelleri ve merkezi projeksiyonları yapılmış, üç boyutlu küpler, dört boyutlu bir küpün üç boyutlu küplerden birine paralel hiperdüzlemlerle kesişmesinden kaynaklanan analitik olarak tanımlanmış nesnelerdir. boyutlu yüzler veya ana köşegenine dik hiperdüzlemler ile.
Yapılan araştırma, farklı boyutlardaki küplerin yapısı ve özelliklerindeki derin analojileri tanımlamayı mümkün kıldı. Kullanılan analoji tekniği araştırmada uygulanabilir, örneğin:boyutlu küre veyaboyutlu simpleks. Yani,boyutlu bir küre bir dizi nokta olarak tanımlanabilirKürenin merkezi olarak adlandırılan belirli bir noktadan eşit uzaklıkta olan boyutlu uzay. Sonraki,boyutlu bir simpleks bir parça olarak tanımlanabilirminimum sayıyla sınırlı boyutsal alanboyutlu hiperdüzlemler. Örneğin, tek boyutlu bir simpleks bir segmenttir (tek boyutlu uzayın iki noktayla sınırlı bir kısmı), iki boyutlu bir simpleks bir üçgendir (iki boyutlu uzayın üç düz çizgiyle sınırlanan bir kısmı), üç boyutlu bir simpleks bir tetrahedrondur (üç boyutlu uzayın dört düzlemle sınırlı bir kısmı). Nihayet,boyutlu simpleksi parça olarak tanımlarızboyutlu uzay, sınırlıboyut hiperdüzlemi.
Tesseract'ın bilimin bazı alanlarındaki sayısız uygulamasına rağmen, bu araştırmanın hala büyük ölçüde matematiksel bir çalışma olduğunu unutmayın.
Referanslar
1) Bugrov Ya.S., Nikolsky S.M.Yüksek matematik, cilt 1 – M.: Bustard, 2005 – 284 s.
2) Kuantum. Dört boyutlu küp / Duzhin S., Rubtsov V., No. 6, 1986.
3) Kuantum. Nasıl çizilir boyutlu küp / Demidovich N.B., No. 8, 1974.
Geometride hiperküp- Bu N bir karenin boyutlu analojisi ( N= 2) ve küp ( N= 3). Şeklin zıt kenarlarında yer alan ve birbirine dik açılarla bağlanan paralel çizgi gruplarından oluşan kapalı dışbükey bir şekildir.
Bu rakam aynı zamanda olarak da bilinir. tesseract(tesseract). Tesseract küpün karesine oranı gibidir. Daha resmi olarak, bir tesseract, sınırları sekiz kübik hücreden oluşan düzenli bir dışbükey dört boyutlu politop (polihedron) olarak tanımlanabilir.
Oxford İngilizce Sözlüğü'ne göre "tesseract" kelimesi 1888 yılında Charles Howard Hinton tarafından türetilmiş ve "Yeni Bir Düşünce Çağı" adlı kitabında kullanılmıştır. Kelime, dört koordinat ekseni biçiminde Yunanca "τεσσερες ακτινες" ("dört ışın") kelimesinden türetilmiştir. Ayrıca bazı kaynaklarda aynı rakamın adı da geçmektedir. tetraküp(tetraküp).
N boyutlu hiperküp de denir n-küp.
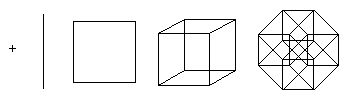
Nokta, boyutu 0 olan bir hiperküptür. Eğer noktayı bir birim uzunlukta kaydırırsanız, birim uzunlukta bir parça elde edersiniz - boyutu 1 olan bir hiperküp. Ayrıca, parçayı dik bir yönde bir birim uzunluk kadar kaydırırsanız parçanın yönüne doğru bir küp elde edersiniz - 2 boyutunda bir hiperküp. Kareyi, karenin düzlemine dik yönde bir birim uzunluk kadar kaydırarak, bir küp elde edilir - 3 boyutunda bir hiperküp. Bu süreç herhangi bir sayıda boyuta genelleştirilebilir. Örneğin, dördüncü boyutta bir küpü bir birim uzunluk hareket ettirirseniz, bir tesseract elde edersiniz.
Hiperküp ailesi, herhangi bir boyutta temsil edilebilen birkaç normal çokyüzlüden biridir.
Bir hiperküpün elemanları
Boyut hiperküpü N 2 tane var N“kenarlar” (tek boyutlu bir çizginin 2 noktası vardır; iki boyutlu bir karenin 4 kenarı vardır; üç boyutlu bir küpün 6 yüzü vardır; dört boyutlu bir tesseractın 8 hücresi vardır). Bir hiperküpün köşe (nokta) sayısı 2'dir N(örneğin, bir küp için - 2 3 köşe).
Miktar M sınırdaki boyutlu hiperküpler N-küp eşittir
Örneğin bir hiperküpün sınırında 8 küp, 24 kare, 32 kenar ve 16 köşe vardır.
| n-küp | İsim | Tepe noktası (0-yüz) |
Kenar (1-yüz) |
Kenar (2 yüzlü) |
Hücre (3-yüzlü) |
(4-yüz) | (5-yüz) | (6 taraflı) | (7-yüz) | (8-yüz) |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 küp | Nokta | 1 | ||||||||
| 1 küp | Segment | 2 | 1 | |||||||
| 2 küp | Kare | 4 | 4 | 1 | ||||||
| 3 küp | Küp | 8 | 12 | 6 | 1 | |||||
| 4 küp | Tesseract | 16 | 32 | 24 | 8 | 1 | ||||
| 5 küp | Penterakt | 32 | 80 | 80 | 40 | 10 | 1 | |||
| 6 küp | Hexeract | 64 | 192 | 240 | 160 | 60 | 12 | 1 | ||
| 7 küp | Hepteract | 128 | 448 | 672 | 560 | 280 | 84 | 14 | 1 | |
| 8 küp | Okterakt | 256 | 1024 | 1792 | 1792 | 1120 | 448 | 112 | 16 | 1 |
| 9 küp | Eneneract | 512 | 2304 | 4608 | 5376 | 4032 | 2016 | 672 | 144 | 18 |
Bir düzleme projeksiyon
Bir hiperküpün oluşumu şu şekilde temsil edilebilir:
- İki A ve B noktası bir AB doğru parçası oluşturacak şekilde birleştirilebilir.
- İki paralel AB ve CD parçası bir ABCD karesi oluşturacak şekilde birleştirilebilir.
- ABCDEFGH küpünü oluşturmak için iki paralel ABCD ve EFGH karesi birleştirilebilir.
- İki paralel küp ABCDEFGH ve IJKLMNOP birleşerek ABCDEFGHIJKLMNOP hiperküpünü oluşturabilir.
İkinci yapının görselleştirilmesi kolay değildir ancak onun iki boyutlu veya üç boyutlu uzaya yansımasını tasvir etmek mümkündür. Ayrıca, iki boyutlu bir düzlem üzerindeki projeksiyonlar, yansıtılan köşelerin konumlarının yeniden düzenlenmesine izin vererek daha kullanışlı olabilir. Bu durumda aşağıdaki örneklerde olduğu gibi artık tesseract içindeki elemanların mekansal ilişkilerini yansıtmayan, köşe bağlantılarının yapısını gösteren görüntüler elde etmek mümkündür.

İlk resim prensip olarak iki küpün birleştirilmesiyle bir tesseratın nasıl oluşturulduğunu göstermektedir. Bu şema, iki kareden küp oluşturma şemasına benzer. İkinci diyagram, tesseratın tüm kenarlarının aynı uzunlukta olduğunu göstermektedir. Bu şema aynı zamanda sizi birbirine bağlı küpleri aramaya da zorlar. Üçüncü diyagramda tesseractın köşeleri, alt noktaya göre yüzler boyunca mesafelere göre konumlandırılmıştır. Bu şema ilginçtir çünkü paralel hesaplamayı düzenlerken işlemcileri birbirine bağlayan ağ topolojisi için temel bir şema olarak kullanılır: herhangi iki düğüm arasındaki mesafe 4 kenar uzunluğunu aşmaz ve yükü dengelemek için birçok farklı yol vardır.
Sanatta hiperküp
Hiperküp, bilim kurgu literatüründe Robert Heinlein'in "Ve Çarpık Bir Ev İnşa Etti" adlı hikayesinde tesseract taraması şeklinde inşa edilmiş bir evi tanımladığı 1940 yılından bu yana ortaya çıktı. Hikayede, bu Sonraki, bu ev çökerek dört boyutlu bir tesseract'a dönüşüyor. Bundan sonra hiperküp birçok kitapta ve kısa öyküde karşımıza çıkıyor.
Cube 2: Hypercube filmi, bir hiperküp ağında sıkışıp kalan yaklaşık sekiz kişiyi konu alıyor.
Salvador Dali'nin 1954 tarihli "Çarmıha Gerilme (Corpus Hypercubus)" adlı tablosu, tesseract taramasında çarmıha gerilen İsa'yı tasvir ediyor. Bu tablo New York'taki Metropolitan Sanat Müzesi'nde görülebilir.
Çözüm
Hiperküp, dördüncü boyutun karmaşıklığını ve olağandışılığını görebileceğiniz en basit dört boyutlu nesnelerden biridir. Ve üç boyutta imkansız görünen şey, dört örneğin imkansız figürlerde mümkündür. Yani örneğin dört boyutlu imkansız bir üçgenin çubukları dik açılarla bağlanacaktır. Ve bu şekil, tüm bakış açılarından böyle görünecek ve üç boyutlu uzayda imkansız bir üçgenin uygulanmasından farklı olarak bozulmayacaktır (bkz.
Birinci sınıf öğrencisiyken sınıf arkadaşlarımdan biriyle hararetli bir tartışma yaşadım. Dört boyutlu bir küpün hiçbir biçimde temsil edilemeyeceğini söyledi ama ben onun oldukça net bir şekilde temsil edilebileceğine dair güvence verdim. Sonra ataçlardan üç boyutlu uzayımıza bir hiperküp projeksiyonu bile yaptım... Ama her şeyi sırasıyla konuşalım.
Hiperküp ve dört boyutlu uzay nedir
Her zamanki uzayımızın üç boyutu vardır. Geometrik açıdan bakıldığında bu, içinde karşılıklı olarak üç dik çizginin gösterilebileceği anlamına gelir. Yani, herhangi bir çizgi için birinciye dik ikinci bir çizgi bulabilirsiniz ve bir çift için ilk ikisine dik üçüncü bir çizgi bulabilirsiniz. Artık mevcut üç çizgiye dik dördüncü bir çizgi bulmak mümkün olmayacak.
Dört boyutlu uzay bizimkinden yalnızca bir ek yönü daha olması bakımından farklıdır. Zaten karşılıklı üç dik çizginiz varsa, o zaman üçüne de dik olacak şekilde dördüncü bir çizgi bulabilirsiniz.
Hiperküp o sadece dört boyutlu uzayda bir küp.
Dört boyutlu uzayı ve hiperküpü hayal etmek mümkün mü?
Bu soru şu soruya benzer: “Leonardo da Vinci'nin (1452-1519) aynı adlı tablosuna (1495-1498) bakarak Son Akşam Yemeği'ni hayal etmek mümkün müdür?”
Bir yandan elbette İsa'nın ne gördüğünü hayal etmeyeceksiniz (izleyiciye dönük oturuyor), özellikle pencerenin dışındaki bahçenin kokusunu almayacağınız ve masadaki yemeğin tadına bakmayacağınız için, kuşları duymayacaksınız. şarkı söylemek... Akşam o saatte yaşananların tam bir resmini elde edemeyeceksiniz ama yeni bir şey öğrenmeyeceğiniz ve resmin ilgi çekici olmadığı söylenemez.
Durum hiperküp sorununa benzer. Bunu tam olarak hayal etmek imkansızdır, ancak nasıl bir şey olduğunu anlamaya daha da yaklaşabilirsiniz.
Bir hiperküp inşaatı
0 boyutlu küp
0 boyutlu bir küple baştan başlayalım. Bu küp karşılıklı olarak dik 0 yüz içerir, yani bu sadece bir noktadır.
1 boyutlu küp
Tek boyutlu uzayda tek yönümüz vardır. Noktayı bu yönde hareket ettirip bir segment elde ediyoruz.
Bu tek boyutlu bir küp.
2 boyutlu küp
İkinci bir boyutumuz var, tek boyutlu küpümüzü (parçamızı) ikinci boyut yönünde kaydırıyoruz ve bir kare elde ediyoruz.
İki boyutlu uzayda bir küptür.
3 boyutlu küp
Üçüncü boyutun gelişiyle benzer şekilde ilerliyoruz: kareyi hareket ettiriyoruz ve sıradan bir üç boyutlu küp elde ediyoruz.

4 boyutlu küp (hiperküp)
Artık dördüncü bir boyutumuz var. Yani, elimizde önceki üç yöne de dik bir yön var. Aynı şekilde kullanalım. Dört boyutlu bir küp buna benzeyecek.

Doğal olarak üç boyutlu ve dört boyutlu küpler iki boyutlu bir ekran düzleminde tasvir edilemez. Çizdiklerim projeksiyonlardır. Tahminler hakkında biraz sonra konuşacağız, ancak şimdilik birkaç çıplak gerçek ve rakam var.
Köşe, kenar ve yüz sayısı
Lütfen bir hiperküpün yüzünün bizim sıradan üç boyutlu küpümüz olduğunu unutmayın. Bir hiperküp çizimine yakından bakarsanız aslında sekiz küp bulabilirsiniz.
Dört boyutlu uzay sakininin projeksiyonları ve vizyonu
Vizyon hakkında birkaç kelime
Üç boyutlu bir dünyada yaşıyoruz ama onu iki boyutlu olarak görüyoruz. Bunun nedeni, gözümüzün retinasının yalnızca iki boyutlu bir düzlemde yer almasıdır. Bu sayede iki boyutlu resimleri algılayıp gerçeğe benzerlerini bulabiliyoruz.
(Elbette uyum sayesinde göz bir nesneye olan mesafeyi tahmin edebilir, ancak bu, gözlerimizde yerleşik olan optikle ilişkili bir yan etkidir.)
Dört boyutlu uzayda yaşayan birinin gözleri üç boyutlu bir retinaya sahip olmalıdır. Böyle bir yaratık, üç boyutlu şeklin tamamını anında görebilir: tüm yüzleri ve iç kısımları. (Aynı şekilde iki boyutlu bir figürün tüm yüzlerini ve içlerini görebiliriz.)
Dolayısıyla dört boyutlu bir küpü, dört boyutlu uzayda yaşayan birinin algıladığı gibi, görme organlarımız sayesinde algılayamayız. Ne yazık ki. Geriye kalan tek şey, neyse ki hiçbir fiziksel sınırlaması olmayan zihin gözüne ve hayal gücüne güvenmek.
Bununla birlikte, bir hiperküpü bir düzlem üzerinde tasvir ederken, onun projeksiyonunu iki boyutlu uzaya yapmak zorunda kalıyorum. Çizimleri incelerken bu gerçeği dikkate alın.
Kenar kesişmeleri
Doğal olarak hiperküpün kenarları kesişmiyor. Kesişmeler yalnızca çizimlerde görünür. Ancak bu durum sürpriz olmamalı çünkü resimlerdeki normal bir küpün kenarları da kesişiyor.
Kaburga uzunlukları
Dört boyutlu bir küpün tüm yüzlerinin ve kenarlarının eşit olduğunu belirtmekte fayda var. Şekilde eşit değiller çünkü bakış yönüne göre farklı açılarda bulunuyorlar. Bununla birlikte, bir hiperküpü tüm projeksiyonların aynı uzunluğa sahip olacağı şekilde döndürmek mümkündür.
Bu arada, bu şekilde bir hiperküpün yüzleri olan sekiz küp açıkça görülüyor.
Hiperküpün içi boş
İnanması zor ama hiperküpü sınırlayan küpler arasında bir miktar boşluk var (dört boyutlu uzayın bir parçası).
Bunu daha iyi anlamak için sıradan bir üç boyutlu küpün iki boyutlu izdüşümüne bakalım (bunu bilinçli olarak biraz şematik yaptım).

Buradan küpün içinde biraz boşluk olduğunu tahmin edebilir misiniz? Evet, ancak yalnızca hayal gücünüzü kullanarak. Göz bu boşluğu görmez.
Bunun nedeni, üçüncü boyutta yer alan (düz bir çizimde gösterilemeyen) kenarların artık çizim düzleminde uzanan parçalara dönüşmesidir. Artık hacim sağlamıyorlar.
Küpün alanını çevreleyen kareler üst üste biniyordu. Ancak orijinal şekilde (üç boyutlu bir küp) bu karelerin, şekilde olduğu gibi aynı düzlemde üst üste değil, farklı düzlemlerde yer aldığı düşünülebilir.
Hiperküpte de durum tamamen aynıdır. Bir hiperküpün küp yüzleri, bize projeksiyonda göründüğü gibi aslında örtüşmez, ancak dört boyutlu uzayda bulunur.
Süpürmeler
Yani dört boyutlu uzayın sakini, üç boyutlu bir nesneyi aynı anda her yönden görebilir. Üç boyutlu bir küpü aynı anda her taraftan görebilir miyiz? Gözle - hayır. Ancak insanlar üç boyutlu bir küpün tüm yüzlerini aynı anda düz bir çizim üzerinde tasvir etmenin bir yolunu buldular. Böyle bir görüntüye tarama denir.
Üç boyutlu bir küpün geliştirilmesi
Muhtemelen herkes üç boyutlu bir küpün gelişiminin nasıl oluştuğunu biliyor. Bu süreç animasyonda gösterilmektedir.

Netlik sağlamak için küp yüzlerinin kenarları yarı saydam hale getirildi.
Bu iki boyutlu resmi ancak hayal gücümüz sayesinde algılayabildiğimizi belirtmek gerekir. Gelişmekte olan aşamaları tamamen iki boyutlu bir bakış açısıyla ele alırsak, süreç tuhaf görünecek ve hiç de net olmayacaktır.

Bu, önce çarpık karelerin ana hatlarının kademeli olarak ortaya çıkması, ardından da aynı anda gerekli şekli alırken yerlerine yerleşmeleri gibi görünüyor.
Açılan küpün yüzlerinden birinin yönünde bakarsanız (bu açıdan küp bir kareye benzer), o zaman açılmanın oluşum süreci daha da az açıktır. Her şey ilk kareden (açılmamış küpten değil) dışarı çıkan karelere benziyor.
Ancak görsel değil yalnızca şunun için tara: göz.
4 boyutlu uzay nasıl anlaşılır?
Hayal gücünüz sayesinde ondan birçok bilgi toplayabilirsiniz.
Dört boyutlu bir küpün geliştirilmesi
Bir hiperküpün açılmasına ilişkin animasyonlu süreci en azından biraz görsel hale getirmek kesinlikle imkansızdır. Ancak bu süreç hayal edilebilir. (Bunu yapmak için dört boyutlu bir varlığın gözünden bakmanız gerekir.)
Tarama şuna benziyor.

Hiperküpü çevreleyen sekiz küpün tümü burada görülebilir.
Katlandığında hizalanması gereken kenarlar aynı renklerle boyanmıştır. Çiftlerin görünmediği yüzler gri renkte bırakılır. Katladıktan sonra üstteki küpün en üst yüzü, alttaki küpün alt kenarıyla aynı hizada olmalıdır. (Üç boyutlu bir küpün açılması da benzer şekilde daraltılır.)
Evrişimden sonra sekiz küpün tüm yüzlerinin temas ederek hiperküpü kapatacağını lütfen unutmayın. Ve son olarak, katlama sürecini hayal ederken, katlama sırasında meydana gelen şeyin küplerin üst üste binmesi değil, bunların belirli (hiperkübik) dört boyutlu bir alan etrafına sarılması olduğunu unutmayın.
Salvador Dali (1904-1989) çarmıha gerilmeyi birçok kez resmetmiştir ve resimlerinin çoğunda haçlar görülmektedir. “Çarmıha Gerilme” (1954) tablosu hiperküp taraması kullanıyor.
Uzay-zaman ve Öklidyen dört boyutlu uzay
Umarım hiperküpü hayal edebilmişsindir. Peki, içinde yaşadığımız dört boyutlu uzay-zamanın nasıl çalıştığını anlamaya daha da yaklaşmayı başardınız mı? Ne yazık ki pek değil.
Burada dört boyutlu Öklid uzayından bahsettik ama uzay-zaman tamamen farklı özelliklere sahip. Özellikle, herhangi bir dönüş sırasında bölümler, ya 45 dereceden daha az bir açıyla ya da 45 dereceden daha büyük bir açıyla her zaman zaman eksenine eğimli kalır.
Uzay-zamanın özelliklerine bir dizi not ayırdım.
Görüntünün üç boyutluluğu
Dünya üç boyutludur. Görüntüsü iki boyutludur. Resmin ve artık fotoğrafçılığın önemli bir görevi, mekanın üç boyutluluğunu aktarmaktır. Romalılar zaten bazı tekniklerde ustalaştılar, sonra unutuldular ve Rönesans'la birlikte klasik resme dönmeye başladılar.
 Resimde üç boyutlu mekan yaratmanın ana tekniği perspektiftir. İzleyiciden uzaklaşan demiryolu rayları görsel olarak dardır. Boyamada raylar fiziksel olarak daraltılabilir. Fotoğrafta perspektif otomatik olarak oluşur: Kamera, rayları gözün gördüğü kadar dar bir şekilde fotoğraflayacaktır. Ancak neredeyse kapanmasına izin vermeyin: artık bir perspektif gibi değil, garip bir figür gibi görünecek; Raylar, cadde kenarları ve nehir kıyısı arasında gözle görülür bir boşluk olmalıdır.
Resimde üç boyutlu mekan yaratmanın ana tekniği perspektiftir. İzleyiciden uzaklaşan demiryolu rayları görsel olarak dardır. Boyamada raylar fiziksel olarak daraltılabilir. Fotoğrafta perspektif otomatik olarak oluşur: Kamera, rayları gözün gördüğü kadar dar bir şekilde fotoğraflayacaktır. Ancak neredeyse kapanmasına izin vermeyin: artık bir perspektif gibi değil, garip bir figür gibi görünecek; Raylar, cadde kenarları ve nehir kıyısı arasında gözle görülür bir boşluk olmalıdır.
Doğrusal perspektifin dünyayı aktarmanın en ilkel ve gerçekçi yolu olduğunu anlamak önemlidir.
Gönderi navigasyonu
Görünüşünün tiyatro sahnesiyle ilişkilendirilmesi tesadüf değildir (Florensky, “Ters Perspektif”). Küçük derinlikteki bir tiyatro sahnesini aktarmanın gelenekselliği ve basitliği, resimde mevcut teknik çeşitliliğinden yoksun olan fotoğrafçılık için çok uygundur.
Doğrusal olandan çok daha ilginç perspektifler var. Çinli ustaların eserlerinde nesnelerin aynı anda aşağıdan, yukarıdan ve önden tasvir edildiği yüzen bir perspektif vardır. Bu, beceriksiz sanatçıların yaptığı teknik bir hata değildi: Bu tekniğin efsanevi yazarı Guo Xi, böyle bir gösterinin kişinin dünyayı bütünüyle fark etmesine olanak sağladığını yazdı. İzleyicinin karakterin yüzünü ve sırtını aynı anda görebildiği Rus ikon boyama tekniği de benzerdir. Batı Avrupalı sanatçılar arasında da bulunan ilginç bir ikon boyama tekniği, uzaktaki nesnelerin, aksine, yakın olanlardan daha büyük olduğu ve önemi vurguladığı ters perspektifti. Böyle bir perspektifin doğru olduğu ancak günümüzde kanıtlanmıştır: Uzaktaki nesnelerin aksine, yakın plan aslında ters perspektifte algılanır (Rauschenbach). Photoshop'u kullanarak arka plan nesnelerini büyüterek ters perspektif elde edebilirsiniz. Fotoğrafçılık yasalarına alışkın bir izleyici için böyle bir görüntü tuhaf görünecektir.
Bir binanın köşesinin, duvarların her iki yönde birbirinden ayrıldığı çerçeveye dahil edilmesi, izometrik bir perspektif görünümü yaratır. Beyin duvarların dik açıda olduğunu anlar ve görüntünün geri kalanını buna göre düzenler. Bu perspektif önden perspektife göre daha dinamik ve yakın çekim için daha doğaldır. Nesnelerin ve yakındaki binaların uç açılarını çerçeveye yerleştirmeniz yeterlidir.
Genişleme nedeniyle izometrik perspektif önemlidir ve bu, klasik bir portre için nadiren uygundur. Doğrusal perspektif, daralma nedeniyle küçük duyguları daha iyi aktarır.
Çekim aşamasında fotoğrafçının elinde perspektifi vurgulamak için kullanabileceği bir dizi araç vardır. Eşit genişlikte, mesafeye uzanan nesneler (yollar, sokaklar, sütunlar, oluklar) daralarak ve hatta uzaklaşarak izleyiciye mekanın üç boyutluluğunu gösterir. Perspektif bozulmasını artırmak için düşük açıdan çekim yaparsanız etki daha güçlü olur. Bu manzara fotoğrafçılığı için yeterlidir, ancak iç mekan fotoğrafçılığı için sığ görüntü derinliğinde etki neredeyse hiç fark edilmez. Görüntünün üst kısmı daraltılarak (Dönüştürme Perspektifi) son işlemlerde biraz geliştirilebilir. Ancak bir manzarada bile abartılı bir perspektif ilginç görünebilir.
Görüntünün anlamında derinlik açık olabilir: binalar bir cadde veya nehirle ayrılmıştır. Köşegen üç boyutluluğu vurgular; örneğin bir nehrin üzerindeki köprü.
Arka planda izleyicinin bildiği boyuttaki nesneler ölçeği belirler ve buna göre perspektifi oluşturur. Manzara fotoğrafçılığında bu nesne bir araba olabilir, ancak portre fotoğrafçılığında, görünür kalırken daha küçük görünmesi için bacağınızı (kameradan uzakta) sandalyenin altına bükmeyi deneyin. Hatta işlem sonrası bu bacağı biraz daha küçük hale getirebilirsiniz.
Süsleme, unsurları görsel olarak azaltarak perspektifi aktarır. Bir örnek, yoldaki çizgileri işaretleyen yerdeki büyük fayanslar olabilir.
Hipertrofik ön plan denilen bir teknik var. Orantısız derecede büyük olduğundan görüntüde derinlik yaratır. Ön planın ölçeği ile model karşılaştırıldığında göz, modelin göründüğünden çok daha uzakta olduğu sonucuna varıyor. Görüntünün bir hata olarak algılanmaması için abartının hafif kalması gerekir. Bu teknik yalnızca son işlemler için değil aynı zamanda çekim için de işe yarar: 35 veya 50 mm'lik bir lensle çekim yaparak oranları bozun. Geniş açılı mercekle çekim yapmak alanı genişletir, orantıları bozarak üç boyutluluğunu artırır. Modeli yakın mesafeden çekerseniz etki daha güçlü olur, ancak grotesk oranlara dikkat edin: yalnızca dini resimlerin yazarları bir binadan daha büyük bir kişiyi tasvir edebilir.
Kavşak harika çalışıyor. Elma armutu kısmen kaplıyorsa beyin yanılmayacaktır: elma armutun önündedir. Model mobilyayı kısmen kaplayarak iç mekanda derinlik yaratıyor.
Açık ve koyu noktaların değişimi de görüntüye derinlik kazandırır. Beyin, deneyimlerinden yakındaki nesnelerin yaklaşık olarak eşit şekilde aydınlatıldığını bilir, bu nedenle farklı şekilde aydınlatılan nesneleri farklı mesafelerde konumlanmış olarak yorumlar. Bu etki için, noktalar perspektif ekseni yönünde, görüntünün derinliklerinde değil, görüntünün derinliklerinde dönüşümlü olarak kullanılır. Örneğin, karanlık bir çerçevede kameradan uzakta uzanan bir modeli çekerken, vurguları kalçaların yakınına ve bacakların yakınına yerleştirin. İşlem sonrası alanları aydınlatabilir/koyulaştırabilirsiniz.
Giderek karanlıklaşan nesnelerin sırasının azaldığı algılanıyor. Nesneleri aktif çizgi boyunca kademeli olarak gölgelendirerek ince bir perspektif duygusu elde edebilirsiniz. Benzer şekilde, ışık zayıflatılarak derinlik aktarılır: Mobilyaların üzerine veya zemine bir ışık şeridi dökün.
Sadece ışık değil, renk kontrastı da sayesinde üç boyutlu bir görüntü elde edilebiliyor. Bu teknik, natürmortlarına parlak renkli noktalar yerleştiren Flaman ressamlar tarafından biliniyordu. Yan yana kırmızı bir nar ve sarı bir limon, düz ön aydınlatmada bile üç boyutlu görünecektir. Mor üzümlerin arka planında özellikle iyi öne çıkacaklar: soğuk bir arka plana karşı sıcak bir renk. Parlak renkli yüzeyler, natürmort için tipik olan, zayıf ışıkta bile karanlıktan iyi bir şekilde ortaya çıkar. Renk kontrastı ana renklerle daha iyi çalışır: gölgeler yerine kırmızı, sarı, mavi.
Siyah bir arka planda sarı öne çıkar, mavi ise gizlenir. Beyaz bir arka planda ise durum tam tersidir. Renk doygunluğu bu etkiyi artırır. Bu neden oluyor? Sarı renk asla karanlık değildir, bu nedenle beyin, sarı bir nesnenin aydınlatılmayan, karanlık bir arka plana gömülebileceğine inanmayı reddeder. Mavi ise tam tersine karanlıktır.
İşlem sonrası perspektifi geliştirmek, atmosferik algıyı simüle etmeye dayanır: uzaktaki nesneler daha hafif, daha bulanık görünür; parlaklık, doygunluk ve ton kontrastı azalır.
Uzun mesafelerin yanı sıra, atmosferik etkiler sabah pusunda, siste veya dumanlı bir barda doğal görünür. Hava durumunu düşünün: Bulutlu bir günde veya alacakaranlıkta ön plan ile arka plan arasında önemli bir fark olmayabilir.
En güçlü faktör parlaklık kontrastıdır. Ayarlarda bu olağan kontrasttır. Uzak nesnelerin kontrastını azaltın, ön planın kontrastını artırın; görüntü dışbükey hale gelecektir. Ön plan ile arka plan arasındaki kontrasttan değil, ön planın kontrastından daha düşük olması gereken arka planın kontrastından bahsediyoruz. Bu yöntem yalnızca manzara ve tür fotoğrafçılığı için değil aynı zamanda stüdyo portreleri için de uygundur: yüzün ön kısmının kontrastını artırın, saç, elmacık kemikleri ve kıyafetlerin kontrastını azaltın. Portre filtreleri de benzer bir şey yaparak modelin cildini bulanıklaştırıyor ve gözleri ve dudakları sertleştiriyor.
Kontrast ayarı, 3D görüntünün son işlemesini yapmanın en kolay yoludur. Diğer süreçlerin aksine izleyici, maksimum doğallığın korunmasına olanak sağlayacak herhangi bir değişikliği neredeyse hiç fark etmeyecektir.
Bulanıklaştırma, kontrast azaltma işlemine benzer ancak farklı işlemlerdir. Görüntü keskin kalırken kontrastı düşük olabilir. Sınırlı alan derinliği nedeniyle, uzaktaki nesnelerin bulanıklaştırılması fotoğrafçılıkta üç boyutluluğu aktarmanın en popüler yolu olmaya devam ediyor ve post prodüksiyonda uzaktaki nesnelerin bulanıklaştırılmasıyla bu durum kolaylıkla geliştirilebilir. Bu nedenle arka plana daha az ayrıntı yerleştirilmelidir; beyin uzaktaki nesnelerin ayırt edilebilir olmasını beklemez. Bu arada, kontrastın azaltılması doğal algıya daha iyi karşılık gelir: Uzak dağlar düşük kontrastta görülebilir ve bulanık değildir, çünkü manzarayı tararken göz sürekli olarak yeniden odaklanır ve alan derinliği sorunu ona yabancıdır. Arka planı bulanıklaştırarak aynı zamanda ön planı da keskinleştirebilirsiniz. Ayrıca ön planda görüntü çizgilerini iyileştirebilirsiniz (Yüksek Geçiş Filtresi veya Netlik). Yüksek kaliteli lenslerin görüntüsündeki karakteristik çıkıntıyı açıklayan, ön planın yüksek keskinliğidir. Dikkat: 3D'yi biraz artırmak adına görüntüyü çok sert hale getirebilirsiniz.
Daha hafif nesneler daha uzakta görünür. Bunun nedeni, doğada ışık saçan havanın kalınlığı boyunca uzaktaki nesneleri görmemizdir; uzak dağlar hafif görünür. Bu nedenle manzara fotoğrafçılığında hafif nesnelerin ön plana yerleştirilmesine dikkat etmelisiniz.
Uzaktaki nesneleri aydınlatın. Ne kadar uzakta olursa gökyüzünün parlaklığına ve tonuna o kadar uyum sağlarlar. Yatay nesnelerin (zemin, deniz) dikey olanlardan (duvarlar, ağaçlar) daha iyi aydınlatıldığını lütfen unutmayın, bu nedenle ikincisini aydınlatarak aşırıya kaçmayın. Her durumda, nesnelerin gökyüzünden belirgin şekilde daha hafif kalması gerekir.
 Peki, kaçmanın arka planın parlaklığındaki kontrastı azaltmanın başka bir yolu olduğunu fark ederseniz. Çarpma efektini arttırmak için ön planı hafifçe karartın.
Peki, kaçmanın arka planın parlaklığındaki kontrastı azaltmanın başka bir yolu olduğunu fark ederseniz. Çarpma efektini arttırmak için ön planı hafifçe karartın.
Görünüşe göre iç mekanda her şey tam tersi. Sokakta göz, mesafenin parlak olduğu gerçeğine alışmışsa, o zaman odada ışık genellikle kişinin üzerinde yoğunlaşır ve iç kısım karanlığa gömülür; beyin arka plan aydınlatmasına değil, ön plan aydınlatmasına alışkındır.
Sığ sahne derinliğine sahip iç mekan görüntülerinde, manzara fotoğraflarından farklı olarak aydınlatılmış model, karanlık bir arka plandan dışarı çıkar. Ancak bunun tersi bir faktör de var: Evriminin %99'u boyunca insan perspektifi açık alanlarda gözlemledi ve odaların ortaya çıkışıyla birlikte beynin yeniden yapılanma için zamanı henüz olmamıştı. Vermeer portrelerinde açık renkli bir fon tercih etmiş ve portreleri oldukça ön plana çıkmış. Fotoğrafçılıkta önerilen dikey bir arka planın aydınlatılması, yalnızca modeli modelden ayırmakla kalmaz, aynı zamanda arka planı aydınlatarak görüntüye hafif bir üç boyutluluk kazandırır. Burada beynin nesnelerin konumunu çeşitli faktörlere göre analiz ettiği ve bunların çelişkili olabileceği gerçeğiyle karşı karşıyayız.
Modelin kameradan uzak alanlarında ışık noktalarının bulunduğu stüdyo aydınlatması ilginç görünüyor. Örneğin kameraya en uzak olan meme vurgulanır.
Uzak nesnelerdeki renk doygunluğunu azaltın: Bizi ayıran havanın kalınlığından dolayı uzak dağların doygunluğu neredeyse tek renkli seviyeye kadar azalır ve mavi bir pusla kaplanır. Ön plan doygunluğu artırılabilir.
Sarı açık, mavi ve kırmızı ise koyu olduğundan renk kontrastı aynı zamanda parlaklık kontrastıdır.
Uzak arka planın doygunluğunu giderirken, onun görüş alanından kaybolmasına izin vermeyin. Çoğu zaman tam tersine, arka planı ortaya çıkarmak için doygunluğunu artırmanız gerekir. Bu üç boyutluluktan daha önemlidir.
3D fotoğrafçılık tavsiyelerinin çoğu sıcaklık kontrastına odaklanır. Aslında bu etki çok zayıftır ve parlaklık kontrastı nedeniyle kolayca kesintiye uğrar. Ayrıca sıcaklık kontrastı can sıkıcı ve dikkat çekicidir.
Hava sıcak turuncu ışığı emdiği için çok uzaktaki nesnelerin rengi daha soğuk görünür. Arka planda ufukta gemiler varken kumsalda bir modelin fotoğrafını çekerken, son işlemde uzaktaki denizin ve gemilerin renk sıcaklığını düşürün. Mavi denizden kırmızı mayolu bir model çıkıyor, mavimsi alacakaranlıktan sokak lambasının sarı ışığında bir model çıkıyor.
Ayrı tonlamanın özü budur: Modeli daha sıcak, arka planı daha serin yaparız. Beyin, aynı düzlemde farklı renk sıcaklıklarının olmadığını anlar ve modelin arka plandan çıktığı üç boyutlu bir görüntüyü algılar. Bölünmüş tonlama manzaralara derinlik katar: ön planı daha sıcak, arka planı daha soğuk yapın.
Ayrı tonlamanın önemli bir istisnası: gün doğumu ve gün batımında, uzaktaki arka plan hiç soğuk değil, sarı ve kırmızı-turuncu tonlarla sıcaktır. Açık çözüm - mor bir mayo içinde beyaz bir model kullanmak - işe yaramıyor çünkü gün batımı ışığı modelin vücuduna da sıcak bir renk katıyor.
Özetleyelim: atmosferik etkilere dayalı bir fotoğrafa üç boyutluluk kazandırmak için ön plan ve arka planın kontrastını oluşturmak gerekir. Ana kontrast olağan kontrasta dayanmaktadır: ön plan yüksek kontrastlıdır, arka plan düşük kontrastlıdır. İkinci kontrast keskinlik açısındandır: Ön plan keskindir, arka plan bulanıktır. Üçüncü kontrast açıklık açısındandır: ön plan karanlık, arka plan aydınlıktır. Dördüncü kontrast doygunluk açısındandır: ön plan renkleri doygundur, arka plan renkleri doygunluğu giderilmiştir. Beşinci kontrast sıcaklıktadır: ön plan sıcak, arka plan soğuktur.
Listelenen faktörler genellikle çok yönlüdür. Sarı maviden daha parlaktır ve açık renkli nesneler karanlık olanlardan daha uzakta görünür. Sarının geri çekilip mavinin izleyiciye yaklaşmasını beklemek doğal olurdu. Aslında durum tam tersidir: Soğuk bir arka plandan sıcak bir renk ortaya çıkar. Yani renk, parlaklıktan daha güçlü bir faktör olarak ortaya çıkıyor. Düşünüldüğünde bu şaşırtıcı değil: sarı ve kırmızı yalnızca yakın mesafeden açıkça ayırt edilebiliyor ve izleyici onları çok uzakta görmeyi beklemiyor.
Özetle: arka planı düşük kontrastlı, soluk, açık, doygunluğu giderilmiş, mavimsi tutun. Ve filmlerin abartılı 3D'sine alışkın olan izleyicinin, yarattığınız üç boyutluluğun neredeyse hiç fark edilmediğini veya yok olduğunu göreceği gerçeğine hazırlıklı olun.
Portre fotoğrafçılığında, kanıtlanmış chiaroscuro efektine (modelin yüzündeki ışık ve gölge oyunu) güvenmek daha iyidir, bu da görüntüyü oldukça dışbükey hale getirir. Tür fotoğrafçılığında perspektif en dikkat çekici üç boyutlu etkiyi verir. Natürmortta ana faktör nesnelerin kesişimi (üst üste binmesi) olacaktır.
Potansiyel müşteriye kendinizi kaptırmayın; bu yalnızca görüntünüzün üzerinde titreştiği ön düzlem için bir arka plandır. Gerçekçilikten uzak olan modern resimde perspektife pek önem verilmemektedir.
Kitabın tamamını indirin: pdfepubazw3mobifb2litİçindekiler
Puanlar (±1, ±1, ±1, ±1). Başka bir deyişle aşağıdaki kümeyle temsil edilebilir:
Tesseract, tesseract'ın kendisi ile kesişimi üç boyutlu yüzlerini (sıradan küpler olan) tanımlayan sekiz hiperdüzlemle sınırlıdır. Paralel olmayan 3B yüzlerin her çifti, 2B yüzler (kareler) vb. oluşturacak şekilde kesişir. Son olarak tesseractın 8 adet 3 boyutlu yüzü, 24 adet 2 boyutlu yüzü, 32 kenarı ve 16 köşesi vardır.
Popüler açıklama
Üç boyutlu uzaydan ayrılmadan bir hiperküpün nasıl görüneceğini hayal etmeye çalışalım.
Tek boyutlu bir "uzayda" - bir çizgi üzerinde - L uzunluğunda bir AB parçası seçiyoruz. AB'den L mesafesindeki iki boyutlu bir düzlemde, ona paralel bir DC parçası çiziyoruz ve uçlarını birleştiriyoruz. Sonuç kare bir CDBA'dır. Bu işlemi düzlemle tekrarlayarak üç boyutlu bir küp CDBAGHFE elde ediyoruz. Ve dördüncü boyuttaki (ilk üçe dik) küpü L kadar kaydırarak CDBAGHFEKLJIOPNM hiperküpünü elde ederiz.
Uçakta tesseract inşaatı
Tek boyutlu AB parçası, iki boyutlu CDBA karesinin kenarı olarak hizmet eder, kare ise CDBAGHFE küpünün kenarı olarak hizmet eder ve bu da dört boyutlu hiperküpün kenarı olacaktır. Düz bir çizgi parçasının iki sınır noktası vardır, bir karenin dört köşesi vardır, bir küpün sekiz köşesi vardır. Dolayısıyla dört boyutlu bir hiperküpte 16 köşe olacaktır: 8'i orijinal küpün köşesi ve 8'i dördüncü boyutta kaydırılmış olanın köşesi. 32 kenarı vardır - 12'sinin her biri orijinal küpün başlangıç ve son konumlarını verir ve diğer 8 kenar da dördüncü boyuta taşınan sekiz köşesini "çizir". Aynı mantık hiperküpün yüzleri için de yapılabilir. İki boyutlu uzayda yalnızca bir tane vardır (karenin kendisi), bir küpün 6 tanesi vardır (hareket ettirilen kareden iki yüz ve kenarlarını tanımlayan dört yüz daha). Dört boyutlu bir hiperküpün 24 kare yüzü vardır - iki konumdaki orijinal küpün 12 karesi ve on iki kenarından 12 kare.
Bir karenin kenarlarının 4 adet tek boyutlu parça olması ve bir küpün kenarlarının (yüzlerinin) 6 adet iki boyutlu kare olması gibi, bir “dört boyutlu küp” (tesseract) için de kenarları 8 adet üç boyutlu küptür. . Karşılıklı tesseract küp çiftlerinin uzayları (yani bu küplerin ait olduğu üç boyutlu uzaylar) paraleldir. Şekilde küpler şunlardır: CDBAGHFE ve KLJIOPNM, CDBAKLJI ve GHFEOPNM, EFBAMNJI ve GHDCOPLK, CKIAGOME ve DLJBHPNF.
Benzer şekilde, daha fazla boyuttaki hiperküpler için akıl yürütmemize devam edebiliriz, ancak dört boyutlu bir hiperküpün, üç boyutlu uzayın sakinleri olan bizler için nasıl görüneceğini görmek çok daha ilginç. Bunun için zaten bilinen analoji yöntemini kullanacağız.
ABCDHEFG tel küpünü alalım ve kenarından tek gözle bakalım. Düzlem üzerinde dört çizgiyle - yan kenarlarla birbirine bağlanan iki kareyi (yakın ve uzak kenarları) göreceğiz ve çizebiliriz. Benzer şekilde, üç boyutlu uzayda dört boyutlu bir hiperküp, birbirine yerleştirilmiş ve sekiz kenarla birbirine bağlanmış iki kübik "kutu" gibi görünecektir. Bu durumda, "kutuların" kendileri - üç boyutlu yüzler - "bizim" alanımıza yansıtılacak ve bunları birbirine bağlayan çizgiler dördüncü eksen yönünde uzanacaktır. Ayrıca küpü projeksiyonda değil, mekansal bir görüntüde hayal etmeye çalışabilirsiniz.
Üç boyutlu bir küpün, yüzünün uzunluğu kadar kaydırılan bir kareden oluşması gibi, dördüncü boyuta kaydırılan bir küp de bir hiperküp oluşturacaktır. Perspektifte oldukça karmaşık bir figür gibi görünecek olan sekiz küple sınırlıdır. Dört boyutlu hiperküpün kendisi de sonsuz sayıda küpten oluşur, tıpkı üç boyutlu bir küpün sonsuz sayıda düz kareye "kesilebilmesi" gibi.
Üç boyutlu bir küpün altı yüzünü keserek, onu düz bir şekle, yani bir gelişmeye ayrıştırabilirsiniz. Orijinal yüzün her iki tarafında bir kare artı bir tane daha olacak - onun karşısındaki yüz. Ve dört boyutlu bir hiperküpün üç boyutlu gelişimi, orijinal küpten, ondan "büyüyen" altı küpten ve bir tane daha - son "hiper yüz"den oluşacaktır.
Bir tesseractın özellikleri, daha düşük boyuttaki geometrik şekillerin özelliklerinin dört boyutlu uzayda devamını temsil eder.
Projeksiyonlar
İki boyutlu uzaya
Bu yapıyı hayal etmek zordur ancak bir tesseractı iki boyutlu veya üç boyutlu uzaylara yansıtmak mümkündür. Ayrıca bir düzleme yansıtmak, hiperküpün köşelerinin konumunun anlaşılmasını kolaylaştırır. Bu sayede artık tesseract içindeki mekansal ilişkileri yansıtmayan, ancak aşağıdaki örneklerde olduğu gibi köşe bağlantı yapısını gösteren görüntüler elde etmek mümkündür:

Üçüncü resim, inşaat noktasına göre izometrideki tesseratı göstermektedir. Bu gösterim, paralel hesaplamada birden fazla işlemciyi birbirine bağlamak için topolojik bir ağın temeli olarak tesseract kullanıldığında ilgi çekicidir.
Üç boyutlu uzaya
Bir tesseractın üç boyutlu uzay üzerindeki çıkıntılarından biri, karşılık gelen köşeleri bölümlerle birbirine bağlanan, iç içe geçmiş iki üç boyutlu küpü temsil eder. Üç boyutlu uzayda iç ve dış küplerin farklı boyutları vardır, ancak dört boyutlu uzayda bunlar eşit küplerdir. Tüm tesseract küplerinin eşitliğini anlamak için dönen bir tesseract modeli oluşturuldu.
|
|
- Tesseractın kenarları boyunca uzanan altı kesik piramit, eşit altı küpün görüntüleridir. Bununla birlikte, karelerin (yüzlerin) bir küpe göre olması gibi, bu küpler de bir tesseracta göredir. Ama aslında tesseract, tıpkı bir küpün sonsuz sayıda kareye veya bir karenin sonsuz sayıda parçaya bölünebilmesi gibi, sonsuz sayıda küpe bölünebilir.
Tesseract'ın üç boyutlu uzaya bir başka ilginç yansıması, eşkenar dörtgenlerin geniş açılarında karşıt köşe çiftlerini birbirine bağlayan dört köşegenli eşkenar dörtgen bir dodekahedrondur. Bu durumda, tesseractın 16 köşesinden 14'ü eşkenar dörtgen dodekahedronun 14 köşesine yansıtılır ve geri kalan 2'sinin çıkıntıları merkezde çakışır. Üç boyutlu uzaya yapılan bu tür bir projeksiyonda, tek boyutlu, iki boyutlu ve üç boyutlu tüm kenarların eşitliği ve paralelliği korunur.
Stereo çifti
Bir tesseractın stereo çifti, üç boyutlu uzaya iki projeksiyon olarak tasvir edilmiştir. Tesseract'ın bu görüntüsü, dördüncü boyut olarak derinliği temsil edecek şekilde tasarlandı. Stereo çift, her göz bu görüntülerden yalnızca birini görecek şekilde görüntülenir; tesseratın derinliğini yeniden üreten stereoskopik bir resim ortaya çıkar.
Tesseract paketini açma
Bir tesseractın yüzeyi sekiz küp halinde açılabilir (bir küpün yüzeyinin altı kareye açılmasına benzer şekilde). 261 farklı tesseract tasarımı var. Bir tesseratın açılması, bağlantılı açıların bir grafik üzerinde çizilmesiyle hesaplanabilir.
Sanatta Tesseract
- Edwina A.'nın "Yeni Abbott Ovası"nda hiperküp bir anlatıcı görevi görüyor.
- Jimmy Neutron'un Maceraları'nın bir bölümünde, "dahi çocuk" Jimmy, Robert Heinlein'in Glory Road (1963) romanındaki katlama kutusuyla aynı olan dört boyutlu bir hiperküp icat eder.
- Robert E. Heinlein en az üç bilim kurgu öyküsünde hiperküplerden bahsetmiştir. "Dört Boyutlu Ev"de ("Deniz Mavisi İnşa Edilen Ev"), bir evin açılmamış bir tesseract olarak inşa edildiğini ve daha sonra bir deprem nedeniyle dördüncü boyutta "katlandığını" ve "gerçek" bir tesseract haline geldiğini anlattı. .
- Heinlein'in romanı Glory Road, içi dışarıdan daha büyük olan hiper boyutlu bir kutuyu anlatıyor.
- Henry Kuttner'ın "All Tenali Borogov" hikayesi, yapı olarak tesseract'a benzer, uzak gelecekten gelen çocuklar için eğitici bir oyuncağı anlatıyor.
- Alex Garland'ın () romanında "tesseract" terimi, hiperküpün kendisinden ziyade dört boyutlu bir hiperküpün üç boyutlu açılımı için kullanılıyor. Bu, bilişsel sistemin bilinenden daha geniş olması gerektiğini göstermek için tasarlanmış bir metafordur.
- Cube 2: Hypercube'un konusu, bir "hiperküp" veya birbirine bağlı küplerden oluşan bir ağ içinde hapsolmuş sekiz yabancıya odaklanıyor.
- Andromeda televizyon dizisi tesseract üreteçlerini bir komplo cihazı olarak kullanıyor. Öncelikle uzayı ve zamanı manipüle etmek için tasarlandılar.
- Salvador Dali'nin () “Çarmıha Gerilme” (Corpus Hypercubus) tablosu.
- Nextwave çizgi romanı, 5 tesseract bölgesi içeren bir aracı tasvir ediyor.
- Voivod Nothingface albümündeki bestelerden birinin adı “In my hypercube”.
- Anthony Pearce'in Route Cube adlı romanında, Uluslararası Kalkınma Birliği'nin yörüngedeki uydularından birine, 3 boyuta sıkıştırılmış tesseract adı veriliyor.
- Üçüncü sezondaki “Black Hole School” dizisinde “Tesseract” bölümü var. Lucas gizli bir düğmeye basıyor ve okul "matematiksel bir tesseract gibi şekillenmeye" başlıyor.
- "Tesseract" terimi ve onun türevi olan "tesseract", Madeleine L'Engle'nin "A Wrinkle in Time" adlı öyküsünde bulunur.
- TesseracT bir İngiliz djent grubunun adıdır.
- Marvel Sinematik Evreni film serisinde Tesseract, hiperküp şeklindeki kozmik bir eser olan önemli bir olay örgüsü öğesidir.
- Robert Sheckley'in "Bayan Fare ve Dördüncü Boyut" adlı öyküsünde, yazarın tanıdığı ezoterik bir yazar, tasarladığı cihaza saatlerce bakarak tesseract'ı görmeye çalışır: bacağın üzerinde, içine çubuklar saplanmış bir top. hangi küpler monte edilir, üzerine her türlü ezoterik sembol yapıştırılır. Hikaye Hinton'un çalışmalarından bahsediyor.
- İlk İntikamcı, Yenilmezler filmlerinde. Tesseract - tüm evrenin enerjisi
Diğer isimler
- Heksadekakoron Heksadekakoron)
- Oktokoron (İngilizce) sekizlik)
- Tetraküp
- 4-Küp
- Hypercube (boyut sayısı belirtilmemişse)
Notlar
Edebiyat
- Charles H. Hinton. Dördüncü Boyut, 1904. ISBN 0-405-07953-2
- Martin Gardner, Matematiksel Karnaval, 1977. ISBN 0-394-72349-X
- Ian Stewart, Modern Matematik Kavramları, 1995. ISBN 0-486-28424-7
Bağlantılar
Rusça- Transformator4D programı. Dört boyutlu nesnelerin (Hypercube dahil) üç boyutlu projeksiyon modellerinin oluşturulması.
- C++ kaynak koduyla bir tesseractın oluşturulmasını ve tüm afin dönüşümlerini uygulayan bir program.
İngilizce
- Mushware Limited - tesseract çıktı programı ( Tesseract Eğitmeni, GPLv2 ile uyumlu lisans) ve dört boyutlu alanda birinci şahıs nişancı ( Adaksis; grafikler çoğunlukla üç boyutludur; İşletim sistemi depolarında bir GPL sürümü vardır).
| Çokyüzlüler | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Doğru (Platonik katılar) |
|||||||||
| Yıldız şeklinde dodekahedron Yıldız şeklinde ikosidodekahedron Yıldız şeklinde ikosahedron Yıldız şeklinde çokyüzlü Yıldız şeklinde oktahedron | |||||||||
| Dışbükey |
|
||||||||
| Formüller, teoremler, teoriler |
|||||||||
| Diğer | |||||||||
Wikimedia Vakfı.









