Ters trigonometrik fonksiyonların Taylor serisi açılımı. Taylor serisi açılımı

"F(x) fonksiyonunun Maclaurin serisi açılımını bulun"- yüksek matematikteki görev tam olarak buna benziyor, bazı öğrenciler bunu yapabilirken diğerleri örneklerle baş edemiyor. Bir kuvvet serisini genişletmenin birkaç yolu vardır; burada fonksiyonları Maclaurin serisine genişletme tekniğini vereceğiz. Bir seride bir fonksiyon geliştirirken türevleri hesaplamada iyi olmanız gerekir.

Örnek 4.7 Bir fonksiyonu x'in kuvvetlerine göre genişletme

Hesaplamalar: Fonksiyonun açılımını Maclaurin formülüne göre yapıyoruz. Öncelikle fonksiyonun paydasını bir seriye genişletelim

Son olarak genişlemeyi pay ile çarpın.
İlk terim fonksiyonun sıfırdaki değeridir f(0) = 1/3.
Birinci ve daha yüksek mertebeden f(x) fonksiyonunun türevlerini ve bu türevlerin x=0 noktasındaki değerini bulalım.




Daha sonra, 0'daki türevlerin değerindeki değişim modeline dayanarak, n'inci türevin formülünü yazıyoruz.

Yani paydayı Maclaurin serisinde bir genişleme şeklinde temsil ediyoruz

Pay ile çarpıyoruz ve fonksiyonun x'in kuvvetleri cinsinden istenen açılımını elde ediyoruz

Gördüğünüz gibi burada karmaşık bir şey yok.
Tüm önemli noktalar, türevleri hesaplama ve yüksek dereceli türevin değerini sıfırda hızlı bir şekilde genelleştirme yeteneğine dayanmaktadır. Aşağıdaki örnekler, bir fonksiyonu seri halinde hızlı bir şekilde nasıl düzenleyeceğinizi öğrenmenize yardımcı olacaktır.

Örnek 4.10 Fonksiyonun Maclaurin serisi açılımını bulun

Hesaplamalar: Tahmin edebileceğiniz gibi paydaki kosinüsü seri halinde koyacağız. Bunu yapmak için sonsuz küçük miktarlar için formüller kullanabilir veya kosinüs açılımını türevler aracılığıyla türetebilirsiniz. Sonuç olarak x'in kuvvetleri cinsinden aşağıdaki seriye ulaşıyoruz:

Gördüğünüz gibi elimizde minimum hesaplamalar ve seri açılımının kompakt bir temsili var.

Örnek 4.16 Bir fonksiyonu x'in kuvvetlerine göre genişletin:
7/(12-x-x^2)
Hesaplamalar: Bu tür örneklerde kesri basit kesirlerin toplamına göre genişletmek gerekir.
Şimdi bunun nasıl yapılacağını göstermeyeceğiz, ancak belirsiz katsayıların yardımıyla kesirlerin toplamına ulaşacağız.
Daha sonra paydaları üstel biçimde yazıyoruz

Maclaurin formülünü kullanarak terimleri genişletmeye devam ediyor. Terimleri "x"in aynı kuvvetleriyle toplayarak, bir fonksiyonun serideki açılımının genel terimi için bir formül oluşturuyoruz



Seriye geçişin son bölümünü başlangıçta uygulamak zordur, çünkü eşleştirilmiş ve eşleştirilmemiş endeksler (dereceler) için formülleri birleştirmek zordur, ancak pratik yaptıkça bu konuda daha iyi olacaksınız.

Örnek 4.18 Fonksiyonun Maclaurin serisi açılımını bulun

Hesaplamalar: Bu fonksiyonun türevini bulalım:

McLaren formüllerinden birini kullanarak fonksiyonu bir seriye genişletelim:

Her ikisinin de tamamen aynı olduğu gerçeğine dayanarak seriyi terim terim özetliyoruz. Tüm seriyi terim terim entegre ettikten sonra, fonksiyonun x'in kuvvetleri cinsinden bir seriye genişletilmesini elde ederiz.

Genişlemenin son iki satırı arasında başlangıçta çok zamanınızı alacak bir geçiş var. Bir seri formülünü genelleştirmek herkes için kolay değildir; bu nedenle güzel ve derli toplu bir formül elde edememe konusunda endişelenmeyin.

Örnek 4.28 Fonksiyonun Maclaurin serisi açılımını bulun:

Logaritmayı şu şekilde yazalım

Maclaurin formülünü kullanarak logaritma fonksiyonunu x'in kuvvetleri cinsinden bir seriye genişletiyoruz

Son evrişim ilk bakışta karmaşıktır, ancak işaretleri değiştirdiğinizde her zaman benzer bir şey elde edersiniz. Fonksiyonların art arda programlanması konusundaki giriş dersi tamamlandı. Eşit derecede ilginç olan diğer ayrıştırma şemaları, aşağıdaki materyallerde ayrıntılı olarak tartışılacaktır.

16.1. Temel fonksiyonların Taylor serilerine genişletilmesi ve

Maclaurin

Bir küme üzerinde keyfi bir fonksiyonun tanımlandığını gösterelim.
, noktanın yakınında
birçok türevi vardır ve bir kuvvet serisinin toplamıdır:

o zaman bu serinin katsayılarını bulabilirsiniz.

Bir kuvvet serisinde yerine koyalım
. Daha sonra
.

Fonksiyonun ilk türevini bulalım
:

Şu tarihte:
:
.

İkinci türev için şunu elde ederiz:

Şu tarihte:
:
.

Bu prosedüre devam etmek N bir kez elde ettiğimizde:
.

Böylece şu formda bir kuvvet serisi elde ettik:

,

buna denir Taylor'ın yanında fonksiyon için
noktanın yakınında
.

Taylor serisinin özel bir durumu Maclaurin serisi en
:

Taylor (Maclaurin) serisinin geri kalanı ana serinin atılmasıyla elde edilir. N ilk üyeler ve şu şekilde gösterilir:
. Daha sonra fonksiyon
toplam olarak yazılabilir N serinin ilk üyeleri
ve geri kalanı
:,

.

Geriye kalan kısım genellikle
farklı formüllerle ifade edilir.

Bunlardan biri Lagrange formundadır:

, Nerede
.
.

Pratikte Maclaurin serisinin daha sık kullanıldığını unutmayın. Bu nedenle fonksiyonu yazmak için
kuvvet serisi toplamı şeklinde gereklidir:

1) Maclaurin (Taylor) serisinin katsayılarını bulun;

2) ortaya çıkan kuvvet serisinin yakınsaklık bölgesini bulun;

3) bu serinin fonksiyona yakınsak olduğunu kanıtlayın
.

Teorem1 (Maclaurin serisinin yakınsaması için gerekli ve yeterli koşul). Serinin yakınsaklık yarıçapı olsun
. Bu serinin aralıkta yakınsaması için
işlev görmek
Koşulun gerçekleşmesi için gerekli ve yeterlidir:
belirtilen aralıkta.

Teorem 2. Fonksiyonun herhangi bir mertebeden türevleri ise
belli bir aralıkta
mutlak değer olarak aynı sayıyla sınırlı M, yani
, o zaman bu aralıkta fonksiyon
Maclaurin serisine genişletilebilir.

Örnek1 . Nokta etrafında Taylor serisini genişletin
işlev.

Çözüm.

.

,;

,
;

,
;

,

.......................................................................................................................................

,
;

Yakınsama bölgesi
.

Örnek2 . Bir işlevi genişlet bir nokta etrafındaki Taylor serisinde
.

Çözüm:

Fonksiyonun değerini ve türevlerini bulun
.

,
;

,
;

...........……………………………

,
.

Bu değerleri sıralayalım. Şunu elde ederiz:

veya
.

Bu serinin yakınsaklık bölgesini bulalım. D'Alembert testine göre bir seri şu durumda yakınsar:

.

Bu nedenle herhangi bir kişi için bu limit 1'den küçüktür ve bu nedenle serinin yakınsaklık aralığı şöyle olacaktır:
.

Temel temel fonksiyonların Maclaurin serisi açılımının birkaç örneğini ele alalım. Maclaurin serisini hatırlayın:

.

aralıkta yakınsar
işlev görmek
.

Bir fonksiyonu bir seriye genişletmek için aşağıdakilerin gerekli olduğunu unutmayın:

a) bu fonksiyon için Maclaurin serisinin katsayılarını bulun;

b) ortaya çıkan serinin yakınsama yarıçapını hesaplayın;

c) Ortaya çıkan serinin fonksiyona yakınsak olduğunu kanıtlayın
.

Örnek 3.İşlevi düşünün
.

Çözüm.

Fonksiyonun değerini ve türevlerini hesaplayalım.
.

O halde serinin sayısal katsayıları şu şekildedir:

herkes için N. Bulunan katsayıları Maclaurin serisine koyalım ve şunu elde edelim:

Ortaya çıkan serinin yakınsaklık yarıçapını bulalım:

.

Bu nedenle seri aralıkta yakınsar
.

Bu seri fonksiyona yakınsar herhangi bir değer için , çünkü herhangi bir aralıkta
işlev ve mutlak değerli türevlerinin sayısı sınırlıdır .

Örnek4 . İşlevi düşünün
.

Çözüm.

:

Eşit mertebeden türevlerin olduğunu görmek kolaydır
ve türevler tek sıralıdır. Bulunan katsayıları Maclaurin serisine koyalım ve açılımı elde edelim:

Bu serinin yakınsaklık aralığını bulalım. D'Alembert'in işaretine göre:

herkes için . Bu nedenle seri aralıkta yakınsar
.

Bu seri fonksiyona yakınsar
Çünkü tüm türevleri birlikle sınırlıdır.

Örnek5 .
.

Çözüm.

Fonksiyonun değerini ve türevlerini bulalım.
:

Böylece bu serinin katsayıları:
Ve
, buradan:

Önceki satıra benzer şekilde yakınsama alanı
. Seri fonksiyona yakınsar
Çünkü tüm türevleri birlikle sınırlıdır.

Lütfen işlevin
Tek kuvvetlerde tek ve seri açılım, fonksiyon
– çift ve çift kuvvetlerde bir seriye genişleme.

Örnek6 . Binom serisi:
.

Çözüm.

Fonksiyonun değerini ve türevlerini bulalım.
:

Bundan şunu görmek mümkündür:

Bu katsayı değerlerini Maclaurin serisine koyalım ve bu fonksiyonun bir kuvvet serisine genişletilmesini elde edelim:

Bu serinin yakınsaklık yarıçapını bulalım:

Bu nedenle seri aralıkta yakınsar
. Sınırlayıcı noktalarda
Ve
üsse bağlı olarak bir seri yakınsak olabilir veya olmayabilir
.

İncelenen seriler aralıkta yakınsaktır
işlev görmek
yani serinin toplamı
en
.

Örnek7 . Fonksiyonu Maclaurin serisine genişletelim
.

Çözüm.

Bu fonksiyonu bir seriye genişletmek için binom serisini kullanırız.
. Şunu elde ederiz:

Kuvvet serisinin özelliğine dayanarak (bir kuvvet serisi yakınsaklık bölgesinde entegre edilebilir), bu serinin sol ve sağ taraflarının integralini buluruz:

Bu serinin yakınsaklık alanını bulalım:
,

yani bu serinin yakınsaklık alanı aralıktır
. Serinin aralığın uçlarındaki yakınsaklığını belirleyelim. Şu tarihte:

. Bu seri uyumlu bir seridir, yani ıraksamaktadır. Şu tarihte:
ortak terimli bir sayı serisi elde ederiz
.

Seri Leibniz testine göre yakınsaktır. Dolayısıyla bu serinin yakınsaklık bölgesi aralıktır.
.

16.2. Güç serilerinin yaklaşık hesaplamalarda uygulanması

Yaklaşık hesaplamalarda kuvvet serileri son derece önemli bir rol oynamaktadır. Onların yardımıyla, örneğin olasılık teorisi ve matematiksel istatistik gibi çeşitli bilgi alanlarında kullanılan trigonometrik fonksiyon tabloları, logaritma tabloları, diğer fonksiyonların değer tabloları derlenmiştir. Ek olarak, fonksiyonların kuvvet serilerine genişletilmesi teorik çalışmaları açısından faydalıdır. Yaklaşık hesaplamalarda kuvvet serilerini kullanırken asıl sorun, bir serinin toplamını ilk serinin toplamı ile değiştirirken hatayı tahmin etme sorunudur. Nüyeler.

İki durumu ele alalım:

fonksiyon alternatif bir seriye genişletilir;

fonksiyon bir dizi sabit işarete genişletilir.

Alternatif serileri kullanarak hesaplama

Fonksiyona izin ver
alternatif kuvvet serisine genişletildi. Daha sonra bu fonksiyonu belirli bir değer için hesaplarken Leibniz kriterini uygulayabileceğimiz bir sayı serisi elde ederiz. Bu kritere göre bir serinin toplamı ilk serinin toplamı ile değiştirilirse N Bu durumda mutlak hata bu serinin geri kalanının ilk terimini aşmaz, yani:
.

Örnek8 . Hesaplamak
0,0001 doğrulukla.

Çözüm.

Maclaurin serisini kullanacağız
radyan cinsinden açı değerini değiştirerek:

Serinin birinci ve ikinci terimlerini belirli bir doğrulukla karşılaştırırsak: .

Üçüncü genişleme dönemi:

Belirtilen hesaplama doğruluğundan daha az. Bu nedenle hesaplamak
serinin iki terimini bırakmak yeterlidir, yani

.

Böylece
.

Örnek9 . Hesaplamak
0,001 doğrulukla.

Çözüm.

Binom serisi formülünü kullanacağız. Bunu yapmak için yazalım
gibi:
.

Bu ifadede
,

Serinin her terimini belirtilen doğrulukla karşılaştıralım. Açık ki
. Bu nedenle hesaplamak
serinin üç terimini bırakmak yeterlidir.

veya
.

Pozitif serileri kullanarak hesaplama

Örnek10 . Numarayı hesapla 0,001 doğrulukla.

Çözüm.

Bir işlev için arka arkaya
hadi değiştirelim
. Şunu elde ederiz:

Bir serinin toplamını ilk serinin toplamıyla değiştirirken ortaya çıkan hatayı tahmin edelim. üyeler. Açık eşitsizliği yazalım:

bu 2<<3. Используем формулу остаточного члена ряда в форме Лагранжа:
,
.

Soruna göre bulmanız gerekir Nöyle ki aşağıdaki eşitsizlik sağlanır:
veya
.

Bunu ne zaman kontrol etmek kolaydır N= 6:
.

Buradan,
.

Örnek11 . Hesaplamak
0,0001 doğrulukla.

Çözüm.

Logaritmaları hesaplamak için fonksiyona yönelik bir seri kullanabileceğimizi unutmayın.
ancak bu seri çok yavaş yakınsar ve verilen doğruluğu elde etmek için 9999 terimin alınması gerekir! Bu nedenle, logaritmaları hesaplamak için kural olarak fonksiyona yönelik bir seri kullanılır.
aralıkta birleşen
.

Haydi hesaplayalım
bu seriyi kullanıyoruz. İzin vermek
, Daha sonra .

Buradan,
,

Hesaplamak için
Belirli bir doğrulukla ilk dört terimin toplamını alın:
.

Serinin geri kalanı
onu bir kenara atalım. Hatayı tahmin edelim. Açıkça görülüyor ki

veya
.

Böylece hesaplama için kullanılan seride fonksiyon için serideki 9999 yerine sadece ilk dört terimin alınması yeterli olmuştur.
.

Kendi kendine teşhis soruları

1. Taylor serisi nedir?

2. Maclaurin serisinin şekli nasıldı?

3. Bir fonksiyonun Taylor serisindeki açılımına ilişkin bir teorem formüle edin.

4. Ana fonksiyonların Maclaurin serisi açılımını yazın.

5. Ele alınan serilerin yakınsaklık alanlarını belirtiniz.

6. Kuvvet serileri kullanılarak yaklaşık hesaplamalarda hata nasıl tahmin edilir?

Yüksek matematik öğrencileri, bize verilen serinin yakınsaklık aralığına ait belirli bir kuvvet serisinin toplamının, sürekli ve sınırsız sayıda farklılaşmış fonksiyona dönüştüğünü bilmelidir. Şu soru ortaya çıkıyor: Belirli bir keyfi fonksiyonun f(x) belirli bir kuvvet serisinin toplamı olduğunu söylemek mümkün müdür? Yani f(x) fonksiyonu hangi koşullar altında bir kuvvet serisiyle temsil edilebilir? Bu sorunun önemi, f(x) fonksiyonunu yaklaşık olarak bir kuvvet serisinin, yani bir polinomun ilk birkaç teriminin toplamıyla değiştirmenin mümkün olması gerçeğinde yatmaktadır. Bir fonksiyonun oldukça basit bir ifadeyle (bir polinom) bu şekilde değiştirilmesi, belirli problemleri çözerken de kullanışlıdır, yani: integralleri çözerken, hesaplama yaparken vb.

Belirli bir f(x) fonksiyonu için, (α - R; x 0 + R) civarında, sonuncusu da dahil olmak üzere (n+1)'inci mertebeye kadar türevleri hesaplamanın mümkün olduğu kanıtlanmıştır. ) bir x = α noktasında, şu formül doğrudur:

Bu formül adını ünlü bilim adamı Brooke Taylor'dan almıştır. Bir önceki seriden elde edilen seriye Maclaurin serisi adı verilir:

Maclaurin serisinde genişletme yapmayı mümkün kılan kural:

1. Birinci, ikinci, üçüncü... derecelerin türevlerini belirleyin.
2. X=0 noktasındaki türevlerin neye eşit olduğunu hesaplayın.
3. Bu fonksiyonun Maclaurin serisini yazın ve yakınsaklık aralığını belirleyin.
4. Maclaurin formülünün geri kalanının (-R;R) aralığını belirleyin

R n (x) -> 0, n -> sonsuz. Eğer biri varsa, içindeki f(x) fonksiyonu Maclaurin serisinin toplamı ile çakışmalıdır.

Şimdi bireysel fonksiyonlar için Maclaurin serisini ele alalım.

1. Yani ilki f(x) = e x olacaktır. Elbette, özellikleri itibarıyla böyle bir fonksiyonun çok farklı mertebelerde türevleri vardır ve f (k) (x) = e x, burada k, yerine geçen x = 0'a eşittir. f (k) (0) = e 0 =1, k = 1,2 elde ederiz... Yukarıdakilere dayanarak e x serisi şöyle görünecektir:

2. f(x) = sin x fonksiyonu için Maclaurin serisi. Tüm bilinmeyenler için fonksiyonun türevlerinin olacağını hemen açıklayalım, ayrıca f "(x) = cos x = sin(x+n/2), f "" (x) = -sin x = sin(x + 2*n/2)..., f (k) (x) = sin(x+k*n/2), burada k herhangi bir doğal sayıya eşittir. Yani basit hesaplamalar yaptıktan sonra şu sonuca ulaşabiliriz. f(x) = sin x serisi şu şekilde görünecektir:

3. Şimdi f(x) = cos x fonksiyonunu ele almaya çalışalım. Tüm bilinmeyenler için keyfi dereceli türevleri vardır ve |f (k) (x)| = |cos(x+k*n/2)|<=1, k=1,2... Снова-таки, произведя определенные расчеты, получим, что ряд для f(х) = cos х будет выглядеть так:

Yani bir Maclaurin serisinde genişletilebilecek en önemli fonksiyonları listeledik, ancak bazı fonksiyonlar için Taylor serileri tarafından desteklenmiştir. Şimdi bunları listeleyeceğiz. Taylor ve Maclaurin serilerinin yüksek matematikte serilerin çözümüne yönelik pratik çalışmanın önemli bir parçası olduğunu da belirtmekte fayda var. Yani Taylor serisi.

1. İlki f(x) = ln(1+x) fonksiyonuna ait seri olacaktır. Önceki örneklerde olduğu gibi, verilen f(x) = ln(1+x) için Maclaurin serisinin genel formunu kullanarak seriyi toplayabiliriz. ancak bu fonksiyon için Maclaurin serisi çok daha basit bir şekilde elde edilebilir. Belirli bir geometrik serinin entegre edilmesiyle böyle bir numunenin f(x) = ln(1+x) serisini elde ederiz:

2. Makalemizde son olacak olan ikincisi ise f(x) = arctan x serisi olacaktır. [-1;1] aralığına ait x için genişletme geçerlidir:

Bu kadar. Bu makale, yüksek matematikte, özellikle ekonomi ve teknik üniversitelerde en çok kullanılan Taylor ve Maclaurin serilerini inceledi.

Fonksiyonel seriler arasında en önemli yeri kuvvet serileri almaktadır.

Kuvvet serisi bir seridir

terimleri artan negatif olmayan tamsayı kuvvetlerine göre düzenlenmiş kuvvet fonksiyonlarıdır X, A C0 , C 1 , C 2 , C N - sabit değerler. Sayılar C1 , C 2 , C N - seri terimlerinin katsayıları, C0 - Ücretsiz Üye. Kuvvet serisinin terimleri sayı doğrusunun tamamında tanımlanır.

Konsepti tanıyalım kuvvet serilerinin yakınsaklık alanları. Bu bir değişkenin değer kümesidir X, bunun için seri yakınsaktır. Kuvvet serileri oldukça basit bir yakınsama bölgesine sahiptir. Gerçek değişken değerleri için X yakınsama bölgesi ya bir noktadan oluşur ya da belirli bir aralıktır (yakınsama aralığı) ya da tüm eksenle çakışır Öküz .

Değerleri güç serisine yerleştirirken X= 0 bir sayı serisiyle sonuçlanacaktır

C0 +0+0+...+0+... ,

hangi birleşir.

Bu nedenle ne zaman X= 0 herhangi bir kuvvet serisi yakınsar ve bu nedenle, yakınsama alanı boş küme olamaz. Tüm kuvvet serilerinin yakınsaklık bölgesinin yapısı aynıdır. Aşağıdaki teorem kullanılarak belirlenebilir.

Teorem 1 (Abel teoremi). Bir kuvvet serisi belirli bir değerde yakınsarsa X = X 0 sıfırdan farklıysa yakınsar ve dahası, tüm değerler için kesinlikle |X| < |X 0 | . Lütfen unutmayın: hem “X sıfırdır” başlangıç ​​değeri hem de başlangıç ​​değeriyle karşılaştırılan herhangi bir “X” değeri, işaret dikkate alınmaksızın modulo olarak alınır.

Sonuçlar. Eğer kuvvet serisi ıraksar bir değerde X = X 1 , o zaman tüm değerler için ıraksar |X| > |X 1 | .

Daha önce de öğrendiğimiz gibi, herhangi bir kuvvet serisi şu değerde yakınsar: X= 0. Yalnızca aşağıdaki durumlarda yakınsayan kuvvet serileri vardır: X= 0 ve diğer değerler için ıraksak X. Bu durumu göz ardı ederek, kuvvet serilerinin bir değerde yakınsadığını varsayıyoruz. X = X 0 , sıfırdan farklı. O halde Abel teoremine göre ]-| aralığının her noktasında yakınsar. X0 |, |X 0 |[ (sol ve sağ sınırları, güç serisinin yakınlaştığı x değerleri olan, sırasıyla eksi işareti ve artı işaretiyle alınan bir aralık), orijine göre simetrik.

Güç serisi belirli bir değerde ıraksaıyorsa X = X 1 , bu durumda, Abel teoreminin bir sonucuna dayanarak, [-| doğru parçasının dışındaki tüm noktalarda ıraksar. X1 |, |X 1 |] . Herhangi bir kuvvet serisi için orijine göre simetrik bir aralık vardır. yakınsama aralığı , serinin yakınlaştığı her noktada, sınırlarda yakınlaşabilir veya uzaklaşabilir ve mutlaka aynı anda olması gerekmez ve segmentin dışında seri ıraksar. Sayı R kuvvet serisinin yakınsaklık yarıçapı denir.

Özel durumlarda kuvvet serilerinin yakınsama aralığı bir noktaya kadar yozlaşabilir (bu durumda seri ancak X= 0 ve öyle kabul edilir R= 0) veya sayı doğrusunun tamamını temsil eder (bu durumda seri sayı doğrusu üzerindeki tüm noktalarda yakınsar ve öyle olduğu varsayılır).

Bu nedenle, bir kuvvet serisinin yakınsaklık bölgesinin belirlenmesi, onun yakınsaklığının belirlenmesinden oluşur. yakınsama yarıçapı R ve yakınsama aralığı sınırlarında ('da) serinin yakınsaklığının incelenmesi.

Teorem 2. Belirli bir seriden başlayarak bir güç serisinin tüm katsayıları sıfırdan farklıysa, yakınsama yarıçapı, serinin aşağıdaki ortak üyelerinin katsayılarının mutlak değerleri oranındaki limite eşittir. , yani

Örnek 1. Kuvvet serisinin yakınsaklık bölgesini bulun

Çözüm. Burada

Formül (28)'i kullanarak bu serinin yakınsama yarıçapını buluruz:

Yakınsaklık aralığının uçlarındaki serilerin yakınsaklığını inceleyelim. Örnek 13, bu serinin şu noktada yakınsadığını göstermektedir: X= 1 ve ıraksar X= -1. Sonuç olarak, yakınsama bölgesi yarı aralıktır.

Örnek 2. Kuvvet serisinin yakınsaklık bölgesini bulun

Çözüm. Serinin katsayıları pozitiftir ve

Bu oranın limitini bulalım. kuvvet serilerinin yakınsama yarıçapı:

Serinin aralığın sonlarındaki yakınsaklığını inceleyelim. Değer İkamesi X= -1/5 ve X= 1/5 bu satırda şunu verir:

Bu serilerden ilki yakınsar (bkz. Örnek 5). Ancak o zaman “Mutlak yakınsaklık” bölümündeki teorem gereği ikinci seri de yakınsar ve yakınsaklığının bölgesi segmenttir.

Örnek 3. Kuvvet serisinin yakınsaklık bölgesini bulun

Çözüm. Burada

Formül (28)'i kullanarak serinin yakınsaklık yarıçapını buluruz:

değerleri için serinin yakınsaklığını inceleyelim. Bunları bu seride yerine koyarsak sırasıyla şunu elde ederiz:

Her iki seri de ıraksaktır çünkü yakınsama için gerekli koşul sağlanmamıştır (ortak terimleri sıfıra yönelmemektedir). Yani yakınsama aralığının her iki ucunda da bu seri ıraksar ve yakınsaklık bölgesi aralıktır.

Örnek 5. Kuvvet serisinin yakınsaklık bölgesini bulun

Çözüm. İlişkiyi nerede buluyoruz ve :

Formül (28)'e göre, bu serinin yakınsama yarıçapı

,

yani seri yalnızca şu durumlarda yakınsar X= 0 ve diğer değerler için ıraksar X.

Örnekler, yakınsama aralığının sonlarında serinin farklı davrandığını göstermektedir. Örnek 1'de seri yakınsama aralığının bir ucunda yakınsar, diğer ucunda ıraksar; örnek 2'de her iki uçta da yakınsar, örnek 3'te her iki uçta da ıraksar.

Bir güç serisinin yakınsama yarıçapı formülü, seri terimlerinin belirli bir noktadan başlayarak tüm katsayılarının sıfırdan farklı olduğu varsayımıyla elde edilir. Bu nedenle formül (28)'in kullanımına yalnızca bu durumlarda izin verilir. Bu koşul ihlal edilirse, güç serisinin yakınsaklık yarıçapı kullanılarak aranmalıdır. d'Alembert'in işareti veya değişkeni değiştirerek seriyi belirtilen koşulun sağlandığı bir forma dönüştürmek.

Örnek 6. Kuvvet serisinin yakınsaklık aralığını bulun

Çözüm. Bu seri tek dereceli terimler içermiyor X. Bu nedenle diziyi ayarlayarak dönüştürüyoruz. Sonra diziyi alıyoruz

formül (28)'i uygulayabileceğimiz yakınsama yarıçapını bulmak için. a olduğundan bu serinin yakınsaklık yarıçapı

Dolayısıyla elde ettiğimiz eşitlikten bu seri aralıkta yakınsar.

Güç serilerinin toplamı. Güç serilerinin farklılaşması ve entegrasyonu

Güç serisi için izin ver

yakınsama yarıçapı R> 0, yani bu seri aralıkta yakınsar.

Daha sonra her değer X yakınsama aralığından serinin belirli bir toplamına karşılık gelir. Bu nedenle güç serilerinin toplamı şuna bağlıdır: X yakınsama aralığında. Şununla belirtmek F(X), eşitliği yazabiliriz

bunu her noktadaki serinin toplamı anlamında anlamak X yakınsama aralığından fonksiyonun değerine eşittir F(X) Bu noktada. Aynı anlamda kuvvet serisinin (29) fonksiyona yakınsadığını söyleyeceğiz. F(X) yakınsama aralığında.

Yakınsama aralığının dışında eşitliğin (30) hiçbir anlamı yoktur.

Örnek 7. Güç serisinin toplamını bulun

Çözüm. Bu geometrik bir seridir A= 1, bir Q= X. Bu nedenle toplamı bir fonksiyondur . Bir seri eğer yakınsar ve onun yakınsama aralığıdır. Bu nedenle eşitlik

işlev yalnızca değerler için geçerlidir, ancak işlev tüm değerler için tanımlanmış X, hariç X= 1.

Güç serilerinin toplamının olduğu kanıtlanabilir. F(X) yakınsama aralığındaki herhangi bir aralıkta, özellikle serinin yakınsama aralığındaki herhangi bir noktada sürekli ve türevlenebilirdir.

Kuvvet serilerinin terim terim türevi ve integrali ile ilgili teoremleri sunalım.

Teorem 1. Yakınsama aralığındaki kuvvet serileri (30), sınırsız sayıda terim terim farklılaştırılabilir ve elde edilen kuvvet serileri, orijinal seri ile aynı yakınsama yarıçapına sahiptir ve bunların toplamları sırasıyla eşittir.

Teorem 2. Kuvvet serisi (30), 0 ile 0 arasında sınırsız sayıda terim terim entegre edilebilir. X, if , ve ortaya çıkan kuvvet serileri orijinal seriyle aynı yakınsaklık yarıçapına sahiptir ve toplamları buna uygun olarak eşittir

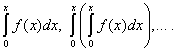
Fonksiyonların kuvvet serilerine genişletilmesi

Fonksiyon verilsin F(X), bunun bir kuvvet serisine genişletilmesi gerekiyor, yani. (30) formunda temsil edilir:

Görev katsayıları belirlemektir. sıra (30). Bunu yapmak için eşitliği (30) terimden terime ayırarak tutarlı bir şekilde şunu buluruz:

……………………………………………….. (31)

(30) ve (31) eşitliklerini varsayarsak X= 0, buluruz

Bulunan ifadeleri eşitlik (30) ile değiştirerek şunu elde ederiz:

(32)

Bazı temel fonksiyonların Maclaurin serisi açılımını bulalım.

Örnek 8. Fonksiyonu Maclaurin serisinde genişletin

Çözüm. Bu fonksiyonun türevleri fonksiyonun kendisiyle çakışmaktadır:

Bu nedenle ne zaman X= 0 elimizde

Bu değerleri formül (32)'ye değiştirerek istenen genişlemeyi elde ederiz:

(33)

Bu seri tüm sayı doğrusu üzerinde (yakınsaklık yarıçapı) yakınsar.

Eğer f(x) fonksiyonunun a noktasını içeren belirli bir aralıktaki tüm mertebelerden türevleri varsa, Taylor formülü ona uygulanabilir:
,
Nerede r n– kalan terim veya serinin geri kalanı olarak adlandırılan Lagrange formülü kullanılarak tahmin edilebilir:
burada x sayısı x ile a arasındadır.

İşlev girme kuralları:

Eğer bir değer için X r n→0 saat N→∞, limitte Taylor formülü bu değer için yakınsak hale gelir Taylor serisi:
,
Dolayısıyla, f(x) fonksiyonu aşağıdaki durumlarda x noktasında bir Taylor serisine genişletilebilir:
1) tüm mertebelerden türevleri vardır;
2) Oluşturulan seri bu noktada yakınsar.

a = 0 olduğunda, adı verilen bir seri elde ederiz. Maclaurin yakınında:
,
Maclaurin serisindeki en basit (temel) fonksiyonların genişletilmesi:
Üstel fonksiyonlar
, R=∞
Trigonometrik fonksiyonlar
, R=∞
, R=∞
, (-π/2< x < π/2), R=π/2
Actgx fonksiyonu x'in kuvvetlerine göre genişlemez çünkü ctg0=∞
Hiperbolik fonksiyonlar


Logaritmik fonksiyonlar
, -1
Binom serisi
.

Örnek No.1. Fonksiyonu bir kuvvet serisine genişletin f(x)= 2X.
Çözüm. Fonksiyonun değerlerini ve türevlerini bulalım. X=0
f(x) = 2X, F( 0) = 2 0 =1;
f"(x) = 2X In2, F"( 0) = 2 0 ln2= ln2;
f""(x) = 2X 2 2'de, F""( 0) = 2 0 ln 2 2= ln 2 2;
…
f(n)(x) = 2X içinde N 2, f(n)( 0) = 2 0 içinde N 2=ln N 2.
Türevlerin elde edilen değerlerini Taylor serisi formülüne değiştirerek şunu elde ederiz:

Bu serinin yakınsaklık yarıçapı sonsuza eşit olduğundan bu genişleme -∞ için geçerlidir.<X<+∞.

Örnek No. 2. Taylor serisini kuvvetlerle yazın ( X+4) işlev için f(x)= e X.
Çözüm. e fonksiyonunun türevlerini bulma X ve değerleri bu noktada X=-4.
f(x)= e X, F(-4) = e -4 ;
f"(x)= e X, F"(-4) = e -4 ;
f""(x)= e X, F""(-4) = e -4 ;
…
f(n)(x)= e X, f(n)( -4) = e -4 .
Bu nedenle, fonksiyonun gerekli Taylor serisi şu şekildedir:

Bu genişleme -∞ için de geçerlidir.<X<+∞.

Örnek No. 3. Bir işlevi genişlet f(x)=n X bir dizi güçte ( X- 1),
(yani noktanın yakınındaki Taylor serisinde X=1).
Çözüm. Bu fonksiyonun türevlerini bulun.
f(x)=lnx , , , ,

f(1)=ln1=0, f"(1)=1, f""(1)=-1, f"""(1)=1*2,..., f (n) =(- 1) n-1 (n-1)!
Bu değerleri formülde değiştirerek istenilen Taylor serisini elde ederiz:

D'Alembert testini kullanarak serinin ½x-1½ noktasında yakınsadığını doğrulayabilirsiniz.<1 . Действительно,

½ ise seri yakınsar X- 1½<1, т.е. при 0<X<2. При X=2 Leibniz kriterinin koşullarını karşılayan bir alternatif seri elde ederiz. x=0 olduğunda fonksiyon tanımlı değildir. Dolayısıyla Taylor serisinin yakınsaklık bölgesi yarı açık aralıktır (0;2).

Örnek No. 4. Fonksiyonu bir kuvvet serisine genişletin.
Çözüm. Genişletme (1)'de x'i -x 2 ile değiştirirsek şunu elde ederiz:
, -∞

Örnek No. 5. Fonksiyonu bir Maclaurin serisine genişletin.
Çözüm. Sahibiz
Formül (4)'ü kullanarak şunu yazabiliriz:

Formülde x yerine –x koyarsak şunu elde ederiz:

Buradan şunu buluruz: ln(1+x)-ln(1-x) = -
Parantezleri açıp serinin terimlerini yeniden düzenleyip benzer terimleri getirerek şunu elde ederiz:
. Bu seri (-1;1) aralığında yakınsar çünkü her biri bu aralıkta yakınsayan iki seriden elde edilir.

Yorum .
Formüller (1)-(5), karşılık gelen fonksiyonları bir Taylor serisine genişletmek için de kullanılabilir; fonksiyonları pozitif tamsayı kuvvetleriyle genişletmek için ( Ha). Bunu yapmak için, (1)-(5) fonksiyonlarından birini elde etmek amacıyla belirli bir fonksiyon üzerinde bu tür özdeş dönüşümleri gerçekleştirmek gerekir; bunun yerine X maliyetler k( Ha) m , burada k sabit bir sayıdır, m ise pozitif bir tam sayıdır. Değişkende değişiklik yapmak genellikle uygundur T=Ha ve elde edilen fonksiyonu Maclaurin serisinde t'ye göre genişletin.

Bu yöntem, bir fonksiyonun kuvvet serisindeki açılımının benzersizliği hakkındaki teoreme dayanmaktadır. Bu teoremin özü, açılımı ne şekilde yapılırsa yapılsın, aynı noktanın komşuluğunda aynı fonksiyona yakınsayacak iki farklı kuvvet serisinin elde edilememesidir.

Örnek No. 5a. Fonksiyonu bir Maclaurin serisinde genişletin ve yakınsaklık bölgesini belirtin.
Çözüm. İlk önce 1-x-6x 2 =(1-3x)(1+2x) ,'yi buluyoruz.
ilkokula:

3/(1-3x) kesri, |3x| ise, paydası 3x olan sonsuz azalan geometrik ilerlemenin toplamı olarak düşünülebilir.< 1. Аналогично, дробь 2/(1+2x) как сумму бесконечно убывающей геометрической прогрессии знаменателем -2x, если |-2x| < 1. В результате получим разложение в степенной ряд

yakınsama bölgesi ile |x|< 1/3.

Örnek No. 6. Fonksiyonu x = 3 noktası civarında bir Taylor serisine genişletin.
Çözüm. Bu problem, daha önce olduğu gibi, fonksiyonun türevlerini ve değerlerini bulmamız gereken Taylor serisinin tanımı kullanılarak çözülebilir. X=3. Ancak mevcut genişletmeyi kullanmak daha kolay olacaktır (5):
=
Ortaya çıkan seri veya –3'te yakınsar

Örnek No. 7. Taylor serisini ln(x+2) fonksiyonunun (x -1) kuvvetlerine yazın.
Çözüm.


Seri , veya -2'de yakınsar< x < 5.

Örnek No. 8. f(x)=sin(πx/4) fonksiyonunu x =2 noktası yakınındaki bir Taylor serisine genişletin.
Çözüm. Değiştirmeyi t=x-2 yapalım:

X'in yerine π / 4 t'yi koyduğumuz genişleme (3)'ü kullanarak şunu elde ederiz:

Ortaya çıkan seri verilen fonksiyona -∞ noktasında yakınsar< π / 4 t<+∞, т.е. при (-∞Böylece,
, (-∞

Güç serilerini kullanarak yaklaşık hesaplamalar

• ortaya çıkan seri dönüşümlü ise aşağıdaki özellik kullanılır: Leibniz koşullarını karşılayan alternatif bir seri için serinin geri kalanı mutlak değer olarak ilk atılan terimi aşmaz.
• Belirli bir seri sabit işaretliyse, o zaman atılan terimlerden oluşan seri, sonsuz azalan geometrik ilerlemeyle karşılaştırılır.
• genel durumda Taylor serisinin geri kalanını tahmin etmek için Lagrange formülünü kullanabilirsiniz: a X ).

Örnek No.1. ln(3)'ü en yakın 0,01'e kadar hesaplayın.
Çözüm. x=1/2 olan açılımı kullanalım (önceki konudaki örnek 5'e bakınız):

Açılımın ilk üç teriminden sonra kalan kısmı atıp atamayacağımızı kontrol edelim; bunu yapmak için sonsuz azalan geometrik ilerlemenin toplamını kullanarak hesaplayacağız:

Böylece bu kalanı atıp şunu elde edebiliriz:

Örnek No. 2. En yakın 0,0001'e kadar hesaplayın.
Çözüm. Binom serisini kullanalım. 5 3, 130'a en yakın bir tam sayının küpü olduğundan, 130 sayısının 130 = 5 3 +5 olarak temsil edilmesi önerilir.



Leibniz kriterini karşılayan sonuçta ortaya çıkan alternatif serinin dördüncü terimi zaten gerekli doğruluktan daha az olduğundan:
, dolayısıyla o ve onu takip eden terimler atılabilir.
Pratik olarak gerekli olan pek çok belirli veya uygunsuz integral, Newton-Leibniz formülü kullanılarak hesaplanamaz, çünkü uygulaması, temel fonksiyonlarda genellikle bir ifadeye sahip olmayan antiderivatifin bulunmasıyla ilişkilidir. Aynı zamanda bir antiderivatif bulmak da mümkündür, ancak bu gereksiz derecede emek yoğundur. Bununla birlikte, eğer integral fonksiyonu bir kuvvet serisine genişletilirse ve integralin sınırları bu serinin yakınsama aralığına aitse, o zaman integralin önceden belirlenmiş bir doğrulukla yaklaşık olarak hesaplanması mümkündür.

Örnek No. 3. ∫ 0 1 4 sin (x) x'in integralini 10 -5 dahilinde hesaplayın.
Çözüm. Karşılık gelen belirsiz integral temel fonksiyonlarda ifade edilemez, yani. “kalıcı olmayan bir integrali” temsil eder. Newton-Leibniz formülü burada uygulanamaz. İntegrali yaklaşık olarak hesaplayalım.
Günah serisini terime bölme X Açık X, şunu elde ederiz:

Bu seriyi terim terim entegre ederek (integrasyonun sınırları bu serinin yakınsama aralığına ait olduğundan bu mümkündür), şunu elde ederiz:

Ortaya çıkan seri Leibniz koşullarını sağladığından ve istenilen değeri belirli bir doğrulukla elde etmek için ilk iki terimin toplamını almak yeterlidir.
Böylece buluyoruz
.

Örnek No. 4. ∫ 0 1 4 e x 2 integralini 0,001 doğrulukla hesaplayın.
Çözüm.
. Ortaya çıkan serinin ikinci teriminden sonra kalan kısmı atıp atamayacağımızı kontrol edelim.
0,0001<0.001. Следовательно, .