Trigonometrik fonksiyonların değer tablosu
Not. Bu trigonometrik fonksiyon değerleri tablosu, karekökü temsil etmek için √ işaretini kullanır. Kesir belirtmek için “/” sembolünü kullanın.
Ayrıca bakınız faydalı malzemeler:
İçin trigonometrik bir fonksiyonun değerini belirleme trigonometrik fonksiyonu gösteren çizginin kesişiminde bulun. Örneğin, sinüs 30 derece - günah (sinüs) başlıklı sütunu ararız ve bu tablo sütununun "30 derece" satırıyla kesişimini buluruz, kesişme noktalarında sonucu okuruz - yarım. Benzer şekilde buluyoruz kosinüs 60 derece, sinüs 60 derece (bir kez daha günah sütunu ile 60 derece çizgisinin kesişiminde sin 60 = √3/2 değerini buluyoruz), vb. Diğer “popüler” açıların sinüs, kosinüs ve teğet değerleri de aynı şekilde bulunur.
Radyan cinsinden sinüs pi, kosinüs pi, teğet pi ve diğer açılar
Aşağıdaki kosinüs, sinüs ve tanjant tablosu aynı zamanda bağımsız değişkeni olan trigonometrik fonksiyonların değerini bulmak için de uygundur. radyan cinsinden verilmiştir. Bunu yapmak için açı değerlerinin ikinci sütununu kullanın. Bu sayede popüler açıların değerini dereceden radyana çevirebilirsiniz. Örneğin ilk satırdaki 60 derecelik açıyı bulalım ve altındaki değerini radyan cinsinden okuyalım. 60 derece π/3 radyana eşittir.
Pi sayısı, çevrenin açının derece ölçüsüne bağımlılığını açıkça ifade eder. Böylece pi radyan 180 dereceye eşittir.
Pi (radyan) cinsinden ifade edilen herhangi bir sayı, pi (π) 180 ile değiştirilerek kolaylıkla dereceye dönüştürülebilir..
Örnekler:
1. sinüs pi.
günah π = günah 180 = 0
dolayısıyla pi'nin sinüsü 180 derecenin sinüsüne eşittir ve sıfıra eşittir.
2. Kosinüs pi.
cos π = cos 180 = -1
dolayısıyla pi'nin kosinüsü 180 derecenin kosinüsüne eşittir ve eksi bire eşittir.
3. Teğet pi
tg π = tg 180 = 0
dolayısıyla teğet pi, 180 derece teğet ile aynıdır ve sıfıra eşittir.
0 - 360 derece açılar için sinüs, kosinüs, teğet değerleri tablosu (ortak değerler)
|
açı α değeri (derece) |
açı α değeri (pi aracılığıyla) |
günah (sinüs) |
çünkü (kosinüs) |
tg (teğet) |
ctg (kotanjant) |
saniye (sekant) |
kosaniye (kosekant) |
| 0 | 0 | 0 | 1 | 0 | - | 1 | - |
| 15 | π/12 | 2 - √3 | 2 + √3 | ||||
| 30 | π/6 | 1/2 | √3/2 | 1/√3 | √3 | 2/√3 | 2 |
| 45 | π/4 | √2/2 | √2/2 | 1 | 1 | √2 | √2 |
| 60 | π/3 | √3/2 | 1/2 | √3 | 1/√3 | 2 | 2/√3 |
| 75 | 5π/12 | 2 + √3 | 2 - √3 | ||||
| 90 | π/2 | 1 | 0 | - | 0 | - | 1 |
| 105 | 7π/12 |
- |
- 2 - √3 | √3 - 2 | |||
| 120 | 2π/3 | √3/2 | -1/2 | -√3 | -√3/3 | ||
| 135 | 3π/4 | √2/2 | -√2/2 | -1 | -1 | -√2 | √2 |
| 150 | 5π/6 | 1/2 | -√3/2 | -√3/3 | -√3 | ||
| 180 | π | 0 | -1 | 0 | - | -1 | - |
| 210 | 7π/6 | -1/2 | -√3/2 | √3/3 | √3 | ||
| 240 | 4π/3 | -√3/2 | -1/2 | √3 | √3/3 | ||
| 270 | 3π/2 | -1 | 0 | - | 0 | - | -1 |
| 360 | 2π | 0 | 1 | 0 | - | 1 | - |
Trigonometrik fonksiyonların değerleri tablosunda fonksiyon değeri yerine bir çizgi belirtilirse (teğet (tg) 90 derece, kotanjant (ctg) 180 derece), o zaman açının derece ölçüsünün belirli bir değeri için fonksiyon belirli bir değeri yoktur. Çizgi yoksa hücre boştur, bu da gerekli değeri henüz girmediğimiz anlamına gelir. En yaygın açı değerlerinin kosinüs, sinüs ve teğet değerlerine ilişkin mevcut verilerin çoğunu çözmek için oldukça yeterli olmasına rağmen, kullanıcıların bize hangi sorguları getirdiğiyle ilgileniyoruz ve tabloyu yeni değerlerle destekliyoruz. sorunlar.
En popüler açılar için sin, cos, tg trigonometrik fonksiyonların değer tablosu
0, 15, 30, 45, 60, 90... 360 derece
(sayısal değerler “Bradis tablolarına göre”)
| açı α değeri (derece) | radyan cinsinden açı α değeri | günah (sinüs) | çünkü (kosinüs) | tg (teğet) | ctg (kotanjant) |
|---|---|---|---|---|---|
| 0 | 0 | ||||
| 15 |
0,2588 |
0,9659
|
0,2679 |
||
| 30 |
0,5000 |
0,5774 |
|||
| 45 |
0,7071 |
||||
|
0,7660 |
|||||
| 60 |
0,8660 |
0,5000
|
1,7321 |
||
|
7π/18 |
TRİGONOMETRİK FONKSİYONLARIN DEĞERLERİ TABLOSU
Trigonometrik fonksiyonların değer tablosu 0, 30, 45, 60, 90, 180, 270 ve 360 derecelik açılar ve vradyan cinsinden karşılık gelen açı değerleri için derlenmiştir. Trigonometrik fonksiyonlardan tabloda sinüs, kosinüs, tanjant, kotanjant, sekant ve kosekant gösterilmektedir. Okul örneklerini çözmenin kolaylığı için, tablodaki trigonometrik fonksiyonların değerleri, sayıların karekökünü çıkarmaya yönelik işaretleri korurken, çoğu zaman karmaşık matematiksel ifadeleri azaltmaya yardımcı olan kesir şeklinde yazılır. Teğet ve kotanjant için bazı açıların değerleri belirlenemez. Bu açıların teğet ve kotanjant değerleri için trigonometrik fonksiyonların değer tablosunda bir çizgi vardır. Bu açıların tanjant ve kotanjantlarının sonsuza eşit olduğu genel olarak kabul edilir. Ayrı bir sayfada trigonometrik fonksiyonları azaltmak için formüller vardır.
Trigonometrik fonksiyon sinüsünün değer tablosu, aşağıdaki açılara ilişkin değerleri gösterir: sin 0, sin 30, sin 45, sin 60, sin 90, sin 180, sin 270, sin 360, derece ölçüsünde karşılık gelir radyan açı ölçüsü cinsinden sin 0 pi, sin pi/6, sin pi/4, sin pi/3, sin pi/2, sin pi, sin 3 pi/2, sin 2 pi. Okul sinüs tablosu.
Trigonometrik kosinüs fonksiyonu için tablo aşağıdaki açıların değerlerini gösterir: cos 0, cos 30, cos 45, cos 60, cos 90, cos 180, cos 270, cos 360 derece cinsinden, bu cos 0 pi'ye karşılık gelir , cos pi'ye 6, cos pi'ye 4, cos pi'ye 3, cos pi'ye 2, cos pi, cos 3 pi'ye 2, cos 2 pi'nin radyan açı ölçüsü. Kosinüslerin okul tablosu.
Trigonometrik tanjant fonksiyonu için trigonometrik tablo aşağıdaki açılar için değerler verir: derece ölçüsünde tg 0, tg 30, tg 45, tg 60, tg 180, tg 360, bu da tg 0 pi, tg pi/6'ya karşılık gelir, tg pi/4, tg pi/3, tg pi, tg 2 pi radyan açı ölçüsü olarak. Trigonometrik tanjant fonksiyonlarının aşağıdaki değerleri tan 90, tan 270, tan pi/2, tan 3 pi/2 olarak tanımlanmamıştır ve sonsuza eşit kabul edilir.
Trigonometrik tablodaki trigonometrik fonksiyon kotanjantı için aşağıdaki açıların değerleri verilmiştir: derece ölçüsünde ctg 30, ctg 45, ctg 60, ctg 90, ctg 270, bu da ctg pi/6, ctg pi/4'e karşılık gelir. , ctg pi/3, tg pi/ 2, tan 3 pi/2 radyan açı ölçüsü cinsinden. Trigonometrik kotanjant fonksiyonlarının aşağıdaki değerleri ctg 0, ctg 180, ctg 360, ctg 0 pi, ctg pi, ctg 2 pi olarak tanımlanmamıştır ve sonsuza eşit kabul edilir.
Trigonometrik fonksiyonların sekant ve kosekant değerleri sinüs, kosinüs, tanjant, kotanjant gibi derece ve radyan cinsinden aynı açılar için verilmiştir.

Standart olmayan açıların trigonometrik fonksiyonlarının değer tablosu, açılar için sinüs, kosinüs, teğet ve kotanjant değerlerini 15, 18, 22,5, 36, 54, 67,5 72 derece ve radyan pi/12 cinsinden gösterir. , pi/10, pi/ 8, pi/5, 3pi/8, 2pi/5 radyan. Okul örneklerinde kesirlerin azaltılmasını kolaylaştırmak için trigonometrik fonksiyonların değerleri kesir ve karekök cinsinden ifade edilmiştir.

Üç trigonometri canavarı daha. Birincisi 1,5 bir buçuk derecenin tanjantı veya pi'nin 120'ye bölümüdür. İkincisi pi'nin kosinüsünün 240'a bölümüdür, pi/240. En uzun olanı pi'nin kosinüsünün 17'ye bölümüdür, pi/17.

Sinüs ve kosinüs fonksiyonlarının trigonometrik değer çemberi, açının büyüklüğüne bağlı olarak sinüs ve kosinüs işaretlerini görsel olarak temsil eder. Özellikle sarışınlar için karışıklığı azaltmak amacıyla kosinüs değerlerinin altı yeşil çizgi ile çizilmiştir. Radyanlar pi cinsinden ifade edildiğinde derecelerin radyana dönüşümü de çok açık bir şekilde sunulur.

Bu trigonometrik tablo, bir derecelik aralıklarla 0 sıfırdan 90 doksan dereceye kadar olan açılar için sinüs, kosinüs, tanjant ve kotanjant değerlerini sunar. İlk kırk beş derece için tablonun üst kısmındaki trigonometrik fonksiyonların adlarına bakılmalıdır. İlk sütunda dereceler bulunur, sonraki dört sütunda sinüs, kosinüs, teğet ve kotanjantların değerleri yazılır.
Kırk beş dereceden doksan dereceye kadar olan açılar için trigonometrik fonksiyonların isimleri tablonun alt kısmına yazılmıştır. Son sütunda dereceler bulunur; kosinüslerin, sinüslerin, kotanjantların ve teğetlerin değerleri önceki dört sütunda yazılmıştır. Trigonometrik tablonun alt kısmında yer alan trigonometrik fonksiyonların adları, tablonun üst kısmındaki adlardan farklı olduğundan dikkatli olmalısınız. Sinüsler ve kosinüsler tıpkı teğet ve kotanjant gibi yer değiştirir. Bunun nedeni trigonometrik fonksiyonların değerlerinin simetrisidir.

Trigonometrik fonksiyonların işaretleri yukarıdaki şekilde gösterilmiştir. Sinüs, 0 ila 180 derece veya 0 ila pi arasında pozitif değerlere sahiptir. Sinüs, 180'den 360 dereceye veya pi'den 2 pi'ye kadar negatif değerlere sahiptir. Kosinüs değerleri 0 ila 90 ve 270 ila 360 derece veya 0 ila 1/2 pi ve 3/2 ila 2 pi arasında pozitiftir. Teğet ve kotanjant, 0 ila 90 derece ve 180 ila 270 derece pozitif değerlere sahiptir ve 0 ila 1/2 pi ve pi ila 3/2 pi değerlerine karşılık gelir. Teğet ve kotanjantın negatif değerleri 90 ila 180 derece ve 270 ila 360 derece veya 1/2 pi ila pi ve 3/2 pi ila 2 pi arasındadır. 360 dereceden veya 2 pi'den büyük açılar için trigonometrik fonksiyonların işaretlerini belirlerken bu fonksiyonların periyodiklik özelliklerini kullanmalısınız.
Trigonometrik fonksiyonlar sinüs, tanjant ve kotanjant tek fonksiyonlardır. Negatif açılar için bu fonksiyonların değerleri negatif olacaktır. Kosinüs çift trigonometrik bir fonksiyondur; negatif bir açının kosinüs değeri pozitif olacaktır. Trigonometrik fonksiyonları çarparken ve bölerken işaret kurallarına uyulmalıdır.
Trigonometrik sinüs fonksiyonuna ilişkin değer tablosu aşağıdaki açılara ilişkin değerleri gösterir
BelgeAyrı bir sayfada azaltma formülleri var trigonometrikişlevler. İÇİNDE masadeğerlerİçintrigonometrikişlevlersinüsverildideğerlerİçinaşağıdakiköşeler: günah 0, günah 30, günah 45 ...
Önerilen matematiksel aparat, herhangi bir sayıda n serbestlik derecesine sahip n boyutlu hiper karmaşık sayılar için karmaşık hesabın tam bir analoğudur ve doğrusal olmayan matematiksel modelleme için tasarlanmıştır.
Belge... işlevler eşittir işlevler görüntüler. Bu teoremden yapmalı, Ne İçin U, V koordinatlarını bulmak, hesaplamak için yeterlidir işlev... geometri; polinar işlevler(iki boyutlunun çok boyutlu analogları trigonometrikişlevler), bunların özellikleri, tablolar ve başvuru; ...
- MÖ beşinci yüzyılda, antik Yunan filozofu Elea'lı Zeno, en ünlüsü "Aşil ve Kaplumbağa" aporia'sı olan ünlü aporialarını formüle etti. İşte kulağa nasıl geliyor:
Diyelim ki Aşil kaplumbağadan on kat daha hızlı koşuyor ve onun bin adım gerisinde. Aşil'in bu mesafeyi koştuğu süre boyunca kaplumbağa aynı yönde yüz adım kadar sürünecektir. Aşil yüz adım koştuğunda kaplumbağa on adım daha sürünür ve bu böyle devam eder. Bu süreç sonsuza kadar devam edecek, Aşil kaplumbağaya asla yetişemeyecek.
Bu akıl yürütme sonraki tüm nesiller için mantıksal bir şok oldu. Aristoteles, Diogenes, Kant, Hegel, Hilbert... Hepsi öyle ya da böyle Zeno'nun açmazını değerlendirdiler. Şok o kadar güçlüydü ki " ... tartışmalar bugüne kadar devam ediyor; bilim camiası paradoksların özü hakkında henüz ortak bir görüşe varamadı ... konunun incelenmesine matematiksel analiz, küme teorisi, yeni fiziksel ve felsefi yaklaşımlar dahil edildi. ; hiçbiri soruna genel kabul görmüş bir çözüm olmadı..."[Wikipedia, "Zeno'nun Aporia'sı". Herkes kandırıldığını anlıyor ama kimse aldatmanın neyden oluştuğunu anlamıyor.
Matematiksel bir bakış açısından Zeno, çıkmazında nicelikten niceliğe geçişi açıkça gösterdi. Bu geçiş, kalıcı olanların yerine uygulamayı ima etmektedir. Anladığım kadarıyla değişken ölçü birimlerini kullanmaya yönelik matematiksel aparat ya henüz geliştirilmedi ya da Zeno'nun açmazına uygulanmadı. Her zamanki mantığımızı uygulamak bizi tuzağa düşürür. Biz, düşüncenin ataleti nedeniyle, karşılıklı değere sabit zaman birimleri uyguluyoruz. Fiziksel açıdan bakıldığında bu, Aşil'in kaplumbağaya yetiştiği anda tamamen durana kadar zamanın yavaşlaması gibi görünüyor. Zaman durursa Aşil kaplumbağadan daha fazla koşamaz.
Her zamanki mantığımızı tersine çevirirsek her şey yerli yerine oturur. Aşil sabit hızla koşar. Yolunun sonraki her bölümü bir öncekinden on kat daha kısadır. Buna göre, bunun üstesinden gelmek için harcanan süre bir öncekine göre on kat daha azdır. Bu duruma “sonsuzluk” kavramını uygularsak o zaman “Aşil kaplumbağaya sonsuz hızla yetişecek” demek doğru olur.
Bu mantıksal tuzaktan nasıl kaçınılır? Sabit zaman birimlerinde kalın ve karşılıklı birimlere geçmeyin. Zeno'nun dilinde şöyle görünür:
Aşil'in bin adım koşması gereken sürede kaplumbağa aynı yönde yüz adım koşacaktır. Bir sonraki birinciye eşit zaman aralığında Aşil bin adım daha koşacak ve kaplumbağa yüz adım daha sürünecektir. Artık Aşil kaplumbağanın sekiz yüz adım ilerisindedir.
Bu yaklaşım, herhangi bir mantıksal paradoks olmaksızın gerçekliği yeterince tanımlamaktadır. Ancak bu soruna tam bir çözüm değildir. Einstein'ın ışık hızının karşı konulmazlığıyla ilgili açıklaması Zeno'nun "Aşil ve Kaplumbağa" açmazına çok benziyor. Hala bu sorunu incelememiz, yeniden düşünmemiz ve çözmemiz gerekiyor. Ve çözümün sonsuz büyük sayılarda değil, ölçü birimlerinde aranması gerekiyor.
Zeno'nun bir başka ilginç açmazı da uçan bir oktan bahseder:
Uçan ok, zamanın her anında hareketsiz olduğundan hareketsizdir ve zamanın her anında hareketsiz olduğundan daima hareketsizdir.
Bu açmazda, mantıksal paradoksun üstesinden çok basit bir şekilde gelinir - uçan bir okun uzayın farklı noktalarında hareketsiz olduğunu, yani aslında hareket olduğunu açıklığa kavuşturmak yeterlidir. Burada bir başka noktaya dikkat çekmek gerekiyor. Yoldaki bir arabanın bir fotoğrafından ne hareketinin gerçekliğini ne de ona olan mesafeyi belirlemek imkansızdır. Bir arabanın hareket edip etmediğini belirlemek için aynı noktadan farklı zamanlarda çekilmiş iki fotoğrafa ihtiyacınız vardır, ancak onlara olan mesafeyi belirleyemezsiniz. Bir arabaya olan mesafeyi belirlemek için, uzayın farklı noktalarından aynı anda çekilmiş iki fotoğrafa ihtiyacınız vardır, ancak bunlardan hareketin gerçeğini belirleyemezsiniz (tabii ki hesaplamalar için yine de ek verilere ihtiyacınız var, trigonometri size yardımcı olacaktır) ). Özellikle dikkat çekmek istediğim şey, zamandaki iki nokta ile uzaydaki iki noktanın birbirine karıştırılmaması gereken farklı şeyler olmasıdır, çünkü bunlar araştırma için farklı fırsatlar sunar.
4 Temmuz 2018 Çarşamba
Küme ve çoklu küme arasındaki farklar Vikipedi'de çok iyi anlatılmıştır. Görelim.
Gördüğünüz gibi “bir kümede iki özdeş eleman olamaz” ama bir kümede özdeş elemanlar varsa bu kümeye “çoklu küme” denir. Makul varlıklar bu kadar saçma mantığı asla anlayamayacaklar. Bu, “tamamen” kelimesinden zekası olmayan, konuşan papağanların ve eğitimli maymunların seviyesidir. Matematikçiler bize saçma fikirlerini vaaz eden sıradan eğitmenler gibi davranırlar.
Bir zamanlar köprüyü inşa eden mühendisler, köprüyü test ederken köprünün altında bir teknedeydiler. Köprü çökerse, vasat mühendis, yarattığı eserin enkazı altında öldü. Köprünün yüke dayanabilmesi durumunda yetenekli mühendis başka köprüler de inşa etti.
Matematikçiler "dikkat edin, evdeyim" veya daha doğrusu "matematik soyut kavramları inceler" ifadesinin arkasına ne kadar saklanırsa saklansınlar, onları gerçeklikle ayrılmaz bir şekilde bağlayan bir göbek bağı vardır. Bu göbek bağı paradır. Matematiksel küme teorisini matematikçilerin kendilerine uygulayalım.
Matematiği çok iyi çalıştık ve şimdi kasanın başında oturup maaş dağıtıyoruz. Yani bir matematikçi parası için bize geliyor. Tutarın tamamını ona sayıyoruz ve içine aynı değerdeki banknotları koyduğumuz farklı yığınlar halinde masamızın üzerine koyuyoruz. Daha sonra her yığından bir banknot alıyoruz ve matematikçiye "matematiksel maaş seti"ni veriyoruz. Matematikçiye, kalan banknotları ancak özdeş elemanları olmayan bir kümenin, aynı elemanları olan bir kümeye eşit olmadığını kanıtladığında alacağını açıklayalım. Eğlencenin başladığı yer burasıdır.
Öncelikle milletvekillerinin mantığı işleyecek: “Bu başkalarına da uygulanabilir ama bana uygulanamaz!” Daha sonra bize, aynı değerdeki banknotların farklı banknot numaralarına sahip olduğu, yani aynı unsurlar olarak kabul edilemeyecekleri konusunda güvence vermeye başlayacaklar. Tamam, maaşları madeni para cinsinden sayalım - madeni paraların üzerinde rakam yok. Burada matematikçi çılgınca fiziği hatırlamaya başlayacak: farklı madeni paraların farklı miktarda kirleri var, kristal yapısı ve atomların düzeni her madeni para için benzersizdir...
Ve şimdi en ilginç sorum var: Çoklu kümenin elemanlarının bir kümenin elemanlarına dönüştüğü ve bunun tersinin de geçerli olduğu çizgi nerede? Böyle bir çizgi yok - her şeye şamanlar karar veriyor, bilim burada yalan söylemeye bile yakın değil.
Buraya bak. Aynı saha alanına sahip futbol stadyumlarını seçiyoruz. Alanların alanları aynıdır; bu da bir çoklu kümeye sahip olduğumuz anlamına gelir. Ancak aynı stadyumların isimlerine baktığımızda çok sayıda isim görüyoruz çünkü isimler farklı. Gördüğünüz gibi aynı eleman kümesi hem bir küme hem de çoklu kümedir. Hangisi doğru? Ve burada matematikçi-şaman-keskinci kolundan bir koz çıkarır ve bize ya bir kümeden ya da bir çoklu kümeden bahsetmeye başlar. Her durumda bizi haklı olduğuna ikna edecektir.
Modern şamanların küme teorisini gerçekliğe bağlayarak nasıl çalıştığını anlamak için bir soruyu yanıtlamak yeterlidir: Bir kümenin öğeleri başka bir kümenin öğelerinden nasıl farklıdır? Size "tek bir bütün olarak düşünülemez" veya "tek bir bütün olarak düşünülemez" olmadan göstereceğim.
18 Mart 2018 Pazar
Bir sayının rakamlarının toplamı, şamanların tef ile dansıdır ve bunun matematikle hiçbir ilgisi yoktur. Evet, matematik derslerinde bize bir sayının rakamlarının toplamını bulmamız ve bunu kullanmamız öğretilir, ancak bu yüzden onlar şamandırlar, nesillerine becerilerini ve bilgeliğini öğretmek için çalışırlar, aksi takdirde şamanlar yok olup giderler.
Kanıta mı ihtiyacınız var? Wikipedia'yı açın ve "Bir sayının rakamlarının toplamı" sayfasını bulmaya çalışın. O yok. Matematikte herhangi bir sayının rakamlarının toplamını bulmak için kullanılabilecek bir formül yoktur. Sonuçta sayılar, sayıları yazdığımız grafik sembollerdir ve matematik dilinde görev şu şekildedir: "Herhangi bir sayıyı temsil eden grafik sembollerin toplamını bulun." Matematikçiler bu problemi çözemezler ama şamanlar bunu kolaylıkla yapabilirler.
Belirli bir sayının rakamlarının toplamını bulmak için ne ve nasıl yapacağımızı bulalım. Peki elimizde 12345 sayısı var. Bu sayının rakamlarının toplamını bulmak için ne yapılması gerekiyor? Tüm adımları sırayla ele alalım.
1. Numarayı bir kağıda yazın. Ne yaptık? Sayıyı grafiksel sayı sembolüne dönüştürdük. Bu matematiksel bir işlem değil.
2. Ortaya çıkan bir resmi, ayrı sayılar içeren birkaç resme kesin. Bir resmi kesmek matematiksel bir işlem değildir.
3. Bireysel grafik sembollerini sayılara dönüştürün. Bu matematiksel bir işlem değil.
4. Ortaya çıkan sayıları ekleyin. İşte bu matematik.
12345 sayısının rakamlarının toplamı 15'tir. Bunlar matematikçilerin kullandığı şamanların "kesme ve dikme kurslarıdır". Ama hepsi bu değil.
Matematiksel açıdan bakıldığında bir sayıyı hangi sayı sisteminde yazdığımız önemli değildir. Yani farklı sayı sistemlerinde aynı sayının rakamlarının toplamı farklı olacaktır. Matematikte sayı sistemi sayının sağında alt simge olarak gösterilir. Büyük sayı olan 12345 ile kafamı kandırmak istemem, yazıdaki 26 sayısını ele alalım. Bu sayıyı ikili, sekizli, onlu ve onaltılı sayı sistemlerinde yazalım. Her adıma mikroskop altında bakmayacağız; bunu zaten yaptık. Sonuca bakalım.
Gördüğünüz gibi farklı sayı sistemlerinde aynı sayının rakamlarının toplamı farklıdır. Bu sonucun matematikle hiçbir ilgisi yoktur. Aynı dikdörtgenin alanını metre ve santimetre olarak belirlerseniz tamamen farklı sonuçlar elde edersiniz.
Sıfır tüm sayı sistemlerinde aynı görünür ve rakam toplamı yoktur. Bu, gerçeğin lehine başka bir argümandır. Matematikçilere soru: Matematikte sayı olmayan bir şey nasıl belirlenir? Ne yani, matematikçiler için sayılardan başka hiçbir şey yok mu? Buna şamanlar için izin verebilirim ama bilim adamları için izin veremem. Gerçeklik sadece sayılardan ibaret değildir.
Elde edilen sonuç, sayı sistemlerinin sayıların ölçü birimleri olduğunun kanıtı olarak değerlendirilmelidir. Sonuçta sayıları farklı ölçü birimleriyle karşılaştıramayız. Aynı niceliğin farklı ölçü birimleriyle yapılan aynı eylemler, karşılaştırıldıktan sonra farklı sonuçlara yol açıyorsa, bunun matematikle hiçbir ilgisi yoktur.
Gerçek matematik nedir? Bu, bir matematiksel işlemin sonucunun sayının büyüklüğüne, kullanılan ölçü birimine ve bu işlemi kimin yaptığına bağlı olmadığı durumdur.
Kapıya imza at Ah! Burası kadınlar tuvaleti değil mi?
- Genç kadın! Burası, cennete yükselişleri sırasında ruhların ölümsüz kutsallığının incelenmesine yönelik bir laboratuvardır! Halo üstte ve yukarı ok. Başka hangi tuvalet?Dişi... Üstteki hale ve aşağı ok erkektir.
Böyle bir tasarım sanatı eseri günde birkaç kez gözünüzün önünden geçiyorsa,
O halde arabanızda aniden garip bir simge bulmanız şaşırtıcı değil:
Kişisel olarak ben kaka yapan bir insanda eksi dört dereceyi görmeye çalışıyorum (bir resim) (birkaç resmin birleşimi: bir eksi işareti, dört rakamı, derecelerin gösterimi). Ve bu kızın fizik bilmeyen bir aptal olduğunu düşünmüyorum. Sadece grafik görüntüleri algılama konusunda güçlü bir stereotipi var. Ve matematikçiler bize bunu her zaman öğretiyorlar. İşte bir örnek.
1A “eksi dört derece” veya “bir a” değildir. Bu "kaka yapan adam" veya onaltılık gösterimle "yirmi altı" sayısıdır. Sürekli olarak bu sayı sisteminde çalışan kişiler, sayıyı ve harfi otomatik olarak tek bir grafik sembol olarak algılarlar.
Bu makale şunları içerir: sinüs, kosinüs, teğet ve kotanjant tabloları. İlk olarak, trigonometrik fonksiyonların temel değerlerinin bir tablosunu, yani 0, 30, 45, 60, 90, ..., 360 derecelik açıların sinüs, kosinüs, teğet ve kotanjant tablosunu sunacağız ( 0, π/6, π/4, π/3, π/2, …, 2π radyan). Bundan sonra V. M. Bradis'in sinüs ve kosinüs tablosunun yanı sıra teğet ve kotanjant tablosunu vereceğiz ve trigonometrik fonksiyonların değerlerini bulurken bu tabloların nasıl kullanılacağını göstereceğiz.
Sayfada gezinme.
0, 30, 45, 60, 90, ... derecelik açılar için sinüs, kosinüs, teğet ve kotanjant tablosu
Referanslar.
- Cebir: Ders Kitabı 9. sınıf için. ortalama okul / Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova; Ed. S. A. Telyakovsky. - M .: Eğitim, 1990. - 272 s.: - ISBN 5-09-002727-7.
- Bashmakov M. I. Cebir ve analizin başlangıcı: Ders kitabı. 10-11 sınıflar için. ortalama okul - 3. baskı. - M.: Eğitim, 1993. - 351 s.: hasta. - ISBN 5-09-004617-4.
- Cebir ve analizin başlangıcı: Proc. 10-11 sınıflar için. genel eğitim kurumlar / A.N. Kolmogorov, A.M. Abramov, Yu.P. Dudnitsyn ve diğerleri; Ed. A. N. Kolmogorov - 14. baskı - M.: Eğitim, 2004. - 384 s.: - ISBN 5-09-013651-3.
- Gusev V.A., Mordkovich A.G. Matematik (teknik okullara girenler için bir el kitabı): Proc. ödenek.- M.; Daha yüksek okul, 1984.-351 s., hasta.
- Bradis V.M. Dört basamaklı matematik tabloları: Genel eğitim için. ders kitabı kuruluşlar. - 2. baskı. - M.: Bustard, 1999.- 96 s.: hasta. ISBN 5-7107-2667-2
Makalede neye benzediğini tam olarak anlayacağız trigonometrik değerler tablosu, sinüs, kosinüs, tanjant ve kotanjant. Trigonometrik fonksiyonların temel anlamını 0,30,45,60,90,...,360 derecelik açılardan ele alalım. Ve trigonometrik fonksiyonların değerlerinin hesaplanmasında bu tabloların nasıl kullanılacağını görelim.
İlk önce şuna bakalım kosinüs, sinüs, tanjant ve kotanjant tablosu 0, 30, 45, 60, 90,... derecelik bir açıdan. Bu büyüklüklerin tanımı, 0 ve 90 derecelik açıların fonksiyonlarının değerini belirlememizi sağlar:sin 0 0 =0, cos 0 0 = 1. tg 00 = 0, 00'dan kotanjant tanımsız olacaktır
sin 90 0 = 1, cos 90 0 =0, ctg90 0 = 0, 90 0'dan teğet belirsiz olacaktırAçıları 30 ile 90 derece arasında olan dik üçgenleri alırsanız. Şunu elde ederiz:
günah 30 0 = 1/2, cos 30 0 = √3/2, tan 30 0 = √3/3, cos 30 0 = √3
günah 45 0 = √2/2, cos 45 0 = √2/2, tan 45 0 = 1, cos 45 0 = 1
günah 60 0 = √3/2, cos 60 0 = 1/2, tan 60 0 =√3, cos 60 0 = √3/3Elde edilen tüm değerleri formda temsil edelim trigonometrik tablo:
Sinüs, kosinüs, teğet ve kotanjant tablosu!
İndirgeme formülünü kullanırsak tablomuz artacak ve 360 dereceye kadar olan açılar için değerler eklenecektir. Şöyle görünecek:

Ayrıca periyodiklik özelliklerine bağlı olarak açıları 0 0 +360 0 *z .... 330 0 +360 0 *z ile değiştirirsek tablo büyütülebilir; burada z bir tam sayıdır. Bu tabloda tek bir çemberdeki noktalara karşılık gelen tüm açıların değerini hesaplamak mümkündür.

Tablonun bir çözümde nasıl kullanılacağına bakalım.
Her şey çok basit. Çünkü ihtiyacımız olan değer, ihtiyacımız olan hücrelerin kesişme noktasında yatıyor. Örneğin, 60 derecelik bir açının cos değerini alın, tabloda şöyle görünecektir:
Trigonometrik fonksiyonların ana değerlerinin son tablosunda da aynı şekilde ilerliyoruz. Ancak bu tabloda 1020 derecelik açıdan tanjantın ne kadar olduğunu bulmak mümkün, = -√3 1020 0 = 300 0 +360 0 *2'yi kontrol edelim. Tabloyu kullanarak bulalım.

Bradi'nin masası. Sinüs, kosinüs, teğet ve kotanjant için.
Bradis tabloları, kosinüs ve sinüs, teğet ve kotanjant tablolarından oluşan birkaç parçaya bölünmüştür - bunlar iki parçaya bölünmüştür (90 dereceye kadar açıların tg'si ve küçük açıların ctg'si).
Sinüs ve kosinüs


00'dan başlayıp 760 ile biten açının tg'si, 140 ile başlayan ve 900 ile biten açının ctg'si.
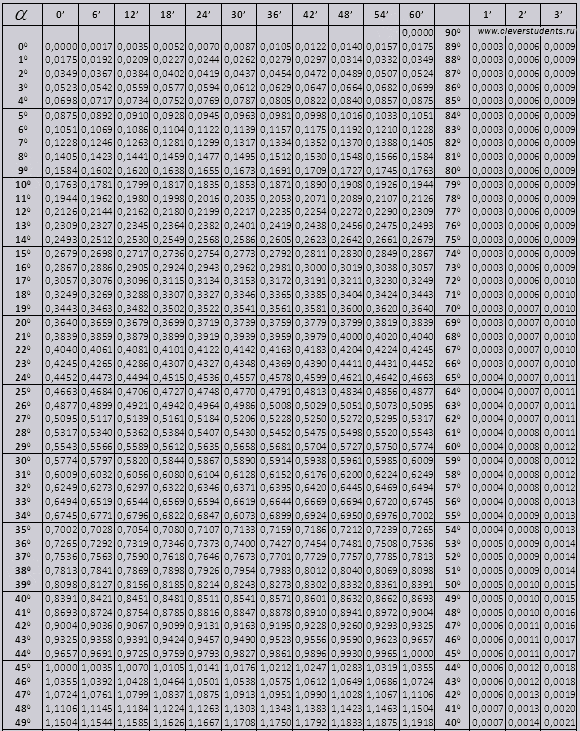

900'e kadar tg ve küçük açılardan ctg.
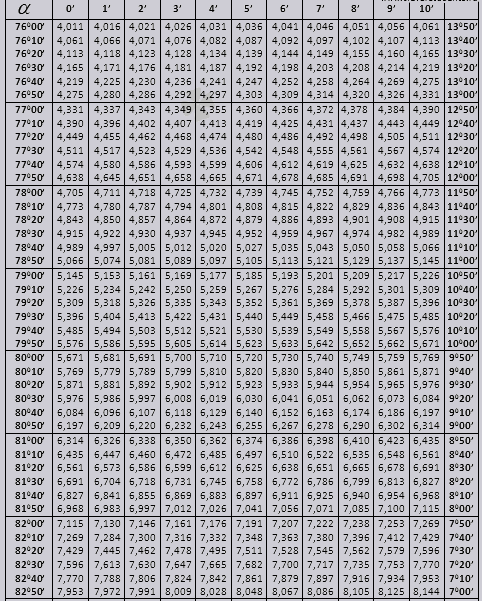

Bradis tablolarını problem çözmede nasıl kullanabileceğimizi bulalım.
Tanımlama günahını (sol kenardaki sütunda tanımlama) 42 dakika (atama üst satırda) bulalım. Kesişim yoluyla atamayı ararız, bu = 0,3040.
Dakika değerleri altı dakikalık aralıklarla belirtilir, ihtiyacımız olan değer tam olarak bu aralığın içine düşerse ne yapmalıyız. 44 dakika alalım ama tabloda sadece 42 var. 42'yi baz alıyoruz ve sağ taraftaki ek sütunları kullanarak 2. değişikliği alıp 0,3040 + 0,0006'yı ekliyoruz ve 0,3046 elde ediyoruz.
Günah 47 dakika ile 48 dakikayı esas alıyoruz ve bundan 1 düzeltme çıkarıyoruz yani 0,3057 - 0,0003 = 0,3054
Cos'u hesaplarken sin'e benzer şekilde çalışıyoruz, sadece tablonun en alt sırasını baz alıyoruz. Örneğin cos 20 0 = 0,9397
90 0'a kadar olan tg açısı ve küçük açılı cot değerleri doğrudur ve bunlarda herhangi bir düzeltme yoktur. Örneğin, tg 78 0 37dk = 4,967'yi bulun
ve ctg 20 0 13 dk = 25,83
Temel trigonometrik tablolara baktık. Bu bilgilerin sizin için son derece yararlı olduğunu umuyoruz. Tablolarla ilgili sorularınız varsa yorumlara yazmayı unutmayın!
Not: Duvar tamponları, duvarları korumaya yönelik bir tampon panelidir. Çerçevesiz duvar tamponları (http://www.spi-polymer.ru/otboyniki/) bağlantısını takip edin ve daha fazlasını öğrenin.








