Tablo açıları trigonometrisi. Tanım ve değer alanları, artan, azalan

TRİGONOMETRİK FONKSİYONLARIN DEĞERLERİ TABLOSU

Trigonometrik fonksiyonların değer tablosu 0, 30, 45, 60, 90, 180, 270 ve 360 ​​derecelik açılar ve vradyan cinsinden karşılık gelen açı değerleri için derlenmiştir. Trigonometrik fonksiyonlardan tabloda sinüs, kosinüs, tanjant, kotanjant, sekant ve kosekant gösterilmektedir. Okul örneklerini çözmenin kolaylığı için, tablodaki trigonometrik fonksiyonların değerleri, sayıların karekökünü çıkarmaya yönelik işaretleri korurken, çoğu zaman karmaşık matematiksel ifadeleri azaltmaya yardımcı olan kesir şeklinde yazılır. Teğet ve kotanjant için bazı açıların değerleri belirlenemez. Bu açıların teğet ve kotanjant değerleri için trigonometrik fonksiyonların değer tablosunda bir çizgi vardır. Bu açıların tanjant ve kotanjantlarının sonsuza eşit olduğu genel olarak kabul edilir. Ayrı bir sayfada trigonometrik fonksiyonları azaltmak için formüller vardır.

Trigonometrik fonksiyon sinüsünün değer tablosu, aşağıdaki açılara ilişkin değerleri gösterir: sin 0, sin 30, sin 45, sin 60, sin 90, sin 180, sin 270, sin 360, derece ölçüsünde karşılık gelir radyan açı ölçüsü cinsinden sin 0 pi, sin pi/6, sin pi/4, sin pi/3, sin pi/2, sin pi, sin 3 pi/2, sin 2 pi. Okul sinüs tablosu.

Trigonometrik kosinüs fonksiyonu için tablo aşağıdaki açıların değerlerini gösterir: cos 0, cos 30, cos 45, cos 60, cos 90, cos 180, cos 270, cos 360 derece cinsinden, bu cos 0 pi'ye karşılık gelir , cos pi'ye 6, cos pi'ye 4, cos pi'ye 3, cos pi'ye 2, cos pi, cos 3 pi'ye 2, cos 2 pi'nin radyan açı ölçüsü. Kosinüslerin okul tablosu.

Trigonometrik fonksiyonun tanjantı için trigonometrik tablo aşağıdaki açılar için değerler verir: derece ölçüsünde tg 0, tg 30, tg 45, tg 60, tg 180, tg 360, bu da tg 0 pi, tg pi/6'ya karşılık gelir, tg pi/4, tg pi/3, tg pi, tg 2 pi radyan açı ölçüsü olarak. Trigonometrik tanjant fonksiyonlarının aşağıdaki değerleri tan 90, tan 270, tan pi/2, tan 3 pi/2 olarak tanımlanmamıştır ve sonsuza eşit kabul edilir.

Trigonometrik tablodaki trigonometrik fonksiyon kotanjantı için aşağıdaki açıların değerleri verilmiştir: derece ölçüsünde ctg 30, ctg 45, ctg 60, ctg 90, ctg 270, bu da ctg pi/6, ctg pi/4'e karşılık gelir. , ctg pi/3, tg pi/ 2, tan 3 pi/2 radyan açı ölçüsü cinsinden. Trigonometrik kotanjant fonksiyonlarının aşağıdaki değerleri ctg 0, ctg 180, ctg 360, ctg 0 pi, ctg pi, ctg 2 pi olarak tanımlanmamıştır ve sonsuza eşit kabul edilir.

Trigonometrik fonksiyonların sekant ve kosekant değerleri sinüs, kosinüs, tanjant, kotanjant gibi derece ve radyan cinsinden aynı açılar için verilmiştir.

Standart olmayan açıların trigonometrik fonksiyonlarının değer tablosu, açılar için sinüs, kosinüs, teğet ve kotanjant değerlerini 15, 18, 22,5, 36, 54, 67,5 72 derece ve radyan pi/12 cinsinden gösterir. , pi/10, pi/ 8, pi/5, 3pi/8, 2pi/5 radyan. Okul örneklerinde kesirlerin azaltılmasını kolaylaştırmak için trigonometrik fonksiyonların değerleri kesir ve karekök cinsinden ifade edilmiştir.

Üç trigonometri canavarı daha. Birincisi 1,5 bir buçuk derecenin tanjantı veya pi'nin 120'ye bölümüdür. İkincisi pi'nin kosinüsünün 240'a bölümüdür, pi/240. En uzun olanı pi'nin kosinüsünün 17'ye bölümüdür, pi/17.

Sinüs ve kosinüs fonksiyonlarının trigonometrik değer çemberi, açının büyüklüğüne bağlı olarak sinüs ve kosinüs işaretlerini görsel olarak temsil eder. Özellikle sarışınlar için karışıklığı azaltmak amacıyla kosinüs değerlerinin altı yeşil çizgi ile çizilmiştir. Radyanlar pi cinsinden ifade edildiğinde derecelerin radyana dönüşümü de çok açık bir şekilde sunulur.

Bu trigonometrik tablo, bir derecelik aralıklarla 0 sıfırdan 90 doksan dereceye kadar olan açılar için sinüs, kosinüs, tanjant ve kotanjant değerlerini sunar. İlk kırk beş derece için tablonun üst kısmındaki trigonometrik fonksiyonların adlarına bakılmalıdır. İlk sütunda dereceler bulunur, sonraki dört sütunda sinüs, kosinüs, teğet ve kotanjantların değerleri yazılır.

Kırk beş dereceden doksan dereceye kadar olan açılar için trigonometrik fonksiyonların isimleri tablonun alt kısmına yazılmıştır. Son sütunda dereceler bulunur; kosinüslerin, sinüslerin, kotanjantların ve teğetlerin değerleri önceki dört sütunda yazılmıştır. Trigonometrik tablonun alt kısmında yer alan trigonometrik fonksiyonların adları, tablonun üst kısmındaki adlardan farklı olduğundan dikkatli olmalısınız. Sinüsler ve kosinüsler tıpkı teğet ve kotanjant gibi yer değiştirir. Bunun nedeni trigonometrik fonksiyonların değerlerinin simetrisidir.

Trigonometrik fonksiyonların işaretleri yukarıdaki şekilde gösterilmiştir. Sinüs, 0 ila 180 derece veya 0 ila pi arasında pozitif değerlere sahiptir. Sinüs, 180'den 360 dereceye veya pi'den 2 pi'ye kadar negatif değerlere sahiptir. Kosinüs değerleri 0 ila 90 ve 270 ila 360 derece veya 0 ila 1/2 pi ve 3/2 ila 2 pi arasında pozitiftir. Teğet ve kotanjant, 0 ila 90 derece ve 180 ila 270 derece arasında pozitif değerlere sahiptir ve 0 ila 1/2 pi ve pi ila 3/2 pi değerlerine karşılık gelir. Teğet ve kotanjantın negatif değerleri 90 ila 180 derece ve 270 ila 360 derece veya 1/2 pi ila pi ve 3/2 pi ila 2 pi arasındadır. 360 dereceden veya 2 pi'den büyük açılar için trigonometrik fonksiyonların işaretlerini belirlerken bu fonksiyonların periyodiklik özelliklerini kullanmalısınız.

Trigonometrik fonksiyonlar sinüs, tanjant ve kotanjant tek fonksiyonlardır. Negatif açılar için bu fonksiyonların değerleri negatif olacaktır. Kosinüs çift trigonometrik bir fonksiyondur; negatif bir açının kosinüs değeri pozitif olacaktır. Trigonometrik fonksiyonları çarparken ve bölerken işaret kurallarına uyulmalıdır.

1. Trigonometrik sinüs fonksiyonuna ilişkin değer tablosu aşağıdaki açılara ilişkin değerleri gösterir

   Belge

   Ayrı bir sayfada azaltma formülleri var trigonometrikişlevler. İÇİNDE masadeğerlerİçintrigonometrikişlevlersinüsverildideğerlerİçinaşağıdakiköşeler: günah 0, günah 30, günah 45 ...

2. Önerilen matematiksel aparat, herhangi bir sayıda serbestlik derecesi n'ye sahip n boyutlu hiper karmaşık sayılar için karmaşık hesabın tam bir analoğudur ve doğrusal olmayan matematiksel modelleme için tasarlanmıştır.

   Belge

   ... işlevler eşittir işlevler görüntüler. Bu teoremden yapmalı, Ne İçin U, V koordinatlarını bulmak, hesaplamak için yeterlidir işlev... geometri; polinar işlevler(iki boyutlunun çok boyutlu analogları trigonometrikişlevler), bunların özellikleri, tablolar ve başvuru; ...

3. Dikkat!
   Ek var
   Özel Bölüm 555'teki materyaller.
   Çok "pek değil..." olanlar için
   Ve “çok…” diyenler için)

   Öncelikle “Sinüs ve kosinüs nedir? Teğet ve kotanjant nedir?” dersinden çıkan basit ama çok faydalı bir sonucu hatırlatayım.

   Bu çıktıdır:

   Sinüs, kosinüs, teğet ve kotanjant açılarına sıkı sıkıya bağlıdır. Bir şeyi biliyoruz, bu da başka bir şeyi bildiğimiz anlamına geliyor.

   Başka bir deyişle, her açının kendine ait sabit sinüsü ve kosinüsü vardır. Ve neredeyse herkesin kendi teğet ve kotanjantı vardır. Neden neredeyse? Aşağıda bu konuda daha fazla bilgi bulabilirsiniz.

   Bu bilgi çalışmalarınızda çok yardımcı olur! Sinüslerden açılara ve sinüslerden açılara geçmeniz gereken birçok görev vardır. Bunun için var sinüs tablosu. Benzer şekilde kosinüslü görevler için - kosinüs tablosu. Ve tahmin edebileceğiniz gibi, teğet tablosu Ve kotanjant tablosu.)

   Tablolar farklı. Uzun olanlar, mesela sin37°6'nın neye eşit olduğunu görebileceğiniz yerler. Bradis tablolarını açıyoruz, otuz yedi derece altı dakikalık bir açı arıyoruz ve 0,6032 değerini görüyoruz. Bu sayıyı (ve diğer binlerce tablo değerini) hatırlamaya kesinlikle gerek olmadığı açıktır.

   Aslında günümüzde uzun kosinüs, sinüs, teğet, kotanjant tablolarına pek ihtiyaç duyulmuyor. İyi bir hesap makinesi bunların tamamen yerini alır. Ancak bu tür tabloların varlığını bilmekten zarar gelmez. Genel bilgi için.)

   Peki o zaman neden bu ders?! - sen sor.

   Ama neden? Sonsuz sayıdaki açılar arasında özel, bilmeniz gerekenler Tüm. Tüm okul geometrisi ve trigonometri bu açılar üzerine inşa edilmiştir. Bu bir tür trigonometri "çarpım tablosudur". Örneğin günah 50°'nin neye eşit olduğunu bilmiyorsanız, kimse sizi yargılamayacaktır.) Ancak günah 30°'nin neye eşit olduğunu bilmiyorsanız, hak ettiğiniz iki değeri almaya hazır olun...

   Çok özel Açılar da oldukça iyi. Okul ders kitapları genellikle nazikçe ezberleme olanağı sunar sinüs tablosu ve kosinüs tablosu on yedi açı için. Ve tabii ki teğet tablosu ve kotanjant tablosu aynı on yedi açı için... yani. 68 değerin hatırlanması önerilmektedir. Bu arada bunlar birbirine çok benziyor, ara sıra kendilerini tekrarlıyor ve işaret değiştiriyorlar. Mükemmel bir görsel hafızaya sahip olmayan bir kişi için bu oldukça zor bir görevdir...)

   Farklı bir rota izleyeceğiz. Ezberlemeyi mantık ve ustalıkla değiştirelim. Daha sonra sinüs tablosu ve kosinüs tablosu için 3 (üç!) değeri ezberlememiz gerekecek. Ve teğet tablosu ve kotanjant tablosu için 3 (üç!) değer. Hepsi bu. Bana öyle geliyor ki altı değeri hatırlamak 68'i hatırlamaktan daha kolay...)

   Güçlü bir yasal hile sayfası kullanarak bu altı kişiden gerekli diğer tüm değerleri alacağız - trigonometrik daire. Bu konuyu incelemediyseniz bağlantıyı takip edin, tembel olmayın. Bu çember sadece bu ders için gerekli değildir. O yeri doldurulamaz tüm trigonometri için aynı anda. Böyle bir aracı kullanmamak kesinlikle günahtır! İstemiyor musun? Bu senin bileceğin iş. Ezberle sinüs tablosu. Kosinüs tablosu. Teğet tablosu. Kotanjant tablosu.Çeşitli açılar için 68 değerin tümü.)

   Öyleyse başlayalım. Öncelikle tüm bu özel açıları üç gruba ayıralım.

   Birinci grup açılar.

   İlk grubu ele alalım on yedi açı özel. Bunlar 5 açıdır: 0°, 90°, 180°, 270°, 360°.

   Bu açılar için sinüs, kosinüs, teğet ve kotanjant tablosu şu şekilde görünür:

   Açı x (derece olarak)	0	90	180	270	360
   Açı x (radyan cinsinden)	0
   günah x	0	1	0	-1	0
   çünkü x	1	0	-1	0	1
   tgx	0	isim	0	isim	0
   ctgx	isim	0	isim	0	isim

   Hatırlamak isteyenler hatırlasın. Ama hemen söyleyeyim ki tüm bu birler ve sıfırlar kafada çok karışıyor. İstediğinizden çok daha güçlü.) Bu nedenle mantığı ve trigonometrik çemberi açıyoruz.

   Bir daire çiziyoruz ve üzerine aynı açıları işaretliyoruz: 0°, 90°, 180°, 270°, 360°. Bu köşeleri kırmızı noktalarla işaretledim:

   

   Bu açıların özelliğinin ne olduğu hemen anlaşılıyor. Evet! Bunlar düşen açılar tam olarak koordinat ekseninde! Aslında insanların kafası da bu yüzden karışıyor... Ama biz karışmayacağız. Fazla ezbere gerek kalmadan bu açıların trigonometrik fonksiyonlarını nasıl bulacağımızı bulalım.

   Bu arada açı konumu 0 derece tamamen örtüşüyor 360 derecelik açı pozisyonuna sahip. Bu, bu açıların sinüsleri, kosinüsleri ve teğetlerinin tamamen aynı olduğu anlamına gelir. Daireyi tamamlamak için 360 derecelik bir açı işaretledim.

   Diyelim ki Birleşik Devlet Sınavının zorlu stresli ortamında bir şekilde şüphe duydunuz... 0 derecenin sinüsü nedir? Sıfır gibi görünüyor... Ya bir olursa?! Mekanik ezberleme böyle bir şeydir. Zor şartlarda şüpheler kemirmeye başlar...)

   Sakin olun, sadece sakin olun!) Size %100 doğru cevap verecek ve tüm şüphelerinizi tamamen ortadan kaldıracak pratik bir teknik anlatacağım.

   Örnek olarak, örneğin 0 derecenin sinüsünü nasıl net ve güvenilir bir şekilde belirleyeceğimizi bulalım. Ve aynı zamanda kosinüs 0. İşin garibi, insanların çoğu zaman bu değerlerde kafası karışıyor.

   Bunu yapmak için bir daire çizin keyfi köşe X. İlk çeyrekte sıcaklık 0 dereceye yakındı. Bu açının sinüsünü ve kosinüsünü eksenlerde işaretleyelim X, her şey yolunda. Bunun gibi:

   Ve şimdi - dikkat! Açıyı azaltalım X, hareketli tarafı eksene yaklaştırın AH. İmlecinizi resmin üzerine getirin (veya tabletinizdeki resme dokunun) ve her şeyi göreceksiniz.

   Şimdi temel mantığı açalım! Bakalım ve düşünelim: X açısı azaldıkça sinx nasıl davranır? Açı sıfıra yaklaşırken? Küçülüyor! Ve cosx artar! Açı tamamen çöktüğünde sinüse ne olacağını bulmaya devam ediyor? Açının hareketli tarafı (A noktası) ne zaman OX eksenine yerleşir ve açı sıfıra eşit olur? Açıkçası, açının sinüsü sıfıra gidecek. Ve kosinüs artacak... şuna... Açının hareketli tarafının uzunluğu (trigonometrik dairenin yarıçapı) nedir? Bir!

   İşte cevap. 0 derecenin sinüsü 0'a eşittir. 0 derecenin kosinüsü 1'e eşittir. Kesinlikle çok sert ve hiç şüphe yok!) Basitçe çünkü aksi halde olamaz.

   Tam olarak aynı şekilde, örneğin 270 derecenin sinüsünü bulabilir (veya netleştirebilirsiniz). Veya kosinüs 180. Bir daire çizin, keyfiİlgimizi çeken koordinat ekseninin yanında çeyreklik bir açı, açının kenarını zihinsel olarak hareket ettirin ve açının kenarı eksene düştüğünde sinüs ve kosinüsün ne olacağını kavrayın. İşte bu.

   Gördüğünüz gibi bu açı grubu için herhangi bir şeyi ezberlemenize gerek yok. Burada gerekli değil sinüs tablosu... Evet ve kosinüs tablosu- da.) Bu arada, trigonometrik dairenin birkaç kullanımından sonra tüm bu değerler kendiliğinden hatırlanacak. Unuturlarsa 5 saniyede bir daire çizip netleştirdim. Bir arkadaşınızı tuvaletten arayıp sertifikanızı riske atmaktan çok daha kolay, değil mi?)

   Teğet ve kotanjanta gelince, her şey aynıdır. Çemberin üzerine teğet (kotanjant) bir çizgi çiziyoruz - ve her şey hemen görülebilir. Sıfıra eşit oldukları ve bulunmadığı yerler. Ne, teğet ve kotanjant doğrularını bilmiyor musun? Bu üzücü ama düzeltilebilir.) Trigonometrik çemberde Bölüm 555 Teğet ve kotanjant'ı ziyaret ettik - ve hiçbir sorun yok!

   Bu beş açı için sinüs, kosinüs, tanjant ve kotanjantı nasıl net bir şekilde tanımlayacağınızı anladıysanız tebrikler! Her ihtimale karşı, artık fonksiyonları tanımlayabileceğinizi size bildiriyorum eksenlere düşen herhangi bir açı. Ve bu 450°, 540°, 1800° ve sonsuz sayıda diğerleri...) Çemberin açısını (doğru!) saydım - ve işlevlerde herhangi bir sorun yok.

   Ancak sorunlar ve hatalar tam olarak açıların ölçülmesiyle ortaya çıkar... Bunlardan nasıl kaçınılacağı derste yazılmıştır: Trigonometrik bir daire üzerinde herhangi bir açı derece cinsinden nasıl çizilir (sayılır). Temeldir ancak hatalara karşı mücadelede çok faydalıdır.)

   İşte bir ders: Trigonometrik bir daire üzerinde herhangi bir açı radyan cinsinden nasıl çizilir (ölçülür) - daha havalı olacaktır. Olasılıklar açısından. Diyelim ki açının dört yarı eksenden hangisine düştüğünü belirleyin

   bunu birkaç saniye içinde yapabilirsiniz. Şaka yapmıyorum! Sadece birkaç saniye içinde. Tabii ki sadece 345 pi değil...) Ve 121, 16 ve -1345. Herhangi bir tam sayı katsayısı anında cevap için uygundur.

   Ve eğer köşe

   Sadece düşün! Paydası iki olan radyanların herhangi bir kesirli değeri için doğru cevap 10 saniyede elde edilir.

   Aslında trigonometrik çemberin iyi yanı da budur. Çünkü birlikte çalışabilme yeteneği bazı köşelere otomatik olarak genişler sonsuz küme köşeler

   Böylece on yedi köşeden beşini sıraladık.

   İkinci grup açılar.

   Bir sonraki açı grubu 30°, 45° ve 60° açılardır. Neden tam olarak bunlar, örneğin 20, 50 ve 80 değil? Evet, bir şekilde bu şekilde oldu... Tarihsel olarak.) Ayrıca bu açıların neden iyi olduğu da görülecek.

   Bu açılar için sinüs kosinüs teğet kotanjant tablosu şuna benzer:

   Açı x (derece olarak)	0	30	45	60	90
   Açı x (radyan cinsinden)	0
   günah x	0				1
   çünkü x	1				0
   tgx	0		1		isim
   ctgx	isim		1		0

   Resmi tamamlamak için önceki tablodaki 0° ve 90° değerlerini bıraktım.) Böylece bu açıların ilk çeyrekte yattığını ve arttığını görebilirsiniz. 0'dan 90'a. Bu daha sonra işimize yarayacak.

   30°, 45° ve 60° açılar için tablo değerleri mutlaka hatırlanmalıdır. İsterseniz ezberleyin. Ancak burada da hayatınızı kolaylaştıracak bir fırsat var.) sinüs tablosu değerleri bu açılar. Ve şununla karşılaştır: kosinüs tablosu değerleri...

   Evet! Onlar aynı olanlar! Sadece ters sırada düzenlenmiştir. Açılar artar (0, 30, 45, 60, 90) - ve sinüs değerleri arttırmak 0'dan 1'e kadar. Hesap makinesiyle kontrol edebilirsiniz. Ve kosinüs değerleri azalıyor 1'den sıfıra. Üstelik değerlerin kendisi aynı olanlar. 20, 50, 80'lik açılar için bu işe yaramaz...

   Bu yararlı bir sonuçtur. Öğrenmen yeterli üç 30, 45, 60 derecelik açılar için değerler. Ve sinüs için arttığını ve kosinüs için azaldıklarını unutmayın. Sinüse doğru.) Yarı yolda buluşurlar (45°), yani 45 derecenin sinüsü 45 derecenin kosinüsüne eşittir. Sonra yine ayrışıyorlar... Üç anlam öğrenilebilir değil mi?

   Teğetler - kotanjantlar ile resim tamamen aynıdır. Bire bir. Sadece anlamları farklıdır. Bu değerlerin (üç tane daha!) öğrenilmesi de gerekiyor.

   Eh, ezberlemenin neredeyse tamamı bitti. Eksene düşen beş açının değerlerinin nasıl belirleneceğini (umarız) anladınız ve 30, 45, 60 derecelik açıların değerlerini öğrendiniz. Toplam 8.

   Geriye 9 kornerden oluşan son grupla ilgilenmek kalıyor.

   Bunlar açılardır:
   120°; 135°; 150°; 210°; 225°; 240°; 300°; 315°; 330°. Bu açılar için sinüs tablosunu, kosinüs tablosunu vb. bilmeniz gerekir.

   Kabus, değil mi?)

   Peki buraya 405°, 600° veya 3000° gibi açılar ve eşit derecede güzel birçok açı eklerseniz?)

   Veya radyan cinsinden açılar mı? Örneğin açılar hakkında:

   

   ve bilmeniz gereken daha birçok kişi Tüm.

   En komik şey bunu bilmek Tüm - prensipte imkansızdır. Mekanik bellek kullanıyorsanız.

   Ve eğer trigonometrik bir daire kullanırsanız, bu çok kolaydır, aslında basittir. Trigonometrik çemberle çalışmayı bir kez öğrendiğinizde, derece cinsinden tüm bu korkulan açılar, kolayca ve zarif bir şekilde eski güzel açılara indirgenecektir:

   Bu arada, sizin için birkaç ilginç sitem daha var.)

   Örnek çözerek pratik yapabilir ve seviyenizi öğrenebilirsiniz. Anında doğrulama ile test etme. Hadi öğrenelim - ilgiyle!)

   Fonksiyonlar ve türevler hakkında bilgi sahibi olabilirsiniz.

   Sinüs (), kosinüs (), tanjant (), kotanjant () kavramları, açı kavramıyla ayrılmaz bir şekilde bağlantılıdır. İlk bakışta karmaşık (birçok okul çocuğunda dehşet durumuna neden olan) kavramları iyi anlayabilmek ve “şeytanın resmedildiği kadar korkunç olmadığından” emin olmak için, şu örnekten başlayalım: açı kavramını daha başlangıç ​​aşamasında anlayabilir ve anlayabilirsiniz.

   Açı kavramı: radyan, derece

   Şimdi resme bakalım. Vektör noktaya göre belirli bir miktarda “dönmüştür”. Yani bu dönmenin başlangıç ​​konumuna göre ölçüsü şu şekilde olacaktır: köşe.

   Açı kavramı hakkında bilmeniz gereken başka ne var? Tabii ki açı birimleri!

   Açı, hem geometride hem de trigonometride derece ve radyan cinsinden ölçülebilir.

   Açı (bir derece), dairenin bir kısmına eşit bir dairesel yay tarafından çevrelenen bir dairedeki merkezi açıdır. Böylece, dairenin tamamı dairesel yayların "parçalarından" oluşur veya dairenin tarif ettiği açı eşittir.

   

   Yani yukarıdaki şekil şuna eşit bir açıyı göstermektedir, yani bu açı, çevre büyüklüğünde bir dairesel yayın üzerinde durmaktadır.

   Radyan cinsinden bir açı, uzunluğu dairenin yarıçapına eşit olan bir daire yayının çevrelediği bir dairedeki merkezi açıdır. Peki anladın mı? Değilse, çizimden çözelim.

   

   Yani, şekil bir radyana eşit bir açıyı göstermektedir, yani bu açı, uzunluğu dairenin yarıçapına eşit olan (uzunluk uzunluğa eşittir veya yarıçap eşittir) dairesel bir yay üzerinde durmaktadır. yayın uzunluğu). Böylece yay uzunluğu aşağıdaki formülle hesaplanır:

   Radyan cinsinden merkez açı nerede?

   Peki bunu bildiğinize göre, dairenin tarif ettiği açının kaç radyan içerdiğini cevaplayabilir misiniz? Evet bunun için çevre formülünü hatırlamanız gerekiyor. İşte:

   Şimdi bu iki formülü ilişkilendirelim ve dairenin tarif ettiği açının eşit olduğunu bulalım. Yani değeri derece ve radyan cinsinden ilişkilendirerek bunu elde ederiz. Sırasıyla . Gördüğünüz gibi, "derece"den farklı olarak "radyan" kelimesi atlanmıştır, çünkü ölçü birimi genellikle bağlamdan açıkça anlaşılmaktadır.

   Kaç radyan var? Bu doğru!

   Anladım? Sonra devam edin ve düzeltin:

   Zorluk mu yaşıyorsunuz? O zaman bak cevaplar:

   Sağ üçgen: sinüs, kosinüs, tanjant, açının kotanjantı

   Böylece açı kavramını anladık. Peki bir açının sinüsü, kosinüsü, teğeti ve kotanjantı nedir? Hadi çözelim. Bunu yapmak için dik üçgen bize yardımcı olacaktır.

   

   Dik üçgenin kenarlarına ne denir? Aynen öyle, hipotenüs ve bacaklar: hipotenüs dik açının karşısındaki kenardır (örneğimizde bu kenardır); bacaklar kalan iki taraftır ve (dik açıya bitişik olanlar) ve bacakları açıya göre düşünürsek, o zaman bacak bitişik bacaktır ve bacak bunun tersidir. Şimdi şu soruyu cevaplayalım: Bir açının sinüs, kosinüs, teğet ve kotanjantı nedir?

   Açının sinüsü- bu, karşı (uzak) bacağın hipotenüse oranıdır.

   Bizim üçgenimizde.

   Açının kosinüsü- bu, bitişik (yakın) bacağın hipotenüse oranıdır.

   Bizim üçgenimizde.

   Açının tanjantı- bu, karşı (uzak) tarafın bitişik (yakın) tarafa oranıdır.

   Bizim üçgenimizde.

   Açının kotanjantı- bu, bitişik (yakın) bacağın karşıt (uzak) bacağına oranıdır.

   Bizim üçgenimizde.

   Bu tanımlar gerekli Unutma! Hangi bacağın neye bölüneceğini hatırlamayı kolaylaştırmak için bunu açıkça anlamalısınız. teğet Ve kotanjant yalnızca bacaklar oturur ve hipotenüs yalnızca sinüs Ve kosinüs. Ve sonra bir çağrışımlar zinciri oluşturabilirsiniz. Örneğin, bu:

   Kosinüs → dokunma → dokunma → bitişik;

   Kotanjant → dokunma → dokunma → bitişik.

   Her şeyden önce, bir üçgenin kenarlarının oranları bu kenarların uzunluklarına (aynı açıda) bağlı olmadığından sinüs, kosinüs, teğet ve kotanjantın olduğunu hatırlamanız gerekir. Bana inanmıyor musun? Daha sonra resme bakarak emin olun:

   

   Örneğin bir açının kosinüsünü düşünün. Tanım gereği bir üçgenden: , ancak bir açının kosinüsünü bir üçgenden hesaplayabiliriz: . Görüyorsunuz, kenarların uzunlukları farklı ama bir açının kosinüsünün değeri aynı. Dolayısıyla sinüs, kosinüs, teğet ve kotanjant değerleri yalnızca açının büyüklüğüne bağlıdır.

   Tanımları anlıyorsanız, devam edin ve bunları pekiştirin!

   Aşağıdaki şekilde gösterilen üçgen için şunu buluyoruz.

   

   Peki, anladın mı? O halde kendiniz deneyin: aynısını açı için hesaplayın.

   Birim (trigonometrik) daire

   Derece ve radyan kavramlarını anlayarak yarıçapı eşit olan bir daire düşündük. Böyle bir daireye denir Bekar. Trigonometri çalışırken çok faydalı olacaktır. Bu nedenle biraz daha detaylı bakalım.

   

   Gördüğünüz gibi bu daire Kartezyen koordinat sistemine göre inşa edilmiştir. Dairenin yarıçapı bire eşittir, dairenin merkezi koordinatların başlangıç ​​noktasında yer alırken, yarıçap vektörünün başlangıç ​​konumu eksenin pozitif yönü boyunca sabittir (örneğimizde bu yarıçaptır).

   Çember üzerindeki her nokta iki sayıya karşılık gelir: eksen koordinatı ve eksen koordinatı. Nedir bu koordinat numaraları? Ve genel olarak, bunların elimizdeki konuyla ne ilgisi var? Bunu yapmak için, dikkate alınan dik üçgeni hatırlamamız gerekir. Yukarıdaki şekilde iki tam dik üçgeni görüyorsunuz. Bir üçgen düşünün. Eksene dik olduğundan dikdörtgendir.

   Üçgen neye eşittir? Bu doğru. Ayrıca bunun birim çemberin yarıçapı olduğunu da biliyoruz, yani . Bu değeri kosinüs formülümüzde yerine koyalım. İşte olanlar:

   Üçgen neye eşittir? Tabii ki! Yarıçap değerini bu formülde değiştirin ve şunu elde edin:

   Peki bir çembere ait bir noktanın hangi koordinatlara sahip olduğunu söyleyebilir misiniz? Peki, mümkün değil mi? Peki ya bunun farkına varırsanız ve yalnızca rakamlardan ibaretseniz? Hangi koordinata karşılık geliyor? Tabii ki koordinatlar! Peki hangi koordinata karşılık geliyor? Doğru, koordinatlar! Böylece dönem.

   

   O halde ve eşittir nedir? Aynen öyle, teğet ve kotanjantın karşılık gelen tanımlarını kullanalım ve şunu elde edelim, a.

   Ya açı daha büyükse? Örneğin bu resimdeki gibi:

   

   Bu örnekte ne değişti? Hadi çözelim. Bunu yapmak için tekrar dik üçgene dönelim. Bir dik üçgen düşünün: açı (bir açıya bitişik olarak). Bir açı için sinüs, kosinüs, teğet ve kotanjant değerleri nelerdir? Doğru, trigonometrik fonksiyonların ilgili tanımlarına uyuyoruz:

   Gördüğünüz gibi açının sinüs değeri hala koordinata karşılık geliyor; açının kosinüsünün değeri - koordinat; ve karşılık gelen oranlara teğet ve kotanjant değerleri. Dolayısıyla bu ilişkiler yarıçap vektörünün herhangi bir dönüşüne uygulanır.

   Yarıçap vektörünün başlangıç ​​konumunun eksenin pozitif yönü boyunca olduğundan daha önce bahsedilmişti. Şu ana kadar bu vektörü saat yönünün tersine döndürdük ama saat yönünde döndürürsek ne olur? Olağanüstü bir şey yok, ayrıca belli bir değerde bir açı elde edeceksiniz, ancak yalnızca negatif olacaktır. Böylece, yarıçap vektörünü saat yönünün tersine döndürdüğümüzde, şunu elde ederiz: pozitif açılar ve saat yönünde döndürüldüğünde - negatif.

   Yani yarıçap vektörünün bir daire etrafındaki tam devriminin veya olduğunu biliyoruz. Yarıçap vektörünü şuna veya şuna döndürmek mümkün mü? Tabii ki yapabilirsin! Dolayısıyla ilk durumda yarıçap vektörü bir tam tur yapacak ve veya konumunda duracaktır.

   İkinci durumda, yarıçap vektörü üç tam devir yapacak ve veya konumunda duracaktır.

   Böylece, yukarıdaki örneklerden, veya (herhangi bir tamsayı olduğunda) farklı olan açıların, yarıçap vektörünün aynı konumuna karşılık geldiği sonucuna varabiliriz.

   Aşağıdaki şekil bir açıyı göstermektedir. Aynı görüntü köşeye vs. karşılık gelir. Bu listeye süresiz olarak devam edilebilir. Tüm bu açılar genel formülle veya (herhangi bir tamsayı olduğunda) yazılabilir.

   

   Şimdi temel trigonometrik fonksiyonların tanımlarını bilerek ve birim çemberi kullanarak değerlerin ne olduğunu cevaplamaya çalışın:

   İşte size yardımcı olacak bir birim çember:

   

   Zorluk mu yaşıyorsunuz? O zaman çözelim. Yani şunu biliyoruz:

   Buradan belirli açı ölçülerine karşılık gelen noktaların koordinatlarını belirliyoruz. Pekala, sırayla başlayalım: açısı koordinatları olan bir noktaya karşılık gelir, bu nedenle:

   Mevcut değil;

   Ayrıca aynı mantığa bağlı kalarak köşelerin sırasıyla koordinatlı noktalara karşılık geldiğini buluyoruz. Bunu bilerek trigonometrik fonksiyonların değerlerini karşılık gelen noktalarda belirlemek kolaydır. Önce kendiniz deneyin, ardından cevapları kontrol edin.

   Cevaplar:

   mevcut değil

   mevcut değil

   mevcut değil

   mevcut değil

   Böylece aşağıdaki tabloyu yapabiliriz:

   

   Tüm bu değerleri hatırlamanıza gerek yok. Birim çember üzerindeki noktaların koordinatları ile trigonometrik fonksiyonların değerleri arasındaki yazışmayı hatırlamak yeterlidir:

   Ancak aşağıdaki tabloda verilen ve açılarının trigonometrik fonksiyonlarının değerleri, hatırlanmalıdır:

   

   Korkmayın, şimdi size bir örnek göstereceğiz karşılık gelen değerleri hatırlamak oldukça basit:

   Bu yöntemi kullanmak için, açının tanjantının yanı sıra, üç açı ölçüsünün () tümü için sinüs değerlerini hatırlamak hayati önem taşır. Bu değerleri bilerek tüm tabloyu geri yüklemek oldukça basittir - kosinüs değerleri oklara göre aktarılır, yani:

   Bunu bilerek değerleri geri yükleyebilirsiniz. " " payı eşleşecek ve " " paydası eşleşecektir. Kotanjant değerleri şekilde gösterilen oklara göre aktarılır. Bunu anlayıp okların olduğu diyagramı hatırlarsanız tablodaki tüm değerleri hatırlamanız yeterli olacaktır.

   Çember üzerindeki bir noktanın koordinatları

   Bir daire üzerinde bir noktayı (koordinatlarını) bulmak mümkün mü? Çemberin merkezinin koordinatlarını, yarıçapını ve dönme açısını bilmek?

   Tabii ki yapabilirsin! Hadi çıkaralım Bir noktanın koordinatlarını bulmak için genel formül.

   Örneğin önümüzde bir daire var:

   

   Bize bu noktanın çemberin merkezi olduğu söylendi. Çemberin yarıçapı eşittir. Noktanın derece derece döndürülmesiyle elde edilen bir noktanın koordinatlarını bulmak gerekir.

   Şekilden de görülebileceği gibi noktanın koordinatı parçanın uzunluğuna karşılık gelmektedir. Segmentin uzunluğu dairenin merkezinin koordinatına karşılık gelir, yani eşittir. Bir segmentin uzunluğu kosinüs tanımı kullanılarak ifade edilebilir:

   Sonra nokta koordinatı için elimizde bu var.

   Aynı mantığı kullanarak noktanın y koordinat değerini buluyoruz. Böylece,

   Dolayısıyla genel olarak noktaların koordinatları aşağıdaki formüllerle belirlenir:

   Çemberin merkezinin koordinatları,

   Daire yarıçapı,

   Vektör yarıçapının dönme açısı.

   Gördüğünüz gibi, düşündüğümüz birim daire için, merkezin koordinatları sıfıra ve yarıçap bire eşit olduğundan bu formüller önemli ölçüde azaltılmıştır:

   Peki çember üzerindeki noktaları bulma alıştırması yaparak bu formülleri deneyelim mi?

   1. Birim çember üzerindeki bir noktanın, noktanın döndürülmesiyle elde edilen koordinatlarını bulun.

   2. Birim çember üzerindeki bir noktanın, noktanın döndürülmesiyle elde edilen koordinatlarını bulun.

   3. Birim çember üzerindeki bir noktanın, noktanın döndürülmesiyle elde edilen koordinatlarını bulun.

   4. Nokta dairenin merkezidir. Çemberin yarıçapı eşittir. Başlangıç ​​yarıçap vektörünü döndürerek elde edilen noktanın koordinatlarını bulmak gerekir.

   5. Nokta çemberin merkezidir. Çemberin yarıçapı eşittir. Başlangıç ​​yarıçap vektörünü döndürerek elde edilen noktanın koordinatlarını bulmak gerekir.

   Bir daire üzerindeki bir noktanın koordinatlarını bulmakta sorun mu yaşıyorsunuz?

   Bu beş örneği çözün (ya da çözmede ustalaşın) ve onları bulmayı öğreneceksiniz!

   1.

   Bunu fark edebilirsiniz. Ancak başlangıç ​​noktasının tam bir devrimine neyin karşılık geldiğini biliyoruz. Böylece istenilen nokta döndürüldüğü zamankiyle aynı konumda olacaktır. Bunu bilerek noktanın gerekli koordinatlarını buluyoruz:

   2. Birim çember bir noktada ortalanmıştır; bu, basitleştirilmiş formülleri kullanabileceğimiz anlamına gelir:

   Bunu fark edebilirsiniz. Başlangıç ​​noktasının iki tam dönüşüne neyin karşılık geldiğini biliyoruz. Böylece istenilen nokta döndürüldüğü zamankiyle aynı konumda olacaktır. Bunu bilerek noktanın gerekli koordinatlarını buluyoruz:

   Sinüs ve kosinüs tablo değerleridir. Anlamlarını hatırlıyoruz ve şunu elde ediyoruz:

   Böylece istenilen noktanın koordinatları olur.

   3. Birim çember bir noktada ortalanmıştır; bu, basitleştirilmiş formülleri kullanabileceğimiz anlamına gelir:

   Bunu fark edebilirsiniz. Söz konusu örneği şekilde tasvir edelim:

   

   Yarıçap eksene eşit ve eksenle açı yapar. Kosinüs ve sinüsün tablo değerlerinin eşit olduğunu bilerek ve buradaki kosinüsün negatif, sinüsün ise pozitif değer aldığını belirledikten sonra:

   Bu tür örnekler, konuyla ilgili trigonometrik fonksiyonların azaltılmasına yönelik formüller incelenirken daha ayrıntılı olarak tartışılmaktadır.

   Böylece istenilen noktanın koordinatları olur.

   4.

   Vektörün yarıçapının dönme açısı (koşula göre)

   Karşılık gelen sinüs ve kosinüs işaretlerini belirlemek için bir birim daire ve açı oluştururuz:

   

   Gördüğünüz gibi değer pozitif, yani değer negatiftir. İlgili trigonometrik fonksiyonların tablo değerlerini bilerek şunu elde ederiz:

   Elde edilen değerleri formülümüzde yerine koyalım ve koordinatları bulalım:

   Böylece istenilen noktanın koordinatları olur.

   5. Bu sorunu çözmek için genel formdaki formülleri kullanırız;

   Çemberin merkezinin koordinatları (örneğimizde,

   Daire yarıçapı (koşula göre)

   Vektörün yarıçapının dönme açısı (koşula göre).

   Tüm değerleri formülde yerine koyalım ve şunu elde edelim:

   ve - tablo değerleri. Bunları hatırlayalım ve formülde yerine koyalım:

   Böylece istenilen noktanın koordinatları olur.

   ÖZET VE TEMEL FORMÜLLER

   Bir açının sinüsü, karşı (uzak) bacağın hipotenüse oranıdır.

   Bir açının kosinüsü, bitişik (yakın) kenarın hipotenüse oranıdır.

   Bir açının tanjantı, karşı (uzak) tarafın bitişik (yakın) tarafa oranıdır.

   Bir açının kotanjantı, bitişik (yakın) tarafın karşı (uzak) tarafa oranıdır.

   Trigonometri çalışmamıza dik üçgenle başlayacağız. Bir akut açının teğet ve kotanjantının yanı sıra sinüs ve kosinüsün ne olduğunu tanımlayalım. Bu trigonometrinin temelidir.

   şunu hatırlatalım dik açı 90 dereceye eşit bir açıdır. Başka bir deyişle, yarım dönüş açısı.

   Dar açı- 90 dereceden az.

   Geniş açı- 90 dereceden büyük. Böyle bir açıyla ilgili olarak "geniş" hakaret değil matematiksel bir terimdir :-)

   Bir dik üçgen çizelim. Dik açı genellikle ile gösterilir. Lütfen köşenin karşısındaki tarafın aynı harfle, yalnızca küçük olarak gösterildiğini unutmayın. Böylece A açısının karşısındaki taraf gösterilir.

   Açı karşılık gelen Yunanca harfle gösterilir.

   

   Hipotenüs Bir dik üçgenin dik açının karşısındaki kenardır.

   Bacaklar- dar açıların karşısında yer alan kenarlar.

   Açının karşısında uzanan bacağa denir zıt(açıya göre). Açının kenarlarından birinde yer alan diğer bacağa denir. bitişik.

   Sinüs Bir dik üçgende dar açı, karşı kenarın hipotenüse oranıdır:

   Kosinüs Dik üçgende dar açı - bitişik bacağın hipotenüse oranı:

   Teğet dik üçgende dar açı - karşı tarafın bitişik tarafa oranı:

   Başka bir (eşdeğer) tanım: bir dar açının tanjantı, açının sinüsünün kosinüsüne oranıdır:

   Kotanjant dik üçgende dar açı - bitişik tarafın karşı tarafa oranı (veya aynı şekilde kosinüsün sinüse oranı):

   Aşağıdaki sinüs, kosinüs, teğet ve kotanjant için temel ilişkilere dikkat edin. Sorunları çözerken bize faydalı olacaklar.

   

   Bunlardan bazılarını kanıtlayalım.

   Tamam, tanımları verdik ve formülleri yazdık. Peki neden hala sinüs, kosinüs, teğet ve kotanjanta ihtiyacımız var?

   Bunu biliyoruz herhangi bir üçgenin açılarının toplamı eşittir.

   arasındaki ilişkiyi biliyoruz. partiler sağ üçgen. Bu Pisagor teoremidir: .

   Bir üçgendeki iki açıyı bilerek üçüncüyü bulabileceğiniz ortaya çıktı. Bir dik üçgenin iki kenarını bilerek üçüncüsünü bulabilirsiniz. Bu, açıların kendi oranlarına ve kenarların kendilerine ait olduğu anlamına gelir. Peki, bir dik üçgende bir açıyı (dik açı hariç) ve bir kenarı biliyorsanız ancak diğer kenarları bulmanız gerekiyorsa ne yapmalısınız?

   

   Geçmişte insanların bölgenin ve yıldızlı gökyüzünün haritasını çıkarırken karşılaştığı şey budur. Sonuçta bir üçgenin tüm kenarlarını doğrudan ölçmek her zaman mümkün değildir.

   Sinüs, kosinüs ve teğet - bunlara aynı zamanda denir trigonometrik açı fonksiyonları-arasındaki ilişkileri vermek partiler Ve köşelerüçgen. Açıyı bilerek, tüm trigonometrik fonksiyonlarını özel tablolar kullanarak bulabilirsiniz. Ve bir üçgenin açılarının ve kenarlarından birinin sinüslerini, kosinüslerini ve teğetlerini bilerek gerisini bulabilirsiniz.

   Ayrıca 'iyi' açılar için sinüs, kosinüs, tanjant ve kotanjant değerlerinin bir tablosunu da çizeceğiz.

   Lütfen tablodaki iki kırmızı çizgiye dikkat edin. Uygun açı değerlerinde teğet ve kotanjant mevcut değildir.

   FIPI Görev Bankasındaki çeşitli trigonometri problemlerine bakalım.

   1. Bir üçgende açı , dir. Bulmak .

   Sorun dört saniyede çözüldü.

   O zamandan beri , .

   2. Bir üçgende açı , , dir. Bulmak .

   

   Bunu Pisagor teoremini kullanarak bulalım.

   Sorun çözüldü.

   Genellikle problemlerde açılı ve veya açılı üçgenler vardır. Onlar için temel oranları ezbere hatırlayın!

   

   Açıları olan bir üçgen için ve açının karşısındaki bacak eşittir hipotenüsün yarısı.

   Açıları olan ve ikizkenar olan bir üçgen. İçinde hipotenüs bacaktan kat kat daha büyüktür.

   Dik üçgenleri çözme, yani bilinmeyen kenarları veya açıları bulma problemlerine baktık. Ama hepsi bu değil! Matematikte Birleşik Durum Sınavında bir üçgenin dış açısının sinüs, kosinüs, tanjant veya kotanjantını içeren birçok problem vardır. Bir sonraki makalede bu konuda daha fazla bilgi vereceğiz.

   Makalede neye benzediğini tam olarak anlayacağız trigonometrik değerler tablosu, sinüs, kosinüs, tanjant ve kotanjant. Trigonometrik fonksiyonların temel anlamını 0,30,45,60,90,...,360 derecelik açılardan ele alalım. Ve trigonometrik fonksiyonların değerlerinin hesaplanmasında bu tabloların nasıl kullanılacağını görelim.
   İlk önce şuna bakalım kosinüs, sinüs, tanjant ve kotanjant tablosu 0, 30, 45, 60, 90,... derecelik bir açıdan. Bu büyüklüklerin tanımı, 0 ve 90 derecelik açıların fonksiyonlarının değerini belirlememizi sağlar:

   sin 0 0 =0, cos 0 0 = 1. tg 00 = 0, 00'dan kotanjant tanımsız olacaktır
   sin 90 0 = 1, cos 90 0 =0, ctg90 0 = 0, 90 0'dan teğet belirsiz olacaktır

   Açıları 30 ile 90 derece arasında olan dik üçgenleri alırsanız. Şunu elde ederiz:

   günah 30 0 = 1/2, cos 30 0 = √3/2, tan 30 0 = √3/3, cos 30 0 = √3
   günah 45 0 = √2/2, cos 45 0 = √2/2, tan 45 0 = 1, cos 45 0 = 1
   sin 60 0 = √3/2, cos 60 0 = 1/2, tg 60 0 =√3, bebek karyolası 60 0 = √3/3

   Elde edilen tüm değerleri formda temsil edelim trigonometrik tablo:

   Sinüs, kosinüs, teğet ve kotanjant tablosu!

   İndirgeme formülünü kullanırsak tablomuz artacak ve 360 ​​dereceye kadar olan açılar için değerler eklenecektir. Şöyle görünecek:

   

   Ayrıca periyodiklik özelliklerine bağlı olarak açıları 0 0 +360 0 *z .... 330 0 +360 0 *z ile değiştirirsek tablo büyütülebilir; burada z bir tam sayıdır. Bu tabloda tek bir çemberdeki noktalara karşılık gelen tüm açıların değerini hesaplamak mümkündür.

   

   Tabloyu bir çözümde nasıl kullanabileceğimize bakalım.
   Her şey çok basit. Çünkü ihtiyacımız olan değer, ihtiyacımız olan hücrelerin kesişme noktasında yatıyor. Örneğin, 60 derecelik bir açının cos değerini alın, tabloda şöyle görünecektir:

   

   Trigonometrik fonksiyonların ana değerlerinin son tablosunda da aynı şekilde ilerliyoruz. Ancak bu tabloda 1020 derecelik açıdan tanjantın ne kadar olduğunu bulmak mümkün, = -√3 1020 0 = 300 0 +360 0 *2'yi kontrol edelim. Tabloyu kullanarak bulalım.

   

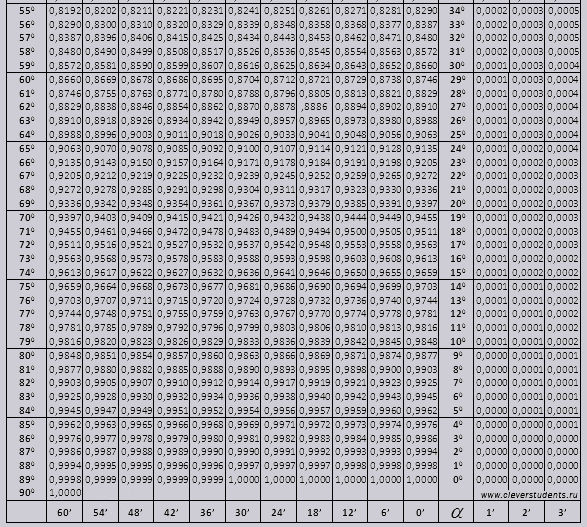
   Bradi'nin masası. Sinüs, kosinüs, teğet ve kotanjant için.

   Bradis tabloları, kosinüs ve sinüs, teğet ve kotanjant tablolarından oluşan birkaç parçaya bölünmüştür - bunlar iki parçaya bölünmüştür (90 dereceye kadar açıların tg'si ve küçük açıların ctg'si).

   Sinüs ve kosinüs

   
   
   

   00'dan başlayıp 760 ile biten açının tg'si, 140 ile başlayan ve 900 ile biten açının ctg'si.

   
   
   

   900'e kadar tg ve küçük açılardan ctg.

   
   

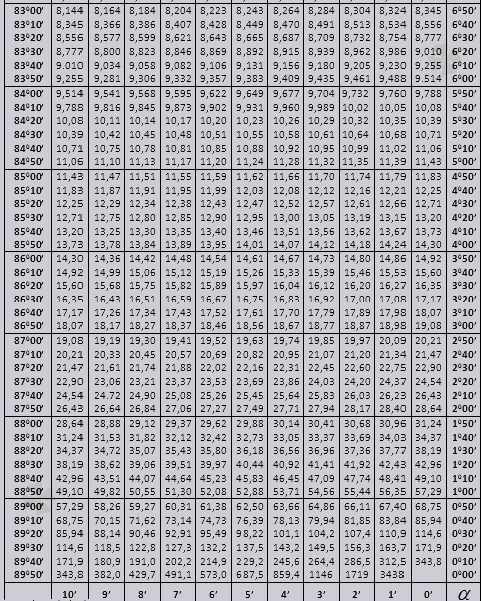
   Sorunların çözümünde Bradis tablolarının nasıl kullanılacağını bulalım.

   Tanımlama günahını (sol kenardaki sütunda tanımlama) 42 dakika (atama üst satırda) bulalım. Kesişim yoluyla atamayı ararız, bu = 0,3040.
   
   Dakika değerleri altı dakikalık aralıklarla belirtilir, ihtiyacımız olan değer tam olarak bu aralığın içine düşerse ne yapmalıyız. 44 dakika alalım ama tabloda sadece 42 var. 42'yi baz alıyoruz ve sağ taraftaki ek sütunları kullanarak 2. değişikliği alıp 0,3040 + 0,0006'yı ekliyoruz ve 0,3046 elde ediyoruz.
   
   Günah 47 dakika ile 48 dakikayı esas alıyoruz ve bundan 1 düzeltme çıkarıyoruz yani 0,3057 - 0,0003 = 0,3054
   
   Cos'u hesaplarken sin'e benzer şekilde çalışıyoruz, sadece tablonun en alt sırasını baz alıyoruz. Örneğin cos 20 0 = 0,9397
   
   90 0'a kadar olan tg açısı ve küçük açılı cot değerleri doğrudur ve bunlarda herhangi bir düzeltme yoktur. Örneğin, tg 78 0 37dk = 4,967'yi bulun
   
   
   ve ctg 20 0 13 dk = 25,83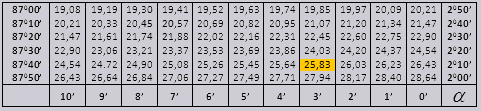
   
   

   Temel trigonometrik tablolara baktık. Bu bilgilerin sizin için son derece yararlı olduğunu umuyoruz. Tablolarla ilgili sorularınız varsa yorumlara yazmayı unutmayın!

   Not: Duvar tamponları, duvarları korumaya yönelik bir tampon panelidir. Çerçevesiz duvar tamponları (http://www.spi-polymer.ru/otboyniki/) bağlantısını takip edin ve daha fazlasını öğrenin.