The straight line y = f(x) will be tangent to the graph shown in the figure at point x0 provided that it passes through this point with coordinates (x0; f(x0)) and has slope f"(x0). Finding this coefficient, taking into account the features of the tangent, is not difficult.
You will need
- - mathematical reference book;
- - notebook;
- - a simple pencil;
- - pen;
- - protractor;
- - compass.
Instructions
- Please note that the graph of the differentiable function f(x) at the point x0 is no different from the tangent segment. Therefore, it is quite close to the segment l, passing through the points (x0; f(x0)) and (x0+Δx; f(x0 + Δx)). To specify a straight line passing through point A with coefficients (x0; f(x0)), indicate its slope. Moreover, it is equal to Δy/Δx secant tangent (Δх→0), and also tends to the number f‘(x0).
- If there are no values for f‘(x0), then perhaps there is no tangent, or perhaps it runs vertically. Based on this, the presence of the derivative of the function at the point x0 is explained by the existence of a non-vertical tangent, which is in contact with the graph of the function at the point (x0, f(x0)). IN in this case the angular coefficient of the tangent is equal to f"(x0). It becomes clear geometric meaning derivative, that is, calculating the slope of the tangent.
- That is, in order to find the slope of the tangent, you need to find the value of the derivative of the function at the point of tangency. Example: find the angular coefficient of the tangent to the graph of the function y = x³ at the point with abscissa X0 = 1. Solution: Find the derivative of this function y΄(x) = 3x²; find the value of the derivative at the point X0 = 1. у΄(1) = 3 × 1² = 3. The angle coefficient of the tangent at the point X0 = 1 is 3.
- Draw additional tangents in the figure so that they touch the graph of the function at the following points: x1, x2 and x3. Mark the angles formed by these tangents with the abscissa axis (the angle is counted in the positive direction - from the axis to the tangent line). For example, the first angle α1 will be acute, the second (α2) will be obtuse, and the third (α3) will be equal to zero, since the tangent line drawn is parallel to the OX axis. In this case, tangent obtuse angle There is negative value, and tangent acute angle– positive, at tg0 and the result is zero.
You are already familiar with the concept of a tangent to the graph of a function. The graph of the function f differentiable at the point x 0 near x 0 practically does not differ from the tangent segment, which means it is close to the secant segment l passing through the points (x 0 ; f (x 0)) and (x 0 +Δx; f ( x 0 + Δx)). Any of these secants passes through point A (x 0 ; f (x 0)) of the graph (Fig. 1). In order to uniquely define a line passing through a given point A, it is enough to indicate its slope. The angular coefficient Δy/Δx of the secant as Δх→0 tends to the number f ‘(x 0) (we will take it as the angular coefficient of the tangent) They say that the tangent is the limiting position of the secant at Δх→0.
If f'(x 0) does not exist, then the tangent either does not exist (like the function y = |x| at the point (0; 0), see figure) or is vertical (like the graph of the function at the point (0 ; 0), Fig. 2).
So, the existence of a derivative of the function f at the point xo is equivalent to the existence of a (non-vertical) tangent at the point (x 0, f (x 0)) of the graph, while tangent slope is equal to f" (x 0). This is geometric meaning of derivative

The tangent to the graph of a function f differentiable at the point xo is a straight line passing through the point (x 0 ; f (x 0)) and having an angular coefficient f ‘(x 0).
Let's draw tangents to the graph of the function f at points x 1, x 2, x 3 (Fig. 3) and note the angles they form with the abscissa axis. (This is the angle measured in the positive direction from the positive direction of the axis to the straight line.) We see that angle α 1 is acute, angle α 3 is obtuse, and angle α 2 is zero, since straight line l is parallel to the Ox axis. The tangent of an acute angle is positive, the tangent of an obtuse angle is negative, tan 0 = 0. Therefore
F"(x 1)>0, f’(x 2)=0, f’(x 3)
Constructing tangents at individual points allows you to more accurately sketch graphs. So, for example, to construct a sketch of a graph of the sine function, we first find that at points 0; π/2 and π derivative of sine is equal to 1; 0 and -1 respectively. Let's construct straight lines passing through the points (0; 0), (π/2,1) and (π, 0) with angular coefficients of 1, 0 and -1, respectively (Fig. 4). It remains to fit into the resulting trapezoid formed by these straight lines and straight line Ox, graph of the sine so that for x equal to 0, π/2 and π, it touches the corresponding straight lines.
Note that the graph of the sine in the vicinity of zero is practically indistinguishable from the straight line y = x. Let, for example, the scales along the axes be chosen so that a unit corresponds to a segment of 1 cm. We have sin 0.5 ≈ 0.479425, i.e. |sin 0.5 - 0.5| ≈ 0.02, and on the chosen scale this corresponds to a segment 0.2 mm long. Therefore, the graph of the function y = sin x in the interval (-0.5; 0.5) will deviate (in the vertical direction) from the straight line y = x by no more than 0.2 mm, which approximately corresponds to the thickness of the drawn line.
A tangent is a straight line , which touches the graph of the function at one point and all points of which are at the shortest distance from the graph of the function. Therefore, the tangent passes tangent to the graph of the function at a certain angle and several tangents at a certain angle cannot pass through the point of tangency. different angles. Tangent equations and normal equations to the graph of a function are constructed using the derivative.
The tangent equation is derived from the line equation .
Let us derive the equation of the tangent, and then the equation of the normal to the graph of the function.
y = kx + b .
In it k- angular coefficient.
From here we get the following entry:
y - y 0 = k(x - x 0 ) .
Derivative value f "(x 0 ) functions y = f(x) at the point x0 equal to the slope k= tg φ tangent to the graph of a function drawn through a point M0 (x 0 , y 0 ) , Where y0 = f(x 0 ) . This is geometric meaning of derivative .
Thus, we can replace k on f "(x 0 ) and get the following equation of the tangent to the graph of a function :
y - y 0 = f "(x 0 )(x - x 0 ) .
In problems involving composing the equation of a tangent to the graph of a function (and we will move on to them soon), it is required to reduce the equation obtained from the above formula to equation of a straight line in general form. To do this, you need to transfer all letters and numbers to left side equation, and leave zero on the right side.
Now about the normal equation. Normal - this is a straight line passing through the point of tangency to the graph of the function perpendicular to the tangent. Normal equation :
(x - x 0 ) + f "(x 0 )(y - y 0 ) = 0
To warm up, you are asked to solve the first example yourself, and then look at the solution. There is every reason to hope that this task will not be a “cold shower” for our readers.
Example 0. Create a tangent equation and a normal equation for the graph of a function at a point M (1, 1) .
Example 1. Write a tangent equation and a normal equation for the graph of a function ![]() , if the abscissa is tangent .
, if the abscissa is tangent .
Let's find the derivative of the function:
Now we have everything that needs to be substituted into the entry given in the theoretical help to get the tangent equation. We get
![]()
In this example, we were lucky: the slope turned out to be equal to zero, therefore, there was no need to separately bring the equation to a general form. Now we can create the normal equation:
![]()
In the figure below: graph of a function in burgundy color, tangent green, orange normal.

The next example is also not complicated: the function, as in the previous one, is also a polynomial, but the slope will not be equal to zero, so one more step will be added - bringing the equation to a general form.
Example 2.
Solution. Let's find the ordinate of the tangent point:
Let's find the derivative of the function:
![]() .
.
Let's find the value of the derivative at the point of tangency, that is, the slope of the tangent:
We substitute all the obtained data into the “blank formula” and get the tangent equation:
![]()
We bring the equation to its general form (we collect all letters and numbers other than zero on the left side, and leave zero on the right):
We compose the normal equation:

Example 3. Write a tangent equation and a normal equation to the graph of the function if the abscissa is the tangent point.
Solution. Let's find the ordinate of the tangent point:
Let's find the derivative of the function:
![]() .
.
Let's find the value of the derivative at the point of tangency, that is, the slope of the tangent:
![]() .
.
We find the tangent equation:
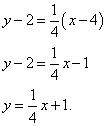
Before bringing the equation to its general form, you need to “comb it” a little: multiply term by term by 4. We do this and bring the equation to its general form:
We compose the normal equation:

Example 4. Write a tangent equation and a normal equation to the graph of the function if the abscissa is the tangent point.
Solution. Let's find the ordinate of the tangent point:
![]() .
.
Let's find the derivative of the function:
Let's find the value of the derivative at the point of tangency, that is, the slope of the tangent:
![]() .
.
We get the tangent equation:
We bring the equation to its general form:
We compose the normal equation:
![]()
A common mistake when writing tangent and normal equations is not to notice that the function given in the example is complex and to calculate its derivative as the derivative of a simple function. The following examples- already since complex functions(the corresponding lesson will open in a new window).
Example 5. Write a tangent equation and a normal equation to the graph of the function if the abscissa is the tangent point.
Solution. Let's find the ordinate of the tangent point:
Attention! This function- complex, since the tangent argument (2 x) is itself a function. Therefore, we find the derivative of a function as the derivative of a complex function.
In mathematics, one of the parameters describing the position of a line on Cartesian plane coordinates is the slope of this line. This parameter characterizes the slope of the straight line to the abscissa axis. To understand how to find the slope, first recall the general form of the equation of a straight line in the XY coordinate system.
IN general view any straight line can be represented by the expression ax+by=c, where a, b and c are arbitrary real numbers, but necessarily a 2 + b 2 ≠ 0.
Using simple transformations, such an equation can be brought to the form y=kx+d, in which k and d are real numbers. The number k is the slope, and the equation of a line of this type is called an equation with a slope. It turns out that to find the angular coefficient, you just need to bring original equation to the above type. For a more complete understanding, consider a specific example:
Problem: Find the slope of the line given by the equation 36x - 18y = 108
Solution: Let's transform the original equation.
Answer: The required slope of this line is 2.
If, during the transformation of the equation, we received an expression like x = const and as a result we cannot represent y as a function of x, then we are dealing with a straight line parallel to the X axis. The angular coefficient of such a straight line is equal to infinity.
For lines expressed by an equation like y = const, the slope is zero. This is typical for straight lines parallel to the abscissa axis. For example:
Problem: Find the slope of the line given by the equation 24x + 12y - 4(3y + 7) = 4
Solution: Let's bring the original equation to its general form
24x + 12y - 12y + 28 = 4
It is impossible to express y from the resulting expression, therefore the angular coefficient of this line is equal to infinity, and the line itself will be parallel to the Y axis.
Geometric meaning
For a better understanding, let's look at the picture:
In the figure we see a graph of a function like y = kx. To simplify, let’s take the coefficient c = 0. In the triangle OAB, the ratio of side BA to AO will be equal to the angular coefficient k. At the same time, the ratio VA/AO is the tangent of the acute angle α in right triangle OAV. It turns out that the angular coefficient of the straight line is equal to the tangent of the angle that this straight line makes with the abscissa axis of the coordinate grid.
Solving the problem of how to find the angular coefficient of a straight line, we find the tangent of the angle between it and the X axis of the coordinate grid. Boundary cases, when the line in question is parallel to the coordinate axes, confirm the above. Indeed, for a straight line described by the equation y=const, the angle between it and the abscissa axis is zero. The tangent of the zero angle is also zero and the slope is also zero.
For straight lines perpendicular to the x-axis and described by the equation x=const, the angle between them and the X-axis is 90 degrees. Tangent right angle is equal to infinity, and the angular coefficient of similar straight lines is also equal to infinity, which confirms what was written above.
Tangent slope
A common task often encountered in practice is also to find the slope of a tangent to the graph of a function at a certain point. A tangent is a straight line, therefore the concept of slope is also applicable to it.
To figure out how to find the slope of a tangent, we will need to recall the concept of derivative. The derivative of any function at some point is a constant, numerically equal to tangent the angle formed between the tangent at a specified point to the graph of this function and the abscissa axis. It turns out that to determine the angular coefficient of the tangent at the point x 0, we need to calculate the value of the derivative of the original function at this point k = f"(x 0). Let's look at the example:
Problem: Find the slope of the line tangent to the function y = 12x 2 + 2xe x at x = 0.1.
Solution: Find the derivative of the original function in general form
y"(0.1) = 24. 0.1 + 2. 0.1. e 0.1 + 2. e 0.1
Answer: The required slope at point x = 0.1 is 4.831
Let a function f be given, which at some point x 0 has a finite derivative f (x 0). Then the straight line passing through the point (x 0 ; f (x 0)), having an angular coefficient f ’(x 0), is called a tangent.
What happens if the derivative does not exist at the point x 0? There are two options:
- There is no tangent to the graph either. Classic example- function y = |x | at point (0; 0).
- The tangent becomes vertical. This is true, for example, for the function y = arcsin x at the point (1; π /2).
Tangent equation
Any non-vertical straight line is given by an equation of the form y = kx + b, where k is the slope. The tangent is no exception, and in order to create its equation at some point x 0, it is enough to know the value of the function and the derivative at this point.
So, let a function y = f (x) be given, which has a derivative y = f ’(x) on the segment. Then at any point x 0 ∈ (a ; b) a tangent can be drawn to the graph of this function, which is given by the equation:
y = f ’(x 0) (x − x 0) + f (x 0)
Here f ’(x 0) is the value of the derivative at point x 0, and f (x 0) is the value of the function itself.
Task. Given the function y = x 3 . Write an equation for the tangent to the graph of this function at the point x 0 = 2.
Tangent equation: y = f ’(x 0) · (x − x 0) + f (x 0). The point x 0 = 2 is given to us, but the values f (x 0) and f ’(x 0) will have to be calculated.
First, let's find the value of the function. Everything is easy here: f (x 0) = f (2) = 2 3 = 8;
Now let’s find the derivative: f ’(x) = (x 3)’ = 3x 2;
We substitute x 0 = 2 into the derivative: f ’(x 0) = f ’(2) = 3 2 2 = 12;
In total we get: y = 12 · (x − 2) + 8 = 12x − 24 + 8 = 12x − 16.
This is the tangent equation.
Task. Write an equation for the tangent to the graph of the function f (x) = 2sin x + 5 at point x 0 = π /2.
This time we will not describe each action in detail - we will only indicate the key steps. We have:
f (x 0) = f (π /2) = 2sin (π /2) + 5 = 2 + 5 = 7;
f ’(x) = (2sin x + 5)’ = 2cos x;
f ’(x 0) = f ’(π /2) = 2cos (π /2) = 0;
Tangent equation:
y = 0 · (x − π /2) + 7 ⇒ y = 7
IN the latter case the straight line turned out to be horizontal, because its angular coefficient k = 0. There is nothing wrong with this - we just stumbled upon an extremum point.








