આંકડાઓમાં ભિન્નતાના મુખ્ય સામાન્યીકરણ સૂચકાંકો વિખેરાઈ અને પ્રમાણભૂત વિચલનો છે.
વિખેરી નાખવું આ અંકગણિત સરેરાશ એકંદર સરેરાશમાંથી દરેક લાક્ષણિક મૂલ્યના વર્ગ વિચલનો. વિચલનને સામાન્ય રીતે વિચલનોનો સરેરાશ વર્ગ કહેવામાં આવે છે અને તેને 2 દ્વારા સૂચિત કરવામાં આવે છે. સ્ત્રોત ડેટાના આધારે, વિચલનની ગણતરી સરળ અથવા ભારિત અંકગણિત સરેરાશનો ઉપયોગ કરીને કરી શકાય છે:
વજન વિનાનું (સરળ) ભિન્નતા;
 વેરિઅન્સ વેઇટેડ.
વેરિઅન્સ વેઇટેડ.
પ્રમાણભૂત વિચલન આ નિરપેક્ષ કદની સામાન્ય લાક્ષણિકતા છે વિવિધતા એકંદરમાં ચિહ્નો. તે એટ્રિબ્યુટ (મીટર, ટન, ટકાવારી, હેક્ટર, વગેરેમાં) તરીકે માપનના સમાન એકમોમાં વ્યક્ત થાય છે.
પ્રમાણભૂત વિચલન એ ભિન્નતાનું વર્ગમૂળ છે અને તેને દ્વારા સૂચિત કરવામાં આવે છે:
 પ્રમાણભૂત વિચલન વજન વિનાનું;
પ્રમાણભૂત વિચલન વજન વિનાનું;
 ભારિત પ્રમાણભૂત વિચલન.
ભારિત પ્રમાણભૂત વિચલન.
પ્રમાણભૂત વિચલન એ સરેરાશની વિશ્વસનીયતાનું માપ છે. પ્રમાણભૂત વિચલન જેટલું નાનું છે, તેટલું સારું અંકગણિત સરેરાશ સમગ્ર પ્રતિનિધિત્વ વસ્તીને પ્રતિબિંબિત કરે છે.
પ્રમાણભૂત વિચલનની ગણતરી ભિન્નતાની ગણતરી દ્વારા આગળ આવે છે.
ભારિત ભિન્નતાની ગણતરી કરવાની પ્રક્રિયા નીચે મુજબ છે:
1) ભારિત અંકગણિત સરેરાશ નક્કી કરો:
2) સરેરાશમાંથી વિકલ્પોના વિચલનોની ગણતરી કરો:
3) સરેરાશમાંથી દરેક વિકલ્પના વિચલનનો વર્ગ કરો:
4) વિચલનોના વર્ગોને વજન (આવર્તન) દ્વારા ગુણાકાર કરો:
5) પરિણામી ઉત્પાદનોનો સારાંશ આપો:
![]()
6) પરિણામી રકમ વજનના સરવાળા દ્વારા વિભાજિત થાય છે:

ઉદાહરણ 2.1

ચાલો ભારિત અંકગણિત સરેરાશની ગણતરી કરીએ:

સરેરાશ અને તેમના ચોરસમાંથી વિચલનોના મૂલ્યો કોષ્ટકમાં રજૂ કરવામાં આવ્યા છે. ચાલો તફાવત વ્યાખ્યાયિત કરીએ:

પ્રમાણભૂત વિચલન સમાન હશે:

જો સ્રોત ડેટા અંતરાલના સ્વરૂપમાં રજૂ કરવામાં આવે છે વિતરણ શ્રેણી , તો તમારે પહેલા એટ્રિબ્યુટનું અલગ મૂલ્ય નક્કી કરવાની જરૂર છે, અને પછી વર્ણવેલ પદ્ધતિ લાગુ કરો.
ઉદાહરણ 2.2
ચાલો ઘઉંની ઉપજ અનુસાર સામૂહિક ખેતરના વાવણી વિસ્તારના વિતરણ પરના ડેટાનો ઉપયોગ કરીને અંતરાલ શ્રેણી માટે તફાવતની ગણતરી બતાવીએ.

અંકગણિતનો અર્થ છે:

ચાલો વિભિન્નતાની ગણતરી કરીએ:

6.3. વ્યક્તિગત ડેટા પર આધારિત સૂત્રનો ઉપયોગ કરીને વિચલનની ગણતરી
ગણતરી તકનીક ભિન્નતા જટિલ, અને વિકલ્પો અને ફ્રીક્વન્સીઝના મોટા મૂલ્યો સાથે તે બોજારૂપ હોઈ શકે છે. વિક્ષેપના ગુણધર્મોનો ઉપયોગ કરીને ગણતરીઓને સરળ બનાવી શકાય છે.
વિક્ષેપમાં નીચેના ગુણધર્મો છે.
1. વિભિન્ન લાક્ષણિકતાના વજન (ફ્રિકવન્સી)ને અમુક ચોક્કસ સંખ્યામાં ઘટાડવાથી અથવા વધારવાથી વિક્ષેપ બદલાતો નથી.
2. સમાન સ્થિર રકમ દ્વારા લાક્ષણિકતાના દરેક મૂલ્યમાં ઘટાડો અથવા વધારો એવિક્ષેપ બદલાતો નથી.
3. દરેક એટ્રિબ્યુટ વેલ્યુને અમુક ચોક્કસ સંખ્યામાં ઘટાડો અથવા વધારો kમાં ભિન્નતા અનુક્રમે ઘટાડે છે અથવા વધે છે k 2 વખત અને પ્રમાણભૂત વિચલન માં kએકવાર
4. સરેરાશ અને મનસ્વી મૂલ્યો વચ્ચેના તફાવતના ચોરસ દીઠ અંકગણિત સરેરાશને સંબંધિત વિક્ષેપ કરતાં મનસ્વી મૂલ્યની તુલનામાં લાક્ષણિકતાનું વિક્ષેપ હંમેશા વધારે હોય છે:
![]()
જો એ 0, પછી આપણે નીચેની સમાનતા પર પહોંચીએ છીએ:
એટલે કે, લાક્ષણિકતાનો તફાવત એ લાક્ષણિક મૂલ્યોના સરેરાશ વર્ગ અને સરેરાશના વર્ગ વચ્ચેના તફાવત જેટલો છે.
ભિન્નતાની ગણતરી કરતી વખતે દરેક મિલકતનો સ્વતંત્ર રીતે અથવા અન્ય લોકો સાથે સંયોજનમાં ઉપયોગ કરી શકાય છે.
વિભિન્નતાની ગણતરી કરવાની પ્રક્રિયા સરળ છે:
1) નક્કી કરો અંકગણિત સરેરાશ :
2) અંકગણિત સરેરાશનો વર્ગ કરો:

3) શ્રેણીના દરેક પ્રકારના વિચલનનો વર્ગ કરો:
એક્સ i 2 .
4) વિકલ્પોના ચોરસનો સરવાળો શોધો:
5) વિકલ્પોના ચોરસના સરવાળાને તેમની સંખ્યા દ્વારા વિભાજીત કરો, એટલે કે સરેરાશ ચોરસ નક્કી કરો:
6) લાક્ષણિકતાના સરેરાશ ચોરસ અને સરેરાશના ચોરસ વચ્ચેનો તફાવત નક્કી કરો:
ઉદાહરણ 3.1કામદારોની ઉત્પાદકતા પર નીચેનો ડેટા ઉપલબ્ધ છે:

ચાલો નીચેની ગણતરીઓ કરીએ:
![]()
પગલાં
સેમ્પલ વેરિઅન્સની ગણતરી
-
નમૂના મૂલ્યો રેકોર્ડ કરો.મોટા ભાગના કિસ્સાઓમાં, આંકડાશાસ્ત્રીઓ પાસે ચોક્કસ વસ્તીના નમૂનાઓ જ હોય છે. ઉદાહરણ તરીકે, એક નિયમ તરીકે, આંકડાશાસ્ત્રીઓ રશિયામાં તમામ કારની સંપૂર્ણતા જાળવવાની કિંમતનું વિશ્લેષણ કરતા નથી - તેઓ ઘણી હજાર કારના રેન્ડમ નમૂનાનું વિશ્લેષણ કરે છે. આવા નમૂના કારની સરેરાશ કિંમત નક્કી કરવામાં મદદ કરશે, પરંતુ, સંભવત,, પરિણામી મૂલ્ય વાસ્તવિક કરતાં દૂર હશે.
- ઉદાહરણ તરીકે, ચાલો રેન્ડમ ક્રમમાં લેવામાં આવેલા 6 દિવસમાં કેફેમાં વેચાયેલા બન્સની સંખ્યાનું વિશ્લેષણ કરીએ. નમૂના આના જેવો દેખાય છે: 17, 15, 23, 7, 9, 13. આ એક નમૂનો છે, વસ્તી નથી, કારણ કે અમારી પાસે કૅફે ખુલ્લી હોય તે દિવસ માટે વેચાતા બન્સનો ડેટા નથી.
- જો તમને મૂલ્યોના નમૂનાને બદલે વસ્તી આપવામાં આવી હોય, તો આગલા વિભાગમાં ચાલુ રાખો.
-
નમૂનાના તફાવતની ગણતરી કરવા માટે એક સૂત્ર લખો.વિક્ષેપ એ ચોક્કસ જથ્થાના મૂલ્યોના પ્રસારનું માપ છે. ભિન્નતા મૂલ્ય શૂન્યની જેટલી નજીક છે, મૂલ્યો એકસાથે જૂથબદ્ધ છે. મૂલ્યોના નમૂના સાથે કામ કરતી વખતે, ભિન્નતાની ગણતરી કરવા માટે નીચેના સૂત્રનો ઉપયોગ કરો:
- s 2 (\ ડિસ્પ્લેસ્ટાઈલ s^(2)) = ∑[(x i (\displaystyle x_(i))- x̅) 2 (\Displaystyle ^(2))] / (એન - 1)
- s 2 (\ ડિસ્પ્લેસ્ટાઈલ s^(2))- આ વિક્ષેપ છે. વિક્ષેપ ચોરસ એકમોમાં માપવામાં આવે છે.
- x i (\displaystyle x_(i))- નમૂનામાં દરેક મૂલ્ય.
- x i (\displaystyle x_(i))તમારે x̅ બાદબાકી કરવાની, તેને ચોરસ કરવાની અને પછી પરિણામો ઉમેરવાની જરૂર છે.
- x̅ - નમૂનાનો સરેરાશ (નમૂનો સરેરાશ).
- n - નમૂનામાં મૂલ્યોની સંખ્યા.
-
નમૂનાના સરેરાશની ગણતરી કરો.તે x̅ તરીકે સૂચવવામાં આવે છે. નમૂનાના સરેરાશની ગણતરી એક સરળ અંકગણિત સરેરાશ તરીકે કરવામાં આવે છે: નમૂનામાં તમામ મૂલ્યો ઉમેરો અને પછી પરિણામને નમૂનામાં મૂલ્યોની સંખ્યા દ્વારા વિભાજીત કરો.
- અમારા ઉદાહરણમાં, નમૂનામાં મૂલ્યો ઉમેરો: 15 + 17 + 23 + 7 + 9 + 13 = 84
હવે પરિણામને નમૂનામાં મૂલ્યોની સંખ્યા દ્વારા વિભાજીત કરો (અમારા ઉદાહરણમાં 6 છે): 84 ÷ 6 = 14.
નમૂનાનો અર્થ x̅ = 14. - નમૂનાનો અર્થ એ કેન્દ્રિય મૂલ્ય છે જેની આસપાસ નમૂનામાં મૂલ્યો વિતરિત કરવામાં આવે છે. જો નમૂનાની આસપાસના નમૂના ક્લસ્ટરમાંના મૂલ્યોનો અર્થ છે, તો પછી તફાવત નાનો છે; અન્યથા તફાવત મોટો છે.
- અમારા ઉદાહરણમાં, નમૂનામાં મૂલ્યો ઉમેરો: 15 + 17 + 23 + 7 + 9 + 13 = 84
-
નમૂનાના દરેક મૂલ્યમાંથી નમૂનાના સરેરાશને બાદ કરો.હવે તફાવતની ગણતરી કરો x i (\displaystyle x_(i))- x̅, ક્યાં x i (\displaystyle x_(i))- નમૂનામાં દરેક મૂલ્ય. પ્રાપ્ત થયેલ દરેક પરિણામ એ દર્શાવે છે કે ચોક્કસ મૂલ્ય નમૂનાના સરેરાશથી કેટલી હદે વિચલિત થાય છે, એટલે કે, આ મૂલ્ય નમૂનાના સરેરાશથી કેટલું દૂર છે.
- અમારા ઉદાહરણમાં:
x 1 (\પ્રદર્શન શૈલી x_(1))- x = 17 - 14 = 3
x 2 (\Displaystyle x_(2))- x̅ = 15 - 14 = 1
x 3 (\displaystyle x_(3))- x = 23 - 14 = 9
x 4 (\displaystyle x_(4))- x̅ = 7 - 14 = -7
x 5 (\displaystyle x_(5))- x̅ = 9 - 14 = -5
x 6 (\displaystyle x_(6))- x̅ = 13 - 14 = -1 - પ્રાપ્ત પરિણામોની ચોકસાઈ તપાસવી સરળ છે, કારણ કે તેમનો સરવાળો શૂન્ય સમાન હોવો જોઈએ. આ સરેરાશની વ્યાખ્યા સાથે સંબંધિત છે, કારણ કે નકારાત્મક મૂલ્યો (સરેરાશથી નાના મૂલ્યો સુધીનું અંતર) હકારાત્મક મૂલ્યો (સરેરાશથી મોટા મૂલ્યો સુધીનું અંતર) દ્વારા સંપૂર્ણપણે સરભર થાય છે.
- અમારા ઉદાહરણમાં:
-
ઉપર નોંધ્યા પ્રમાણે, તફાવતોનો સરવાળો x i (\displaystyle x_(i))- x̅ શૂન્યની બરાબર હોવી જોઈએ. આનો અર્થ એ છે કે સરેરાશ તફાવત હંમેશા શૂન્ય હોય છે, જે ચોક્કસ જથ્થાના મૂલ્યોના ફેલાવા વિશે કોઈ ખ્યાલ આપતું નથી. આ સમસ્યાને ઉકેલવા માટે, દરેક તફાવતને ચોરસ કરો x i (\displaystyle x_(i))- x̅. આના પરિણામે તમને માત્ર હકારાત્મક સંખ્યા જ મળશે, જે ક્યારેય 0 સુધી ઉમેરશે નહીં.
- અમારા ઉદાહરણમાં:
(x 1 (\પ્રદર્શન શૈલી x_(1))- x̅) 2 = 3 2 = 9 (\displaystyle ^(2)=3^(2)=9)
(x 2 (\Displaystyle (x_(2))- x̅) 2 = 1 2 = 1 (\displaystyle ^(2)=1^(2)=1)
9 2 = 81
(-7) 2 = 49
(-5) 2 = 25
(-1) 2 = 1 - તમને તફાવતનો વર્ગ મળ્યો - x̅) 2 (\Displaystyle ^(2))નમૂનામાં દરેક મૂલ્ય માટે.
- અમારા ઉદાહરણમાં:
-
તફાવતોના વર્ગોના સરવાળાની ગણતરી કરો.એટલે કે, સૂત્રનો તે ભાગ શોધો જે આ રીતે લખાયેલ છે: ∑[( x i (\displaystyle x_(i))- x̅) 2 (\Displaystyle ^(2))]. અહીં ચિહ્ન Σ નો અર્થ દરેક મૂલ્ય માટે વર્ગના તફાવતોનો સરવાળો છે x i (\displaystyle x_(i))નમૂનામાં. તમે પહેલાથી જ વર્ગના તફાવતો શોધી લીધા છે (x i (\displaystyle (x_(i))- x̅) 2 (\Displaystyle ^(2))દરેક મૂલ્ય માટે x i (\displaystyle x_(i))નમૂનામાં; હવે ફક્ત આ ચોરસ ઉમેરો.
- અમારા ઉદાહરણમાં: 9 + 1 + 81 + 49 + 25 + 1 = 166 .
-
પરિણામને n - 1 વડે વિભાજીત કરો, જ્યાં n એ નમૂનામાં મૂલ્યોની સંખ્યા છે.થોડા સમય પહેલા, નમૂનાના તફાવતની ગણતરી કરવા માટે, આંકડાશાસ્ત્રીઓએ પરિણામને n વડે વિભાજિત કર્યું હતું; આ કિસ્સામાં તમને સ્ક્વેર વેરિઅન્સનો સરેરાશ મળશે, જે આપેલ નમૂનાના ભિન્નતાનું વર્ણન કરવા માટે આદર્શ છે. પરંતુ યાદ રાખો કે કોઈપણ નમૂના મૂલ્યોની વસ્તીનો માત્ર એક નાનો ભાગ છે. જો તમે બીજો નમૂનો લો અને સમાન ગણતરીઓ કરો, તો તમને અલગ પરિણામ મળશે. જેમ તે તારણ આપે છે, n - 1 (ફક્ત n ને બદલે) વડે ભાગવાથી વસ્તીના તફાવતનો વધુ સચોટ અંદાજ મળે છે, જેમાં તમને રુચિ છે. n – 1 દ્વારા વિભાજન સામાન્ય બની ગયું છે, તેથી તે નમૂનાના તફાવતની ગણતરી માટેના સૂત્રમાં શામેલ છે.
- અમારા ઉદાહરણમાં, નમૂનામાં 6 મૂલ્યો છે, એટલે કે, n = 6.
નમૂના ભિન્નતા = s 2 = 166 6 − 1 = (\displaystyle s^(2)=(\frac (166)(6-1))=) 33,2
- અમારા ઉદાહરણમાં, નમૂનામાં 6 મૂલ્યો છે, એટલે કે, n = 6.
-
વિચલન અને પ્રમાણભૂત વિચલન વચ્ચેનો તફાવત.નોંધ કરો કે સૂત્રમાં ઘાતાંકનો સમાવેશ થાય છે, તેથી વિક્ષેપ વિશ્લેષણ કરવામાં આવી રહેલા મૂલ્યના ચોરસ એકમોમાં માપવામાં આવે છે. કેટલીકવાર આવી તીવ્રતાનું સંચાલન કરવું ખૂબ મુશ્કેલ છે; આવા કિસ્સાઓમાં, પ્રમાણભૂત વિચલનનો ઉપયોગ કરો, જે વિચલનના વર્ગમૂળની બરાબર છે. એટલા માટે સેમ્પલ વેરિઅન્સ તરીકે સૂચવવામાં આવે છે s 2 (\ ડિસ્પ્લેસ્ટાઈલ s^(2)), અને નમૂનાનું પ્રમાણભૂત વિચલન આ પ્રમાણે છે s (\ડિસ્પ્લેસ્ટાઈલ ઓ).
- અમારા ઉદાહરણમાં, નમૂનાનું પ્રમાણભૂત વિચલન છે: s = √33.2 = 5.76.
વસ્તી તફાવતની ગણતરી
-
મૂલ્યોના કેટલાક સમૂહનું વિશ્લેષણ કરો.સમૂહમાં વિચારણા હેઠળના જથ્થાના તમામ મૂલ્યોનો સમાવેશ થાય છે. ઉદાહરણ તરીકે, જો તમે લેનિનગ્રાડ પ્રદેશના રહેવાસીઓની ઉંમરનો અભ્યાસ કરી રહ્યાં છો, તો સંપૂર્ણતામાં આ પ્રદેશના તમામ રહેવાસીઓની ઉંમરનો સમાવેશ થાય છે. વસ્તી સાથે કામ કરતી વખતે, ટેબલ બનાવવાની અને તેમાં વસ્તીના મૂલ્યો દાખલ કરવાની ભલામણ કરવામાં આવે છે. નીચેના ઉદાહરણને ધ્યાનમાં લો:
- ચોક્કસ રૂમમાં 6 માછલીઘર છે. દરેક માછલીઘરમાં નીચેની સંખ્યામાં માછલીઓ હોય છે:
x 1 = 5 (\displaystyle x_(1)=5)
x 2 = 5 (\displaystyle x_(2)=5)
x 3 = 8 (\displaystyle x_(3)=8)
x 4 = 12 (\displaystyle x_(4)=12)
x 5 = 15 (\displaystyle x_(5)=15)
x 6 = 18 (\displaystyle x_(6)=18)
- ચોક્કસ રૂમમાં 6 માછલીઘર છે. દરેક માછલીઘરમાં નીચેની સંખ્યામાં માછલીઓ હોય છે:
-
વસ્તી તફાવતની ગણતરી કરવા માટે એક સૂત્ર લખો.વસ્તીમાં ચોક્કસ જથ્થાના તમામ મૂલ્યોનો સમાવેશ થતો હોવાથી, નીચેનું સૂત્ર તમને વસ્તી તફાવતનું ચોક્કસ મૂલ્ય મેળવવા માટે પરવાનગી આપે છે. સેમ્પલ વેરિઅન્સ (જે માત્ર એક અંદાજ છે) થી વસ્તીના તફાવતને અલગ પાડવા માટે, આંકડાશાસ્ત્રીઓ વિવિધ ચલોનો ઉપયોગ કરે છે:
- σ 2 (\Displaystyle ^(2)) = (∑(x i (\displaystyle x_(i)) - μ) 2 (\Displaystyle ^(2)))/એન
- σ 2 (\Displaystyle ^(2))- વસ્તી ફેલાવો ("સિગ્મા સ્ક્વેર્ડ" તરીકે વાંચો). વિક્ષેપ ચોરસ એકમોમાં માપવામાં આવે છે.
- x i (\displaystyle x_(i))- કુલ દરેક મૂલ્ય.
- Σ - રકમનું ચિહ્ન. એટલે કે, દરેક મૂલ્યમાંથી x i (\displaystyle x_(i))તમારે μ બાદબાકી કરવાની, તેને ચોરસ કરવાની અને પછી પરિણામો ઉમેરવાની જરૂર છે.
- μ - વસ્તી સરેરાશ.
- n - વસ્તીમાં મૂલ્યોની સંખ્યા.
-
સરેરાશ વસ્તીની ગણતરી કરો.વસ્તી સાથે કામ કરતી વખતે, તેનો સરેરાશ μ (mu) તરીકે સૂચવવામાં આવે છે. વસ્તીના સરેરાશની ગણતરી એક સરળ અંકગણિત સરેરાશ તરીકે કરવામાં આવે છે: વસ્તીમાં તમામ મૂલ્યો ઉમેરો અને પછી પરિણામને વસ્તીમાં મૂલ્યોની સંખ્યા દ્વારા વિભાજીત કરો.
- ધ્યાનમાં રાખો કે સરેરાશ હંમેશા અંકગણિત સરેરાશ તરીકે ગણવામાં આવતી નથી.
- અમારા ઉદાહરણમાં, વસ્તીનો અર્થ છે: μ = 5 + 5 + 8 + 12 + 15 + 18 6 (\Displaystyle (\frac (5+5+8+12+15+18)(6))) = 10,5
-
વસ્તીના દરેક મૂલ્યમાંથી વસ્તીના સરેરાશને બાદ કરો.તફાવત શૂન્યની નજીક છે, ચોક્કસ મૂલ્ય વસ્તીના સરેરાશની નજીક છે. વસ્તીમાં દરેક મૂલ્ય અને તેના સરેરાશ વચ્ચેનો તફાવત શોધો અને તમને મૂલ્યોના વિતરણનો પ્રથમ ખ્યાલ આવશે.
- અમારા ઉદાહરણમાં:
x 1 (\પ્રદર્શન શૈલી x_(1))- μ = 5 - 10.5 = -5.5
x 2 (\Displaystyle x_(2))- μ = 5 - 10.5 = -5.5
x 3 (\displaystyle x_(3))- μ = 8 - 10.5 = -2.5
x 4 (\displaystyle x_(4))- μ = 12 - 10.5 = 1.5
x 5 (\displaystyle x_(5))- μ = 15 - 10.5 = 4.5
x 6 (\displaystyle x_(6))- μ = 18 - 10.5 = 7.5
- અમારા ઉદાહરણમાં:
-
મેળવેલ દરેક પરિણામને ચોરસ કરો.તફાવત મૂલ્યો હકારાત્મક અને નકારાત્મક બંને હશે; જો આ મૂલ્યો સંખ્યા રેખા પર રચાયેલ છે, તો તેઓ વસ્તીના સરેરાશની જમણી અને ડાબી બાજુએ આવેલા હશે. ભિન્નતાની ગણતરી કરવા માટે આ સારું નથી કારણ કે હકારાત્મક અને નકારાત્મક સંખ્યાઓ એકબીજાને રદ કરે છે. તેથી વિશિષ્ટ રીતે હકારાત્મક સંખ્યાઓ મેળવવા માટે દરેક તફાવતનો વર્ગ કરો.
- અમારા ઉદાહરણમાં:
(x i (\displaystyle x_(i)) - μ) 2 (\Displaystyle ^(2))દરેક વસ્તી મૂલ્ય માટે (i = 1 થી i = 6 સુધી):
(-5,5)2 (\Displaystyle ^(2)) = 30,25
(-5,5)2 (\Displaystyle ^(2)), ક્યાં x n (\displaystyle x_(n))- વસ્તીમાં છેલ્લું મૂલ્ય. - પ્રાપ્ત પરિણામોના સરેરાશ મૂલ્યની ગણતરી કરવા માટે, તમારે તેનો સરવાળો શોધીને તેને n:(( વડે ભાગવાની જરૂર છે. x 1 (\પ્રદર્શન શૈલી x_(1)) - μ) 2 (\Displaystyle ^(2)) + (x 2 (\Displaystyle x_(2)) - μ) 2 (\Displaystyle ^(2)) + ... + (x n (\displaystyle x_(n)) - μ) 2 (\Displaystyle ^(2)))/એન
- હવે ચલોનો ઉપયોગ કરીને ઉપરોક્ત સમજૂતી લખીએ: (∑( x i (\displaystyle x_(i)) - μ) 2 (\Displaystyle ^(2))) / n અને વસ્તી તફાવતની ગણતરી માટે એક સૂત્ર મેળવો.
- અમારા ઉદાહરણમાં:
જો વસ્તીને અભ્યાસ કરવામાં આવતી લાક્ષણિકતા અનુસાર જૂથોમાં વિભાજિત કરવામાં આવે છે, તો પછી આ વસ્તી માટે નીચેના પ્રકારના વિભિન્નતાની ગણતરી કરી શકાય છે: કુલ, જૂથ (જૂથની અંદર), જૂથની સરેરાશ (જૂથની અંદરની સરેરાશ), આંતર જૂથ.
શરૂઆતમાં, તે નિર્ધારણના ગુણાંકની ગણતરી કરે છે, જે દર્શાવે છે કે અભ્યાસ કરવામાં આવી રહેલા લક્ષણની કુલ વિવિધતાનો કયો ભાગ આંતરજૂથ વિવિધતા છે, એટલે કે. જૂથની લાક્ષણિકતાને કારણે:
પ્રયોગમૂલક સહસંબંધ સંબંધ જૂથ (ફેક્ટોરિયલ) અને પ્રદર્શન લાક્ષણિકતાઓ વચ્ચેના જોડાણની નિકટતાને દર્શાવે છે.
પ્રયોગમૂલક સહસંબંધ ગુણોત્તર 0 થી 1 સુધીના મૂલ્યો લઈ શકે છે.
પ્રયોગમૂલક સહસંબંધ ગુણોત્તરના આધારે જોડાણની નિકટતાનું મૂલ્યાંકન કરવા માટે, તમે ચૅડૉક સંબંધોનો ઉપયોગ કરી શકો છો:
ઉદાહરણ 4.માલિકીના વિવિધ સ્વરૂપોની ડિઝાઇન અને સર્વેક્ષણ સંસ્થાઓ દ્વારા કામના પ્રદર્શન પર નીચેનો ડેટા ઉપલબ્ધ છે:
વ્યાખ્યાયિત કરો:
1) કુલ વિચલન;
2) જૂથ ભિન્નતા;
3) જૂથ તફાવતોની સરેરાશ;
4) આંતરજૂથ તફાવત;
5) ભિન્નતા ઉમેરવા માટેના નિયમના આધારે કુલ વિચલન;
6) નિર્ધારણનો ગુણાંક અને પ્રયોગમૂલક સહસંબંધ ગુણોત્તર.
તારણો દોરો.
ઉકેલ:
1. ચાલો માલિકીના બે સ્વરૂપોના સાહસો દ્વારા કરવામાં આવતા કામનું સરેરાશ પ્રમાણ નક્કી કરીએ:
ચાલો કુલ ભિન્નતાની ગણતરી કરીએ:
![]()
2. જૂથ સરેરાશ નક્કી કરો:
![]() મિલિયન રુબેલ્સ;
મિલિયન રુબેલ્સ;
![]() મિલિયન રુબેલ્સ
મિલિયન રુબેલ્સ
જૂથ તફાવતો:
![]() ;
;
3. જૂથ ભિન્નતાઓની સરેરાશની ગણતરી કરો:
4. ચાલો આંતરજૂથ તફાવત નક્કી કરીએ:
5. ભિન્નતા ઉમેરવા માટેના નિયમના આધારે કુલ ભિન્નતાની ગણતરી કરો:
6. ચાલો નિર્ધારણનો ગુણાંક નક્કી કરીએ:
![]() .
.
આમ, ડિઝાઇન અને મોજણી સંસ્થાઓ દ્વારા કરવામાં આવેલ કાર્યનું પ્રમાણ એંટરપ્રાઇઝની માલિકીના સ્વરૂપ પર 22% દ્વારા નિર્ભર છે.
પ્રયોગમૂલક સહસંબંધ ગુણોત્તર સૂત્રનો ઉપયોગ કરીને ગણવામાં આવે છે
![]() .
.
ગણતરી કરેલ સૂચકનું મૂલ્ય સૂચવે છે કે એન્ટરપ્રાઇઝની માલિકીના સ્વરૂપ પર કામના વોલ્યુમની અવલંબન નાની છે.
ઉદાહરણ 5.ઉત્પાદન ક્ષેત્રોની તકનીકી શિસ્તના સર્વેક્ષણના પરિણામે, નીચેનો ડેટા પ્રાપ્ત થયો હતો:
નિર્ધારણનો ગુણાંક નક્કી કરો
અપેક્ષા અને ભિન્નતા એ રેન્ડમ ચલની સૌથી સામાન્ય રીતે ઉપયોગમાં લેવાતી સંખ્યાત્મક લાક્ષણિકતાઓ છે. તેઓ વિતરણની સૌથી મહત્વપૂર્ણ લાક્ષણિકતાઓ દર્શાવે છે: તેની સ્થિતિ અને સ્કેટરિંગની ડિગ્રી. ઘણી વ્યવહારુ સમસ્યાઓમાં, રેન્ડમ ચલની સંપૂર્ણ, સંપૂર્ણ લાક્ષણિકતા - વિતરણ કાયદો - કાં તો બિલકુલ મેળવી શકાતો નથી, અથવા તેની બિલકુલ જરૂર નથી. આ કિસ્સાઓમાં, સંખ્યાત્મક લાક્ષણિકતાઓનો ઉપયોગ કરીને રેન્ડમ ચલના અંદાજિત વર્ણન સુધી મર્યાદિત છે.
અપેક્ષિત મૂલ્યને ઘણીવાર રેન્ડમ ચલનું સરેરાશ મૂલ્ય કહેવામાં આવે છે. રેન્ડમ ચલનું વિક્ષેપ એ વિક્ષેપની લાક્ષણિકતા છે, તેની ગાણિતિક અપેક્ષાની આસપાસ રેન્ડમ ચલનો ફેલાવો.
એક અલગ રેન્ડમ ચલની અપેક્ષા
ચાલો આપણે એક અલગ રેન્ડમ ચલના વિતરણના યાંત્રિક અર્થઘટન પર આધારિત, ગાણિતિક અપેક્ષાના ખ્યાલનો સંપર્ક કરીએ. એકમ સમૂહને x-અક્ષના બિંદુઓ વચ્ચે વિતરિત કરવા દો x1 , x 2 , ..., x n, અને દરેક મટીરીયલ પોઈન્ટનું અનુરૂપ માસ હોય છે પી1 , પી 2 , ..., પી n. એબ્સિસા અક્ષ પર એક બિંદુ પસંદ કરવું જરૂરી છે, ભૌતિક બિંદુઓની સમગ્ર સિસ્ટમની સ્થિતિને દર્શાવતા, તેમના સમૂહને ધ્યાનમાં લેતા. ભૌતિક બિંદુઓની સિસ્ટમના દળના કેન્દ્રને આવા બિંદુ તરીકે લેવું સ્વાભાવિક છે. આ રેન્ડમ ચલની ભારિત સરેરાશ છે એક્સ, જેમાં પ્રત્યેક બિંદુનો અબ્સિસા xiઅનુરૂપ સંભાવનાના સમાન "વજન" સાથે પ્રવેશ કરે છે. આ રીતે મેળવેલ રેન્ડમ ચલનું સરેરાશ મૂલ્ય એક્સતેની ગાણિતિક અપેક્ષા કહેવાય છે.
એક અલગ રેન્ડમ ચલની ગાણિતિક અપેક્ષા તેના તમામ સંભવિત મૂલ્યોના ઉત્પાદનોનો સરવાળો અને આ મૂલ્યોની સંભાવનાઓ છે:

ઉદાહરણ 1.જીત-જીત લોટરીનું આયોજન કરવામાં આવ્યું છે. ત્યાં 1000 જીત છે, જેમાંથી 400 10 રુબેલ્સ છે. 300 - 20 રુબેલ્સ દરેક. 200 - 100 રુબેલ્સ દરેક. અને 100 - 200 રુબેલ્સ દરેક. એક ટિકિટ ખરીદનાર વ્યક્તિ માટે સરેરાશ જીત કેટલી છે?
ઉકેલ. જો આપણે જીતની કુલ રકમને 10*400 + 20*300 + 100*200 + 200*100 = 50,000 રુબેલ્સ, 1000 (જીતની કુલ રકમ) દ્વારા વિભાજીત કરીએ તો અમને સરેરાશ જીત મળશે. પછી આપણને 50000/1000 = 50 રુબેલ્સ મળે છે. પરંતુ સરેરાશ જીતની ગણતરી માટે અભિવ્યક્તિ નીચેના સ્વરૂપમાં રજૂ કરી શકાય છે:

બીજી બાજુ, આ શરતો હેઠળ, વિજેતા કદ એ રેન્ડમ ચલ છે, જે 10, 20, 100 અને 200 રુબેલ્સના મૂલ્યો લઈ શકે છે. અનુક્રમે 0.4 ની સમાન સંભાવનાઓ સાથે; 0.3; 0.2; 0.1. તેથી, અપેક્ષિત સરેરાશ જીત એ જીતના કદના ઉત્પાદનોના સરવાળા અને તેમને પ્રાપ્ત કરવાની સંભાવના સમાન છે.
ઉદાહરણ 2.પ્રકાશકે નવું પુસ્તક પ્રકાશિત કરવાનું નક્કી કર્યું. તે પુસ્તકને 280 રુબેલ્સમાં વેચવાની યોજના ધરાવે છે, જેમાંથી તે પોતે 200, 50 - પુસ્તકની દુકાન અને 30 - લેખકને પ્રાપ્ત કરશે. કોષ્ટક પુસ્તક પ્રકાશિત કરવાના ખર્ચ અને પુસ્તકની ચોક્કસ સંખ્યામાં નકલો વેચવાની સંભાવના વિશે માહિતી પ્રદાન કરે છે.
પ્રકાશકનો અપેક્ષિત નફો શોધો.
ઉકેલ. રેન્ડમ ચલ "નફો" વેચાણમાંથી આવક અને ખર્ચની કિંમત વચ્ચેના તફાવતની બરાબર છે. ઉદાહરણ તરીકે, જો કોઈ પુસ્તકની 500 નકલો વેચાય છે, તો વેચાણમાંથી આવક 200 * 500 = 100,000 છે, અને પ્રકાશનની કિંમત 225,000 રુબેલ્સ છે. આમ, પ્રકાશકને 125,000 રુબેલ્સના નુકસાનનો સામનો કરવો પડે છે. નીચેનું કોષ્ટક રેન્ડમ ચલ - નફોના અપેક્ષિત મૂલ્યોનો સારાંશ આપે છે:
| નંબર | નફો xi | સંભાવના પીi | xi પી i |
| 500 | -125000 | 0,20 | -25000 |
| 1000 | -50000 | 0,40 | -20000 |
| 2000 | 100000 | 0,25 | 25000 |
| 3000 | 250000 | 0,10 | 25000 |
| 4000 | 400000 | 0,05 | 20000 |
| કુલ: | 1,00 | 25000 |
આમ, અમે પ્રકાશકના નફાની ગાણિતિક અપેક્ષા મેળવીએ છીએ:
![]() .
.
ઉદાહરણ 3.એક શોટ સાથે હિટ થવાની સંભાવના પી= 0.2. 5 જેટલી હિટની સંખ્યાની ગાણિતિક અપેક્ષા પૂરી પાડતા અસ્ત્રોનો વપરાશ નક્કી કરો.
ઉકેલ. એ જ ગાણિતિક અપેક્ષા સૂત્રમાંથી જેનો આપણે અત્યાર સુધી ઉપયોગ કર્યો છે, આપણે વ્યક્ત કરીએ છીએ x- શેલ વપરાશ:
![]() .
.
ઉદાહરણ 4.રેન્ડમ ચલની ગાણિતિક અપેક્ષા નક્કી કરો xત્રણ શોટ સાથે હિટની સંખ્યા, જો દરેક શોટ સાથે હિટની સંભાવના પી = 0,4 .
સંકેત: દ્વારા રેન્ડમ ચલ મૂલ્યોની સંભાવના શોધો બર્નૌલીનું સૂત્ર .
ગાણિતિક અપેક્ષાના ગુણધર્મો
ચાલો ગાણિતિક અપેક્ષાના ગુણધર્મોને ધ્યાનમાં લઈએ.
મિલકત 1.સ્થિર મૂલ્યની ગાણિતિક અપેક્ષા આ સ્થિરાંક જેટલી છે:
મિલકત 2.સતત પરિબળને ગાણિતિક અપેક્ષા ચિહ્નમાંથી બહાર લઈ શકાય છે:
![]()
મિલકત 3.રેન્ડમ ચલોના સરવાળા (તફાવત)ની ગાણિતિક અપેક્ષા તેમની ગાણિતિક અપેક્ષાઓના સરવાળા (તફાવત) જેટલી છે:
મિલકત 4.રેન્ડમ ચલોના ઉત્પાદનની ગાણિતિક અપેક્ષા તેમની ગાણિતિક અપેક્ષાઓના ઉત્પાદનની સમાન છે:
મિલકત 5.જો રેન્ડમ ચલના તમામ મૂલ્યો એક્સસમાન સંખ્યામાં ઘટાડો (વધારો). સાથે, પછી તેની ગાણિતિક અપેક્ષા સમાન સંખ્યામાં ઘટાડો (વધારો) થશે:
![]()
જ્યારે તમે તમારી જાતને માત્ર ગાણિતિક અપેક્ષાઓ સુધી મર્યાદિત કરી શકતા નથી
મોટા ભાગના કિસ્સાઓમાં, માત્ર ગાણિતિક અપેક્ષા જ પર્યાપ્ત રીતે રેન્ડમ ચલને લાક્ષણિકતા આપી શકતી નથી.
રેન્ડમ ચલો દો એક્સઅને વાયનીચેના વિતરણ કાયદા દ્વારા આપવામાં આવે છે:
| અર્થ એક્સ | સંભાવના |
| -0,1 | 0,1 |
| -0,01 | 0,2 |
| 0 | 0,4 |
| 0,01 | 0,2 |
| 0,1 | 0,1 |
| અર્થ વાય | સંભાવના |
| -20 | 0,3 |
| -10 | 0,1 |
| 0 | 0,2 |
| 10 | 0,1 |
| 20 | 0,3 |
આ જથ્થાઓની ગાણિતિક અપેક્ષાઓ સમાન છે - શૂન્યની બરાબર:


જો કે, તેમની વિતરણ પદ્ધતિ અલગ છે. રેન્ડમ ચલ એક્સમાત્ર એવા મૂલ્યો લઈ શકે છે જે ગાણિતિક અપેક્ષા અને રેન્ડમ ચલથી થોડા અલગ હોય વાયએવા મૂલ્યો લઈ શકે છે જે ગાણિતિક અપેક્ષાથી નોંધપાત્ર રીતે વિચલિત થાય છે. એક સમાન ઉદાહરણ: સરેરાશ વેતન ઉચ્ચ અને ઓછા પગારવાળા કામદારોના હિસ્સાનો નિર્ણય કરવાનું શક્ય બનાવતું નથી. બીજા શબ્દોમાં કહીએ તો, કોઈ ગાણિતિક અપેક્ષાથી નક્કી કરી શકતું નથી કે તેમાંથી કયા વિચલનો, ઓછામાં ઓછા સરેરાશ, શક્ય છે. આ કરવા માટે, તમારે રેન્ડમ ચલનો તફાવત શોધવાની જરૂર છે.
એક અલગ રેન્ડમ ચલનો ભિન્નતા
ભિન્નતાઅલગ રેન્ડમ ચલ એક્સગાણિતિક અપેક્ષામાંથી તેના વિચલનના વર્ગની ગાણિતિક અપેક્ષા કહેવાય છે:

રેન્ડમ ચલનું પ્રમાણભૂત વિચલન એક્સતેના વિચલનના વર્ગમૂળનું અંકગણિત મૂલ્ય કહેવાય છે:
![]() .
.
ઉદાહરણ 5.રેન્ડમ ચલોના ભિન્નતા અને પ્રમાણભૂત વિચલનોની ગણતરી કરો એક્સઅને વાય, જેના વિતરણ કાયદાઓ ઉપરના કોષ્ટકોમાં આપવામાં આવ્યા છે.
ઉકેલ. રેન્ડમ ચલોની ગાણિતિક અપેક્ષાઓ એક્સઅને વાય, ઉપર મળ્યા મુજબ, શૂન્યની બરાબર છે. ખાતે વિક્ષેપ સૂત્ર મુજબ ઇ(એક્સ)=ઇ(y)=0 અમને મળે છે:


પછી રેન્ડમ ચલોના પ્રમાણભૂત વિચલનો એક્સઅને વાયમેક અપ
![]() .
.
આમ, સમાન ગાણિતિક અપેક્ષાઓ સાથે, રેન્ડમ ચલનો તફાવત એક્સખૂબ નાનું, પરંતુ રેન્ડમ ચલ વાય- નોંધપાત્ર. આ તેમના વિતરણમાં તફાવતનું પરિણામ છે.
ઉદાહરણ 6.રોકાણકાર પાસે 4 વૈકલ્પિક રોકાણ પ્રોજેક્ટ છે. કોષ્ટક આ પ્રોજેક્ટ્સમાં અનુરૂપ સંભાવના સાથે અપેક્ષિત નફાનો સારાંશ આપે છે.
| પ્રોજેક્ટ 1 | પ્રોજેક્ટ 2 | પ્રોજેક્ટ 3 | પ્રોજેક્ટ 4 |
| 500, પી=1 | 1000, પી=0,5 | 500, પી=0,5 | 500, પી=0,5 |
| 0, પી=0,5 | 1000, પી=0,25 | 10500, પી=0,25 | |
| 0, પી=0,25 | 9500, પી=0,25 |
દરેક વિકલ્પ માટે ગાણિતિક અપેક્ષા, ભિન્નતા અને પ્રમાણભૂત વિચલન શોધો.
ઉકેલ. ચાલો બતાવીએ કે 3જી વિકલ્પ માટે આ મૂલ્યોની ગણતરી કેવી રીતે કરવામાં આવે છે:
કોષ્ટક બધા વિકલ્પો માટે મળેલા મૂલ્યોનો સારાંશ આપે છે.
બધા વિકલ્પો સમાન ગાણિતિક અપેક્ષાઓ ધરાવે છે. મતલબ કે લાંબા ગાળે દરેકની આવક સરખી છે. પ્રમાણભૂત વિચલનને જોખમના માપ તરીકે અર્થઘટન કરી શકાય છે - તે જેટલું ઊંચું છે, રોકાણનું જોખમ વધારે છે. જે રોકાણકાર વધુ જોખમ ન ઇચ્છતા હોય તે પ્રોજેક્ટ 1 પસંદ કરશે કારણ કે તેમાં સૌથી નાનું પ્રમાણભૂત વિચલન (0) છે. જો રોકાણકાર ટૂંકા ગાળામાં જોખમ અને ઉચ્ચ વળતર પસંદ કરે છે, તો તે સૌથી મોટા પ્રમાણભૂત વિચલન સાથે પ્રોજેક્ટ પસંદ કરશે - પ્રોજેક્ટ 4.
વિક્ષેપ ગુણધર્મો
ચાલો વિક્ષેપના ગુણધર્મો રજૂ કરીએ.
મિલકત 1.સ્થિર મૂલ્યનો તફાવત શૂન્ય છે:
મિલકત 2.અચળ પરિબળને વિક્ષેપ ચિન્હમાંથી વર્ગીકરણ કરીને બહાર લઈ શકાય છે:
![]() .
.
મિલકત 3.રેન્ડમ ચલનો તફાવત આ મૂલ્યના વર્ગની ગાણિતિક અપેક્ષા સમાન છે, જેમાંથી મૂલ્યની ગાણિતિક અપેક્ષાનો વર્ગ પોતે જ બાદ કરવામાં આવે છે:
![]() ,
,
જ્યાં ![]() .
.
મિલકત 4.રેન્ડમ ચલોના સરવાળા (તફાવત) નું વિચલન તેમના ચલોના સરવાળા (તફાવત) જેટલું છે:
ઉદાહરણ 7.તે જાણીતું છે કે એક અલગ રેન્ડમ ચલ એક્સમાત્ર બે મૂલ્યો લે છે: −3 અને 7. વધુમાં, ગાણિતિક અપેક્ષા જાણીતી છે: ઇ(એક્સ) = 4 . એક અલગ રેન્ડમ ચલનો તફાવત શોધો.
ઉકેલ. ચાલો દ્વારા સૂચિત કરીએ પીસંભાવના કે જેની સાથે રેન્ડમ ચલ મૂલ્ય લે છે x1 = −3 . પછી મૂલ્યની સંભાવના x2 = 7 1 - હશે પી. ચાલો ગાણિતિક અપેક્ષા માટે સમીકરણ મેળવીએ:
ઇ(એક્સ) = x 1 પી + x 2 (1 − પી) = −3પી + 7(1 − પી) = 4 ,
જ્યાં આપણને સંભાવનાઓ મળે છે: પી= 0.3 અને 1 − પી = 0,7 .
રેન્ડમ ચલના વિતરણનો કાયદો:
| એક્સ | −3 | 7 |
| પી | 0,3 | 0,7 |
અમે વિક્ષેપના ગુણધર્મ 3માંથી સૂત્રનો ઉપયોગ કરીને આ રેન્ડમ ચલના ભિન્નતાની ગણતરી કરીએ છીએ:
ડી(એક્સ) = 2,7 + 34,3 − 16 = 21 .
રેન્ડમ ચલની ગાણિતિક અપેક્ષા જાતે શોધો અને પછી ઉકેલ જુઓ
ઉદાહરણ 8.અલગ રેન્ડમ ચલ એક્સમાત્ર બે મૂલ્યો લે છે. તે સંભાવના 0.4 સાથે 3 ના મોટા મૂલ્યોને સ્વીકારે છે. વધુમાં, રેન્ડમ ચલનો તફાવત જાણીતો છે ડી(એક્સ) = 6 રેન્ડમ ચલની ગાણિતિક અપેક્ષા શોધો.
ઉદાહરણ 9.કલરમાં 6 સફેદ અને 4 કાળા દડા છે. કલગીમાંથી 3 બોલ દોરવામાં આવે છે. દોરેલા દડાઓમાં સફેદ દડાઓની સંખ્યા એક અલગ રેન્ડમ ચલ છે એક્સ. આ રેન્ડમ ચલની ગાણિતિક અપેક્ષા અને ભિન્નતા શોધો.
ઉકેલ. રેન્ડમ ચલ એક્સમૂલ્યો 0, 1, 2, 3 લઈ શકે છે. અનુરૂપ સંભાવનાઓની ગણતરી અહીંથી કરી શકાય છે સંભાવના ગુણાકાર નિયમ. રેન્ડમ ચલના વિતરણનો કાયદો:
| એક્સ | 0 | 1 | 2 | 3 |
| પી | 1/30 | 3/10 | 1/2 | 1/6 |
તેથી આ રેન્ડમ ચલની ગાણિતિક અપેક્ષા:
એમ(એક્સ) = 3/10 + 1 + 1/2 = 1,8 .
આપેલ રેન્ડમ ચલનો તફાવત છે:
ડી(એક્સ) = 0,3 + 2 + 1,5 − 3,24 = 0,56 .
સતત રેન્ડમ ચલની અપેક્ષા અને વિચલન
સતત રેન્ડમ ચલ માટે, ગાણિતિક અપેક્ષાનું યાંત્રિક અર્થઘટન એ જ અર્થ જાળવી રાખશે: ઘનતા સાથે x-અક્ષ પર સતત વિતરિત એકમ સમૂહ માટે દળનું કેન્દ્ર f(x). એક અલગ રેન્ડમ ચલથી વિપરીત, જેનું કાર્ય દલીલ xiસતત રેન્ડમ ચલ માટે અચાનક બદલાય છે, દલીલ સતત બદલાય છે. પરંતુ સતત રેન્ડમ ચલની ગાણિતિક અપેક્ષા તેના સરેરાશ મૂલ્ય સાથે પણ સંબંધિત છે.
સતત રેન્ડમ ચલની ગાણિતિક અપેક્ષા અને ભિન્નતા શોધવા માટે, તમારે ચોક્કસ પૂર્ણાંકો શોધવાની જરૂર છે . જો સતત રેન્ડમ ચલનું ઘનતા કાર્ય આપવામાં આવે છે, તો તે સીધું ઇન્ટિગ્રેન્ડમાં પ્રવેશ કરે છે. જો સંભાવના વિતરણ કાર્ય આપવામાં આવે છે, તો તેને અલગ કરીને, તમારે ઘનતા કાર્ય શોધવાની જરૂર છે.
સતત રેન્ડમ ચલના તમામ સંભવિત મૂલ્યોની અંકગણિત સરેરાશ કહેવાય છે ગાણિતિક અપેક્ષા, અથવા દ્વારા સૂચવવામાં આવે છે.
જૂથ ડેટા માટે શેષ તફાવત- ઇન્ટ્રાગ્રુપ ભિન્નતાની સરેરાશ:જ્યાં σ 2 j એ jth જૂથનું આંતર-જૂથ વિચલન છે.
જૂથ વિનાના ડેટા માટે શેષ તફાવત- અંદાજની ચોકસાઈનું માપ, એટલે કે. મૂળ ડેટા માટે રીગ્રેસન લાઇનનો અંદાજ: 
જ્યાં y(t) એ વલણ સમીકરણનો ઉપયોગ કરીને આગાહી છે; y t - પ્રારંભિક ગતિશીલતા શ્રેણી; n - પોઈન્ટની સંખ્યા; p – રીગ્રેસન સમીકરણ ગુણાંકની સંખ્યા (સ્પષ્ટીકરણાત્મક ચલોની સંખ્યા).
આ ઉદાહરણમાં તેને કહેવામાં આવે છે નિષ્પક્ષ ભિન્નતા અનુમાનક.
ઉદાહરણ નંબર 1. ટેરિફ શ્રેણીઓ અનુસાર એક સંગઠનના ત્રણ સાહસોના કામદારોનું વિતરણ નીચેના ડેટા દ્વારા વર્ગીકૃત થયેલ છે:
| કામદારની ટેરિફ શ્રેણી | એન્ટરપ્રાઇઝમાં કામદારોની સંખ્યા | ||
| એન્ટરપ્રાઇઝ 1 | એન્ટરપ્રાઇઝ 2 | એન્ટરપ્રાઇઝ 3 | |
| 1 | 50 | 20 | 40 |
| 2 | 100 | 80 | 60 |
| 3 | 150 | 150 | 200 |
| 4 | 350 | 300 | 400 |
| 5 | 200 | 150 | 250 |
| 6 | 150 | 100 | 150 |
વ્યાખ્યાયિત કરો:
1. દરેક એન્ટરપ્રાઈઝ માટે ભિન્નતા (અંતર-જૂથ ભિન્નતા);
2. જૂથની અંદરની ભિન્નતાઓની સરેરાશ;
3. આંતરજૂથ વિખેરી;
4. કુલ વિચલન.
ઉકેલ.
સમસ્યાનો ઉકેલ લાવવાનું શરૂ કરતા પહેલા, તે શોધવાનું જરૂરી છે કે કઈ સુવિધા અસરકારક છે અને કઈ હકીકતલક્ષી છે. વિચારણા હેઠળના ઉદાહરણમાં, પરિણામી એટ્રિબ્યુટ "ટેરિફ કેટેગરી" છે, અને પરિબળ એટ્રિબ્યુટ "એન્ટરપ્રાઇઝનો નંબર (નામ)" છે.
પછી અમારી પાસે ત્રણ જૂથો (ઉદ્યોગો) છે, જેના માટે જૂથ સરેરાશ અને ઇન્ટ્રાગ્રુપ ભિન્નતાની ગણતરી કરવી જરૂરી છે:

| એન્ટરપ્રાઇઝ | જૂથ સરેરાશ, | જૂથમાં તફાવત, |
| 1 | 4 | 1,8 |
જૂથની અંદરના તફાવતોની સરેરાશ ( શેષ તફાવત) સૂત્રનો ઉપયોગ કરીને ગણતરી કરવામાં આવશે:

જ્યાં તમે ગણતરી કરી શકો છો:

અથવા:

પછી:
કુલ ભિન્નતા સમાન હશે: s 2 = 1.6 + 0 = 1.6.
નીચેના બે સૂત્રોમાંથી એકનો ઉપયોગ કરીને પણ કુલ તફાવતની ગણતરી કરી શકાય છે:
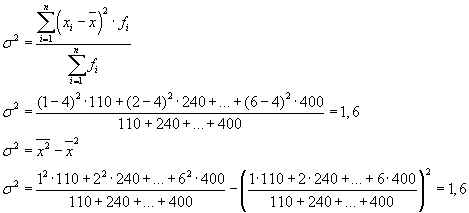
વ્યવહારિક સમસ્યાઓ હલ કરતી વખતે, વ્યક્તિએ ઘણી વાર એવી સુવિધાનો સામનો કરવો પડે છે જે ફક્ત બે વૈકલ્પિક મૂલ્યો લે છે. આ કિસ્સામાં, અમે કોઈ વિશેષતાના ચોક્કસ મૂલ્યના વજન વિશે નથી, પરંતુ એકંદરમાં તેના શેર વિશે વાત કરી રહ્યા છીએ. જો અભ્યાસ કરવામાં આવતી લાક્ષણિકતા ધરાવતા વસ્તી એકમોનું પ્રમાણ " દ્વારા સૂચવવામાં આવે છે આર", અને જેની પાસે નથી - દ્વારા" q", પછી ફોર્મ્યુલાનો ઉપયોગ કરીને વિભિન્નતાની ગણતરી કરી શકાય છે:
s 2 = p×q
ઉદાહરણ નંબર 2. એક ટીમમાં છ કામદારોના ઉત્પાદન ડેટાના આધારે, આંતર-જૂથ તફાવત નક્કી કરો અને જો કુલ તફાવત 12.2 હોય તો તેમની શ્રમ ઉત્પાદકતા પર કામના શિફ્ટની અસરનું મૂલ્યાંકન કરો.
| ટીમ વર્કર નં. | વર્કર આઉટપુટ, પીસી. | |
| પ્રથમ પાળીમાં | બીજી પાળીમાં | |
| 1 | 18 | 13 |
| 2 | 19 | 14 |
| 3 | 22 | 15 |
| 4 | 20 | 17 |
| 5 | 24 | 16 |
| 6 | 23 | 15 |
ઉકેલ. પ્રારંભિક ડેટા
| એક્સ | f 1 | f 2 | f 3 | f 4 | f 5 | f 6 | કુલ |
| 1 | 18 | 19 | 22 | 20 | 24 | 23 | 126 |
| 2 | 13 | 14 | 15 | 17 | 16 | 15 | 90 |
| કુલ | 31 | 33 | 37 | 37 | 40 | 38 |
પછી અમારી પાસે 6 જૂથો છે જેના માટે જૂથના સરેરાશ અને ઇન્ટ્રાગ્રુપ ભિન્નતાની ગણતરી કરવી જરૂરી છે.
1. દરેક જૂથના સરેરાશ મૂલ્યો શોધો.
2. દરેક જૂથનો સરેરાશ ચોરસ શોધો.
ચાલો કોષ્ટકમાં ગણતરીના પરિણામોનો સારાંશ આપીએ:
| જૂથ નંબર | જૂથ સરેરાશ | જૂથમાં તફાવત |
| 1 | 1.42 | 0.24 |
| 2 | 1.42 | 0.24 |
| 3 | 1.41 | 0.24 |
| 4 | 1.46 | 0.25 |
| 5 | 1.4 | 0.24 |
| 6 | 1.39 | 0.24 |
3. જૂથમાં તફાવતજૂથની અંતર્ગતના પરિબળને બાદ કરતાં, તેના પરના તમામ પરિબળોના પ્રભાવ હેઠળ જૂથની અંદર અભ્યાસ કરેલ (પરિણામાત્મક) લાક્ષણિકતાના ફેરફાર (વિવિધતા)ને લાક્ષણિકતા આપે છે:
અમે સૂત્રનો ઉપયોગ કરીને ઇન્ટ્રાગ્રુપ ભિન્નતાની સરેરાશની ગણતરી કરીએ છીએ:
4. આંતરજૂથ તફાવતજૂથનો આધાર બનાવે છે તે પરિબળ (ફેક્ટેરિયલ લાક્ષણિકતા) ના પ્રભાવ હેઠળ અભ્યાસ કરેલ (પરિણામાત્મક) લાક્ષણિકતાના ફેરફાર (વિવિધતા) ની લાક્ષણિકતા.
અમે આંતરજૂથ તફાવતને આ રીતે વ્યાખ્યાયિત કરીએ છીએ:
જ્યાં
પછી
કુલ વિચલનઅપવાદ વિના તમામ પરિબળો (ફેક્ટેરિયલ લાક્ષણિકતાઓ) ના પ્રભાવ હેઠળ અભ્યાસ કરેલ (પરિણામાત્મક) લાક્ષણિકતાના ફેરફાર (વિવિધતા) ની લાક્ષણિકતા. સમસ્યાની શરતો અનુસાર, તે 12.2 ની બરાબર છે.
પ્રયોગમૂલક સહસંબંધ સંબંધપરિણામી લાક્ષણિકતાની કુલ પરિવર્તનશીલતાનો કયો ભાગ અભ્યાસ કરવામાં આવતા પરિબળને કારણે થાય છે તે માપે છે. આ પરિબળ ભિન્નતા અને કુલ ભિન્નતાનો ગુણોત્તર છે:
અમે પ્રયોગમૂલક સહસંબંધ સંબંધને વ્યાખ્યાયિત કરીએ છીએ:
લાક્ષણિકતાઓ વચ્ચેના જોડાણો નબળા અને મજબૂત (નજીક) હોઈ શકે છે. તેમના માપદંડોનું મૂલ્યાંકન ચૅડૉક સ્કેલ પર કરવામાં આવે છે:
0.1 0.3 0.5 0.7 0.9 અમારા ઉદાહરણમાં, લક્ષણ Y અને પરિબળ X વચ્ચેનો સંબંધ નબળો છે
નિર્ધારણ ગુણાંક.
ચાલો નિર્ધારણનો ગુણાંક નક્કી કરીએ:
આમ, 0.67% વિવિધતા લક્ષણો વચ્ચેના તફાવતને કારણે છે, અને 99.37% અન્ય પરિબળોને કારણે છે.
નિષ્કર્ષ: આ કિસ્સામાં, કામદારોનું આઉટપુટ ચોક્કસ પાળી પરના કામ પર આધારિત નથી, એટલે કે. તેમની શ્રમ ઉત્પાદકતા પર કામની પાળીનો પ્રભાવ નોંધપાત્ર નથી અને તે અન્ય પરિબળોને કારણે છે.
ઉદાહરણ નંબર 3. સરેરાશ વેતન પરના ડેટાના આધારે અને કામદારોના બે જૂથો માટે તેના મૂલ્યમાંથી વર્ગીકૃત વિચલનોના આધારે, ભિન્નતા ઉમેરવાનો નિયમ લાગુ કરીને કુલ તફાવત શોધો:
ઉકેલ:જૂથની અંદરની ભિન્નતાઓની સરેરાશ
અમે આંતરજૂથ તફાવતને આ રીતે વ્યાખ્યાયિત કરીએ છીએ:
કુલ તફાવત હશે: 480 + 13824 = 14304








