周期 T、パルス幅、最大値を持つ方形パルスの周期的なシーケンスを考えてみましょう。。図に示すように座標の原点を選択して、このような信号の級数展開を求めてみましょう。この場合、関数は縦軸に関して対称です。正弦波成分のすべての係数 =0、係数のみを計算する必要がある .

- 0 tt

定数成分
(28)

一定成分は、期間にわたる平均値です。ここは衝動の領域です
を期間全体で割った値、つまり
、つまり厳密な形式的な計算でも同じことが起こりました (28)。

最初の高調波の周波数  1 = であることを思い出してください。ここで、T は方形信号の周期です。高調波間の距離= 1. 高調波数 n が正弦関数の引数であることが判明した場合、
、どこ。その振幅が初めて消失する高調波番号は次のように呼ばれます。 「最初のゼロ」この高調波の特別な特性を強調して、文字 N でそれを表します。

(29)

一方、パルスのデューティサイクル S は、パルス持続時間 t u に対する周期 T の比です。。したがって、「最初のゼロ」はパルスのデューティサイクルと数値的に同じです。 N= S。  の倍数である引数のすべての値についてサインがゼロになるため、「最初のゼロ」の数の倍数である数値を持つすべての高調波の振幅もゼロになります。あれは
で
、どこ k– 任意の整数。したがって、たとえば、(22) と (23) から、デューティサイクル 2 の方形パルスのスペクトルは奇数高調波のみで構成されていることがわかります。なぜなら S=2 、それから N=2 、つまり 2 次高調波の振幅が初めてゼロになります。これが「最初のゼロ」です。ただし、2 で割り切れる数の他のすべての高調波の振幅は次のようになります。すべての偶数もゼロにならなければなりません。デューティサイクル S=3 の場合、ゼロ振幅は 3、6、9、12、... 高調波になります。

デューティサイクルが増加すると、「最初のゼロ」が大きな数の高調波の領域に移動し、その結果、高調波振幅の減少率が減少します。での最初の高調波の振幅の簡単な計算 U メートル=100V (デューティサイクル) S=2, U メートル 1 =63.7V、at S=5, U メートル 1 =37.4V および S=10, U メートル 1 =19.7V、つまりデューティサイクルが増加すると、第 1 高調波の振幅は急激に減少します。たとえば5次高調波の振幅比を求めると、 U メートル 5 第一高調波の振幅に U メートル 1 、次に、 S=2, U メートル 5 /U メートル 1 =0.2、および S=10, U メートル 5 / U メートル 1 = 0.9、つまり高調波の減衰率は、デューティサイクルが増加するにつれて減少します。

したがって、デューティサイクルが増加すると、一連の矩形パルスのスペクトルはより均一になります。

2.5. パルス幅と信号周期が減少するスペクトル。

デューティサイクルを調整する S= T/ t nパルス幅を変更することもできます t nで T=const、または周期 T を変更することで t n=定数。この場合の信号スペクトルを考えてみましょう。

T =定数、t n =var.第一高調波周波数 f 1 =1/ T= 定数と  f= f 1 = 定数。最初のゼロ N= T/ t nそして脈拍が短くなるにつれて t n数値の大きい高調波の領域に移行します。で t n 0 N、スペクトルは離散的であり、  f= f 1 、無限に広く、無限小の高調波振幅を持ちます。

t n =定数、T =var.期間を延長させていただきます T、次に最初の高調波の周波数 f 1 とスペクトル線間の距離  f減少します。なぜなら  f= f 1 =1/T、その後、スペクトル線はより低い周波数にシフトし、スペクトルの「密度」が増加します。もし T の場合、周期的な信号は非周期的 (単一パルス) になります。この場合 f 1 =  f0、つまりスペクトルは離散的なものから連続的なものに変化し、互いに無限小の距離にある無限の数のスペクトル線で構成されます。

これにより、次のルールが導かれます。周期信号は離散 (線) スペクトルを生成し、非周期信号は連続 (連続) スペクトルを生成します。

離散スペクトルから連続スペクトルに移行するとき、フーリエ級数はフーリエ積分に置き換えられます。この置換は、複素形式 (16) および (17) のフーリエ級数の表現を使用する場合に最も簡単に実行されます。連続スペクトルのフーリエ積分は次のように書かれます。

, (30)

どこ
(31)

関数 F(j ) 呼ばれた スペクトル関数または スペクトル密度、周波数によって異なります。式(30)と式(31)を総称して 一方向フーリエ変換これは、より一般的なラプラス変換の特殊なケースであり、ラプラス変換の複素数変数を置き換えることによって取得されます。 Rの上 j .

スペクトル関数は、フーリエ級数の係数の包絡線として表すことができます。における周期関数の線スペクトルの限界として T。関数 F(j ) 実数の場合もあれば、複雑な場合もあります。一般的なケースで考えると
、次の 2 つの周波数特性が得られます。
-振幅スペクトル、つまりスペクトル成分の振幅の周波数依存性、および  ( ) – 位相スペクトル、つまり周波数に応じて信号のスペクトル成分の位相が変化する法則。それは次のことを示すことができます振幅スペクトルは常に偶関数であり、位相スペクトルは常に奇関数です。 . 多くの非周期信号 (さまざまな形状の単一パルス) のスペクトル関数は、教育文献や参考文献に記載されている、ラプラス変換の元の表と画像を使用することで最も簡単かつ簡単に見つけることができます。ラプラスに従って画像を見つけた後 F(p) 特定の非周期関数の場合 f(t) 、スペクトル関数が見つかります

(32)

したがって、(30) によれば、非周期関数は f(t) 無限に小さい振幅を持つ無限に多数の高調波の集合であるように見える
- から + までの周波数範囲全体にわたって、つまりパフォーマンス f(t) フーリエ積分の形では、無限の連続周波数スペクトルの減衰されていない調和振動の合計を意味します。

研究室のセットアップの説明

この作業は「Signal Synthesizer」ブロックで実行されます。その機能図を図に示します。 16.

このブロックには、信号の最初の 6 つの高調波のジェネレーター G1 ～ G6 が含まれています。第 1 高調波の周波数は 10 kHz です。 n 番目の発生器の出力からの高調波信号は、移相器 Ф n と減衰器 A n を介して加算器に供給されます。移相器は  n 高調波の初期位相を設定し、減衰器はその振幅 A n を設定します。

一般に、信号の 6 つの高調波の合計が加算器の出力で得られます。

信号は加算器の出力からオシロスコープの Y 入力に供給されます。外部同期には、「Sync」ソケットから供給される特別なパルス信号が使用されます。オシロスコープのX入力に接続します。高調波の振幅を設定および制御するために、いずれかの高調波を無効にすることができます。 n 次高調波発生器のみをオンにすると、アッテネータ A n を使用してその振幅を設定し、オシロスコープを使用してその値を評価できます。スイッチを使用すると、各移相器で高調波の初期位相に必要な離散値を設定したり、発電機をオフにしたりできます。

信号とそのパラメータの分類。

電気信号は、情報の送信または保存に使用される電気プロセスです。

信号は、決定的信号とランダム信号という 2 つの大きなクラスに分類できます。決定論的信号とは、その瞬間値がいつでも 1 に等しい確率で予測でき、特定の時間関数の形式で指定される信号です。典型的な例をいくつか示します。振幅が既知の高調波信号あそして期間 T(図1.1 あ); 既知の繰り返し周期を持つ一連の方形パルス T、持続時間 t および振幅あ(図1.1 b); 既知の持続時間 t と振幅を持つ任意の形状のパルスのシーケンスあそして期間 T(図1.1 V）。確定的な信号には情報が含まれません。

ランダム信号は時間のカオス関数であり、その値は事前には不明であり、1 に等しい確率で予測することはできません (持続時間 t と振幅を持つ単一パルス) あ(図1.1 G) 電気量の表現における音声、音楽)。ランダム信号にはノイズも含まれます。

決定論的な信号は、条件が満たされる周期的な信号に分割されます。 S(t)=S(t+kT）、どこ T- 期間、 k- 任意の整数以下 S(t) 時間の経過とともに変化する電流、電圧、または電荷を指します (図 1.1) ＢＣ).

明らかに、条件が満たされる決定論的な信号は非周期的です。 S(t)¹ S(t+kT).

最も単純な周期信号は、次の形式の高調波信号です。 .

複雑な周期信号はすべて高調波成分に分解できます。以下では、そのような分解をいくつかの特定のタイプの信号に対して実行します。

変調により情報が埋め込まれた高周波の高調波信号を無線信号と呼びます（図1.1） d).

周期的な信号。

任意の複雑な周期信号 S(t)=S(t+kT) (図 1.2)、値の範囲で指定 t–¥ から +¥ までは、基本高調波信号の和として表すことができます。指定された周期関数のみがディリクレ条件を満たす場合、この表現はフーリエ級数の形式で実行されます。

1. 任意の有限時間間隔で関数 S(t) は連続的であるか、有限数の第 1 種の不連続性を持たなければなりません。

2. 1 つの期間内で、関数は有限数の最大値と最小値を持たなければなりません。

通常、実際の無線信号はすべてこれらの条件を満たします。三角関数形式では、フーリエ級数は次の形式になります (1.1)

ここで、定数コンポーネントは次の値に等しい (1.2)

そして係数ん、そして bnコサイン項と正弦波項の場合、展開は次の式によって決まります。 (1.3)

振幅 (係数) と位相 (引数) n番目高調波は係数によって表現されますん、そして bn次の方法で (1.4)

複雑な表記形式を使用する場合、信号 S(t) の式は次の形式になります。。ここに係数があります複素振幅と呼ばれる、等しいそして、次の式によって数量 a n および b n に関連付けられます: n>0 の場合、および n の場合<0. С учётом обозначений .

周期関数のスペクトルは、離散周波数 0、w、2w、3w ... に対応する個々の線で構成されます。つまり、線または離散的な性質を持ちます (図 1.3)。フーリエ級数を重ね合わせの原理と組み合わせて使用することは、線形システムを通過するさまざまな種類の周期信号の通過に対する線形システムの影響を分析する強力な手段です。

周期関数をフーリエ級数に拡張するときは、計算を簡素化できるため、関数自体の対称性を考慮する必要があります。対称性のタイプに応じて、フーリエ級数で表される関数は次のことができます。

1. 正の半サイクルの図形の面積が負の半サイクルの図形の面積と等しい場合、定数成分は存在しません。

2. 関数値が半周期後に反対の符号で繰り返される場合、偶数高調波と定数成分は存在しません。

デューティサイクルの異なる周期における一連の矩形パルスのスペクトル構成。

方形パルスの周期的シーケンスを図に示します。 1.4. フーリエ級数の定数成分は次の式から求められます。この場合、それは次と等しくなります .

cos成分の振幅 そしてnに等しい

、およびsin成分の振幅 b nに等しい .

振幅 n次高調波

教育団体名:

国家予算の専門教育機関「スタヴロポリ通信大学」はソ連の英雄、バージニア州の英雄にちなんで名付けられました。ペトロワ」

作品の制作年と場所： 2016 年、自然および一般的な専門分野のサイクル委員会。

「電気通信理論」という学問の実践のためのガイドライン

「方形パルスの周期的シーケンスのスペクトルの計算と構築」

学生のための 2 専門コース:

02/11/11 通信ネットワークと交換システム

02/11/09 多チャンネル通信システム

フルタイム教育

仕事の目標:理論授業で得た知識を強化し、周期的な一連の矩形パルスのスペクトルを計算するスキルを開発します。

文学： P.A. ウシャコフ「通信回路と信号」 M.: パブリッシングセンター「アカデミー」、2010 年、24-27 ページ。

1. 設備:

1.パソコン

2.実務の説明

2. 理論資料

2.1. 任意の形状の周期信号は、さまざまな周波数の調和振動の合計として表すことができ、これを信号のスペクトル分解と呼びます。

2.2 。高調波は、その周波数が信号のパルス繰り返し率の整数倍である振動です。

2.3. 周期微分波形の瞬時電圧値は次のように記述できます。

ここで、定数成分は、期間にわたる平均信号値に等しいです。

第一高調波の正弦波電圧の瞬時値。

高調波周波数はパルス繰り返し周波数に等しい。

第一高調波の振幅。

第一高調波振動の初期位相。

第 2 高調波正弦波電圧の瞬時値。

第二高調波周波数;

第二高調波振幅。

第 2 高調波振動の初期位相。

3 次高調波正弦波電圧の瞬時値。

第三高調波周波数。

3 次高調波の振幅。

3 次高調波振動の初期位相。

2.4. 信号のスペクトルは、信号の合計を形成する周波数、振幅、初期位相の特定の値を持つ一連の高調波成分です。実際には、振幅図が最もよく使用されます。

信号が方形パルスの周期的なシーケンスである場合、定数成分は次のようになります。

ここで、Um は PPIP の電圧振幅です。

s - 信号デューティサイクル (S - T/t);

T - パルス繰り返し周期。

t - パルス持続時間。

すべての高調波の振幅は次の式で決定されます。

ウムク = 2ウム | sin kπ/s | /kπ

ここで、k は高調波数です。

2.5. 振幅がゼロとなる高調波の数

ここで、n は任意の整数 1、2、3…..

振幅が初めてゼロになる高調波の数は、PPIP のデューティサイクルに等しい

2.6. 隣接するスペクトル線間の間隔は、第 1 高調波の周波数またはパルス繰り返し周波数に等しくなります。

2.7 信号の振幅スペクトルの包絡線（図1に点線で示す）

ローブと呼ばれるスペクトル線のグループを識別します。図によると。図１に示すように、スペクトル包絡線の各ローブには、信号デューティサイクルに等しい数のラインが含まれています。

3 。 P作業命令.

3.1. グループジャーナルリストの番号と一致する個別のタスクオプションを受け取ります (付録を参照)。

3.2. 計算例を読んでください (セクション 4 を参照)

4. 例

4.1. パルス繰り返し周期 T=.1 μs、パルス持続時間 t=0.25 μs、パルス振幅 = 10V とします。

4.2. AEFI 時間図の計算と構築。

4.2.1 。 PPIP の時間図を作成するには、問題の条件から分かるパルス繰り返し周期 T、パルスの振幅と持続時間 t を知る必要があります。

4.2.2. SAI の時間図を作成するには、応力軸と時間軸に沿ってスケールを選択する必要があります。スケールは、1、2、4 の数値に 10 n - を乗算したものに対応する必要があります (n=0、1、2、3...)。時間軸はシートの幅の約 3/4 を占め、その上に 2 ～ 3 個の信号周期を配置する必要があります。応力の縦軸は 5 ～ 10 cm で、シート幅が 20 cm の場合、時間軸の長さは約 15 cm になるように、15 cm 上に 3 つの期間を配置すると便利です。 L1=5cmとなります。なぜなら

Mt=T/Lt=1μs/5cm=0.2μs/cm

得られた結果は上記の条件に矛盾しません。応力軸では、Mu = 2V/cm のスケールを取ると便利です (図 2 を参照)。

4.3.スペクトル図の計算と構築。

4.3.1.FITR のデューティサイクルは次と等しい

4.3.2. デューティサイクルは S=4 であるため、3 枚の花びらを計算する必要があります。 12倍音。

4.3.3. 高調波成分の周波数は等しい

ここで、k は高調波数、l は SAI 周期です。

4.3.4. AEFI 成分の振幅は等しい

4.3.5. 電圧SAIの数学モデル

4.3.6.スケールの選択。

周波数軸は水平に配置されており、シートの幅が 20 cm の場合、長さは約 15 cm になります。周波数軸上に 12 MHz の最高周波数を表示する必要があるため、これに沿ってスケールを取ると便利です。軸 Mf = 1 MHz/cm。

応力軸は垂直に配置されており、応力軸から最大の応力を示す必要があるため、長さは 4 ～ 5 cm である必要があります。

この軸 M=1V/cm に沿ってスケールを取ると便利です。

4.3.7. スペクトル図を図 3 に示します。

エクササイズ：

T=0.75ミリ秒; τ=0.15ms 21.T=24μs; τ=8μs

T=1.5μs; τ=0.25μs 22. T=6.4ms; τ=1.6ms

T=2.45ミリ秒; τ=0.35ms 23. T=7ms; τ=1.4ms

T=13.5μs; τ=4.5μs 24. T=5.4ms; τ=0.9ms

T=0.26ミリ秒; τ=0.65μs 25. T=17.5μs; τ=2.5μs

T=0.9ミリ秒; τ=150μs 26. T=1.4μs; τ=0.35μs

T=0.165ミリ秒; τ=55μs 27. T=5.4μs; τ=1.8μs

T=0.3ミリ秒; τ=75μs 28. T=2.1ms; τ=0.3ms

T=42.5μs; τ=8.5μs 29. T=3.5ms; τ=7ms

T=0.665ミリ秒; τ=95μs 30. T=27μs; τ=4.5μs

T=12.5μs; τ=2.5μs 31. T=4.2μs; τ=0.7μs

T=38μs; τ=9.5μs 32.T=28μs; τ=7μs

T=0.9μs; τ=0.3μs 33. T=0.3ms; τ=60μs

T=38.5μs; τ=5.5μs

T=0.21ミリ秒; τ=35ms

T=2.25ミリ秒; τ=0.45ms

T=39μs; τ=6.5μs

T=5.95ミリ秒; τ=0.85ms

T=48μs; τ=16μs

時間関数のスペクトル表現は、コミュニケーション理論で広く使用されています。電気回路の特性や通信チャネルを介したメッセージの送信に関する理論的および実験的研究には、高調波振動、一定の電圧レベル、一連の矩形パルスや無線パルスなど、さまざまなタイプの信号が使用されます。単位関数は、電気回路とインパルス関数 (ディラック関数) の理論的研究において特に重要な役割を果たします。最も一般的な典型的な信号のスペクトルを決定してみましょう。

11.1 一連の矩形パルスのスペクトル

周期 T、パルス持続時間 t、振幅 A を持つ方形パルスの周期シーケンスがあるとします。セグメント上のパルスを記述する関数の解析式は次の形式になります。

(11.1)

周期的なパルスシーケンスのグラフを図 11.1 に示します。

図11.1

この関数は、グラフが縦軸に関して対称であるため、偶数です。次に、これらの関数のフーリエ係数が式 (KFT2) を使用して計算されます。

この数値は期間にわたる関数の平均値を表し、定数コンポーネントと呼ばれます。周波数は基本波または第 1 高調波と呼ばれ、k 個の周波数は高調波と呼ばれます。ここで、k = 2、3、4、...

考慮されている一連の矩形パルスの振幅スペクトルを構築してみましょう。関数は周期的であるため、その振幅スペクトルは線状になります。隣接する高調波間の距離で表しましょう。明らかに、それはに等しい。 (11.2) による k 次高調波の振幅は次の形式になります。

(11.3)

周期 T と k 次高調波の振幅がゼロになるパルス幅の関係を求めます。

A2≈32V、A3≈15V、A4≈0、A5≈6.36V、A6≈10.5V、A7≈6.36V、A8≈0、A9≈4.95V、A10≈6.37V。

計算の結果得られた振幅スペクトルを図11.2に示します。

図11.2

このようなスペクトルは、線スペクトルまたは離散スペクトルと呼ばれます。

q=8 および q=16 のスペクトルも同様に計算され、プロットされました。それらをそれぞれ図 11.3 と図 11.4 に示します。

図11.3

図11.4

この図は、方形パルスのデューティサイクルが大きくなるほど、第 1 高調波の振幅は小さくなりますが、スペクトルの減少が遅くなることがわかります。

11.2 単一方形パルスのスペクトル

T→∞、つまりパルスの周期シーケンスが持続時間 t u の単一の矩形パルスに縮退する場合の Ф (11.1) を考えてみましょう。

このインパルスの分析式は次のように記述されます。

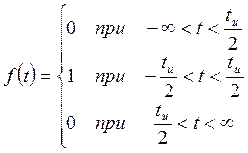
この関数のグラフを図 11.5 に示します。

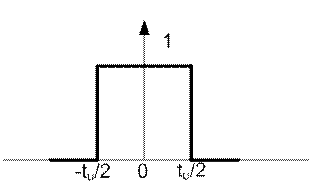
図11.5

この場合、最初の高調波の周波数と高調波間の距離は 0 に等しくなるため、スペクトルは離散的なものから連続的なものになり、互いに無限小の距離にある無数のスペクトル線で構成されます。このようなスペクトルは連続スペクトルと呼ばれます。これは最も重要なルールにつながります。つまり、周期信号は離散スペクトルを生成し、非周期信号は連続スペクトルを生成します。

方形単一パルスのスペクトルは、直接フーリエ変換 (10.1) から直接求めることができます。

周期信号のスペクトル解析

知られているように、ディリクレ条件を満たす (実際の信号のモデルが条件を満たす) 時間の周期関数で記述される信号 S(t) は、フーリエ級数と呼ばれる調和振動の和として表すことができます。

ここで、は期間にわたる信号の平均値、または信号の一定成分です。

フーリエ級数係数。

基本周波数 (第 1 高調波周波数); n=1,2,3,…

値 An と n (または正弦関数 n に展開される場合) のセットは、周期関数のスペクトルと呼ばれます。高調波振幅 An は振幅スペクトルを特徴付け、初期位相 n (または「n」) は位相スペクトルを特徴付けます。

したがって、周期信号のスペクトルは、一定の成分と、対応する振幅と初期位相を持つ無限の調和振動 (サインまたはコサイン) として表されます。すべての高調波周波数は基本周波数の倍数です。これは、周期信号がたとえば 1 kHz の周波数に従う場合、そのスペクトルには 0 kHz、1 kHz、2 kHz などの周波数のみが含まれることを意味します。このような周期信号のスペクトルには、たとえば 1.5 kHz や 1.2 kHz の周波数を含めることはできません。

図では、 1. 特定の周期信号の振幅と位相のスペクトルが表示されます。各高調波成分は垂直セグメントとして表され、その長さは (あるスケールで) その振幅と位相に等しくなります。ご覧のとおり、周期信号のスペクトルは離散的、またはいわゆる「線状」です。

計算を簡素化するために、フーリエ級数を三角関数形式で記述する代わりに、係数 An と n を組み合わせた複雑な形式のフーリエ級数を使用することがよくあります。