Enačbe s spremembo spremenljivke. Metoda integracije s spremembo spremenljivke

Matematika je luknja, skozi katero lahko logični um pokuka v idealni svet.

Krotov Viktor

V šoli zavzemajo racionalne enačbe vodilno mesto pri tečaju algebre. Njihovemu študiju se posveti več časa kot kateri koli drugi temi. To je predvsem posledica dejstva, da enačbe nimajo le pomembnega teoretičnega pomena, ampak služijo tudi mnogim praktičnim namenom. Ogromno število problemov v resničnem svetu se spusti na reševanje različnih enačb in šele ko obvladate metode njihovega reševanja, boste našli odgovore na različna vprašanja znanosti in tehnologije.

Za razvijanje sposobnosti reševanja racionalnih enačb je zelo pomembno študentovo samostojno delo. Preden pa preidete na samostojno delo, morate jasno poznati in znati v praksi uporabiti vse možne metode za reševanje racionalnih enačb.

Oglejmo si ga podrobno na primerih. variabilna metoda zamenjave za reševanje racionalnih enačb.

Primer 1.

Rešite enačbo (2x 2 – 3x + 1) 2 = 22x 2 – 33x + 1.

rešitev.

Prepišimo enačbo v obliki

(2x 2 – 3x + 1) 2 = 11(2x 2 – 3x) + 1. Naredimo zamenjavo. Naj bo 2x 2 – 3x = t, potem bo enačba v obliki:

(t + 1) 2 = 11t + 1.

Zdaj pa odpremo oklepaje in podamo podobne, dobimo:

t 2 + 2t + 1 = 11t + 1;

V nastali nepopolni kvadratni enačbi vzamemo skupni faktor iz oklepaja in imamo:

t = 0 ali t = 9.

Zdaj morate narediti obratno zamenjavo in rešiti vsako od nastalih enačb:

2x 2 – 3x = 0 ali 2x 2 – 3x = 9

x(2x – 3) = 0 2x 2 – 3x – 9 = 0

x = 0 ali x = 3/2 x = 3 ali x = -3/2

Odgovor: -1,5; 0; 1,5; 3.

Primer 2.

Rešite enačbo (x 2 – 6x) 2 – 2(x – 3) 2 = 81.

rešitev.

Uporabimo formulo za kvadrat razlike (a – b) 2 = a 2 – 2ab + b 2 . Zapišimo izvirno enačbo v obliki

(x 2 – 6x) 2 – 2(x 2 – 6x + 9) = 81. Zdaj lahko opravite zamenjavo.

Naj bo x 2 – 6x = t, potem bo enačba videti takole:

t 2 – 2(t + 9) = 81.

t 2 – 2t – 18 – 81 = 0;

t 2 – 2t – 99 = 0.

Po Vietovem izreku bodo korenine nastale enačbe števili -9 in 11.

Naredimo obratno zamenjavo:

x 2 – 6x = -9 ali x 2 – 6x = 11

x 2 – 6x + 9 = 0 x 2 – 6x – 11 = 0

(x – 3) 2 = 0 D = 80

x = 3 x 1 = 3 + 2√5; x 2 = 3 – 2√5.

Odgovor: 3 – 2√5; 3; 3 + 2√5.

Primer 3.

Rešite enačbo (x – 1)(x – 3)(x + 5)(x + 7) = 297 in poiščite produkt njenih korenin.

rešitev.

Poiščimo "dobičkonosen" način za združevanje faktorjev in odprimo pare oklepajev:

((x – 1)(x + 5))((x – 3)(x + 7)) = 297;

(x 2 + 5x – x – 5)(x 2 + 7x – 3x – 21) = 297;

(x 2 + 4x – 5) (x 2 + 4x – 21) = 297.

Naredimo zamenjavo x 2 + 4x = t, potem bo enačba videti takole:

(t – 5)(t – 21) = 297.

Odprimo oklepaje in predstavimo podobne izraze:

t 2 – 21t – 5t + 105 = 297;

t 2 – 26t – 192 = 0.

Z uporabo Vietovega izreka določimo, da bosta korena dobljene enačbe števili -6 in 32.

Po obratni zamenjavi bomo imeli:

x 2 + 4x = -6 ali x 2 + 4x = 32

x 2 + 4x + 6 = 0 x 2 + 4x – 32 = 0

D = 16 – 24< 0 D = 16 + 128 > 0

Brez korenin x 1 = -8; x 2 = 4

Poiščemo produkt korenin: -8 · 4 = -32.

Odgovor: -32.

Primer 4.

Poiščite vsoto korenov enačbe (x 2 – 2x + 2) 2 + 3x(x 2 – 2x + 2) = 10x 2.

rešitev.

Naj bo x 2 – 2x + 2 = t, potem bo enačba v obliki:

t 2 + 3xt – 10x 2 = 0.

Vzemimo dobljeno enačbo kot kvadratno glede na t.

D = (3x) 2 – 4 · (-10x 2) = 9x 2 + 40x 2 = 49x 2 ; ≥≤

t 1 = (-3x – 7x) / 2 in t 2 = (-3x + 7x) / 2;

t 1 = -5x in t 2 = 2x.

Ker je t = x 2 – 2x + 2, potem

x 2 – 2x + 2 = -5x ali x 2 – 2x + 2 = 2x. Rešimo vsako od nastalih enačb.

x 2 + 3x + 2 = 0 ali x 2 – 4x + 2 = 0.

Obe enačbi imata korenine, ker D > 0.

Z uporabo Vietovega izreka lahko sklepamo, da je vsota korenov prve enačbe -3, druge enačbe pa 4. Ugotovimo, da je vsota korenov prvotne enačbe -3 + 4 = 1

Odgovor: 1.

Primer 5.

Poiščite koren enačbe (x + 1) 4 + (x + 5) 4 = 32, ki pripada intervalu [-5; 10].

rešitev.

Naj bo x = t – 3, potem je x + 1 = t – 2; x + 5 = t + 2 in izvirna enačba ima obliko:

(t – 2) 4 + (t + 2) 4 = 32. Če želite izraze dvigniti na četrto potenco, lahko uporabite Pascalov trikotnik (slika 1);

(t – 2) 4 = t 4 – 4t 3 2 + 6t 2 2 2 – 4t 2 3 + 2 4 ;

(t + 2) 4 = t 4 + 4t 3 2 + 6t 2 2 2 + 4t 2 3 + 2 4.

Po zmanjšanju podobnih izrazov dobimo:

2t 4 – 2 6t 2 2 2 + 2 2 4 = 32;

t 4 + 6t 2 2 2 + 2 4 = 16;

t 4 + 24t 2 + 16 = 16;

t 4 + 24t 2 = 0;

t 2 (t 2 + 24) = 0;

t = 0 ali t 2 = -24.

Druga enačba je brez korenin, kar pomeni t = 0 tudi po obratni zamenjavi

x = t – 3 = 0 – 3 = -3. Koren enačbe -3 pripada intervalu [-5; 10].

Odgovor: -3.

Kot lahko vidite, morate pri reševanju racionalnih enačb poznati zgornje formule in znati pravilno šteti. Najpogosteje pride do napak pri izbiri zamenjave in pri obratni zamenjavi. Da bi se temu izognili, morate vsako dejanje podrobno opisati, potem pri vaših odločitvah ne bo napak.

blog.site, pri celotnem ali delnem kopiranju gradiva je obvezna povezava do izvirnega vira.

Reševanje enačb z metodo menjave spremenljivk

Večino življenjskih nalog

se rešujejo kot algebraične enačbe:

jih pripeljejo do najpreprostejše oblike.

L.N. Tolstoj.

Namen lekcije: organizira izobraževalno dejavnost študentov za obvladovanje metod za reševanje celotnih enačb višjih stopenj z metodo substitucije spremenljivke; seznaniti študente s koncepti in tehnikami za reševanje recipročnih in simetričnih enačb.

Naloge:izobraževalni:še naprej razvijati sposobnost uporabe nadomestne metode

spremenljivka pri reševanju enačb; razvijanje sposobnosti videti isto metodo za reševanje enačb v različnih situacijah; oblikovati idejo o metodah in tehnikah za reševanje nestandardnih problemov in algebrskih enačb na ravni, ki presega raven državnih izobraževalnih standardov;

razvoj: razvoj mišljenja učencev; razvoj spomina; razvoj

logično razmišljanje, sposobnost jasnega oblikovanja svojih misli; razvoj domišljije učencev; razvoj ustnega govora.

izobraževalni: izobraževanje sposobnosti opazovanja; vzgoja urejenosti

pri zapisovanju na tablo in v zvezek; negovanje samostojnosti pri praktičnem delu.

Napredek lekcije

Organizacijski trenutek.

Posodobitev in sistematizacija znanja.

Naloga št. 1. Reši križanko. Odgovore zapišite samo v imenovalniku.

4.Kaj je izraz za kvadratno enačbo? (diskriminator)

6. Vrednost spremenljivke, pri kateri se enačba spremeni v pravo enakost. (koren)

8.Enačba oblike
, Kje
. (bikvadraten)

9.Francoski matematik, povezan s kvadratnimi enačbami. (Viet)

10. Enačba, v kateri sta leva in desna stran celoštevilski izraz. (celo)

11. Enačbe z eno spremenljivko, ki imajo enako množico korenov. (enakovredno)

Navpično:

1. Številni koreni enačbe. (rešitev)

2. Rešitev enačbe
. (nič)

3. Enačba, ki vsebuje spremenljivko. (enačba)

5. Kvadratna enačba, v kateri je eden od koeficientov b ali c enak 0. (nepopolno)

7. Kvadratna enačba, v kateri je prvi koeficient enak ena. (podano)

Čemu bomo danes posvetili lekcijo? ( Reševanje enačb )

Naloga št. 2. Kako bi rešili enačbe za vsako skupino?

ODGOVORI: Primere skupine 1) je najbolje rešiti z faktorizacijo tako, da skupni faktor postavite iz oklepaja ali uporabite skrajšane formule za množenje.

Primere skupine 2) je bolje rešiti z združevanjem in faktorizacijo.

Primere skupine 3) je bolje rešiti z uvedbo nove spremenljivke in prehodom na kvadratno enačbo.

1 Kateri dejavnik bi dal iz oklepaja v primerih skupine 1?

ODGOVORI:

Kako bi združili izraze v skupini 2 primerov?

ODGOVORI:

Kaj bi mislili z novo spremenljivko v skupini 3 primerov?

ODGOVORI:

Kako lahko faktoriziraš polinom?
?

ODGOVORI: .

Danes boste v lekciji pokazali svoje znanje na temo "Reševanje enačb z metodo zamenjave spremenljivk"

Temo lekcije zapišite v zvezke.

Danes si bomo pri pouku ogledali enega izmed načinov reševanja enačb višjih stopenj – metodo zamenjave spremenljivke; Spoznajmo koncepte in tehnike reševanja recipročnih in simetričnih enačb.

Umetnost izvajanja spremenljivih zamenjav je ugotoviti, katera zamenjava je najbolj smiselna in hitreje vodi do uspeha.

Naloga št. 3.

Reši enačbo.(2 učenca istočasno rešujeta nalogo ob tabli.)

A) (Prvi učenec rešuje ob tabli z razlago.)

b) (Drugi učenec tiho reši enačbo, nato razloži rešitev, razred posluša in sprašuje, če kaj ni jasno.)

1 študent Zamenjava:
.

2 študent Zamenjava:
.

(Dodatno za tiste, ki so prej obvladali prejšnje enačbe).

. .

3 študent

(Učenci s sedeža komentirajo potek reševanja.)

REŠITEV: Dodajmo skupni faktor: ,

kjer
oz
, tj.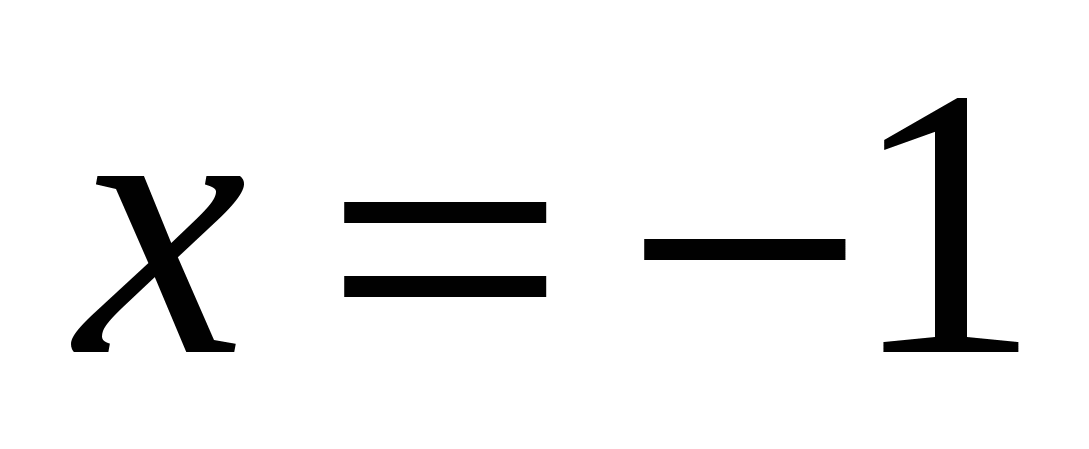

odgovor:

Poglabljanje in širjenje znanja

Nadaljujemo z delom. Na prosojnici vidite enačbo: x 4 -5x 3 +6x 2 -5x+1=0.

Kako predlagate rešitev? Kaj naj storimo?

Ali jo je mogoče rešiti v okviru šolskih programov matematike? Odgovor je ne. Navsezadnje standardne metode reševanja enačb v šoli vključujejo reševanje enačb največ druge stopnje. Spomnimo pa se lahko, da so posamezne enačbe višjih stopenj reševali še v šoli. Res je, metode za njihovo reševanje so kreativna uporaba znanih metod, ki jih zmanjšajo na rešitev ene ali več enačb stopnje, ki ni višja od druge.

Poglejte zelo natančno to enačbo? Kaj si opazil ?(v tej enačbi so koeficienti, enako oddaljeni od koncev, enaki)

Fantje, enačba te vrste, ko koeficienti, enako oddaljeni od koncev sovpadajo, se imenuje povratno. To enačbo je mogoče zmanjšati na kvadratno enačbo z uporabo substitucije.

Ponujam vam naslednji algoritem za njihovo reševanje:

Algoritem za reševanje recipročnih enačb.

1. Obe strani enačbe delite z x 2.

2.Združi izraze (prvi z zadnjim, drugi s četrtim).

Zmanjšajte enačbo na obliko A + c = 0

3.Uvedite novo spremenljivko t = ,tedaj izpolnjena t 2 = , tj.

= t 2 – 2.

4. Nadomestite in rešite kvadratno enačbo.

5. Vrnite se k zamenjavi in ​​rešite nastale enačbe.

6. Zapišite odgovor.

Fantje preučujejo algoritem.

Učenec ob tabli rešuje enačbo po algoritmu in s pomočjo učitelja, ostali pišejo v zvezke. 4 6x 3 – 5x 2 – 38x

rešitev.

– 5x + 6 = 0.

6x 2 – 5x – 38 – 5/x + 6/x 2 = 0.

6(x 2 + 1/x 2) – 5(x + 1/x) – 38 = 0.

Vnesite t: zamenjava (x + 1/x) = t. Zamenjava: (x 2 + 1/x 2) = t 2 – 2, imamo:

6t 2 – 5t – 50 = 0.

t = -5/2 ali t = 10/3.

Vrnimo se k spremenljivki x. Po obratni zamenjavi rešimo dobljeni enačbi:

1) x + 1/x = -5/2;

x 2 + 5/2 x +1 = 0;

x = -2 ali x = -1/2.

2) x + 1/x = 10/3;

x 2 – 10/3 x + 1 = 0;

x = 3 ali x = 1/3.

Odgovor: -2; -1/2; 1/3; 3.

K problemu enačb 3. in 4. stopnje so veliko prispevali italijanski matematiki 16. stoletja N. Tartaglia, A. Fiore, D. Cardano in drugi. Leta 1535 je potekal znanstveni dvoboj med A. Fiorejem in N. Tartaglia, na kateri je zmagal slednji. V 2 urah je rešil 30 problemov, ki jih je predlagal Fiore, sam Fiore pa ni mogel rešiti niti enega, ki mu ga je dal Tartaglia.

. Fantje, danes vam želim ponuditi še eno enačbo; vzel sem jo iz zbirke nalog za pripravo na OGE.

((x + 1)(x + 4))((x + 2)(x + 3)) = 24,

(x 2 + 5x + 4) (x 2 + 5x + 6) = 24.

Če zamenjamo x 2 + 5x + 4 = t, dobimo enačbo

t(t + 2) = 24, je kvadrat:

t 2 + 2t – 24 = 0.

t = -6 ali t = 4.

Ko izvedemo obratno zamenjavo, zlahka najdemo korene prvotne enačbe.

Odgovor: -5; 0.

Kreativni prenos znanja in veščin v nove razmere.

Na začetku lekcije smo govorili o dejstvu, da če se v enačbi ponavljajo elementi, potem lahko uporabite metodo zamenjave spremenljivke. Trigonometričnih in iracionalnih enačb še ne znamo reševati. Poglejmo, ali lahko to metodo uporabimo pri njih, če znamo reševati preproste trigonometrične in iracionalne enačbe. Naloga 1:

Poimenujte spremembo spremenljivke v naslednjih enačbah. Naloga 2:

Sestavite več enačb, katerih rešitev temelji na metodi zamenjave spremenljivke.

Če povzamem.

Torej, fantje, naša lekcija se je končala. Povzemimo našo lekcijo.

Kakšne cilje smo si zastavili na začetku lekcije?

Ali so naši cilji doseženi?

Kaj novega smo se naučili v lekciji?

4x 4 – 8x 3 + 3x 2 – 8x + 4 = 0

(x+1)(x+2)(x+4)(x+5) = 40

. (enačba italijanskih matematikov)

Lekcijo bi rad zaključil z besedami velikega znanstvenika Einsteina A.:

»Svoj čas moram razdeliti med politiko in enačbe. Vendar je enačba po mojem mnenju veliko pomembnejša, saj politika obstaja samo ta trenutek, enačba pa bo obstajala večno.”

Hvala za lekcijo! Adijo!

Ohranjanje vaše zasebnosti je za nas pomembno. Iz tega razloga smo razvili Politiko zasebnosti, ki opisuje, kako uporabljamo in shranjujemo vaše podatke. Preglejte naše postopke varovanja zasebnosti in nam sporočite, če imate kakršna koli vprašanja.

Zbiranje in uporaba osebnih podatkov

Osebni podatki se nanašajo na podatke, ki jih je mogoče uporabiti za identifikacijo ali vzpostavitev stika z določeno osebo.

Kadar koli stopite v stik z nami, boste morda morali posredovati svoje osebne podatke.

Spodaj je nekaj primerov vrst osebnih podatkov, ki jih lahko zbiramo, in kako lahko te podatke uporabimo.

Katere osebne podatke zbiramo:

• Ko na spletnem mestu oddate prijavo, lahko zberemo različne podatke, vključno z vašim imenom, telefonsko številko, e-poštnim naslovom itd.

Kako uporabljamo vaše osebne podatke:

• Osebni podatki, ki jih zbiramo, nam omogočajo, da vas kontaktiramo z edinstvenimi ponudbami, promocijami in drugimi dogodki ter prihajajočimi dogodki.
• Občasno lahko uporabimo vaše osebne podatke za pošiljanje pomembnih obvestil in sporočil.
• Osebne podatke lahko uporabljamo tudi za interne namene, kot so izvajanje revizij, analize podatkov in različne raziskave, da bi izboljšali storitve, ki jih nudimo, in vam dali priporočila glede naših storitev.
• Če sodelujete v nagradni igri, tekmovanju ali podobni promociji, lahko podatke, ki nam jih posredujete, uporabimo za upravljanje takih programov.

Razkritje informacij tretjim osebam

Prejetih podatkov ne razkrivamo tretjim osebam.

Izjeme:

• Če je potrebno - v skladu z zakonom, sodnim postopkom, v sodnem postopku in/ali na podlagi javnih zahtev ali zahtev državnih organov na ozemlju Ruske federacije - za razkritje vaših osebnih podatkov. Podatke o vas lahko razkrijemo tudi, če ugotovimo, da je takšno razkritje potrebno ali primerno za varnostne namene, namene kazenskega pregona ali druge javno pomembne namene.
• V primeru reorganizacije, združitve ali prodaje lahko osebne podatke, ki jih zberemo, prenesemo na ustrezno naslednico tretje osebe.

Varstvo osebnih podatkov

Izvajamo previdnostne ukrepe – vključno z administrativnimi, tehničnimi in fizičnimi – za zaščito vaših osebnih podatkov pred izgubo, krajo in zlorabo ter nepooblaščenim dostopom, razkritjem, spreminjanjem in uničenjem.

Spoštovanje vaše zasebnosti na ravni podjetja

Da bi zagotovili varnost vaših osebnih podatkov, svojim zaposlenim sporočamo standarde zasebnosti in varnosti ter strogo uveljavljamo prakse glede zasebnosti.

Uvod

Matematična izobrazba, pridobljena v srednji šoli, je bistvena sestavina splošne izobrazbe in splošne kulture sodobnega človeka. Skoraj vse, kar obdaja sodobnega človeka, je tako ali drugače povezano z matematiko. In nedavni napredek v fiziki, tehniki in informacijski tehnologiji ne pušča nobenega dvoma, da bo stanje v prihodnosti ostalo enako. Zato se reševanje številnih praktičnih problemov zmanjša na reševanje različnih vrst enačb, ki se jih morate naučiti reševati.

V osnovni matematiki obstajata dve vrsti enačb: algebraične in transcendentalne enačbe.

kubični;

dvočlenska algebrska enačba n-te stopnje; potenčna algebraika; – refleksivna (algebraična); – algebraična enačba th stopnje splošne oblike;

10. ulomljene algebrske enačbe, tj. enačbe, ki vsebujejo polinome in algebraične ulomke (ulomke oblike

Enačbe, ki vsebujejo transcendentne funkcije, kot so logaritemske, eksponentne ali trigonometrične funkcije, imenujemo transcendentne. V našem delu bomo podrobneje obravnavali algebraične enačbe.

Učna in metodološka literatura tradicionalno obravnava posebne tehnike reševanja enačb. Medtem pa so posebnosti reševanja enačb vsakega odseka drugotnega pomena. V bistvu obstajajo štiri glavne metode:

Zamenjava enačbe h (f(x))=h (g(x)) z enačbo f(x)=g(x);

Metoda variabilne zamenjave;

Metoda faktorizacije;

Funkcionalno-grafične metode in njihove različne modifikacije.

Najpogostejša med njimi je metoda variabilne zamenjave.

Na podlagi tega oblikujemo cilj našega dela: preučiti možnosti metode zamenjave neznanke pri reševanju algebrskih enačb in prikazati njihovo uporabo v standardnih in nestandardnih situacijah. Za dosego tega cilja je potrebno rešiti naslednje naloge:

1. Razkrijte vsebino osnovnih pojmov in trditev, povezanih s teorijo reševanja enačb: reševanje enačbe, ekvivalenca in posledica, splošne metode reševanja enačb.

2. Ugotovite možnosti uporabe metode zamenjave neznanke pri reševanju algebrskih enačb v standardnih in nestandardnih situacijah.

3. Tipizirati metode za uvajanje novih neznank pri reševanju algebrskih enačb in identificirati kriterije njihove uporabnosti.

4. Sestavite niz tipičnih nalog, ki se nanašajo na uporabo substitucijske metode pri reševanju enačb, in pokažite njihovo rešitev.

1. Osnovni pojmi in trditve v zvezi s teorijo reševanja enačb

V prvem poglavju našega dela bomo razkrili vsebino osnovnih pojmov in trditev, povezanih s teorijo reševanja enačb.

S pojmom »enačba« se pri pouku matematike seznanimo že v osnovni šoli, naloga »reši enačbo« pa je verjetno najpogostejša težava. Kljub temu ne moremo podati natančne definicije pojma "enačba", natančno definirati, kaj pomeni "rešiti enačbo", ne da bi šli daleč preko okvira predmeta osnovne matematike. Za to je potrebno vključiti zelo resne logične in celo filozofske kategorije. Seznanjenost s temi koncepti na ravni "zdrave pameti" je za nas povsem dovolj.

Razmislite o dveh enačbah A in B z isto neznanko. Rekli bomo, da je enačba B posledica enačba A, če je kateri koli koren enačbe A koren enačbe B.

Enačbe se imenujejo enakovreden,če je kateri koli koren enega od njih koren drugega in obratno. Enačbe so torej enakovredne, če je vsaka posledica druge.

Iz teh definicij sledi na primer, da sta dve enačbi, ki nimata rešitev, enakovredni. Če A nima rešitve, potem B je posledica A, karkoli je enačba B.

Opredelimo pojem "reševanje enačbe". Reši enačbo- pomeni iskanje vseh vrednosti neznank, ki enačbo spremenijo v identiteto. Te vrednosti se imenujejo korenine enačbe.

Postopek reševanja enačb je v glavnem sestavljen iz zamenjave dane enačbe z drugo, ki ji je enakovredna.

Kot smo že omenili, obstajajo štiri najpogostejše metode, ki se uporabljajo pri reševanju kakršnih koli enačb. Oglejmo si podrobneje vsako metodo.

Metoda zamenjave enačbe h (f(x))=h (g(x)) z enačbo f(x)=g(x) se lahko uporabi le, če

Bistvo metode faktorizacije je naslednje: enačba

Ko rešite enačbe tega niza, morate vzeti tiste korene, ki spadajo v domeno definicije prvotne enačbe, in zavreči ostalo kot tujo idejo o grafični metodi za reševanje enačbe

Razkrijmo bistvo metode zamenjave spremenljivke: če enačba

Lekcija in predstavitev na temo: "Metoda zamenjave spremenljivk. Primeri"

Dodatni materiali
Dragi uporabniki, ne pozabite pustiti svojih komentarjev, mnenj, želja! Vsa gradiva so bila preverjena s protivirusnim programom.

Učni pripomočki in simulatorji v spletni trgovini Integral za 11. razred
1C: Šola. Rešujemo naloge iz geometrije. Interaktivne naloge o gradnji v prostoru za 10.–11
Algebraične naloge s parametri, 9.–11

Ta metoda je precej pogosta pri reševanju enačb in smo jo uporabili že večkrat. Uporabimo jo lahko v naslednjih primerih:

• Če ima izvirna enačba $f(x)=0$ kompleksno obliko, vendar jo je bilo mogoče transformirati v enačbo oblike $h(g(x))=0$.
• Potrebno je narediti spremembo spremenljivk $u=g(x)$.
• Rešite enačbo $h(u)=0$, poiščite korene $u_1$, $u_2$, … $u_n$.
• Vnesite obratno zamenjavo $g(x)=u_1$, $g(x)=u_2$, … , $g(x)=u_n$.
• Rešite vsako od enačb $g(x)=u_1$, $g(x)=u_2$, …, $g(x)=u_n$. Koreni vsake enačbe bodo rešitve izvirne enačbe.

Primer.
Rešite enačbo: $8x^6+7x^3-1=0$.

rešitev.
Uvedimo zamenjavo $y=x^3$. Nato se naša enačba zmanjša na kvadratno enačbo:
$8y^2+7y-1=0$,
$(8y-1)(y+1)=0$,
$y_1=\frac(1)(8)$ in $y_2=-1$.

Na tej stopnji pri reševanju zahtevnejših enačb preverite dobljene korene.
Uvedimo obratno zamenjavo: $x^3=\frac(1)(8)$ in $x^3=-1$.
Korenine teh enačb je enostavno najti: $x_1=\frac(1)(2)$ in $x_2=-1$.

Odgovor: $x=0,5$ in $x=-1$.

Primer.
Rešite enačbo: $\sqrt(\frac(2x+3)(2x-1))+4\sqrt(\frac(2x-1)(2x+3))=4$.

rešitev.
Izvedimo enakovredne transformacije:
$\sqrt(\frac(2x-1)(2x+3))=(\frac(2x-1)(2x+3))^(\frac(1)(2))=(\frac(2x+ 3) )(2x-1))^(-\frac(1)(2))=((\frac(2x+3)(2x-1))^(\frac(1)(2)))^( - 1)=\frac(1)(\sqrt(\frac(2x+3)(2x-1)))$.

Vstavimo zamenjavo: $u=\sqrt(\frac(2x+3)(2x-1))$, potem se naša enačba zmanjša na $u+\frac(4)(u)=4$. $u^2-4u+4=0$, od koder je $u=2$.

Uvedimo obratno spremembo: $\sqrt(\frac(2x+3)(2x-1))=2$.

$2x+3=4(2x-1)$ z reševanjem linearne enačbe $x=1\frac(1)(6)$.

Primer.
Rešite enačbo: $2^x+2^(1-x)=3$.

rešitev.
Naša enačba se zmanjša na enakovredno enačbo: $2^x+\frac(2)(2^x)=3$.

Predstavimo zamenjavo: $t=2^x$.
$t+\frac(2)(t)=3$,
$t^2-3t+2=0$,
$(t-2)(t-1)=0$,
$t_1=2$ in $t_2=1$.

Predstavimo obratno zamenjavo: $2^x=2$ in $2^x=1$. Od: $x=1$ in $x=0$.

Odgovor: $x=1$ in $x=0$.

Primer.
Rešite enačbo: $lg^2(x^2)+lg(10x)-6=0$.

rešitev.
Preoblikujemo našo enačbo.
$lg^2(x^2)=(lg(x^2))^2=(2lg(x))^2=4lg^2x$.
$lg(10x)=lg10+lgx=1+lgx$.

Prvotna enačba je enakovredna enačbi: $4lg^2x+lgx-5=0$.

Uvedemo zamenjavo: $u=lg(x)$.
$4u^2+u-5=0$,
$(4u+5)(u-1)=0$.

Uvedimo obratno zamenjavo: $lgx=-1,25$ in $lgx=1$.
Odgovor: $x=10^(-\frac(5)(4))$ in $x=10$.

Primer.
Rešite enačbo: $sin(x)cos(x)-6sin(x)+6cos(x)+6=0$.

rešitev.
Predstavimo zamenjavo: $cos(x)-sin(x)=y$.

Potem: $(cos(x)-sin(x))^2=1-2sin(x)cos(x)$.
$sin(x)cos(x)=\frac(1-y^2)(2)$.

Prvotna enačba je enakovredna:
$\frac(1-y^2)(2)+6y+6=0$,
$1-y^2+12y+12=0$,
$y^2-12y-13=0$,
$(y-13)(y+1)=0$.

Vstavimo inverzno zamenjavo: $cos(x)-sin(x)=13$ - očitno je, da rešitev ni, saj sta kosinus in sinus omejena na modul z ena.

$cos(x)-sin(x)=-1$ - pomnožite obe strani enačbe z $\frac(\sqrt(2))(2)$.
$\frac(\sqrt(2))(2)cos(x)-\frac(\sqrt(2))(2)sin(x)=-\frac(\sqrt(2))(2)$.
$sin(\frac(π)(4)-x)=-\frac(\sqrt(2))(2)$.
$\begin (primeri) \frac(π)(4)-x=-\frac(π)(4)+2πn, \\ \frac(π)(4)-x=-\frac(3π)(4 )+2πn. \konec (primeri)$
$\begin (primeri) x=\frac(π)(2)+2πn, \\ x=π+2πn. \konec (primeri)$

Odgovor: $x=\frac(π)(2)+2πn$ in $π+2πn$.

Težave, ki jih je treba rešiti neodvisno

2. $\sqrt(\frac(5x-1)(x+3))+5\sqrt(\frac(x+3)(5x-1))=6$.

3. $5^x+5^(2x+1)=-4$.
4. $2cos^2(x)-7cos-4=0$.
5. $5sin(2x)-11sin(x)=11cos(x)-7$.