TABELA E VLERAVE TË FUNKSIONET TRIGONOMETRIKE
Tabela e vlerave të funksioneve trigonometrike është përpiluar për këndet 0, 30, 45, 60, 90, 180, 270 dhe 360 gradë dhe vlerat përkatëse të këndeve në vradiane. Nga funksionet trigonometrike, tabela tregon sinusin, kosinusin, tangjentën, kotangjentin, sekantin dhe kosekantin. Për lehtësinë e zgjidhjes së shembujve shkollorë, vlerat e funksioneve trigonometrike në tabelë shkruhen në formën e një thyese duke ruajtur shenjat për nxjerrjen e rrënjës katrore të numrave, gjë që shumë shpesh ndihmon në reduktimin e shprehjeve komplekse matematikore. Për tangjenten dhe kotangjenten, vlerat e disa këndeve nuk mund të përcaktohen. Për vlerat e tangjentes dhe të kotangjentës së këndeve të tilla, ka një vizë në tabelën e vlerave të funksioneve trigonometrike. Në përgjithësi pranohet se tangjentja dhe kotangjentja e këndeve të tilla është e barabartë me pafundësinë. Në një faqe të veçantë ka formula për reduktimin e funksioneve trigonometrike.
Tabela e vlerave për funksionin trigonometrik sinus tregon vlerat për këndet e mëposhtme: sin 0, sin 30, sin 45, sin 60, sin 90, sin 180, sin 270, sin 360 në masën e shkallës, që korrespondon to sin 0 pi, sin pi/6 , sin pi/4, sin pi/3, sin pi/2, sin pi, sin 3 pi/2, sin 2 pi në masën radiane të këndeve. Tabela shkollore e sinuseve.
Për funksionin kosinus trigonometrik, tabela tregon vlerat për këndet e mëposhtme: cos 0, cos 30, cos 45, cos 60, cos 90, cos 180, cos 270, cos 360 në gradë, që korrespondon me cos 0 pi , cos pi me 6, cos pi me 4, cos pi me 3, cos pi me 2, cos pi, cos 3 pi me 2, cos 2 pi në masën radiane të këndeve. Tabela shkollore e kosinusit.
Tabela trigonometrike për tangjenten e funksionit trigonometrik jep vlerat për këndet e mëposhtme: tg 0, tg 30, tg 45, tg 60, tg 180, tg 360 në masë, që korrespondon me tg 0 pi, tg pi/6, tg pi/4, tg pi/3, tg pi, tg 2 pi në masën radiane të këndeve. Vlerat e mëposhtme të funksioneve tangjente trigonometrike nuk janë të përcaktuara tan 90, tan 270, tan pi/2, tan 3 pi/2 dhe konsiderohen të barabarta me pafundësi.
Për funksionin trigonometrik kotangjent në tabelën trigonometrike janë dhënë vlerat e këndeve të mëposhtme: ctg 30, ctg 45, ctg 60, ctg 90, ctg 270 në masën e shkallës, që i përgjigjet ctg pi/6, ctg pi/4. , ctg pi/3, tg pi/ 2, tan 3 pi/2 në masën radiane të këndeve. Vlerat e mëposhtme të funksioneve kotangjente trigonometrike nuk janë të përcaktuara ctg 0, ctg 180, ctg 360, ctg 0 pi, ctg pi, ctg 2 pi dhe konsiderohen të barabarta me pafundësi.
Vlerat e funksioneve trigonometrike sekant dhe kosekant janë dhënë për të njëjtat kënde në gradë dhe radiane si sinusi, kosinusi, tangjentja, kotangjentja.

Tabela e vlerave të funksioneve trigonometrike të këndeve jo standarde tregon vlerat e sinusit, kosinusit, tangjentës dhe kotangjentit për këndet në shkallët 15, 18, 22,5, 36, 54, 67,5 72 gradë dhe në radian pi/12 , pi/10, pi/ 8, pi/5, 3pi/8, 2pi/5 radian. Vlerat e funksioneve trigonometrike shprehen në fraksione dhe rrënjë katrore për ta bërë më të lehtë reduktimin e thyesave në shembujt e shkollës.

Tre përbindësha të tjera trigonometrike. E para është tangjentja prej 1,5 një gradë e gjysmë ose pi e ndarë me 120. E dyta është kosinusi i pi i pjesëtuar me 240, pi/240. Më i gjati është kosinusi i pi i ndarë me 17, pi/17.

Rrethi trigonometrik i vlerave të funksioneve sinus dhe kosinus përfaqëson vizualisht shenjat e sinusit dhe kosinusit në varësi të madhësisë së këndit. Sidomos për biondet, vlerat e kosinusit nënvizohen me një vizë të gjelbër për të reduktuar konfuzionin. Shndërrimi i shkallëve në radiane paraqitet gjithashtu shumë qartë kur radianët shprehen në terma pi.

Kjo tabelë trigonometrike paraqet vlerat e sinusit, kosinusit, tangjentës dhe kotangjentës për këndet nga 0 zero deri në 90 nëntëdhjetë gradë në intervale një shkallë. Për dyzet e pesë shkallët e para, emrat e funksioneve trigonometrike duhet të shihen në krye të tabelës. Kolona e parë përmban shkallë, vlerat e sinuseve, kosinuseve, tangjentëve dhe kotangjentave shkruhen në katër kolonat e ardhshme.
Për këndet nga dyzet e pesë gradë deri në nëntëdhjetë gradë, emrat e funksioneve trigonometrike shkruhen në fund të tabelës. Kolona e fundit përmban shkallët, vlerat e kosinuseve, sinuseve, kotangjentave dhe tangjentëve janë shkruar në katër kolonat e mëparshme. Duhet të keni kujdes sepse emrat e funksioneve trigonometrike në fund të tabelës trigonometrike janë të ndryshëm nga emrat në krye të tabelës. Sinuset dhe kosinuset ndërrohen, ashtu si tangjentja dhe kotangjentja. Kjo është për shkak të simetrisë së vlerave të funksioneve trigonometrike.

Shenjat e funksioneve trigonometrike janë paraqitur në figurën e mësipërme. Sinusi ka vlera pozitive nga 0 në 180 gradë, ose 0 në pi. Sinusi ka vlera negative nga 180 në 360 gradë ose nga pi në 2 pi. Vlerat e kosinusit janë pozitive nga 0 në 90 dhe 270 në 360 gradë, ose 0 në 1/2 pi dhe 3/2 në 2 pi. Tangjentja dhe kotangjentja kanë vlera pozitive nga 0 deri në 90 gradë dhe 180 deri në 270 gradë, që korrespondojnë me vlerat nga 0 deri në 1/2 pi dhe pi deri në 3/2 pi. Vlerat negative të tangjentës dhe kotangjentës janë nga 90 në 180 gradë dhe nga 270 në 360 gradë, ose nga 1/2 pi në pi dhe nga 3/2 pi në 2 pi. Kur përcaktoni shenjat e funksioneve trigonometrike për kënde më të mëdha se 360 gradë ose 2 pi, duhet të përdorni vetitë e periodicitetit të këtyre funksioneve.
Funksionet trigonometrike sinus, tangjente dhe kotangjente janë funksione tek. Vlerat e këtyre funksioneve për kënde negative do të jenë negative. Kosinusi është një funksion trigonometrik i barabartë - vlera e kosinusit për një kënd negativ do të jetë pozitive. Rregullat e shenjave duhet të ndiqen gjatë shumëzimit dhe pjesëtimit të funksioneve trigonometrike.
Tabela e vlerave për funksionin e sinusit trigonometrik tregon vlerat për këndet e mëposhtme
DokumentiKa formula reduktimi në një faqe të veçantë trigonometrikefunksionet. NË tabelavleratPërtrigonometrikefunksionetsinusitdhënëvleratPërnë vijimqoshet: mëkati 0, mëkati 30, mëkati 45 ...
Aparati matematikor i propozuar është një analog i plotë i llogaritjes komplekse për numrat hiperkompleks n-dimensionale me çdo numër të shkallëve të lirisë n dhe është menduar për modelimin matematikor jolinear.
Dokumenti... funksionet barazohet funksionet imazhe. Nga kjo teoremë duhet, Çfarë Për duke gjetur koordinatat U, V, mjafton të llogarisim funksionin... gjeometria; polinar funksionet(analoge shumëdimensionale të dydimensionale trigonometrikefunksionet), vetitë e tyre, tabelat dhe aplikimi; ...
-
Kujdes!
Ka shtesë
materialet në Seksionin Special 555.
Për ata që janë shumë "jo shumë..."
Dhe për ata që "shumë ...")Fillimisht, më lejoni t'ju kujtoj një përfundim të thjeshtë por shumë të dobishëm nga mësimi "Çfarë janë sinusi dhe kosinusi?"
Ky është dalja:
Sinusi, kosinusi, tangjentja dhe kotangjentja janë të lidhura ngushtë me këndet e tyre. Ne dimë një gjë, që do të thotë se dimë një tjetër.
Me fjalë të tjera, çdo kënd ka sinusin dhe kosinusin e tij konstant. Dhe pothuajse të gjithë kanë tangjenten dhe kotangjenten e tyre. Pse pothuajse? Më shumë për këtë më poshtë.
Kjo njohuri ju ndihmon shumë në studimet tuaja! Ka shumë detyra ku duhet të kaloni nga sinuset në kënde dhe anasjelltas. Për këtë ka tabela e sinuseve. Në mënyrë të ngjashme, për detyrat me kosinus - tabelë kosinusi. Dhe, siç mund ta keni marrë me mend, ka tabelë tangjente Dhe tabela e kotangjenteve.)
Tabelat janë të ndryshme. Të gjata, ku mund të shihni se me çfarë është, të themi, sin37°6'. Hapim tabelat Bradis, kërkojmë një kënd prej tridhjetë e shtatë gradë gjashtë minuta dhe shohim vlerën 0.6032. Është e qartë se nuk ka absolutisht nevojë të mbani mend këtë numër (dhe mijëra vlera të tjera të tabelës).
Në fakt, në kohën tonë, tabelat e gjata të kosinuseve, sinuseve, tangjentave, kotangjentave nuk janë vërtet të nevojshme. Një kalkulator i mirë i zëvendëson ato plotësisht. Por nuk është e dëmshme të dini për ekzistencën e tabelave të tilla. Për erudicionin e përgjithshëm.)
Dhe pse atëherë ky mësim?! - pyet ti.
Por pse. Midis numrit të pafund të këndeve ka e veçantë, për të cilat duhet të dini Të gjitha. E gjithë gjeometria dhe trigonometria e shkollës janë ndërtuar mbi këto kënde. Kjo është një lloj "tabela e shumëzimit" të trigonometrisë. Nëse nuk e dini se me çfarë është mëkati 50°, për shembull, askush nuk do t'ju gjykojë.) Por nëse nuk e dini se me çfarë është mëkati30°, përgatituni të merrni një dy të merituar...
Të tillë e veçantë Këndet janë gjithashtu mjaft të mira. Tekstet shkollore zakonisht ofrojnë me dashamirësi mësim përmendësh tabela sinusale dhe tabela e kosinusit për shtatëmbëdhjetë kënde. Dhe, sigurisht, tabela tangjente dhe tabela kotangjente për të njëjtat shtatëmbëdhjetë kënde... D.m.th. Propozohet të mbani mend 68 vlera. Të cilat, nga rruga, janë shumë të ngjashme me njëra-tjetrën, përsëriten herë pas here dhe ndryshojnë shenja. Për një person pa kujtesë të përsosur vizuale, kjo është një detyrë mjaft...)
Ne do të marrim një rrugë tjetër. Le ta zëvendësojmë memorizimin përmendësh me logjikën dhe zgjuarsinë. Atëherë do të duhet të mësojmë përmendësh 3 (tre!) vlera për tabelën e sinuseve dhe tabelën e kosinuseve. Dhe 3 (tre!) vlera për tabelën e tangjentëve dhe tabelën e kotangjentave. Kjo është e gjitha. Gjashtë vlera janë më të lehta për t'u mbajtur mend se 68, më duket ...)
Ne do të marrim të gjitha vlerat e tjera të nevojshme nga këto gjashtë duke përdorur një fletë mashtrimi të fuqishëm ligjor - rrethi trigonometrik. Nëse nuk e keni studiuar këtë temë, ndiqni lidhjen, mos u bëni dembel. Ky rreth nuk është i nevojshëm vetëm për këtë mësim. Ai është i pazëvendësueshëm për të gjitha trigonometritë në të njëjtën kohë. Mos përdorimi i një mjeti të tillë është thjesht një mëkat! Nuk dëshiron? Kjo është puna juaj. Mësoni përmendësh tabela e sinuseve. Tabela e kosinuseve. Tabela e tangjentëve. Tabela e kotangjenteve. Të gjitha 68 vlerat për një shumëllojshmëri këndesh.)
Pra, le të fillojmë. Së pari, le t'i ndajmë të gjitha këto kënde të veçanta në tre grupe.
Grupi i parë i këndeve.
Le të shqyrtojmë grupin e parë shtatëmbëdhjetë kënde e veçantë. Këto janë 5 kënde: 0°, 90°, 180°, 270°, 360°.
Kështu duket tabela e sinuseve, kosinuseve, tangjentëve, kotangjenteve për këto kënde:
Këndi x
(në gradë)0
90
180
270
360
Këndi x
(në radianë)0
mëkat x
0
1
0
-1
0
cos x
1
0
-1
0
1
tg x
0
emër
0
emër
0
ctg x
emër
0
emër
0
emër
Ata që duan të kujtojnë, mbani mend. Por unë do të them menjëherë se të gjitha këto njëshe dhe zero më ngatërrohen shumë në kokën time. Shumë më e fortë se sa dëshironi.) Prandaj, ne ndezim logjikën dhe rrethin trigonometrik.
Vizatojmë një rreth dhe shënojmë të njëjtat kënde mbi të: 0°, 90°, 180°, 270°, 360°. I shënova këto qoshe me pika të kuqe:

Është menjëherë e qartë se çfarë është e veçantë për këto kënde. po! Këto janë këndet që bien pikërisht në boshtin koordinativ! Në fakt, kjo është arsyeja pse njerëzit ngatërrohen... Por ne nuk do të ngatërrohemi. Le të kuptojmë se si të gjejmë funksionet trigonometrike të këtyre këndeve pa shumë memorizim.
Nga rruga, pozicioni i këndit është 0 gradë përkon plotësisht me një pozicion këndi 360 gradë. Kjo do të thotë se sinuset, kosinuset dhe tangjentet e këtyre këndeve janë saktësisht të njëjta. Kam shënuar një kënd 360 gradë për të përfunduar rrethin.
Supozoni se në mjedisin e vështirë stresues të Provimit të Unifikuar të Shtetit, ju dyshoni disi... Cili është sinusi i 0 gradë? Duket si zero... Po sikur të jetë një?! Memorizimi mekanik është një gjë e tillë. Në kushte të vështira, dyshimet fillojnë të gërryen...)
Qetë, vetëm qetë!) Unë do t'ju tregoj një teknikë praktike që do t'ju japë një përgjigje 100% të saktë dhe do t'ju heqë plotësisht të gjitha dyshimet.
Si shembull, le të kuptojmë se si të përcaktojmë qartë dhe me besueshmëri, të themi, sinusin prej 0 gradë. Dhe në të njëjtën kohë, kosinusi 0. Pikërisht në këto vlera, çuditërisht, njerëzit shpesh ngatërrohen.
Për ta bërë këtë, vizatoni një rreth arbitrare qoshe X. Në tremujorin e parë ishte afër 0 gradë. Le të shënojmë sinusin dhe kosinusin e këtij këndi në boshte X,çdo gjë është në rregull. Si kjo:
Dhe tani - vëmendje! Le të zvogëlojmë këndin X, afrojeni anën lëvizëse më afër boshtit Oh. Lëvizni kursorin mbi foto (ose prekni figurën në tablet) dhe do të shihni gjithçka.
Tani le të kalojmë në logjikën elementare! Le të shohim dhe të mendojmë: Si sillet sinx kur këndi x zvogëlohet? Ndërsa këndi i afrohet zeros? Po zvogëlohet! Dhe cosx rritet! Mbetet për të kuptuar se çfarë do të ndodhë me sinusin kur këndi të shembet plotësisht? Kur ana lëvizëse e këndit (pika A) vendoset në boshtin OX dhe këndi bëhet i barabartë me zero? Natyrisht, sinusi i këndit do të shkojë në zero. Dhe kosinusi do të rritet në... në... Sa është gjatësia e anës lëvizëse të këndit (rrezja e rrethit trigonometrik)? Një!
Këtu është përgjigja. Sinusi i 0 gradë është i barabartë me 0. Kosinusi i 0 gradë është i barabartë me 1. Absolutisht i hekurt dhe pa asnjë dyshim!) Thjesht sepse ndryshe nuk mund të jetë.
Në të njëjtën mënyrë, ju mund të zbuloni (ose sqaroni) sinusin prej 270 gradë, për shembull. Ose kosinusi 180. Vizatoni një rreth, arbitrare një kënd në një të katërtën pranë boshtit koordinativ që na intereson, lëvizni mendërisht anën e këndit dhe kuptoni se çfarë do të bëhen sinusi dhe kosinusi kur ana e këndit bie mbi bosht. Kjo është ajo.
Siç mund ta shihni, nuk ka nevojë të mësoni përmendësh asgjë për këtë grup këndesh. Nuk nevojitet këtu tabela e sinuseve... Po dhe tabelë kosinusi- gjithashtu.) Nga rruga, pas disa përdorimeve të rrethit trigonometrik, të gjitha këto vlera do të mbahen mend vetë. Dhe nëse harrojnë, unë vizatova një rreth në 5 sekonda dhe e sqarova. Shumë më e lehtë sesa të telefonosh një mik nga tualeti dhe të rrezikosh certifikatën tënde, apo jo?)
Sa i përket tangjentës dhe kotangjentës, gjithçka është e njëjtë. Ne vizatojmë një vijë tangjente (kotangjente) në rreth - dhe gjithçka është menjëherë e dukshme. Ku janë të barabarta me zero dhe ku nuk ekzistojnë. Çfarë, nuk dini për linjat tangjente dhe kotangjente? Kjo është e trishtueshme, por e rregullueshme.) Ne vizituam seksionin 555 Tangjentja dhe kotangjentja në rrethin trigonometrik - dhe nuk ka probleme!
Nëse keni kuptuar se si të përcaktoni qartë sinusin, kosinusin, tangjentën dhe kotangjentën për këto pesë kënde, urime! Për çdo rast, ju informoj se tani mund të përcaktoni funksionet çdo kënd që bie mbi boshtet. Dhe kjo është 450°, dhe 540°, dhe 1800°, dhe një numër i pafund të tjerash...) Kam numëruar (saktë!) këndin në rreth - dhe nuk ka probleme me funksionet.
Por është pikërisht me matjen e këndeve që shfaqen probleme dhe gabime... Si t'i shmangni ato shkruhet në mësim: Si të vizatoni (numëroni) çdo kënd në një rreth trigonometrik në gradë. Elementare, por shumë e dobishme në luftën kundër gabimeve.)
Ja një mësim: Si të vizatoni (matni) çdo kënd në një rreth trigonometrik në radianë - do të jetë më i ftohtë. Për sa i përket mundësive. Le të themi, të përcaktojmë se në cilin nga katër gjysmëboshtet bie këndi
ju mund ta bëni atë në disa sekonda. nuk po tallej! Vetëm në disa sekonda. Epo, sigurisht, jo vetëm 345 pi...) Dhe 121, dhe 16, dhe -1345. Çdo koeficient i plotë është i përshtatshëm për një përgjigje të menjëhershme.
Dhe nëse këndi
Vetëm mendoni! Përgjigja e saktë merret në 10 sekonda Për çdo vlerë thyesore të radianeve me një dy në emërues.
Në fakt, kjo është ajo që është e mirë për rrethin trigonometrik. Për shkak të aftësisë për të punuar me disa qoshet në të cilat zgjerohet automatikisht grup i pafund qoshet
Pra, ne kemi renditur pesë qoshe nga shtatëmbëdhjetë.
Grupi i dytë i këndeve.
Grupi tjetër i këndeve janë këndet 30°, 45° dhe 60°. Pse pikërisht këto, dhe jo, për shembull, 20, 50 dhe 80? Po, disi doli kështu... Historikisht.) Më tej do të shihet pse këto kënde janë të mira.
Tabela e sinuseve kosinus tangjentet kotangjente për këto kënde duket si kjo:
Këndi x
(në gradë)0
30
45
60
90
Këndi x
(në radianë)0
mëkat x
0
1
cos x
1
0
tg x
0
1
emër
ctg x
emër
1
0
I lashë vlerat për 0° dhe 90° nga tabela e mëparshme për të plotësuar figurën.) Kështu që ju mund të shihni se këto kënde qëndrojnë në tremujorin e parë dhe rriten. Nga 0 në 90. Kjo do të jetë e dobishme për ne më vonë.
Vlerat e tabelës për këndet 30°, 45° dhe 60° duhet të mbahen mend. Mësoni përmendësh nëse dëshironi. Por edhe këtu ka një mundësi për ta bërë jetën tuaj më të lehtë.) Kushtojini vëmendje vlerat e tabelës sinus këto kënde. Dhe krahasoni me Vlerat e tabelës së kosinusit...
po! Ata të njëjtat! Sapo rregulluar në rend të kundërt. Këndet rriten (0, 30, 45, 60, 90) - dhe vlerat e sinusit rriten nga 0 në 1. Mund të kontrolloni me një kalkulator. Dhe vlerat kosinus janë janë në rënie nga 1 në zero. Për më tepër, vlerat e tyre të njëjtat. Për këndet 20, 50, 80 kjo nuk do të funksiononte...
Ky është një përfundim i dobishëm. Mjaft për të mësuar tre vlerat për këndet 30, 45, 60 gradë. Dhe mbani mend se për një sinus rriten dhe për një kosinus zvogëlohen. Drejt sinusit.) Ata takohen në gjysmë të rrugës (45°), domethënë, sinusi 45 gradë është i barabartë me kosinusin 45 gradë. Dhe pastaj ato ndryshojnë përsëri... Tre kuptime mund të mësohen, apo jo?
Me tangjente - kotangjente fotografia është saktësisht e njëjtë. Një me një. Vetëm kuptimet janë të ndryshme. Këto vlera (tre të tjera!) gjithashtu duhet të mësohen.
Epo, pothuajse i gjithë memorizimi ka mbaruar. Ju keni kuptuar (shpresojmë) se si të përcaktoni vlerat për pesë këndet që bien në bosht dhe keni mësuar vlerat për këndet 30, 45, 60 gradë. Gjithsej 8.
Mbetet të merremi me grupin e fundit prej 9 këndesh.
Këto janë këndet:
120°; 135°; 150°; 210°; 225°; 240°; 300°; 315°; 330°. Për këto kënde duhet të dini tabelën e sinuseve, tabelën e kosinuseve etj.Makth, apo jo?)
Dhe nëse shtoni kënde këtu, si p.sh.: 405°, 600° ose 3000° dhe shumë e shumë kënde po aq të bukura?)
Apo kënde në radianë? Për shembull, në lidhje me këndet:

dhe shumë të tjera që duhet të dini Të gjitha.
Gjëja më qesharake është ta dish këtë Të gjitha - e pamundur në parim. Nëse përdorni memorie mekanike.
Dhe është shumë e lehtë, në fakt elementare - nëse përdorni një rreth trigonometrik. Sapo të filloni të punoni me rrethin trigonometrik, të gjitha ato kënde të frikshme në gradë do të reduktohen lehtësisht dhe në mënyrë elegante në ato të modës së vjetër:
Nga rruga, unë kam disa faqe më interesante për ju.)
Ju mund të praktikoni zgjidhjen e shembujve dhe të zbuloni nivelin tuaj. Testimi me verifikim të menjëhershëm. Le të mësojmë - me interes!)
Mund të njiheni me funksionet dhe derivatet.
Konceptet e sinusit (), kosinusit (), tangjentes (), kotangjentës () janë të lidhura pazgjidhshmërisht me konceptin e këndit. Për t'i kuptuar mirë këto, në shikim të parë, koncepte komplekse (të cilat shkaktojnë një gjendje tmerri te shumë nxënës) dhe për t'u siguruar që "djalli nuk është aq i tmerrshëm sa është pikturuar", le të fillojmë nga në fillim dhe të kuptojë konceptin e një këndi.
Koncepti i këndit: radian, shkallë
Le të shohim foton. Vektori është "kthyer" në lidhje me pikën me një sasi të caktuar. Pra, masa e këtij rrotullimi në lidhje me pozicionin fillestar do të jetë qoshe.
Çfarë tjetër duhet të dini për konceptin e këndit? Epo, njësitë e këndit, sigurisht!
Këndi, si në gjeometri ashtu edhe në trigonometri, mund të matet në gradë dhe radianë.
Këndi (një shkallë) është këndi qendror në një rreth të nënshtruar nga një hark rrethor i barabartë me një pjesë të rrethit. Kështu, i gjithë rrethi përbëhet nga "copë" harqesh rrethore, ose këndi i përshkruar nga rrethi është i barabartë.

Kjo do të thotë, figura e mësipërme tregon një kënd të barabartë me, domethënë, ky kënd mbështetet në një hark rrethor me madhësinë e perimetrit.
Një kënd në radianë është këndi qendror në një rreth të nënshtruar nga një hark rrethor, gjatësia e të cilit është e barabartë me rrezen e rrethit. Epo, e kuptove? Nëse jo, atëherë le ta kuptojmë nga vizatimi.

Pra, figura tregon një kënd të barabartë me një radian, domethënë, ky kënd mbështetet në një hark rrethor, gjatësia e të cilit është e barabartë me rrezen e rrethit (gjatësia është e barabartë me gjatësinë ose rrezja është e barabartë me gjatësia e harkut). Kështu, gjatësia e harkut llogaritet me formulën:
Ku është këndi qendror në radianë.
Epo, duke e ditur këtë, a mund të përgjigjeni se sa radianë përmbahen në këndin e përshkruar nga rrethi? Po, për këtë ju duhet të mbani mend formulën për perimetrin. Këtu është:
Epo, tani le t'i lidhim këto dy formula dhe të gjejmë se këndi i përshkruar nga rrethi është i barabartë. Kjo do të thotë, duke korreluar vlerën në gradë dhe radianë, ne e marrim atë. Përkatësisht,. Siç mund ta shihni, ndryshe nga "gradat", fjala "radian" është lënë jashtë, pasi njësia e matjes zakonisht është e qartë nga konteksti.
Sa radianë ka? Kjo është e drejtë!
E kuptove? Pastaj vazhdoni dhe rregulloni:
Keni vështirësi? Pastaj shikoni përgjigjet:
Trekëndëshi kënddrejtë: sinusi, kosinusi, tangjentja, kotangjentja e këndit
Pra, ne kuptuam konceptin e një këndi. Por çfarë është sinusi, kosinusi, tangjentja dhe kotangjentja e një këndi? Le ta kuptojmë. Për ta bërë këtë, një trekëndësh kënddrejtë do të na ndihmojë.

Si quhen brinjët e trekëndëshit kënddrejtë? Kjo është e drejtë, hipotenuza dhe këmbët: hipotenuza është ana që shtrihet përballë këndit të duhur (në shembullin tonë kjo është ana); këmbët janë dy anët e mbetura dhe (ato ngjitur me këndin e duhur), dhe nëse i konsiderojmë këmbët në lidhje me këndin, atëherë këmba është këmba ngjitur dhe këmba është e kundërta. Pra, tani le t'i përgjigjemi pyetjes: çfarë janë sinusi, kosinusi, tangjentja dhe kotangjentja e një këndi?
Sinusi i këndit- ky është raporti i këmbës së kundërt (të largët) me hipotenuzën.
Në trekëndëshin tonë.
Kosinusi i këndit- ky është raporti i këmbës ngjitur (të afërt) me hipotenuzën.
Në trekëndëshin tonë.
Tangjentja e këndit- ky është raporti i anës së kundërt (të largët) me atë ngjitur (të afërt).
Në trekëndëshin tonë.
Kotangjentja e këndit- ky është raporti i këmbës ngjitur (të afërt) me të kundërtën (larg).
Në trekëndëshin tonë.
Këto përkufizime janë të nevojshme mbaj mend! Për ta bërë më të lehtë të mbani mend se cilën këmbë të ndani në çfarë, duhet ta kuptoni qartë këtë tangjente Dhe kotangjent vetëm këmbët ulen, dhe hipotenuza shfaqet vetëm në sinusit Dhe kosinusi. Dhe pastaj mund të dilni me një zinxhir shoqatash. Për shembull, ky:
Kosinus→prek→prek→ ngjitur;
Kotangjent→prek→prek→ ngjitur.
Para së gjithash, duhet të mbani mend se sinusi, kosinusi, tangjentja dhe kotangjentja pasi raportet e brinjëve të një trekëndëshi nuk varen nga gjatësitë e këtyre brinjëve (në të njëjtin kënd). Nuk më besoni? Pastaj sigurohuni duke parë foton:

Konsideroni, për shembull, kosinusin e një këndi. Sipas përkufizimit, nga një trekëndësh: , por mund të llogarisim kosinusin e një këndi nga një trekëndësh: . E shihni, gjatësitë e brinjëve janë të ndryshme, por vlera e kosinusit të një këndi është e njëjtë. Kështu, vlerat e sinusit, kosinusit, tangjentës dhe kotangjentës varen vetëm nga madhësia e këndit.
Nëse i kuptoni përkufizimet, atëherë vazhdoni dhe konsolidoni ato!
Për trekëndëshin e paraqitur në figurën më poshtë, gjejmë.

Epo, e kuptove? Pastaj provojeni vetë: llogarisni të njëjtën gjë për këndin.
Rrethi njësi (trigonometrik).
Duke kuptuar konceptet e shkallës dhe radianit, ne konsideruam një rreth me një rreze të barabartë me. Një rreth i tillë quhet beqare. Do të jetë shumë e dobishme kur studioni trigonometrinë. Prandaj, le ta shohim atë pak më në detaje.

Siç mund ta shihni, ky rreth është ndërtuar në sistemin e koordinatave karteziane. Rrezja e rrethit është e barabartë me një, ndërsa qendra e rrethit qëndron në origjinën e koordinatave, pozicioni fillestar i vektorit të rrezes është i fiksuar përgjatë drejtimit pozitiv të boshtit (në shembullin tonë, kjo është rrezja).
Çdo pikë në rreth korrespondon me dy numra: koordinata e boshtit dhe koordinata e boshtit. Cilët janë këta numra koordinativ? Dhe në përgjithësi, çfarë lidhje kanë ato me temën në fjalë? Për ta bërë këtë, duhet të kujtojmë për trekëndëshin kënddrejtë të konsideruar. Në figurën e mësipërme, mund të shihni dy trekëndësha të tërë kënddrejtë. Konsideroni një trekëndësh. Ai është drejtkëndor sepse është pingul me boshtin.
Me çfarë është i barabartë trekëndëshi? Kjo është e drejtë. Përveç kësaj, ne e dimë se është rrezja e rrethit të njësisë, që do të thotë . Le ta zëvendësojmë këtë vlerë në formulën tonë për kosinusin. Ja çfarë ndodh:
Me çfarë është i barabartë trekëndëshi? Epo sigurisht! Zëvendësoni vlerën e rrezes në këtë formulë dhe merrni:
Pra, a mund të thoni se çfarë koordinatash ka një pikë që i përket një rrethi? Epo, në asnjë mënyrë? Po sikur ta kuptoni këtë dhe të jeni vetëm numra? Cilës koordinatë i përgjigjet? Epo, sigurisht, koordinatat! Dhe me çfarë koordinate korrespondon? Kjo është e drejtë, koordinatat! Kështu, periudha.

Atëherë me çfarë janë dhe të barabarta? Është e drejtë, le të përdorim përkufizimet përkatëse të tangjentes dhe kotangjentës dhe të marrim atë, a.
Po sikur këndi të jetë më i madh? Për shembull, si në këtë foto:

Çfarë ka ndryshuar në këtë shembull? Le ta kuptojmë. Për ta bërë këtë, le të kthehemi përsëri në një trekëndësh kënddrejtë. Konsideroni një trekëndësh kënddrejtë: kënd (si ngjitur me një kënd). Cilat janë vlerat e sinusit, kosinusit, tangjentës dhe kotangjentës për një kënd? Kjo është e drejtë, ne i përmbahemi përkufizimeve përkatëse të funksioneve trigonometrike:
Epo, siç mund ta shihni, vlera e sinusit të këndit ende korrespondon me koordinatat; vlera e kosinusit të këndit - koordinata; dhe vlerat e tangjentes dhe kotangjentes me raportet përkatëse. Kështu, këto marrëdhënie zbatohen për çdo rrotullim të vektorit të rrezes.
Është përmendur tashmë se pozicioni fillestar i vektorit të rrezes është përgjatë drejtimit pozitiv të boshtit. Deri më tani ne e kemi rrotulluar këtë vektor në drejtim të kundërt të akrepave të orës, por çfarë ndodh nëse e rrotullojmë në drejtim të akrepave të orës? Asgjë e jashtëzakonshme, do të merrni edhe një kënd me një vlerë të caktuar, por vetëm ai do të jetë negativ. Kështu, kur rrotullojmë vektorin e rrezes në drejtim të kundërt të akrepave të orës, marrim kënde pozitive, dhe kur rrotullohet në drejtim të akrepave të orës - negative.
Pra, ne e dimë se një rrotullim i tërë i vektorit të rrezes rreth një rrethi është ose. A është e mundur të rrotullohet vektori i rrezes në ose në? Epo, sigurisht që mundesh! Prandaj, në rastin e parë, vektori i rrezes do të bëjë një rrotullim të plotë dhe do të ndalet në pozicionin ose.
Në rastin e dytë, domethënë, vektori i rrezes do të bëjë tre rrotullime të plota dhe do të ndalet në pozicionin ose.
Kështu, nga shembujt e mësipërm mund të konkludojmë se këndet që ndryshojnë nga ose (ku është ndonjë numër i plotë) korrespondojnë me të njëjtin pozicion të vektorit të rrezes.
Figura më poshtë tregon një kënd. I njëjti imazh korrespondon me këndin, etj. Kjo listë mund të vazhdojë pafundësisht. Të gjitha këto kënde mund të shkruhen me formulën e përgjithshme ose (ku është ndonjë numër i plotë)

Tani, duke ditur përkufizimet e funksioneve bazë trigonometrike dhe duke përdorur rrethin e njësisë, përpiquni të përgjigjeni se cilat janë vlerat:
Këtu është një rreth njësi për t'ju ndihmuar:

Keni vështirësi? Atëherë le ta kuptojmë. Pra, ne e dimë se:
Nga këtu, ne përcaktojmë koordinatat e pikave që korrespondojnë me masa të caktuara të këndit. Epo, le të fillojmë me radhë: këndi në korrespondon me një pikë me koordinata, prandaj:
Nuk ekziston;
Më tej, duke iu përmbajtur të njëjtës logjikë, zbulojmë se qoshet në korrespondojnë me pikat me koordinata, përkatësisht. Duke e ditur këtë, është e lehtë të përcaktohen vlerat e funksioneve trigonometrike në pikat përkatëse. Provojeni vetë fillimisht dhe më pas kontrolloni përgjigjet.
Përgjigjet:
Nuk ekziston
Nuk ekziston
Nuk ekziston
Nuk ekziston
Kështu, mund të bëjmë tabelën e mëposhtme:

Nuk ka nevojë të mbani mend të gjitha këto vlera. Mjafton të mbani mend korrespondencën midis koordinatave të pikave në rrethin e njësisë dhe vlerave të funksioneve trigonometrike:
Por vlerat e funksioneve trigonometrike të këndeve në dhe, të dhëna në tabelën më poshtë, duhet mbajtur mend:

Mos kini frikë, tani do t'ju tregojmë një shembull mjaft e thjeshtë për të mbajtur mend vlerat përkatëse:
Për të përdorur këtë metodë, është thelbësore të mbani mend vlerat e sinusit për të tre masat e këndit (), si dhe vlerën e tangjentës së këndit. Duke ditur këto vlera, është mjaft e thjeshtë të rivendosni të gjithë tabelën - vlerat e kosinusit transferohen në përputhje me shigjetat, domethënë:
Duke e ditur këtë, ju mund të rivendosni vlerat për. Numëruesi " " do të përputhet dhe emëruesi " " do të përputhet. Vlerat kotangjente transferohen në përputhje me shigjetat e treguara në figurë. Nëse e kuptoni këtë dhe mbani mend diagramin me shigjeta, atëherë do të jetë e mjaftueshme të mbani mend të gjitha vlerat nga tabela.
Koordinatat e një pike në një rreth
A është e mundur të gjesh një pikë (koordinatat e saj) në një rreth, njohja e koordinatave të qendrës së rrethit, rrezes dhe këndit të rrotullimit të tij?
Epo, sigurisht që mundesh! Le ta nxjerrim atë formula e përgjithshme për gjetjen e koordinatave të një pike.
Për shembull, këtu është një rreth para nesh:

Na është dhënë se pika është qendra e rrethit. Rrezja e rrethit është e barabartë. Është e nevojshme të gjenden koordinatat e një pike të përftuara duke rrotulluar pikën me gradë.
Siç shihet nga figura, koordinata e pikës korrespondon me gjatësinë e segmentit. Gjatësia e segmentit korrespondon me koordinatat e qendrës së rrethit, domethënë është e barabartë. Gjatësia e një segmenti mund të shprehet duke përdorur përkufizimin e kosinusit:
Pastaj e kemi atë për koordinatën e pikës.
Duke përdorur të njëjtën logjikë, gjejmë vlerën e koordinatave y për pikën. Kështu,
Pra, në përgjithësi, koordinatat e pikave përcaktohen nga formula:
Koordinatat e qendrës së rrethit,
Rrezja e rrethit,
Këndi i rrotullimit të rrezes vektoriale.
Siç mund ta shihni, për rrethin e njësisë që po shqyrtojmë, këto formula janë zvogëluar ndjeshëm, pasi koordinatat e qendrës janë të barabarta me zero dhe rrezja është e barabartë me një:
Epo, le t'i provojmë këto formula duke praktikuar gjetjen e pikave në një rreth?
1. Gjeni koordinatat e një pike në rrethin njësi të përftuar duke rrotulluar pikën në.
2. Gjeni koordinatat e një pike në rrethin njësi të përftuar duke rrotulluar pikën në.
3. Gjeni koordinatat e një pike në rrethin njësi të përftuar duke rrotulluar pikën në.
4. Pika është qendra e rrethit. Rrezja e rrethit është e barabartë. Është e nevojshme të gjenden koordinatat e pikës së fituar duke rrotulluar vektorin e rrezes fillestare me.
5. Pika është qendra e rrethit. Rrezja e rrethit është e barabartë. Është e nevojshme të gjenden koordinatat e pikës së fituar duke rrotulluar vektorin e rrezes fillestare me.
Keni vështirësi në gjetjen e koordinatave të një pike në një rreth?
Zgjidhini këto pesë shembuj (ose bëhuni të mirë në zgjidhjen e tyre) dhe do të mësoni t'i gjeni!
1.
Ju mund ta vini re atë. Por ne e dimë se çfarë korrespondon me një revolucion të plotë të pikës fillestare. Kështu, pika e dëshiruar do të jetë në të njëjtin pozicion si kur kthehet në. Duke e ditur këtë, gjejmë koordinatat e kërkuara të pikës:
2. Rrethi i njësisë është i përqendruar në një pikë, që do të thotë se mund të përdorim formula të thjeshtuara:
Ju mund ta vini re atë. Ne e dimë se çfarë korrespondon me dy revolucione të plota të pikës së fillimit. Kështu, pika e dëshiruar do të jetë në të njëjtin pozicion si kur kthehet në. Duke e ditur këtë, gjejmë koordinatat e kërkuara të pikës:
Sinusi dhe kosinusi janë vlera të tabelës. Ne kujtojmë kuptimet e tyre dhe marrim:
Kështu, pika e dëshiruar ka koordinata.
3. Rrethi i njësisë është i përqendruar në një pikë, që do të thotë se mund të përdorim formula të thjeshtuara:
Ju mund ta vini re atë. Le të përshkruajmë shembullin në fjalë në figurë:

Rrezja bën kënde të barabarta me dhe me boshtin. Duke ditur që vlerat e tabelës së kosinusit dhe sinusit janë të barabarta dhe pasi kemi përcaktuar që kosinusi këtu merr një vlerë negative dhe sinusi një vlerë pozitive, kemi:
Shembuj të tillë diskutohen më në detaje kur studiohen formulat për zvogëlimin e funksioneve trigonometrike në temë.
Kështu, pika e dëshiruar ka koordinata.
4.
Këndi i rrotullimit të rrezes së vektorit (sipas gjendjes)
Për të përcaktuar shenjat përkatëse të sinusit dhe kosinusit, ne ndërtojmë një rreth njësi dhe kënd:

Siç mund ta shihni, vlera, domethënë është pozitive, dhe vlera, domethënë është negative. Duke ditur vlerat tabelare të funksioneve trigonometrike përkatëse, marrim se:
Le të zëvendësojmë vlerat e marra në formulën tonë dhe të gjejmë koordinatat:
Kështu, pika e dëshiruar ka koordinata.
5. Për të zgjidhur këtë problem, ne përdorim formula në formë të përgjithshme, ku
Koordinatat e qendrës së rrethit (në shembullin tonë,
Rrezja e rrethit (sipas gjendjes)
Këndi i rrotullimit të rrezes së vektorit (sipas gjendjes).
Le të zëvendësojmë të gjitha vlerat në formulë dhe të marrim:
dhe - vlerat e tabelës. Le të kujtojmë dhe t'i zëvendësojmë ato në formulën:
Kështu, pika e dëshiruar ka koordinata.
PËRMBLEDHJE DHE FORMULA BAZË
Sinusi i një këndi është raporti i këmbës së kundërt (të largët) me hipotenuzën.
Kosinusi i një këndi është raporti i këmbës ngjitur (të afërt) me hipotenuzën.
Tangjenti i një këndi është raporti i anës së kundërt (të largët) me anën fqinje (të afërt).
Kotangjentja e një këndi është raporti i këmbës ngjitur (të afërt) me këmbën e kundërt (larg).
Ne do të fillojmë studimin tonë të trigonometrisë me trekëndëshin kënddrejtë. Le të përcaktojmë se çfarë janë sinusi dhe kosinusi, si dhe tangjentja dhe kotangjentja e një këndi akut. Këto janë bazat e trigonometrisë.
Le të kujtojmë atë kënd i drejtëështë një kënd i barabartë me 90 gradë. Me fjalë të tjera, gjysmë këndi i kthyer.
Këndi akut- më pak se 90 gradë.
Këndi i mpirë- më shumë se 90 gradë. Kur zbatohet në një kënd të tillë, "i trashë" nuk është një fyerje, por një term matematikor :-)
Le të vizatojmë një trekëndësh kënddrejtë. Një kënd i drejtë zakonisht shënohet me . Ju lutemi vini re se ana përballë këndit tregohet me të njëjtën shkronjë, vetëm e vogël. Kështu, caktohet ana përballë këndit A.
Këndi shënohet me shkronjën përkatëse greke.

Hipotenuza e një trekëndëshi kënddrejtë është brinja përballë këndit të drejtë.
Këmbët- anët që shtrihen përballë këndeve akute.
Këmba e shtrirë përballë këndit quhet përballë(në lidhje me këndin). Këmba tjetër, e cila shtrihet në njërën nga anët e këndit, quhet ngjitur.
Sinus Këndi akut në një trekëndësh kënddrejtë është raporti i anës së kundërt me hipotenuzën:
Kosinusi këndi akut në një trekëndësh të drejtë - raporti i këmbës ngjitur me hipotenuzën:
Tangjente këndi akut në një trekëndësh kënddrejtë - raporti i anës së kundërt me fqinjin:
Një përkufizim tjetër (ekuivalent): tangjentja e një këndi akut është raporti i sinusit të këndit me kosinusin e tij:
Kotangjente këndi akut në një trekëndësh kënddrejtë - raporti i anës ngjitur me të kundërtën (ose, që është i njëjtë, raporti i kosinusit me sinusin):
Vini re marrëdhëniet bazë për sinusin, kosinusin, tangjentën dhe kotangjentën më poshtë. Ata do të jenë të dobishëm për ne kur zgjidhim problemet.

Le të vërtetojmë disa prej tyre.
Mirë, ne kemi dhënë përkufizime dhe kemi shkruar formula. Por pse kemi ende nevojë për sinus, kosinus, tangjentë dhe kotangjent?
Ne e dimë atë shuma e këndeve të çdo trekëndëshi është e barabartë me.
Ne e dimë marrëdhënien ndërmjet partive trekëndësh kënddrejtë. Kjo është teorema e Pitagorës: .
Rezulton se duke ditur dy kënde në një trekëndësh, mund të gjesh të tretin. Duke ditur dy anët e një trekëndëshi kënddrejtë, mund të gjeni të tretën. Kjo do të thotë që këndet kanë raportin e tyre, dhe anët kanë të tyren. Por çfarë duhet të bëni nëse në një trekëndësh kënddrejtë njihni një kënd (përveç këndit të drejtë) dhe njërën anë, por duhet të gjeni anët e tjera?

Kjo është ajo që njerëzit në të kaluarën hasnin kur bënin harta të zonës dhe qiellit me yje. Në fund të fundit, nuk është gjithmonë e mundur të maten drejtpërdrejt të gjitha anët e një trekëndëshi.
Sinus, kosinus dhe tangjent - quhen gjithashtu funksionet e këndit trigonometrik- japin marrëdhënie ndërmjet partive Dhe qoshet trekëndëshi. Duke ditur këndin, mund të gjeni të gjitha funksionet e tij trigonometrike duke përdorur tabela të veçanta. Dhe duke ditur sinuset, kosinuset dhe tangjentet e këndeve të një trekëndëshi dhe njërës prej brinjëve të tij, mund të gjeni pjesën tjetër.
Ne gjithashtu do të vizatojmë një tabelë të vlerave të sinusit, kosinusit, tangjentës dhe kotangjentës për kënde "të mira" nga në.
Ju lutemi vini re dy vijat e kuqe në tabelë. Në vlerat e duhura të këndit, tangjentja dhe kotangjentja nuk ekzistojnë.
Le të shohim disa probleme të trigonometrisë nga Banka e Detyrave FIPI.
1. Në një trekëndësh, këndi është , . Gjeni.
Problemi zgjidhet në katër sekonda.
Që nga , .
2. Në një trekëndësh, këndi është , , . Gjeni.

Le ta gjejmë duke përdorur teoremën e Pitagorës.
Problemi është zgjidhur.
Shpesh në problema ka trekëndësha me kënde dhe ose me kënde dhe. Mos harroni raportet bazë për ta përmendësh!

Për një trekëndësh me kënde dhe këmbën përballë këndit në është e barabartë me gjysma e hipotenuzës.
Një trekëndësh me kënde dhe është dykëndësh. Në të, hipotenuza është herë më e madhe se këmba.
Ne shikuam problemet për zgjidhjen e trekëndëshave kënddrejtë - domethënë gjetjen e brinjëve ose këndeve të panjohura. Por kjo nuk është e gjitha! Ka shumë probleme në Provimin e Unifikuar të Shtetit në matematikë që përfshijnë sinusin, kosinusin, tangjentën ose kotangjentën e një këndi të jashtëm të një trekëndëshi. Më shumë për këtë në artikullin vijues.
Në artikull, ne do të kuptojmë plotësisht se si duket tabela e vlerave trigonometrike, sinus, kosinus, tangent dhe kotangjent. Le të shqyrtojmë kuptimin bazë të funksioneve trigonometrike, nga një kënd prej 0,30,45,60,90,...,360 gradë. Dhe le të shohim se si t'i përdorim këto tabela në llogaritjen e vlerave të funksioneve trigonometrike.
Së pari le të shohim tabela e kosinusit, sinusit, tangjentes dhe kotangjentes nga një kënd prej 0, 30, 45, 60, 90, ... gradë. Përcaktimi i këtyre sasive na lejon të përcaktojmë vlerën e funksioneve të këndeve 0 dhe 90 gradë:sin 0 0 =0, cos 0 0 = 1. tg 00 = 0, kotangjentja nga 00 do të jetë e papërcaktuar
sin 90 0 = 1, cos 90 0 = 0, ctg90 0 = 0, tangjentja nga 90 0 do të jetë e pasigurtNëse merrni trekëndësha kënddrejtë, këndet e të cilëve janë nga 30 në 90 gradë. Ne marrim:
sin 30 0 = 1/2, cos 30 0 = √3/2, tan 30 0 = √3/3, cos 30 0 = √3
sin 45 0 = √2/2, cos 45 0 = √2/2, tan 45 0 = 1, cos 45 0 = 1
sin 60 0 = √3/2, cos 60 0 = 1/2, tan 60 0 =√3, cos 60 0 = √3/3Le të përfaqësojmë të gjitha vlerat e marra në formë tabelë trigonometrike:
Tabela e sinuseve, kosinuseve, tangjentëve dhe kotangjenteve!
Nëse përdorim formulën e reduktimit, tabela jonë do të rritet, duke shtuar vlera për kënde deri në 360 gradë. Do të duket si kjo:

Gjithashtu, në bazë të vetive të periodicitetit, tabela mund të rritet nëse i zëvendësojmë këndet me 0 0 +360 0 *z .... 330 0 +360 0 *z, në të cilin z është një numër i plotë. Në këtë tabelë është e mundur të llogaritet vlera e të gjitha këndeve që korrespondojnë me pikat në një rreth të vetëm.

Le të shohim se si të përdorim tabelën në një zgjidhje.
Gjithçka është shumë e thjeshtë. Meqenëse vlera që na nevojitet qëndron në pikën e kryqëzimit të qelizave që na duhen. Për shembull, merrni cos-in e një këndi prej 60 gradë, në tabelë do të duket si kjo:
Në tabelën përfundimtare të vlerave kryesore të funksioneve trigonometrike, ne vazhdojmë në të njëjtën mënyrë. Por në këtë tabelë mund të zbulohet se sa është tangjentja nga këndi 1020 gradë, ajo = -√3 Le të kontrollojmë 1020 0 = 300 0 +360 0 *2. Le ta gjejmë duke përdorur tabelën.

Tabela Bradis. Për sinusin, kosinusin, tangjentën dhe kotangjentin.
Tabelat Bradis ndahen në disa pjesë, të përbëra nga tabelat e kosinusit dhe sinusit, tangjentes dhe kotangjentes - e cila është e ndarë në dy pjesë (tg këndesh deri në 90 gradë dhe ctg kënde të vogla).
Sinusi dhe kosinusi

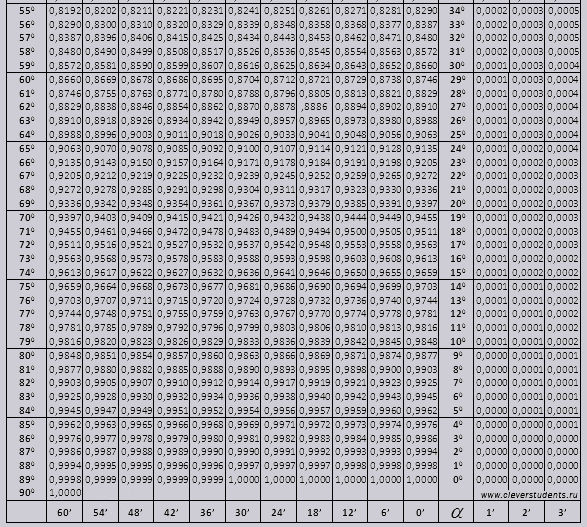
tg e këndit që fillon nga 00 duke përfunduar me 760, ctg e këndit duke filluar nga 140 duke përfunduar me 900.


tg deri në 900 dhe ctg kënde të vogla.

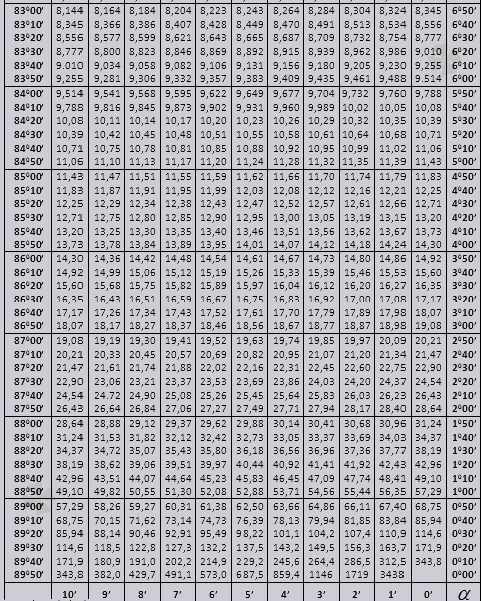
Le të kuptojmë se si të përdorim tabelat Bradis në zgjidhjen e problemeve.
Le të gjejmë përcaktimin sin (përcaktimi në kolonën në skajin e majtë) 42 minuta (përcaktimi është në vijën e sipërme). Nga kryqëzimi ne kërkojmë përcaktimin, ai = 0.3040.
Vlerat e minutave tregohen me një interval prej gjashtë minutash, çfarë të bëjmë nëse vlera që na nevojitet bie pikërisht brenda këtij intervali. Le të marrim 44 minuta, por në tabelë janë vetëm 42. Ne marrim 42 si bazë dhe përdorim kolonat shtesë në anën e djathtë, marrim ndryshimin e dytë dhe shtojmë në 0.3040 + 0.0006 marrim 0.3046.
Me sin 47 minuta, marrim 48 minuta si bazë dhe i heqim 1 korrigjim, pra 0,3057 - 0,0003 = 0,3054
Gjatë llogaritjes së cos-it, ne punojmë në mënyrë të ngjashme me mëkatin, vetëm se marrim rreshtin e poshtëm të tabelës si bazë. Për shembull cos 20 0 = 0.9397
Vlerat e këndit tg deri në 90 0 dhe shtratit të një këndi të vogël janë të sakta dhe nuk ka korrigjim në to. Për shembull, gjeni tg 78 0 37min = 4,967
dhe ctg 20 0 13min = 25,83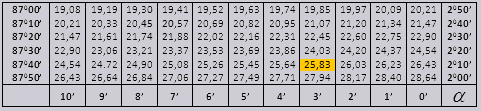
Epo, ne kemi parë tabelat bazë trigonometrike. Shpresojmë që ky informacion të ishte jashtëzakonisht i dobishëm për ju. Nëse keni ndonjë pyetje në lidhje me tabelat, sigurohuni që t'i shkruani ato në komente!
Shënim: Parakolpët e murit janë një dërrasë parakolp për mbrojtjen e mureve. Ndiqni lidhjen e parakolpëve të murit pa kornizë (http://www.spi-polymer.ru/otboyniki/) dhe zbuloni më shumë.








