Başvuru

İşlenen materyali pekiştirmek amacıyla pratik alıştırmalar için sitedeki güç serileri. Ve bir kuvvet serisinin yakınsaklığının benzersiz bir şekilde nasıl belirleneceğini öğrenmek için öğrencilerin becerilerini geliştirmek. Uygulamalı alıştırmalar, çalışma sırasında yeterli sayıda ders tahsis edilmesi durumunda istenen sonucu tam olarak verir. Bu, öğrenciler için yüksek kaliteli eğitimin tam olarak sağlanmasını sağlayacaktır. Ama orada olmadıklarında ne yapmalı? Bu durumda web sitemiz veya benzer bir kaynak, kuvvet serilerini çevrimiçi çözmenize yardımcı olacaktır. Ancak bu tür hesap makineleri her zaman soruna doğru cevabı sağlayamayacaktır. Tam da bu amaçla, tek bir koşul örneğini kullanarak, benzer sitelerin çözümleri arasında alınan yanıtları karşılaştırmanız gerekir. Bir serinin yakınsaklık bölgesinin bazen farklı teoremler kullanılarak hesaplandığını ve cevabın doğru olmasına rağmen farklı gösterim biçimleriyle ifade edilebildiğini fark edebilirsiniz. Elbette bu bir hata olarak kabul edilmeyecektir; asıl mesele bunu nasıl algılamanızın sizin için daha uygun olacağıdır. Kısacası, bir siteyi veya diğerini kullanarak bir güç serisinin yakınsamasını, yani cevabın daha sonraki uygulamaları için sizin için ne kadar uygun olacağını bulmak size kalmıştır. Bazen bir kuvvet serisinin çözümü eşitsizlik işaretli notasyonlarla ve çoğunlukla da modül işaretiyle ifade edilir. Pratikte kullanılan en yaygın yöntemler bir serinin ortak üyelerinin modüller kullanılarak karşılaştırılması olduğundan, bu bir tesadüf değildir. Bir dizi dönüşüm yoluyla, bir modül içine alınmış bir değişken izole edilir ve çözümün anlaşılması için normalde algılanan kısa bir gösterim kalır. Görsel bir gösterim için, bir serinin yakınsaklık yarıçapı, sınır noktalarını gösteren sayısal eksen üzerinde temsil edilebilir; bu arada, bu da bazı durumlarda memnuniyetle karşılanır. Ufkunuzu daraltacak herhangi bir spesifik çerçeveye kendinizi zorlamanıza gerek yok. Genel olarak konuşursak, kuvvet serileri matematikte önemli bir konudur çünkü karmaşıktır ve bunu anlamak için birkaç ders almanız gerekecektir. Örneğin, limit ve integral hesabına geçiş teorisi, çünkü bir güç serisinin yakınsamasını kanıtlamak için genellikle bu eylemlerin mevcut olduğu teknikleri tam olarak kullanırlar. Size pratik dersler almanızı ve güç serilerini inceleme bilginizi doğrudan sitede çevrimiçi olarak test etmenizi öneriyoruz, çünkü çözülen tüm sorunların birkaç saniye içinde ve gerçek zamanlı olarak tamamen ücretsiz olarak doğru bir cevapla verildiğini garanti ediyoruz. Serilerin yakınsama aralığına ek olarak veya serinin yakınsama yarıçapı olarak da adlandırıldığı için, kesinlikle en üst düzeyde takdir edeceğiniz birçok ilgili hesap makinesini size sunuyoruz. Bir kuvvet serisinin yakınsaklığını bulmanız gerekiyorsa, site doğruluğun garantisi ve kusursuz kalitede yanıtın garantisi olduğundan, bunu sizin için yapmamıza izin verin. Pek çok öğrenci genellikle bir güç serisini çözmeye nasıl hızlı bir şekilde hazırlanılacağı gibi bir soru sorar, ancak yalnızca bir çözüm değil, aynı zamanda yüksek kaliteli ve doğru bir çözümdür. Kuvvet serileri her zaman şu anda öğrencilere öğretilenden daha geniş bir anlama sahip olmuştur. Bu anlaşılabilir bir durumdur çünkü bu, daha önemli konuların derinlemesine incelenmesi ihtiyacı nedeniyle zamanın olmamasıyla açıklanmaktadır. Bir yandan - EVET ama bu, kuvvet serilerinin yakınsamasını ihmal edebileceğimiz anlamına mı geliyor? Büyük olasılıkla hayır, çünkü kuvvet serilerini çevrimiçi olarak düzgün bir şekilde çalışmadan, ders çalışmanızdaki veya tez savunmanızdaki bariz soruları yetkin bir şekilde yanıtlayamazsınız. Diyelim ki konu alanınız sürekli ortam mekaniği veya yapı mekaniği gibi bir disiplini içeriyor. Stratejik nesnelerin tasarımında özellikle insan hayatının korunmasını doğrudan ilgilendiriyorsa sistemlerin istikrarının önemli olduğu açıktır. Bir serinin yakınsama alanını nasıl bulacağınızın özünü öğrenirseniz veya en azından anlarsanız ne gibi yararlı şeyler öğrenilebileceği anlaşılıyor? Bu tanımın önemini tek bir cümleyle anlatmak zordur. Ancak benim sözüme güvenin, bir kuvvet serisinin yakınsaklığını bulmak, örneğin Pisagor teoremini bilmek kadar önemli ve gerekli bir prosedürdür. Eğer bir kuvvet serisinin çözümü hatayla yapılırsa, daha sonraki hesaplamalarda bu kesinlikle öğrenciye acımasız bir şaka yapacaktır. Bazen, bir hatadaki can sıkıcı bir yanlışlık nedeniyle uçağın ilk testler sırasında düşmesi meydana gelir. Katılıyorum, yapılan işten ve muazzam zaman yatırımından sonra bu bir utanç. Bu nedenle, bir serinin yakınsaklık yarıçapını bulmayı öğrenin ve tekrar öğrenin, böylece problemlerin çözümünde en başından itibaren doğruluk ve titizlik aşılayın. Şimdi kuvvet serileri konusuna dönelim ve bu bölüm hakkında size biraz daha bilgi verelim. Uygulamada birçok kuvvet serisi birinci terimle başlar, ancak birinci terimin hem ikinci hem de üçüncü terimle başlayabileceği seriler de vardır. Bu büyük ölçüde, örneğin ilk terimden başlayarak serinin tüm toplamının anında sonsuza gitmesinden kaynaklanmaktadır ki bu aslında özünde elbette önemsizdir. Yakınsaklık alanını incelemek için bir konu olarak bir kuvvet serisinin yakınsaklığı, özellikle matematiksel analiz bölümünde çalışmayan öğrenciler tarafından pratikte sıklıkla kullanılmaz. İşin özü açıktır ve görevlerin tümü belirlenmiştir. Hesap makinemiz online olarak kuvvet serilerini hesaplıyor ayrıca serilerin yakınsaklığından da bahsediyor, bir sayı serisinin hangi kriterlere göre yakınsadığını kısacası kuvvet serilerinin yakınsaklığını belirleyebiliyor. Bir değişken, belirli bir tek koşulu karşılıyorsa, yani karşılık gelen sayısal serinin sonlu bir gerçek sayısal değere yakınsaması durumunda, bir serinin yakınsaklık bölgesine düşebilir. Belki de bu sadece bir koşul değildir; n parametresinin herhangi bir sıralı doğal değeri için serinin tüm terimlerinin var olması ve benzersiz bir şekilde belirlenmesi de gereklidir. Bir kuvvet serisinin yakınsaklığını bulmak, eğer Kartezyen koordinat sisteminden bahsediyorsak, onun x ekseni üzerindeki yakınsaklık bölgesini belirlemek anlamına gelir. Bunu D'Alembert ilkesini kullanarak yapmak mümkün görünüyor, ancak bunu yalnızca kritere göre anlamanız gerekir, çünkü ilkenin kendisi yalnızca değişkenin düşeceği aralığı belirler. Unutmayın, d'Alembert testi fonksiyonel seriler için geçerli değildir, yalnızca sayı serileri için geçerlidir. Bir kuvvet serisini çözmek doğrudan bu serinin yakınsaklık yarıçapını bulmakla ilgilidir, ancak kısaca bu şekilde ifade edilir. Bilim dünyasındaki trende ayak uydurabilmek için biz de bu terimi kullanacağız. Sınır noktalarındaki kuvvet serileri ayrı ayrı incelenmiştir. Elbette bu, kuvvet serilerinin yakınsaklığını incelemenin genel probleminin bir parçasıdır. Bu sınır noktalarında seri, serinin genel teriminin türüne göre sayısal seri - sabit işaretli veya alternatif işaretli olarak incelenir. Üyeleri kuvvet fonksiyonu olan serilere kuvvet serileri denir ve hesap makinesi bunları çevrimiçi olarak çözebilir. Bunu deyince akıllarına hemen şu varsayım geliyor ve eğer serinin üyeleri periyodik fonksiyonlar ise o zaman böyle bir seriye muhtemelen fonksiyonel periyodik seri denmesi gerekir! Komik bir şey ama her şey çok ciddi. Serinin yakınsaklık alanını belirlediğimizde, son hesaplamaları yapmak, yani x değişkeni yerine belirli bir aralığın sınırlarını koyarak elde edilen sayısal serileri yakınsaklık açısından incelemek gerekir. güç serisi. Daha sonra çözümüyle birlikte tam bir cevap yazabilirsiniz. Bir kuvvet serisinin yakınsaklığını ana teoremleri kullanmadan, yalnızca karşılaştırmalı olarak nasıl bulabileceğinize dair bir örnek düşünelim. Bu durumda, orijinal seriyi uzun süredir üzerinde çalışılan temel seriye basitleştirene kadar iki fonksiyonel serinin karşılaştırmasını yetkin bir şekilde yapmamız gerekiyor. Bu prensibe göre, herkesin uzun zamandır önceden bildiği sonucu cevap olarak alacağız. Bir güç serisinin çözümüne dayanarak, serinin yakınsama yarıçapının tam olarak ne olacağını kesin olarak tahmin etmek henüz mümkün değildir, çünkü bundan önce, serinin sınırlarının her biri üzerinde en az iki sayı serisini incelemek hala gereklidir. Görünüşte tüm kuvvet serileri aynıdır, çünkü ortak terimleri argümanın düzenli bir fonksiyonunu temsil eder. Çalışmanın özü, serinin yakınsaması için bu argümanın kabul edilebilir değerlerini (koşullu veya koşulsuz) ve karşılık gelen sayısal serilerin hangi aralıklarla ayrılacağını kesin olarak belirlemektir. Yakınsaklık için güç serilerini incelemek çok zaman alır ve web sitesinde hazır bir hesap makinesi kullanmanızı öneririz. Aralığın sınırlarını da incelemek gerekiyor, aksi takdirde görev tam olarak tamamlanamayacak, bu da iki puanın düşülmesinin garanti olduğu anlamına geliyor. Web sitemizde çevrimiçi olarak kuvvet serilerinin toplamını hesaplayabilirsiniz. Her zaman hızlı, güvenilir ve en önemlisi ücretsiz! Kullanışlı arayüz ve net veri talebi Doğru olarak, bir serinin yakınsaklık alanı, sayısal bir serinin toplamının varlığı için özel bir durumdur. Aralığın sınırındaki değer, ortaya çıkan alternatif serinin ıraksamasını veriyorsa. sonra serinin koşullu yakınsadığını yani bu bölgede mutlaka yakınsadığını ama belirli koşullar altında ki bu her durumda önemli diyorlar. Kuvvet serisi kavramından soyutlarsak ve bir an için kuvvet serisinin toplamının x değişkenindeki belirli bir fonksiyon olduğunu hayal edersek, o zaman artık bir kuvvet serisinin yakınsaklığını bulmaktan değil, kuvvet serisinin yakınsamasını bulmaktan bahsediyoruz demektir. fonksiyonun değerinin argüman x'in farklı değerlerinde bulunacağı koşullar. Kısacası problemi, bir fonksiyonun tanım kümesinin en basit bulgusuna indirgemekteyiz. Gerçek çok basit ve açıktır! Bir güç serisine yönelik herhangi bir çözüm her zaman böyle bir güç serisinin yakınsama yarıçapından bahseder ve genellikle D'Alembert kriteri aracılığıyla belirlenir, ancak doğrudan değil, yalnızca bir koşulla belirlenir. Bundan sonra ortaya çıkan eşitsizliğin modülü ortaya çıkarılır ve sayısal seriler mutlak veya koşullu yakınsaklık açısından incelenir. Sonra bir sonuca varırlar. Orijinal formundaki kuvvet serilerinin entegre edilmesi veya farklılaştırılması ve ardından yeni kuvvet serisinden elde edilen serilerin toplamının hesaplanması çok ilginçtir. Bu, bir serinin belirli koşullar altında nasıl davranacağına ilişkin birçok seçeneğe yol açar. Orijinal serinin bütünleşik terimleriyle bulunan kuvvet serilerinin toplamı aslında orijinal güç serisinin bütünleşik toplamıdır. İlginç ve bilgilendirici, değil mi? Sorunun metnini doğru bir şekilde formüle ederseniz, şuna benzer: Güç serisinin yakınsama aralığını bulun ve onu bulunan aralığın sınırları üzerinde inceleyin. Buradan itibaren seriler mutlak olarak yakınlaşabilir veya uzaklaşabilir, bu da ek bir araştırma gerektirmez. Düzgün yakınsaklık, üniversitedeki gibi klasik biçimde yazılmış orijinal serinin tüm terimlerini birer birer ekleyerek çevrimiçi hesaplamada kuvvet serilerini gösterir. Sadece içgüdülerine güvenen bir öğrenci, öğreniminin en başında bir web sitesi hesaplayıcısını alıp kullanmak armut kabuğunu soymak kadar kolayken, deneyimsizliği nedeniyle kendine olan güveninin tuzağına düşme riskiyle karşı karşıya kalır. Serinin yakınsama alanından, fonksiyonel veya daha doğrusu güç serisinin yakınsaması hakkında sonuçlar çıkarılır, yani koşullu veya mutlak olarak yakınlaştığı tespit edilir. Bütün bunlar nihai yanıtın son kaydı için gereklidir. Durumu karmaşıklaştırmadan ve karmaşık teoremlerin isimlerini kullanmadan diyelim ki, bir kuvvet serisinin yakınsaklığını bulmanın anlaşılması, belirli bir fonksiyonu serinin toplamı olarak hayal edip çalışırsanız daha kolay olacaktır. Ve bu uzun zamandır herkes için açık ve nasıl yapılacağını anlıyor! Bir serinin yakınsaklık yarıçapı ve bir kuvvet serisinin çözümü aynı kavramlardır, çünkü aynı şeyi ifade ederler; daha kesin olarak, karşılık gelen sayı serisinin yakınsamasının oluştuğu bölgeyi, değişkenin değerlerini benzersiz bir şekilde tanımlarlar. verir.

Fonksiyonel seriler arasında en önemli yeri kuvvet serileri almaktadır.

Kuvvet serisi bir seridir

terimleri artan negatif olmayan tamsayı kuvvetlerine göre düzenlenmiş kuvvet fonksiyonlarıdır X, A C0 , C 1 , C 2 , C N - sabit değerler. Sayılar C1 , C 2 , C N - seri terimlerinin katsayıları, C0 - ücretsiz üye. Kuvvet serisinin terimleri sayı doğrusunun tamamında tanımlanır.

Konsepti tanıyalım kuvvet serilerinin yakınsaklık alanları. Bu bir dizi değişken değerdir X, bunun için seri yakınsaktır. Kuvvet serileri oldukça basit bir yakınsama bölgesine sahiptir. Gerçek değişken değerleri için X yakınsama bölgesi ya bir noktadan oluşur ya da belirli bir aralıktır (yakınsama aralığı) ya da tüm eksenle çakışır Öküz .

Değerleri güç serisine yerleştirirken X= 0 bir sayı serisiyle sonuçlanacaktır

C0 +0+0+...+0+... ,

hangi birleşir.

Bu nedenle ne zaman X= 0 herhangi bir kuvvet serisi yakınsar ve bu nedenle, yakınsama alanı boş küme olamaz. Tüm kuvvet serilerinin yakınsama bölgesinin yapısı aynıdır. Aşağıdaki teorem kullanılarak belirlenebilir.

Teorem 1 (Abel teoremi). Bir kuvvet serisi belirli bir değerde yakınsarsa X = X 0 sıfırdan farklıysa yakınsar ve dahası, tüm değerler için kesinlikle |X| < |X 0 | . Lütfen unutmayın: hem “X sıfırdır” başlangıç değeri hem de başlangıç değeriyle karşılaştırılan herhangi bir “X” değeri, işaret dikkate alınmaksızın modulo olarak alınır.

Sonuçlar. Eğer kuvvet serisi ıraksar bir değerde X = X 1 , o zaman tüm değerler için ıraksar |X| > |X 1 | .

Daha önce öğrendiğimiz gibi, herhangi bir kuvvet serisi şu değerde yakınsar: X= 0. Yalnızca şu durumlarda yakınsayan kuvvet serileri vardır: X= 0 ve diğer değerler için ıraksak X. Bu durumu göz önünde bulundurmadan, kuvvet serilerinin bir değerde yakınsadığını varsayıyoruz. X = X 0 , sıfırdan farklı. O halde Abel teoremine göre ]-| aralığının her noktasında yakınsar. X0 |, |X 0 |[ (sol ve sağ sınırları, güç serisinin yakınlaştığı x değerleri olan, sırasıyla eksi işareti ve artı işaretiyle alınan bir aralık), orijine göre simetrik.

Kuvvet serisi belirli bir değerde ıraksaıyorsa X = X 1 , bu durumda, Abel teoreminin bir sonucuna dayanarak, [-| segmentinin dışındaki tüm noktalarda ıraksar. X1 |, |X 1 |] . Herhangi bir kuvvet serisi için orijine göre simetrik bir aralık vardır. yakınsama aralığı , serinin yakınlaştığı her noktada, sınırlarda yakınlaşabilir veya uzaklaşabilir ve mutlaka aynı anda olması gerekmez ve segmentin dışında seri ıraksar. Sayı R kuvvet serisinin yakınsaklık yarıçapı denir.

Özel durumlarda kuvvet serilerinin yakınsama aralığı bir noktaya kadar yozlaşabilir (bu durumda seri ancak X= 0 ve öyle kabul edilir R= 0) veya sayı doğrusunun tamamını temsil eder (bu durumda seri sayı doğrusu üzerindeki tüm noktalarda yakınsar ve öyle olduğu varsayılır).

Dolayısıyla bir kuvvet serisinin yakınsaklık bölgesinin belirlenmesi, onun yakınsaklığının belirlenmesinden ibarettir. yakınsama yarıçapı R ve yakınsama aralığı sınırlarında ('da) serinin yakınsaklığının incelenmesi.

Teorem 2. Belirli bir seriden başlayarak bir güç serisinin tüm katsayıları sıfırdan farklıysa, yakınsama yarıçapı, serinin aşağıdaki ortak üyelerinin katsayılarının mutlak değerleri oranındaki limite eşittir. yani

Örnek 1. Kuvvet serisinin yakınsaklık bölgesini bulun

Çözüm. Burada

Formül (28)'i kullanarak bu serinin yakınsama yarıçapını buluruz:

Yakınsaklık aralığının uçlarındaki serilerin yakınsaklığını inceleyelim. Örnek 13 bu serinin şu noktada yakınsadığını göstermektedir: X= 1 ve ıraksar X= -1. Sonuç olarak, yakınsama bölgesi yarı aralıktır.

Örnek 2. Kuvvet serisinin yakınsaklık bölgesini bulun

Çözüm. Serinin katsayıları pozitiftir ve

Bu oranın limitini bulalım. kuvvet serilerinin yakınsama yarıçapı:

Serinin aralığın sonlarındaki yakınsaklığını inceleyelim. Değerlerin değiştirilmesi X= -1/5 ve X= 1/5 bu satırda şunu verir:

Bu serilerden ilki yakınsar (bkz. Örnek 5). Ancak o zaman “Mutlak yakınsaklık” bölümündeki teorem gereği ikinci seri de yakınsar ve yakınsaklığının bölgesi segmenttir.

Örnek 3. Kuvvet serisinin yakınsaklık bölgesini bulun

Çözüm. Burada

Formül (28)'i kullanarak serinin yakınsaklık yarıçapını buluruz:

değerleri için serinin yakınsaklığını inceleyelim. Bunları bu seride yerine koyarsak sırasıyla şunu elde ederiz:

Her iki seri de ıraksaktır çünkü yakınsama için gerekli koşul sağlanmamıştır (ortak terimleri sıfıra yönelmemektedir). Yani yakınsama aralığının her iki ucunda da bu seri ıraksar ve yakınsaklık bölgesi aralıktır.

Örnek 5. Kuvvet serisinin yakınsaklık bölgesini bulun

Çözüm. İlişkiyi nerede buluyoruz ve :

Formül (28)'e göre, bu serinin yakınsama yarıçapı

yani seri yalnızca şu durumlarda yakınsar X= 0 ve diğer değerler için ıraksar X.

Örnekler, yakınsama aralığının sonlarında serinin farklı davrandığını göstermektedir. Örnek 1'de seri yakınsaklık aralığının bir ucunda yakınsar, diğer ucunda ıraksar; örnek 2'de her iki uçta da yakınsar, örnek 3'te her iki uçta da ıraksar.

Bir güç serisinin yakınsama yarıçapı formülü, seri terimlerinin belirli bir noktadan başlayarak tüm katsayılarının sıfırdan farklı olduğu varsayımıyla elde edilir. Bu nedenle formül (28)'in kullanımına yalnızca bu durumlarda izin verilir. Bu koşul ihlal edilirse, güç serisinin yakınsaklık yarıçapı kullanılarak aranmalıdır. d'Alembert'in işareti veya değişkeni değiştirerek seriyi belirtilen koşulun sağlandığı bir forma dönüştürmek.

Örnek 6. Kuvvet serisinin yakınsaklık aralığını bulun

Çözüm. Bu seri tek dereceli terimler içermiyor X. Bu nedenle diziyi ayarlayarak dönüştürüyoruz. Sonra diziyi alıyoruz

formül (28)'i uygulayabileceğimiz yakınsama yarıçapını bulmak için. a olduğundan bu serinin yakınsaklık yarıçapı

Dolayısıyla elde ettiğimiz eşitlikten bu seri aralıkta yakınsar.

Güç serilerinin toplamı. Güç serilerinin farklılaşması ve entegrasyonu

Güç serisi için izin ver

yakınsama yarıçapı R> 0, yani bu seri aralıkta yakınsar.

Daha sonra her değer X yakınsama aralığından serinin belirli bir toplamına karşılık gelir. Bu nedenle güç serilerinin toplamı şuna bağlıdır: X yakınsama aralığında. Şununla belirtmek F(X), eşitliği yazabiliriz

bunu her noktadaki serinin toplamı anlamında anlamak X yakınsama aralığından fonksiyonun değerine eşittir F(X) Bu noktada. Aynı anlamda kuvvet serisinin (29) fonksiyona yakınsadığını söyleyeceğiz. F(X) yakınsama aralığında.

Yakınsama aralığının dışında eşitliğin (30) hiçbir anlamı yoktur.

Örnek 7. Güç serisinin toplamını bulun

Çözüm. Bu geometrik bir seridir A= 1, bir Q= X. Bu nedenle toplamı bir fonksiyondur . Bir seri eğer yakınsar ve onun yakınsama aralığıdır. Bu nedenle eşitlik

işlev yalnızca değerler için geçerlidir, ancak işlev tüm değerler için tanımlanmış X, hariç X= 1.

Güç serilerinin toplamının olduğu kanıtlanabilir. F(X) yakınsama aralığındaki herhangi bir aralıkta, özellikle serinin yakınsama aralığındaki herhangi bir noktada sürekli ve türevlenebilirdir.

Kuvvet serilerinin terim terim türevi ve integrali ile ilgili teoremleri sunalım.

Teorem 1. Yakınsama aralığındaki kuvvet serileri (30), sınırsız sayıda terim terim farklılaştırılabilir ve elde edilen kuvvet serileri, orijinal seri ile aynı yakınsama yarıçapına sahiptir ve bunların toplamları sırasıyla eşittir.

Teorem 2. Kuvvet serisi (30), 0 ile 0 arasında sınırsız sayıda terim terim entegre edilebilir. X, if , ve ortaya çıkan kuvvet serileri orijinal seriyle aynı yakınsaklık yarıçapına sahiptir ve toplamları buna uygun olarak eşittir

Fonksiyonların kuvvet serilerine genişletilmesi

Fonksiyon verilsin F(X), bunun bir kuvvet serisine genişletilmesi gerekiyor, yani. (30) formunda temsil edilir:

Görev katsayıları belirlemektir. sıra (30). Bunu yapmak için eşitliği (30) terimden terime ayırarak tutarlı bir şekilde şunu buluruz:

……………………………………………….. (31)

(30) ve (31) eşitliklerini varsayarsak X= 0, buluruz

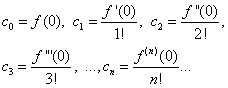
Bulunan ifadeleri eşitlik (30) ile değiştirerek şunu elde ederiz:

(32)

Bazı temel fonksiyonların Maclaurin serisi açılımını bulalım.

Örnek 8. Fonksiyonu Maclaurin serisinde genişletin

Çözüm. Bu fonksiyonun türevleri fonksiyonun kendisiyle çakışmaktadır:

Bu nedenle ne zaman X= 0 elimizde

Bu değerleri formül (32)'ye değiştirerek istenen genişlemeyi elde ederiz:

(33)

Bu seri tüm sayı doğrusu üzerinde (yakınsaklık yarıçapı) yakınsar.

Örnek 1. Kuvvet serisinin yakınsaklık bölgesini bulun:

A) ; B) ;

V) ; G)
;

D)
.

A) Yakınsama yarıçapını bulalım R. Çünkü
,
, O

X
yani serinin yakınsaklık aralığı
.

Şu tarihte:
bir sayı serisi elde ederiz . Bu seri genelleştirilmiş bir harmonik seri olduğundan yakınsar en
.

Şu tarihte:
bir sayı serisi elde ederiz
. Terimlerinin mutlak değerlerinden oluşan bir seri olduğundan bu seri kesinlikle yakınsaktır. , yakınsak.

B) Yakınsama yarıçapını bulalım R. Çünkü
, O
.

Yani serinin yakınsama aralığı
.

Bu serinin yakınsaklığını yakınsama aralığının sonlarında inceliyoruz.

Şu tarihte:
bir sayı serimiz var

.

Şu tarihte:
bir sayı serimiz var
. Bu seri farklı çünkü
mevcut değil.

Yani bu serinin yakınsaklık bölgesi
.

V) Yakınsama yarıçapını bulalım R. Çünkü
,
O
.

Yani yakınsama aralığı
. Bu serinin yakınsama bölgesi yakınsama aralığına denk gelir, yani seri değişkenin herhangi bir değeri için yakınsar X.

G) Yakınsama yarıçapını bulalım R. Çünkü
,
O
.

Çünkü
, bu durumda seri yalnızca noktada yakınsar
. Bu, bu serinin yakınsaklık bölgesinin bir nokta olduğu anlamına gelir
.

D) Yakınsama yarıçapını bulalım R.

Çünkü
,
, O

Yani seri kesinlikle herkes için birleşiyor X eşitsizliğin sağlanması
yani
.

Buradan
- yakınsama aralığı,
- yakınsama yarıçapı.

Bu serinin yakınsaklık aralığının uçlarındaki yakınsaklığını inceleyelim.

Şu tarihte:
bir sayı serisi elde ederiz

ıraksak olan (harmonik seri).

Şu tarihte:
bir sayı serisi elde ederiz
Koşullu olarak yakınsak olan (dizi Leibniz kriterine göre yakınsar ve üyelerinin mutlak değerlerinden oluşan seri harmonik olduğundan ıraksar).

Yani serinin yakınsaklık bölgesi
.

2.3. Taylor ve Maclaurin serileri.

Fonksiyonların kuvvet serilerine genişletilmesi.

Güç serilerinin yaklaşık hesaplamalara uygulanması

Problem çözme örnekleri

Örnek 1. Fonksiyonu bir kuvvet serisine genişletin:

A)
; B)
;

V)
; G)
.

A) Formülde değiştirme
X Açık
İstenilen genişlemeyi elde ederiz:

Nerede

B) Eşitlik içinde değiştirme

Nerede
X Açık
İstenilen genişlemeyi elde ederiz:

V) Bu fonksiyon şu şekilde yazılabilir:
. İstenilen seriyi bulmak için genişletmeniz yeterlidir

Nerede
yerine geçmek
. Sonra şunu elde ederiz:

G) Bu fonksiyon şu şekilde yeniden yazılabilir: .

İşlev
bir binom serisi yerleştirilerek kuvvet serisine genişletilebilir
, alacağız.

Nerede
.

İstenilen genişlemeyi elde etmek için ortaya çıkan seriyi çarpmak yeterlidir (bu serilerin mutlak yakınsamasından dolayı).

Buradan,

, Nerede
.

Örnek 2. Bu fonksiyonların yaklaşık değerlerini bulun:

A)
0,0001 doğrulukla;

B)
0,00001 doğrulukla.

A)Çünkü
, daha sonra fonksiyonun genişletilmesine, burada
hadi değiştirelim
:

veya

Çünkü
, kendimizi sonuçta ortaya çıkan genişlemenin yalnızca ilk iki terimiyle sınırlandırırsak gerekli doğruluk sağlanacaktır.

Binom serisini kullanıyoruz

Nerede
.

İnanmak
Ve
aşağıdaki genişlemeyi elde ederiz:

Son alternatif seride yalnızca ilk iki terim dikkate alınır ve geri kalanı atılırsa hesaplamada hata olur
mutlak değer olarak 0,000006'yı geçmeyecektir. O zaman hesaplamadaki hata
sayısını aşamaz. Buradan,

Örnek 3. En yakın 0,001'e kadar hesaplayın:

A)
; B)
.

A)
.

İntegrali bir kuvvet serisine genişletelim. Bunu yapmak için binom serisinde yerine koyalım
ve değiştir X Açık :

Entegrasyon segmentinden bu yana
ortaya çıkan serinin yakınsaklık bölgesine aittir
, daha sonra belirtilen sınırlar dahilinde terimi terim olarak entegre edeceğiz:

Sonuçta ortaya çıkan alternatif işaretler dizisinde dördüncü terimin mutlak değeri 0,001'den küçüktür. Sonuç olarak serinin sadece ilk üç terimi dikkate alındığında gerekli doğruluk sağlanacaktır.

Atılan terimlerden ilki eksi işaretine sahip olduğundan, ortaya çıkan yaklaşık değer fazla olacaktır. Bu nedenle 0,001 dahilindeki cevap 0,487'dir.

B)İlk önce integrali bir kuvvet serisi olarak temsil edelim. Fonksiyonun açılımında yerine koyalım

Nerede

X Açık
, şunu elde ederiz:

Daha sonra
.

Ortaya çıkan alternatif seri, Leibniz'in kriterinin koşullarını karşılıyor. Serinin dördüncü teriminin mutlak değeri 0,001'den küçüktür. Gerekli doğruluğu sağlamak için ilk üç terimin toplamını bulmak yeterlidir.

Buradan,
.

Fonksiyonel seri. Güç serileri.
Serinin yakınsaklık aralığı

Sebepsiz gülmek d'Alembert'in işaretidir

İşlevsel rütbelerin saati geldi. Konuya ve özellikle de bu derse başarılı bir şekilde hakim olmak için sıradan sayı serileri hakkında iyi bir anlayışa sahip olmanız gerekir. Bir serinin ne olduğunu iyi anlamanız ve seriyi yakınsaklık açısından incelemek için karşılaştırma kriterlerini uygulayabilmeniz gerekir. Bu nedenle, konuyu incelemeye yeni başladıysanız veya yüksek matematiğe yeni başlıyorsanız, gerekliüç dersi sırayla çalışın: Aptallar için satırlar,D'Alembert'in işareti. Cauchy'nin işaretleri Ve Alternatif satırlar. Leibniz'in testi. Kesinlikle üçü de! Sayı serileriyle ilgili problemleri çözme konusunda temel bilgi ve becerilere sahipseniz, çok fazla yeni materyal olmadığı için fonksiyonel serilerle baş etmek oldukça basit olacaktır.

Bu derste fonksiyonel seri kavramına (hatta ne olduğuna) bakacağız, pratik görevlerin %90'ında bulunan kuvvet serileri hakkında bilgi sahibi olacağız ve yarıçapı bulma konusunda yaygın olarak karşılaşılan tipik bir problemin nasıl çözüleceğini öğreneceğiz. Bir kuvvet serisinin yakınsaklığı, yakınsaklık aralığı ve yakınsama bölgesi. Daha sonra, ilgili materyali düşünmenizi öneririm fonksiyonların kuvvet serilerine genişletilmesi ve yeni başlayanlara ilk yardım sağlanacaktır. Biraz nefesimizi tuttuktan sonra bir sonraki aşamaya geçiyoruz:

Ayrıca fonksiyonel seriler bölümünde bunlardan çok sayıda var hesaplamaya yaklaşmak için uygulamalar ve bazıları, eğitim literatüründe kural olarak ayrı bir bölüm verilen Fourier Serisi ile öne çıkıyor. Elimde yalnızca bir makale var ama bu uzun bir makale ve çok çok fazla ek örnek var!

Yani, yer işaretleri belirlendi, hadi gidelim:

Fonksiyonel seriler ve kuvvet serileri kavramı

Limitin sonsuz olduğu ortaya çıkarsa, daha sonra çözüm algoritması da işini bitirir ve göreve son cevabı veririz: "Seri " (veya ikisinden birinde ") yakınsar. Önceki paragrafın 3 numaralı durumuna bakın.

Limitin ne sıfır ne de sonsuz olduğu ortaya çıkarsa, o zaman pratikte 1 numaralı en yaygın duruma sahibiz - seri belirli bir aralıkta yakınsar.

Bu durumda sınır . Bir serinin yakınsaklık aralığı nasıl bulunur? Eşitsizliği oluşturuyoruz:

İÇİNDE Bu türden HERHANGİ bir görev eşitsizliğin sol tarafında olmalıdır limit hesaplama sonucu ve eşitsizliğin sağ tarafında – kesinlikle birim. Neden böyle bir eşitsizliğin olduğunu ve neden sağda bir eşitsizliğin olduğunu tam olarak açıklamayacağım. Dersler uygulamaya yönelik ve hikayelerimin öğretim elemanlarını asmaması ve bazı teoremlerin netleşmesi zaten çok iyi.

Makalede bir modülle çalışma ve çift eşitsizlikleri çözme tekniği ilk yılda ayrıntılı olarak tartışıldı. İşlev Etki Alanı, ancak kolaylık olması açısından tüm eylemler hakkında mümkün olduğunca ayrıntılı yorum yapmaya çalışacağım. Eşitsizliğin okul kuralına göre modül ile genişletilmesi . Bu durumda:

Yolun yarısı bitti.

İkinci aşamada serilerin bulunan aralığın uçlarındaki yakınsaklığının araştırılması gerekmektedir.

Öncelikle aralığın sol ucunu alıp kuvvet serimizde yerine koyarız:

Şu tarihte:

Bir sayı serisi elde ettik ve onu yakınsaklık açısından incelememiz gerekiyor (önceki derslerden zaten aşina olduğumuz bir görev).

1) Seri dönüşümlüdür.
2) – serinin terimlerinin modülü azalır. Üstelik serinin her bir sonraki üyesi mutlak değer bakımından bir öncekinden daha azdır: Bu da düşüşün monoton olduğu anlamına geliyor.
Sonuç: Seri yakınsaktır.

Modüllerden oluşan bir dizi kullanarak tam olarak nasıl olduğunu öğreneceğiz:
– yakınsar (genelleştirilmiş harmonik seriler ailesinden “standart” seriler).

Böylece elde edilen sayı serileri mutlak yakınsaktır.

en – yakınsar.

! sana hatırlatıyorum herhangi bir yakınsak pozitif seri aynı zamanda mutlak yakınsaktır.

Böylece kuvvet serisi, bulunan aralığın her iki ucunda da mutlak olarak yakınsar.

Cevap: incelenen güç serisinin yakınsama alanı:

Başka bir cevap biçimi de yaşam hakkına sahiptir: Bir seri şu şekilde yakınsar:

Bazen problem ifadesi yakınsama yarıçapını belirtmenizi gerektirir. Ele alınan örnekte açıkça görülmektedir.

Örnek 2

Güç serisinin yakınsaklık bölgesini bulun

Çözüm: serinin yakınsaklık aralığını buluyoruz kullanarak d'Alembert'in işareti (fakat BY özelliği değil! – böyle bir özellik fonksiyonel seriler için mevcut değildir):

Seri şu noktada birleşiyor:

Sol ayrılmamız lazım sadece eşitsizliğin her iki tarafını da 3 ile çarpıyoruz:

– Seri dönüşümlüdür.
– – serinin terimlerinin modülü azalır. Serinin her bir sonraki üyesi bir öncekinden modülo daha azdır: Bu da düşüşün monoton olduğu anlamına geliyor.

Sonuç: Seri yakınsaktır.

Yakınsamanın doğası açısından inceleyelim:

Bu diziyi farklı bir diziyle karşılaştıralım.
Sınırlayıcı karşılaştırma kriterini kullanıyoruz:

Sıfırdan farklı sonlu bir sayı elde edilir, bu da serinin seriden ıraksadığı anlamına gelir.

Yani seri koşullu yakınsaktır.

2) Ne zaman – farklılaşıyor (kanıtlanmış olana göre).

Cevap:İncelenen güç serisinin yakınsaklık alanı: . Seri koşullu yakınsak olduğunda.

Ele alınan örnekte, güç serisinin yakınsaklık bölgesi yarım aralıktır ve aralığın tüm noktalarında güç serisi kesinlikle yakınsar ve bu noktada, ortaya çıktığı üzere – şartlı olarak.

Örnek 3

Kuvvet serisinin yakınsaklık aralığını bulun ve bulunan aralığın uçlarındaki yakınsaklığını araştırın

Bu kendi başınıza çözebileceğiniz bir örnektir.

Nadir görülen ancak meydana gelen birkaç örneğe bakalım.

Örnek 4

Serinin yakınsaklık alanını bulun:

Çözüm: D'Alembert testini kullanarak bu serinin yakınsaklık aralığını buluruz:

(1) Serinin bir sonraki üyesinin bir öncekine oranını oluştururuz.

(2) Dört katlı kesirden kurtuluyoruz.

(3) Kuvvetli işlemler kuralına göre küpleri tek kuvvet altına alıyoruz. Payda dereceyi akıllıca genişletiyoruz, yani. Bir sonraki adımda kesri azaltabileceğimiz şekilde düzenliyoruz. Faktöriyelleri ayrıntılı olarak açıklıyoruz.

(4) Küpün altında payı paydaya, terime ve terime bölerek şunu belirtiriz: . Azaltılabilecek her şeyi bir kesir halinde azaltıyoruz. Faktörü limit işaretinin ötesine alıyoruz; içinde “dinamik” değişken “en”e bağlı hiçbir şey olmadığından çıkarılabilir. Herhangi bir "x" için negatif olmayan değerler alması nedeniyle modül işaretinin çizilmediğine lütfen dikkat edin.

Limitte sıfır elde edilir, bu da son cevabı verebileceğimiz anlamına gelir:

Cevap: Seri şu noktada birleşiyor:

Ancak ilk başta "korkunç dolgulu" bu sıranın çözülmesi zor görünüyordu. Sınırın sıfır veya sonsuz olması neredeyse bir hediyedir, çünkü çözüm gözle görülür derecede azalır!

Örnek 5

Serinin yakınsaklık alanını bulun

Bu kendi başınıza çözebileceğiniz bir örnektir. Dikkatli olun;-) Tam çözüm dersin sonundadır.

Teknik tekniklerin kullanımı açısından yenilik unsuru içeren birkaç örneğe daha bakalım.

Örnek 6

Serinin yakınsaklık aralığını bulun ve bulunan aralığın uçlarındaki yakınsaklığını araştırın

Çözüm: Kuvvet serisinin ortak terimi işaret dönüşünü sağlayan bir faktör içerir. Çözüm algoritması tamamen korunur, ancak limiti çizerken, modül tüm "eksileri" yok ettiği için bu faktörü göz ardı ederiz (yazmayız).

Serinin yakınsaklık aralığını d'Alembert testini kullanarak buluyoruz:

Standart bir eşitsizlik oluşturalım:
Seri şu noktada birleşiyor:
Sol ayrılmamız lazım yalnızca modül eşitsizliğin her iki tarafını da 5 ile çarpıyoruz:

Şimdi modülü tanıdık bir şekilde açıyoruz:

Çifte eşitsizliğin ortasında sadece “X” bırakmanız gerekiyor, bunun için eşitsizliğin her bir kısmından 2 çıkarıyoruz:

– incelenen güç serisinin yakınsama aralığı.

Bulunan aralığın sonlarında serinin yakınsaklığını araştırıyoruz:

1) Değeri kuvvet serimize yazın :

Son derece dikkatli olun, çarpan herhangi bir doğal “en” için işaret değişimi sağlamaz. Ortaya çıkan eksiyi serinin dışına alıyoruz ve unutuyoruz çünkü (herhangi bir faktör sabiti gibi) sayı serisinin yakınsamasını veya ıraksamasını hiçbir şekilde etkilemez.

Lütfen tekrar not edin değeri kuvvet serisinin genel terimine koyarken faktörümüz azaltıldı. Eğer bu gerçekleşmediyse ya limiti yanlış hesaplamışız ya da modülü yanlış genişletmişiz demektir.

Bu nedenle yakınsaklık için sayı serilerini incelememiz gerekir. Burada en kolay yol sınırlayıcı karşılaştırma kriterini kullanmak ve bu seriyi ıraksak bir harmonik seriyle karşılaştırmaktır. Ancak dürüst olmak gerekirse, karşılaştırmanın sınırlayıcı işaretinden çok yoruldum, bu yüzden çözüme biraz çeşitlilik katacağım.

Yani seri şu noktada yakınsaktır:

Eşitsizliğin her iki tarafını da 9 ile çarpıyoruz:

Eski okul şakasını hatırlayarak her iki parçanın da kökünü çıkarıyoruz:

Modülü genişletme:

ve tüm parçalara bir tane ekleyin:

– incelenen güç serisinin yakınsama aralığı.

Bulunan aralığın uçlarındaki kuvvet serilerinin yakınsaklığını araştırıyoruz:

1) Eğer ise aşağıdaki sayı serisi elde edilir: