A10 simplest trigonometric equations. The simplest trigonometric equations

Concept of solving trigonometric equations.

• To solve a trigonometric equation, convert it into one or more basic trigonometric equations. Solving a trigonometric equation ultimately comes down to solving the four basic trigonometric equations.

Class: 10

“The equations will last forever.”

A. Einstein

Lesson objectives:

• Educational:
  • deepening understanding of methods for solving trigonometric equations;
  • to develop the skills to distinguish and correctly select methods for solving trigonometric equations.
• Educational:
  • nurturing cognitive interest in the educational process;
  • developing the ability to analyze a given task;
  • contribute to improving the psychological climate in the classroom.
• Developmental:
  • promote the development of the skill of independent acquisition of knowledge;
  • promote students’ ability to argue their point of view;

Equipment: poster with basic trigonometric formulas, computer, projector, screen.

1 lesson

I. Updating of reference knowledge

Solve the equations orally:

1) cosx = 1;
2) 2 cosx = 1;
3) cosx = –;
4) sin2x = 0;
5) sinx = –;
6) sinx = ;
7) tgx = ;
8) cos 2 x – sin 2 x = 0

1) x = 2k;
2) x = ± + 2k;
3) x =± + 2k;
4) x = k;
5) x = (–1) + k;
6) x = (–1) + 2k;
7) x = + k;
8) x = + k;

to Z.

– Today we will look at more complex trigonometric equations. Let's look at 10 ways to solve them. Next there will be two lessons for consolidation, and for the next lesson there will be a test. At the “For Lesson” stand there are tasks posted that are similar to those that will be on the test; you need to solve them before the test. (The day before the test, post the solutions to these tasks on the stand).

So, let's move on to considering ways to solve trigonometric equations. Some of these methods will probably seem difficult to you, while others will seem easy, because... You already know some techniques for solving equations.

Four students in the class received an individual task: to understand and show you 4 ways to solve trigonometric equations.

(Speaking students have prepared slides in advance. The rest of the class writes down the main steps for solving equations in a notebook.)

1 student: 1 way. Solving equations by factoring

sin 4x = 3 cos 2x

To solve the equation, we use the double angle sine formula sin 2 = 2 sin cos
2 sin 2x cos 2x – 3 cos 2x = 0,
cos 2x (2 sin 2x – 3) = 0. The product of these factors is equal to zero if at least one of the factors is equal to zero.

2x = + k, k Z or sin 2x = 1.5 – there are no solutions, because | sin| 1
x = + k; to Z.
Answer: x = + k, k Z.

2 student. Method 2. Solving equations by converting the sum or difference of trigonometric functions into a product

cos 3x + sin 2x – sin 4x = 0.

To solve the equation, we use the formula sin– sin = 2 sin сos

cos 3x + 2 sin cos = 0,

сos 3x – 2 sin x cos 3x = 0,

cos 3x (1 – 2 sinx) = 0. The resulting equation is equivalent to a set of two equations:

The set of solutions to the second equation is completely included in the set of solutions to the first equation. Means

Answer:

3 student. 3 way. Solving equations by converting the product of trigonometric functions into a sum

sin 5x cos 3x = sin 6x cos2x.

To solve the equation, we use the formula

Answer:

4 student. 4 way. Solving equations that reduce to quadratic equations

3 sin x – 2 cos 2 x = 0,
3 sin x – 2 (1 – sin 2 x) = 0,
2 sin 2 x + 3 sin x – 2 = 0,

Let sin x = t, where | t |. We obtain the quadratic equation 2t 2 + 3t – 2 = 0,

D = 9 + 16 = 25.

Thus . does not satisfy the condition | t |.

So sin x = . That's why .

Answer:

III. Consolidation of what has been learned from the textbook by A. N. Kolmogorov

1. No. 164 (a), 167 (a) (quadratic equation)
2. No. 168 (a) (factorization)
3. No. 174 (a) (converting a sum into a product)
4. (convert product to sum)

(At the end of the lesson, show the solution to these equations on the screen for verification)

№ 164 (A)

2 sin 2 x + sin x – 1 = 0.
Let sin x = t, | t | 1. Then
2 t 2 + t – 1 = 0, t = – 1, t= . Where

Answer: - .

№ 167 (A)

3 tg 2 x + 2 tg x – 1 = 0.

Let tg x = 1, then we get the equation 3 t 2 + 2 t – 1 = 0.

Answer:

№ 168 (A)

Answer:

№ 174 (A)

Solve the equation:

Answer:

Lesson 2 (lesson-lecture)

IV. Learning new material(continuation)

– So, let's continue to study ways to solve trigonometric equations.

5 way. Solving homogeneous trigonometric equations

Equations of the form a sin x + b cos x = 0, where a and b are some numbers, are called homogeneous equations of the first degree with respect to sin x or cos x.

Consider the equation

sin x – cos x = 0. Let's divide both sides of the equation by cos x. This can be done; root loss will not occur, because , If cos x = 0, That sin x = 0. But this contradicts the basic trigonometric identity sin 2 x+cos 2 x = 1.

We get tan x – 1 = 0.

tan x = 1,

Equations of the form a sin 2 x + bcos 2 x + c sin x cos x = 0 , Where a, b, c – some numbers are called homogeneous equations of the second degree with respect to sin x or cos x.

Consider the equation

sin 2 x – 3 sin x cos x + 2 cos 2 = 0. Let’s divide both sides of the equation by cos x, and the root will not be lost, because cos x = 0 is not the root of this equation.

tg 2 x – 3tg x + 2 = 0.

Let tg x = t. D = 9 – 8 = 1.

Then hence tg x = 2 or tg x = 1.

As a result, x = arctan 2 + , x =

Answer: arctg 2 + ,

Consider another equation: 3 sin 2 x – 3 sin x cos x + 4 cos 2 x = 2.
Let's transform the right side of the equation in the form 2 = 2 · 1 = 2 · (sin 2 x + cos 2 x). Then we get:
3sin 2 x – 3sin x cos x + 4cos 2 x = 2 (sin 2 x + cos 2 x),
3sin 2 x – 3sin x cos x + 4cos 2 x – 2sin 2 x – 2 cos 2 x = 0,
sin 2 x – 3sin x cos x + 2cos 2 x = 0. (We got the 2nd equation, which we have already analyzed).

Answer: arctan 2 + k,

6 way. Solving Linear Trigonometric Equations

A linear trigonometric equation is an equation of the form a sin x + b cos x = c, where a, b, c are some numbers.

Consider the equation sin x + cos x= – 1.
Let's rewrite the equation as:

Considering that and, we get:

Answer:

7 way. Introducing an additional argument

Expression a cos x + b sin x can be converted:

(we have already used this transformation when simplifying trigonometric expressions)

Let us introduce an additional argument - the angle is such that

Then

Consider the equation: 3 sinx + 4 cosx = 1. =

Homework: No. 164 -170 (c, d).

You can order a detailed solution to your problem!!!

An equality containing an unknown under the sign of a trigonometric function (`sin x, cos x, tan x` or `ctg x`) is called a trigonometric equation, and it is their formulas that we will consider further.

The simplest equations are `sin x=a, cos x=a, tg x=a, ctg x=a`, where `x` is the angle to be found, `a` is any number. Let us write down the root formulas for each of them.

1. Equation `sin x=a`.

For `|a|>1` it has no solutions.

When `|a| \leq 1` has an infinite number of solutions.

Root formula: `x=(-1)^n arcsin a + \pi n, n \in Z`

2. Equation `cos x=a`

For `|a|>1` - as in the case of sine, it has no solutions among real numbers.

When `|a| \leq 1` has an infinite number of solutions.

Root formula: `x=\pm arccos a + 2\pi n, n \in Z`

Special cases for sine and cosine in graphs.

3. Equation `tg x=a`

Has an infinite number of solutions for any values ​​of `a`.

Root formula: `x=arctg a + \pi n, n \in Z`

4. Equation `ctg x=a`

Also has an infinite number of solutions for any values ​​of `a`.

Root formula: `x=arcctg a + \pi n, n \in Z`

Formulas for the roots of trigonometric equations in the table

For sine:
For cosine:
For tangent and cotangent:
Formulas for solving equations containing inverse trigonometric functions:

Methods for solving trigonometric equations

Solving any trigonometric equation consists of two stages:

• with the help of transforming it to the simplest;
• solve the simplest equation obtained using the root formulas and tables written above.

Let's look at the main solution methods using examples.

Algebraic method.

This method involves replacing a variable and substituting it into an equality.

Example. Solve the equation: `2cos^2(x+\frac \pi 6)-3sin(\frac \pi 3 - x)+1=0`

`2cos^2(x+\frac \pi 6)-3cos(x+\frac \pi 6)+1=0`,

make a replacement: `cos(x+\frac \pi 6)=y`, then `2y^2-3y+1=0`,

we find the roots: `y_1=1, y_2=1/2`, from which two cases follow:

1. `cos(x+\frac \pi 6)=1`, `x+\frac \pi 6=2\pi n`, `x_1=-\frac \pi 6+2\pi n`.

2. `cos(x+\frac \pi 6)=1/2`, `x+\frac \pi 6=\pm arccos 1/2+2\pi n`, `x_2=\pm \frac \pi 3- \frac \pi 6+2\pi n`.

Answer: `x_1=-\frac \pi 6+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.

Factorization.

Example. Solve the equation: `sin x+cos x=1`.

Solution. Let's move all the terms of the equality to the left: `sin x+cos x-1=0`. Using , we transform and factorize the left-hand side:

`sin x — 2sin^2 x/2=0`,

`2sin x/2 cos x/2-2sin^2 x/2=0`,

`2sin x/2 (cos x/2-sin x/2)=0`,

1. `sin x/2 =0`, `x/2 =\pi n`, `x_1=2\pi n`.
2. `cos x/2-sin x/2=0`, `tg x/2=1`, `x/2=arctg 1+ \pi n`, `x/2=\pi/4+ \pi n` , `x_2=\pi/2+ 2\pi n`.

Answer: `x_1=2\pi n`, `x_2=\pi/2+ 2\pi n`.

Reduction to a homogeneous equation

First, you need to reduce this trigonometric equation to one of two forms:

`a sin x+b cos x=0` (homogeneous equation of the first degree) or `a sin^2 x + b sin x cos x +c cos^2 x=0` (homogeneous equation of the second degree).

Then divide both parts by `cos x \ne 0` - for the first case, and by `cos^2 x \ne 0` - for the second. We obtain equations for `tg x`: `a tg x+b=0` and `a tg^2 x + b tg x +c =0`, which need to be solved using known methods.

Example. Solve the equation: `2 sin^2 x+sin x cos x - cos^2 x=1`.

Solution. Let's write the right side as `1=sin^2 x+cos^2 x`:

`2 sin^2 x+sin x cos x — cos^2 x=` `sin^2 x+cos^2 x`,

`2 sin^2 x+sin x cos x — cos^2 x -` ` sin^2 x — cos^2 x=0`

`sin^2 x+sin x cos x — 2 cos^2 x=0`.

This is a homogeneous trigonometric equation of the second degree, we divide its left and right sides by `cos^2 x \ne 0`, we get:

`\frac (sin^2 x)(cos^2 x)+\frac(sin x cos x)(cos^2 x) — \frac(2 cos^2 x)(cos^2 x)=0`

`tg^2 x+tg x — 2=0`. Let's introduce the replacement `tg x=t`, resulting in `t^2 + t - 2=0`. The roots of this equation are `t_1=-2` and `t_2=1`. Then:

1. `tg x=-2`, `x_1=arctg (-2)+\pi n`, `n \in Z`
2. `tg x=1`, `x=arctg 1+\pi n`, `x_2=\pi/4+\pi n`, ` n \in Z`.

Answer. `x_1=arctg (-2)+\pi n`, `n \in Z`, `x_2=\pi/4+\pi n`, `n \in Z`.

Moving to Half Angle

Example. Solve the equation: `11 sin x - 2 cos x = 10`.

Solution. Let's apply the double angle formulas, resulting in: `22 sin (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 sin^2 x/2=` `10 sin^2 x/2 +10 cos^2 x/2`

`4 tg^2 x/2 — 11 tg x/2 +6=0`

Applying the algebraic method described above, we obtain:

1. `tg x/2=2`, `x_1=2 arctg 2+2\pi n`, `n \in Z`,
2. `tg x/2=3/4`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.

Answer. `x_1=2 arctg 2+2\pi n, n \in Z`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.

Introduction of auxiliary angle

In the trigonometric equation `a sin x + b cos x =c`, where a,b,c are coefficients and x is a variable, divide both sides by `sqrt (a^2+b^2)`:

`\frac a(sqrt (a^2+b^2)) sin x +` `\frac b(sqrt (a^2+b^2)) cos x =` `\frac c(sqrt (a^2) +b^2))`.

The coefficients on the left side have the properties of sine and cosine, namely the sum of their squares is equal to 1 and their modules are not greater than 1. Let us denote them as follows: `\frac a(sqrt (a^2+b^2))=cos \varphi` , ` \frac b(sqrt (a^2+b^2)) =sin \varphi`, `\frac c(sqrt (a^2+b^2))=C`, then:

`cos \varphi sin x + sin \varphi cos x =C`.

Let's take a closer look at the following example:

Example. Solve the equation: `3 sin x+4 cos x=2`.

Solution. Divide both sides of the equality by `sqrt (3^2+4^2)`, we get:

`\frac (3 sin x) (sqrt (3^2+4^2))+` `\frac(4 cos x)(sqrt (3^2+4^2))=` `\frac 2(sqrt (3^2+4^2))`

`3/5 sin x+4/5 cos x=2/5`.

Let's denote `3/5 = cos \varphi` , `4/5=sin \varphi`. Since `sin \varphi>0`, `cos \varphi>0`, then we take `\varphi=arcsin 4/5` as an auxiliary angle. Then we write our equality in the form:

`cos \varphi sin x+sin \varphi cos x=2/5`

Applying the formula for the sum of angles for the sine, we write our equality in the following form:

`sin (x+\varphi)=2/5`,

`x+\varphi=(-1)^n arcsin 2/5+ \pi n`, `n \in Z`,

`x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.

Answer. `x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.

Fractional rational trigonometric equations

These are equalities with fractions whose numerators and denominators contain trigonometric functions.

Example. Solve the equation. `\frac (sin x)(1+cos x)=1-cos x`.

Solution. Multiply and divide the right side of the equality by `(1+cos x)`. As a result we get:

`\frac (sin x)(1+cos x)=` `\frac ((1-cos x)(1+cos x))(1+cos x)`

`\frac (sin x)(1+cos x)=` `\frac (1-cos^2 x)(1+cos x)`

`\frac (sin x)(1+cos x)=` `\frac (sin^2 x)(1+cos x)`

`\frac (sin x)(1+cos x)-` `\frac (sin^2 x)(1+cos x)=0`

`\frac (sin x-sin^2 x)(1+cos x)=0`

Considering that the denominator cannot be equal to zero, we get `1+cos x \ne 0`, `cos x \ne -1`, ` x \ne \pi+2\pi n, n \in Z`.

Let's equate the numerator of the fraction to zero: `sin x-sin^2 x=0`, `sin x(1-sin x)=0`. Then `sin x=0` or `1-sin x=0`.

1. `sin x=0`, `x=\pi n`, `n \in Z`
2. `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.

Given that ` x \ne \pi+2\pi n, n \in Z`, the solutions are `x=2\pi n, n \in Z` and `x=\pi /2+2\pi n` , `n \in Z`.

Answer. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.

Trigonometry, and trigonometric equations in particular, are used in almost all areas of geometry, physics, and engineering. Studying begins in the 10th grade, there are always tasks for the Unified State Exam, so try to remember all the formulas of trigonometric equations - they will definitely be useful to you!

However, you don’t even need to memorize them, the main thing is to understand the essence and be able to derive it. It's not as difficult as it seems. See for yourself by watching the video.

When solving many mathematical problems, especially those that occur before grade 10, the order of actions performed that will lead to the goal is clearly defined. Such problems include, for example, linear and quadratic equations, linear and quadratic inequalities, fractional equations and equations that reduce to quadratic ones. The principle of successfully solving each of the mentioned problems is as follows: you need to establish what type of problem you are solving, remember the necessary sequence of actions that will lead to the desired result, i.e. answer and follow these steps.

It is obvious that success or failure in solving a particular problem depends mainly on how correctly the type of equation being solved is determined, how correctly the sequence of all stages of its solution is reproduced. Of course, in this case it is necessary to have the skills to perform identical transformations and calculations.

The situation is different with trigonometric equations. It is not at all difficult to establish the fact that the equation is trigonometric. Difficulties arise when determining the sequence of actions that would lead to the correct answer.

It is sometimes difficult to determine its type based on the appearance of an equation. And without knowing the type of equation, it is almost impossible to choose the right one from several dozen trigonometric formulas.

To solve a trigonometric equation, you need to try:

1. bring all functions included in the equation to “the same angles”;
2. bring the equation to “identical functions”;
3. factor the left side of the equation, etc.

Let's consider basic methods for solving trigonometric equations.

I. Reduction to the simplest trigonometric equations

Solution diagram

Step 1. Express a trigonometric function in terms of known components.

Step 2. Find the function argument using the formulas:

cos x = a; x = ±arccos a + 2πn, n ЄZ.

sin x = a; x = (-1) n arcsin a + πn, n Є Z.

tan x = a; x = arctan a + πn, n Є Z.

ctg x = a; x = arcctg a + πn, n Є Z.

Step 3. Find the unknown variable.

Example.

2 cos(3x – π/4) = -√2.

Solution.

1) cos(3x – π/4) = -√2/2.

2) 3x – π/4 = ±(π – π/4) + 2πn, n Є Z;

3x – π/4 = ±3π/4 + 2πn, n Є Z.

3) 3x = ±3π/4 + π/4 + 2πn, n Є Z;

x = ±3π/12 + π/12 + 2πn/3, n Є Z;

x = ±π/4 + π/12 + 2πn/3, n Є Z.

Answer: ±π/4 + π/12 + 2πn/3, n Є Z.

II. Variable replacement

Solution diagram

Step 1. Reduce the equation to algebraic form with respect to one of the trigonometric functions.

Step 2. Denote the resulting function by the variable t (if necessary, introduce restrictions on t).

Step 3. Write down and solve the resulting algebraic equation.

Step 4. Make a reverse replacement.

Step 5. Solve the simplest trigonometric equation.

Example.

2cos 2 (x/2) – 5sin (x/2) – 5 = 0.

Solution.

1) 2(1 – sin 2 (x/2)) – 5sin (x/2) – 5 = 0;

2sin 2 (x/2) + 5sin (x/2) + 3 = 0.

2) Let sin (x/2) = t, where |t| ≤ 1.

3) 2t 2 + 5t + 3 = 0;

t = 1 or e = -3/2, does not satisfy the condition |t| ≤ 1.

4) sin(x/2) = 1.

5) x/2 = π/2 + 2πn, n Є Z;

x = π + 4πn, n Є Z.

Answer: x = π + 4πn, n Є Z.

III. Equation order reduction method

Solution diagram

Step 1. Replace this equation with a linear one, using the formula for reducing the degree:

sin 2 x = 1/2 · (1 – cos 2x);

cos 2 x = 1/2 · (1 + cos 2x);

tg 2 x = (1 – cos 2x) / (1 + cos 2x).

Step 2. Solve the resulting equation using methods I and II.

Example.

cos 2x + cos 2 x = 5/4.

Solution.

1) cos 2x + 1/2 · (1 + cos 2x) = 5/4.

2) cos 2x + 1/2 + 1/2 · cos 2x = 5/4;

3/2 cos 2x = 3/4;

2x = ±π/3 + 2πn, n Є Z;

x = ±π/6 + πn, n Є Z.

Answer: x = ±π/6 + πn, n Є Z.

IV. Homogeneous equations

Solution diagram

Step 1. Reduce this equation to the form

a) a sin x + b cos x = 0 (homogeneous equation of the first degree)

or to the view

b) a sin 2 x + b sin x · cos x + c cos 2 x = 0 (homogeneous equation of the second degree).

Step 2. Divide both sides of the equation by

a) cos x ≠ 0;

b) cos 2 x ≠ 0;

and get the equation for tan x:

a) a tan x + b = 0;

b) a tan 2 x + b arctan x + c = 0.

Step 3. Solve the equation using known methods.

Example.

5sin 2 x + 3sin x cos x – 4 = 0.

Solution.

1) 5sin 2 x + 3sin x · cos x – 4(sin 2 x + cos 2 x) = 0;

5sin 2 x + 3sin x · cos x – 4sin² x – 4cos 2 x = 0;

sin 2 x + 3sin x · cos x – 4cos 2 x = 0/cos 2 x ≠ 0.

2) tg 2 x + 3tg x – 4 = 0.

3) Let tg x = t, then

t 2 + 3t – 4 = 0;

t = 1 or t = -4, which means

tg x = 1 or tg x = -4.

From the first equation x = π/4 + πn, n Є Z; from the second equation x = -arctg 4 + πk, k Є Z.

Answer: x = π/4 + πn, n Є Z; x = -arctg 4 + πk, k Є Z.

V. Method of transforming an equation using trigonometric formulas

Solution diagram

Step 1. Using all possible trigonometric formulas, reduce this equation to an equation solved by methods I, II, III, IV.

Step 2. Solve the resulting equation using known methods.

Example.

sin x + sin 2x + sin 3x = 0.

Solution.

1) (sin x + sin 3x) + sin 2x = 0;

2sin 2x cos x + sin 2x = 0.

2) sin 2x (2cos x + 1) = 0;

sin 2x = 0 or 2cos x + 1 = 0;

From the first equation 2x = π/2 + πn, n Є Z; from the second equation cos x = -1/2.

We have x = π/4 + πn/2, n Є Z; from the second equation x = ±(π – π/3) + 2πk, k Є Z.

As a result, x = π/4 + πn/2, n Є Z; x = ±2π/3 + 2πk, k Є Z.

Answer: x = π/4 + πn/2, n Є Z; x = ±2π/3 + 2πk, k Є Z.

The ability and skill to solve trigonometric equations is very important, their development requires significant effort, both on the part of the student and on the part of the teacher.

Many problems of stereometry, physics, etc. are associated with the solution of trigonometric equations. The process of solving such problems embodies many of the knowledge and skills that are acquired by studying the elements of trigonometry.

Trigonometric equations occupy an important place in the process of learning mathematics and personal development in general.

Still have questions? Don't know how to solve trigonometric equations?
To get help from a tutor, register.
The first lesson is free!

website, when copying material in full or in part, a link to the source is required.

Solving a trigonometric equation consists of two stages: equation transformation to get it simplest type (see above) and solutionthe resulting simplest trigonometric equation. There are seven basic methods for solving trigonometric equations.

1. Algebraic method.

(variable replacement and substitution method).

2. Factorization.

Example 1. Solve the equation: sin x+cos x = 1 .

Solution. Let's move all the terms of the equation to the left:

Sin x+cos x – 1 = 0 ,

Let us transform and factorize the expression in

Left side of the equation:

Example 2. Solve the equation: cos 2 x+ sin x cos x = 1.

Solution: cos 2 x+ sin x cos x– sin 2 x– cos 2 x = 0 ,

Sin x cos x– sin 2 x = 0 ,

Sin x· (cos x– sin x ) = 0 ,

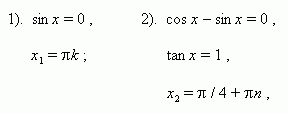
Example 3. Solve the equation: cos 2 x–cos 8 x+ cos 6 x = 1.

Solution: cos 2 x+ cos 6 x= 1 + cos 8 x,

2 cos 4 x cos 2 x= 2cos² 4 x ,

Cos 4 x · (cos 2 x– cos 4 x) = 0 ,

Cos 4 x · 2 sin 3 x sin x = 0 ,

1). cos 4 x= 0, 2). sin 3 x= 0, 3). sin x = 0 ,

4. Transition to half angle.

Let's look at this method using an example:

EXAMPLE Solve equation: 3 sin x– 5 cos x = 7.

Solution: 6 sin ( x/ 2) cos ( x/ 2) – 5 cos² ( x/ 2) + 5 sin² ( x/ 2) =

7 sin² ( x/ 2) + 7 cos² ( x/ 2) ,

2 sin² ( x/ 2) – 6 sin ( x/ 2) cos ( x/ 2) + 12 cos² ( x/ 2) = 0 ,

tan²( x/ 2) – 3 tan ( x/ 2) + 6 = 0 ,

. . . . . . . . . .

5. Introduction of an auxiliary angle.

Consider an equation of the form:

a sin x + b cos x = c ,

Where a, b, c– coefficients;x– unknown.

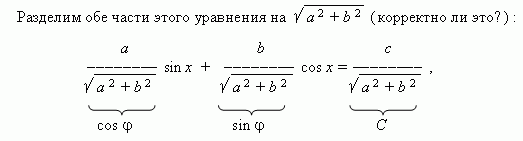
Now the coefficients of the equation have the properties of sine and cosine, namely: modulus (absolute value) of each of which no more than 1, and the sum of their squares is 1. Then we can denote them accordingly How cos and sin (here - so-called auxiliary angle), Andtake our equation