Examples:
\(\log_(2)(x) = 32\)
\(\log_3x=\log_39\)
\(\log_3((x^2-3))=\log_3((2x))\)
\(\log_(x+1)((x^2+3x-7))=2\)
\(\lg^2((x+1))+10=11 \lg((x+1))\)
How to solve logarithmic equations:
When solving a logarithmic equation, you should strive to transform it to the form \(\log_a(f(x))=\log_a(g(x))\), and then make the transition to \(f(x)=g(x) \).
\(\log_a(f(x))=\log_a(g(x))\) \(⇒\) \(f(x)=g(x)\).
Example:\(\log_2(x-2)=3\)
|
Solution: |
ODZ: |
Very important! This transition can only be made if:
You have written for the original equation, and at the end you will check whether those found are included in the DL. If this is not done, extra roots may appear, which means a wrong decision.
The number (or expression) on the left and right is the same;
The logarithms on the left and right are “pure”, that is, there should be no multiplications, divisions, etc. – only single logarithms on either side of the equal sign.
For example:
Note that equations 3 and 4 can be easily solved by applying required properties logarithms.
Example . Solve the equation \(2\log_8x=\log_82.5+\log_810\)
Solution :
|
Let's write the ODZ: \(x>0\). |
||
|
\(2\log_8x=\log_82.5+\log_810\) ODZ: \(x>0\) |
On the left in front of the logarithm is the coefficient, on the right is the sum of the logarithms. This bothers us. Let's move the two to the exponent \(x\) according to the property: \(n \log_b(a)=\log_b(a^n)\). Let us represent the sum of logarithms as one logarithm according to the property: \(\log_ab+\log_ac=\log_a(bc)\) |
|
|
\(\log_8(x^2)=\log_825\) |
We reduced the equation to the form \(\log_a(f(x))=\log_a(g(x))\) and wrote down the ODZ, which means we can move to the form \(f(x)=g(x)\ ). |
|
|
It worked. We solve it and get the roots. |
||
|
\(x_1=5\) \(x_2=-5\) |
We check whether the roots are suitable for ODZ. To do this, in \(x>0\) instead of \(x\) we substitute \(5\) and \(-5\). This operation can be performed orally. |
|
|
\(5>0\), \(-5>0\) |
The first inequality is true, the second is not. This means that \(5\) is the root of the equation, but \(-5\) is not. We write down the answer. |
Answer : \(5\)
Example : Solve the equation \(\log^2_2(x)-3 \log_2(x)+2=0\)
Solution :
|
Let's write the ODZ: \(x>0\). |
||
|
\(\log^2_2(x)-3 \log_2(x)+2=0\) ODZ: \(x>0\) |
A typical equation solved using . Replace \(\log_2x\) with \(t\). |
|
|
\(t=\log_2x\) |
||
|
We got the usual one. We are looking for its roots. |
||
|
\(t_1=2\) \(t_2=1\) |
Making a reverse replacement |
|
|
\(\log_2(x)=2\) \(\log_2(x)=1\) |
We transform the right-hand sides, representing them as logarithms: \(2=2 \cdot 1=2 \log_22=\log_24\) and \(1=\log_22\) |
|
|
\(\log_2(x)=\log_24\) \(\log_2(x)=\log_22 \) |
Now our equations are \(\log_a(f(x))=\log_a(g(x))\), and we can transition to \(f(x)=g(x)\). |
|
|
\(x_1=4\) \(x_2=2\) |
We check the correspondence of the roots of the ODZ. To do this, substitute \(4\) and \(2\) into the inequality \(x>0\) instead of \(x\). |
|
|
\(4>0\) \(2>0\) |
Both inequalities are true. This means that both \(4\) and \(2\) are roots of the equation. |
Answer : \(4\); \(2\).
On this lesson we will repeat the main ones theoretical facts about logarithms and consider solving the simplest logarithmic equations.
Let us remind you central definition- definition of logarithm. It is related to the decision exponential equation. This equation has a single root, it is called the logarithm of b to base a:
Definition:
The logarithm of b to base a is the exponent to which base a must be raised to get b.
Let us remind you basic logarithmic identity .
The expression (expression 1) is the root of the equation (expression 2). Substitute the value x from expression 1 instead of x into expression 2 and get the main logarithmic identity:
So we see that each value is associated with a value. We denote b by x(), c by y, and thus obtain a logarithmic function:
For example: ![]()
Let's remember the basic properties logarithmic function.
Let us pay attention once again, here, since under the logarithm there can be a strictly positive expression, as the base of the logarithm.

Rice. 1. Graph of a logarithmic function in different bases
The graph of the function at is shown in black. Rice. 1. If the argument increases from zero to infinity, the function increases from minus to plus infinity.
The graph of the function at is shown in red. Rice. 1.
Properties of this function:
Scope: ;
Range of values: ;
The function is monotonic throughout its entire domain of definition. When monotonically (strictly) increases, higher value the argument corresponds to the larger value of the function. When monotonically (strictly) decreases, the larger value of the argument corresponds to lower value functions.
The properties of the logarithmic function are the key to solving a variety of logarithmic equations.
Let's consider the simplest logarithmic equation; all other logarithmic equations, as a rule, are reduced to this form.
Since the bases of logarithms and the logarithms themselves are equal, the functions under the logarithm are also equal, but we must not miss the domain of definition. The logarithm can only stand positive number, we have:
We found out that the functions f and g are equal, so it is enough to choose any one inequality to comply with the ODZ.
Thus, we have a mixed system in which there is an equation and an inequality:
![]()
As a rule, it is not necessary to solve an inequality; it is enough to solve the equation and substitute the found roots into the inequality, thus performing a check.
Let us formulate a method for solving the simplest logarithmic equations:
Equalize the bases of logarithms;
Equate sublogarithmic functions;
Perform check.
Let's look at specific examples.
Example 1 - solve the equation:
The bases of logarithms are initially equal, we have the right to equate sublogarithmic expressions, do not forget about the ODZ, we choose the first logarithm to compose the inequality:
![]()
![]()
Example 2 - solve the equation:
![]()
This equation differs from the previous one in that the bases of the logarithms are less than one, but this does not affect the solution in any way:
![]()
Let's find the root and substitute it into the inequality:
![]()
We received an incorrect inequality, which means that the found root does not satisfy the ODZ.
Example 3 - solve the equation:
The bases of logarithms are initially equal, we have the right to equate sublogarithmic expressions, do not forget about the ODZ, we choose the second logarithm to compose the inequality:
Let's find the root and substitute it into the inequality:
![]()
![]()
Obviously, only the first root satisfies the ODZ.
Logarithmic expressions, solving examples. In this article we will look at problems related to solving logarithms. The tasks ask the question of finding the meaning of an expression. It should be noted that the concept of logarithm is used in many tasks and understanding its meaning is extremely important. As for the Unified State Exam, the logarithm is used when solving equations, in applied problems, also in tasks related to the study of functions.
Let us give examples to understand the very meaning of the logarithm:
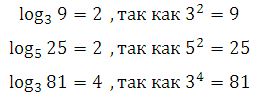

Basic logarithmic identity:

Properties of logarithms that must always be remembered:

*Logarithm of the product equal to the sum logarithms of factors.
* * *

*Logarithm of the quotient (fraction) equal to the difference logarithms of factors.
* * *
![]()
*Logarithm of degree equal to the product exponent by the logarithm of its base.
* * *

*Transition to a new foundation
* * *
More properties:

* * *
The calculation of logarithms is closely related to the use of properties of exponents.
Let's list some of them:
The essence of this property lies in the fact that when transferring the numerator to the denominator and vice versa, the sign of the exponent changes to the opposite. For example:

A corollary from this property:
* * *
![]()
When raising a power to a power, the base remains the same, but the exponents are multiplied.
* * *
As you have seen, the concept of a logarithm itself is simple. The main thing is what is needed good practice, which gives a certain skill. Of course, knowledge of formulas is required. If the skill in converting elementary logarithms has not been developed, then when solving simple tasks It's easy to make a mistake.
Practice, solve the simplest examples from the mathematics course first, then move on to more complex ones. In the future, I will definitely show how “ugly” logarithms are solved; these won’t appear on the Unified State Examination, but they are of interest, don’t miss them!
That's all! Good luck to you!
Sincerely, Alexander Krutitskikh
P.S: I would be grateful if you tell me about the site on social networks.
Preparation for the final test in mathematics includes an important section - “Logarithms”. Tasks from this topic are necessarily contained in the Unified State Examination. Experience from past years shows that logarithmic equations have caused difficulties for many schoolchildren. Therefore, students with different levels preparation.
Pass the certification test successfully using the Shkolkovo educational portal!
In preparation for the unified state exam high school graduates require a reliable source that provides the most complete and accurate information for a successful solution test problems. However, the textbook is not always at hand, and searching necessary rules and formulas on the Internet often takes time.
The Shkolkovo educational portal allows you to prepare for the Unified State Exam anywhere at any time. Our website offers the most convenient approach to repeating and assimilating a large amount of information on logarithms, as well as with one and several unknowns. Start with easy equations. If you cope with them without difficulty, move on to more complex ones. If you have trouble solving a particular inequality, you can add it to your Favorites so you can return to it later.
Find necessary formulas To complete the task, you can repeat special cases and methods for calculating the root of a standard logarithmic equation by looking at the “Theoretical Help” section. Shkolkovo teachers collected, systematized and outlined everything necessary for successful completion materials in the simplest and most understandable form.
In order to easily cope with tasks of any complexity, on our portal you can familiarize yourself with the solution of some standard logarithmic equations. To do this, go to the “Catalogues” section. We present large number examples, including profile equations Unified State Exam level in mathematics.
Students from schools throughout Russia can use our portal. To start classes, simply register in the system and start solving equations. To consolidate the results, we advise you to return to the Shkolkovo website daily.
Logarithmic equations. We continue to consider problems from Part B of the Unified State Examination in mathematics. We have already examined solutions to some equations in the articles “”, “”. In this article we will look at logarithmic equations. I’ll say right away that there will be no complex transformations when solving such equations on the Unified State Exam. They are simple.
It is enough to know and understand the basic logarithmic identity, to know the properties of the logarithm. Please note that after solving a solution, you MUST do a check - substitute the resulting value into original equation and calculate, the result should be a correct equality.
Definition:
The logarithm of a number to base b is the exponent,to which b must be raised to obtain a.


For example:
Log 3 9 = 2, since 3 2 = 9
Properties of logarithms:

Special cases of logarithms:

Let's solve problems. In the first example we will do a check. Do the subsequent check yourself.
Find the root of the equation: log 3 (4–x) = 4
Since log b a = x b x = a, then
3 4 = 4 – x
x = 4 – 81
x = – 77
Examination:
log 3 (4–(–77)) = 4
log 3 81 = 4
3 4 = 81 Correct.
Answer: – 77
Decide for yourself:
Find the root of the equation: log 2 (4 – x) = 7
Find the root of the equation log 5(4 + x) = 2
We use the basic logarithmic identity.
Since log a b = x b x = a, then
5 2 = 4 + x
x =5 2 – 4
x = 21
Examination:
log 5 (4 + 21) = 2
log 5 25 = 2
5 2 = 25 Correct.
Answer: 21
Find the root of the equation log 3 (14 – x) = log 3 5.
Takes place next property, its meaning is as follows: if on the left and right sides of the equation we have logarithms with the same basis, then we can equate the expressions under the signs of logarithms.
14 – x = 5
x=9
Do a check.
Answer: 9
Decide for yourself:
Find the root of the equation log 5 (5 – x) = log 5 3.
Find the root of the equation: log 4 (x + 3) = log 4 (4x – 15).
If log c a = log c b, then a = b
x + 3 = 4x – 15
3x = 18
x = 6
Do a check.
Answer: 6
Find the root of the equation log 1/8 (13 – x) = – 2.
(1/8) –2 = 13 – x
8 2 = 13 – x
x = 13 – 64
x = – 51
Do a check.
A small addition - the property is used here
degrees ().
Answer: – 51
Decide for yourself:
Find the root of the equation: log 1/7 (7 – x) = – 2
Find the root of the equation log 2 (4 – x) = 2 log 2 5.
Let's transform right side. Let's use the property:
log a b m = m∙log a b
log 2 (4 – x) = log 2 5 2
If log c a = log c b, then a = b
4 – x = 5 2
4 – x = 25
x = – 21
Do a check.
Answer: – 21
Decide for yourself:
Find the root of the equation: log 5 (5 – x) = 2 log 5 3
Solve the equation log 5 (x 2 + 4x) = log 5 (x 2 + 11)
If log c a = log c b, then a = b
x 2 + 4x = x 2 + 11
4x = 11
x = 2.75
Do a check.
Answer: 2.75
Decide for yourself:
Find the root of the equation log 5 (x 2 + x) = log 5 (x 2 + 10).
Solve the equation log 2 (2 – x) = log 2 (2 – 3x) +1.
Required with right side equations obtain an expression of the form:
log 2 (......)
We represent 1 as a base 2 logarithm:
1 = log 2 2
log c (ab) = log c a + log c b
log 2 (2 – x) = log 2 (2 – 3x) + log 2 2
We get:
log 2 (2 – x) = log 2 2 (2 – 3x)
If log c a = log c b, then a = b, then
2 – x = 4 – 6x
5x = 2
x = 0.4
Do a check.
Answer: 0.4
Decide for yourself: Next you need to decide quadratic equation. By the way,
the roots are 6 and – 4.
Root "–4" is not a solution since the base of the logarithm must be greater than zero, and when "– 4" it is equal to " – 5". The solution is root 6.Do a check.
Answer: 6.
R eat on your own:
Solve the equation log x –5 49 = 2. If the equation has more than one root, answer with the smaller one.
As you have seen, no complicated transformations with logarithmic equationsNo. It is enough to know the properties of the logarithm and be able to apply them. IN Unified State Examination tasks related to transformation logarithmic expressions, more serious transformations are performed and deeper solution skills are required. We will look at such examples, don’t miss them!Good luck to you!!!
Sincerely, Alexander Krutitskikh.
P.S: I would be grateful if you tell me about the site on social networks.








