Circumference is a figure consisting of all points of the plane located at a given distance from a given point. This point is called center circle, and the segment connecting the center with any point on the circle is radius circles.
The part of the plane bounded by a circle is called all around.
Circular sector or just sector is the part of a circle bounded by an arc and two radii connecting the ends of the arc to the center of the circle.
Segment is the part of a circle bounded by an arc and a chord subtending it.
Basic terms
Tangent
A straight line with only one common point is called tangent to a circle, and their common point is called point of contact straight line and circle.
Tangent Properties
A tangent to a circle is perpendicular to the radius drawn to the point of tangency.
Segments of tangents to a circle drawn from one point are equal and make equal angles with a straight line passing through this point and the center of the circle.
Chord
A segment connecting two points on a circle is called its chord. A chord passing through the center of a circle is called diameter
Properties of chords
The diameter (radius), perpendicular to the chord, divides this chord and both arcs subtended by it in half. The converse theorem is also true: if the diameter (radius) bisects a chord, then it is perpendicular to this chord.
The arcs contained between parallel chords are equal.
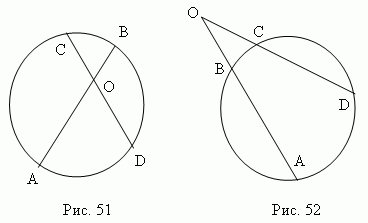
If two chords of a circle, AB And CD intersect at a point M, then the product of segments of one chord is equal to the product of segments of another chord: AM MB = CM MD.
Properties of a circle
A straight line may not have common points with a circle; have one common point with the circle ( tangent); have two points in common with her ( secant).
Through three points that do not lie on the same line, you can draw a circle, and only one.
The point of contact of two circles lies on the line connecting their centers.

Tangent and secant theorem
If a tangent and a secant are drawn from a point lying outside the circle, then the square of the length of the tangent is equal to the product of the secant and its outer part: M.C. 2 = MA MB.
The secant theorem
If two secants are drawn from a point lying outside the circle, then the product of one secant and its external part is equal to the product of the other secant and its external part. MA MB = MC MD.
Angles in a circle
Central An angle in a circle is a plane angle with a vertex at its center.
An angle whose vertex lies on a circle and whose sides intersect this circle is called inscribed angle.
Any two points on a circle divide it into two parts. Each of these parts is called arc circles. The measure of an arc can be the measure of its corresponding central angle.
The arc is called semicircle, if the segment connecting its ends is a diameter.
Properties of angles associated with a circle
An inscribed angle is either equal to half of its corresponding central angle or complements half of this angle to 180°.

Angles inscribed in the same circle and resting on the same arc are equal.
The inscribed angle subtended by the diameter is 90°.
The angle formed by a tangent to a circle and a secant drawn through the point of contact is equal to half the arc enclosed between its sides.

Lengths and areas
Circumference C radius R calculated by the formula:
C= 2 R.
Square S circle radius R calculated by the formula:
S= R 2 .
Inscribed and circumscribed circles
Circle and triangle 
the center of the incircle is the point of intersection of the bisectors of the triangle, its radius r calculated by the formula:
r = ,
Where S is the area of the triangle, and - semiperimeter;
R= ,
R= ;
here a, b, c are the sides of the triangle, is the angle opposite the side a, S- area of the triangle;
the center of the circle circumscribed about a right triangle lies at the middle of the hypotenuse;
The centers of the circumscribed and inscribed circles of a triangle coincide only if this triangle is regular.
Circle and quadrilaterals
a circle can be described around a convex quadrilateral if and only if the sum of its internal opposite angles is equal to 180°:
180°;
A circle can be inscribed in a quadrilateral if and only if its sums of opposite sides are equal:
a + c = b + d;
a parallelogram can be described as a circle if and only if it is a rectangle;
it is possible to describe a circle around a trapezoid if and only if this trapezoid is isosceles; the center of the circle lies at the intersection of the axis of symmetry of the trapezoid with the perpendicular bisector to the side;
A circle can be inscribed in a parallelogram if and only if it is a rhombus.
Circle- a geometric figure consisting of all points of the plane located at a given distance from a given point.
This point (O) is called center of the circle.
Circle radius- this is a segment connecting the center with any point on the circle. All radii have the same length (by definition).
Chord- a segment connecting two points on a circle. A chord passing through the center of a circle is called diameter. The center of a circle is the midpoint of any diameter.
Any two points on a circle divide it into two parts. Each of these parts is called arc of a circle. The arc is called semicircle, if the segment connecting its ends is a diameter.
The length of a unit semicircle is denoted by π
.
The sum of the degree measures of two arcs of a circle with common ends is equal to 360º.
The part of the plane bounded by a circle is called all around.
Circular sector- a part of a circle bounded by an arc and two radii connecting the ends of the arc to the center of the circle. The arc that limits the sector is called arc of the sector.
Two circles having a common center are called concentric.
Two circles intersecting at right angles are called orthogonal.
The relative position of a straight line and a circle
- If the distance from the center of the circle to the straight line is less than the radius of the circle ( d), then the straight line and the circle have two common points. In this case the line is called secant in relation to the circle.
- If the distance from the center of the circle to the straight line is equal to the radius of the circle, then the straight line and the circle have only one common point. This line is called tangent to the circle, and their common point is called point of tangency between a line and a circle.
- If the distance from the center of the circle to the straight line is greater than the radius of the circle, then the straight line and the circle have no common points .
Central and inscribed angles
Central angle is an angle with its vertex at the center of the circle.
Inscribed angle- an angle whose vertex lies on a circle and whose sides intersect the circle.
Inscribed angle theorem
An inscribed angle is measured by the half of the arc on which it subtends.
- Corollary 1.
Inscribed angles subtending the same arc are equal. - Corollary 2.
An inscribed angle subtended by a semicircle is a right angle.
Theorem on the product of segments of intersecting chords.
If two chords of a circle intersect, then the product of the segments of one chord is equal to the product of the segments of the other chord.
Basic formulas
- Circumference:
- Circular arc length:
- Diameter:
- Circular arc length:
Where α - degree measure of the length of a circular arc)
- Circle area:
- Area of the circular sector:
Equation of a circle
- In a rectangular coordinate system, the equation of a circle with radius is r centered at a point C(x o;y o) has the form:
- The equation of a circle of radius r with center at the origin has the form:
Geometric locus of points. Median perpendicular. Angle bisector.
Circle. Circle . Center of the circle. Radius. Arc. Secant. Chord.
Diameter. Tangent and its properties. Segment. Sector. Angles in a circle.
Arc length . Radian. Relationships between the elements of a circle.
Geometric locus – this is a set everyone points, satisfying given a certain conditions.
Example 1. The median perpendicular of any segment is a geometric
place of points (i.e. the set of all points), equidistant from
ends of this segment. Let PO AB and AO = OB:
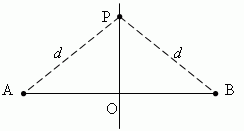
Then, the distances from any point P , lying on the median perpendicular PO, to ends A and B of segment AB same and equald.
Thus, each point of the median perpendicular segment has the following property: it is equidistant from the ends of the segment.
Example 2. Angle bisector There is locus of points equidistant from its sides .
Example 3 . A circle is the locus of points (i.e. many quality
all points), equidistant from its center ( in Fig. Bye zana alone
from these points – A).

Circle - This locus of points (i.e. the set of all points) on the plane ,equidistant from one pointcalled the center of the circle. A segment connecting the center of a circle with any point on it is called radius and is designatedr or R. The part of the plane bounded by a circle is called all around. Part of a circle (
A m B, Fig.39) called arc. Straight PQpassing through points M And N circles (Fig. 39 ), called secant and its segment MN , lying inside the circle - chord.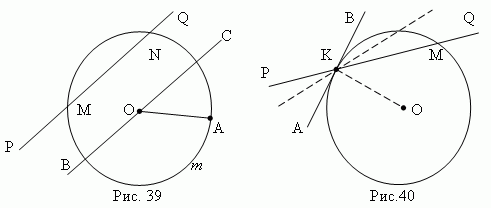
A chord passing through the center of a circle (for example,
B.C. , Fig. 39), is calleddiameter and is designated d or D.Diameter is the largest chord equal to two radii (d= 2 r).
Tangent. Suppose the secant PQ (Fig. 40) passes through the points K and M circles. Let us also assume that the point M moves along a circle, approaching a point K. Then the secant PQ will change its position, rotating around the point K . As the point approaches M to point K secant PQ will tend to some limiting position AB. Straight AB called tangent to the circle at a point K. Point K called point of contact. The tangent and the circle have only one common point - the point of contact.
Properties of a tangent.
1) TOthe tangent to the circle is perpendicular to the radius drawn to the point of contact(AB OK, Fig.40) .
2) From a point outside the circle, two tangents can be drawn to
the same circle; their segments are equal (Fig. 41).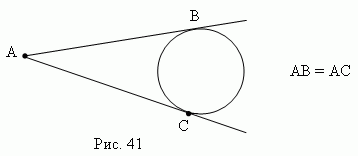
Segment - this is part of a circle, bounded by an arc ACB and the corresponding chord AB (Fig. 42). Perpendicular length CD drawn from the middle of the chord AB until it intersects with the arc ACB , called height segment.
Sector – is the part of a circle bounded by an arc A m B and two radii OA and OB, drawn to the ends of this arc (Fig. 43).
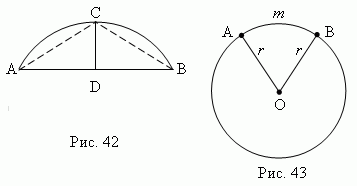
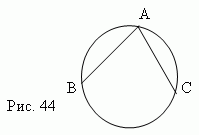
Angles in a circle. Central angle – the angle formed by two radii ( A.O.B. Fig.43). Inscribed angle– the angle formed by two chords AB and AC , drawn from their one common point ( BA C, fig.44). Circumscribed angle– angle formed by two tangents AB and AC drawn from one common point ( BAC, Fig. 41).
Arc length of a circle is proportional to its radiusr and the corresponding central angle :
l = r
Thus, if we know the arc length
l and radius r, then the value of the corresponding central angle can be determined by their relation: = l/r.This formula is the basis for determining radian measurement corners So, ifl = r, That = 1 and we say that the angle equal to 1 radian (this is denoted by: = 1 glad). Thus, we have the following definition of the radian as a unit of measurement of angles: radian is the central angle ( AOB, Fig.43), whose arc length is equal to its radius (A m B = AO, Fig.43). So, The radian measure of any angle is the ratio of the length of an arc drawn with an arbitrary radius and enclosed between the sides of this angle to its radius. Specifically, according to the arc length formula, the circumferenceCcan be expressed as follows:
Where defined as the ratioCto circle diameter 2r :
= C/ 2 r.
Irrational number; its approximate value 3.1415926…
On the other side, 2- This circular angle circle, which in the degree system of measurement is equal to 360º. In practice, it often happens that both the arc radius and the angle are unknown. In this case, the arc length can be calculated using the approximate Huygens formula:
p 2l + (2l–L) / 3 ,
where (see Fig. 42): p– arc length ACB; l– chord length AC; L– chord length AB. If the arc contains no more than 60º , the relative error of this formula does not exceed 0.5%.
Relationships between the elements of a circle. Inscribed angle (ABC, fig.45) equal to half the central angle , resting on the same arc A mC (AOC, fig.45) . That's why, all inscribed angles(Fig.45), resting on one and that one the same arc(A m C , Fig.45), are equal. And since the central angle contains the same number of degrees as its arc ( A m C ,Fig.45), then any inscribed angle is measured by half the arc on which it subtends(in our case A m C).

All inscribed angles subtending a semicircle (APB, AQB, ..., Fig. 46), straight (Prove it, please!).
Corner(AOD, Fig.47 ), formed by two chords( AB and CD), measures being the half-sum of arcs enclosed between its sides: (A n D+C m B) / 2 .

Corner(AOD, fig.48) , formed by two secants (AO and OD ), is measured by the half-difference of arcs, concluded between its parties: (A n D–B m C ) / 2. secant(CO and BO ), measured by half difference arcs enclosed between its sides: (B m C – C n D ) / 2 .
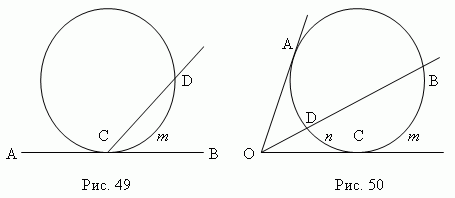
Circumscribed angle(AOC, Fig.50 ), formed by two tangents( CO and AO ), measured by the half-difference of arcs enclosed between it parties:( ABC – CDA) / 2 .
Products of segments of chords ( AB and CD , Fig.51 or Fig.52), into which they are divided by the point of intersection, are equal: AO·BO = CO·DO.
K square of a tangent is equal to the product of a secant and its outer part (fig.50): OA 2 = O B O D (prove it!). This property can be considered as a special case Fig.52.
Chord(AB , fig.53) , perpendicular to the diameter( CD ), is divided at their point of intersection O in half: AO = OB.
( Try to prove it!).
Versatile. Bisector. Sign of equality. Any triangle has three heights. Any triangle has three medians. Height. Two triangles are said to be congruent if they can be brought together by overlapping. Test for equality of triangles. Classification of triangles. A side and two adjacent angles. Each of the triangles. Median. Let's apply a triangle. Triangle. The triangles are equal. In any triangle, the medians intersect at one point.
“Basic concepts of geometry” - Equal segments have equal lengths. Construction of a triangle. Consequence. Triangle equality sign. The lines are parallel. Parallel lines. How many lines can be drawn through two points? The simplest geometric shapes. Degree measure of angle. Medians. Secant line. Angle bisector segment. An angle is a geometric figure that consists of a point and two rays. Beam and angle. Beam. The triangles are equal.
“Geometry problems” 7th grade - Measuring segments. AOB = 45. OC – bisector. MP segment. OE – bisector. ABD = 100. Section KN. Section FD. Angles. Adjacent corners. OD – bisector. Section KE. Section AC. Vertical angles. Section DF. BOC = 23. AOB = 55. Line segment AB. Measuring angles. Basic geometric information. EDK = 36. ABC = 72. Segment AD.
“Defining an angle” - Angles. Preparatory stage of the lesson. Development of logical thinking. Acute angle. Concepts of angles. Paint the inside area of the corner. Explanation of new material. Types of angles. Definition of a straight angle. Obtuse angle. The ray in the figure divides the angle. First geometry lessons. Angles. Right angle. An angle divides a plane. Get interested in the subject. Ray BM divides angle ABC into two angles. Write down the symbols for all angles.
“Isosceles triangle” - AFD – isosceles. List the congruent elements of triangles. Classification of triangles according to the size of their angles. A triangle is the simplest closed rectilinear figure. In an isosceles triangle AMK AM = AK. Test questions. A triangle with all sides equal. ABC - isosceles. A triangle is called isosceles if its two sides are equal. Isosceles triangle. Equality of triangles.
“Initial concepts of geometry” - How geometry arose. You can draw any number of different straight lines through one point. Basic geometric knowledge. Geometric information. Introduction to geometry. Points belonging to a line. Geometric terms. Segment. What does geometry study? The work of the Greek scientist Euclid. Checking the mathematical dictation. Practical conduct of direct lines. Practical tasks. Geometry. Basic geometric information.
Maintaining your privacy is important to us. For this reason, we have developed a Privacy Policy that describes how we use and store your information. Please review our privacy practices and let us know if you have any questions.
Collection and use of personal information
Personal information refers to data that can be used to identify or contact a specific person.
You may be asked to provide your personal information at any time when you contact us.
Below are some examples of the types of personal information we may collect and how we may use such information.
What personal information do we collect:
- When you submit an application on the site, we may collect various information, including your name, telephone number, email address, etc.
How we use your personal information:
- The personal information we collect allows us to contact you with unique offers, promotions and other events and upcoming events.
- From time to time, we may use your personal information to send important notices and communications.
- We may also use personal information for internal purposes, such as conducting audits, data analysis and various research in order to improve the services we provide and provide you with recommendations regarding our services.
- If you participate in a prize draw, contest or similar promotion, we may use the information you provide to administer such programs.
Disclosure of information to third parties
We do not disclose the information received from you to third parties.
Exceptions:
- If necessary - in accordance with the law, judicial procedure, in legal proceedings, and/or on the basis of public requests or requests from government bodies in the Russian Federation - to disclose your personal information. We may also disclose information about you if we determine that such disclosure is necessary or appropriate for security, law enforcement, or other public importance purposes.
- In the event of a reorganization, merger, or sale, we may transfer the personal information we collect to the applicable successor third party.
Protection of personal information
We take precautions - including administrative, technical and physical - to protect your personal information from loss, theft, and misuse, as well as unauthorized access, disclosure, alteration and destruction.
Respecting your privacy at the company level
To ensure that your personal information is secure, we communicate privacy and security standards to our employees and strictly enforce privacy practices.








