Mathematical expectation. Mathematical expectation discrete random variable X, taking a finite number of values Xi with probabilities ri, the amount is called:
Mathematical expectation continuous random variable X is called the integral of the product of its values X on the probability distribution density f(x):
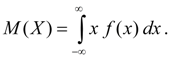(6b)
Improper integral (6 b) is assumed to be absolutely convergent (otherwise they say that the mathematical expectation M(X) does not exist). The mathematical expectation characterizes average value random variable X. Its dimension coincides with the dimension of the random variable.
Properties of mathematical expectation:
Dispersion. Variance random variable X the number is called:
The variance is scattering characteristic random variable values X relative to its average value M(X). The dimension of variance is equal to the dimension of the random variable squared. Based on the definitions of variance (8) and mathematical expectation (5) for a discrete random variable and (6) for a continuous random variable, we obtain similar expressions for the variance:
(9)
Here m = M(X).
Dispersion properties:
Standard deviation:
(11)
Since the standard deviation has the same dimension as a random variable, it is more often used as a measure of dispersion than variance.
Moments of distribution. The concepts of mathematical expectation and dispersion are special cases of a more general concept for the numerical characteristics of random variables – distribution moments. The moments of distribution of a random variable are introduced as mathematical expectations of some simple functions of a random variable. So, moment of order k relative to the point X 0 is called the mathematical expectation M(X–X 0 )k. Moments about the origin X= 0 are called initial moments and are designated:
(12)
The initial moment of the first order is the center of the distribution of the random variable under consideration:
(13)
Moments about the center of distribution X= m are called central points and are designated:
(14)
From (7) it follows that the first-order central moment is always equal to zero:
The central moments do not depend on the origin of the values of the random variable, since when shifted by a constant value WITH its center of distribution shifts by the same value WITH, and the deviation from the center does not change: X – m = (X – WITH) – (m – WITH).
Now it's obvious that dispersion- This second order central moment:
Asymmetry. Third order central moment:
(17)
serves for evaluation distribution asymmetries. If the distribution is symmetrical about the point X= m, then the third-order central moment will be equal to zero (like all central moments of odd orders). Therefore, if the third-order central moment is different from zero, then the distribution cannot be symmetric. The magnitude of asymmetry is assessed using a dimensionless asymmetry coefficient:
(18)
The sign of the asymmetry coefficient (18) indicates right-sided or left-sided asymmetry (Fig. 2).
Rice. 2. Types of distribution asymmetry.
Excess. Fourth order central moment:
(19)
serves to evaluate the so-called excess, which determines the degree of steepness (peakedness) of the distribution curve near the center of the distribution in relation to the normal distribution curve. Since for a normal distribution, the value taken as kurtosis is:
(20)
In Fig. Figure 3 shows examples of distribution curves with different kurtosis values. For normal distribution E= 0. Curves that are more peaked than normal have a positive kurtosis, those that are more flat-topped have a negative kurtosis.
Rice. 3. Distribution curves with varying degrees of steepness (kurtosis).
Higher order moments are not usually used in engineering applications of mathematical statistics.
Fashion
discrete a random variable is its most probable value. Fashion continuous a random variable is its value at which the probability density is maximum (Fig. 2). If the distribution curve has one maximum, then the distribution is called unimodal. If a distribution curve has more than one maximum, then the distribution is called multimodal. Sometimes there are distributions whose curves have a minimum rather than a maximum. Such distributions are called anti-modal. In the general case, the mode and mathematical expectation of a random variable do not coincide. In the special case, for modal, i.e. having a mode, symmetrical distribution and provided that there is a mathematical expectation, the latter coincides with the mode and center of symmetry of the distribution.
Median random variable X- this is its meaning Meh, for which equality holds: i.e. it is equally probable that the random variable X will be less or more Meh. Geometrically median is the abscissa of the point at which the area under the distribution curve is divided in half (Fig. 2). In the case of a symmetric modal distribution, the median, mode and mathematical expectation are the same.
Let's consider a discrete random variable given by the distribution law:
Expectation equals:
We see that it is much more. This can be explained by the fact that the value x= –150, much different from the other values, increased sharply when squared; the probability of this value is low (0.02). Thus, the transition from M(X) To M(X 2) made it possible to better take into account the influence on the mathematical expectation of such values of a random variable that are large in absolute value, but the probability of their occurrence is low. Of course, if the quantity had several large and unlikely values, then the transition to the quantity X 2, and even more so to the quantities , etc., would allow us to further “strengthen the role” of these large but unlikely possible values. That is why it turns out to be advisable to consider the mathematical expectation of an integer positive power of a random variable, not only discrete, but also continuous.
Definition 6.10. The initial moment of the th order of a random variable is the mathematical expectation of the quantity:
In particular:
Using these points, the formula for calculating the variance can be written differently
In addition to the moments of a random variable, it is advisable to consider the moments of deviation.
Definition 6.11. The central moment of the th order of a random variable is the mathematical expectation of the quantity.
(6.23)
In particular,
Relationships connecting the initial and central moments are easily derived. So, comparing (6.22) and (6.24), we get:
It is not difficult to prove the following relations:
Likewise:
Higher order moments are rarely used. In determining the central moments, deviations of a random variable from its mathematical expectation (center) are used. That's why moments are called central.
In determining the initial moments, deviations of a random variable are also used, but not from the mathematical expectation, but from the point whose abscissa is equal to zero, which is the origin of coordinates. That's why moments are called initial.
In the case of a continuous random variable, the initial moment of the 1st order is calculated by the formula:
(6.27)
The central moment of the th order of a continuous random variable is calculated by the formula:
(6.28)
Let us assume that the distribution of the random variable is symmetrical with respect to the mathematical expectation. Then all central moments of odd order are equal to zero. This can be explained by the fact that for each positive value of the quantity X-M(X) there is (due to the symmetry of the distribution relative to M(X)) equal in absolute value to the negative value of this quantity, and their probabilities will be the same.
If the central moment of an odd order is not equal to zero, then this indicates an asymmetry of the distribution, and the greater the moment, the greater the asymmetry. Therefore, it is most reasonable to take some odd central moment as a characteristic of the distribution asymmetry. Since the first-order central moment is always zero, it is advisable to use the third-order central moment for this purpose.
Definition 6.12. The asymmetry coefficient is the quantity:
If the asymmetry coefficient is negative, then this indicates a large influence on the magnitude of negative deviations. In this case, the distribution curve (Fig. 6.1 A) is more flat to the left of . If the coefficient is positive, which means that the influence of positive deviations predominates, then the distribution curve is flatter on the right.
As is known, the second central moment (variance) serves to characterize the dispersion of the values of a random variable around its mathematical expectation. If this moment for some random variable is large enough, i.e. If the dispersion is large, then the corresponding distribution curve is flatter than the distribution curve of a random variable with a smaller second-order moment. However, the moment cannot serve this purpose due to the fact that for any distribution 
.
In this case, the fourth order central moment is used.
Definition 6.13. Kurtosis is the quantity:
For the most common normal distribution law in nature, the ratio is . Therefore, the kurtosis given by formula (6.28) serves to compare this distribution with the normal one (Fig. 6.1 b).
In addition to position characteristics - average, typical values of a random variable - a number of characteristics are used, each of which describes one or another property of the distribution. The so-called moments are most often used as such characteristics.
The concept of moment is widely used in mechanics to describe the distribution of masses (static moments, moments of inertia, etc.). Exactly the same techniques are used in probability theory to describe the basic properties of the distribution of a random variable. Most often, two types of moments are used in practice: initial and central.
The initial moment of the sth order of a discontinuous random variable is a sum of the form:
. (5.7.1)
Obviously, this definition coincides with the definition of the initial moment of order s in mechanics, if masses are concentrated on the abscissa axis at points.
For a continuous random variable X, the initial moment of sth order is called the integral
. (5.7.2)
It is easy to see that the main characteristic of the position introduced in the previous n° - the mathematical expectation - is nothing more than the first initial moment of the random variable.
Using the mathematical expectation sign, you can combine two formulas (5.7.1) and (5.7.2) into one. Indeed, formulas (5.7.1) and (5.7.2) are completely similar in structure to formulas (5.6.1) and (5.6.2), with the difference that instead of and there are, respectively, and . Therefore, we can write a general definition of the initial moment of the th order, valid for both discontinuous and continuous quantities:
, (5.7.3)
those. The initial moment of the th order of a random variable is the mathematical expectation of the th degree of this random variable.
Before defining the central moment, we introduce a new concept of “centered random variable.”
Let there be a random variable with mathematical expectation. A centered random variable corresponding to the value is the deviation of the random variable from its mathematical expectation:
In the future, we will agree to denote everywhere the centered random variable corresponding to a given random variable by the same letter with a symbol at the top.
It is easy to verify that the mathematical expectation of a centered random variable is equal to zero. Indeed, for a discontinuous quantity
similarly for a continuous quantity.
Centering a random variable is obviously equivalent to moving the origin of coordinates to the middle, “central” point, the abscissa of which is equal to the mathematical expectation.
The moments of a centered random variable are called central moments. They are analogous to moments about the center of gravity in mechanics.
Thus, the central moment of order s of a random variable is the mathematical expectation of the th power of the corresponding centered random variable:
, (5.7.6)
and for continuous – by the integral
. (5.7.8)
In what follows, in cases where there is no doubt about which random variable a given moment belongs to, for brevity we will write simply and instead of and .
Obviously, for any random variable the central moment of the first order is equal to zero:
, (5.7.9)
since the mathematical expectation of a centered random variable is always equal to zero.
Let us derive relations connecting the central and initial moments of different orders. We will carry out the conclusion only for discontinuous quantities; it is easy to verify that exactly the same relations are valid for continuous quantities if we replace finite sums with integrals, and probabilities with elements of probability.
Let's consider the second central point:
Similarly for the third central moment we obtain:
Expressions for etc. can be obtained in a similar way.
Thus, for the central moments of any random variable the formulas are valid:
(5.7.10)
Generally speaking, moments can be considered not only relative to the origin (initial moments) or mathematical expectation (central moments), but also relative to an arbitrary point:
. (5.7.11)
However, central moments have an advantage over all others: the first central moment, as we have seen, is always equal to zero, and the next one, the second central moment, with this reference system has a minimum value. Let's prove it. For a discontinuous random variable at, formula (5.7.11) has the form:
. (5.7.12)
Let's transform this expression:
Obviously, this value reaches its minimum when , i.e. when the moment is taken relative to the point.
Of all the moments, the first initial moment (mathematical expectation) and the second central moment are most often used as characteristics of a random variable.
The second central moment is called the variance of the random variable. In view of the extreme importance of this characteristic, among other points, we introduce a special designation for it:
According to the definition of the central moment
those. the variance of a random variable X is the mathematical expectation of the square of the corresponding centered variable.
Replacing the quantity in expression (5.7.13) with its expression, we also have:
. (5.7.14)
To directly calculate the variance, use the following formulas:
, (5.7.15)
(5.7.16)
Accordingly for discontinuous and continuous quantities.
The dispersion of a random variable is a characteristic of dispersion, the scattering of the values of a random variable around its mathematical expectation. The word “dispersion” itself means “dispersion”.
If we turn to the mechanical interpretation of the distribution, then the dispersion is nothing more than the moment of inertia of a given mass distribution relative to the center of gravity (mathematical expectation).
The variance of a random variable has the dimension of the square of the random variable; To visually characterize dispersion, it is more convenient to use a quantity whose dimension coincides with the dimension of the random variable. To do this, take the square root of the variance. The resulting value is called the standard deviation (otherwise “standard”) of the random variable. We will denote the standard deviation:
, (5.7.17)
To simplify notations, we will often use the abbreviations for standard deviation and dispersion: and . In the case when there is no doubt which random variable these characteristics relate to, we will sometimes omit the symbol x y and and write simply and . The words “standard deviation” will sometimes be abbreviated to be replaced by the letters r.s.o.
In practice, a formula is often used that expresses the dispersion of a random variable through its second initial moment (the second of formulas (5.7.10)). In the new notation it will look like:
Expectation and variance (or standard deviation) are the most commonly used characteristics of a random variable. They characterize the most important features of the distribution: its position and degree of scattering. For a more detailed description of the distribution, moments of higher orders are used.
The third central point serves to characterize the asymmetry (or “skewness”) of the distribution. If the distribution is symmetrical with respect to the mathematical expectation (or, in a mechanical interpretation, the mass is distributed symmetrically with respect to the center of gravity), then all odd-order moments (if they exist) are equal to zero. Indeed, in total
when the distribution law is symmetrical with respect to the law and odd, each positive term corresponds to a negative term equal in absolute value, so that the entire sum is equal to zero. The same is obviously true for the integral
,
which is equal to zero as an integral in the symmetric limits of an odd function.
It is natural, therefore, to choose one of the odd moments as a characteristic of the distribution asymmetry. The simplest of these is the third central moment. It has the dimension of the cube of a random variable: to obtain a dimensionless characteristic, the third moment is divided by the cube of the standard deviation. The resulting value is called the “asymmetry coefficient” or simply “asymmetry”; we will denote it:
In Fig. 5.7.1 shows two asymmetric distributions; one of them (curve I) has a positive asymmetry (); the other (curve II) is negative ().
The fourth central point serves to characterize the so-called “coolness”, i.e. peaked or flat-topped distribution. These distribution properties are described using the so-called kurtosis. The kurtosis of a random variable is the quantity
The number 3 is subtracted from the ratio because for the very important and widespread in nature normal distribution law (which we will get to know in detail later) . Thus, for a normal distribution the kurtosis is zero; curves that are more peaked compared to the normal curve have a positive kurtosis; Curves that are more flat-topped have negative kurtosis.
In Fig. 5.7.2 shows: normal distribution (curve I), distribution with positive kurtosis (curve II) and distribution with negative kurtosis (curve III).
In addition to the initial and central moments discussed above, in practice the so-called absolute moments (initial and central) are sometimes used, determined by the formulas
Obviously, absolute moments of even orders coincide with ordinary moments.
Of the absolute moments, the most commonly used is the first absolute central moment.
, (5.7.21)
called the arithmetic mean deviation. Along with dispersion and standard deviation, arithmetic mean deviation is sometimes used as a characteristic of dispersion.
Expectation, mode, median, initial and central moments and, in particular, dispersion, standard deviation, skewness and kurtosis are the most commonly used numerical characteristics of random variables. In many practical problems, a complete characteristic of a random variable - the distribution law - is either not needed or cannot be obtained. In these cases, one is limited to an approximate description of the random variable using help. Numerical characteristics, each of which expresses some characteristic property of the distribution.
Very often, numerical characteristics are used to approximately replace one distribution with another, and usually they try to make this replacement in such a way that several important points remain unchanged.
Example 1. One experiment is carried out, as a result of which an event may or may not appear, the probability of which is equal to . A random variable is considered - the number of occurrences of an event (characteristic random variable of an event). Determine its characteristics: mathematical expectation, dispersion, standard deviation.
Solution. The value distribution series has the form:
where is the probability of the event not occurring.
Using formula (5.6.1) we find the mathematical expectation of the value:
The dispersion of the value is determined by formula (5.7.15):
(We suggest that the reader obtain the same result by expressing the dispersion in terms of the second initial moment).
Example 2. Three independent shots are fired at a target; The probability of hitting each shot is 0.4. random variable – number of hits. Determine the characteristics of a quantity - mathematical expectation, dispersion, r.s.d., asymmetry.
Solution. The value distribution series has the form:
We calculate the numerical characteristics of the quantity.
3.4. Moments of a random variable.
Above we got acquainted with the comprehensive characteristics of the SV: the distribution function and the distribution series for a discrete SV, the distribution function and probability density for a continuous SV. These pairwise equivalent characteristics in terms of information content are functions and fully describe the SV from a probabilistic point of view. However, in many practical situations it is either impossible or unnecessary to characterize a random variable in an exhaustive manner. Often it is enough to specify one or more numerical parameters that to some extent describe the main features of the distribution, and sometimes finding exhaustive characteristics is, although desirable, too difficult mathematically, and operating with numerical parameters, we are limited to an approximate, but simpler description. The specified numerical parameters are called numerical characteristics random variables and play a major role in the applications of probability theory to various fields of science and technology, facilitating the solution of problems and allowing the results of the solution to be presented in a simple and visual form.
The most commonly used numerical characteristics can be divided into two types: moments and position characteristics. There are several types of moments, of which the two most commonly used are: primary and central. Other types of moments, e.g. absolute moments, factorial moments, we do not consider. In order to avoid the use of a generalization of the integral - the so-called Stieltjes integral, we will give definitions of moments separately for continuous and discrete SVs.
Definitions. 1. The starting momentk-th order discrete SV is called the quantity
Where f(x) is the probability density of a given SV.
3. Central momentk-th order discrete SV is called the quantity
In cases where several SVs are simultaneously under consideration, it is convenient, in order to avoid misunderstandings, to indicate the identity of the moment; we will do this by indicating the designation of the corresponding SV in brackets, for example, 
, etc. This designation should not be confused with the function notation, and the letter in parentheses should not be confused with the function argument. Sums and integrals on the right-hand sides of equalities (3.4.1 - 3.4.4) can converge or diverge depending on the value k and specific distribution. In the first case they say that the moment does not exist or diverges, in the second - what moment exists or converges. If a discrete SV has a finite number of finite values ( N of course), then all its moments are of finite order k exist. At infinite N, starting from some k and for higher orders, the moments of a discrete SV (both initial and central) may not exist. The moments of a continuous SV, as can be seen from the definitions, are expressed by improper integrals, which can diverge starting from a certain k and for higher orders (simultaneously initial and central). Zeroth order moments always converge.
Let us consider in more detail first the initial and then the central moments. From a mathematical point of view, the initial moment k-th order is the “weighted average” k-th degrees of SV values; in the case of a discrete SV, the weights are the probabilities of values; in the case of a continuous SV, the weight function is the probability density. Operations of this kind are widely used in mechanics to describe the distribution of masses (static moments, moments of inertia, etc.); The analogies arising in this regard are discussed below.
For a better understanding of the initial moments, we consider them separately for given k. In probability theory, the moments of lower orders are most important, i.e. at small k, therefore, consideration should be carried out in order of increasing values k. The initial moment of zero order is equal to
1, for discrete SV;
=1, for continuous SV,
those. for any SV it is equal to the same value - one, and therefore does not carry any information about the statistical properties of the SV.
The first order initial moment (or first initial moment) is equal to
For discrete SV;
, for continuous SV.
This point is the most important numerical characteristic of any SV, for which there are several interrelated reasons. Firstly, according to Chebyshev’s theorem (see section 7.4), with an unlimited number of tests on the SV, the arithmetic mean of the observed values tends (in a sense) to , thus, for any SV, this is a characteristic number around which its values are grouped on experience. Secondly, for a continuous CV it is numerically equal to X-th coordinate of the center of gravity of the curvilinear trapezoid formed by the curve f(x) (a similar property occurs for a discrete SV), therefore this moment could be called the “center of gravity of the distribution.” Thirdly, this moment has remarkable mathematical properties that will become clear during the course, in particular, therefore its value is included in the expressions for central moments (see (3.4.3) and (3.4.4)).
The importance of this moment for theoretical and practical problems of probability theory and its remarkable mathematical properties have led to the fact that in addition to the designation and name “first initial moment”, other designations and names are used in the literature, more or less convenient and reflecting the mentioned properties. The most common names are: mathematical expectation, average value, and notation: m, M[X], . We will most often use the term “mathematical expectation” and the notation m; if there are several SVs, we will use a subscript indicating the identity of the mathematical expectation, for example, m x , m y etc.
The second-order initial moment (or second initial moment) is equal to
For discrete SV;
, for continuous SV;
sometimes it's called mean square of the random variable and is designated M.
The third order initial moment (or third initial moment) is equal to
For discrete SV;
, for continuous SV
sometimes it's called average cube of a random variable and is designated M[X 3 ].
There is no point in continuing to list the initial points. Let us dwell on the important interpretation of moments of order k>1. Let, along with SV X there is also a SV Y, and Y=X k (k=2, 3, ...). This equality means that the random variables X And Y are connected deterministically in the sense that when SV X takes on the value x, NE Y takes on the value y=x k(in the future, this connection of SV will be considered in more detail). Then, according to (3.4.1) and (3.4.2)
=m y
, k=2,
3, ...,
i.e. k The th initial moment of SV is equal to the mathematical expectation k-th power of this random variable. For example, the third initial moment of the edge length of a random cube is equal to the mathematical expectation of the volume of the cube. The possibility of understanding moments as certain mathematical expectations is another facet of the importance of the concept of mathematical expectation.
Let's move on to consider the central points. Since, as will become clear below, central moments are unambiguously expressed through initial moments and vice versa, the question arises of why central moments are needed at all and why initial moments are not enough. Let's consider SV X(continuous or discrete) and another SV Y, related to the first one as Y=X+a, Where a 0 is a non-random real number. Each value x random variable X corresponds to value y=x+a random variable Y, therefore the distribution of SV Y will have the same shape (expressed by the distribution polygon in the discrete case or the probability density in the continuous case) as the SV distribution X, but shifted along the x-axis by the amount a. Consequently, the initial moments of SV Y will differ from the corresponding moments of SV X. For example, it is easy to see m y =m x +a(moments of a higher order are connected by more complex relations). So we have established that the initial moments are not invariant with respect to the shift of the distribution as a whole. The same result will be obtained if you shift not the distribution, but the beginning of the x-axis horizontally by an amount - a, i.e. The equivalent conclusion is also valid: the initial moments are not invariant with respect to the horizontal shift of the beginning of the x-axis.
Central moments, intended to describe those properties of distributions that do not depend on their shift as a whole, are free from this drawback. Indeed, as can be seen from (3.4.3) and (3.4.4), when the distribution as a whole shifts by an amount a, or, what is the same, shifting the beginning of the x-axis by the amount - a, all values x, with the same probabilities (in the discrete case) or the same probability density (in the continuous case), will change by the amount a, but the quantity will change by the same amount m, so the values of the parentheses on the right sides of the equalities will not change. Thus, the central moments are invariant with respect to the shift of the distribution as a whole, or, what is the same, with respect to the horizontal shift of the beginning of the x-axis. These moments received the name “central” in those days when the first initial moment was called “center”. It is useful to note that the central moment of SV X can be understood as the corresponding initial moment of SV X 0 equal
|
X 0 =X-m x . |
NE X 0 is called centered(relative to SV X), and the operation leading to it, i.e. subtracting its mathematical expectation from a random variable, is called centering. As we will see later, this concept and this operation will be useful throughout the course. Note that the central moment of order k>1 can be considered as the mathematical expectation (average) k th degree of centered SV: 
.
Let us consider separately the central moments of the lower orders. The zeroth order central moment is equal to
, for discrete SVs;
, for continuous SV;
i.e. for any SV and does not carry any information about the statistical properties of this SV.
The first order central moment (or first central moment) is equal to
for discrete SV;
for continuous CB; i.e. for any SV and does not carry any information about the statistical properties of this SV.
The second order central moment (or second central moment) is equal to
, for discrete SV;
, for continuous SV.
As will become clear below, this point is one of the most important in probability theory, since it is used as a characteristic of the measure of dispersion (or dispersion) of SV values, therefore it is often called dispersion and is designated D X. Note that this can be understood as the mean square of the centered SV.
The third order central moment (third central moment) is equal to
Central moments are called distribution moments, when calculating which the deviation of the options from the arithmetic mean of a given series is taken as the initial value.
1. Calculate the first order central moment using the formula:
2. Calculate the second-order central moment using the formula:
where is the value of the middle of the intervals;
This is a weighted average;
Fi is the number of values.
3. Calculate the third-order central moment using the formula:
where is the value of the middle of the intervals; - this is the weighted average; - fi-number of values.
4. Calculate the fourth-order central moment using the formula:
where is the value of the middle of the intervals; - this is the weighted average; - fi-number of values.
Calculation for table 3.2
Calculation for table 3.4
1. Calculate the first-order central moment using formula (7.1):
2. Calculate the second-order central moment using formula (7.2):
3. Calculate the third-order central moment using formula (7.3):
4. Calculate the fourth-order central moment using formula (7.4):
Calculation for table 3.6
1. Calculate the first-order central moment using formula (7.1):
2. Calculate the second-order central moment using formula (7.2):
3. Calculate the third-order central moment using formula (7.3):
4. Calculate the fourth-order central moment using formula (7.4):
Moments of orders 1, 2, 3, 4 were calculated for three problems. Where the third order moment is needed to calculate asymmetry, and the fourth order moment is needed to calculate kurtosis.
CALCULATION OF DISTRIBUTION ASYMMETRY
In statistical practice, various distributions are encountered. There are the following types of distribution curves:
· single-vertex curves: symmetrical, moderately asymmetrical and extremely asymmetrical;
· multivertex curves.
Homogeneous populations, as a rule, are characterized by single-vertex distributions. Multivertex indicates the heterogeneity of the population being studied. The appearance of two or more vertices makes it necessary to regroup the data in order to identify more homogeneous groups.
Determining the general nature of the distribution involves assessing its homogeneity, as well as calculating indicators of asymmetry and kurtosis. For symmetric distributions, the frequencies of any two options that are equally located on both sides of the distribution center are equal to each other. The mean, mode and median calculated for such distributions are also equal.
When comparatively studying the asymmetry of several distributions with different units of measurement, the relative asymmetry indicator () is calculated:
where is the weighted average; Mo-fashion; - root mean square weighted dispersion; Me-median.
Its value can be positive or negative. In the first case, we are talking about right-sided asymmetry, and in the second, about left-sided asymmetry.
With right-sided asymmetry Mo>Me >x. The most widely used (as an indicator of asymmetry) is the ratio of the third-order central moment to the standard deviation of a given series cubed:
where is the third-order central moment; - standard deviation cubed.
The use of this indicator makes it possible to determine not only the magnitude of asymmetry, but also to check its presence in the general population. It is generally accepted that skewness greater than 0.5 (regardless of sign) is considered significant; if it is less than 0.25, then it is insignificant.
The significance assessment is based on the mean square error, the asymmetry coefficient (), which depends on the number of observations (n) and is calculated using the formula:
where n is the number of observations.
In this case, the asymmetry is significant and the distribution of the characteristic in the population is asymmetrical. Otherwise, the asymmetry is insignificant and its presence may be caused by random circumstances.
Calculation for table 3.2 Grouping of the population by average monthly salary, rub.
Left-sided, significant asymmetry.
Calculation for table 3.4 Grouping of stores by retail turnover, million rubles.
1. Let us determine the asymmetries using formula (7.5):
Right-sided, significant asymmetry.
Calculation for table 3.6 Grouping of transport organizations by freight turnover of public transport (million t.km)
1. Let us determine the asymmetries using formula (7.5):
Right-sided, slight asymmetry.
CALCULATION OF KURTESS OF DISTRIBUTION
For symmetric distributions, the kurtosis index () can be calculated:
where is the fourth-order central moment; - standard deviation to the fourth power.
Calculation for table 3.2 Grouping of the population by average monthly salary, rub.
Calculation for table 3.4 Grouping of stores by retail turnover, million rubles.
Let's calculate the kurtosis indicator using formula (7.7)
Peak distribution.
Calculation for table 3.6 Grouping of transport organizations by freight turnover of public transport (million t.km)
Let's calculate the kurtosis indicator using formula (7.7)
Flat top distribution.
ASSESSMENT OF THE HOMOGENEOUSNESS OF THE POPULATION
Homogeneity assessment for table 3.2 Grouping of the population by average monthly salary, rub.
It should be noted that although the indicators of asymmetry and kurtosis directly characterize only the form of distribution of the characteristic within the population being studied, their definition has not only descriptive significance. Often asymmetry and kurtosis provide certain indications for further research of socio-economic phenomena. The result obtained indicates the presence of asymmetry that is significant in magnitude and negative in nature; it should be noted that the asymmetry is left-sided. In addition, the population has a flat-top distribution.
Homogeneity assessment for table 3.4 Grouping of stores by retail turnover, million rubles.
The result obtained indicates the presence of asymmetry that is significant in magnitude and positive in nature; it should be noted that the asymmetry is right-sided. And also the population has a sharp-vertex distribution.
Homogeneity assessment for table 3.6 Grouping of transport organizations by freight turnover of public transport (million t.km)
The obtained result indicates the presence of asymmetry that is insignificant in magnitude and positive in nature; it should be noted that the asymmetry is right-sided. In addition, the population has a flat-topped distribution.
