Logarithmic Expressions, solving examples. In this article we will look at problems related to solving logarithms. The tasks ask the question of finding the meaning of an expression. It should be noted that the concept of logarithm is used in many tasks and understanding its meaning is extremely important. As for the Unified State Exam, the logarithm is used when solving equations, in applied problems, also in tasks related to the study of functions.
Let us give examples to understand the very meaning of the logarithm:
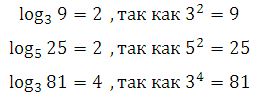

Basic logarithmic identity:

Properties of logarithms that must always be remembered:

*Logarithm of the product equal to the sum logarithms of factors.
* * *

*Logarithm of the quotient (fraction) equal to the difference logarithms of factors.
* * *
![]()
*Logarithm of degree equal to the product exponent by the logarithm of its base.
* * *

*Transition to a new foundation
* * *
More properties:

* * *
The calculation of logarithms is closely related to the use of properties of exponents.
Let's list some of them:
The essence of this property lies in the fact that when transferring the numerator to the denominator and vice versa, the sign of the exponent changes to the opposite. For example:

A corollary from this property:
* * *
![]()
When raising a power to a power, the base remains the same, but the exponents are multiplied.
* * *
As you have seen, the concept of a logarithm itself is simple. The main thing is what is needed good practice, which gives a certain skill. Of course, knowledge of formulas is required. If the skill in converting elementary logarithms has not been developed, then when solving simple tasks It's easy to make a mistake.
Practice, solve the simplest examples from the mathematics course first, then move on to more complex ones. In the future, I will definitely show how “ugly” logarithms are solved; these won’t appear on the Unified State Examination, but they are of interest, don’t miss them!
That's all! Good luck to you!
Sincerely, Alexander Krutitskikh
P.S: I would be grateful if you tell me about the site on social networks.
Solving logarithmic equations. Part 1.
Logarithmic equation is an equation in which the unknown is contained under the sign of the logarithm (in particular, in the base of the logarithm).
The simplest logarithmic equation has the form:
Solving any logarithmic equation involves a transition from logarithms to expressions under the sign of logarithms. However, this action expands the scope acceptable values equations and can lead to the appearance extraneous roots. To avoid the appearance of foreign roots, you can do one of three ways:
1. Make an equivalent transition from the original equation to a system including


depending on which inequality or simpler.
If the equation contains an unknown in the base of the logarithm:
then we go to the system:

2. Separately find the range of acceptable values of the equation, then solve the equation and check whether the solutions found satisfy the equation.
3. Solve the equation, and then check: substitute the solutions found into original equation, and check if we get the correct equality.
A logarithmic equation of any level of complexity always ultimately reduces to the simplest logarithmic equation.
All logarithmic equations can be divided into four types:
1 . Equations that contain logarithms only to the first power. With the help of transformations and use, they are brought to the form
Example. Let's solve the equation:
Let us equate the expressions under the logarithm sign:
Let's check whether our root of the equation satisfies:
Yes, it satisfies.
Answer: x=5
2 . Equations that contain logarithms to powers other than 1 (particularly in the denominator of a fraction). Such equations can be solved using introducing a change of variable.
Example. Let's solve the equation:
Let's find the ODZ equation:
The equation contains logarithms squared, so it can be solved using a change of variable.
Important! Before introducing a replacement, you need to “pull apart” the logarithms that are part of the equation into “bricks”, using the properties of logarithms.
When “pulling apart” logarithms, it is important to use the properties of logarithms very carefully:
In addition, there is one more subtle point here, and in order to avoid a common mistake, we will use an intermediate equality: we will write the degree of the logarithm in this form:
Likewise,
Let's substitute the resulting expressions into the original equation. We get:
Now we see that the unknown is contained in the equation as part of . Let's introduce the replacement: . Since it can take any real value, we do not impose any restrictions on the variable.
Algebra 11th grade
Topic: “Methods for solving logarithmic equations”
Lesson objectives:
educational: formation of knowledge about in different ways solving logarithmic equations, skills to apply them in each specific situation and choose any method to solve;
developmental: development of skills to observe, compare, apply knowledge in new situation, identify patterns, generalize; developing skills of mutual control and self-control;
educational: fostering a responsible attitude towards educational work, attentive perception of the material in the lesson, careful note-taking.
Lesson type: lesson on introducing new material.
“The invention of logarithms, while reducing the work of the astronomer, extended his life.”
French mathematician and astronomer P.S. Laplace
Lesson progress
I. Setting the lesson goal
The studied definition of logarithm, properties of logarithms and logarithmic function will allow us to solve logarithmic equations. All logarithmic equations, no matter how complex they are, are solved using uniform algorithms. We'll look at these algorithms in today's lesson. There are not many of them. If you master them, then any equation with logarithms will be feasible for each of you.
Write down the topic of the lesson in your notebook: “Methods for solving logarithmic equations.” I invite everyone to cooperate.
II. Update background knowledge
Let's prepare to study the topic of the lesson. You solve each task and write down the answer; you don’t have to write the condition. Work in pairs.
1) For what values of x does the function make sense:
(Answers are checked for each slide and errors are sorted out)
2) Do the graphs of the functions coincide?
3) Rewrite the equalities as logarithmic equalities:
4) Write the numbers as logarithms with base 2:
5) Calculate:
6) Try to restore or supplement the missing elements in these equalities.
III. Introduction to new material
The following statement is displayed on the screen:
“The equation is the golden key that opens all mathematical sesames.”
Modern Polish mathematician S. Kowal
Try to formulate the definition of a logarithmic equation. (An equation containing an unknown under the logarithm sign).
Let's consider the simplest logarithmic equation:logAx = b(where a>0, a ≠ 1). Because logarithmic function increases (or decreases) on the set positive numbers and accepts everything real values, then by the root theorem it follows that for any b given equation has, and moreover, only one, solution, and a positive one.
Remember the definition of logarithm. (The logarithm of a number x to the base a is an indicator of the power to which the base a must be raised to obtain the number x). From the definition of logarithm it immediately follows that AV is such a solution.
Write down the title: Methods for solving logarithmic equations
1. By definition of logarithm.
This is how the simplest equations of the form are solved.
Let's consider No. 514(a)): Solve the equation
How do you propose to solve it? (By definition of logarithm)
Solution. , Hence 2x - 4 = 4; x = 4.
In this task, 2x - 4 > 0, since > 0, so no extraneous roots can appear, and there is no need to check. The condition 2x - 4 > 0 does not need to be written out in this task.
2. Potentization(transition from logarithm given expression to this expression itself).
Let's consider No. 519(g): log5(x2+8)-log5(x+1)=3log5 2
What feature did you notice? (The bases are the same and the logarithms of the two expressions are equal.) What can be done? (Potentize).
It should be taken into account that any solution is contained among all x for which the logarithmic expressions are positive.
Solution: ODZ:
X2+8>0 is an unnecessary inequality
log5(x2+8) =log5 23+ log5(x+1)
log5(x2+8)= log5 (8 x+8)
Let's potentiate the original equation
we get the equation x2+8= 8x+8
Let's solve it: x2-8x=0
Answer: 0; 8
IN general view transition to an equivalent system:
Equation
(The system contains a redundant condition - one of the inequalities need not be considered).
Question for the class: Which of these three solutions did you like best? (Discussion of methods).
You have the right to decide in any way.
3. Introduction of a new variable.
Let's consider No. 520(g). .
What did you notice? (This quadratic equation regarding log3x) Your suggestions? (Introduce a new variable)
Solution. ODZ: x > 0.
Let , then the equation takes the form:. Discriminant D > 0. Roots according to Vieta's theorem:.
Let's go back to the replacement: or.
Having solved the simplest logarithmic equations, we get:
Answer: 27;
4. Logarithm both sides of the equation.
Solve the equation:.
Solution: ODZ: x>0, take the logarithm of both sides of the equation in base 10:
Let's apply the property of the logarithm of a power:
(logx + 3) logx = 4
Let logx = y, then (y + 3)y = 4
, (D > 0) roots according to Vieta’s theorem: y1 = -4 and y2 = 1.
Let's go back to the replacement, we get: lgx = -4,; lgx = 1, .
Answer: 0.0001; 10.
5. Reduction to one base.
No. 523(c). Solve the equation:
Solution: ODZ: x>0. Let's move on to base 3.
6. Functional-graphic method.
№ 509(d). Solve the equation graphically: = 3 - x.
How do you propose to solve? (Build graphs of two functions y = log2x and y = 3 - x using points and look for the abscissa of the points of intersection of the graphs).
Look at your solution on the slide.
There is a way to avoid making graphs . It is as follows : if one of the functions y = f(x) increases, and the other y = g(x) decreases on the interval X, then the equation f(x)= g(x) has at most one root on the interval X.
If there is a root, then it can be guessed.
In our case, the function increases for x>0, and the function y = 3 - x decreases for all values of x, including for x>0, which means that the equation has no more than one root. Note that at x = 2 the equation turns into a true equality, since .
« Correct use methods can be learned
only by applying them to various examples».
Danish historian of mathematics G. G. Zeiten
IV. Homework
P. 39 consider example 3, solve No. 514(b), No. 529(b), No. 520(b), No. 523(b)
V. Summing up the lesson
What methods of solving logarithmic equations did we look at in class?
In the next lessons we will look at more complex equations. To solve them, the studied methods will be useful.
Last slide shown:
“What is more than anything in the world?
Space.
What is the wisest thing?
Time.
What's the best part?
Achieve what you want."
Thales
I wish everyone to achieve what they want. Thank you for your cooperation and understanding.
We are all familiar with equations primary classes. There we also learned to solve the simplest examples, and we must admit that they find their application even in higher mathematics. Everything is simple with equations, including quadratic equations. If you are having trouble with this topic, we highly recommend that you review it.
You've probably already gone through logarithms too. However, we consider it important to tell what it is for those who do not yet know. A logarithm is equated to the power to which the base must be raised to obtain the number to the right of the logarithm sign. Let's give an example based on which everything will become clear to you.
If you raise 3 to the fourth power, you get 81. Now substitute the numbers by analogy, and you will finally understand how logarithms are solved. Now all that remains is to combine the two concepts discussed. Initially, the situation seems extremely complicated, but upon closer examination the weight falls into place. We are sure that after this short article you will not have problems in this part of the Unified State Exam.
Today there are many ways to solve such structures. We will tell you about the simplest, most effective and most applicable in the case of Unified State Examination tasks. Solving logarithmic equations must start from the very beginning. simple example. The simplest logarithmic equations consist of a function and one variable in it.

It's important to note that x is inside the argument. A and b must be numbers. In this case, you can simply express the function in terms of a number to a power. It looks like this.

Of course, solving a logarithmic equation using this method will lead you to the correct answer. The problem for the vast majority of students in this case is that they do not understand what comes from and where it comes from. As a result, you have to put up with mistakes and not get the desired points. The most offensive mistake will be if you mix up the letters. To solve an equation this way, you need to memorize this standard school formula because it is difficult to understand.
To make it easier, you can resort to another method - the canonical form. The idea is extremely simple. Turn your attention back to the problem. Remember that the letter a is a number, not a function or variable. A is not equal to one and greater than zero. There are no restrictions on b. Now, of all the formulas, let us remember one. B can be expressed as follows.

It follows from this that all original equations with logarithms can be represented in the form:

Now we can drop the logarithms. It will work out simple design, which we have already seen earlier.

The convenience of this formula lies in the fact that it can be used in the most different cases, and not just for the simplest designs.
Don't worry about OOF!
Many experienced mathematicians will notice that we have not paid attention to the domain of definition. The rule boils down to the fact that F(x) is necessarily greater than 0. No, we did not miss this point. Now we are talking about another serious advantage of the canonical form.
There will be no extra roots here. If a variable will only appear in one place, then a scope is not necessary. It is done automatically. To verify this judgment, try solving several simple examples.
How to solve logarithmic equations with different bases
These are already complex logarithmic equations, and the approach to solving them must be special. Here it is rarely possible to limit ourselves to the notorious canonical form. Let's start our detailed story. We have the following construction.

Pay attention to the fraction. It contains the logarithm. If you see this in a task, it’s worth remembering one interesting trick.

What does it mean? Each logarithm can be represented as the quotient of two logarithms with a convenient base. And this formula has special case, which is applicable with this example (meaning if c=b).

This is exactly the fraction we see in our example. Thus.

Essentially, we turned the fraction around and got a more convenient expression. Remember this algorithm!
Now we need that the logarithmic equation did not contain different reasons. Let's represent the base as a fraction.

In mathematics there is a rule based on which you can derive a degree from a base. The following construction results.

It would seem that what is stopping us from now turning our expression into canonical form and just solve it? It's not that simple. There should be no fractions before the logarithm. Let's fix this situation! A fraction is allowed to be used as a degree.

Respectively.

If the bases are the same, we can remove the logarithms and equate the expressions themselves. This way the situation will become much simpler than it was. Will remain elementary equation, which each of us knew how to solve back in 8th or even 7th grade. You can do the calculations yourself.

We have obtained the only true root of this logarithmic equation. Examples of solving a logarithmic equation are quite simple, aren't they? Now you will be able to deal with even the most difficult problems on your own. complex tasks for preparing and passing the Unified State Exam.
What's the result?
In the case of any logarithmic equations, we start from one very important rule. It is necessary to act in such a way as to bring the expression to the maximum simple view. In this case you will have more chances not only solve the task correctly, but also do it in the simplest and most logical way possible. This is exactly how mathematicians always work.
We strongly do not recommend that you look for difficult paths, especially in this case. Remember a few simple rules, which will allow you to transform any expression. For example, reduce two or three logarithms to the same base or derive a power from the base and win on this.
It is also worth remembering that solving logarithmic equations requires constant practice. Gradually you will move on to more and more complex structures, and this will lead you to confidently solving all variants of problems on the Unified State Exam. Prepare well in advance for your exams, and good luck!
Algebra 11th grade
Topic: “Methods for solving logarithmic equations”
Lesson objectives:
educational: developing knowledge about different ways to solve logarithmic equations, the ability to apply them in each specific situation and choose any method for solving;
developing: development of skills to observe, compare, apply knowledge in a new situation, identify patterns, generalize; developing skills of mutual control and self-control;
educational: nurturing a responsible attitude to educational work, attentive perception of the material in the lesson, and careful note-taking.
Lesson type : lesson on introducing new material.
“The invention of logarithms, while reducing the work of the astronomer, extended his life.”
French mathematician and astronomer P.S. Laplace
Lesson progress
I. Setting the lesson goal
The studied definition of logarithm, properties of logarithms and logarithmic function will allow us to solve logarithmic equations. All logarithmic equations, no matter how complex they are, are solved using uniform algorithms. We'll look at these algorithms in today's lesson. There are not many of them. If you master them, then any equation with logarithms will be feasible for each of you.
Write down the topic of the lesson in your notebook: “Methods for solving logarithmic equations.” I invite everyone to cooperate.
II. Updating of reference knowledge
Let's prepare to study the topic of the lesson. You solve each task and write down the answer; you don’t have to write the condition. Work in pairs.
1) For what values of x does the function make sense:
A)
b)
V)![]()
d)
(Answers are checked for each slide and errors are sorted out)
2) Do the graphs of the functions coincide?
a) y = x and
b)And![]()
3) Rewrite the equalities as logarithmic equalities:
4) Write the numbers as logarithms with base 2:
4 =
2 =
0,5 =
1 =
5) Calculate :
6) Try to restore or supplement the missing elements in these equalities.

III. Introduction to new material
The following statement is displayed on the screen:
“The equation is the golden key that opens all mathematical sesames.”
Modern Polish mathematician S. Kowal
Try to formulate the definition of a logarithmic equation. (Equation containing an unknown under the logarithm sign ).
Let's considerthe simplest logarithmic equation: log A x = b (where a>0, a ≠ 1). Since the logarithmic function increases (or decreases) on the set of positive numbers and takes all real values, then by the root theorem it follows that for any b this equation has, and only one, solution, and a positive one.
Remember the definition of logarithm. (The logarithm of a number x to the base a is an indicator of the power to which the base a must be raised to obtain the number x ). From the definition of logarithm it immediately follows thatA V is such a solution.
Write down the title:Methods for solving logarithmic equations
1. By definition of logarithm .
This is how the simplest equations of the form are solved.
Let's considerNo. 514(a)
): Solve the equation![]()
How do you propose to solve it? (By definition of logarithm )
Solution
.
 , Hence 2x – 4 = 4; x = 4.
, Hence 2x – 4 = 4; x = 4.
Answer: 4.
In this task 2x – 4 > 0, since> 0, so no extraneous roots can appear, andno need to check . There is no need to write out the condition 2x – 4 > 0 in this task.
2. Potentization (transition from the logarithm of a given expression to this expression itself).
Let's considerNo. 519(g): log 5 ( x 2 +8)- log 5 ( x+1)=3 log 5 2
What feature did you notice?(The bases are the same and the logarithms of the two expressions are equal) . What can be done?(Potentize).
It should be taken into account that any solution is contained among all x for which the logarithmic expressions are positive.
Solution: ODZ:
X 2 +8>0 unnecessary inequality
log 5 ( x 2 +8) = log 5 2 3 + log 5 ( x+1)
log 5 ( x 2 +8)= log 5 (8 x+8)
Let's potentiate the original equation
x 2 +8= 8 x+8
we get the equationx 2 +8= 8 x+8
Let's solve it:x 2 -8 x=0
x=0, x=8
Answer: 0; 8
In generaltransition to an equivalent system :
Equation![]()

(The system contains a redundant condition - one of the inequalities need not be considered).
Question for the class : Which of these three solutions did you like best? (Discussion of methods).
You have the right to decide in any way.
3. Introduction of a new variable .
Let's considerNo. 520(g) . .
What did you notice? (This is a quadratic equation with respect to log3x) What are your suggestions? (Introduce a new variable)
Solution . ODZ: x > 0.
Let, then the equation will take the form:![]() . Discriminant D > 0. Roots according to Vieta’s theorem:
. Discriminant D > 0. Roots according to Vieta’s theorem:![]() .
.
Let's go back to the replacement:or.
Having solved the simplest logarithmic equations, we get:
; .
Answer : 27;
4. Logarithm both sides of the equation.
Solve the equation:![]() .
.
Solution : ODZ: x>0, let's take the logarithm of both sides of the equation in base 10:
![]() . Let's apply the property of the logarithm of a power:
. Let's apply the property of the logarithm of a power:
(lgx + 3) lgx =
(logx + 3) logx = 4
Let logx = y, then (y + 3)y = 4
![]() , (D > 0) roots according to Vieta’s theorem: y1 = -4 and y2 = 1.
, (D > 0) roots according to Vieta’s theorem: y1 = -4 and y2 = 1.
Let's go back to the replacement, we get: lgx = -4,![]() ; logx = 1,
; logx = 1,![]() .
.
It is as follows:
if one of the functions
y = f(x)
increases, and the other
y = g(x)
decreases on the interval X, then the equation
f(x)= g(x)
has at most one root on the interval X
.
.
.
It is as follows:
if one of the functions
y = f(x)
increases, and the other
y = g(x)
decreases on the interval X, then the equation
f(x)= g(x)
has at most one root on the interval X
.
If there is a root, then it can be guessed. .
Answer : 2
“The correct application of methods can be learned by
only by applying them to various examples.”
Danish historian of mathematics G. G. Zeiten
I V. Homework
P. 39 consider example 3, solve No. 514(b), No. 529(b), No. 520(b), No. 523(b)
V. Summing up the lesson
What methods of solving logarithmic equations did we look at in class?
In the next lessons we will look at more complex equations. To solve them, the studied methods will be useful.
Last slide shown:
“What is more than anything in the world?
Space.
What is the wisest thing?
Time.
What's the best part?
Achieve what you want."
Thales
I wish everyone to achieve what they want. Thank you for your cooperation and understanding.








