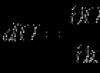Corresponding to such a vector space. In this article, the first definition will be taken as the starting point.

N (\displaystyle n)-dimensional Euclidean space is usually denoted E n (\displaystyle \mathbb (E) ^(n)); the notation is also often used when it is clear from the context that the space is provided with a natural Euclidean structure.

Formal definition

To define Euclidean space, the easiest way is to take as the main concept the scalar product. A Euclidean vector space is defined as a finite-dimensional vector space over the field of real numbers, on whose pairs of vectors a real-valued function is specified (⋅ , ⋅) , (\displaystyle (\cdot ,\cdot),) having the following three properties:

Example of Euclidean space - coordinate space R n , (\displaystyle \mathbb (R) ^(n),) consisting of all possible sets of real numbers (x 1 , x 2 , … , x n) , (\displaystyle (x_(1),x_(2),\ldots ,x_(n)),) scalar product in which is determined by the formula (x , y) = ∑ i = 1 n x i y i = x 1 y 1 + x 2 y 2 + ⋯ + x n y n . (\displaystyle (x,y)=\sum _(i=1)^(n)x_(i)y_(i)=x_(1)y_(1)+x_(2)y_(2)+\cdots +x_(n)y_(n).)

Lengths and angles

The scalar product defined on Euclidean space is sufficient to introduce the geometric concepts of length and angle. Vector length u (\displaystyle u) is defined as (u , u) (\displaystyle (\sqrt ((u,u)))) and is designated | u | . (\displaystyle |u|.) The positive definiteness of the scalar product guarantees that the length of the nonzero vector is nonzero, and from bilinearity it follows that | a u | = | a | | u | , (\displaystyle |au|=|a||u|,) that is, the lengths of proportional vectors are proportional.

Angle between vectors u (\displaystyle u) And v (\displaystyle v) determined by the formula φ = arccos ⁡ ((x , y) | x | | y |) . (\displaystyle \varphi =\arccos \left((\frac ((x,y))(|x||y|))\right).) From the cosine theorem it follows that for a two-dimensional Euclidean space ( Euclidean plane) this definition of angle coincides with the usual one. Orthogonal vectors, as in three-dimensional space, can be defined as vectors the angle between which is equal to π 2. (\displaystyle (\frac (\pi )(2)).)

The Cauchy-Bunyakovsky-Schwartz inequality and the triangle inequality

There is one gap left in the definition of angle given above: in order to arccos ⁡ ((x , y) | x | | y |) (\displaystyle \arccos \left((\frac ((x,y))(|x||y|))\right)) has been defined, it is necessary that the inequality | (x, y) | x | | y | | ⩽ 1. (\displaystyle \left|(\frac ((x,y))(|x||y|))\right|\leqslant 1.) This inequality does hold in an arbitrary Euclidean space, and is called the Cauchy–Bunyakovsky–Schwartz inequality. From this inequality, in turn, follows the triangle inequality: | u + v | ⩽ | u | + | v | . (\displaystyle |u+v|\leqslant |u|+|v|.) The triangle inequality, together with the length properties listed above, means that the length of a vector is a norm on Euclidean vector space, and the function d(x, y) = | x − y | (\displaystyle d(x,y)=|x-y|) defines the structure of a metric space on Euclidean space (this function is called the Euclidean metric). In particular, the distance between elements (points) x (\displaystyle x) And y (\displaystyle y) coordinate space R n (\displaystyle \mathbb (R) ^(n)) is given by the formula d (x , y) = ‖ x − y ‖ = ∑ i = 1 n (x i − y i) 2 . (\displaystyle d(\mathbf (x) ,\mathbf (y))=\|\mathbf (x) -\mathbf (y) \|=(\sqrt (\sum _(i=1)^(n) (x_(i)-y_(i))^(2))).)

Algebraic properties

Orthonormal bases

Conjugate spaces and operators

Any vector x (\displaystyle x) Euclidean space defines a linear functional x ∗ (\displaystyle x^(*)) on this space, defined as x ∗ (y) = (x , y) . (\displaystyle x^(*)(y)=(x,y).) This comparison is an isomorphism between Euclidean space and its dual space and allows them to be identified without compromising calculations. In particular, conjugate operators can be considered as acting on the original space, and not on its dual, and self-adjoint operators can be defined as operators that coincide with their conjugates. In an orthonormal basis, the matrix of the adjoint operator is transposed to the matrix of the original operator, and the matrix of the self-adjoint operator is symmetric.

Movements of Euclidean space

Motions of Euclidean space are metric-preserving transformations (also called isometries). Motion example - parallel translation to vector v (\displaystyle v), which translates the point p (\displaystyle p) to the point p + v (\displaystyle p+v). It is easy to see that any movement is a composition of parallel translation and transformation that keeps one point fixed. By choosing a fixed point as the origin of coordinates, any such movement can be considered as

4.3.1 Definition of linear space

Let ā , , - elements of some set ā , , L and λ , μ - real numbers, λ , μ R..

The set L is calledlinear orvector space, if two operations are defined:

1 0 . Addition. Each pair of elements of this set is associated with an element of the same set, called their sum

ā + =

2°.Multiplying by a number. Any real number λ and element ā L matches an element of the same set λ ā L and the following properties are satisfied:

1. ā+= + ā;

2. ā+(+ )=(ā+ )+ ;

3. exists zero element
, such that ā +=ā ;

4. exists opposite element -
such that ā +(-ā )=.

If λ , μ - real numbers, then:

5. λ(μ , ā)= λ μ ā ;

6. 1ā= ā;

7. λ(ā +)= λ ā+λ ;

8. (λ+ μ ) ā=λ ā + μ ā

Elements of linear space ā, , ... are called vectors.

Exercise. Show yourself that these sets form linear spaces:

1) A set of geometric vectors on a plane;

2) Many geometric vectors in three-dimensional space;

3) A set of polynomials of some degree;

4) A set of matrices of the same dimension.

4.3.2 Linearly dependent and independent vectors. Dimension and basis of space

Linear combination vectors ā 1 , ā 2 , …, ā n Lis called a vector of the same space of the form:

Where λ i are real numbers.

Vectors ā 1 , .. , ā n are calledlinearly independent, if their linear combination is a zero vector if and only if all λ i are equal to zero, that is

λ i =0

If the linear combination is a zero vector and at least one of λ i is different from zero, then these vectors are called linearly dependent. The latter means that at least one of the vectors can be represented as a linear combination of other vectors. Indeed, even if, for example,
. Then,
, Where

.

A maximally linearly independent ordered system of vectors is called basis space L. The number of basis vectors is called dimension space.

Let's assume that there is n linearly independent vectors, then the space is called n-dimensional. Other space vectors can be represented as a linear combination n basis vectors. Per basis n- dimensional space can be taken any n linearly independent vectors of this space.

Example 17. Find the basis and dimension of these linear spaces:

a) a set of vectors lying on a line (collinear to some line)

b) a set of vectors belonging to the plane

c) a set of vectors of three-dimensional space

d) a set of polynomials of degree no higher than two.

Solution.

A) Any two vectors lying on a straight line will be linearly dependent, since the vectors are collinear
, That
, λ - scalar. Consequently, the basis of a given space is only one (any) vector different from zero.

Usually this space is designated R, its dimension is 1.

b) any two non-collinear vectors
will be linearly independent, and any three vectors on the plane will be linearly independent. For any vector , there are numbers  And  such that
. The space is called two-dimensional, denoted by R 2 .

The basis of a two-dimensional space is formed by any two non-collinear vectors.

V) Any three non-coplanar vectors will be linearly independent, they form the basis of three-dimensional space R 3 .

G) As a basis for the space of polynomials of degree no higher than two, we can choose the following three vectors: ē 1 = x 2 ; ē 2 = x; ē 3 =1 .

(1 is a polynomial identically equal to one). This space will be three-dimensional.

Linear (vector) A space is a set V of arbitrary elements called vectors, in which the operations of adding vectors and multiplying a vector by a number are defined, i.e. any two vectors \mathbf(u) and (\mathbf(v)) are associated with the vector \mathbf(u)+\mathbf(v), called the sum of vectors \mathbf(u) and (\mathbf(v)), any vector (\mathbf(v)) and any number \lambda from the field of real numbers \mathbb(R) is associated with a vector \lambda\mathbf(v), called the product of the vector \mathbf(v) by the number \lambda ; so the following conditions are satisfied:

1. \mathbf(u)+ \mathbf(v)=\mathbf(v)+\mathbf(u)\,~\forall \mathbf(u),\mathbf(v)\in V(commutativity of addition);
2. \mathbf(u)+(\mathbf(v)+\mathbf(w))=(\mathbf(u)+\mathbf(v))+\mathbf(w)\,~\forall \mathbf(u), \mathbf(v),\mathbf(w)\in V(associativity of addition);
3. there is an element \mathbf(o)\in V , called the zero vector, such that \mathbf(v)+\mathbf(o)=\mathbf(v)\,~\forall \mathbf(v)\in V;
4. for each vector (\mathbf(v)) there is a vector called opposite to the vector \mathbf(v) such that \mathbf(v)+(-\mathbf(v))=\mathbf(o);
5. \lambda(\mathbf(u)+\mathbf(v))=\lambda \mathbf(u)+\lambda \mathbf(v)\,~\forall \mathbf(u),\mathbf(v)\in V ,~\forall \lambda\in \mathbb(R);
6. (\lambda+\mu)\mathbf(v)=\lambda \mathbf(v)+\mu \mathbf(v)\,~ \forall \mathbf(v)\in V,~\forall \lambda,\mu\ in\mathbb(R);
7. \lambda(\mu \mathbf(v))=(\lambda\mu)\mathbf(v)\,~ \forall \mathbf(v)\in V,~\forall \lambda,\mu\in \mathbb( R);
8. 1\cdot \mathbf(v)=\mathbf(v)\,~\forall \mathbf(v)\in V.

Conditions 1-8 are called axioms of linear space. The equal sign placed between the vectors means that the left and right sides of the equality represent the same element of the set V; such vectors are called equal.

In the definition of linear space, the operation of multiplying a vector by a number is introduced for real numbers. Such a space is called linear space over the field of real numbers, or, in short, real linear space. If in the definition, instead of the field \mathbb(R) of real numbers, we take the field of complex numbers \mathbb(C) , then we get linear space over the field of complex numbers, or, in short, complex linear space. As a number field, we can also choose the field \mathbb(Q) of rational numbers, and in this case we obtain a linear space over the field of rational numbers. In what follows, unless otherwise stated, real linear spaces will be considered. In some cases, for brevity, we will talk about space, omitting the word linear, since all the spaces discussed below are linear.

Notes 8.1

1. Axioms 1-4 show that a linear space is a commutative group with respect to the operation of addition.

2. Axioms 5 and 6 determine the distributivity of the operation of multiplying a vector by a number in relation to the operation of adding vectors (axiom 5) or to the operation of adding numbers (axiom 6). Axiom 7, sometimes called the law of associativity of multiplication by a number, expresses the connection between two different operations: multiplying a vector by a number and multiplying numbers. The property defined by Axiom 8 is called the unitarity of the operation of multiplying a vector by a number.

3. Linear space is a non-empty set, since it necessarily contains a zero vector.

4. The operations of adding vectors and multiplying a vector by a number are called linear operations on vectors.

5. The difference between the vectors \mathbf(u) and \mathbf(v) is the sum of the vector \mathbf(u) with the opposite vector (-\mathbf(v)) and is denoted: \mathbf(u)-\mathbf(v)=\mathbf(u)+(-\mathbf(v)).

6. Two non-zero vectors \mathbf(u) and \mathbf(v) are called collinear (proportional) if there is a number \lambda such that \mathbf(v)=\lambda \mathbf(u). The concept of collinearity extends to any finite number of vectors. The zero vector \mathbf(o) is considered collinear with any vector.

Corollaries of the linear space axioms

1. There is only one zero vector in linear space.

2. In linear space, for any vector \mathbf(v)\in V there is a unique opposite vector (-\mathbf(v))\in V.

3. The product of an arbitrary space vector and the number zero is equal to the zero vector, i.e. 0\cdot \mathbf(v)=\mathbf(o)\,~\forall \mathbf(v)\in V.

4. The product of a zero vector by any number is equal to a zero vector, that is, for any number \lambda.

5. The vector opposite to a given vector is equal to the product of this vector by the number (-1), i.e. (-\mathbf(v))=(-1)\mathbf(v)\,~\forall \mathbf(v)\in V.

6. In expressions of the form \mathbf(a+b+\ldots+z)(sum of a finite number of vectors) or \alpha\cdot\beta\cdot\ldots\cdot\omega\cdot \mathbf(v)(the product of a vector and a finite number of factors) you can place the brackets in any order or not specify them at all.

Let us prove, for example, the first two properties. Uniqueness of the zero vector. If \mathbf(o) and \mathbf(o)" are two zero vectors, then by Axiom 3 we obtain two equalities: \mathbf(o)"+\mathbf(o)=\mathbf(o)" or \mathbf(o)+\mathbf(o)"=\mathbf(o), the left sides of which are equal according to Axiom 1. Consequently, the right sides are also equal, i.e. \mathbf(o)=\mathbf(o)". Uniqueness of the opposite vector. If the vector \mathbf(v)\in V has two opposite vectors (-\mathbf(v)) and (-\mathbf(v))", then by axioms 2, 3,4 we obtain their equality:

(-\mathbf(v))"=(-\mathbf(v))"+\underbrace(\mathbf(v)+(-\mathbf(v)))_(\mathbf(o))= \underbrace( (-\mathbf(v))"+\mathbf(v))_(\mathbf(o))+(-\mathbf(v))=(-\mathbf(v)).

The remaining properties are proved similarly.

Examples of linear spaces

1. Let us denote \(\mathbf(o)\) - a set containing one zero vector, with the operations \mathbf(o)+ \mathbf(o)=\mathbf(o) And \lambda \mathbf(o)=\mathbf(o). For the indicated operations, axioms 1-8 are satisfied. Consequently, the set \(\mathbf(o)\) is a linear space over any number field. This linear space is called null.

2. Let us denote V_1,\,V_2,\,V_3 - sets of vectors (directed segments) on a straight line, on a plane, in space, respectively, with the usual operations of adding vectors and multiplying vectors by a number. The fulfillment of axioms 1-8 of linear space follows from the course of elementary geometry. Consequently, the sets V_1,\,V_2,\,V_3 are real linear spaces. Instead of free vectors, we can consider the corresponding sets of radius vectors. For example, a set of vectors on a plane that have a common origin, i.e. plotted from one fixed point of the plane is a real linear space. The set of radius vectors of unit length does not form a linear space, since for any of these vectors the sum \mathbf(v)+\mathbf(v) does not belong to the set under consideration.

3. Let us denote \mathbb(R)^n - a set of matrix-columns of sizes n\times1 with the operations of adding matrices and multiplying matrices by a number. Axioms 1-8 of linear space are satisfied for this set. The zero vector in this set is the zero column o=\begin(pmatrix)0&\cdots&0\end(pmatrix)^T. Consequently, the set \mathbb(R)^n is a real linear space. Similarly, a set \mathbb(C)^n of columns of size n\times1 with complex elements is a complex linear space. The set of column matrices with non-negative real elements, on the contrary, is not a linear space, since it does not contain opposite vectors.

4. Let us denote \(Ax=o\) - the set of solutions of a homogeneous system Ax=o of linear algebraic equations with and unknowns (where A is the real matrix of the system), considered as a set of columns of sizes n\times1 with the operations of adding matrices and multiplying matrices by a number . Note that these operations are indeed defined on the set \(Ax=o\) . From Property 1 of solutions to a homogeneous system (see Section 5.5) it follows that the sum of two solutions of a homogeneous system and the product of its solution by a number are also solutions of a homogeneous system, i.e. belong to the set \(Ax=o\) . The axioms of linear space for columns are satisfied (see point 3 in examples of linear spaces). Therefore, the set of solutions of a homogeneous system is a real linear space.

The set \(Ax=b\) of solutions to the inhomogeneous system Ax=b,~b\ne o , on the contrary, is not a linear space, if only because it does not contain a zero element (x=o is not a solution to the inhomogeneous system).

5. Let us denote M_(m\times n) - a set of matrices of size m\times n with the operations of adding matrices and multiplying matrices by a number. Axioms 1-8 of linear space are satisfied for this set. The zero vector is a zero matrix O of appropriate sizes. Therefore, the set M_(m\times n) is a linear space.

6. Let us denote P(\mathbb(C)) - the set of polynomials of one variable with complex coefficients. The operations of adding many terms and multiplying a polynomial by a number considered as a polynomial of degree zero are defined and satisfy axioms 1-8 (in particular, a zero vector is a polynomial that is identically equal to zero). Therefore, the set P(\mathbb(C)) is a linear space over the field of complex numbers. The set P(\mathbb(R)) of polynomials with real coefficients is also a linear space (but, of course, over the field of real numbers). The set P_n(\mathbb(R)) of polynomials of degree at most n with real coefficients is also a real linear space. Note that the operation of addition of many terms is defined on this set, since the degree of the sum of polynomials does not exceed the degrees of the terms.

The set of polynomials of degree n is not a linear space, since the sum of such polynomials may turn out to be a polynomial of lower degree that does not belong to the set under consideration. The set of all polynomials of degree no higher than n with positive coefficients is also not a linear space, since multiplying such a polynomial by a negative number will result in a polynomial that does not belong to this set.

7. Let us denote C(\mathbb(R)) - the set of real functions defined and continuous on \mathbb(R) . The sum (f+g) of the functions f,g and the product \lambda f of the function f and the real number \lambda are defined by the equalities:

(f+g)(x)=f(x)+g(x),\quad (\lambda f)(x)=\lambda\cdot f(x) for all x\in \mathbb(R)

These operations are indeed defined on C(\mathbb(R)) since the sum of continuous functions and the product of a continuous function and a number are continuous functions, i.e. elements of C(\mathbb(R)) . Let us check the fulfillment of the axioms of linear space. Since the addition of real numbers is commutative, it follows that the equality f(x)+g(x)=g(x)+f(x) for any x\in \mathbb(R) . Therefore f+g=g+f, i.e. axiom 1 is satisfied. Axiom 2 follows similarly from the associativity of addition. The zero vector is the function o(x), identically equal to zero, which, of course, is continuous. For any function f the equality f(x)+o(x)=f(x) holds, i.e. Axiom 3 is true. The opposite vector for the vector f will be the function (-f)(x)=-f(x) . Then f+(-f)=o (axiom 4 is true). Axioms 5, 6 follow from the distributivity of the operations of addition and multiplication of real numbers, and axiom 7 - from the associativity of multiplication of numbers. The last axiom is satisfied, since multiplication by one does not change the function: 1\cdot f(x)=f(x) for any x\in \mathbb(R), i.e. 1\cdot f=f . Thus, the considered set C(\mathbb(R)) with the introduced operations is a real linear space. Similarly, it is proved that C^1(\mathbb(R)),C^2(\mathbb(R)), \ldots, C^m(\mathbb(R))- sets of functions that have continuous derivatives of the first, second, etc. orders, respectively, are also linear spaces.

Let us denote the set of trigonometric binomials (often \omega\ne0 ) with real coefficients, i.e. many functions of the form f(t)=a\sin\omega t+b\cos\omega t, Where a\in \mathbb(R),~b\in \mathbb(R). The sum of such binomials and the product of a binomial by a real number are trigonometric binomials. The linear space axioms for the set under consideration are satisfied (since T_(\omega)(\mathbb(R))\subset C(\mathbb(R))). Therefore, many T_(\omega)(\mathbb(R)) with the usual operations of addition and multiplication by a number for functions, it is a real linear space. The zero element is the binomial o(t)=0\cdot\sin\omega t+0\cdot\cos\omega t, identically equal to zero.

The set of real functions defined and monotone on \mathbb(R) is not a linear space, since the difference of two monotone functions may turn out to be a non-monotone function.

8. Let us denote \mathbb(R)^X - the set of real functions defined on the set X with the operations:

(f+g)(x)=f(x)+g(x),\quad (\lambda f)(x)=\lambda\cdot f(x)\quad \forall x\in X

It is a real linear space (the proof is the same as in the previous example). In this case, the set X can be chosen arbitrarily. In particular, if X=\(1,2,\ldots,n\), then f(X) is an ordered set of numbers f_1,f_2,\ldots,f_n, Where f_i=f(i),~i=1,\ldots,n Such a set can be considered a matrix-column of dimensions n\times1 , i.e. many \mathbb(R)^(\(1,2,\ldots,n\)) coincides with the set \mathbb(R)^n (see point 3 for examples of linear spaces). If X=\mathbb(N) (recall that \mathbb(N) is the set of natural numbers), then we obtain a linear space \mathbb(R)^(\mathbb(N))- many number sequences \(f(i)\)_(i=1)^(\infty). In particular, the set of convergent number sequences also forms a linear space, since the sum of two convergent sequences converges, and when all terms of a convergent sequence are multiplied by a number, we obtain a convergent sequence. In contrast, the set of divergent sequences is not a linear space, since, for example, the sum of divergent sequences may have a limit.

9. Let us denote \mathbb(R)^(+) - the set of positive real numbers in which the sum a\oplus b and the product \lambda\ast a (the notations in this example differ from the usual ones) are defined by the equalities: a\oplus b=ab,~ \lambda\ast a=a^(\lambda), in other words, the sum of elements is understood as a product of numbers, and multiplication of an element by a number is understood as raising to a power. Both operations are indeed defined on the set \mathbb(R)^(+) since the product of positive numbers is a positive number and any real power of a positive number is a positive number. Let's check the validity of the axioms. Equalities

a\oplus b=ab=ba=b\oplus a,\quad a\oplus(b\oplus c)=a(bc)=(ab)c=(a\oplus b)\oplus c

show that axioms 1 and 2 are satisfied. The zero vector of this set is one, since a\oplus1=a\cdot1=a, i.e. o=1 . The opposite vector for a is the vector \frac(1)(a) , which is defined since a\ne o . In fact, a\oplus\frac(1)(a)=a\cdot\frac(1)(a)=1=o. Let's check the fulfillment of axioms 5, 6,7,8:

\begin(gathered) \mathsf(5))\quad \lambda\ast(a\oplus b)=(a\cdot b)^(\lambda)= a^(\lambda)\cdot b^(\lambda) = \lambda\ast a\oplus \lambda\ast b\,;\hfill\\ \mathsf(6))\quad (\lambda+ \mu)\ast a=a^(\lambda+\mu)=a^( \lambda)\cdot a^(\mu)=\lambda\ast a\oplus\mu\ast a\,;\hfill\\ \mathsf(7)) \quad \lambda\ast(\mu\ast a) =(a^(\mu))^(\lambda)=a^(\lambda\mu)=(\lambda\cdot \mu)\ast a\,;\hfill\\ \mathsf(8))\quad 1\ast a=a^1=a\,.\hfill \end(gathered)

All axioms are satisfied. Consequently, the set under consideration is a real linear space.

10. Let V be a real linear space. Let us consider the set of linear scalar functions defined on V, i.e. functions f\colon V\to \mathbb(R), taking real values and satisfying the conditions:

f(\mathbf(u)+\mathbf(v))=f(u)+f(v)~~ \forall u,v\in V(additivity);

f(\lambda v)=\lambda\cdot f(v)~~ \forall v\in V,~ \forall \lambda\in \mathbb(R)(homogeneity).

Linear operations on linear functions are specified in the same way as in paragraph 8 of examples of linear spaces. The sum f+g and the product \lambda\cdot f are defined by the equalities:

(f+g)(v)=f(v)+g(v)\quad \forall v\in V;\qquad (\lambda f)(v)=\lambda f(v)\quad \forall v\ in V,~ \forall \lambda\in \mathbb(R).

The fulfillment of the linear space axioms is confirmed in the same way as in paragraph 8. Therefore, the set of linear functions defined on the linear space V is a linear space. This space is called conjugate to the space V and is denoted by V^(\ast) . Its elements are called covectors.

For example, the set of linear forms of n variables, considered as the set of scalar functions of the vector argument, is the linear space conjugate to the space \mathbb(R)^n.

CHAPTER 8. LINEAR SPACES § 1. Definition of a linear space

Generalizing the concept of a vector, known from school geometry, we will define algebraic structures (linear spaces) in which it is possible to construct n-dimensional geometry, a special case of which will be analytical geometry.

Definition 1. Given a set L=(a,b,c,…) and a field P=( ,…). Let the algebraic operation of addition be defined in L and the multiplication of elements from L by elements of the field P be defined:

The set L is called linear space over the field P, if the following requirements are met (axioms of linear space):

1. L commutative group with respect to addition;

2. α(βa)=(αβ)a α,β P, a L;

3. α(a+b)=αa+αb α P, a,b L;

4. (α+β)a=αa+βa α,β P, a L;

5. a L the following equality is true: 1 a=a (where 1 is the unit of the field P).

The elements of the linear space L are called vectors (we note once again that they will be denoted by the Latin letters a, b, c,...), and the elements of the field P are called numbers (we will denote them by the Greek letters α,

Remark 1. We see that the well-known properties of “geometric” vectors are taken as axioms of linear space.

Remark 2. Some well-known algebra textbooks use different notations for numbers and vectors.

Basic examples of linear spaces

1. R 1 is the set of all vectors on some line.

IN in what follows we will call such vectorssegment vectors on a straight line. If we take R as P, then obviously R1 is a linear space over the field R.

2. R 2 , R3 – segment vectors on the plane and in three-dimensional space. It is easy to see that R2 and R3 are linear spaces over R.

3. Let P be an arbitrary field. Consider the set P(n) all ordered sets of n elements of the field P:

P(n) = (α1 ,α2 ,α3 ,...,αn )| αi P, i=1,2,..,n .

The set a=(α1,α2,…,αn) will be called n-dimensional row vector. The numbers i will be called components

vector a.

For vectors from P(n) , by analogy with geometry, we naturally introduce the operations of addition and multiplication by a number, assuming for any (α1 ,α2 ,…,αn ) P(n) and (β1 ,β2 ,...,βn ) P(n) :

(α1 ,α2 ,…,αn )+(β1 ,β2 ,...,βn )=(α1 +β1 ,α2 +b2 ,...,αn +βn ),
(α1 ,α2 ,…,αn )= (α1 , α2 ,…, αn ) R.

From the definition of addition of row vectors it is clear that it is performed componentwise. It is easy to check that P(n) is a linear space over P.

Vector 0=(0,…,0) is the zero vector (a+0=a a P(n)), and vector -a=(-α1,-α2,…,-αn) is the opposite of a (since . a+(-a)=0).

Linear space P(n) is called the n-dimensional space of row vectors, or n-dimensional arithmetic space.

Remark 3. Sometimes we will also denote by P(n) the n-dimensional arithmetic space of column vectors, which differs from P(n) only in the way the vectors are written.

4. Consider the set M n (P) of all matrices of nth order with elements from the field P. This is a linear space over P, where the zero matrix is a matrix in which all elements are zeros.

5. Consider the set P[x] of all polynomials in the variable x with coefficients from the field P. It is easy to verify that P[x] is a linear space over P. Let us call itspace of polynomials.

6. Let P n [x]=( 0 xn +…+ n | i P, i=0,1,..,n) the set of all polynomials of degree not higher than n together with

0. It is a linear space over the field P. P n [x] we will call space of polynomials of degree at most n.

7. Let us denote by Ф the set of all functions of a real variable with the same domain of definition. Then Ф is a linear space over R.

IN In this space one can find other linear spaces, for example the space of linear functions, differentiable functions, continuous functions, etc.

8. Every field is a linear space above itself.

Some corollaries from the axioms of linear space

Corollary 1. Let L be a linear space over the field P. L contains the zero element 0 and a L (-a) L (since L is an addition group).

IN In what follows, the zero element of the field P and the linear space L will be denoted identically by

0. This usually does not cause confusion.

Corollary 2. 0 a=0 a L (0 P on the left side, 0 L on the right side).

Proof. Let's consider α a, where α is any number from P. We have: α a=(α+0)a=α a+0 a, whence 0 a= α a +(-α a)=0.

Corollary 3. α 0=0 α P.

Proof. Consider α a=α(a+0)=α a+α 0; hence α 0=0. Corollary 4. α a=0 if and only if either α=0 or a=0.

Proof. Adequacy proven in Corollaries 2 and 3.

Let's prove the necessity. Let α a=0 (2). Let us assume that α 0. Then, since α P, then there exists α-1 P. Multiplying (2) by α-1, we obtain:

α-1 (α a)=α-1 0. By Corollary 2 α-1 0=0, i.e. α-1 (α a)=0. (3)

On the other hand, using axioms 2 and 5 of linear space, we have: α-1 (α a)=(α-1 α) a=1 a=a.

From (3) and (4) it follows that a=0. The investigation has been proven.

We present the following statements without proof (their validity is easily verified).

Corollary 5. (-α) a=-α a α P, a L. Corollary 6. α (-a)=-α a α P, a L. Corollary 7. α (a–b)=α a–α b α P, a,b L.

§ 2. Linear dependence of vectors

Let L be a linear space over the field P and a1 ,a2 ,…as (1) be some finite set of vectors from L.

The set a1 ,a2 ,…as will be called a system of vectors.

If b = α1 a1 +α2 a2 +…+αs as , (αi P), then they say that the vector b linearly expressed through system (1), or is linear combination vectors of system (1).

As in analytical geometry, in linear space one can introduce the concepts of linearly dependent and linearly independent systems of vectors. Let's do this in two ways.

Definition I. The finite system of vectors (1) for s 2 is called linearly dependent, if at least one of its vectors is a linear combination of the others. Otherwise (i.e., when none of its vectors is a linear combination of the others), it is called linearly independent.

Definition II. The finite system of vectors (1) is called linearly dependent, if there is a set of numbers α1 ,α2 ,…,αs , αi P, at least one of which is not equal to 0 (such a set is called non-zero), then the equality holds: α1 a1 +…+αs as =0 (2).

From Definition II we can obtain several equivalent definitions of a linearly independent system:

Definition 2.

a) system (1) linearly independent, if from (2) it follows that α1 =…=αs =0.

b) system (1) linearly independent, if equality (2) is satisfied only for all αi =0 (i=1,…,s).

c) system (1) linearly independent, if any non-trivial linear combination of vectors of this system is different from 0, i.e. if β1 , …,βs is any non-zero set of numbers, then β1 a1 +…βs as 0.

Theorem 1. For s 2, the definitions of linear dependence I and II are equivalent.

Proof.

I) Let (1) be linearly dependent by definition I. Then we can assume, without loss of generality, that as =α1 a1 +…+αs-1 as-1 . Let's add the vector (-as) to both sides of this equality. We get:

0= α1 a1 +…+αs-1 as-1 +(-1) as (3) (since by Corollary 5

(–as ) =(-1) as ). In equality (3) the coefficient (-1) is 0, and therefore system (1) is linearly dependent and by definition

II) Let system (1) be linearly dependent by definition II, i.e. there is a non-zero set α1 ,…,αs, which satisfies (2). Without loss of generality, we can assume that αs 0. In (2) we add (-αs as) to both sides. We get:

α1 a1 +α2 a2 +…+αs as - αs as = -αs as , whence α1 a1 +…+αs-1 as-1 = -αs as .

Because αs 0, then there is αs -1 P. Let's multiply both sides of equality (4) by (-αs -1 ) and use some axioms of linear space. We get:

(-αs -1 ) (-αs as )= (-αs -1 )(α1 a1 +…+αs-1 as-1 ), which follows: (-αs -1 α1 ) a1 +…+(-αs - 1) αs-1 as-1 =as.

Let us introduce the notation β1 = -αs -1 α1 ,…, βs-1 =(-αs -1 ) αs-1 . Then the equality obtained above will be rewritten as:

as = β1 a1 +…+ βs-1 as-1 .

Since s 2, there will be at least one vector ai on the right side. We found that system (1) is linearly dependent by Definition I.

The theorem has been proven.

By virtue of Theorem 1, if necessary, for s 2 we can apply any of the above definitions of linear dependence.

Remark 1. If the system consists of only one vector a1, then only the definition is applicable to it

Let a1 =0; then 1a1 =0. Because 1 0, then a1 =0 is a linearly dependent system.

Let a1 0; then α1 a1 ≠0, for any α1 0. This means that the non-zero vector a1 is linearly independent

There are important connections between the linear dependence of the vector system and its subsystems.

Theorem 2. If some subsystem (i.e. part) of a finite system of vectors is linearly dependent, then the entire system is linearly dependent.

The proof of this theorem is not difficult to do on your own. It can be found in any algebra or analytical geometry textbook.

Corollary 1. All subsystems of a linearly independent system are linearly independent. Obtained from Theorem 2 by contradiction.

Remark 2. It is easy to see that linearly dependent systems can have subsystems as linearly

Corollary 2. If a system contains 0 or two proportional (equal) vectors, then it is linearly dependent (since a subsystem of 0 or two proportional vectors is linearly dependent).

§ 3. Maximal linearly independent subsystems

Definition 3. Let a1, a2,…,ak,…. (1) is a finite or infinite system of vectors of linear space L. Its finite subsystem ai1, ai2, …, air (2) is called basis of the system (1) or maximum linearly independent subsystem this system if the following two conditions are met:

1) subsystem (2) is linearly independent;

2) if any vector aj of system (1) is assigned to subsystem (2), then we obtain a linearly dependent

system ai1, ai2, …, air, aj (3).

Example 1. In the space Pn [x], consider the system of polynomials 1,x1 , …, xn (4). Let us prove that (4) is linearly independent. Let α0, α1,…, αn be numbers from P such that α0 1+α1 x+...+αn xn =0. Then, by the definition of equality of polynomials, α0 =α1 =…=αn =0. This means that the system of polynomials (4) is linearly independent.

Let us now prove that system (4) is a basis of the linear space Pn [x].

For any f(x) Pn [x] we have: f(x)=β0 xn +…+βn 1 Pn [x]; therefore, f(x) is a linear combination of vectors (4); then the system 1,x1 , …, xn ,f(x) is linearly dependent (by definition I). Thus, (4) is a basis of the linear space Pn [x].

Example 2. In Fig. 1 a1, a3 and a2, a3 – bases of the system of vectors a1,a2,a3.

Theorem 3. Subsystem (2) ai1 ,…, air of a finite or infinite system (1) a1 , a2 ,…,as ,… is a maximal linearly independent subsystem (basis) of system (1) if and only if

a) (2) linearly independent; b) any vector from (1) is linearly expressed through (2).

Necessity . Let (2) be a maximal linearly independent subsystem of system (1). Then two conditions from Definition 3 are satisfied:

1) (2) linearly independent.

2) For any vector a j from (1) the system ai1 ,…, ais ,aj (5) is linearly dependent. It is necessary to prove that statements a) and b) are true.

Condition a) coincides with 1); therefore, a) is satisfied.

Further, by virtue of 2) there is a non-zero set α1 ,...,αr ,β P (6) such that α1 ai1 +…+αr air +βaj =0 (7). Let us prove that β 0 (8). Let's assume that β=0 (9). Then from (7) we obtain: α1 ai1 +…+αr air =0 (10). From the fact that set (6) is non-zero and β=0 it follows that α1 ,...,αr is a non-zero set. And then from (10) it follows that (2) is linearly dependent, which contradicts condition a). This proves (8).

By adding the vector (-βaj) to both sides of equalities (7), we obtain: -βaj = α1 ai1 +…+αr air. Since β 0, then

there is β-1 P; multiply both sides of the last equality by β-1: (β-1 α1 )ai1 +…+ (β-1 αr )air =aj . Let's introduce

notation: (β-1 α1 )= 1 ,…, (β-1 αr )= r ; thus, we got: 1 ai1 +…+ r air =aj ; therefore, the satisfiability of condition b) has been proven.

The need has been proven.

Sufficiency. Let conditions a) and b) from Theorem 3 be satisfied. It is necessary to prove that conditions 1) and 2) from Definition 3 are satisfied.

Since condition a) coincides with condition 1), then 1) is satisfied.

Let us prove that 2) holds. By condition b), any vector aj (1) is linearly expressed through (2). Consequently, (5) is linearly dependent (by definition 1), i.e. 2) is fulfilled.

The theorem has been proven.

Comment. Not every linear space has a basis. For example, there is no basis in the space P[x] (otherwise, the degrees of all polynomials in P[x] would be, as follows from paragraph b) of Theorem 3, collectively bounded).

§ 4. The main theorem about linear dependence. Its consequences

Definition 4. Let two finite systems of vectors of linear space L:a1 ,a2 ,…,al (1) and

b1 ,b2 ,…,bs (2).

If each vector of system (1) is linearly expressed through (2), then we will say that system (1)

is linearly expressed through (2). Examples:

1. Any subsystem of a system 1 ,…,ai ,…,ak is linearly expressed through the entire system, because

ai =0 a1 +…+1 ai +…+0 ak .

2. Any system of segment vectors from R2 is linearly expressed through a system consisting of two non-collinear plane vectors.

Definition 5. If two finite systems of vectors are linearly expressed through each other, then they are called equivalent.

Note 1. The number of vectors in two equivalent systems may be different, as can be seen from the following examples.

3. Each system is equivalent to its basis (this follows from Theorem 3 and Example 1).

4. Any two systems segment vectors from R2, each of which contains two non-collinear vectors, are equivalent.

The following theorem is one of the most important statements in the theory of linear spaces. Basic theorem about linear dependence. Let in a linear space L over a field P be given two

vector systems:

a1 ,a2 ,…,al (1) and b1 ,b2 ,…,bs (2), and (1) is linearly independent and linearly expressed through (2). Then l s (3). Proof. We need to prove inequality (3). Let us assume the opposite, let l>s (4).

By condition, each vector ai from (1) is linearly expressed through system (2):

a1 =α11 b1 +α12 b2 +…+α1s bs a2 =α21 b1 +a22 b2 +…+α2s bs

…………………... (5)

al =αl1 b1 +αl2 b2 +…+αls bs .

Let's make the following equation: x1 a1 +x2 a2 +…+x1 al =0 (6), where xi are unknowns taking values from the field P (i=1,…,s).

Let's multiply each of the equalities (5), respectively, by x1,x2,...,xl, substitute into (6) and put together the terms containing b1, then b2 and, finally, bs. We get:

x1 a1 +…+xl al = (α11 x1 +α21 x2 + … +αl1 xl )b1	+ (α12 x1 +α22 x2 + … +αl2 xl )b2 + …+(α1s x1 +α2s x2 +…+αls xl )bs =0.

Let's try to find a non-zero solution	equation (6). To do this, let us equate to zero all
coefficients for bi (i=1, 2,…,s) and compose the following system of equations:
α11 x1 +α21 x2 + … +αl1 xl =0
α12 x1 +α22 x2 +…+αl2 xl =0
…………………….

α1s x1 +α2s x2 +…+αls xl =0.

(8) homogeneous system s of equations for unknowns x 1 ,…,xl . She is always cooperative.

IN By virtue of inequality (4), in this system the number of unknowns is greater than the number of equations, and therefore, as follows from the Gauss method, it is reduced to a trapezoidal form. This means that there are non-zero

solutions to system (8). Let us denote one of them by x1 0 ,x2 0 ,…,xl 0 (9), xi 0 P (i=1, 2,…s).

Substituting numbers (9) into the left side of (7), we obtain: x1 0 a1 +x2 0 a2 +…+xl 0 al =0 b1 +0 b2 +…+0 bs =0. (10)

So, (9) is a non-zero solution to equation (6). Therefore, system (1) is linearly dependent, and this contradicts the condition. Therefore, our assumption (4) is incorrect and l s.

The theorem has been proven.

Corollaries from the main theorem about linear dependence Corollary 1. Two finite equivalent linearly independent vector systems consist of

the same number of vectors.

Proof. Let the systems of vectors (1) and (2) be equivalent and linearly independent. To prove this, we apply the main theorem twice.

Because system (2) is linearly independent and linearly expressed through (1), then by the main theorem l s (11).

On the other hand, (1) is linearly independent and is linearly expressed through (2), and by the main theorem s l (12).

From (11) and (12) it follows that s=l. The statement has been proven.

Corollary 2. If in some system of vectors a1 ,…,as ,… (13) (finite or infinite) there are two bases, then they consist of the same number of vectors.

Proof. Let ai1 ,…,ail (14) and aj1 ,..ajk (15) be the bases of system (13). Let us show that they are equivalent.

According to Theorem 3, each vector of system (13) is linearly expressed through its basis (15), in particular, any vector of system (14) is linearly expressed through system (15). Similarly, system (15) is linearly expressed through (14). This means that systems (14) and (15) are equivalent and by Corollary 1 we have: l=k.

The statement has been proven.

Definition 6. The number of vectors in an arbitrary basis of a finite (infinite) system of vectors is called the rank of this system (if there are no bases, then the rank of the system does not exist).

By Corollary 2, if system (13) has at least one basis, its rank is unique.

Remark 2. If a system consists only of zero vectors, then we assume that its rank is 0. Using the concept of rank, we can strengthen the main theorem.

Corollary 3. Given two finite systems of vectors (1) and (2), and (1) is linearly expressed through (2). Then the rank of system (1) does not exceed the rank of system (2).

Proof . Let us denote the rank of system (1) by r1, the rank of system (2) by r2. If r1 =0, then the statement is true.

Let r1 0. Then r2 0, because (1) is linearly expressed through (2). This means that systems (1) and (2) have bases.

Let a1 ,…,ar1 (16) be the basis of system (1) and b1 ,…,br2 (17) be the basis of system (2). They are linearly independent by definition of the basis.

Because (16) is linearly independent, then the main theorem can be applied to the pair of systems (16), (17). According to this

theorem r1 r2 . The statement has been proven.

Corollary 4. Two finite equivalent systems of vectors have the same ranks. To prove this statement, we need to apply Corollary 3 twice.

Remark 3. Note that the rank of a linearly independent system of vectors is equal to the number of its vectors (since in a linearly independent system its only basis coincides with the system itself). Therefore, Corollary 1 is a special case of Corollary 4. But without proof of this special case, we would not be able to prove Corollary 2, introduce the concept of the rank of a system of vectors and obtain Corollary 4.

§ 5. Finite-dimensional linear spaces

Definition 7. A linear space L over a field P is called finite-dimensional if there is at least one basis in L.

Basic examples of finite-dimensional linear spaces:

1. Vector segments on a straight line, a plane and in space (linear spaces R1, R2, R3).

2. n-dimensional arithmetic space P(n) . Let us show that in P(n) there is the following basis: e1 =(1,0,…,0)

e2 =(0,1,…,0) (1)

en =(0,0,…1).

Let us first prove that (1) is a linearly independent system. Let's create the equation x1 e1 +x2 e2 +…+xn en =0 (2).

Using the form of vectors (1), we rewrite equation (2) as follows: x1 (1,0,…,0)+x2 (0,1,…,0)+…+xn (0,0,…,1)=( x1 , x2 , …,xn )=(0,0,…,0).

By the definition of equality of row vectors, it follows:

x1 =0, x2 =0,…, xn =0 (3). Therefore, (1) is a linearly independent system. Let us prove that (1) is a basis of the space P(n) using Theorem 3 on bases.

For any a=(α1 ,α2 ,…,αn ) Pn we have:

а=(α1 ,α2 ,…,αn )=(α1 ,0,…,0)+(0,α2 ,…,0)+(0,0,…,αn )= 1 e1 + 2 e2 +…+ n en .

This means that any vector in the space P(n) can be linearly expressed through (1). Consequently, (1) is a basis of the space P(n), and therefore P(n) is a finite-dimensional linear space.

3. Linear space Pn [x]=(α0 xn +...+αn | αi P).

It is easy to verify that the basis of the space Pn [x] is the system of polynomials 1,x,…,xn. So Pn

[x] is a finite-dimensional linear space.

4. Linear space M n(P). It can be verified that the set of matrices of the form Eij , in which the only non-zero element 1 is at the intersection of the i-th row and the j-th column (i,j=1,…,n), constitute the basis Mn (P).

Corollaries from the main theorem on linear dependence for finite-dimensional linear spaces

Along with the corollaries of the main linear dependence theorem 1–4, several other important statements can be obtained from this theorem.

Corollary 5. Any two bases of a finite-dimensional linear space consist of the same number of vectors.

This statement is a special case of Corollary 2 from the main linear dependence theorem applied to the entire linear space.

Definition 8. The number of vectors in an arbitrary basis of a finite-dimensional linear space L is called the dimension of this space and is denoted by dim L.

By Corollary 5, every finite-dimensional linear space has a unique dimension. Definition 9. If a linear space L has dimension n, then it is called n-dimensional

linear space. Examples:

1. dim R 1 =1;

2. dimR 2 =2;

3. dimP (n) =n, i.e. P(n) is an n-dimensional linear space, because above, in example 2 it is shown that (1) is the basis

P(n);

4. dimP n [x]=(n+1), because, as is easy to check, 1,x,x2 ,…,xn is a basis of n+1 vectors of this space;

5. dimM n (P)=n2, because there are exactly n2 matrices of the form Eij indicated in example 4.

Corollary 6. In an n-dimensional linear space L, any n+1 vectors a1 ,a2 ,…,an+1 (3) constitute a linearly dependent system.

Proof. By definition of the dimension of space in L, there is a basis of n vectors: e1 ,e2 ,…,en (4). Let's consider a pair of systems (3) and (4).

Let us assume that (3) is linearly independent. Because (4) is a basis of L, then any vector of the space L can be linearly expressed through (4) (by Theorem 3 from §3). In particular, system (3) is linearly expressed through (4). By assumption (3) it is linearly independent; then the main theorem on linear dependence can be applied to the pair of systems (3) and (4). We get: n+1 n, which is impossible. The contradiction proves that (3) is linearly dependent.

The investigation has been proven.

Remark 1. From Corollary 6 and Theorem 2 from §2 we obtain that in an n-dimensional linear space any finite system of vectors containing more than n vectors is linearly dependent.

From this remark it follows

Corollary 7. In an n-dimensional linear space, any linearly independent system contains at most n vectors.

Remark 2. Using this statement we can establish that some linear spaces are not finite-dimensional.

Example. Let us consider the space of polynomials P[x] and prove that it is not finite-dimensional. Let us assume that dim P[x]=m, m N. Consider 1, x,…, xm – a set of (m+1) vectors from P[x]. This system of vectors, as noted above, is linearly independent, which contradicts the assumption that the dimension of P[x] is equal to m.

It is easy to check (using P[x]) that finite-dimensional linear spaces are not the spaces of all functions of a real variable, spaces of continuous functions, etc.

Corollary 8. Any finite linearly independent system of vectors a1 , a2 ,…,ak (5) of a finite-dimensional linear space L can be supplemented to the basis of this space.

Proof. Let n=dim L. Let's consider two possible cases.

1. If k=n, then a 1 , a2 ,…,ak is a linearly independent system of n vectors. By Corollary 7, for any b L the system a1 , a2 ,…,ak , b is linearly dependent, i.e. (5) – basis L.

2. Let k n. Then system (5) is not a basis of L, which means there exists a vector a k+1 L, that a1 , a2 ,…,ak , ak+1 (6) is a linearly independent system. If (k+1)

By Corollary 7, this process ends after a finite number of steps. We obtain a basis a1 , a2 ,…,ak , ak+1 ,…,an of the linear space L, containing (5).

The investigation has been proven.

From Corollary 8 it follows

Corollary 9. Any non-zero vector of a finite-dimensional linear space L is contained in some basis L (since such a vector is a linearly independent system).

It follows that if P is an infinite field, then in a finite-dimensional linear space over the field P there are infinitely many bases (since in L there are infinitely many vectors of the form a, a 0, P\0).

§ 6. Isomorphism of linear spaces

Definition 10. Two linear spaces L and L` over one field P are called isomorphic if there is a bijection: L L` satisfying the following conditions:

1. (a+b)= (a)+ (b) a, b L,

2. (a)= (a) P, a L.

Such a mapping itself is called an isomorphism or isomorphic mapping.

Properties of isomorphisms.

1. With isomorphism, the zero vector becomes zero.

Proof. Let a L and: L L` be an isomorphism. Since a=a+0, then (a)= (a+0)= (a)+ (0).

Because (L)=L` then from the last equality it is clear that (0) (we denote it by 0`) is the zero vector from

2. With isomorphism, a linearly dependent system transforms into a linearly dependent system. Proof. Let a1 , a2 ,…,as (2) be some linearly dependent system from L. Then there exists

a non-zero set of numbers 1 ,…, s (3) from P, such that 1 a1 +…+ s as =0. Let us subject both sides of this equality to an isomorphic mapping. Taking into account the definition of isomorphism, we get:

1 (a1 )+…+ s (as )= (0)=0` (we used property 1). Because set (3) is non-zero, then from the last equality it follows that (1),..., (s) is a linearly dependent system.

3. If: L L` is an isomorphism, then -1 : L` L is also an isomorphism.

Proof. Since is a bijection, then there is a bijection -1 : L` L. We need to prove that if a`,

Since it is an isomorphism, then a`+b`= (a)+ (b) = (a+b). It follows from this:

a+b= -1 ((a+b))= -1 ((a)+ (b)).

From (5) and (6) we have -1 (a`+b`)=a+b= -1 (a`)+ -1 (b`).

Similarly, it is checked that -1 (a`)= -1 (a`). So, -1 is an isomorphism.

The property has been proven.

4. With isomorphism, a linearly independent system transforms into a linearly independent system. Proof. Let: L L` is an isomorphism and a1, a2,…,as (2) is a linearly independent system. Required

prove that (a1), (a2),…, (as) (7) is also linearly independent.

Let us assume that (7) is linearly dependent. Then, when displaying -1, it goes into the system a1,...,as.

By property 3 -1 is an isomorphism, and then by property 2, system (2) will also be linearly dependent, which contradicts the condition. Therefore, our assumption is incorrect.

The property has been proven.

5. With isomorphism, the basis of any system of vectors goes into the basis of the system of its images. Proof. Let a1 , a2 ,…,as ,… (8) be a finite or infinite system of linear vectors

space L, : L L` is an isomorphism. Let system (8) have basis ai1 , …,air (9). Let us show that the system

(a1),…, (ak),… (10) has a basis (ai1),…, (air) (11).

Since (9) is linearly independent, then by property 4 system (11) is linearly independent. Let us assign to (11) any vector from (10); we get: (ai1), …, (air), (aj) (12). Consider the system ai1 , …,air , aj (13). It is linearly dependent, since (9) is the basis of system (8). But (13) under isomorphism turns into (12). Since (13) is linearly dependent, then by property 2 system (12) is also linearly dependent. This means that (11) is the basis of system (10).

Applying Property 5 to the entire finite-dimensional linear space L, we obtain

Statement 1. Let L be an n-dimensional linear space over the field P, : L L` isomorphism. Then L` is also a finite-dimensional space and dim L`= dim L = n.

In particular, Statement 2 is true. If finite-dimensional linear spaces are isomorphic, then their dimensions are equal.

Comment. In §7 the validity of the converse to this statement will also be established.

§ 7. Vector coordinates

Let L be a finite-dimensional linear space over the field P and e1 ,...,en (1) be some basis of L.

Definition 11. Let a L. Let us express the vector a through basis (1), i.e. a= 1 e1 +…+ n en (2), i P (i=1,…,n). Column (1,…, n)t (3) is called coordinate column vector a in basis (1).

The coordinate column of vector a in basis e is also denoted by [a], [a]e or [1,.., n].

As in analytical geometry, the uniqueness of the vector expression through the basis is proved, i.e. the uniqueness of the coordinate column of the vector in a given basis.

Note 1. In some textbooks, instead of coordinate columns, coordinate lines are considered (for example, in the book). In this case, the formulas obtained there in the language of coordinate columns look different.

Theorem 4. Let L be an n-dimensional linear space over the field P and (1) be some basis of L. Consider the mapping: a (1,..., n)t, which associates any vector a from L with its coordinate column in basis (1). Then is an isomorphism of the spaces L and P(n) (P(n) is an n-dimensional arithmetic space of column vectors).

Proof . The mapping is unique due to the uniqueness of the vector coordinates. It is easy to check that is a bijection and (a)= (a), (a)+ (b)= (a+b). This means isomorphism.

The theorem has been proven.

Corollary 1. A system of vectors a1 ,a2 ,…,as of a finite-dimensional linear space L is linearly dependent if and only if the system consisting of the coordinate columns of these vectors in some basis of the space L is linearly dependent.

The validity of this statement follows from Theorem 1 and the second and fourth properties of isomorphism. Remark 2. Corollary 1 allows us to study the question of the linear dependence of systems of vectors in

in a finite-dimensional linear space can be reduced to solving the same question for the columns of a certain matrix.

Theorem 5 (criterion for isomorphism of finite-dimensional linear spaces). Two finite-dimensional linear spaces L and L` over one field P are isomorphic if and only if they have the same dimension.

Necessity. Let L L` By virtue of Statement 2 from §6, the dimension of L coincides with the dimension of L1.

Adequacy. Let dim L = dim L`= n. Then, by Theorem 4, we have: L P(n)		and L` P(n) . From here
it is not difficult to obtain that L L`.
The theorem has been proven.
Note. In what follows, we will often denote an n-dimensional linear space by Ln.
§ 8. Transition matrix
Definition 12. Let in the linear space Ln	two bases are given:
e= (е1,...еn) and e`=(e1`,...,e`n) (old and new).
Let us expand the vectors of the basis e` into the basis e:
e`1 =t11 e1 +…+tn1 en
…………………..

e`n =t1n e1 +…+tnn en .

t11………t1n

T= ……………

tn1………tnn

called transition matrix from basis e to basis e`.

Note that it is convenient to write equalities (1) in matrix form as follows: e` = eT (2). This equality is equivalent to defining the transition matrix.

Remark 1. Let us formulate a rule for constructing a transition matrix: to construct a transition matrix from a basis e to a basis e`, for all vectors ej` of the new basis e`, we need to find their coordinate columns in the old basis e and write them as the corresponding columns of the matrix T.

Note 2. In the book, the transition matrix is compiled row by row (from the coordinate rows of the vectors of the new basis in the old one).

Theorem 6. The transition matrix from one basis of the n-dimensional linear space Ln over the field P to its other basis is a non-degenerate matrix of nth order with elements from the field P.

Proof. Let T be the transition matrix from basis e to basis e`. The columns of the matrix T, by definition 12, are the coordinate columns of the vectors of the basis e` in the basis e. Since e` is a linearly independent system, then by Corollary 1 of Theorem 4 the columns of the matrix T are linearly independent, and therefore |T|≠0.

The theorem has been proven.

The converse is also true.

Theorem 7. Any non-degenerate square matrix of the nth order with elements from the field P serves as a transition matrix from one basis of the n-dimensional linear space Ln over the field P to some other basis Ln.

Proof . Let the basis e = (e1, ..., en) of the linear space L and a non-singular square matrix be given

Т= t11………t1n

tn1………tnn

nth order with elements from the field P. In the linear space Ln, consider an ordered system of vectors e`=(e1 `,…,e`n), for which the columns of the matrix T are coordinate columns in the basis e.

The system of vectors e` consists of n vectors and, by virtue of Corollary 1 of Theorem 4, is linearly independent, since the columns of a non-singular matrix T are linearly independent. Therefore, this system is the basis of the linear space Ln, and due to the choice of system vectors e` the equality e`=eT holds. This means that T is the transition matrix from basis e to basis e`.

The theorem has been proven.

Relationship between the coordinates of vector a in different bases

Let the bases e=(е1,...еn) and e`=(e1`,...,e`n) be given in the linear space Ln with the transition matrix T from the basis e to the basis e`, i.e. (2) is true. Vector a has coordinates in the bases e and e` [a]e =(1 ,…, n)T and [a]e` =(1 `,…,

n `)T , i.e. a=e[a]e and a=e`[a]e` .

Then, on the one hand, a=e[a]e , and on the other a=e`[a]e` =(eT)[a]e` =e(T[a]e` ) (we used the equality ( 2)). From these equalities we get: a=e[a]e =e(T[a]e` ). Hence, due to the uniqueness of the expansion of the vector in basis

This implies the equality [a]e =Т[a]e` (3), or




	n` .

Relations (3) and (4) are called coordinate transformation formulas when the basis of linear space changes. They express the old vector coordinates in terms of the new ones. These formulas can be resolved relative to the new vector coordinates by multiplying (4) on the left by T-1 (such a matrix exists, since T is a non-singular matrix).

Then we get: [a]e` =T-1 [a]e . Using this formula, knowing the coordinates of the vector in the old basis e of the linear space Ln, you can find its coordinates in the new basis, e`.

§ 9. Subspaces of linear space

Definition 13. Let L be a linear space over the field P and H L. If H is also a linear space over P with respect to the same operations as L, then H is called subspace linear space L.

Statement 1. A subset H of a linear space L over a field P is a subspace of L if the following conditions are satisfied:

1. h 1 +h2 H for any h1 , h2 H;

2. h H for any h H and P.

Proof. If conditions 1 and 2 are satisfied in H, then addition and multiplication by elements of the field P are specified in H. The validity of most of the linear space axioms for H follows from their validity for L. Let us check some of them:

a) 0 h=0 H (due to condition 2);

b) h H we have: (-h)=(-1)h H (due to condition 2).

The statement has been proven.

1. The subspaces of any linear space L are 0 and L.

2. R 1 – subspace of the space R2 of segment vectors on the plane.

3. The space of functions of a real variable has, in particular, the following subspaces:

a) linear functions of the form ax+b;

b) continuous functions; c) differentiable functions.

One universal way of identifying subspaces of any linear space is associated with the concept of a linear hull.

Definition 14. Let a1 ,…as (1) be an arbitrary finite system of vectors in linear space L. Let us call linear shell of this system set ( 1 a1 +…+ s as | i P) = . The linear shell of system (1) is also denoted by L(a1 ,…,as ).

Theorem 8. The linear hull H of any finite system of vectors (1) of a linear space L is a finite-dimensional subspace of the linear space L. The basis of system (1) is also a basis of H, and the dimension of H is equal to the rank of system (1).

Proof. Let H= . From the definition of a linear hull it easily follows that conditions 1 and 2 of Statement 1 are satisfied. By virtue of this statement, H is a subspace of the linear space L. Let ai1 ,….,air (2) be the basis of system (1). Then we have: any vector h H is linearly expressed through (1) - by definition of a linear shell, and (1) is linearly expressed through its basis (2). Since (2) is a linearly independent system, it is the basis of N. But the number of vectors in (2) is equal to the rank of system (1). This means dimH=r.

The theorem has been proven.

Remark 1. If H is a finite-dimensional subspace of the linear space L and h1 ,...,hm is a basis of H, then it is easy to see that H=