Apibrėžtinis integralas ir jo skaičiavimo metodai. Apibrėžtasis integralas

Trapecijos metodas

Pagrindinis straipsnis:Trapecijos metodas

Jei funkcija kiekviename iš dalinių atkarpų yra aproksimuota tiese, einančia per baigtines reikšmes, tada gauname trapecijos metodą.

Trapecijos plotas kiekviename segmente:

Apytikslė kiekvieno segmento klaida:

Kur

Visa trapecijos formulė, padalijus visą integravimo intervalą į vienodo ilgio segmentus:

Kur

Trapecijos formulės klaida:

Kur

Simpsono metodas.

Integrand f(x) pakeičiamas antrojo laipsnio interpoliacijos daugianario P(x)– parabolė, einanti per tris mazgus, pavyzdžiui, kaip parodyta paveiksle ((1) – funkcija, (2) – daugianomas).

Panagrinėkime du integravimo etapus ( h= const = x i+1 – x i), tai yra trys mazgai x 0, x 1, x 2, per kurią nubrėžiame parabolę naudodami Niutono lygtį:

Leiskite z = x - x 0,
Tada

Dabar, naudodamiesi gautu ryšiu, apskaičiuojame integralą per šį intervalą:

.
Už vienodas tinklelis Ir lyginis žingsnių skaičius n Simpsono formulė yra tokia:

Čia , A darant ketvirtosios integrando išvestinės tęstinumo prielaidą.

[taisyti] Padidėjęs tikslumas

Funkcijos aproksimavimas vienu polinomu per visą integravimo intervalą, kaip taisyklė, lemia didelę integralo vertės įvertinimo paklaidą.

Siekiant sumažinti paklaidą, integravimo segmentas yra padalintas į dalis ir kiekvienoje iš jų integralas įvertinamas skaitmeniniu metodu.

Kadangi skaidinių skaičius linkęs į begalybę, integralo įvertis linkęs į jo tikrąją reikšmę bet kurio skaitmeninio metodo analitinėms funkcijoms.

Aukščiau pateikti metodai leidžia atlikti paprastą žingsnio sumažinimo per pusę procedūrą, kai kiekvieno žingsnio funkcijos reikšmės turi būti skaičiuojamos tik naujai pridėtuose mazguose. Skaičiavimo paklaidai įvertinti naudojama Runge taisyklė.

Runge taisyklės taikymas

redaguoti]Tam tikro integralo skaičiavimo tikslumo įvertinimas

Integralas apskaičiuojamas naudojant pasirinktą formulę (stačiakampiai, trapecijos, Simpsono parabolės), kai žingsnių skaičius lygus n, o tada žingsnių skaičius lygus 2n. Klaida apskaičiuojant integralo vertę, kai žingsnių skaičius lygus 2n, nustatoma pagal Runge formulę:
, stačiakampių ir trapecijų formulėms bei Simpsono formulei.
Taigi integralas apskaičiuojamas nuoseklioms žingsnių skaičiaus reikšmėms, kur n 0 yra pradinis žingsnių skaičius. Skaičiavimo procesas baigiamas, kai įvykdoma kitos reikšmės N sąlyga, kur ε yra nurodytas tikslumas.

Klaidų elgesio ypatybės.

Atrodytų, kam analizuoti skirtingus integravimo metodus, jei didelio tikslumo galime pasiekti tiesiog sumažinę integravimo žingsnio dydį. Tačiau apsvarstykite užpakalinės klaidos elgesio grafiką R skaitinio skaičiavimo rezultatai priklausomai nuo ir iš numerio n intervalų skaidiniai (tai yra žingsnyje . (1) sekcijoje paklaida sumažėja dėl žingsnio h sumažėjimo. Tačiau (2) sekcijoje pradeda dominuoti skaičiavimo paklaida, kuri kaupiasi dėl daugybės aritmetinių operacijų. Taigi metodas turi savo Rmin, kuris priklauso nuo daugelio veiksnių, bet pirmiausia nuo metodo klaidos a priori reikšmės R.

Rombergo aiškinamoji formulė.

Rombergo metodas susideda iš nuoseklaus integralo vertės patikslinimo, daug kartų padidinus skaidinių skaičių. Pagrindas gali būti trapecijos formulė su vienodais žingsniais h.
Pažymime integralą skaidinių skaičiumi n= 1 as .
Sumažinus žingsnį per pusę, gauname .
Jei paeiliui sumažinsime žingsnį 2 n kartų, gausime pasikartojimo santykį, skirtą apskaičiuoti .

Programos vertė vidutinės vertės teoremos slypi galimybėje gauti kokybinį tam tikro integralo vertės įvertį jo neskaičiuojant. Suformuluokime : jei funkcija yra ištisinė intervale, tai šiame intervale yra taškas, kad .

Ši formulė yra gana tinkama apytiksliai įvertinti sudėtingos ar sudėtingos funkcijos integralą. Vienintelis dalykas, kuris sudaro formulę apytikslis , yra būtinybė nepriklausomas pasirinkimas taškais Jei eisime paprasčiausiu keliu – integravimo intervalo viduriu (kaip siūloma daugelyje vadovėlių), tai klaida gali būti gana didelė. Norėdami gauti tikslesnį rezultatą rekomenduojame atlikite skaičiavimus tokia seka:

Sukurkite funkcijos grafiką intervale ;

Nubrėžkite viršutinę stačiakampio ribą taip, kad funkcijos grafiko ribinės dalys būtų maždaug vienodo ploto (būtent tai pavaizduota aukščiau esančiame paveikslėlyje – du kreiviniai trikampiai yra beveik identiški);

Nustatykite pagal figūrą;

Naudokite vidutinės vertės teoremą.

Pavyzdžiui, apskaičiuokime paprastą integralą:

Tiksli vertė;

Intervalo viduriui taip pat gauname apytikslę reikšmę, t.y. aiškiai netikslus rezultatas;

Sudarę grafiką, kurio viršutinė stačiakampio pusė nubrėžta pagal rekomendacijas, gauname , taigi apytikslę reikšmę . Gana patenkinamas rezultatas, paklaida 0,75%.

Trapecijos formulė

Skaičiavimų, naudojant vidutinės vertės teoremą, tikslumas labai priklauso, kaip buvo parodyta, nuo vizualinis tikslas pagal punktų tvarkaraštį. Iš tiesų, tame pačiame pavyzdyje pasirinkę taškus arba , galite gauti kitas integralo reikšmes ir paklaida gali padidėti. Subjektyvūs veiksniai, grafiko mastelis ir piešimo kokybė labai įtakoja rezultatą. Tai nepriimtina atliekant kritinius skaičiavimus, todėl vidutinės reikšmės teorema taikoma tik greitai kokybės integraliniai įverčiai.

Šiame skyriuje apžvelgsime vieną iš populiariausių apytikslės integracijos metodų - trapecijos formos formulė . Pagrindinė šios formulės sukūrimo idėja pagrįsta tuo, kad kreivę galima apytiksliai pakeisti laužta linija, kaip parodyta paveikslėlyje.

Tikslumui (ir pagal paveikslą) tarkime, kad integravimo intervalas yra padalintas į lygus (tai neprivaloma, bet labai patogu) dalių. Kiekvienos iš šių dalių ilgis apskaičiuojamas pagal formulę ir vadinamas žingsnis . Perskirstymo taškų abscisės, jei nurodytos, nustatomos pagal formulę, kur . Naudojant žinomas abscises, lengva apskaičiuoti ordinates. Taigi,

Tai yra atvejo trapecijos formos formulė. Atkreipkite dėmesį, kad pirmasis skliausteliuose esantis narys yra pradinių ir galutinių ordinačių pusė, prie kurios pridedamos visos tarpinės ordinatės. Savavališkam integravimo intervalo skaidinių skaičiui bendroji trapecijos formulė turi formą: kvadratūros formulės: stačiakampiai, Simpsonai, Gauso ir kt. Jie pagrįsti ta pačia idėja vaizduoti kreivinę trapeciją įvairių formų elementariais plotais, todėl įvaldžius trapecijos formulę suprasti panašias formules nebus sunku. Daugelis formulių nėra tokios paprastos kaip trapecijos formos formulės, tačiau jos leidžia gauti didelio tikslumo rezultatus su nedideliu skaičiumi skaidinių.

Naudodami trapecijos formulę (ar panašias), praktikoje reikalaujamu tikslumu galite apskaičiuoti tiek „neatliekamus“ integralus, tiek sudėtingų ar sudėtingų funkcijų integralus.

Pagal apibrėžtą integralą iš nuolatinės funkcijos f(x) paskutiniame segmente [ a, b] (kur ) yra kai kurių jo antidarinių padidėjimas šiame segmente. (Apskritai, supratimas bus pastebimai lengvesnis, jei kartosite neapibrėžto integralo temą) Šiuo atveju naudojamas žymėjimas

Kaip matyti iš toliau pateiktų grafikų (antidarinės funkcijos padidėjimas pažymėtas ), apibrėžtasis integralas gali būti teigiamas arba neigiamas skaičius(Jis apskaičiuojamas kaip skirtumas tarp antidarinio vertės viršutinėje riboje ir vertės apatinėje riboje, t.y. F(b) - F(a)).

Skaičiai a Ir b vadinamos atitinkamai apatine ir viršutine integracijos ribomis, o segmentas [ a, b] – integracijos segmentas.

Taigi, jei F(x) – tam tikra antiderivatinė funkcija f(x), tada pagal apibrėžimą

(38)

Lygybė (38) vadinama Niutono-Leibnizo formulė . Skirtumas F(b) – F(a) trumpai parašyta taip:

Todėl Niutono-Leibnizo formulę parašysime taip:

(39)

Įrodykime, kad apibrėžtasis integralas nepriklauso nuo to, kuri integrando antidarinė imama jį skaičiuojant. Leiskite F(x) ir F( X) yra savavališki integrando antidariniai. Kadangi tai yra tos pačios funkcijos antidariniai, jie skiriasi pastoviu terminu: Ф( X) = F(x) + C. Štai kodėl

Tai nustato, kad segmente [ a, b] visų funkcijos antidarinių prieaugiai f(x) rungtynės.

Taigi, norint apskaičiuoti apibrėžtąjį integralą, reikia rasti bet kurią integrando antidarinę, t.y. Pirmiausia reikia rasti neapibrėžtą integralą. Pastovus SU neįtraukti į tolesnius skaičiavimus. Tada taikoma Niutono-Leibnizo formulė: viršutinės ribos reikšmė pakeičiama antiderivatine funkcija b , toliau – apatinės ribos reikšmė a ir skirtumas apskaičiuojamas F(b) – F(a) . Gautas skaičius bus apibrėžtas integralas..

At a = b pagal apibrėžimą priimtas

1 pavyzdys.

Sprendimas. Pirmiausia suraskime neapibrėžtą integralą:

Niutono-Leibnizo formulės taikymas antidariniui

(at SU= 0), gauname

Tačiau skaičiuojant apibrėžtąjį integralą, geriau neieškoti antidarinio atskirai, o iš karto integralą rašyti formoje (39).

2 pavyzdys. Apskaičiuokite apibrėžtąjį integralą

Sprendimas. Naudojant formulę

Apibrėžtinio integralo savybės

2 teorema.Apibrėžtinio integralo reikšmė nepriklauso nuo integravimo kintamojo žymėjimo, t.y.

(40)

Leiskite F(x) – antidarinis skirtas f(x). Už f(t) antidarinys atlieka tą pačią funkciją F(t), kuriame nepriklausomas kintamasis žymimas tik skirtingai. Vadinasi,

Remiantis (39) formule, paskutinė lygybė reiškia integralų lygybę

3 teorema.Pastovųjį veiksnį galima išimti iš apibrėžtojo integralo ženklo, t.y.

(41)

4 teorema.Baigtinio skaičiaus funkcijų algebrinės sumos apibrėžtasis integralas yra lygus šių funkcijų apibrėžtųjų integralų algebrinei sumai, t.y.

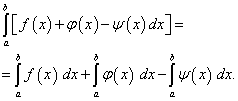(42)

5 teorema.Jei integralinis segmentas yra padalintas į dalis, tai viso segmento apibrėžtasis integralas yra lygus jo dalių apibrėžtųjų integralų sumai, t.y. Jeigu

(43)

6 teorema.Perstatant integravimo ribas, absoliuti apibrėžtojo integralo reikšmė nekinta, o keičiasi tik jo ženklas, t.y.

(44)

7 teorema(vidutinės vertės teorema). Apibrėžiamasis integralas yra lygus integravimo atkarpos ilgio sandaugai ir integrando vertei tam tikrame jo viduje, t.y.

(45)

8 teorema.Jei integravimo viršutinė riba yra didesnė už apatinę, o integrandas yra neneigiamas (teigiamas), tai apibrėžtasis integralas taip pat yra neneigiamas (teigiamas), t.y. Jeigu

9 teorema.Jei integracijos viršutinė riba yra didesnė už apatinę, o funkcijos ir yra tolydžios, tada nelygybė

gali būti integruotas po termino, t.y.

(46)

Apibrėžtinio integralo savybės leidžia supaprastinti tiesioginį integralų skaičiavimą.

5 pavyzdys. Apskaičiuokite apibrėžtąjį integralą

Naudodami 4 ir 3 teoremas ir radę antidarinius - lentelės integralus (7) ir (6), gauname

Apibrėžiamasis integralas su kintama viršutine riba

Leiskite f(x) – ištisinis segmente [ a, b] funkcija ir F(x) yra jo antidarinys. Apsvarstykite apibrėžtąjį integralą

(47)

ir per t integravimo kintamasis nurodomas taip, kad nebūtų painiojamas su viršutine riba. Keičiant X kinta ir apibrėžtasis integralas (47), t.y. tai yra viršutinės integracijos ribos funkcija X, kurį žymime F(X), t.y.

(48)

Įrodykime, kad funkcija F(X) yra antidarinys, skirtas f(x) = f(t). Iš tiesų, diferencijavimas F(X), gauname

nes F(x) – antidarinis skirtas f(x), A F(a) yra pastovi reikšmė.

Funkcija F(X) – vienas iš begalinio skaičiaus antidarinių, skirtų f(x), būtent tą x = a eina į nulį. Šis teiginys gaunamas, jei į lygybę (48) įdedame x = a ir naudokite ankstesnės pastraipos 1 teoremą.

Apibrėžtinių integralų skaičiavimas integravimo dalimis metodu ir kintamojo kaitos metodu

kur pagal apibrėžimą F(x) – antidarinis skirtas f(x). Jei integrande pakeisime kintamąjį

tada pagal (16) formulę galime rašyti

Šioje išraiškoje

antiderivatinė funkcija

Tiesą sakant, jo išvestinė, anot sudėtingų funkcijų diferenciacijos taisyklė, yra lygus

Tegul α ir β yra kintamojo reikšmės t, kuriai skirta funkcija

atitinkamai paima vertybes a Ir b, t.y.

Tačiau pagal Niutono-Leibnizo formulę skirtumas F(b) – F(a) Yra

Teorema. Jei funkcija f(x) integruojamas intervale [ a, b], kur a< b , ir visiems x ∈ nelygybė galioja

Naudojant teoremos nelygybes, galima įvertinti apibrėžtąjį integralą, t.y. nurodykite ribas, tarp kurių yra jo reikšmė. Šios nelygybės išreiškia apibrėžtojo integralo įvertį.

Teorema [Mean Theorem]. Jei funkcija f(x) integruojamas intervale [ a, b] ir visiems x ∈ nelygybės tenkinamos m ≤ f(x) ≤ M, Tai

Kur m ≤ μ ≤ M.

komentuoti. Tuo atveju, kai funkcija f(x) yra nuolatinis intervale [ a, b], lygybė iš teoremos įgauna formą

Kur c ∈. Skaičius μ=f(c), apibrėžiamas šia formule, vadinamas vidutinė vertė funkcijas f(x) segmente [ a, b]. Ši lygybė turi šiuos dalykus geometrine prasme: išlenktos trapecijos, apribotos ištisine linija, plotas y=f(x) (f(x) ≤ 0), yra lygus stačiakampio plotui su tuo pačiu pagrindu ir aukščiu, lygus kurio nors šios linijos taško ordinatėms.

Antidarinio buvimas nuolatinei funkcijai

Pirmiausia pristatome integralo su kintama viršutine riba sąvoką.

Tegul funkcija f(x) integruojamas intervale [ a, b]. Tada kad ir koks būtų skaičius x iš [ a, b], funkcija f(x) integruojamas intervale [ a, b]. Todėl intervalu [ a, b] funkcija apibrėžta

kuris vadinamas integralu su kintama viršutine riba.

Teorema. Jei integrandas yra tęstinis intervale [ a, b], tada apibrėžtojo integralo su kintamąja viršutine riba išvestinė egzistuoja ir yra lygi šios ribos integrando reikšmei, tai yra

Pasekmė. Apibrėžtas integralas su kintama viršutine riba yra vienas iš ištisinio integrando antidarinių. Kitaip tariant, bet kuriai funkcijai, kuri tęsiasi intervale, yra antidarinys.

1 pastaba. Atkreipkite dėmesį, kad jei funkcija f(x) integruojamas intervale [ a, b], tada integralas su kintama viršutine riba yra viršutinės ribos funkcija, ištisinė šiame segmente. Iš tiesų, iš St.2 ir vidutinės vertės teoremos turime

2 pastaba. Integralas su kintama viršutine integravimo riba naudojamas apibrėžiant daugybę naujų funkcijų, pavyzdžiui, . Šios funkcijos nėra pagrindinės; kaip jau buvo pažymėta, nurodytų integrandų antidariniai nėra išreikšti elementariomis funkcijomis.

Pagrindinės integracijos taisyklės

Niutono-Leibnizo formulė

Kadangi bet kurios dvi antiderivatinės funkcijos f(x) skiriasi konstanta, tai pagal ankstesnę teoremą galima teigti, kad bet koks antidarinys Φ(x) ištisinis segmente [ a, b] funkcijas f(x) atrodo kaip

Kur C- kai kurie pastovūs.

Darant prielaidą, kad šioje formulėje x=a Ir x=b, naudojant st.1 apibrėžtuosius integralus, randame

Šios lygybės reiškia santykį

kuris vadinamas Niutono-Leibnizo formulė.

Taigi mes įrodėme tokią teoremą:

Teorema. Nenutrūkstamos funkcijos apibrėžtasis integralas yra lygus skirtumui tarp bet kurio iš jo antidarinių verčių viršutinei ir apatinei integracijos riboms.

Niutono-Leibnizo formulę galima perrašyti kaip

Kintamojo keitimas apibrėžtajame integrale

Teorema. Jeigu

• funkcija f(x) yra nuolatinis intervale [ a, b];
• segmentas [ a, b] yra funkcijos reikšmių rinkinys φ(t), apibrėžtas segmente α ≤ t ≤ β ir turintis ištisinę išvestinę priemonę;
• φ(α)=a, φ(β)=b

tada formulė teisinga

Integravimo pagal dalis formulė

Teorema. Jei funkcijos u=u(x), v=v(x) turi tęstines išvestines intervale [ a, b], tada formulė galioja

Anksčiau apibrėžtą integralą laikėme integrando antidarinio verčių skirtumu. Buvo daroma prielaida, kad integrandas turi antidarinį integravimo intervale.

Tuo atveju, kai antidarinys išreiškiamas elementariomis funkcijomis, galime būti tikri jo egzistavimu. Bet jei tokios išraiškos nėra, tada klausimas apie antidarinės egzistavimą lieka atviras, ir mes nežinome, ar egzistuoja atitinkamas apibrėžtasis integralas.

Geometriniai svarstymai rodo, kad nors, pavyzdžiui, funkcijai y=e^(-x^2) neįmanoma išreikšti antidarinės elementariomis funkcijomis, integralas \textstyle(\int\limits_(a)^(b)e^(-x^2)\,dx) egzistuoja ir yra lygus figūros plotui, kurį riboja x ašis, funkcijos y=e^(-x^2) grafikas ir tiesės x=a,~ x=b (6 pav. ). Tačiau atlikus kruopštesnę analizę paaiškėja, kad pati srities samprata turi būti pagrįsti, todėl negalima ja remtis sprendžiant antidarinio ir apibrėžtojo integralo egzistavimo klausimus.

Įrodykime tai bet kuri intervalo tęstinė funkcija turi šio intervalo antidarinį, todėl šiame segmente yra tam tikras integralas. Kad tai padarytume, mums reikia kitokio požiūrio į apibrėžtojo integralo sąvoką, kuris nesiremtų prielaida, kad egzistuoja antidarinys.

Pirmiausia nustatykime keletą apibrėžtojo integralo savybės, suprantamas kaip antidarinio verčių skirtumas.

Apibrėžtųjų integralų įverčiai

1 teorema. Tegul funkcija y=f(x) apribota intervale ir m=\min_(x\in)f(x) Ir M=\max_(x\in)f(x), atitinkamai, mažiausia ir didžiausia funkcijos y=f(x) reikšmės ant , o šiame segmente funkcija y=f(x) turi antidarinę. Tada

m(b-a)\leqslant \int\limits_(a)^(b)f(x)\,dx\leqslant M(b-a).

Įrodymas. Tegu F(x) yra vienas iš funkcijos y=f(x) atkarpoje antidarinių. Tada

\int\limits_(a)^(b)f(x)\,dx=\Bigl.(F(x))\Bigr|_(a)^(b)=F(b)-F(a).

Pagal Lagranžo teoremą F(b)-F(a)=F"(c)(b-a), kur a \int\limits_(a)^(b)f(x)\,dx=f(c)(b-a).

Pagal sąlygą visoms segmento x reikšmėms galioja ši nelygybė: m\leqslant f(x)\leqslant M, Štai kodėl m\leqslant f(c)\leqslant M ir todėl

m(b-a)\leqslant f(c)(b-a)\leqslant M(b-a), tai yra m(b-a)\leqslant \int\limits_(a)^(b)f(x)\,dx\leqslant M(b-a),

Q.E.D.

Dviguba nelygybė (1) suteikia tik labai apytikslį apibrėžtojo integralo vertės įvertinimą. Pavyzdžiui, atkarpoje funkcijos y=x^2 reikšmės yra nuo 1 iki 25, todėl atsiranda nelygybės

4=1\cdot(5-1)\leqslant\int\limits_(1)^(5)x^2\,dx\leqslant 25\cdot(5-1)=100.

Norėdami gauti tikslesnį įvertinimą, padalinkite segmentą į kelias dalis su taškais a=x_0 ir kiekvienai daliai taikoma nelygybė (1). Jei segmente galioja nelygybė, tada

m_k\cdot\Delta x_k\leqslant \int\limits_(x_k)^(x_(k+1)) f(x)\,dx\leqslant M_k\cdot \Delta x_k\,

kur \Delta x_k žymi skirtumą (x_(k+1)-x_k), t.y. atkarpos ilgį. Užrašę šias nelygybes visoms k reikšmėms nuo 0 iki n-1 ir jas sudėjus, gauname:

\sum_(k=0)^(n-1)(m_k\cdot\Delta x_k) \leqslant \sum_(k=0)^(n-1) \int\limits_(x_k)^(x_(k+1) ))f(x)\,dx\leqslant \sum_(k=0)^(n-1) (M_k\cdot \Delta x_k),

Bet pagal adityvią apibrėžtojo integralo savybę integralų suma per visas atkarpos dalis yra lygi integralui virš šios atkarpos, t.y.

\sum_(k=0)^(n-1) \int\limits_(x_k)^(x_(k+1))f(x)\,dx= \int\limits_a)^(b)f(x) \,dx\,.

Reiškia,

\sum_(k=0)^(n-1)(m_k\cdot\Delta x_k) \leqslant \sum_(k=0)^(n-1) \int\limits_(a)^(b)f(x) )\,dx\leqslant \sum_(k=0)^(n-1) (M_k\cdot \Delta x_k)

Pavyzdžiui, jei padalinsite segmentą į 10 lygių dalių, kurių kiekvienos ilgis yra 0,4, tada į dalinį segmentą nelygybė galioja

(1+0,\!4k)^2\leqslant x^2\leqslant \bigl(1+0,\!4(k+1)\bigr)^2

Todėl mes turime:

0,\!4\sum_(k=0)^(9)(1+0,\!4k)^2\leqslant \int\limits_(1)^(5)x^2\,dx\leqslant 0, \!4\sum_(k=0)^(9)\bigl(1+0,\!4(k+1)\bigr)^2.

Skaičiuodami gauname: 36,\!64\leqslant \int\limits_(1)^(5) x^2\,dx\leqslant 46,\!24. Šis įvertinimas yra daug tikslesnis nei anksčiau gautas 4\leqslant\int\limits_(1)^(5)x^2\,dx\leqslant100.

Norint gauti dar tikslesnį integralo įvertį, atkarpą reikia padalyti ne į 10, o, tarkime, į 100 ar 1000 dalių ir paskaičiuoti atitinkamas sumas. Žinoma, šį integralą lengviau apskaičiuoti naudojant antidarinį:

\int\limits_(1)^(5)x^2\,dx= \left.(\frac(x^3)(3))\right|_(1)^(5)= \frac(1) (3)(125-1)= \frac(124)(3)\,.

Bet jei antidarinės išraiška mums nežinoma, tai nelygybės (2) leidžia įvertinti integralo reikšmę iš apačios ir iš viršaus.

Apibrėžtinis integralas kaip dalijamasis skaičius

Skaičiai m_k ir M_k, įtraukti į nelygybę (2), gali būti pasirinkti savavališkai, jei nelygybė tenkinama kiekvienoje atkarpoje m_k\leqslant f(x)\leqslant M_k. Tiksliausias integralo įvertis tam tikrai atkarpos daliai gaunamas, jei laikysime M_k mažiausią, o m_k kaip didžiausią iš visų galimų reikšmių. Tai reiškia, kad kaip m_k turime paimti tikslią apatinę funkcijos y=f(x) reikšmių ribą segmente, o kaip M_k tikslią viršutinę šių verčių ribą tame pačiame segmente:

m_k=\inf_(x\in)f(x),\qquad M_k=\sup_(x\in)f(x).

Jei y=f(x) yra apribota atkarpos funkcija, tada ji taip pat yra apribota kiekvienoje atkarpoje, todėl jai skaičiai m_k ir M_k,~ 0\leqslant k\leqslant n-1. Pasirinkus skaičius m_k ir M_k, sumos \textstyle(\sum\limits_(k=0)^(n-1)m_k\Delta x_k) Ir \textstyle(\sum\limits_(k=0)^(n-1)M_k\Delta x_k) atitinkamai vadinamos apatine ir viršutine Darboux integralų sumomis funkcijai y=-f(x) tam tikram skirsniui P:

a=x_0

segmentas Šias sumas pažymėsime atitinkamai s_(fP) ir S_(fP), o jei funkcija y=f(x) yra fiksuota, tai tiesiog s_P ir S_P.

Nelygybė (2) reiškia, kad jei funkcija y=f(x), apribota intervalu, turi šio intervalo priešišvestinę, tai apibrėžtasis integralas atskiria skaitines aibes \(s_p\) ir \(S_P\) , kurias sudaro atitinkamai visos apatinės ir viršutinės Darboux sumos visos galimos intervalo pertvaros P. Paprastai tariant, gali atsitikti taip, kad skaičius, skiriantis šias dvi aibes, nėra unikalus. Tačiau toliau pamatysime, kad svarbiausioms funkcijų klasėms (ypač nuolatinėms funkcijoms) jis yra unikalus.

Tai leidžia mums pateikti naują apibrėžimą \textstyle(\int\limits_(a)^(b) f(x)\,dx), kuris nėra pagrįstas antidarinio koncepcija, o naudoja tik Darboux sumas.

Apibrėžimas. Funkcija y=f(x), apribota intervalu, vadinama integruojama šiame intervale, jei yra vienas skaičius \ell, skiriantis apatinių ir viršutinių Darboux sumų aibes, sudarytas visoms galimoms intervalo dalims. Jei funkcija y=f(x) yra integruojama į intervalą, tai vienintelis skaičius, skiriantis šias aibes, vadinamas apibrėžtuoju šios funkcijos integralu per intervalą ir reiškia .

Mes apibrėžėme integralą \textstyle(\int\limits_(a)^(b) f(x)\,dx) tuo atveju, kai a b , tada dedame