Sudėtingas pavyzdys, kaip rasti atvirkštinę matricos vertę. Atvirkštinės matricos radimo metodai

Tam tikros matricos atvirkštinė matrica yra tokia matrica, padauginus pradinę, iš kurios gaunama tapatumo matrica: Privaloma ir pakankama atvirkštinės matricos buvimo sąlyga yra ta, kad pradinės matricos determinantas yra nelygu nuliui (o tai savo ruožtu reiškia, kad matrica turi būti kvadratinė). Jei matricos determinantas yra lygus nuliui, tada jis vadinamas vienaskaita ir tokia matrica neturi atvirkštinės reikšmės. Aukštojoje matematikoje atvirkštinės matricos yra svarbios ir naudojamos sprendžiant daugybę problemų. Pavyzdžiui, ant rasti atvirkštinę matricą buvo sukonstruotas matricinis lygčių sistemų sprendimo metodas. Mūsų paslaugų svetainė leidžia Apskaičiuokite atvirkštinę matricą internete du metodai: Gauso-Jordano metodas ir naudojant algebrinių priedų matricą. Pirmasis apima daugybę elementariųjų transformacijų matricos viduje, antrasis apima determinanto ir algebrinių priedų skaičiavimą prie visų elementų. Norėdami apskaičiuoti matricos determinantą internete, galite pasinaudoti kita mūsų paslauga - Matricos determinanto skaičiavimas internetu

Raskite atvirkštinę svetainės matricą

svetainę leidžia rasti atvirkštinė matrica internete greitai ir nemokamai. Svetainėje atliekami skaičiavimai, naudojant mūsų paslaugą, o rezultatas pateikiamas kartu su išsamiu paieškos sprendimu atvirkštinė matrica. Serveris visada pateikia tik tikslų ir teisingą atsakymą. Užduotyse pagal apibrėžimą atvirkštinė matrica internete, būtina, kad determinantas matricos buvo ne nulis, kitaip svetainę praneš, kad atvirkštinės matricos rasti neįmanoma dėl to, kad pradinės matricos determinantas yra lygus nuliui. Užduotis surasti atvirkštinė matrica randama daugelyje matematikos šakų, yra viena iš pagrindinių algebros sąvokų ir matematinė taikomųjų problemų priemonė. Nepriklausomas atvirkštinės matricos apibrėžimas reikalauja didelių pastangų, daug laiko, skaičiavimų ir didelio kruopštumo, kad būtų išvengta rašybos klaidų ar smulkių klaidų skaičiavimuose. Todėl mūsų paslauga rasti atvirkštinę matricą internetežymiai palengvins jūsų užduotį ir taps nepakeičiamu įrankiu sprendžiant matematinius uždavinius. Net jei tu rasti atvirkštinę matricą patys, rekomenduojame patikrinti sprendimą mūsų serveryje. Įveskite savo pradinę matricą mūsų svetainėje Apskaičiuokite atvirkštinę matricą internete ir patikrinkite savo atsakymą. Mūsų sistema niekada nedaro klaidų ir neranda atvirkštinė matrica duotas matmuo režimu internete iš karto! Svetainėje svetainę simbolių įrašai leidžiami elementuose matricos, šiuo atveju atvirkštinė matrica internete bus pateikta bendra simboline forma.

Tegu pateikta kvadratinė matrica. Turite rasti atvirkštinę matricą.

Pirmas būdas. 4.1 teorema apie atvirkštinės matricos egzistavimą ir unikalumą nurodo vieną iš būdų ją rasti.

1. Apskaičiuokite šios matricos determinantą. Jei, tada atvirkštinė matrica neegzistuoja (matrica yra vienaskaita).

2. Sukurkite matricą iš matricos elementų algebrinių komplementų.

3. Perkelkite matricą, kad gautumėte jungtinę matricą .

4. Raskite atvirkštinę matricą (4.1) padalydami visus adjungtinės matricos elementus iš determinanto

Antras būdas. Norėdami rasti atvirkštinę matricą, galite naudoti elementariąsias transformacijas.

1. Sukurkite bloko matricą, duotai matricai priskirdami tos pačios eilės tapatybės matricą.

2. Naudodami elementarias transformacijas, atliktas matricos eilutėse, perkelkite kairįjį bloką į paprasčiausią formą. Šiuo atveju bloko matrica sumažinama iki formos, kurioje yra kvadratinė matrica, gauta transformuojant tapatybės matricą.

3. Jei , tai blokas yra lygus matricos atvirkštinei, t.y. Jei, tada matrica neturi atvirkštinės.

Tiesą sakant, elementariųjų matricos eilučių transformacijų pagalba galima sumažinti jos kairįjį bloką į supaprastintą formą (žr. 1.5 pav.). Šiuo atveju blokinė matrica transformuojama į formą, kur yra elementarioji matrica, tenkinanti lygybę. Jei matrica yra neišsigimusi, tai pagal 3.3 pastabos 2 pastraipą jos supaprastinta forma sutampa su tapatybės matrica. Tada iš lygybės išplaukia, kad. Jei matrica yra vienaskaita, tada jos supaprastinta forma skiriasi nuo tapatybės matricos, o matrica neturi atvirkštinės.

11. Matricinės lygtys ir jų sprendimas. SLAE įrašymo matricinė forma. Matricos metodas (atvirkštinės matricos metodas) SLAE sprendimui ir jo taikymo sąlygos.

Matricinės lygtys yra tokios formos lygtys: A*X=C; X*A=C; Su kiekvienu SLAE galima susieti keletą matricų; Be to, pats SLAE gali būti parašytas matricos lygties forma. SLAE (1) atveju apsvarstykite šias matricas:

Matrica A vadinama sistemos matrica. Šios matricos elementai atspindi tam tikros SLAE koeficientus.

Matrica A˜ vadinama išplėstinė matricinė sistema. Jis gaunamas į sistemos matricą įtraukus stulpelį, kuriame yra laisvieji terminai b1,b2,...,bm. Paprastai šis stulpelis aiškumo dėlei atskiriamas vertikalia linija.

Stulpelio matrica B vadinama laisvųjų narių matrica, o stulpelio matrica X yra nežinomųjų matrica.

Naudojant aukščiau pateiktą žymėjimą, SLAE (1) galima parašyti matricos lygties forma: A⋅X=B.

Pastaba

Su sistema susietas matricas galima rašyti įvairiai: viskas priklauso nuo nagrinėjamos SLAE kintamųjų ir lygčių eilės. Bet bet kuriuo atveju nežinomųjų tvarka kiekvienoje tam tikros SLAE lygtyje turi būti tokia pati.

Matricos metodas tinka sprendžiant SLAE, kuriose lygčių skaičius sutampa su nežinomų kintamųjų skaičiumi, o pagrindinės sistemos matricos determinantas skiriasi nuo nulio. Jei sistemoje yra daugiau nei trys lygtys, atvirkštinės matricos radimas reikalauja didelių skaičiavimo pastangų, todėl šiuo atveju patartina naudoti Gauso metodas.

12. Homogeniniai SLAE, jų nenulinių sprendimų egzistavimo sąlygos. Vienarūšių SLAE dalinių tirpalų savybės.

Tiesinė lygtis vadinama vienalyte, jei jos laisvasis narys yra lygus nuliui, o nehomogeniška kitaip. Sistema, susidedanti iš vienalyčių lygčių, vadinama vienalyte ir turi bendrą formą:

13 .Tiesinio nepriklausomumo ir vienalytės SLAE dalinių sprendinių priklausomybės samprata. Fundamentali sprendinių sistema (FSD) ir jos nustatymas. Homogeninio SLAE bendro sprendimo vaizdavimas per FSR.

Funkcinė sistema y 1 (x ), y 2 (x ), …, y n (x ) vadinamas tiesiškai priklausomas per intervalą ( a , b ), jei yra pastovių koeficientų, kurie tuo pačiu metu nėra lygūs nuliui, rinkinys, kad tiesinis šių funkcijų derinys būtų identiškas nuliui. a , b ): Už . Jei lygybė už galima tik , funkcijų sistema y 1 (x ), y 2 (x ), …, y n (x ) vadinamas tiesiškai nepriklausomas per intervalą ( a , b ). Kitaip tariant, funkcijos y 1 (x ), y 2 (x ), …, y n (x ) tiesiškai priklausomas per intervalą ( a , b ), jei yra lygus nuliui ( a , b ) jų netrivialus tiesinis derinys. Funkcijos y 1 (x ),y 2 (x ), …, y n (x ) tiesiškai nepriklausomas per intervalą ( a , b ), jei tik jų trivialus tiesinis derinys yra identiškas nuliui ( a , b ).

Fundamentali sprendimų sistema (FSR) Vienalytis SLAE yra šios kolonų sistemos pagrindas.

Elementų skaičius FSR yra lygus sistemos nežinomųjų skaičiui atėmus sistemos matricos rangą. Bet kuris pradinės sistemos sprendimas yra tiesinis FSR sprendimų derinys.

Teorema

Bendras nehomogeninio SLAE sprendimas yra lygus nehomogeninio SLAE konkretaus tirpalo ir atitinkamo vienarūšio SLAE bendrojo sprendinio sumai.

1 . Jei stulpeliai yra vienalytės lygčių sistemos sprendiniai, tai bet koks tiesinis jų derinys taip pat yra vienalytės sistemos sprendimas.

Iš tiesų iš lygybių išplaukia, kad

tie. tiesinis sprendinių derinys yra vienalytės sistemos sprendimas.

2. Jei vienalytės sistemos matricos rangas yra lygus , tai sistema turi tiesiškai nepriklausomus sprendinius.

Iš tiesų, naudodamiesi formulėmis (5.13) bendram homogeninės sistemos sprendimui, randame konkrečius sprendimus, laisviesiems kintamiesiems suteikiant tokius standartinių reikšmių rinkiniai (kiekvieną kartą darant prielaidą, kad vienas iš laisvųjų kintamųjų yra lygus vienetui, o kiti lygūs nuliui):

kurios yra tiesiškai nepriklausomos. Tiesą sakant, jei iš šių stulpelių sukuriate matricą, tada paskutinės jos eilutės sudaro tapatybės matricą. Vadinasi, paskutinėse eilutėse esantis minorinis nėra lygus nuliui (lygus vienetui), t.y. yra pagrindinis. Todėl matricos rangas bus lygus. Tai reiškia, kad visi šios matricos stulpeliai yra tiesiškai nepriklausomi (žr. 3.4 teoremą).

Bet koks tiesiškai nepriklausomų vienalytės sistemos sprendinių rinkinys vadinamas pamatinė sprendinių sistema (aibė). .

14 Antrosios eilės minoras, pagrindinis minoras, matricos rangas. Matricos rango apskaičiavimas.

Matricos A eilės k minor yra kai kurios jos kvadratinės k eilės submatricos determinantas.

Matricoje A, kurios matmenys m x n, r eilės mažoji vadinama bazine, jei ji nėra lygi nuliui, o visos aukštesnės eilės mažosios, jei jos egzistuoja, yra lygios nuliui.

Matricos A stulpeliai ir eilutės, kurių sankirtoje yra pagrindinė mažoji, vadinami A baziniais stulpeliais ir eilutėmis.

1 teorema. (Apie matricos rangą). Bet kurios matricos šalutinis rangas yra lygus eilutės rangui ir lygus stulpelio rangui.

2 teorema. (Pagrindas minor). Kiekvienas matricos stulpelis suskaidomas į linijinį pagrindinių stulpelių derinį.

Matricos rangas (arba šalutinis rangas) yra pagrindinės mažosios eilės arba, kitaip tariant, didžiausios eilės, kuriai egzistuoja ne nulis, eilė. Nulinės matricos rangas pagal apibrėžimą laikomas 0.

Atkreipkime dėmesį į dvi akivaizdžias mažo rango savybes.

1) Transponavimo metu matricos rangas nesikeičia, nes transponuojant matricą, perkeliamos visos jos submatricos, o antraeiliai nesikeičia.

2) Jei A’ yra matricos A submatrica, tai A’ rangas neviršija A rango, nes į A’ įtrauktas nenulinis nepilnametis taip pat įtraukiamas į A.

15. -dimensinio aritmetinio vektoriaus samprata. Vektorių lygybė. Veiksmai su vektoriais (sudėti, atimti, daugyba iš skaičiaus, daugyba iš matricos). Linijinis vektorių derinys.

Užsakyta kolekcija n vadinami tikrieji arba kompleksiniai skaičiai n matmenų vektorius. Skaičiai skambinami vektoriaus koordinates.

Du (ne nuliniai) vektoriai a Ir b yra vienodi, jei yra vienodai nukreipti ir turi tą patį modulį. Visi nuliniai vektoriai laikomi lygiais. Visais kitais atvejais vektoriai nėra lygūs.

Vektorių papildymas. Yra du vektorių pridėjimo būdai: 1. Lygiagretaus taisyklė. Norėdami pridėti vektorius ir, dedame abiejų ištakas tame pačiame taške. Statome iki lygiagretainio ir iš to paties taško nubrėžiame lygiagretainio įstrižainę. Tai bus vektorių suma.

2. Antrasis vektorių pridėjimo būdas yra trikampio taisyklė. Paimkime tuos pačius vektorius ir . Antrojo pradžią pridėsime prie pirmojo vektoriaus pabaigos. Dabar sujungkime pirmojo pradžią ir antrojo pabaigą. Tai vektorių ir suma. Naudodami tą pačią taisyklę, galite pridėti kelis vektorius. Mes juos išdėstome vieną po kito, o tada sujungiame pirmojo pradžią su paskutinio pabaiga.

Vektorių atėmimas. Vektorius nukreiptas priešais vektoriui. Vektorių ilgiai lygūs. Dabar aišku, kas yra vektorinė atimtis. Skirtumas tarp vektorių ir yra vektoriaus ir vektoriaus suma.

Vektoriaus padauginimas iš skaičiaus

Padauginus vektorių iš skaičiaus k, gaunamas vektorius, kurio ilgis yra k kartų didesnis už ilgį. Jis yra kartu su vektoriumi, jei k yra didesnis už nulį, ir priešingas, jei k yra mažesnis už nulį.

Vektorių skaliarinė sandauga yra vektorių ilgių ir kampo tarp jų kosinuso sandauga. Jei vektoriai yra statmeni, jų skaliarinė sandauga yra lygi nuliui. Ir taip skaliarinė sandauga išreiškiama per vektorių koordinates ir .

Linijinis vektorių derinys

Linijinis vektorių derinys vadinamas vektoriumi

Kur - tiesinės kombinacijos koeficientai. Jeigu derinys vadinamas trivialiu, jei jis yra nereikšmingas.

16 .Aritmetinių vektorių skaliarinė sandauga. Vektoriaus ilgis ir kampas tarp vektorių. Vektoriaus ortogonalumo samprata.

Vektorių a ir b skaliarinė sandauga yra skaičius

Skaliarinė sandauga naudojama skaičiuojant: 1) tarp jų esantį kampą 2) vektoriaus ilgio apskaičiavimą 4) vektorių statmenumo sąlygas;

Atkarpos AB ilgis vadinamas atstumu tarp taškų A ir B. Kampas tarp vektorių A ir B vadinamas kampu α = (a, b), 0≤ α ≤P. Pagal kurį reikia pasukti 1 vektorių, kad jo kryptis sutaptų su kitu vektoriumi. Su sąlyga, kad jų kilmė sutampa.

Ortomas a yra vektorius a, turintis ilgio ir krypties a vienetą.

17. Vektorių sistema ir jos tiesinis derinys. Vektorių sistemos tiesinės priklausomybės ir nepriklausomumo samprata. Teorema apie vektorių sistemos tiesinės priklausomybės būtinas ir pakankamas sąlygas.

Vektorių a1,a2,...,an sistema vadinama tiesiškai priklausoma, jei yra tokių skaičių λ1,λ2,...,λn, kad bent vienas iš jų būtų lygus nuliui, o λ1a1+λ2a2+...+λnan=0 . Priešingu atveju sistema vadinama tiesiškai nepriklausoma.

Du vektoriai a1 ir a2 vadinami kolineariniais, jei jų kryptys yra vienodos arba priešingos.

Trys vektoriai a1, a2 ir a3 vadinami lygiagrečiais, jei jie yra lygiagretūs kokiai nors plokštumai.

Geometriniai tiesinės priklausomybės kriterijai:

a) sistema (a1,a2) yra tiesiškai priklausoma tada ir tik tada, kai vektoriai a1 ir a2 yra kolinearūs.

b) sistema (a1,a2,a3) yra tiesiškai priklausoma tada ir tik tada, kai vektoriai a1,a2 ir a3 yra vienodi.

teorema. (Būtina ir pakankama sąlyga tiesinei priklausomybei sistemos vektoriai.)

Vektorinė sistema vektorius erdvė yra linijinis priklausomas tada ir tik tada, kai vienas iš sistemos vektorių yra tiesiškai išreikštas kitais vektoriusšią sistemą.

1 išvada. Vektorių sistema vektorių erdvėje yra tiesiškai nepriklausoma tada ir tik tada, kai nė vienas sistemos vektorius nėra tiesiškai išreikštas kitais šios sistemos vektoriais.2. Vektorių sistema, turinti nulinį vektorių arba du lygius vektorius, yra tiesiškai priklausoma.

Atvirkštinės matricos radimas- problema, kuri dažnai išsprendžiama dviem būdais:

• algebrinių sudėjimų metodas, kai reikia rasti determinantus ir transponuoti matricas;
• Gauso nežinomųjų pašalinimo metodas, kurio metu reikia atlikti elementarias matricų transformacijas (sudėti eilutes, padauginti eilutes iš to paties skaičiaus ir pan.).

Tiems, kuriems ypač įdomu, yra ir kitų metodų, pavyzdžiui, tiesinių transformacijų metodas. Šioje pamokoje analizuosime tris minėtus atvirkštinės matricos radimo metodus ir algoritmus taikant šiuos metodus.

Atvirkštinė matrica A, tokia matrica vadinama

A
. (1)

Atvirkštinė matrica , kurią reikia rasti duotai kvadratinei matricai A, tokia matrica vadinama

kurio sandauga matricos A dešinėje yra tapatybės matrica, t.y.
. (1)

Tapatybės matrica yra įstrižainė, kurioje visi įstrižainės elementai yra lygūs vienetui.

Teorema.Kiekvienai nevienskaitinei (neišsigimusiai, ne vienaskaitinei) kvadratinei matricai galima rasti atvirkštinę matricą ir tik vieną. Specialiai (išsigimusiai, vienaskaitei) kvadratinei matricai atvirkštinė matrica neegzistuoja.

Kvadratinė matrica vadinama neypatingas(arba neišsigimęs, ne vienaskaita), jei jo determinantas nėra nulis, ir ypatingas(arba išsigimęs, vienaskaita), jei jo determinantas lygus nuliui.

Matricos atvirkštinę vertę galima rasti tik kvadratinei matricai. Natūralu, kad atvirkštinė matrica taip pat bus kvadratinė ir tokios pat eilės kaip ir duotoji matrica. Matrica, kuriai galima rasti atvirkštinę matricą, vadinama apverčiamąja matrica.

Už atvirkštinė matrica Yra atitinkama analogija su skaičiaus atvirkštine verte. Už kiekvieną skaičių a, nelygus nuliui, yra toks skaičius b kad darbas a Ir b lygus vienam: ab= 1. Skaičius b vadinamas atvirkštine skaičiaus b. Pavyzdžiui, skaičiaus 7 atvirkštinė vertė yra 1/7, nes 7*1/7=1.

Atvirkštinės matricos radimas naudojant algebrinių priedų metodą (sąjunginę matricą)

Ne vienaskaitos kvadratinei matricai A atvirkštinė yra matrica

kur yra matricos determinantas A, a yra matrica, susieta su matrica A.

Sujungta su kvadratine matrica A yra tos pačios eilės matrica, kurios elementai yra matricos determinanto atitinkamų elementų, perkeltų matricos A atžvilgiu, algebriniai papildiniai.

Tai

Ir

Atvirkštinės matricos radimo algoritmas naudojant algebrinių sudėjimų metodą

1. Raskite šios matricos determinantą A. Jei determinantas lygus nuliui, atvirkštinės matricos paieška sustoja, nes matrica yra vienaskaita, o atvirkštinė neegzistuoja.

2. Raskite matricą, transponuotą atžvilgiu A.

3. Apskaičiuokite sąjungos matricos elementus kaip 2 veiksme rasto marico algebrinius papildinius.

4. Taikykite (2) formulę: padauginkite atvirkštinę matricos determinanto vertę A, į sąjungos matricą, rastą 4 veiksme.

5. Padauginę šią matricą patikrinkite 4 veiksme gautą rezultatą Aį atvirkštinę matricą. Jei šių matricų sandauga yra lygi tapatybės matricai, tada atvirkštinė matrica buvo rasta teisingai. Priešingu atveju iš naujo pradėkite sprendimo procesą.

1 pavyzdys. Dėl matricos

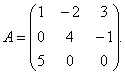
rasti atvirkštinę matricą.

Sprendimas. Norėdami rasti atvirkštinę matricą, turite rasti matricos determinantą A. Pagal trikampių taisyklę randame:

Todėl matrica A– nevienaskaita (neišsigimusi, nevienaskaita) ir jam yra atvirkštinė.

Raskime matricą, susietą su šia matrica A.

Raskime matricą, transponuotą matricos atžvilgiu A:

Mes apskaičiuojame sąjunginės matricos elementus kaip matricos, perkeltos matricos atžvilgiu, algebrinius papildinius A:

Todėl matrica susijungė su matrica A, turi formą

komentuoti. Elementų skaičiavimo ir matricos perkėlimo tvarka gali skirtis. Pirmiausia galite apskaičiuoti matricos algebrinius papildinius A, tada perkelkite algebrinio komplemento matricą. Rezultatas turėtų būti tie patys sąjungos matricos elementai.

Taikydami formulę (2), randame matricą atvirkštinę matricą A:

Atvirkštinės matricos radimas naudojant Gauso nežinomo eliminavimo metodą

Pirmasis žingsnis norint rasti atvirkštinę matricos vertę naudojant Gauso eliminavimo metodą yra priskirti matricą A tos pačios eilės tapatybės matrica, atskiriant jas vertikalia juosta. Gausime dvigubą matricą. Padauginkime abi šios matricos puses iš , tada gausime

,

Atvirkštinės matricos radimo algoritmas naudojant Gauso nežinomo eliminavimo metodą

1. Į matricą A priskirti tos pačios eilės tapatybės matricą.

2. Transformuokite gautą dvigubą matricą taip, kad jos kairėje pusėje gautumėte vienetinę matricą, tada dešinėje, vietoje tapatybės matricos, automatiškai gautumėte atvirkštinę matricą. Matrica A kairėje pusėje elementarios matricos transformacijomis paverčiama tapatybės matrica.

2. Jei matricos transformacijos procese A tapatybės matricoje bet kurioje eilutėje ar bet kuriame stulpelyje bus tik nuliai, tada matricos determinantas yra lygus nuliui, taigi ir matrica A bus vienaskaita ir neturi atvirkštinės matricos. Tokiu atveju tolesnis atvirkštinės matricos nustatymas sustoja.

2 pavyzdys. Dėl matricos

rasti atvirkštinę matricą.

ir transformuosime taip, kad kairėje pusėje gautume tapatybės matricą. Pradedame transformaciją.

Kairiosios ir dešiniosios matricos pirmąją eilutę padauginkite iš (-3) ir pridėkite prie antros eilės, o tada pirmąją eilutę padauginkite iš (-4) ir pridėkite prie trečios eilės, tada gausime

.

Norėdami užtikrinti, kad vėlesnėse transformacijose nebūtų trupmeninių skaičių, pirmiausia sukurkime vienetą antroje eilutėje kairėje dvigubos matricos pusėje. Norėdami tai padaryti, padauginkite antrą eilutę iš 2 ir iš jos atimkite trečią eilutę, tada gausime

.

Sudėkime pirmąją eilutę su antrąja, o antrąją eilutę padauginkime iš (-9) ir pridėkime trečiąja eilute. Tada gauname

.

Tada trečią eilutę padalinkite iš 8

.

Trečią eilutę padauginkite iš 2 ir pridėkite prie antrosios eilutės. Pasirodo:

.

Sukeiskime antrąją ir trečiąją eilutes, tada galiausiai gausime:

.

Matome, kad kairėje pusėje turime tapatybės matricą, todėl dešinėje turime atvirkštinę matricą. Taigi:

.

Skaičiavimų teisingumą galite patikrinti padauginę pradinę matricą iš rastos atvirkštinės matricos:

Rezultatas turėtų būti atvirkštinė matrica.

3 pavyzdys. Dėl matricos

rasti atvirkštinę matricą.

Sprendimas. Dvigubos matricos sudarymas

ir mes jį pakeisime.

Pirmą eilutę padauginame iš 3, o antrąją iš 2 ir atimame iš antrosios, tada padauginame pirmą eilutę iš 5, o trečią iš 2 ir atimame iš trečios eilutės, tada gauname

.

Pirmąją eilutę padauginame iš 2 ir pridedame prie antrosios, o tada iš trečios eilutės atimame antrąją, tada gauname

.

Matome, kad trečioje eilutėje kairėje pusėje visi elementai yra lygūs nuliui. Todėl matrica yra vienaskaita ir neturi atvirkštinės matricos. Mes nustojame toliau ieškoti atvirkštinio maritz.

Daugeliu savybių panašus į atvirkštinį.

Enciklopedinis „YouTube“.

1 / 5

✪ Kaip rasti atvirkštinę matricos vertę - bezbotvy

✪ Atvirkštinė matrica (2 būdai rasti)

✪ Atvirkštinė matrica Nr. 1

✪ 2015-01-28. Atvirkštinė 3x3 matrica

✪ 2015-01-27. Atvirkštinė matrica 2x2

Subtitrai

Atvirkštinės matricos savybės

• det A − 1 = 1 det A (\displaystyle \det A^(-1)=(\frac (1)(\det A))), Kur det (\displaystyle \\det )žymi determinantą.
• (A B) − 1 = B − 1 A − 1 (\displaystyle \ (AB)^(-1)=B^(-1)A^(-1)) dviem kvadratinėms apverčiamoms matricoms A (\displaystyle A) Ir B (\displaystyle B).
• (A T) − 1 = (A − 1) T (\displaystyle \ (A^(T))^(-1)=(A^(-1))^(T)), Kur (. . .) T (\displaystyle (...)^(T))žymi transponuotą matricą.
• (k A) − 1 = k − 1 A − 1 (\displaystyle \ (kA)^(-1)=k^(-1)A^(-1)) bet kokiam koeficientui k ≠ 0 (\displaystyle k\not =0).
• E − 1 = E (\displaystyle \E^(-1)=E).
• Jei reikia išspręsti tiesinių lygčių sistemą, (b yra nulinis vektorius), kur x (\displaystyle x) yra norimas vektorius, o jei A − 1 (\displaystyle A^(-1)) tada egzistuoja x = A − 1 b (\displaystyle x=A^(-1)b). Priešingu atveju arba sprendinių erdvės matmuo yra didesnis už nulį, arba sprendinių visai nėra.

Atvirkštinės matricos radimo metodai

Jei matrica yra apverčiama, tada norėdami rasti atvirkštinę matricą, galite naudoti vieną iš šių metodų:

Tikslieji (tiesioginiai) metodai

Gauss-Jordan metodas

Paimkime dvi matricas: the A ir vienišas E. Pateikiame matricą A tapatybės matricai naudojant Gauss-Jordan metodą, taikant transformacijas išilgai eilučių (taip pat galite taikyti transformacijas išilgai stulpelių, bet ne maišyti). Pritaikę kiekvieną operaciją pirmajai matricai, taikykite tą pačią operaciją antrajai. Kai bus baigtas pirmosios matricos redukavimas į vieneto formą, antroji matrica bus lygi A–1.

Naudojant Gauso metodą, pirmoji matrica kairėje bus padauginta iš vienos iš elementariųjų matricų Λ i (\displaystyle \Lambda _(i))(transvekcinė arba įstrižainė matrica su matricomis pagrindinėje įstrižainėje, išskyrus vieną padėtį):

Antroji matrica pritaikius visas operacijas bus lygi Λ (\displaystyle\Lambda), tai yra, jis bus norimas. Algoritmo sudėtingumas - O (n 3) (\displaystyle O(n^(3))).

Naudojant algebrinę komplemento matricą

Matrica atvirkštinė matrica A (\displaystyle A), gali būti pavaizduotas formoje

A − 1 = adj (A) det (A) (\displaystyle (A)^(-1)=(((\mbox(adj))(A)) \over (\det(A))))

Kur adj (A) (\displaystyle (\mbox(adj))(A))- adjungtinė matrica;

Algoritmo sudėtingumas priklauso nuo determinanto O det skaičiavimo algoritmo sudėtingumo ir yra lygus O(n²)·O det.

Naudojant LU/LUP skaidymą

Matricinė lygtis A X = I n (\displaystyle AX=I_(n)) atvirkštinei matricai X (\displaystyle X) galima laikyti kolekcija n (\displaystyle n) formos sistemos A x = b (\displaystyle Ax=b). Pažymėkime i (\displaystyle i) matricos stulpelis X (\displaystyle X) per X i (\displaystyle X_(i)); Tada A X i = e i (\displaystyle AX_(i)=e_(i)), i = 1 , … , n (\displaystyle i=1,\ldots ,n), nes i (\displaystyle i) matricos stulpelis I n (\displaystyle I_(n)) yra vieneto vektorius e i (\displaystyle e_(i)). kitaip tariant, norint rasti atvirkštinę matricą, reikia išspręsti n lygčių su ta pačia matrica ir skirtingomis dešiniosiomis pusėmis. Atlikus LUP skaidymą (O(n³) laikas), kiekvienai iš n lygčių išspręsti reikia O(n²) laiko, todėl šiai darbo daliai taip pat reikia O(n³) laiko.

Jei matrica A yra ne vienaskaita, tada jai galima apskaičiuoti LUP skaidymą P A = L U (\displaystyle PA = LU). Leiskite P A = B (\displaystyle PA = B), B – 1 = D (\displaystyle B^(-1) = D). Tada iš atvirkštinės matricos savybių galime parašyti: D = U – 1 L – 1 (\displaystyle D=U^(-1)L^(-1)). Jei šią lygybę padauginsite iš U ir L, galite gauti dvi formos lygybes U D = L − 1 (\displaystyle UD=L^(-1)) Ir D L = U − 1 (\displaystyle DL=U^(-1)). Pirmoji iš šių lygčių yra n² tiesinių lygčių sistema n (n + 1) 2 (\displaystyle (\frac (n(n+1))(2))) iš kurių žinomos dešinės pusės (iš trikampių matricų savybių). Antrasis taip pat reiškia n² tiesinių lygčių sistemą n (n − 1) 2 (\displaystyle (\frac (n(n-1))(2))) iš kurių žinomos dešinės pusės (taip pat iš trikampių matricų savybių). Kartu jie sudaro n² lygybių sistemą. Naudodami šias lygybes galime rekursyviai nustatyti visus n² matricos D elementus. Tada iš lygybės (PA) −1 = A −1 P −1 = B −1 = D. gauname lygybę A − 1 = D P (\displaystyle A^(-1) = DP).

Naudojant LU dekompoziciją, matricos D stulpelių permutacija nereikalinga, tačiau sprendimas gali skirtis, net jei matrica A nėra vienaskaita.

Algoritmo sudėtingumas yra O(n³).

Iteraciniai metodai

Schultzo metodai

( Ψ k = E − A U k , U k + 1 = U k ∑ i = 0 n Ψ k i (\displaystyle (\begin(cases)\Psi _(k)=E-AU_(k),),\\U_() k+1)=U_(k)\suma _(i=0)^(n)\Psi _(k)^(i)\pabaiga(atvejai)))

Klaidos įvertinimas

Pradinio aproksimavimo pasirinkimas

Pradinės aproksimacijos pasirinkimo problema čia nagrinėjamuose iteraciniuose matricos inversijos procesuose neleidžia jų traktuoti kaip nepriklausomų universalių metodų, konkuruojančių su tiesioginės inversijos metodais, pagrįstais, pavyzdžiui, matricų LU skaidymu. Yra keletas rekomendacijų, kaip pasirinkti U 0 (\displaystyle U_(0)), užtikrinančios sąlygos įvykdymą ρ (Ψ 0) < 1 {\displaystyle \rho (\Psi _{0})<1} (matricos spektrinis spindulys yra mažesnis už vienetą), kuris yra būtinas ir pakankamas proceso konvergencijai. Tačiau šiuo atveju pirmiausia reikia iš viršaus žinoti apverčiamosios matricos A arba matricos spektro įvertinimą. A A T (\displaystyle AA^(T))(būtent jei A yra simetriška teigiama apibrėžtoji matrica ir ρ (A) ≤ β (\displaystyle \rho (A)\leq \beta ), tada galite pasiimti U 0 = α E (\displaystyle U_(0)=(\alpha )E), kur; jei A yra savavališka nevienetinė matrica ir ρ (A A T) ≤ β (\displaystyle \rho (AA^(T))\leq \beta ), tada jie tiki U 0 = α A T (\displaystyle U_(0)=(\alpha )A^(T)), kur taip pat α ∈ (0 , 2 β) (\displaystyle \alpha \in \left(0,(\frac (2)(\beta ))\right)); Žinoma, galite supaprastinti situaciją ir pasinaudoti tuo ρ (A A T) ≤ k A A T k (\displaystyle \rho (AA^(T))\leq (\mathcal (k))AA^(T)(\mathcal (k))), įdėti U 0 = A T ‖ A A T ‖ (\displaystyle U_(0)=(\frac (A^(T))(\|AA^(T)\|)))). Antra, tokiu būdu nurodant pradinę matricą, nėra garantijos, kad ‖ Ψ 0 ‖ (\displaystyle \|\Psi _(0)\|) bus mažas (gal net pasirodys ‖ Ψ 0 ‖ > 1 (\displaystyle \|\Psi _(0)\|>1)), o aukštas konvergencijos rodiklis nebus atskleistas iš karto.

Pavyzdžiai

Matrica 2x2

(\displaystyle \mathbf (A) ^(-1)=(\begin(bmatrix)a&b\\c&d\\\end(bmatrix))^(-1)=(\frac (1)(\det(\mathbf (A))))(\begin(bmatrix)\,\,\,d&\!\!-b\\-c&\,a\\\end(bmatrix))=(\frac (1)(ad- bc))(\begin(bmatrix)\,\,\,d&\!\!-b\\-c&\,a\\\end(bmatrica)).) 2x2 matricos inversija galima tik su sąlyga, kad.

a d − b c = det A ≠ 0 (\displaystyle ad-bc=\det A\neq 0) 1 apibrėžimas:

matrica vadinama vienaskaita, jei jos determinantas yra nulis. 2 apibrėžimas:

matrica vadinama ne vienaskaita, jei jos determinantas nėra lygus nuliui. Matrica „A“ vadinama atvirkštinė matrica

, jei tenkinama sąlyga A*A-1 = A-1 *A = E (vieneto matrica).

Kvadratinė matrica yra apverčiama tik tuo atveju, jei ji nėra vienaskaita.

Atvirkštinės matricos skaičiavimo schema: ∆ 1) Apskaičiuokite matricos "A" determinantą, jei

A = 0, tada atvirkštinė matrica neegzistuoja.

2) Raskite visus matricos "A" algebrinius papildinius.

3) Sukurkite algebrinių priedų matricą (Aij)

4) Transponuokite algebrinių komplementų matricą (Aij )T

5) Padauginkite perkeltą matricą iš šios matricos determinanto atvirkštinės vertės.

6) Atlikite patikrinimą:

Iš pirmo žvilgsnio tai gali atrodyti sudėtinga, bet iš tikrųjų viskas yra labai paprasta. Visi sprendimai pagrįsti paprastais aritmetiniais veiksmais, sprendžiant svarbiausia nesusipainioti su „-“ ir „+“ ženklais ir jų nepamesti.

Užduotis: suraskite atvirkštinę matricą „A“, parodytą paveikslėlyje žemiau:

1. Pirmas dalykas, kurį reikia padaryti, yra rasti matricos "A" determinantą:

Paaiškinimas:

Supaprastinome determinantą naudodami pagrindines jo funkcijas. Pirmiausia į 2 ir 3 eilutes įtraukėme pirmosios eilutės elementus, padaugintus iš vieno skaičiaus.

Antra, pakeitėme determinanto 2 ir 3 stulpelius, o pagal jo savybes pakeitėme ženklą prieš jį.

Trečia, išėmėme bendrąjį antrosios eilutės koeficientą (-1), taip vėl pakeisdami ženklą, ir jis tapo teigiamas. Mes taip pat supaprastinome 3 eilutę taip pat, kaip ir pačioje pavyzdžio pradžioje.

Turime trikampį determinantą, kurio elementai žemiau įstrižainės yra lygūs nuliui, o pagal savybę 7 lygus įstrižainių elementų sandaugai. Galų gale gavome ∆ A = 26, todėl atvirkštinė matrica egzistuoja.

A11 = 1*(3+1) = 4

A12 = -1*(9+2) = -11

A13 = 1*1 = 1

A21 = -1*(-6) = 6

A22 = 1*(3-0) = 3

A23 = -1*(1+4) = -5

A31 = 1*2 = 2

A32 = -1*(-1) = -1

A33 = 1+(1+6) = 7

3. Kitas žingsnis yra sudaryti matricą iš gautų priedų:

5. Padauginkite šią matricą iš determinanto atvirkštinės vertės, ty iš 1/26:

6. Dabar tereikia patikrinti:

Bandymo metu gavome tapatybės matricą, todėl sprendimas buvo atliktas visiškai teisingai.

2 būdas apskaičiuoti atvirkštinę matricą.

1. Elementariosios matricos transformacija

2. Atvirkštinė matrica per elementarųjį keitiklį.

Elementarioji matricos transformacija apima:

1. Eilutės padauginimas iš skaičiaus, kuris nėra lygus nuliui.

2. Į bet kurią eilutę įtraukiant kitą eilutę, padaugintą iš skaičiaus.

3. Sukeiskite matricos eilutes.

4. Taikydami elementariųjų transformacijų grandinę gauname kitą matricą.

A -1 = ?

1. (A|E) ~ (E|A -1 )

2.A -1 * A = E

Pažvelkime į tai naudodami praktinį pavyzdį su realiais skaičiais.

Pratimas: Raskite atvirkštinę matricą.

Sprendimas:

Patikrinkime:

Šiek tiek paaiškinimo apie sprendimą:

Pirma, mes pertvarkėme 1 ir 2 matricos eilutes, tada padauginome pirmąją eilutę iš (-1).

Po to pirmąją eilutę padauginome iš (-2) ir sudėjome su antrąja matricos eilute. Tada 2 eilutę padauginome iš 1/4.

Paskutinis transformacijos etapas buvo antrosios eilutės padauginimas iš 2 ir pridėjimas prie pirmosios. Dėl to mes turime tapatybės matricą kairėje, todėl atvirkštinė matrica yra dešinėje.

Patikrinę įsitikinome, kad sprendimas buvo teisingas.

Kaip matote, atvirkštinės matricos apskaičiavimas yra labai paprastas.

Šios paskaitos pabaigoje taip pat norėčiau skirti šiek tiek laiko tokios matricos savybėms.