Tarkime, Achilas bėga dešimt kartų greičiau už vėžlį ir atsilieka nuo jo tūkstančiu žingsnių. Per tą laiką, kurio Achilui reikia nubėgti šį atstumą, vėžlys nušliaups šimtą žingsnių ta pačia kryptimi. Kai Achilas nubėga šimtą žingsnių, vėžlys šliaužia dar dešimt žingsnių ir t.t. Procesas tęsis iki begalybės, Achilas niekada nepasivys vėžlio.
Šis samprotavimas tapo logišku šoku visoms vėlesnėms kartoms. Aristotelis, Diogenas, Kantas, Hegelis, Hilbertas... Visi jie vienaip ar kitaip svarstė Zenono aporiją. Šokas buvo toks stiprus, kad " ... diskusijos tęsiasi iki šiol, mokslo bendruomenė dar nesugebėjo prieiti prie bendros nuomonės apie paradoksų esmę... į klausimo tyrimą įtraukta matematinė analizė, aibių teorija, nauji fizikiniai ir filosofiniai požiūriai; ; nė vienas iš jų netapo visuotinai priimtu problemos sprendimu..."[Wikipedia, "Zeno aporia". Visi supranta, kad yra kvailinami, bet niekas nesupranta, iš ko susideda apgaulė.
Matematiniu požiūriu Zenonas savo aporijoje aiškiai pademonstravo perėjimą nuo kiekybės prie . Šis perėjimas reiškia taikymą, o ne nuolatinį. Kiek suprantu, matematinis aparatas kintamiems matavimo vienetams naudoti arba dar nėra sukurtas, arba nebuvo pritaikytas Zenono aporijai. Taikydami savo įprastą logiką, mes patenkame į spąstus. Mes, dėl mąstymo inercijos, abipusei vertei taikome pastovius laiko vienetus. Iš fizinės pusės tai atrodo kaip laikas sulėtėjęs, kol visiškai sustoja tuo metu, kai Achilas pasiveja vėžlį. Jei laikas sustos, Achilas nebegali aplenkti vėžlio.
Jei apverstume savo įprastą logiką, viskas stoja į savo vietas. Achilas bėga pastoviu greičiu. Kiekviena paskesnė jo kelio atkarpa yra dešimt kartų trumpesnė nei ankstesnė. Atitinkamai, laikas, skirtas jai įveikti, yra dešimt kartų mažesnis nei ankstesnis. Jei šioje situacijoje pritaikytume „begalybės“ sąvoką, būtų teisinga sakyti „Achilas be galo greitai pasivys vėžlį“.
Kaip išvengti šių loginių spąstų? Laikykitės pastovių laiko vienetų ir neperjunkite prie abipusių vienetų. Zenono kalba tai atrodo taip:
Per tą laiką, kurio prireiks Achilui nubėgti tūkstantį žingsnių, vėžlys nuropos šimtą žingsnių ta pačia kryptimi. Per kitą laiko intervalą, lygų pirmajam, Achilas nubėgs dar tūkstantį žingsnių, o vėžlys nuropos šimtą žingsnių. Dabar Achilas aštuoniais šimtais žingsnių lenkia vėžlį.
Šis požiūris adekvačiai apibūdina tikrovę be jokių loginių paradoksų. Tačiau tai nėra visiškas problemos sprendimas. Einšteino teiginys apie šviesos greičio nenugalimą yra labai panašus į Zenono aporiją „Achilas ir vėžlys“. Dar turime studijuoti, permąstyti ir išspręsti šią problemą. Ir sprendimo reikia ieškoti ne be galo dideliais skaičiais, o matavimo vienetais.
Kita įdomi Zenono aporija pasakoja apie skraidančią strėlę:
Skraidanti strėlė yra nejudanti, nes kiekvienu laiko momentu ji yra ramybės būsenoje, o kadangi ji ilsisi kiekvienu laiko momentu, ji visada yra ramybės būsenoje.
Šioje aporijoje loginis paradoksas įveikiamas labai paprastai – pakanka paaiškinti, kad kiekvienu laiko momentu skraidanti strėlė ilsisi skirtinguose erdvės taškuose, o tai iš tikrųjų yra judėjimas. Čia reikia atkreipti dėmesį į dar vieną dalyką. Iš vienos automobilio nuotraukos kelyje neįmanoma nustatyti nei jo judėjimo fakto, nei atstumo iki jo. Norint nustatyti, ar automobilis juda, reikia dviejų nuotraukų, padarytų iš to paties taško skirtingu laiku, tačiau negalite nustatyti atstumo nuo jų. Norėdami nustatyti atstumą iki automobilio, jums reikia dviejų nuotraukų, padarytų iš skirtingų erdvės taškų vienu metu, tačiau iš jų negalite nustatyti judėjimo fakto (žinoma, vis tiek reikia papildomų duomenų skaičiavimams, trigonometrija jums padės ). Noriu atkreipti ypatingą dėmesį į tai, kad du laiko taškai ir du erdvės taškai yra skirtingi dalykai, kurių nereikėtų painioti, nes jie suteikia skirtingas tyrimo galimybes.
2018 m. liepos 4 d., trečiadienis
Vikipedijoje labai gerai aprašyti rinkinio ir kelių rinkinių skirtumai. Pažiūrėsim.
Kaip matote, „rinkinyje negali būti dviejų identiškų elementų“, bet jei rinkinyje yra identiškų elementų, toks rinkinys vadinamas „daugiarūšiu“. Protingos būtybės niekada nesupras tokios absurdiškos logikos. Tai kalbančių papūgų ir dresuotų beždžionių lygis, kurie neturi intelekto iš žodžio „visiškai“. Matematikai veikia kaip paprasti treneriai, skelbiantys mums savo absurdiškas idėjas.
Kadaise tiltą statę inžinieriai, bandydami tiltą, buvo valtyje po tiltu. Jei tiltas sugriuvo, vidutinis inžinierius mirė po savo kūrinio griuvėsiais. Jei tiltas atlaikė apkrovą, talentingas inžinierius pastatė kitus tiltus.
Kad ir kaip matematikai slepiasi po fraze „mink mane, aš esu namuose“, tiksliau, „matematika tiria abstrakčias sąvokas“, yra viena virkštelė, neatskiriamai susiejanti jas su tikrove. Ši virkštelė yra pinigai. Taikykime matematinių aibių teoriją patiems matematikams.
Labai gerai mokėmės matematikos, o dabar sėdime prie kasos, išduodame atlyginimus. Taigi matematikas ateina pas mus už savo pinigus. Suskaičiuojame jam visą sumą ir išdėliojame ant savo stalo į skirtingas krūvas, į kurias dedame to paties nominalo kupiūras. Tada paimame vieną sąskaitą iš kiekvienos krūvos ir pateikiame matematikui jo „matematinį atlyginimo rinkinį“. Paaiškinkime matematikui, kad likusias sąskaitas jis gaus tik tada, kai įrodys, kad aibė be identiškų elementų nėra lygi aibei su identiškais elementais. Čia ir prasideda linksmybės.
Visų pirma, pasiteisins deputatų logika: „Tai gali būti taikoma kitiems, bet ne man! Tada jie pradės mus raminti, kad to paties nominalo banknotai turi skirtingus vekselių numerius, o tai reiškia, kad jie negali būti laikomi tais pačiais elementais. Gerai, skaičiuokime atlyginimus monetomis – ant monetų nėra skaičių. Čia matematikas pradės pašėlusiai prisiminti fiziką: skirtingos monetos turi skirtingą kiekį nešvarumų, kiekvienos monetos kristalų struktūra ir atomų išsidėstymas yra unikalus...
Ir dabar man kyla įdomiausias klausimas: kur yra ta riba, už kurios multiaibės elementai virsta aibės elementais ir atvirkščiai? Tokios linijos nėra – viską sprendžia šamanai, mokslas čia nė iš tolo nemeluoja.
Pažiūrėk čia. Mes pasirenkame futbolo stadionus, kurių aikštės plotas yra toks pat. Laukų plotai vienodi – tai reiškia, kad turime multiset. Bet jei pažiūrėtume į tų pačių stadionų pavadinimus, gautume daug, nes pavadinimai skirtingi. Kaip matote, tas pats elementų rinkinys yra ir rinkinys, ir kelių rinkinys. Kuris teisingas? O štai matematikas-šamanas-aštrininkas iš rankovės išsitraukia kozirių tūzą ir pradeda pasakoti arba apie rinkinį, arba apie multisetą. Bet kokiu atveju jis įtikins mus, kad yra teisus.
Norint suprasti, kaip šiuolaikiniai šamanai operuoja su aibių teorija, siedami ją su realybe, pakanka atsakyti į vieną klausimą: kuo vienos aibės elementai skiriasi nuo kitos aibės elementų? Aš jums parodysiu be jokių „neįsivaizduojamų kaip viena visuma“ ar „neįsivaizduojama kaip viena visuma“.
2018 m. kovo 18 d., sekmadienis
Skaičiaus skaitmenų suma – tai šamanų šokis su tamburinu, neturintis nieko bendro su matematika. Taip, matematikos pamokose mus moko rasti skaičiaus skaitmenų sumą ir ja naudotis, bet todėl jie yra šamanai, mokyti savo palikuonis savo įgūdžių ir išminties, kitaip šamanai tiesiog išmirs.
Ar jums reikia įrodymų? Atidarykite Vikipediją ir pabandykite rasti puslapį „Skaičiaus skaitmenų suma“. Ji neegzistuoja. Matematikoje nėra formulės, pagal kurią būtų galima rasti bet kurio skaičiaus skaitmenų sumą. Juk skaičiai yra grafiniai simboliai, kuriais rašome skaičius, o matematikos kalba užduotis skamba taip: „Suraskite bet kurį skaičių grafinių simbolių sumą“. Matematikai negali išspręsti šios problemos, bet šamanai gali tai padaryti lengvai.
Išsiaiškinkime, ką ir kaip darome, kad surastume tam tikro skaičiaus skaitmenų sumą. Taigi, turėkime skaičių 12345. Ką reikia padaryti, norint rasti šio skaičiaus skaitmenų sumą? Apsvarstykime visus veiksmus eilės tvarka.
1. Užrašykite numerį ant popieriaus lapo. Ką mes padarėme? Mes konvertavome skaičių į grafinį skaičiaus simbolį. Tai nėra matematinė operacija.
2. Iškirpkite vieną paveikslėlį į kelias nuotraukas su atskirais skaičiais. Paveikslėlio iškirpimas nėra matematinis veiksmas.
3. Konvertuokite atskirus grafinius simbolius į skaičius. Tai nėra matematinė operacija.
4. Sudėkite gautus skaičius. Dabar tai matematika.
Skaičiaus 12345 skaitmenų suma yra 15. Tai šamanų „kirpimo ir siuvimo kursai“, kuriuos naudoja matematikai. Bet tai dar ne viskas.
Matematiniu požiūriu nesvarbu, kurioje skaičių sistemoje rašome skaičių. Taigi skirtingose skaičių sistemose to paties skaičiaus skaitmenų suma bus skirtinga. Matematikoje skaičių sistema nurodoma kaip indeksas dešinėje nuo skaičiaus. Su dideliu skaičiumi 12345 nenoriu suklaidinti galvos, panagrinėkime skaičių 26 iš straipsnio apie. Parašykime šį skaičių dvejetainėje, aštuntainėje, dešimtainėje ir šešioliktainėje skaičių sistemomis. Mes nežiūrėsime į kiekvieną žingsnį po mikroskopu, mes jau tai padarėme. Pažiūrėkime į rezultatą.
Kaip matote, skirtingose skaičių sistemose to paties skaičiaus skaitmenų suma skiriasi. Šis rezultatas neturi nieko bendra su matematika. Tai tas pats, kaip jei nustatytumėte stačiakampio plotą metrais ir centimetrais, gautumėte visiškai skirtingus rezultatus.
Nulis visose skaičių sistemose atrodo vienodai ir neturi skaitmenų sumos. Tai dar vienas argumentas už tai, kad. Klausimas matematikams: kaip matematikoje įvardijamas tai, kas nėra skaičius? O matematikams nieko nėra, išskyrus skaičius? Galiu tai leisti šamanams, bet ne mokslininkams. Realybė yra ne tik skaičiai.
Gautas rezultatas turėtų būti laikomas įrodymu, kad skaičių sistemos yra skaičių matavimo vienetai. Juk negalime lyginti skaičių su skirtingais matavimo vienetais. Jei tie patys veiksmai su skirtingais to paties dydžio matavimo vienetais, juos palyginus, duoda skirtingus rezultatus, tai tai neturi nieko bendra su matematika.
Kas yra tikroji matematika? Tai yra tada, kai matematinės operacijos rezultatas nepriklauso nuo skaičiaus dydžio, naudojamo matavimo vieneto ir nuo to, kas atlieka šį veiksmą.
O! Ar tai ne moterų tualetas?
- Jauna moteris! Tai laboratorija, skirta sielų nedefiliniam šventumui joms kylant į dangų tirti! Halo viršuje ir rodyklė aukštyn. Koks dar tualetas?
Moteriška... Aureole viršuje ir rodyklė žemyn yra vyriškos lyties.
Jei toks dizaino meno kūrinys prieš akis blyksteli kelis kartus per dieną,
Tada nenuostabu, kad staiga savo automobilyje randate keistą piktogramą:
Asmeniškai aš stengiuosi pamatyti minus keturis laipsnius kakiojančiame žmoguje (viena nuotrauka) (kelių paveikslėlių kompozicija: minuso ženklas, skaičius keturi, laipsnių žymėjimas). Ir nemanau, kad ši mergina yra kvailė, kuri neišmano fizikos. Ji tiesiog turi stiprų grafinių vaizdų suvokimo stereotipą. Ir matematikai mus nuolat to moko. Štai pavyzdys.
1A nėra „minus keturi laipsniai“ arba „vienas a“. Tai yra „pooping man“ arba skaičius „dvidešimt šeši“ šešioliktaine tvarka. Tie žmonės, kurie nuolat dirba šioje skaičių sistemoje, skaičių ir raidę automatiškai suvokia kaip vieną grafinį simbolį.
Skaičiaus x ir skaičiaus y santykis yra skaičių u koeficientas, t.y. y/x arba x: y. Santykis parodo, kiek kartų x yra didesnis už y arba kokia y dalis yra x. Proporcija – tai dviejų santykių lygybė, t.y. a/b = x/y. Skaičiai a ir y vadinami kraštutiniais nariais, o skaičiai x ir b – viduriniais proporcijos nariais.
Proporcingumo savybės
(pagrindinis): proporcijos kraštutinių narių sandauga lygi jos vidurinių narių sandaugai, t.y. jei a / b = x / y, tai ay = bx.
Ir atvirkščiai, skaičiai a, b, x, y sudaro proporciją a/b = x/y, jei ay = bx.
Jei proporcijomis keičiame kraštutinumus, vidurinius terminus arba abu tuo pačiu metu, gauname teisingą proporciją.
Norėdami rasti nežinomą vidurinį (arba kraštutinį) proporcijos narį, turite padalyti kraštutinių (vidurinių) dalių sandaugą iš žinomo vidurinio (kraštutinio) proporcijos nario.
Skaičiaus padalijimas į dalis, tiesiogiai ir atvirkščiai proporcingas duotiesiems skaičiams
Norėdami padalyti skaičių proporcingai duotiesiems skaičiams (padalyti tam tikru santykiu), turite padalyti šį skaičių iš nurodytų skaičių sumos ir padauginti rezultatą iš kiekvieno iš jų.
Norint padalyti skaičių į dalis, atvirkščiai proporcingas duotiesiems skaičiams, pakanka padalyti šį skaičių į dalis, tiesiogiai proporcingas skaičiams, atvirkščiai proporcingiems duotiesiems skaičiams.
Pavyzdžiui, 27 padalinkime atvirkščiai proporcingai skaičiams 4 ir 5. Duomenų atvirkštiniai dydžiai yra susiję taip (1/4) : (1/5) = 5: 4; tada gauname
Procentas yra šimtoji skaičiaus dalis. Procentas nurodomas % ženklu.
Jei šis skaičius laikomas 1, tai 1% yra 0,01 šio skaičiaus, 25% yra 0,25 skaičiaus (arba 1/4 skaičiaus) ir kt. Taigi, norint pateikti procentų skaičių trupmena, pakanka procentų skaičių padalyti iš 100. Pavyzdžiui, 125% = 1,25; 2,3 % = 0,023.
Pagrindinės problemos dėl procentų
Duoto skaičiaus procentinės dalies radimas.
Norint rasti skaičiaus b %, reikia išreikšti procentus trupmena: a /100 ir skaičių b padauginti iš šios trupmenos.
Pavyzdžiui, 30% nuo 60 rublių. yra 0,3 60 = 18 (rub.).
Skaičiaus radimas pagal jo procentą.
Jei žinoma, kad skaičiaus x a% yra lygus b, tada skaičių x randame pagal formulę. Tie. Procentus reikia išreikšti trupmena ir žinomą skaičių b padalyti iš šios trupmenos.
Pavyzdžiui, jei 3% grynųjų pinigų įnašo yra 150 rublių, tada visas indėlis yra lygus 150/0,03 = 5000 (rublių).
Skaičių procentinės dalies radimas.
Norint rasti dviejų skaičių a ir b procentinį santykį, reikia šių skaičių santykį padauginti iš 100, t.y. apskaičiuoti.
Pavyzdžiui, jei planuojama 60 automobilių per dieną gamykla pagamino 90 automobilių, tada ji pasiekė tikslą iki
(90/60) 100% = 150%.
„Komedijos tėvas“ Aristofanas Senovės Graikas Keletą kartų savo komedijose Aristofanas kreipiasi į tokį nemalonų reiškinį kaip informatoriai. Pavyzdžiui, Nikarchui, „Akharnyan“ herojui...
Meilės tema rusų romane (pagal romanus „Oblomovas“, „Tėvai ir sūnūs“, „Karas ir taika“)... Meilės kančios tema labiausiai siejama su pagrindiniu „Tėvų ir sūnų“ veikėju Jevgenijumi Bazarovu. Jo jausmas yra sunkus, visa apimantis...
Sprendžiant daugumą vidurinės mokyklos matematikos uždavinių reikia žinoti proporcijas. Šis paprastas įgūdis padės ne tik atlikti sudėtingus pratimus iš vadovėlio, bet ir įsigilinti į pačią matematikos mokslo esmę. Kaip padaryti proporciją? Išsiaiškinkime tai dabar.
Paprasčiausias pavyzdys yra problema, kai žinomi trys parametrai, o reikia rasti ketvirtą. Proporcijos, žinoma, yra skirtingos, tačiau dažnai reikia rasti tam tikrą skaičių naudojant procentus. Pavyzdžiui, berniukas iš viso turėjo dešimt obuolių. Ketvirtąją dalį atidavė mamai. Kiek obuolių berniukui liko? Tai yra paprasčiausias pavyzdys, kuris leis jums sukurti proporciją. Svarbiausia tai padaryti. Iš pradžių buvo dešimt obuolių. Tebūnie 100%. Pažymėjome visus jo obuolius. Jis atidavė ketvirtadalį. 1/4 = 25/100. Tai reiškia, kad jis išėjo: 100% (tai buvo iš pradžių) - 25% (jis davė) = 75%. Šis skaičius rodo likusio vaisių kiekio procentą, palyginti su iš pradžių turimu kiekiu. Dabar turime tris skaičius, pagal kuriuos jau galime išspręsti proporciją. 10 obuolių – 100 proc. X obuolių – 75%, kur x – reikiamas vaisių kiekis. Kaip padaryti proporciją? Jūs turite suprasti, kas tai yra. Matematiškai tai atrodo taip. Lygybės ženklas dedamas jūsų supratimui.

10 obuolių = 100%;
x obuoliai = 75%.
Pasirodo, 10/x = 100%/75. Tai yra pagrindinė proporcijų savybė. Galų gale, kuo didesnis x, tuo didesnis procentas šio skaičiaus nuo originalo. Išsprendžiame šią proporciją ir nustatome, kad x = 7,5 obuolių. Kodėl berniukas nusprendė atiduoti dalį sumos, nežinome. Dabar jūs žinote, kaip sudaryti proporcijas. Svarbiausia yra rasti du santykius, iš kurių viename yra nežinomas nežinomasis.
Proporcijos sprendimas dažnai yra paprastas dauginimas ir padalijimas. Mokyklos neaiškina vaikams, kodėl taip yra. Nors svarbu suprasti, kad proporciniai santykiai yra matematikos klasika, pati mokslo esmė. Norėdami išspręsti proporcijas, turite mokėti tvarkyti trupmenas. Pavyzdžiui, dažnai reikia konvertuoti procentus į trupmenas. Tai yra, 95% įrašymas neveiks. Ir jei iš karto parašysite 95/100, tada galėsite žymiai sumažinti nepradėję pagrindinio skaičiavimo. Verta iš karto pasakyti, kad jei jūsų proporcija pasirodo esanti su dviem nežinomaisiais, tada to neįmanoma išspręsti. Joks profesorius čia tau nepadės. Ir jūsų užduotis greičiausiai turi sudėtingesnį teisingų veiksmų algoritmą.

Pažiūrėkime į kitą pavyzdį, kur nėra procentų. Vairuotojas nupirko 5 litrus benzino už 150 rublių. Galvojo, kiek mokės už 30 litrų degalų. Norėdami išspręsti šią problemą, pažymime x reikiamą pinigų sumą. Galite patys išspręsti šią problemą ir tada patikrinti atsakymą. Jei dar nesupratote, kaip sudaryti proporciją, pažiūrėkite. 5 litrai benzino yra 150 rublių. Kaip ir pirmame pavyzdyje, užrašome 5l - 150r. Dabar suraskime trečią skaičių. Žinoma, tai yra 30 litrų. Sutikite, kad šioje situacijoje tinka 30 l - x rublių pora. Pereikime prie matematinės kalbos.
5 litrai - 150 rublių;
30 litrų - x rubliai;
Išspręskime šią proporciją:
x = 900 rublių.
Taigi nusprendėme. Atlikdami užduotį nepamirškite patikrinti atsakymo adekvatumo. Pasitaiko, kad netinkamu sprendimu automobiliai pasiekia nerealų 5000 kilometrų per valandą greitį ir pan. Dabar jūs žinote, kaip sudaryti proporcijas. Taip pat galite tai išspręsti. Kaip matote, čia nėra nieko sudėtingo.
Pagrindinės proporcijų savybės
- Proporcingumo pakeitimas. Jeigu a : b = c : d, Tai b : a = d : c
- Proporcijos narių dauginimas skersai. Jeigu a : b = c : d, Tai skelbimas = bc.
- Vidurinių ir kraštutinių terminų pertvarkymas. Jeigu a : b = c : d, Tai
- Didėjančios ir mažėjančios proporcijos. Jeigu a : b = c : d, Tai
- Proporcijų sudarymas sudedant ir atimant. Jeigu a : b = c : d, Tai
Sudėtinės (ištisinės) proporcijos
Istorinis fonas
Literatūra
- van der Waerden, B. L. Pabudimo mokslas. Senovės Egipto, Babilono ir Graikijos matematika. - per. iš olandų kalbos I. N. Veselovskis- M.: GIFML, 1959 m
Taip pat žr
Wikimedia fondas.
2010 m.:Sinonimai
Pažiūrėkite, kas yra „proporcija“ kituose žodynuose: - (lot., iš pro for, ir portio part, porcija). 1) proporcingumas, derinimas. 2) dalių santykis tarpusavyje ir su jų visuma. Ryšys tarp kiekių. 3) architektūroje: geri matmenys. Užsienio žodžių žodynas, įtrauktas į rusų kalbą... ...
Rusų kalbos svetimžodžių žodynas PROporcija, proporcijos, moteriška. (knyga) (lot. proportio). 1. Proporcingumas, tam tikras santykis tarp dalių. Taisyklingos kūno dalių proporcijos. Sumaišykite cukrų su tryniu tokiu santykiu: du šaukštus cukraus vienam tryniui. 2. Dviejų lygybė......
Ušakovo aiškinamasis žodynas Požiūris, santykis; proporcingumo. Ant. disproporcija Rusų sinonimų žodynas. proporciją žr. santykis Rusų kalbos sinonimų žodynas. Praktinis vadovas. M.: Rusų kalba. Z. E. Aleksandrova ...
Sinonimų žodynas Moteris, prancūzė proporcingumas; ką nors atitinkanti vertė arba kiekis; | mat. turinio lygybė, identiški dviženklių keturių skaitmenų santykiai; aritmetika, jei antrasis skaičius yra tiek pat didesnis ar mažesnis nei pirmasis, kiek ketvirtas prieš...
Dahlio aiškinamasis žodynas - (lot. proportio) matematikoje lygybė tarp dviejų keturių dydžių santykių: a/b =c/d ...
Didysis enciklopedinis žodynas PROORCIJA, matematikoje, lygybė tarp dviejų keturių dydžių santykių: a/b=c/d. Nepertraukiama proporcija yra grupė iš trijų ar daugiau dydžių, kurių kiekvienas turi tokį patį ryšį su kitu dydžiu, kaip ir... ...
Mokslinis ir techninis enciklopedinis žodynas PROPORCIJA, ir, moteriška. 1. Matematikoje: dviejų santykių lygybė (3 reikšmėmis). 2. Tam tikras dalių santykis, proporcingumas. P. pastato dalyse. Ožegovo aiškinamąjį žodyną. S.I. Ožegovas, N. Yu. Švedova. 1949 1992…
Ožegovo aiškinamasis žodynas anglų kalba proporcija; vokiečių kalba Proporcija. 1. Proporcingumas, tam tikras santykis tarp visumos dalių. 2. Dviejų santykių lygybė. Antinazi. Sociologijos enciklopedija, 2009 ...
Sociologijos enciklopedija proporcija - [A.S. Goldbergas. Anglų-rusų energetikos žodynas. 2006] Energetikos temos apskritai EN ratedegreeDdegdrratio ...
Techninis vertėjo vadovas- dviejų lygybė (žr.), t.y. a: b = c: d, kur a, b, c, d yra proporcijos nariai, kai a ir d yra kraštutiniai, o b ir c yra viduryje. Pagrindinė proporcijos savybė: kraštutinių proporcijos narių sandauga yra lygi vidurkio sandaugai: ad = bс ... Didžioji politechnikos enciklopedija
Sudarykite proporciją. Šiame straipsnyje noriu pakalbėti su jumis apie proporcijas. Suprasti, kas yra proporcija ir mokėti ją sudaryti, labai svarbu, tai tikrai sutaupo. Atrodo, kad tai maža ir nereikšminga „raidė“ didžiojoje matematikos abėcėlėje, bet be jos matematika pasmerkta būti šlubuota ir nepilna.Pirmiausia priminsiu, kas yra proporcija. Tai yra formos lygybė:

kuris yra tas pats dalykas (tai kita įrašymo forma).
Pavyzdys:
Sakoma, kad vienas yra prieš du, kaip keturi yra aštuoni. Tai yra, tai yra dviejų santykių lygybė (šiame pavyzdyje santykiai yra skaitiniai).
Pagrindinė proporcijų taisyklė:
a:b=c:d
kraštutinių dėmenų sandauga yra lygi viduriniųjų narių sandaugai
tai yra
a∙d=b∙c
*Jei kuri nors proporcijos reikšmė nežinoma, ją visada galima rasti.
Jei apsvarstysime tokią įrašymo formą:
tada galite naudoti tokią taisyklę, kuri vadinama „kryžiaus taisykle“: užrašoma įstrižainėje stovinčių elementų (skaičių ar posakių) sandaugų lygybė.
a∙d=b∙c
Kaip matote, rezultatas yra tas pats.
Jei žinomi trys proporcijos elementai, tadavisada galime rasti ketvirtą.
Būtent tokia yra naudos ir būtinybės esmėproporcijas sprendžiant problemas.
Pažvelkime į visus variantus, kur nežinomas dydis x yra „bet kur“ proporcijoje, kur a, b, c yra skaičiai:

Dydis, esantis įstrižai nuo x, rašomas trupmenos vardikliu, o žinomi dydžiai, stovintys įstrižai, rašomi skaitiklyje kaip sandauga. Nebūtina jo įsiminti, jūs jau viską teisingai apskaičiuosite, jei išmoksite pagrindinę proporcingumo taisyklę.
Dabar pagrindinis klausimas, susijęs su straipsnio pavadinimu. Kada taupo proporcija ir kur ji naudojama? Pavyzdžiui:
1. Visų pirma, tai problemos, susijusios su procentais. Mes pažvelgėme į juos straipsniuose „“ ir „“.
2. Daugelis formulių pateikiamos proporcijų forma:
>sinusų teorema
> elementų santykis trikampyje

> liestinės teorema

> Talio teorema ir kt.
3. Geometrijos uždaviniuose sąlyga dažnai nurodo kraštinių (kitų elementų) arba plotų santykį, pavyzdžiui, 1:2, 2:3 ir kt.
4. Matavimo vienetų perskaičiavimas, nurodant proporciją, naudojamą perskaičiuojant vienetus ir iš vieno mato į kitą:
- nuo valandų iki minučių (ir atvirkščiai).
- tūrio, ploto vienetai.
— ilgiai, pavyzdžiui, mylios į kilometrai (ir atvirkščiai).
— radianų laipsniai (ir atvirkščiai).
čia neapsieisite be proporcijų sudarymo.
Svarbiausia yra tai, kad reikia teisingai nustatyti korespondenciją, pažvelkime į paprastus pavyzdžius:
Turite nustatyti skaičių, kuris yra 35% iš 700.
Problemų, susijusių su procentais, vertė, su kuria mes lyginame, laikoma 100%. Nežinomą skaičių pažymime x. Užmegzkime korespondenciją:
Galime sakyti, kad septyni šimtai trisdešimt penki atitinka 100 proc.
X atitinka 35 proc. Reiškia,
700 – 100%
x – 35 proc.
Nuspręskime

Atsakymas: 245
Paverskime 50 minučių į valandas.
Žinome, kad viena valanda lygi 60 minučių. Pažymėkime korespondenciją -x valandos yra 50 minučių. Reiškia
1 – 60
x – 50
Mes nusprendžiame:
Tai yra, 50 minučių yra penkios šeštosios valandos.
Atsakymas: 5/6
Nikolajus Petrovičius nuvažiavo 3 kilometrus. Kiek tai kainuos myliomis (manykite, kad 1 mylia yra 1,6 km)?
Yra žinoma, kad 1 mylia yra 1,6 kilometro. Paimkime mylių, kurias įveikė Nikolajus Petrovičius, skaičių kaip x. Galime suderinti:
Viena mylia atitinka 1,6 kilometro.
X mylios yra trys kilometrai.
1 – 1,6
x – 3
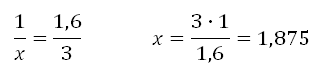
Atsakymas: 1875 mylios
Jūs žinote, kad yra formulės, kaip konvertuoti laipsnius į radianus (ir atvirkščiai). Aš jų neužsirašau, nes manau, kad nereikia jų įsiminti, todėl daug informacijos turite saugoti atmintyje. Visada galite konvertuoti laipsnius į radianus (ir atvirkščiai), jei naudojate proporciją.
Paverskime 65 laipsnius radianiniais vienetais.
Svarbiausia atsiminti, kad 180 laipsnių yra Pi radianas.
Norimą dydį pažymėkime x. Užmezgame susirašinėjimą.
Šimtas aštuoniasdešimt laipsnių atitinka Pi radianus.
Šešiasdešimt penki laipsniai atitinka x radianus. studijuoti straipsnį šia tema tinklaraštyje. Medžiaga joje pateikta kiek kitaip, tačiau principas tas pats. Aš baigsiu tuo. Tikrai bus kažkas įdomesnio, nepraleiskite to!
Jei prisimintume patį matematikos apibrėžimą, jame yra šie žodžiai: matematika tiria kiekybinius RYŠIAS- pagrindinis žodis čia). Kaip matote, pačiame matematikos apibrėžime yra proporcija. Apskritai matematika be proporcijos nėra matematika!!!
Viso geriausio!
Pagarbiai, Aleksandrai
P.S. Būčiau dėkingas, jei papasakotumėte apie svetainę socialiniuose tinkluose.








