- Budeme vychádzať zo spojení, nie z mechanických vzorcov.
- Uvažujme komplexné čísla ako doplnok k našej číselnej sústave, rovnako ako nula, zlomkové alebo záporné čísla.
- Myšlienky vizualizujeme v grafike, aby sme lepšie pochopili podstatu a neprezentovali ich len suchým textom.
A náš Tajná zbraň: učenie podľa analógie. Ku komplexným číslam sa dostaneme tak, že začneme ich predkami, zápornými číslami. Tu je malý návod pre vás:
Zatiaľ má táto tabuľka malý zmysel, ale nech je tam. Na konci článku všetko padne na svoje miesto.
Poďme naozaj pochopiť, čo sú záporné čísla
Záporné čísla nie sú také jednoduché. Predstavte si, že ste európsky matematik v 18. storočí. Máte 3 a 4 a môžete napísať 4 – 3 = 1. Je to jednoduché.
Ale koľko je 3-4? Čo to presne znamená? Ako môžete odobrať 4 kravám 3? Ako môžeš mať menej ako nič?
Záporné čísla boli považované za úplný nezmysel, niečo, čo „vrhlo tieň na celú teóriu rovníc“ (Francis Maceres, 1759). Dnes by to bolo úplný nezmysel Považujte záporné čísla za niečo nelogické a neužitočné. Opýtajte sa svojho učiteľa, či záporné čísla porušujú základnú matematiku.
Čo sa stalo? Vymysleli sme teoretické číslo, ktoré malo užitočné vlastnosti. Záporných čísel sa nemožno dotknúť ani ich cítiť, ale sú dobré na opis určitých vzťahov (napríklad dlhu). Toto je veľmi užitočný nápad.
Namiesto toho, aby som povedal: „Dlžím ti 30“ a čítal som slová, aby som zistil, či som v pluse alebo v pluse, môžem si jednoducho zapísať „-30“ a vedieť, čo to znamená. Ak zarobím a splatím svoje dlhy (-30 + 100 = 70), môžem túto transakciu bez problémov napísať do niekoľkých znakov. Zostane mi +70.
Znamienka plus a mínus automaticky vystihujú smer – na popísanie zmien po každej transakcii nepotrebujete celú vetu. Matematika sa stala jednoduchšou, elegantnejšou. Už nezáleží na tom, či sú záporné čísla „hmatateľné“ – majú prospešné vlastnosti a používali sme ich dovtedy, kým sa pevne neusadili v našom každodennom živote. Ak niekto z vašich známych ešte nepochopil podstatu záporných čísel, teraz mu pomôžete.
Ale neznižujme ľudské utrpenie: záporné čísla boli skutočným posunom vo vedomí. Ani Euler, génius, ktorý objavil číslo e a mnohé ďalšie, nerozumel záporným číslam tak dobre ako my dnes. Boli vnímané ako „nezmyselné“ výsledky výpočtov.
Je zvláštne očakávať, že deti pokojne pochopia myšlienky, ktoré kedysi zmiatli aj tých najlepších matematikov.
Zadávanie imaginárnych čísel
Je to rovnaký príbeh s vymyslenými číslami. Takto môžeme riešiť rovnice celý deň:
Odpovede budú 3 a -3. Ale predstavme si, že nejaký chytrák tu pridal mínus:
![]()
Dobre dobre. To je ten druh otázky, ktorý ľudí škrie, keď to vidia prvýkrát. Chcete vypočítať druhú odmocninu z čísla menšieho ako nula? To je nemysliteľné! (Historicky skutočne existovali podobné otázky, ale je pre mňa pohodlnejšie predstaviť si nejakého múdreho muža bez tváre, aby som neuviedol do rozpakov vedcov minulosti).
Vyzerá to šialene, rovnako ako záporné čísla, nula a iracionálne čísla(neopakujúce sa čísla). Táto otázka nemá žiadny „skutočný“ význam, však?
Nie, nie je to pravda. Takzvané „imaginárne čísla“ sú normálne ako každé iné (alebo rovnako abnormálne): sú nástrojom na opis sveta. V rovnakom duchu, v akom si predstavujeme, že "existuje" -1, 0,3 a 0, predpokladajme, že existuje nejaké číslo i, kde:
![]()
Inými slovami, vynásobíte i samotné, aby ste dostali -1. čo sa deje teraz?
Najprv nás určite bolí hlava. Ale hraním hry „predstierajme, že ja existuje“ v skutočnosti robíme matematiku jednoduchšou a elegantnejšou. Objavujú sa nové súvislosti, ktoré môžeme jednoducho opísať.
Nebudete veriť v i, rovnako ako tí starí nevrlí matematici neverili v existenciu -1. Všetky nové pojmy, ktoré krútia mozog do trubice, sú ťažko vnímateľné a ich význam sa nevynorí okamžite, dokonca ani pre brilantného Eulera. Ale ako nám ukázali záporné čísla, zvláštne nové nápady môžu byť mimoriadne užitočné.
Nepáči sa mi samotný výraz „imaginárne čísla“ – mám pocit, že bol vybraný špeciálne, aby urazil pocity i. Číslo i je normálne ako ostatné, no prilepila sa mu prezývka „imaginárny“, takže ju budeme používať aj my.
Vizuálne chápanie záporných a komplexných čísel
Rovnica x^2 = 9 v skutočnosti znamená toto:
![]()
Ktorá transformácia x, použitá dvakrát, zmení 1 na 9?
Existujú dve odpovede: "x = 3" a "x = -3". To znamená, že môžete „zmenšiť“ 3-krát alebo „zmenšiť o 3 a prevrátiť“ (obrátenie alebo prevrátenie výsledku sú všetky interpretácie násobenia zápornou hodnotou).
Teraz sa zamyslime nad rovnicou x^2 = -1, ktorú možno zapísať takto:
Ktorá transformácia x, použitá dvakrát, zmení 1 na -1? Hm.
- Nemôžeme sa množiť dvakrát kladné číslo pretože výsledok bude pozitívny.
- Záporné číslo nemôžeme vynásobiť dvakrát, pretože výsledok bude opäť kladný.
Čo tak... rotácia! Znie to, samozrejme, nezvyčajne, ale čo ak si predstavíme x ako „otočenie o 90 stupňov“, potom dvojitým použitím x urobíme otočenie o 180 stupňov súradnicová os, a 1 sa zmení na -1!

Wow! A ak sa nad tým trochu zamyslíme, môžeme urobiť dve revolúcie opačný smer, a tiež prejsť z 1 na -1. Toto je "záporná" rotácia alebo násobenie pomocou -i:
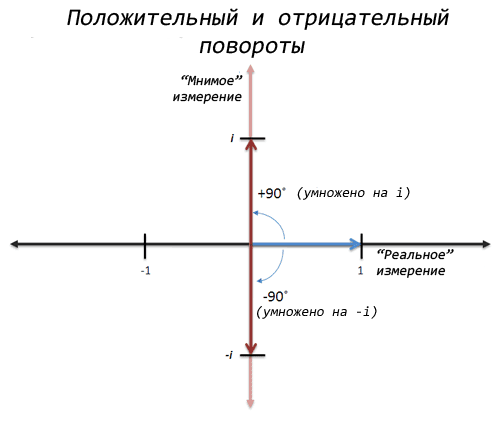
Ak vynásobíme -i dvakrát, potom pri prvom násobení dostaneme -i z 1 a pri druhom -1 z -i. Takže sú vlastne dve odmocniny-1: i a -i.
Toto je celkom fajn! Máme niečo ako riešenie, ale čo to znamená?
- i je "nová imaginárna dimenzia" na meranie čísla
- i (alebo -i) je to, čím sa čísla "stanú" otáčaním
- Násobenie i sa otáča o 90 stupňov proti smeru hodinových ručičiek
- Násobenie -i je otočenie o 90 stupňov v smere hodinových ručičiek.
- Otočenie dvakrát v ľubovoľnom smere dáva -1: vráti nás späť do "normálnej" dimenzie kladných a záporných čísel (os x).
Všetky čísla sú 2-rozmerné. Áno, je to ťažké prijať, ale rovnako ťažko by to prijali aj starí Rimania. desatinné miesta alebo dlhé delenie. (Ako to, že medzi 1 a 2 je viac čísel?). Vyzerá zvláštne ako ktokoľvek iný Nová cesta myslieť v matematike.
Spýtali sme sa "Ako premeniť 1 na -1 v dvoch akciách?" a našiel odpoveď: otočte sa dvakrát o 1 90 stupňov. Celkom zvláštny, nový spôsob myslenia v matematike. Ale veľmi užitočné. (Mimochodom, toto geometrický výklad komplexné čísla sa objavili až desaťročia po objavení čísla i).
Tiež nezabudnite, že otáčanie proti smeru hodinových ručičiek je pozitívny výsledok- to je čisto ľudská konvencia a všetko mohlo byť úplne inak.
Hľadajte súpravy
Poďme trochu hlbšie do detailov. Keď vynásobíte záporné čísla (napríklad -1), dostanete množinu:
- 1, -1, 1, -1, 1, -1, 1, -1
Keďže -1 nemení veľkosť čísla, iba znamienka, dostanete rovnaké číslo buď so znamienkom „+“ alebo so znamienkom „-“. Za číslo x dostanete:
- x, -x, x, -x, x, -x…
Toto je veľmi užitočný nápad. Číslo „x“ môže predstavovať dobré a zlé týždne. Predstavme si to dobrý týždeň nahrádza zlý; Je to dobrý týždeň; Aký bude 47. týždeň?
X znamená, že to bude zlý týždeň. Pozrite sa, ako záporné čísla "nasledujú znamienko" - do kalkulačky môžeme namiesto počítania jednoducho zadať (-1)^47 ("1. týždeň dobrý, 2. týždeň zlý... 3. týždeň dobrý..."). Veci, ktoré sa neustále striedajú, sa dajú dokonale modelovať pomocou záporných čísel.
Dobre, čo sa stane, ak budeme pokračovať v násobení i?
![]()
Veľmi vtipné, poďme to celé trochu zjednodušiť:
Tu je to isté graficky znázornené:

Cyklus opakujeme každé 4. otočenie. To určite dáva zmysel, nie? Každé dieťa vám povie, že 4 otáčky doľava sú rovnaké, ako keby ste sa neotáčali vôbec. Teraz si dajte pauzu od imaginárnych čísel (i, i^2) a pozrite sa na celkovú množinu:
- X, Y, -X, -Y, X, Y, -X, -Y…
Presne tak, ako sa modelujú záporné čísla zrkadlový odrazčísla, imaginárne čísla môžu modelovať čokoľvek, čo sa otáča medzi dvoma rozmermi "X" a "Y". Alebo čokoľvek s cyklickou, kruhovou závislosťou - máte niečo na mysli?
Pochopenie komplexných čísel
Je potrebné zvážiť ešte jeden detail: môže byť číslo „skutočné“ aj „imaginárne“?
O tom ani nepochybuj. Kto povedal, že sa musíme otočiť presne o 90 stupňov? Ak stojíme jednou nohou na „skutočnej“ dimenzii a druhou na „imaginárnej“, bude to vyzerať asi takto:

Sme na 45 stupňovej značke, kde sú skutočné a imaginárne časti rovnaké a samotné číslo je „1 + i“. Je to ako párok v rožku, kde je kečup aj horčica – kto povedal, že si musíte vybrať jedno alebo druhé?
V podstate si môžeme zvoliť ľubovoľnú kombináciu reálnych a imaginárnych častí a z toho všetkého spraviť trojuholník. Uhol sa stáva "uhlom otáčania". Komplexné číslo je vymyslený názov pre čísla, ktoré majú reálnu a imaginárnu časť. Sú napísané ako „a + bi“, kde:
- a - skutočná časť
- b - imaginárna časť

Nie zlé. Zostáva však jedna posledná otázka: aké „veľké“ je komplexné číslo? Skutočnú alebo imaginárnu časť nemôžeme merať oddelene, pretože nám unikne celkový obraz.
Urobme krok späť. Veľkosť záporného čísla je vzdialenosť od nuly:
Toto je ďalší spôsob, ako nájsť absolútna hodnota. Ale ako zmerať obe zložky pod uhlom 90 stupňov pre komplexné čísla?
Je to vták na oblohe... alebo lietadlo... Pytagoras prichádza na záchranu!
Táto veta sa objavuje všade, kde je to možné, dokonca aj v číslach vynájdených 2000 rokov po samotnej vete. Áno, tvoríme trojuholník a jeho prepona sa bude rovnať vzdialenosti od nuly:
Hoci meranie komplexného čísla nie je také jednoduché ako „len vynechanie znamienka -“, komplexné čísla majú veľmi užitočné aplikácie. Pozrime sa na niektoré z nich.
Reálny príklad: Rotácie
S precvičovaním komplexných čísel nebudeme čakať do vysokoškolskej fyziky. Dnes to urobíme. Na tému násobenia komplexných čísel sa dá povedať veľa, ale teraz musíte pochopiť hlavnú vec:
- Násobenie komplexným číslom sa otáča o jeho uhol
Pozrime sa, ako to funguje. Predstavte si, že som na lodi a pohybujem sa kurzom 3 jednotky na východ každé 4 jednotky na sever. Chcem zmeniť kurz o 45 stupňov proti smeru hodinových ručičiek. Aký bude môj nový kurz?

Niekto by mohol povedať: „Je to ľahké! Vypočítajte sínus, kosínus, vygooglite hodnotu dotyčnice... a potom...“ Myslím, že sa mi rozbila kalkulačka...
Vezmime si jednoduchšiu cestu: sme na kurze 3 + 4i (je jedno aký je uhol, teraz je nám to jedno) a chceme sa otočiť o 45 stupňov. No, 45 stupňov je 1 + i (ideálna uhlopriečka). Takže môžeme vynásobiť našu sadzbu týmto číslom!

Tu je podstata:
- Počiatočný kurz: 3 jednotky východ, 4 jednotky sever = 3 + 4i
- Otočte proti smeru hodinových ručičiek o 45 stupňov = vynásobte 1 + i
Po vynásobení dostaneme:

Naša nová smernica je 1 jednotka na západ (-1 na východ) a 7 jednotiek na sever, súradnice si môžete nakresliť do grafu a riadiť sa nimi.
Ale! Odpoveď sme našli za 10 sekúnd, bez akýchkoľvek sínusov a kosínusov. Neexistovali žiadne vektory, žiadne matice, žiadne sledovanie toho, v ktorom kvadrante sme boli. Vypracovať rovnicu bola jednoduchá aritmetika a trocha algebry. Imaginárne čísla sú skvelé na rotáciu!
Okrem toho je výsledok takéhoto výpočtu veľmi užitočný. Máme kurz (-1, 7) namiesto uhla (atan(7/-1) = 98,13 a hneď je jasné, že sme v druhom kvadrante. Ako presne ste plánovali nakresliť a sledovať uvedený uhol Používate uhlomer po ruke?
Nie, previedli by ste uhol na kosínus a sínus (-0,14 a 0,99), našli by ste približný pomer medzi nimi (asi 1 ku 7) a načrtli trojuholník. A tu nepochybne vyhrávajú komplexné čísla - presne, bleskovo a bez kalkulačky!
Ak ste ako ja, tento objav vás ohromí. Ak nie, obávam sa, že matematika vás vôbec nevzrušuje. Prepáč!
Trigonometria je dobrá, ale komplexné čísla výrazne uľahčujú výpočty (napríklad hľadanie cos(a + b)). Toto je len malé oznámenie; v nasledujúcich článkoch vám poskytnem kompletné menu.
Lyrická odbočka: niektorí ľudia si myslia niečo takéto: „Hej, nie je vhodné mať smer sever/východ namiesto jednoduchého uhla, ktorý má loď sledovať!
Je to pravda? Dobre, pozri sa na svoje pravá ruka. Aký je uhol medzi základňou malíčka a špičkou ukazovák? Veľa šťastia s metódou výpočtu.
Alebo môžete jednoducho odpovedať: „No, hrot je X palcov vpravo a Y palcov hore,“ a môžete s tým niečo urobiť.
Približujú sa komplexné čísla?
Moje základné objavy v oblasti komplexných čísel sme prešli ako tornádo. Pozrite sa na úplne prvú ilustráciu, teraz by mala byť jasnejšia.
V týchto krásnych, nádherných číslach je toho ešte oveľa viac, ale môj mozog je už unavený. Môj cieľ bol jednoduchý:
- Presvedčiť vás, že komplexné čísla boli vnímané iba ako „bláznivé“, ale v skutočnosti môžu byť veľmi užitočné (rovnako ako záporné čísla)
- Ukážte, ako zložité čísla môžu zjednodušiť niektoré problémy, ako je rotácia.
Ak sa mi zdá, že ma táto téma príliš znepokojuje, má to svoj dôvod. Vymyslené čísla sú moje už roky posadnutosť- rozčuľoval ma nedostatok porozumenia.
Ale zapáliť sviečku je lepšie ako sa brodiť čiernu tmu: toto sú moje myšlienky a som si istý, že oheň zapáli v mysliach mojich čitateľov.
Epilóg: Ale aj tak sú dosť divní!
Viem, že aj mne sa stále zdajú divné. Snažím sa myslieť ako prvý človek, ktorý objavil nulové myslenie.
Nula je taká zvláštna myšlienka, „niečo“ predstavuje „nič“ a nedá sa to nijako pochopiť Staroveký Rím. Rovnako je to aj s komplexnými číslami – ide o nový spôsob myslenia. Nulové aj komplexné čísla však značne zjednodušujú matematiku. Keby sme nikdy nezaviedli divné veci, ako sú nové číselné sústavy, stále by sme všetko počítali na prstoch.
Opakujem túto analógiu, pretože je také ľahké začať si myslieť, že komplexné čísla „nie sú normálne“. Buďme otvorení inováciám: v budúcnosti budú ľudia iba žartovať o tom, ako niekto až do 21. storočia neveril v komplexné čísla.
23. októbra 2015
MOŽNOSŤ POUŽITIA KOMPLEXNÝCH ČÍSEL
V PREDBEHU MATEMATIKY NA VŠEOBECNEJ ŠKOLE
Vedecký poradca:
Mestská vzdelávacia inštitúcia
Stredná škola Pervomajskaja
s. Mesto Kichmengsky
St. Zarechnaja 38
Predložená práca je venovaná štúdiu komplexných čísel. Relevantnosť: riešenie mnohých problémov vo fyzike a technike vedie ku kvadratickým rovniciam s negatívny diskriminant. Tieto rovnice nemajú riešenie v oblasti reálnych čísel. Ale riešenie mnohých takýchto problémov má veľmi jasný fyzikálny význam.
Praktický význam: komplexné čísla a funkcie komplexných premenných sa používajú v mnohých otázkach vedy a techniky a môžu byť použité v škole pri riešení kvadratických rovníc.
Oblasť objektu: matematika. Predmet výskumu: algebraické pojmy a akcie. Predmet výskumu- komplexné čísla. Problém: komplexné čísla sa v kurzoch matematiky nevyučujú stredná škola, hoci sa dajú použiť na riešenie kvadratických rovníc. Možnosť zavedenia komplexných čísel do Zadania jednotnej štátnej skúšky nabudúce. hypotéza: Komplexné čísla môžete použiť na riešenie kvadratických rovníc na strednej škole. Cieľ: naštudovať si možnosť používania komplexných čísel pri štúdiu matematiky v 10. ročníku strednej školy. Úlohy: 1. Preštudujte si teóriu komplexných čísel 2. Zvážte možnosť využitia komplexných čísel v kurze matematiky pre 10. ročník. 3. Vyvíjajte a testujte úlohy s komplexnými číslami.
Pre riešenia algebraické rovnice Nie je dostatok reálnych čísel. Preto je prirodzené snažiť sa, aby boli tieto rovnice riešiteľné, čo následne vedie k rozšíreniu pojmu číslo..gif" width="10" height="65 src=">
https://pandia.ru/text/78/027/images/image005_18.gif" width="10" height="62">.gif" width="97" height="28 src=">
musíte len súhlasiť s tým, že budete s takýmito výrazmi postupovať podľa pravidiel bežnej algebry a predpokladať to ![]()
V roku 1572 vyšla kniha talianskeho algebraistu R. Bombelliho, v ktorej boli stanovené prvé pravidlá pre aritmetické operácie s takýmito číslami, až po extrakciu z nich kubické korene. Názov „imaginárne čísla“ bol zavedený v roku 1637. francúzsky matematik a filozof R. Descartes a v roku 1777 jeden z najväčších matematikov 8. storočia X..gif" width="58" height="19"> ako príklad využitia komplexných čísel pri štúdiu matematiky v r. 10. ročník. Preto číslo x, ktorého druhá mocnina sa rovná –1, sa nazýva imaginárna jednotka a označuje sa i. Odtiaľ teda pochádza ..gif" width="120" height="27 src=">. gif" width="100" height="27 src=" >8th grade" href="/text/category/8_klass/" rel="bookmark">8. ročník algebry. - M.: Education, 1994.-P 0,134-139.
2. encyklopedický slovník mladý matematik / Comp. E-68. - M.: Pedagogika, 19с
Textová časť publikácie
Obsah
Úvod…………………………………………………………………………..3 Kapitola I. Z histórie komplexných čísel………………………………… ……………………… ............4 Kapitola II. Základy metódy komplexných čísel………………………………………………6 Kapitola III. Geometria trojuholníka v komplexných číslach………………………………12 Kapitola IV. Riešenie Problémy s jednotnou štátnou skúškou a rôzne olympiády metódou komplexných čísel………………………………………………………………....20 Záver………………………………… ………………………………………………….24 Bibliografia………………………………………………………………..25
Úvod
Veľký význam komplexných čísel v matematike a jej aplikáciách je všeobecne známy. Algebru komplexných čísel možno úspešne využiť v elementárnej geometrii, trigonometrii, teórii pohybov a podobností, ako aj v elektrotechnike, rôznych mechanických a fyzické problémy. V planimetrii vám metóda komplexných čísel umožňuje riešiť problémy priamym výpočtom pomocou hotových vzorcov. Toto je jednoduchosť tejto metódy v porovnaní s vektorovou a súradnicové metódy, metódou geometrických transformácií, vyžadujúcich od študentov značnú inteligenciu a zdĺhavé vyhľadávanie. Už niekoľko tisícročí je trojuholník symbolom geometrie. Môžete dokonca povedať, že trojuholník je atóm geometrie. Akýkoľvek mnohouholník možno rozdeliť na trojuholníky a štúdium jeho vlastností spočíva v štúdiu vlastností trojuholníkov jeho komponentov. Pozrime sa, ako funguje metóda komplexných čísel pri dokazovaní vlastností trojuholníka z školský kurz planimetrie, ako aj na riešenie úloh C-4 Jednotnej štátnej skúšky. 2
Kapitola I. Z histórie komplexných čísel,,
Prvýkrát boli zrejme imaginárne množstvá spomenuté v slávnom diele „Veľké umenie alebo o algebraické pravidlá» Cardano (1545), vnútri formálne rozhodnutie problém výpočtu dvoch čísel, ktorých súčet je 10 a po vynásobení dávajú 40. Pre túto úlohu získal kvadratickú rovnicu pre jeden z členov a našiel jej korene: 5 + √ − 15 a 5 − √ − 15. V komentári k riešeniu napísal: „tieto najzložitejšie veličiny sú zbytočné, aj keď sú veľmi dômyselné“ a „aritmetické úvahy sa stávajú čoraz viac neuchopiteľné a dosahujú hranicu, ktorá je taká jemná, ako je zbytočná“. Možnosť využitia imaginárnych veličín pri riešení kubickej rovnice, v takzvanom ireducibilnom prípade (keď sú reálne korene polynómu vyjadrené cez odmocniny imaginárnych veličín), prvýkrát opísal Bombelli (1572). Ako prvý opísal pravidlá sčítania, odčítania, násobenia a delenia komplexných čísel, no stále ich považoval za zbytočný a prefíkaný „vynález“. Výrazy reprezentovateľné v tvare a + b √ − 1, vyskytujúce sa pri riešení kvadratickej a kubické rovnice, sa začalo nazývať „imaginárnym“ v r XVI-XVII storočia na popud Descarta, ktorý ich nazval tak, že odmietajúc ich realitu, a mnohým ďalším významným vedcom 17. storočia sa povaha a právo na existenciu imaginárnych veličín zdali veľmi pochybné, rovnako ako iracionálne čísla a dokonca záporné hodnoty. Napriek tomu sa matematici smelo prihlásili formálne metódy algebry reálnych veličín a ku komplexným, získali správne reálne výsledky aj zo stredne zložitých, a to nemohlo začať vzbudzovať dôveru. Dlho nebolo jasné, či všetky operácie s komplexnými číslami vedú ku komplexným alebo skutočným výsledkom, alebo či napríklad extrakcia koreňa môže viesť k objavu nejakého iného nového typu čísel. Problém vyjadrenia koreňov stupňa n z dané číslo bol riešený v prácach Moivreho (1707) a Cotesa (1722). Symbol pre označenie pomyselná jednotka navrhol Euler (1777, publ. 1794), ktorý za to prevzal prvé písmeno slova lat. imaginarius — imaginárny. Všetko šíril štandardné funkcie vrátane logaritmu do komplexnej domény. Euler tiež v roku 1751 vyjadril myšlienku, že pole komplexných čísel je algebraicky uzavreté. D’Alembert (1747) dospel k rovnakému záveru, ale prvý prísny dôkaz Táto skutočnosť patrí Gaussovi (1799). Bol to Gauss, kto zaviedol v roku 1831 výraz „komplexné číslo“, ktorý sa v roku 1803 začal používať v rovnakom zmysle ako francúzsky matematik Lazare Carnot. 3
Aritmetický (štandardný) model komplexných čísel ako párov reálnych čísel zostrojil Hamilton (1837); to dokázalo konzistentnosť ich vlastností. Oveľa skôr, v roku 1685, Wallis (Anglicko) vo svojom diele „Algebra“ ukázal, že zložité korene kvadratická rovnica s reálnymi koeficientmi možno znázorniť geometricky, bodmi v rovine. Ale zostalo to nepovšimnuté. Nabudúce sa geometrická interpretácia komplexných čísel a operácií s nimi objavila v diele Wessela (1799). Moderné geometrické znázornenie, niekedy nazývané „Argandov diagram“, sa začalo používať po publikovaní práce J. R. Arganda v rokoch 1806 a 1814, ktorá nezávisle zopakovala Wesselove závery. Pojmy „modul“, „argument“ a „konjugované číslo“ zaviedol Cauchy. Zistilo sa teda, že komplexné čísla sú vhodné aj na vykonávanie čisto algebraických operácií sčítania, odčítania, násobenia a delenia vektorov v rovine, čo veľmi zmenilo vektorovú algebru. 4
Kapitola II. Základy metódy komplexných čísel
[
1
]
,
[2], [3] [4] Geometrická interpretácia komplexných čísel Dĺžka úsečky Je daný obdĺžnik karteziánsky systém súradnice na rovine, komplexné číslo z = x+iy (i 2 = -1) môže byť spojené s bodom M roviny jedna k jednej so súradnicami x, y (obr. 1): z = x + iy ↔M (x, y ) ↔M (z) . Číslo z sa potom nazýva komplexná súradnica bodu M. Keďže množina bodov euklidovskej roviny je v zhode jedna ku jednej s množinou komplexných čísel, nazýva sa táto rovina aj rovina komplexných čísel. Počiatok O karteziánskeho súradnicového systému sa nazýva počiatočný alebo nulový bod roviny komplexných čísel. Keď = 0, číslo z je skutočné. Reálne čísla sú reprezentované bodmi na osi x, preto sa nazýva reálna os. Pri x=0 je číslo z čisto imaginárne: z=iy. Imaginárne čísla sú znázornené bodmi na osi y, preto sa nazýva imaginárna os. Nula je skutočné aj čisto imaginárne číslo. Vzdialenosť od začiatku roviny O k bodu M(z) sa nazýva modul komplexného čísla z a označuje sa |z| alebo r: | z | = r = | OM | = √ x 2 + y 2 Ak φ je orientovaný uhol, ktorý zviera vektor ⃗ OM s osou x, potom podľa definície funkcie sínus a kosínus sin φ = y r, cos φ = x r 5
odkiaľ x = r cos φ, y = r sin φ, a teda z = r (cos φ + sin φ). Táto reprezentácia komplexného čísla z sa nazýva jeho
trigonometria
cheskoe
formulár. Pôvodná reprezentácia z=x+iy sa nazýva
algebraické
tvar tohto čísla. V trigonometrickom zobrazení sa uhol nazýva argumentom komplexného čísla a označuje sa aj arg z: φ = arg z Ak je dané komplexné číslo z = x + iy, potom sa nazýva číslo ´ z = x − iy
komplexný konjugát
(alebo jednoducho
konjugovať
) k tomuto číslu z. Potom, samozrejme, číslo z je tiež konjugované s číslom ´z. Body M(z) a M 1 (´ z) sú symetrické okolo osi x. Z rovnosti z = ´ z vyplýva, že y = 0 a naopak. Znamená to, že
číslo rovné
k jeho konjugátu je skutočný a naopak.
Body s komplexnými súradnicami z a -z sú symetrické vzhľadom na počiatočný bod O. Body s komplexnými súradnicami z a − ´z sú symetrické vzhľadom na os y. Z rovnosti z = ´ z vyplýva, že x = 0 a naopak. Preto podmienka z =− ´ z je kritériom pre čisto imaginárne číslo. Pre akékoľvek číslo z samozrejme | z | = | ´z | =¿− z ∨¿∨−´ z ∨¿ .
Súčet a súčin
dve konjugované komplexné čísla sú reálne čísla: z + ´ z = 2 z, z ´ z = x 2 + y 2 =¿ z 2 ∨¿. Číslo konjugované so súčtom, súčinom alebo kvocientom komplexu 6
čísla sú súčtom, súčinom alebo podielom čísel konjugovaných s danými komplexnými číslami: ´ z 1 + z 2 = ´ z 1 + ´ z 2 ; ´z 1 z 2 = ´ z 1 ´ z 2; ´ z 1: z 2 = ´ z 1: ´ z 2 Tieto rovnosti možno ľahko overiť pomocou vzorcov pre operácie s komplexnými číslami. Ak a a b - komplexné súradnice bodov A a B, potom číslo c = a + b je súradnicou bodu C tak, že ⃗ OC = ⃗ OA + ⃗ OB (obr. 3). Komplexné číslo d = a − b zodpovedá bodu D tak, že ⃗ OD = ⃗ OA − ⃗ OB . Vzdialenosť medzi bodmi A a B je | ⃗BA | = | ⃗ OD | =¿ a − b ∨¿: ¿ AB ∨¿∨ a − b ∨¿ (1) Keďže ¿ z ∨ 2 = z ´ z , potom ¿ AB ∨ 2 =(a − b) (´ a − ´ b) . (2)
Rovnica
z ´z = r 2
definuje kruh so stredom
O polomere
r.
Vzťah AC CB = λ, (λ ≠ − 1), v ktorom sa delí bod C tento segment AB, sa vyjadruje prostredníctvom komplexných súradníc týchto bodov takto: λ = c − a b − c, λ = ´ λ, odkiaľ c = a + λb 1 + λ (3) Pre λ = 1 je bod C stredom segmentu AB a naopak. Potom: c = 1 2 (a + b) (4) Násobenie komplexných čísel Násobenie komplexných čísel sa vykonáva podľa vzorca, tj | a b | = | a || b | a 7
Rovnobežnosť a kolmosť Kolinearita troch bodov Nech sú body A(a) a B(b) dané na rovine komplexných čísel. Vektory ⃗ OA a ⃗ OB sú spoluriadené vtedy a len vtedy, ak arg a = arg b, t. j. keď arg a – arg b=arg a b = 0 (pri delení komplexných čísel sa argument deliteľa odčíta od argumentu dividenda). Je tiež zrejmé, že tieto vektory sú nasmerované v opačných smeroch práve vtedy, ak arg a - arg b= arg a b = ± π. Komplexné čísla s argumentmi 0, π, - π sú reálne.
Kritérium kolinearity pre body O, A, B:
Aby body A(a) a B(b) boli kolineárne s počiatočným bodom O, je potrebné a postačujúce, aby bol podiel ab Reálne číslo a b = ´ a ´ b alebo a ´ b = ´ a b (6) Teraz vezmite body A(a), B(b), C(c), D(d). Vektory ⃗ BA a ⃗ DC kólia sú nepárne práve vtedy, ak sú body definované komplexom čísla a-b a с-d, sú kolineárne so začiatkom O. Poznámka: 1. Na základe (6) máme: ⃗ AB ∨¿ ⃗ CD↔ (a − b) (´ c − ´ d) =(´ a − ´ b ) (c - d); (8) 2. Ak body A, B, C, D patria do jednotkovej kružnice z ´ z = 1, potom ´ a = 1 a; 'b = 1 b; c = 1 c; ´ d = 1 d a preto podmienka (8) má tvar: ⃗ AB ∨¿ ⃗ CD↔ ab = cd ; (9) 3. Kolinearita bodov A, B, C je charakterizovaná kolinearitou vektorov ⃗AB a ⃗AC. Pomocou (8) dostaneme: (a − b) (´ a −´ c) =(´ a − ´ b) (a − c) (10) Toto je kritérium pre príslušnosť bodov A, B, C na rovnakú priamku. Môže byť reprezentovaný v symetrickom tvare a (´ b −´ c) + b (´ c −´ a) + c (´ a − ´ b) = 0 (11) 8
Ak body A a B patria do jednotkovej kružnice z ´ z = 1, potom ´ a = 1 a; ´ b = 1 b a preto sa každý zo vzťahov (10) a (11) transformuje (po zmenšení o (a-b) na nasledovné: c + ab ´ c = a + b (12) Body A a B sú pevné, a bod C budeme považovať za premennú, pričom jej súradnicu preznačíme na z. Potom každý z výsledných vzťahov (10), (11), (12) bude rovnicou priamky AB: (´ a − ´ b) z + (b − a) ´ z + a ´ b − b ´ a = 0, (10a) z + ab ´ z = a + b. (12a) Najmä priama OA má rovnicu a ´ z = ´ a z. Komplexné čísla s argumentmi π 2 a − π 2 sú čisto imaginárne, preto OA ⊥ OB↔ a b = − ´ a ´ b alebo OA ⊥ OB↔a ´ b + ´ a b = 0 (13) Kolmosť úsečiek AB a CD je určená rovnosťou (a − b) (´ c − ´ d) + (´ a − ´ b) (c − d) = 0 (14) Najmä ak body A, B, C, D patria do jednotkovej kružnice z ´ z = 1, potom závislosť (14) je zjednodušená: ab + cd = 0 (15) Skalárny súčin vektorov. skalárny produkt vektory ⃗ OA a ⃗ OB cez komplexné súradnice aab bodov A a B. Nech a=x 1 +iy 1 , b=x 2 +iy 2 . Potom a b + a b=(x 1 +iy 1)(x 2 −iy 2)+(x 1 −iy 1)(x 2 +iy 2)=2(x 1 x 2 +y 1 y 2)= 2 ⃗ OA∙⃗OB. Takže ⃗ OA ∙ ⃗ OB = 1 2 (a b + ab) (16) 9
Teraz nech sa dajú štyri ľubovoľné body A(a), B(b), C(c), D(d) ich komplexnými súradnicami. Potom 2 ⃗ AB ∙ ⃗ CB = 1 2 (a-b)(c - d)+(a - b)(c-d) (17) Uhly Dohodneme sa, že symbolom ∠ (AB ,CD) označíme kladne orientovaný uhol cez ktorý musí byť vektor ⃗ otočený AB tak, aby sa stal spolusmerovaným s vektorom ⃗ CD. Potom cos ∠ (AB, CD)= (d − c) (´ b − ´ a) +(´ d −´ c)(b − a) 2 | d − c || b - a | (18) sin ∠ (AB ,CD)= (d − c) (´ b −´ a) +(´ d −´ c)(b − a) 2 i | d − c || b - a | (19) Priesečník sekán ku kružnici Ak body A, B, C a D ležia na kružnici z ´ z = 1, potom zložitú súradnicu priesečníka nájdeme podľa vzorca ´ z = (a + b) − (c + d) ab − cd (20) Ak je AB kolmá na CD, potom z= 1 2 (a+b+c+d) (21) Priesečník dotyčníc ku kružnici 10
Zložitú súradnicu priesečníka dotyčníc ku kružnici z ´ z =1 v jej bodoch A(a) a B(b) nájdeme podľa vzorca z= 2ab a + b (22) Kolmý priemet bodu na priamku Ortogonálny priemet bodu M(m) na priamku AB, kde A(a) a B(b) nájdeme podľa vzorca V prípade, že A a B patria do jednotkovej kružnice z= 1 2 (a + b + m - cb m) .
Kapitola III.
Geometria trojuholníka v komplexných číslach
V rovine komplexných čísel je trojuholník definovaný tromi komplexnými číslami zodpovedajúcimi jeho vrcholom. Ťažisko a ortocentrum trojuholníka. [ 2 ] Je známe, že pre ťažisko G (priesečník stredníc) trojuholníka ABC a ľubovoľného bodu O platí nasledujúca rovnosť: ⃗ OG = 1 3 (⃗ OA + ⃗ OB + ⃗ OC). Preto komplexnú súradnicu g ťažiska G vypočítame podľa vzorca g = 1 3 (a + b + c) (23) Vyjadrime h komplexnú súradnicu ortocentra H trojuholníka ABC cez súradnice a, b, c jeho vrcholov. Nech priamky AH, BH, CH pretínajú kružnicu opísanú trojuholníku v bodoch A1, B1, C1. Nech má tento kruh rovnicu z ´ z =1, potom podľa (15) máme: a 1 = − bc a , b 1 = − ca b , c 1 = − ab c Podľa vzorca (20) h = (a + a 1 ) −(b + b 1) a a 1 − bb 1 = ab + bc + ca abc = 1 a + 1 b + 1 c 11
Odkiaľ pochádza h=a+b+c. (24) Výsledný výraz obsahuje súradnice vrcholov trojuholníka symetricky, preto tretia výška trojuholníka prechádza priesečníkom prvých dvoch Podobné trojuholníky [2,1] Trojuholníky ABC a A 1 B 1 C 1 sú podobné a identicky orientované (podobnosť prvého druhu), ak B 1 =kAB, A 1 B 1 =kAC a uhly B 1 A 1 C 1 a BAC sú rovnaké (uhly sú orientované). Pomocou komplexných čísel možno tieto rovnosti zapísať takto: |a 1 −b 1 |=k|a−b|, |a 1 −c 1 |=k|a−c|,arg c 1 − a 1 b 1 − a 1 =arg c − a b − a . Tieto dve rovnosti sú ekvivalentné jednej s 1 − a 1 c − a = b 1 − a 1 b − a = σ , (25) kde σ je komplexné číslo, |σ|=k-koeficient podobnosti. Ak je σ reálne, potom c 1 − a 1 c − a = ´ c 1 − ´ a 1 ´ c − ´ a , kde AC║A 1 C 1. Trojuholníky ABC a A 1 B 1 C 1 sú teda homotetické. Vzťah (25) je nevyhnutný a dostatočný stav aby trojuholníky ABC a A 1 B 1 C 1 boli podobné a rovnako orientované. Môže dostať symetrický tvar ab 1 +bc 1 +ca 1 =ba 1 +cb 1 +ac 1 (25a) Rovnocenné trojuholníky Ak | σ | = 1, potom sú trojuholníky ABC a A 1 B 1 C 1 rovnaké. Potom vzťah (25) je znakom rovnosti identicky orientovaných trojuholníkov a vzťah (26) je znakom rovnosti opačne orientovaných trojuholníkov. Pravidelné trojuholníky Ak požadujete orientáciu trojuholník ABC bol podobný orientovanému trojuholníku BCA, potom trojuholník ABC bude pravidelný. 12
Preto z (25) dostaneme nevyhnutnú a postačujúcu podmienku, aby trojuholník ABC bol pravidelný (a−b) 2 +(b−c) 2 +(c−a) 2 =0 (27) Plocha trojuholníka (dokázané autorom) Odvodíme vzorec pre obsah S kladne orientovaného trojuholníka ABC: S = 1 2 | AB || AC | sin ∠ (AB, AC)= 1 4i ((c − a) (´ b − ´ a) − (b − a) (´ c − ´ a)) = − 1 4i (a (´ b − ´ c) + b (´ c − ´ a) + c (´ a − ´ b)) alebo S = i 4 (a (´ b − ´ c) + b (´ c − ´ a) + c (´ a − ´ b )) (28) Ak trojuholník ABC vpísanej do kružnice z ´ z = 1, potom sa vzorec (28) pretransformuje do tvaru: S = i 4 (a − b)(b − c)(c − a) abc (29) Veta o stredovej čiare a trojuholník (dokázané autorom)
Veta
. stredná čiara trojuholníka je rovnobežná so základňou a rovná sa jej polovici. Dôkaz. Nech body M a N sú stredy strán AB a BC, potom m = b 2 ; n = b + c2. Keďže z 2 =z ´z, potom MN 2 =(m-n)(´ m - ´ n)=(b 2 - b + c 2)(´ b 2 – ´ b + ´ c 2)= b ´ b 4 − b ´ b + b ´ c 4 − b ´ b + ´ b c 4 + b ´ b + b ´ c + ´ b c + c ´ c 4 = c ´ c 4 13
4MN 2 =c ´c, AC 2 =(c-0)(c-0)=c ´c, teda 4MN 2 = AC 2 alebo 2MN=AC.Podmienka (8) kolinearity vektorov MN a AC je tiež splnená , a teda MN ║AC. Thalesova veta (dokázaná autorom)
Veta
. Ak na jednej strane uhla rovnobežné čiary odrežú rovnaké segmenty, potom na druhej strane uhla odrežú rovnaké segmenty. Dôkaz Predpokladajme, že c=kb. Potom ak BD||CE, potom máme (b-d)(´ c − 2 ´ d ¿= (´ b − ´ d) (c − 2d) Otvorenie zátvoriek a uvedenie podobné výrazy, dostaneme rovnicu b ´ c − 2 b ´ d −´ c d = ´ b c − 2 ´ b d − c ´ d Nahradením c za kb a ´c za k ´b dostaneme bk ´ b -2b ´ d -dk ´b = ´b kb-2 ´b d-kb ´d. Ak opäť privedieme podobné pojmy a všetko presunieme na jednu stranu, dostaneme 2b ´ d + dk ´ b − 2 ´ b d − kb ´ d =0. Vytiahneme to spoločný multiplikátor a dostaneme 2(b ´ d − ´ b d ¿+ k (´ b d − b ´ d) = 0. Preto k=2, t.j. c=2b. Podobne je dokázané, že f=3b, atď. Pytagorova veta ( dokázané autorom) B správny trojuholníkštvorec prepony rovná súčtuštvorcové nohy 14
Dôkaz. Vzdialenosť medzi bodmi B a C sa rovná BC=|b-c|=b, BC 2 =b ´ b. Od |z| 2 = z ´z , potom AC 2 =(a-c)(c ´ a − ´ ¿ ¿=(a − 0) (´ a - 0)=a ´ a. AB 2 =(a-b)(´ a − ´ b ¿= a ´ a − a ´ b - ´ a b+b ´ b. Keďže b je reálne číslo, t.j. b= ´ b, potom -a ´ b =− ab. Keďže bod A leží na osi Oy, potom a = - ´ a, čiže - ´ ab = ab. Teda AB 2 = a ´ a -a ´ b - ´ ab +b ´ b = a ´ a +b ´ b = AC 2 +BC 2. Veta Eulerova priamka (dokázané autorom) Dokážme, že ortocentrum, ťažisko a osnica trojuholníka ležia na tej istej priamke (táto priamka sa nazýva Eulerova priamka) a OG = 1/2GH. 15
Dôkaz: Bod G(g) je ťažisko trojuholníka ABC, H(h) je ortocentrum a O(o) je stred opísanej kružnice trojuholníka. Aby tieto body boli kolineárne, musí byť splnená rovnosť (10): (g-о)(´ g - ´ h ¿ -(´ g − ´ o ¿ (g − h) =0 Vezmime bod O ako počiatok, potom g(´ g - ´ h ¿ - ´ g (g − h) =g 2 -g ´ h −¿ (g 2 - h ´ g ¿ =-g ´ h + h ´ g (30) komplexná súradnica ortocentra sa vypočíta podľa vzorca (24) h=a+b+c, (30a) a ťažisko podľa vzorca (23) g = 1 3 (a + b + c) (30c) Dosadíme do ( 30), dostaneme 1 3 (a+b +c)(´ a + b + c)-(a+b+c)(´ a + b + c 1 3 ¿)) = 0. Rovnosť (10) je splnené teda ťažisko, ortocentrum a stred opísaného trojuholníka kružnice ležia na rovnakej priamke OG=g= 1 3 (a+b+c) GH=h-g=a+b+c- 1 3 (a+ b+c)= 2 3 (a+b+c) Dostali sme, že OG= 1 2 GH. Veta je dokázaná.
Eulerov kruh (deväťbodový kruh). Dokázané autorom Uvažujme trojuholník ABC. Zhodnime sa na tom | OA | = | OB | = | OC | =1, t.j. všetky vrcholy trojuholníka patria do jednotkovej kružnice z ´ z = 1 (stred kružnice opísanej O je počiatok a polomer je jednotka dĺžky). Dokážme, že základne majú tri výšky ľubovoľný trojuholník, stredy jej troch strán a stredy troch úsečiek spájajúcich jej vrcholy s ortocentrom ležia na tej istej kružnici a jej stred je stredom úsečky OH, kde H je ortocentrum trojuholníka ABC. Takýto kruh sa nazýva
Eulerov kruh
. Nech body K, L a M sú stredy strán trojuholníka ABC, body Q, N, P základne jeho výšok, body F, E, D stredy troch úsečiek spájajúcich jeho vrcholy s ortocentrom. Dokážme, že do tej istej kružnice patria body D, E, F, K, L, M, N, P, Q. Bodom priraďte zodpovedajúce komplexné súradnice: k = a + b 2, l = b + c 2 ; m = a + c2,oi = h2 = a + b + c2 d = 2a + b + c2; e = 2 c + a + b2; f = 2 b + a + c 2 n = 1 2 (a + b + c − ab c), q = 1 2 (a + c + b − ac b), p = 1 2 (c + b + a − cb a) O 1 K = | o 1 − k | = | c 2 | ,O 1 L = | o 1 − l | = | a 2 | 01M = | o 1 − m | = | b 2 | O1D = | o 1 − d | = | a 2 | ,01E = | o 1 − e | = | c 2 | ,01F = | o 1 − f | = | b 2 | 01N= | o 1 − n | = 1 2 | ab c | = 1 2 | a || b | | c | 01Q= 12 | a || c | | b | 01F= 12 | b || c | | a | . 17
Pretože trojuholník ABC je vpísaný do kružnice z ´ z = 1, potom | a | = | b | = | c | = 1,→ | a 2 | = | b 2 | = | c 2 | = 1 2 | a || b | | c | = 1 2 | a || c | | b | = 1 2 | b || c | | a | = 1 2 Body D, E, F, K, L, M, N, Q, F patria do tej istej kružnice Gaussova veta Ak priamka pretína priamky so stranami BC, CA, AB trojuholníka ABC, resp. body A 1, B 1 , C 1, potom sú stredy segmentov AA 1, BB 1, СС 1 kolineárne. Pomocou (11) napíšeme podmienky pre kolinearitu trojíc bodov AB 1 C, CA 1 B, BC 1 A, A 1 B 1 C 1: 0,) b - a (c) a - c () c - b (a 0 ,) c - b a() b - a () a - c b(0,) a - c b() c - b () b - a c(0,) b - a (c) a - c () c - b a (1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 ) b c a b, Ps (31) segmenty AA 1, BB 1, CC 1 , potom musíme ukázať, že 0) () () ( n m p m p n p n m (32) Odkedy), (2 1), (2 1), (2 1 1 1 1 c c p b b n a a m potom dokazovaná rovnosť (31) je ekvivalentná tomuto: 0))(())(())((1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 b a c b a s b a c b a c a c b a s b a c b a c b c b a c b a c b a c b a (33) Teraz je ľahké vidieť že (33) sa získa sčítaním rovnosti (31) po členoch. Dôkaz je úplný. 18
Kapitola IV.
Riešenie úloh USE a rôznych olympiád metódou komplexných čísel.
Úloha 1. Jednotná štátna skúška -2012, P-4 Na priamke obsahujúcej medián AD pravouhlého trojuholníka ABC s pravým uhlom C sa vezme bod E vzdialený od vrcholu A vo vzdialenosti rovnajúcej sa 4. Nájdite obsah trojuholník BCE, ak BC=6, AC=4. Prvé riešenie. Podľa Pytagorovej vety AD=5. Potom ED=1 Nech bod E leží na lúči AD. Strednica AD je dlhšia ako AE a bod E leží vo vnútri trojuholníka ABC (obr. 1.) Pustime kolmicu EF z bodu E na priamku BC a uvažujme podobné pravouhlé trojuholníky DEF a DAC. Z podobnosti týchto trojuholníkov zistíme: EF = AC ∙ ED AD = 4 5 19
Preto S BCE = 1 2 ∙ 6 ∙ 4 5 = 2,4. Teraz nech leží bod A medzi E a D (obr. 2). V tomto prípade ED = 9 a EF = AC ∙ ED AD = 36 5 . Potom S BCE = 1 2 ∙ 6 ∙ 36 5 = 21,6. Odpoveď: 2,4; 21.6. Riešenie úlohy pomocou komplexných čísel. Prípad I: bod E leží na lúči AD. Keďže D je stred CB, potom CD=3. A keďže CA = 4, je jasné, že AD = 5, t.j. DE = 1. Zoberme si bod C ako počiatočný bod a priamky CA a CB ako skutočné a imaginárne osi. Potom A(4), C(0), B(6i), D(3i), E(e). Body A, E a D sú kolineárne, potom e − 4 3i − e = 4 t.j. e= 12i + 4 5 . Podľa vzorca (25) S CBE =│ ´ i 4 (e6 ´ i +6i(− ´ e)│= e e − ´ ¿ 6 i 2 4 ¿ ¿ =2.4 Prípad II: bod A leží medzi bodmi D a E , potom 4 − e 3i − 4 = 4 5 , t. j. e= 36 − 12 i 5 S CBE = | 3 i 2 2 (36 − 12 i 5 − − 36 − 12i 5) | =21.6 Odpoveď: 2.4 a 21.6 problém pri použití prvej metódy, je potrebné mať množstvo dohadov, ktoré sa nemusia objaviť hneď, ale až po dosť dlhom uvažovaní. Aj keď, ak je študent dobre pripravený, potom sa samotné riešenie tvorí okamžite. riešenie úlohy pomocou druhej metódy, my Používame hotové vzorce, čím šetríme čas pri hľadaní. Chápeme však, že bez znalosti vzorcov sa problémy nedajú vyriešiť metódou komplexných čísel Ako vidíte, každá metóda má svoje klady a zápory.
Úloha 2 (MIOO, 2011):
„Bod M leží na segmente AB. Na kružnici s priemerom AB sa berie bod C vzdialený od bodov A, M a B vo vzdialenostiach 20, 14 a 15. Nájdite oblasť trojuholníka BMC." 20
Riešenie: Keďže AB je priemer kruhu, potom ∆ ABC je obdĺžnikový, ∠ C = 90 ° Vezmime C ako nulový bod rovina, potom A(20i), B(15), M(z). Pretože CM=14 platí rovnosť z ´z = 196, t.j. bod M ∈ kružnica so stredom v bode C a r=14. Nájdite priesečníky tejto kružnice s priamkou AB: Rovnica priamky AB (10a): 20 i (15 −´ z) + 15 (´ z + 20 i) + z (− 20 i − 15) = 0 Nahradenie ´ z s 196 z a vynásobením celej rovnice číslom (4 i − 3) dostaneme kvadratickú rovnicu pre z: 25 z 2 + 120 i (4 i − 3) z + 196 (4 i − 3) 2 = 0 z 1,2 = 2 (3 − 4 i) (6 i± √ 13) 5 Pomocou vzorca (28) zistíme plochu ∆ MBC: S = i 4 (z (´ b − ´ c) + b (´ c − ´ z) + c (´ z − ´ b)) Kde c = 0, ´ c = 0, b = 15, ´ b = 15, ´ z = 196 ∗ 5 2 (3 − 4 i) (6 i ± √ 13) Po dokončení ekvivalentné transformácie, dostaneme S = 54 ± 12 √ 13 štvorcových. Jednotky Odpoveď. 54 ± 12 √ 13 štvorcových. Jednotky Ak problém vyriešite geometrické metódy, potom je potrebné zvážiť dva rôzne prípady: 1. - bod M leží medzi A a D; 2. - medzi D a B. 21
Pri riešení problému metódou komplexných čísel sa dualita riešenia získa vďaka prítomnosti dvoch priesečníkov kruhu a priamky. Táto okolnosť nám umožňuje vyhnúť sa bežnej chybe.
Problém 3
Strednice AA 1, BB 1 a CC 1 trojuholníka ABC sa pretínajú v bode M. Je známe, že AB=6MC 1. Dokážte, že trojuholník ABC je pravouhlý trojuholník. Riešenie: Nech C je nulový bod roviny a bodu A priraďte skutočnú jednotku. Problém sa potom zredukuje na dôkaz, že b je čisto imaginárne číslo. AB 2 = (b − 1) (´ b − 1) . M je ťažisko, jeho súradnica je 1 3 b + 1 3 MC 1 2 = (1 3 b + 1 3 − 1 2 b − 1 2) (1 3 ´ b + 1 3 − 1 2 ´ b − 1 2) = 1 3 b (b + 1) (´ b + 1) Keďže AB=6MC 1, potom (b − 1) (´ b − 1) = (b + 1) (´ b + 1) . Po vykonaní transformácií dostaneme b =− ´ b, t.j. b je čisto imaginárne číslo, t.j. uhol C je priamka.
Úloha 4.
22
V dôsledku 90° rotácie okolo bodu O sa segment AB zmenil na segment A "B". Dokážte, že strednica OM trojuholníka OAB" je kolmá na priamku A"B. Riešenie: Nech sú súradnice O, A, B rovné 0,1, b. Potom body A " a B " budú mať súradnice a" = i a b" = bi a stred M segmentu AB " bude mať súradnice m = 1 2 (1 + bi). Nájdeme: a " − b m − 0 = i − b 1 2 (1 + bi) = 2 i (i − b) i − b = 2i číslo je čisto imaginárne. Na základe kritéria kolmosti (úsečky AB a CD sú kolmé práve vtedy, ak je číslo a − b c − d čisto imaginárne) sú priamky OM a A ’ B kolmé.
Problém 5
.
23
Od základne nadmorskej výšky trojuholníka sú kolmice spustené na dve strany, ktoré nezodpovedajú tejto výške. Dokážte, že vzdialenosť medzi základňami týchto kolmic nezávisí od voľby výšky trojuholníka. Riešenie: Nech je daný trojuholník ABC a kružnica, ktorá je mu opísaná, má rovnicu z ´z = 1. Ak je CD výška trojuholníka, potom d = 1 2 (a + b + c − ab c) Komplexné súradnice báz M a N kolmice spadnuté z bodu D do bodu AC a BC sa rovnajú m = 1 2 (a + c + d − ac ´ d 2) n = 1 2 (b + c + d − bc ´ d 2) Nájdeme: m − n = 1 2 (a − b + c ´ d ( b − a)) = 1 2 ( a − b) (1 − c ´ d) = (a − b) (a − c) (b − c) 4 ab Keďže | a | = | b | = 1, potom | m - n | = | (a – b) × (b – c) (c – a) | 4. Tento výraz je symetrický vzhľadom na a, b, c, t.j. vzdialenosť MN nezávisí od voľby výšky trojuholníka.
Záver
24
„Určite! Všetky problémy sa dajú vyriešiť bez komplexných čísel. Faktom však je, že algebra komplexných čísel je iná efektívna metóda riešenie planimetrických úloh. Môžeme sa baviť len o výbere metódy, ktorá je pre danú úlohu efektívnejšia. Spory o výhodnosti konkrétnej metódy sú zbytočné, ak tieto metódy berieme do úvahy všeobecne, bez aplikácie na konkrétny problém“ [2]. Veľké miesto v štúdiu metódy zaujíma súbor vzorcov. Toto je
hlavná nevýhoda
metóda a zároveň
dôstojnosť
, keďže vám umožňuje vyriešiť dosť komplexné úlohy podľa hotových vzorcov s elementárnymi výpočtami. Okrem toho verím, že pri riešení úloh planimetrie túto metódu je univerzálny.
Bibliografia
1. Markushevich A.I. Komplexné čísla a konformné zobrazenia - M.: Štátne nakladateľstvo technickej a teoretickej literatúry, 1954. - 52 s. 25
2. Ponarin Ya. P. Algebra komplexných čísel v geometrických úlohách: Kniha pre študentov matematických tried škôl, učiteľov a študentov vysokých škôl pedagogického - M.: MTsNMO, 2004. - 160 s. 3. Shvetsov D. Od Simsonovej línie k Droz-Farnyho vete, Kvant. - č. 6, 2009. – s. 44-48 4. Yaglom I. M. Geometrické transformácie. Lineárne a kruhové transformácie. - Štátne nakladateľstvo technickej a teoretickej literatúry, 1956. – 612 s. 5. Yaglom I.M. Komplexné čísla a ich aplikácia v geometrii - M.: Fizmatgiz, 1963. - 192 s. 6. Morkovich A.G. a iné, Algebra a začiatky matematickej analýzy.10. ročník. Za 2 hod.časť 1. Učebnica pre študentov všeobecnovzdelávacích inštitúcií (profilová úroveň) - M.: Mnemosyne, 2012. - 343 s. 7. Andronov I.K. Matematika reálnych a komplexných čísel - M.: Prosveshchenie, 1975. - 158 s. 26
Aplikácia
Klasické teorémy elementárnej geometrie
Newtonova veta.
V štvoruholníku opísanom okolo kruhu sú stredy uhlopriečok kolineárne so stredom kruhu. 27
Dôkaz. Vezmime stred kruhu ako počiatok, pričom jeho polomer nastavíme na jednu. Body dotyku strán tohto štvoruholníka A o B o C o D o označme A, B, C, D (v kruhovom poradí) (obr. 4). Nech M a N sú stredy uhlopriečok A o C o a B o D o. Potom podľa vzorca pre priesečníky dotyčníc ku kružnici z = 2ab a + b budú mať body A o, B o, C o, Do komplexné súradnice, v tomto poradí: , 2 , 2 , 2 , 2 0 0 0 0 d c cd d c b bc c b a ab b d a ad a kde a, b, c, d sú komplexné súradnice bodov A, B, C, D. Preto.) (2 1 ,) (2 1 0 0 0 0 d c cd b a ab d b n c b bc d a ad c a m Vypočítajte.)) (d b) c Keďže, 1 , 1 b b a a , 1 , 1 d d c c potom je priamo zrejmé, že n m n m Na základe (6) sú body O, M, N kolineárne.
Pascalova veta
.
Priesečníky priamok obsahujúcich protiľahlé strany vpísaného šesťuholníka ležia na tej istej priamke. 28
Dôkaz. Šesťuholník ABCDEF a P FA CD N EF BC M DE AB ) () (,) () (,) () ( (obr. 6) nech je vpísaný do kruhu (obr. 6). Za nulový bod roviny vezmime stred kružnice a jej polomer je na jednotku dĺžky Potom podľa (17) máme: ,) (,) (,) (fa cd a f d c p ef bc f e c b n de ab e d b a m Vypočítať) )())((ef bc de ab ab b c fa ef de c a podobne .))(())((fa cd ef bc bc ab fa ef de cd f c p n Ďalej nájdeme: .))(())((de ab c f fa cd e b Keďže čísla f e d c b a sú rovnaké, resp. f e d c b a 1 , 1 , 1 , 1 , 1, 1, ústna kontrola odhalí, že nájdený výraz sa zhoduje s jeho konjugovaným skutočným číslom, t.j. To znamená kolinearitu bodov M, N, P.
Mongeova veta.
V štvoruholníku vpísanom do kruhu sú čiary prechádzajúce stredmi strán a. Každá uhlopriečka je kolmá na protiľahlé strany a podľa toho sa druhá uhlopriečka pretína v jednom bode. Nazýva sa Mongeovým bodom cyklického štvoruholníka. Dôkaz. Kolmice na strany štvoruholníka ABCD sa pretínajú v strede opísanej kružnice, ktorú berieme ako začiatočný bod. Pre každý bod M(z) kolmica do [AB] čísla b a b a z ) (2 1 čisto imaginárne. 29
Najmä pre z=0 sa rovná) (2) (b a b a . Pre každý bod N(z) priamky prechádzajúcej stredom bočného CD kolmo na (AB) je číslo b a d c z ) (2 1 bude musieť byť čisto imaginárny a naopak. Ale pre z=) (2 1 d c b a sa rovná) (2 b a b a t. j. čisto imaginárny. Preto bod E s komplexnou súradnicou) ( 2 1 d c b a leží na naznačenej priamke A tento výraz je symetrický vzhľadom na písmená a, b, c, d. Preto ďalších päť podobne zostrojených priamok obsahuje bod E. 30







