Ters matrisin hesaplanması. Matris cebiri - matris tersi

Ters matrisi bulma- genellikle iki yöntemle çözülen bir sorun:

• determinantların bulunmasını ve matrislerin yerlerinin değiştirilmesini gerektiren cebirsel toplama yöntemi;
• Matrislerin temel dönüşümlerinin (satırların eklenmesi, satırların aynı sayıyla çarpılması vb.) gerçekleştirilmesini gerektiren, bilinmeyenleri ortadan kaldırmaya yönelik Gauss yöntemi.

Özellikle meraklı olanlar için başka yöntemler de var, örneğin doğrusal dönüşüm yöntemi. Bu dersimizde bahsedilen üç yöntemi ve bu yöntemleri kullanarak ters matrisi bulmak için kullanılan algoritmaları analiz edeceğiz.

Ters matris A böyle bir matris denir

A
. (1)

Ters matris Belirli bir kare matris için bulunması gereken A böyle bir matris denir

matrisleri olan çarpım A sağda kimlik matrisi var, yani.
. (1)

Kimlik matrisi, tüm köşegen elemanların bire eşit olduğu köşegen bir matristir.

Teorem.Tekil olmayan (dejenere olmayan, tekil olmayan) her kare matris için bir ters matris bulunabilir ve yalnızca bir tane bulunabilir. Özel (dejenere, tekil) bir kare matris için ters matris mevcut değildir.

Kare matris denir özel değil(veya dejenere olmayan, tekil olmayan), eğer determinantı sıfır değilse ve özel(veya dejenere, tekil) eğer determinantı sıfır ise.

Bir matrisin tersi yalnızca kare matris için bulunabilir. Doğal olarak ters matris de kare olacak ve verilen matrisle aynı mertebede olacaktır. Ters matrisi bulunabilen bir matrise tersinir matris denir.

İçin ters matris Bir sayının tersiyle ilgili bir benzetme vardır. Her sayı için A sıfıra eşit değil, böyle bir sayı var B bu iş A Ve B bire eşittir: ab= 1 . Sayı B bir sayının tersi denir B. Örneğin 7 sayısının karşılığı 1/7'dir, çünkü 7*1/7=1'dir.

Cebirsel toplama yöntemini kullanarak ters matrisi bulma (müttefik matris)

Tekil olmayan bir kare matris için A tersi matristir

matrisin determinantı nerede A, a matris ile müttefik bir matristir A.

Kare matrisle müttefik A elemanları, A matrisine göre transpoze edilmiş matrisin determinantının karşılık gelen elemanlarının cebirsel tamamlayıcıları olan aynı dereceden bir matristir. Dolayısıyla, eğer

O

Ve

Cebirsel toplama yöntemini kullanarak ters matrisi bulma algoritması

1. Bu matrisin determinantını bulun A. Determinant sıfıra eşitse, matris tekil olduğundan ve tersi mevcut olmadığından ters matrisin bulunması durur.

2. Şuna göre transpoze edilmiş matrisi bulun: A.

3. Birleşim matrisinin elemanlarını, 2. adımda bulunan maritzin cebirsel tamamlayıcıları olarak hesaplayın.

4. Formül (2)'yi uygulayın: matris determinantının tersini çarpın A 4. adımda bulunan birleşim matrisine.

5. Bu matrisi çarparak 4. adımda elde edilen sonucu kontrol edin. A ters matrise. Bu matrislerin çarpımı birim matrise eşitse ters matris doğru bulunmuştur. Aksi takdirde çözüm sürecini yeniden başlatın.

Örnek 1. Matris için

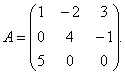
ters matrisi bulun.

Çözüm. Ters matrisi bulmak için matrisin determinantını bulmanız gerekir. A. Üçgen kuralına göre şunu buluruz:

Bu nedenle matris A– tekil olmayan (dejenere olmayan, tekil olmayan) ve bunun tersi de var.

Bu matrisin müttefiki bir matris bulalım A.

Matrise göre transpoze edilmiş matrisi bulalım A:

Müttefik matrisin elemanlarını matrise göre transpoze edilmiş matrisin cebirsel tamamlayıcıları olarak hesaplıyoruz A:

Bu nedenle, matris ile müttefik olan matris A, formu var

Yorum. Elemanların hesaplanması ve matrisin transpoze edilmesinin sırası farklı olabilir. Önce matrisin cebirsel tamamlayıcılarını hesaplayabilirsiniz. A ve sonra cebirsel tümleyen matrisinin devriğini değiştirin. Sonuç, birleşim matrisinin aynı elemanları olmalıdır.

Formül (2)'yi uygulayarak matrisin tersini buluruz. A:

Gaussian bilinmeyen eleme yöntemini kullanarak ters matrisi bulma

Gauss yok etme yöntemini kullanarak bir matrisin tersini bulmanın ilk adımı, matrise atama yapmaktır. A Aynı sıradaki kimlik matrisi, bunları dikey bir çubukla ayırır. İkili bir matris elde edeceğiz. Bu matrisin her iki tarafını da ile çarpalım, sonra şunu elde ederiz:

,

Gaussian bilinmeyen eleme yöntemini kullanarak ters matrisi bulmaya yönelik algoritma

1. Matrise A aynı dereceden bir kimlik matrisi atayın.

2. Ortaya çıkan ikili matrisi, sol tarafında bir birim matris elde edecek şekilde dönüştürün, ardından sağ tarafta birim matrisin yerine otomatik olarak bir ters matris elde edin. Matris A sol taraftaki elemanter matris dönüşümleri ile birim matrise dönüştürülür.

2. Matris dönüşümü sürecinde ise A kimlik matrisinde herhangi bir satırda veya herhangi bir sütunda yalnızca sıfırlar olacaktır, o zaman matrisin determinantı sıfıra eşit olur ve sonuç olarak matris A tekil olacaktır ve ters matrisi yoktur. Bu durumda ters matrisin daha fazla belirlenmesi durur.

Örnek 2. Matris için

ters matrisi bulun.

ve bunu sol tarafta bir birim matris elde edecek şekilde dönüştüreceğiz. Dönüşüme başlıyoruz.

Sol ve sağ matrisin ilk satırını (-3) ile çarpıp ikinci satıra ekleyin, ardından ilk satırı (-4) ile çarpıp üçüncü satıra ekleyin, sonra şunu elde ederiz:

.

Sonraki dönüşümlerde kesirli sayıların kalmamasını sağlamak için öncelikle ikili matrisin sol tarafındaki ikinci satırda bir birim oluşturalım. Bunu yapmak için ikinci satırı 2 ile çarpın ve üçüncü satırı bundan çıkarın, sonra şunu elde ederiz:

.

İlk satırı ikinciyle toplayalım, sonra ikinci satırı (-9) ile çarpıp üçüncü satırla toplayalım. Sonra alırız

.

Üçüncü satırı 8'e bölün, ardından

.

Üçüncü satırı 2 ile çarpın ve ikinci satıra ekleyin. Görünüşe göre:

.

İkinci ve üçüncü satırları yer değiştirelim ve sonunda şunu elde edelim:

.

Sol tarafta birim matrisimiz olduğunu görüyoruz, dolayısıyla sağ tarafta da ters matrisimiz var. Böylece:

.

Orijinal matrisi bulunan ters matrisle çarparak hesaplamaların doğruluğunu kontrol edebilirsiniz:

Sonuç ters bir matris olmalıdır.

Örnek 3. Matris için

ters matrisi bulun.

Çözüm. İkili bir matrisin derlenmesi

ve onu dönüştüreceğiz.

İlk satırı 3 ile, ikinciyi 2 ile çarpıp ikinciden çıkarıyoruz, sonra ilk satırı 5 ile, üçüncü satırı 2 ile çarpıp üçüncü satırdan çıkarıyoruz, sonra şunu elde ediyoruz:

.

İlk satırı 2 ile çarpıp ikinciye ekleriz, sonra ikinciyi üçüncü satırdan çıkarırız, sonra şunu elde ederiz:

.

Sol taraftaki üçüncü satırda tüm elemanların sıfıra eşit olduğunu görüyoruz. Bu nedenle matris tekildir ve ters matrisi yoktur. Ters maritz'i bulmayı bırakıyoruz.

$A^(-1)$ matrisine $A$ kare matrisinin tersi denir, eğer $A^(-1)\cdot A=A\cdot A^(-1)=E$ koşulu sağlanırsa, burada $E $, sırası $A$ matrisinin sırasına eşit olan birim matristir.

Tekil olmayan bir matris, determinantı sıfıra eşit olmayan bir matristir. Buna göre tekil bir matris, determinantı sıfıra eşit olan bir matristir.

Ters matris $A^(-1)$ ancak ve ancak $A$ matrisinin tekil olmaması durumunda mevcuttur. Eğer $A^(-1)$ ters matrisi mevcutsa, bu benzersizdir.

Bir matrisin tersini bulmanın birkaç yolu vardır ve biz bunlardan ikisine bakacağız. Bu sayfada çoğu yüksek matematik dersinde standart olarak kabul edilen birleşik matris yöntemi tartışılacaktır. Gauss yöntemini veya Gauss-Jordan yöntemini kullanmayı içeren ters matrisi bulmanın ikinci yöntemi (temel dönüşümler yöntemi) ikinci bölümde tartışılmaktadır.

Birleşik matris yöntemi

$A_(n\times n)$ matrisi verilsin. $A^(-1)$ ters matrisini bulmak için üç adım gereklidir:

1. $A$ matrisinin determinantını bulun ve $\Delta A\neq 0$ olduğundan emin olun; A matrisi tekil değildir.
2. $A$ matrisinin her bir elemanının cebirsel tamamlayıcılarını $A_(ij)$ oluşturun ve bulunan cebirden $A_(n\times n)^(*)=\left(A_(ij) \right)$ matrisini yazın tamamlar.
3. $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$ formülünü dikkate alarak ters matrisi yazın.

$(A^(*))^T$ matrisine genellikle $A$ matrisine ek (karşılıklı, müttefik) adı verilir.

Çözüm manuel olarak yapılırsa, ilk yöntem yalnızca nispeten küçük dereceli matrisler için iyidir: ikinci (), üçüncü (), dördüncü (). Daha yüksek dereceli bir matrisin tersini bulmak için başka yöntemler kullanılır. Örneğin ikinci bölümde tartışılan Gauss yöntemi.

Örnek No.1

$A=\left(\begin(array) (cccc) 5 & -4 &1 & 0 \\ 12 &-11 &4 & 0 \\ -5 & 58 &4 & 0 \\ 3 & - 1 matrisinin tersini bulun & -9 & 0 \end(array) \right)$.

Dördüncü sütunun tüm elemanları sıfıra eşit olduğundan, $\Delta A=0$ (yani $A$ matrisi tekildir). $\Delta A=0$ olduğundan, $A$ matrisinin ters matrisi yoktur.

Örnek No.2

$A=\left(\begin(array) (cc) -5 & 7 \\ 9 & 8 \end(array)\right)$ matrisinin tersini bulun.

Ek matris yöntemini kullanıyoruz. Öncelikle verilen $A$ matrisinin determinantını bulalım:

$$ \Delta A=\left| \begin(array) (cc) -5 & 7\\ 9 & 8 \end(array)\right|=-5\cdot 8-7\cdot 9=-103. $$

$\Delta A \neq 0$ olduğuna göre ters matris mevcut olduğundan çözüme devam edeceğiz. Cebirsel tamamlayıcıları bulma

\begin(aligned) & A_(11)=(-1)^2\cdot 8=8; \; A_(12)=(-1)^3\cdot 9=-9;\\ & A_(21)=(-1)^3\cdot 7=-7; \; A_(22)=(-1)^4\cdot (-5)=-5.\\ \end(aligned)

Cebirsel toplamalardan oluşan bir matris oluşturuyoruz: $A^(*)=\left(\begin(array) (cc) 8 & -9\\ -7 & -5 \end(array)\right)$.

Ortaya çıkan matrisin yerini değiştiririz: $(A^(*))^T=\left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end(array)\right)$ (the ortaya çıkan matrise genellikle $A$ matrisine ek veya müttefik matris denir. $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$ formülünü kullanarak şunu elde ederiz:

$$ A^(-1)=\frac(1)(-103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end(array)\right) =\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array)\right) $$

Böylece ters matris bulunur: $A^(-1)=\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array )\sağ) $. Sonucun doğruluğunu kontrol etmek için eşitliklerden birinin doğruluğunu kontrol etmek yeterlidir: $A^(-1)\cdot A=E$ veya $A\cdot A^(-1)=E$. $A^(-1)\cdot A=E$ eşitliğini kontrol edelim. Kesirlerle daha az çalışmak için, $A^(-1)$ matrisini $\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 biçiminde değil) değiştireceğiz & 5/103 \ end(array)\right)$ ve $-\frac(1)(103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & biçiminde -5 \end(dizi )\sağ)$:

Cevap: $A^(-1)=\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array)\right)$.

Örnek No.3

$A=\left(\begin(array) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2\end(array) \right)$ matrisinin ters matrisini bulun .

$A$ matrisinin determinantını hesaplayarak başlayalım. Yani $A$ matrisinin determinantı:

$$ \Delta A=\left| \begin(array) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2\end(array) \right| = 18-36+56-12=26. $$

$\Delta A\neq 0$ olduğuna göre ters matris mevcut olduğundan çözüme devam edeceğiz. Belirli bir matrisin her elemanının cebirsel tamamlayıcılarını buluruz:

Cebirsel eklemelerden oluşan bir matris oluşturuyoruz ve onu değiştiriyoruz:

$$ A^*=\left(\begin(array) (ccc) 6 & 8 & -12 \\ -5 & 2 & -3 \\ 1 & -16 & 37\end(array) \right); \; (A^*)^T=\left(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end(array) \right) $$

$A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$ formülünü kullanarak şunu elde ederiz:

$$ A^(-1)=\frac(1)(26)\cdot \left(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & - 3 & 37\end(array) \right)= \left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \ \ -6/13 & -3/26 & 37/26 \end(array) \right) $$

Yani $A^(-1)=\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ - 6 /13 & -3/26 & 37/26 \end(array) \right)$. Sonucun doğruluğunu kontrol etmek için eşitliklerden birinin doğruluğunu kontrol etmek yeterlidir: $A^(-1)\cdot A=E$ veya $A\cdot A^(-1)=E$. $A\cdot A^(-1)=E$ eşitliğini kontrol edelim. Kesirlerle daha az çalışmak için, $A^(-1)$ matrisini $\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \ biçiminde olmayan bir şekilde değiştireceğiz. \ 4/13 & 1/13 & -8/13 \\ -6/13 & -3/26 & 37/26 \end(array) \right)$ ve $\frac(1)(26 biçiminde) )\cdot \left( \begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end(array) \right)$:

Kontrol başarılı oldu, $A^(-1)$ ters matrisi doğru bulundu.

Cevap: $A^(-1)=\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ -6 /13 & -3/26 & 37/26 \end(array) \right)$.

Örnek No. 4

$A=\left(\begin(array) (cccc) 6 & -5 & 8 & 4\\ 9 & 7 & 5 & 2 \\ 7 & 5 & 3 & 7\\ -4 matrisinin tersini bulun & 8 & -8 & -3 \end(array) \right)$.

Dördüncü dereceden bir matris için cebirsel toplamaları kullanarak ters matrisi bulmak biraz zordur. Ancak test kağıtlarında bu tür örneklere rastlanmaktadır.

Bir matrisin tersini bulmak için öncelikle $A$ matrisinin determinantını hesaplamanız gerekir. Bu durumda bunu yapmanın en iyi yolu determinantı bir satır (sütun) boyunca ayrıştırmaktır. Herhangi bir satır veya sütunu seçiyoruz ve seçilen satır veya sütunun her bir öğesinin cebirsel tümleyenlerini buluyoruz.

Tanım 1: determinantı sıfır olan bir matrise tekil matris denir.

Tanım 2: determinantı sıfıra eşit değilse bir matrise tekil olmayan matris denir.

Matris "A" denir ters matris, eğer A*A-1 = A-1 *A = E (birim matris) koşulu karşılanıyorsa.

Bir kare matris yalnızca tekil değilse tersinirdir.

Ters matrisi hesaplama şeması:

1) Eğer "A" matrisinin determinantını hesaplayın: ∆ A = 0 ise ters matris mevcut değildir.

2) "A" matrisinin tüm cebirsel tümleyenlerini bulun.

3) Cebirsel toplamalardan oluşan bir matris oluşturun (Aij)

4) Cebirsel tümleyenler (Aij )T matrisinin transpoze edilmesi

5) Transpoze matrisi bu matrisin determinantının tersiyle çarpın.

6) Kontrolü gerçekleştirin:

İlk bakışta karmaşık görünebilir ama aslında her şey çok basittir. Tüm çözümler basit aritmetik işlemlere dayanmaktadır, çözerken asıl önemli olan “-” ve “+” işaretleriyle karıştırılmaması ve onları kaybetmemektir.

Şimdi ters matrisi hesaplayarak pratik bir görevi birlikte çözelim.

Görev: Aşağıdaki resimde gösterilen "A" ters matrisini bulun:

1. Yapılacak ilk şey "A" matrisinin determinantını bulmaktır:

Açıklama:

Determinantımızı temel fonksiyonlarını kullanarak basitleştirdik. Öncelikle 2. ve 3. satırlara birinci satırın elemanlarını bir sayıyla çarparak ekledik.

İkinci olarak determinantın 2. ve 3. sütunlarını değiştirerek özelliklerine göre önündeki işareti değiştirdik.

Üçüncü olarak ikinci satırın ortak çarpanını (-1) çıkardık ve böylece işareti tekrar değiştirdik ve pozitif oldu. Ayrıca 3. satırı da örneğin en başında olduğu gibi basitleştirdik.

Köşegenin altındaki elemanları sıfıra eşit olan ve 7 özelliği gereği köşegen elemanlarının çarpımına eşit olan bir üçgen determinantımız var. Sonunda elimizde ∆ A = 26, dolayısıyla ters matris mevcuttur.

A11 = 1*(3+1) = 4

A12 = -1*(9+2) = -11

A13 = 1*1 = 1

A21 = -1*(-6) = 6

A22 = 1*(3-0) = 3

A23 = -1*(1+4) = -5

A31 = 1*2 = 2

A32 = -1*(-1) = -1

A33 = 1+(1+6) = 7

3. Bir sonraki adım, elde edilen eklemelerden bir matris derlemektir:

5. Bu matrisi determinantın tersiyle, yani 1/26 ile çarpın:

6. Şimdi şunu kontrol etmemiz gerekiyor:

Test sırasında bir kimlik matrisi aldık, bu nedenle çözüm kesinlikle doğru bir şekilde gerçekleştirildi.

Ters matrisi hesaplamanın 2 yolu.

1. Temel matris dönüşümü

2. Temel bir dönüştürücü aracılığıyla matrisi ters çevirin.

Temel matris dönüşümü şunları içerir:

1. Bir dizeyi sıfıra eşit olmayan bir sayıyla çarpmak.

2. Herhangi bir satıra bir sayıyla çarpılarak başka bir satır eklemek.

3. Matrisin satırlarını değiştirin.

4. Bir temel dönüşüm zinciri uygulayarak başka bir matris elde ederiz.

A -1 = ?

1. (A|E) ~ (E|A -1 )

2.A -1 * A = E

Buna gerçek sayılarla pratik bir örnek kullanarak bakalım.

Egzersiz yapmak: Ters matrisi bulun.

Çözüm:

Kontrol edelim:

Çözüme dair küçük bir açıklama:

Önce matrisin 1. ve 2. satırlarını yeniden düzenledik, ardından ilk satırı (-1) ile çarptık.

Daha sonra ilk satırı (-2) ile çarpıp matrisin ikinci satırına ekledik. Daha sonra 2. satırı 1/4 ile çarptık.

Dönüşümün son aşaması, ikinci satırı 2 ile çarpıp birinciyle eklemekti. Sonuç olarak solda birim matrisimiz var, dolayısıyla ters matris sağdaki matristir.

Kontrol ettikten sonra kararın doğru olduğuna ikna olduk.

Gördüğünüz gibi ters matrisin hesaplanması çok basittir.

Bu dersin sonunda böyle bir matrisin özelliklerine de biraz zaman ayırmak istiyorum.

Matrislerle yapılan eylemler hakkındaki konuşmaya devam edelim. Yani bu dersi incelerken ters matrisin nasıl bulunacağını öğreneceksiniz. Öğrenmek. Matematik zor olsa bile.

Ters matris nedir? Burada ters sayılarla bir benzetme yapabiliriz: örneğin iyimser sayı 5'i ve onun ters sayısını düşünün. Bu sayıların çarpımı bire eşittir: . Matrislerde her şey benzer! Bir matrisin ve ters matrisinin çarpımı şuna eşittir: kimlik matrisi sayısal birimin matris analogudur. Ancak, ilk önce önemli bir pratik sorunu çözelim, yani bu çok ters matrisin nasıl bulunacağını öğrenelim.

Ters matrisi bulmak için neyi bilmeniz ve yapabilmeniz gerekiyor? Karar verebilmelisin elemeler. Ne olduğunu anlamalısın matris ve onlarla bazı eylemler gerçekleştirebiliriz.

Ters matrisi bulmanın iki ana yöntemi vardır:
kullanarak cebirsel eklemeler Ve temel dönüşümleri kullanma.

Bugün ilk, daha basit yöntemi inceleyeceğiz.

En korkunç ve anlaşılmaz olanla başlayalım. düşünelim kare matris. Ters matris aşağıdaki formül kullanılarak bulunabilir:

Matrisin determinantı nerede, matrisin karşılık gelen elemanlarının cebirsel tamamlayıcılarının aktarılmış matrisidir.

Ters matris kavramı yalnızca kare matrisler için mevcuttur, matrisler “ikiye iki”, “üçe üç” vb.

Tanımlar: Daha önce fark etmiş olabileceğiniz gibi, ters matris bir üst simge ile gösterilir

En basit durumla başlayalım; ikiye ikilik bir matris. Elbette çoğu zaman "üçe üç" gereklidir, ancak yine de çözümün genel prensibini anlamak için daha basit bir görev üzerinde çalışmanızı şiddetle tavsiye ederim.

Örnek:

Bir matrisin tersini bulun

Karar verelim. Eylem sırasını noktadan noktaya ayırmak uygundur.

1) İlk önce matrisin determinantını buluyoruz.

Bu eylemi anlamanız iyi değilse materyali okuyun Determinant nasıl hesaplanır?

Önemli! Matrisin determinantı eşitse SIFIR– ters matris MEVCUT DEĞİL.

Söz konusu örnekte, ortaya çıktığı gibi, bu her şeyin yolunda olduğu anlamına geliyor.

2) Küçüklerin matrisini bulun.

Sorunumuzu çözmek için reşit olmayanın ne olduğunu bilmenize gerek yok ancak makaleyi okumanız tavsiye edilir. Determinant nasıl hesaplanır.

Küçüklerin matrisi matrisle aynı boyutlara sahiptir, yani bu durumda.
Geriye kalan tek şey dört sayıyı bulup yıldızların yerine koymak.

Matrisimize dönelim
Önce sol üstteki öğeye bakalım:

Nasıl bulunur? küçük?
Ve bu şu şekilde yapılır: Bu öğenin bulunduğu satır ve sütunu ZİHİNSEL olarak çizin:

Geriye kalan sayı bu elementin küçük, bunu minörler matrisimize yazıyoruz:

Aşağıdaki matris elemanını göz önünde bulundurun:

Bu öğenin göründüğü satır ve sütunu zihinsel olarak çizin:

Geriye kalan, matrisimize yazdığımız bu elemanın minörüdür:

Benzer şekilde ikinci satırın elemanlarını da göz önünde bulundurarak küçüklerini buluyoruz:


Hazır.

Çok basit. Küçüklerin matrisinde ihtiyacınız var İŞARETLERİ DEĞİŞTİR iki sayı:

Bunlar daire içine aldığım rakamlar!

– Matrisin karşılık gelen elemanlarının cebirsel toplamlarının matrisi.

Ve sadece...

4) Cebirsel toplamaların devrik matrisini bulun.

– matrisin karşılık gelen elemanlarının cebirsel tamamlayıcılarının transpoze matrisi.

5) Cevap.

Formülümüzü hatırlayalım
Her şey bulundu!

Yani ters matris:

Cevabı olduğu gibi bırakmak daha iyidir. GEREK YOK sonuç kesirli sayılar olduğundan matrisin her elemanını 2'ye bölün. Bu nüans aynı makalede daha ayrıntılı olarak tartışılmaktadır. Matrislerle eylemler.

Çözüm nasıl kontrol edilir?

Matris çarpımı yapmanız gerekir veya

Muayene:

Daha önce bahsedildiği gibi alındı kimlik matrisi birleri olan bir matristir ana diyagonal ve diğer yerlerde sıfırlar.

Böylece ters matris doğru bir şekilde bulunur.

Eylemi gerçekleştirirseniz sonuç aynı zamanda bir kimlik matrisi olacaktır. Bu, matris çarpımının değişmeli olduğu birkaç durumdan biridir; daha fazla ayrıntıyı makalede bulabilirsiniz. Matrislerdeki işlemlerin özellikleri. Matris İfadeleri. Ayrıca kontrol sırasında sabitin (kesir) matris çarpımından sonra en sonunda öne çıkarıldığını ve işlendiğini unutmayın. Bu standart bir tekniktir.

Pratikte daha yaygın bir duruma geçelim: üçe üç matris:

Örnek:

Bir matrisin tersini bulun

Algoritma “ikiye iki” durumuyla tamamen aynıdır.

Ters matrisi şu formülü kullanarak buluyoruz: matrisin karşılık gelen elemanlarının cebirsel tamamlayıcılarının yer değiştirmiş matrisi burada.

1) Matrisin determinantını bulun.

Burada belirleyici ortaya çıkıyor ilk satırda.

Ayrıca şunu da unutma, bu her şeyin yolunda olduğu anlamına geliyor - ters matris mevcut.

2) Küçüklerin matrisini bulun.

Küçüklerin matrisi “üçe üç” boyutundadır ve dokuz sayı bulmamız gerekiyor.

Birkaç küçük çocuğa daha yakından bakacağım:

Aşağıdaki matris elemanını göz önünde bulundurun:

Bu öğenin bulunduğu satırı ve sütunu ZİHİNSEL olarak çizin:

Kalan dört sayıyı “ikiye iki” determinantına yazıyoruz.

Bu ikiye ikilik determinant ve bu elementin küçüğüdür. Hesaplanması gerekiyor:


İşte bu, küçük bulundu, bunu küçükler matrisimize yazıyoruz:

Muhtemelen tahmin ettiğiniz gibi dokuz adet ikiye iki determinantı hesaplamanız gerekir. Süreç elbette sıkıcı ama durum en ağır değil, daha da kötü olabilir.

Peki, pekiştirmek için - resimlerde başka bir yan dal bulmak:

Kalan reşit olmayanları kendiniz hesaplamaya çalışın.

Nihai sonuç:
– matrisin karşılık gelen elemanlarının küçüklerinin matrisi.

Reşit olmayanların tamamının negatif çıkması tamamen bir kazadır.

3) Cebirsel toplamaların matrisini bulun.

Küçüklerin matrisinde gereklidir İŞARETLERİ DEĞİŞTİR kesinlikle aşağıdaki unsurlar için:

Bu durumda:

"Dörde dört" matris için ters matris bulmayı düşünmüyoruz, çünkü böyle bir görevi yalnızca sadist bir öğretmen verebilir (öğrencinin bir "dörde dört" determinantı ve 16 "üçe üç" determinantı hesaplaması). Uygulamamda böyle tek bir durum vardı ve testin müşterisi işkencemin bedelini oldukça pahalı ödedi =).

Bazı ders kitaplarında ve kılavuzlarda ters matrisi bulmaya yönelik biraz farklı bir yaklaşım bulabilirsiniz, ancak yukarıda özetlenen çözüm algoritmasını kullanmanızı öneririm. Neden? Çünkü hesaplamalarda ve işaretlerde karıştırılma ihtimali çok daha azdır.

Birçok özellikte bunun tersine benzer.

Ansiklopedik YouTube

1 / 5

✪ Bir matrisin tersi nasıl bulunur - bezbotvy

✪ Ters matris (bulmanın 2 yolu)

✪ Ters matris #1

✪ 2015-01-28. Ters 3x3 matris

✪ 2015-01-27. Ters matris 2x2

Altyazılar

Ters bir matrisin özellikleri

• det A − 1 = 1 det A (\displaystyle \det A^(-1)=(\frac (1)(\det A))), Nerede det (\displaystyle \\det) determinantı ifade eder.
• (A B) − 1 = B − 1 A − 1 (\displaystyle \ (AB)^(-1)=B^(-1)A^(-1)) iki kare tersinir matris için bir (\displaystyle A) Ve B (\displaystyle B).
• (A T) - 1 = (A - 1) T (\displaystyle \ (A^(T))^(-1)=(A^(-1))^(T)), Nerede (. . .) T (\displaystyle (...)^(T)) aktarılmış bir matrisi belirtir.
• (k A) − 1 = k − 1 A − 1 (\displaystyle \ (kA)^(-1)=k^(-1)A^(-1)) herhangi bir katsayı için k ≠ 0 (\displaystyle k\değil =0).
• E − 1 = E (\displaystyle \E^(-1)=E).
• Bir doğrusal denklem sistemini çözmek gerekiyorsa (b sıfır olmayan bir vektördür) burada x (\displaystyle x) istenen vektördür ve eğer A − 1 (\displaystyle A^(-1)) var o zaman x = A − 1 b (\displaystyle x=A^(-1)b). Aksi halde ya çözüm uzayının boyutu sıfırdan büyüktür ya da hiç çözüm yoktur.

Ters matrisi bulma yöntemleri

Matris tersinirse, ters matrisi bulmak için aşağıdaki yöntemlerden birini kullanabilirsiniz:

Kesin (doğrudan) yöntemler

Gauss-Jordan yöntemi

İki matris alalım: A ve bekar e. Matris'i sunalım A Gauss-Jordan yöntemini kullanarak birim matrise satırlar boyunca dönüşümler uygulayarak (dönüşümleri sütunlar boyunca da uygulayabilirsiniz, ancak birbirine karıştıramazsınız). Her işlemi birinci matrise uyguladıktan sonra aynı işlemi ikinciye de uygulayın. Birinci matrisin birim forma indirgenmesi tamamlandığında ikinci matris şuna eşit olacaktır: A−1.

Gauss yöntemini kullanırken, sol taraftaki ilk matris temel matrislerden biriyle çarpılacaktır. Λ ben (\displaystyle \Lambda _(i))(bir konum hariç, ana köşegen üzerinde olanlarla transveksiyon veya çapraz matris):

Tüm işlemleri uyguladıktan sonra ikinci matris şuna eşit olacaktır: Λ (\displaystyle \Lambda) yani istenilen olacaktır. Algoritma karmaşıklığı - Ö (n 3) (\displaystyle O(n^(3))).

Cebirsel tamamlayıcı matrisini kullanma

Matrisin tersi matris bir (\displaystyle A)şeklinde temsil edilebilir

A − 1 = adj (A) det (A) (\displaystyle (A)^(-1)=(((\mbox(adj))(A)) \over (\det(A))))

Nerede adj (A) (\displaystyle (\mbox(adj))(A))- ek matris;

Algoritmanın karmaşıklığı, O det determinantının hesaplanmasına yönelik algoritmanın karmaşıklığına bağlıdır ve O(n²)·O det'e eşittir.

LU/LUP Ayrıştırmanın Kullanılması

Matris denklemi bir X = ben n (\displaystyle AX=I_(n)) ters matris için X (\displaystyle X) koleksiyon olarak değerlendirilebilir n (\displaystyle n) form sistemleri A x = b (\displaystyle Ax=b). Haydi belirtelim ben (\displaystyle i) matrisin inci sütunu X (\displaystyle X) başından sonuna kadar X ben (\displaystyle X_(i)); Daha sonra Bir X ben = e ben (\displaystyle AX_(i)=e_(i)), i = 1 , … , n (\displaystyle i=1,\ldots ,n),Çünkü ben (\displaystyle i) matrisin inci sütunu ben n (\displaystyle I_(n)) birim vektör e ben (\displaystyle e_(i)). başka bir deyişle, ters matrisi bulmak, aynı matrise ve farklı sağ taraflara sahip n denklemin çözülmesine indirgenir. LUP ayrıştırması (O(n³) süresi) gerçekleştirildikten sonra, n denklemin her birinin çözümü O(n²) zaman alır, dolayısıyla işin bu kısmı da O(n³) süresi gerektirir.

A matrisi tekil değilse, bunun için LUP ayrıştırması hesaplanabilir. P A = L U (\displaystyle PA=LU). İzin vermek P Bir = B (\displaystyle PA=B), B − 1 = D (\displaystyle B^(-1)=D). O zaman ters matrisin özelliklerinden şunu yazabiliriz: D = U − 1 L − 1 (\displaystyle D=U^(-1)L^(-1)). Bu eşitliği U ve L ile çarparsanız, formdaki iki eşitliği elde edebilirsiniz. U D = L − 1 (\displaystyle UD=L^(-1)) Ve D L = U − 1 (\displaystyle DL=U^(-1)). Bu eşitliklerden ilki n² doğrusal denklem sistemidir. n (n + 1) 2 (\displaystyle (\frac (n(n+1))(2))) sağ tarafların bilindiği (üçgen matrislerin özelliklerinden). İkincisi ayrıca n² doğrusal denklem sistemini temsil eder. n (n - 1) 2 (\displaystyle (\frac (n(n-1))(2))) sağ tarafların bilindiği (ayrıca üçgen matrislerin özelliklerinden). Birlikte n² eşitliklerden oluşan bir sistemi temsil ederler. Bu eşitlikleri kullanarak, D matrisinin tüm n² elemanlarını yinelemeli olarak belirleyebiliriz. Daha sonra (PA) −1 = A −1 P −1 = B −1 = D eşitliğinden eşitliği elde ederiz. A − 1 = DP (\displaystyle A^(-1)=DP).

LU ayrıştırmasının kullanılması durumunda, D matrisinin sütunlarının permütasyonuna gerek yoktur, ancak A matrisi tekil olmasa bile çözüm ıraksak olabilir.

Algoritmanın karmaşıklığı O(n³)'tür.

Yinelemeli yöntemler

Schultz yöntemleri

( Ψ k = E − A U k , U k + 1 = U k ∑ ben = 0 n Ψ k ben (\displaystyle (\begin(case)\Psi _(k)=E-AU_(k),\\U_( k+1)=U_(k)\sum _(i=0)^(n)\Psi _(k)^(i)\end(cases)))

Hata tahmini

İlk Yaklaşımın Seçilmesi

Burada ele alınan yinelemeli matris ters çevirme süreçlerinde bir başlangıç ​​yaklaşımı seçme sorunu, bunları, örneğin matrislerin LU ayrıştırmasına dayanan doğrudan ters çevirme yöntemleriyle rekabet eden bağımsız evrensel yöntemler olarak ele almamıza izin vermez. Seçim için bazı öneriler var U 0 (\displaystyle U_(0)) koşulun yerine getirilmesini sağlamak ρ (Ψ 0) < 1 {\displaystyle \rho (\Psi _{0})<1} (matrisin spektral yarıçapı birden küçüktür), bu sürecin yakınsaması için gerekli ve yeterlidir. Ancak bu durumda öncelikle tersinir matris A veya matrisin spektrumuna ilişkin tahminin yukarıdan bilinmesi gerekir. A A T (\displaystyle AA^(T))(yani, eğer A simetrik bir pozitif tanımlı matris ise ve ρ (A) ≤ β (\displaystyle \rho (A)\leq \beta ), o zaman alabilirsin U 0 = α E (\displaystyle U_(0)=(\alpha )E), Nerede ; A keyfi tekil olmayan bir matris ise ve ρ (A A T) ≤ β (\displaystyle \rho (AA^(T))\leq \beta ) o zaman inanırlar U 0 = α A T (\displaystyle U_(0)=(\alpha )A^(T)), ayrıca nerede α ∈ (0 , 2 β) (\displaystyle \alpha \in \left(0,(\frac (2)(\beta))\right)); Elbette durumu basitleştirebilir ve bunun avantajından yararlanabilirsiniz. ρ (A A T) ≤ k A A T k (\displaystyle \rho (AA^(T))\leq (\mathcal (k))AA^(T)(\mathcal (k))), koymak U 0 = A T ‖ A A T ‖ (\displaystyle U_(0)=(\frac (A^(T))(\|AA^(T)\|)))). İkinci olarak, başlangıç ​​matrisini bu şekilde belirlerken, bunun garantisi yoktur. ‖ Ψ 0 ‖ (\displaystyle \|\Psi _(0)\|) küçük olacak (hatta belki de ortaya çıkacak) ‖ Ψ 0 ‖ > 1 (\displaystyle \|\Psi _(0)\|>1)) ve yüksek düzeyde yakınsama oranı hemen ortaya çıkmayacaktır.

Örnekler

Matris 2x2

(\displaystyle \mathbf (A) ^(-1)=(\begin(bmatrix)a&b\\c&d\\\end(bmatrix))^(-1)=(\frac (1)(\det(\mathbf (A))))(\begin(bmatrix)\,\,\,d&\!\!-b\\-c&\,a\\\end(bmatrix))=(\frac (1)(ad- bc))(\begin(bmatrix)\,\,\,d&\!-b\\-c&\,a\\\end(bmatrix))).) 2x2'lik bir matrisin ters çevrilmesi ancak şu koşullar altında mümkündür:.